Thangka Hyperspectral Image Super-Resolution Based on a Spatial–Spectral Integration Network

Abstract

Thangka refers to a form of Tibetan Buddhist painting on a fabric, scroll, or Thangka, often depicting deities, scenes, or mandalas. Deep-learning-based super-resolution techniques have been applied to improve the spatial resolution of hyperspectral images (HSIs), especially for the preservation and analysis of Thangka cultural heritage. However, existing CNN-based methods encounter difficulties in effectively preserving spatial information, due to challenges such as registration errors and spectral variability. To overcome these limitations, we present a novel cross-sensor super-resolution (SR) framework that utilizes high-resolution RGBs (HR-RGBs) to enhance the spectral features in low-resolution hyperspectral images (LR-HSIs). Our approach utilizes spatial–spectral integration (SSI) blocks and spatial–spectral restoration (SSR) blocks to effectively integrate and reconstruct spatial and spectral features. Furthermore, we introduce a frequency multi-head self-attention (F-MSA) mechanism that treats high-, medium-, and low-frequency features as tokens, enabling self-attention computations across the frequency dimension. We evaluate our method on a custom dataset of ancient Thangka paintings and demonstrate its effectiveness in enhancing the spectral resolution in high-resolution hyperspectral images (HR-HSIs), while preserving the spatial characteristics of Thangka artwork with minimal information loss.

1. Introduction

Thangka paintings are culturally significant artifacts in Tibetan culture, created as painted scrolls. These works of art are typically composed of cotton fabric with an underlayer and are often framed with a textile mount. The paintings are adorned with mineral pigments, adding vibrancy and beauty to the artwork [1]. However, Thangkas are susceptible to degradation caused by various environmental factors, such as temperature, humidity, light, radiation, toxic gases, and dust. This deterioration creates challenges in observing and identifying the content of the paintings [2]. Researchers have been actively studying the traditional materials and techniques used in Thangka production to aid in the preservation of this artwork. Image processing and computer vision techniques, including region filling and object removal, have been applied to the virtual restoration of damaged patches in Thangka paintings [3,4]. Advanced edge detection techniques, such as the Cross Dense Residual architecture (CDR), have also enabled the creation of highly realistic and detailed Thangka edge line drawings [5]. Spectral imaging methods, which offer non-invasive analyses, have provided valuable insights into the layers, visual characteristics, spatial details, and chemical composition of Thangka paintings, minimizing the need for invasive measurements [6]. The analysis of mineral pigments used in Thangka paintings has been instrumental to understanding their origin, production dates, and the evolution of their painting traditions [7]. Non-destructive testing techniques play a crucial role in Thangka studies, as the mechanical sampling of pigments from this precious artwork is strongly discouraged. The conservators and curators responsible for preserving Thangka paintings in public collections rely on non-destructive methods, such as X-ray fluorescence (XRF), Raman microspectroscopy (Raman), polarizing light microscopy (PLM), and scanning electron microscopy with energy dispersive X-ray spectrometry (SEM-EDS), to analyze the materials and painting techniques used to create Thangka paintings [8,9]. X-ray radiography and infrared reflectography have also been employed for examining the technical aspects of these paintings, including their underdrawings, concealed mantras, and color symbols. However, the use of these techniques may be limited in non-laboratory storage conditions, such as in temples, due to the requirements for specialized equipment and controlled analysis conditions.

With the rapid advancement of imaging spectroscopy, hyperspectral imaging (HSI) has gained significant popularity in the monitoring and preservation of cultural heritage artwork [10]. HSI technology captures data cubes that consist of numerous narrow and contiguous spectral bands, each with a bandwidth of less than 10 nm [11]. These spectral bands cover various ranges, including the visible (VIS) range of 400–700 nm, the near-infrared (NIR) range of 700–1000 nm, the short-wave infrared (SWIR) range of 1000–2500 nm, and the mid-infrared (MWIR) range of 2500–15,000 nm. The resulting series of images form a three-dimensional spectral cube, accompanied by a two-dimensional wavelength sequence. Each pixel in the image corresponds to a continuous reflectance spectrum. Unlike multispectral images (MSIs) that utilize the RGB color model, hyperspectral data cubes provide detailed information about the chemical composition and spatial characteristics of artwork surfaces, making them a valuable source of information. HSI has a wide range of applications, including the protection of artwork [12], non-destructive identification of the material components in cultural relics [13], and extraction of faded pattern information [14]. HR-HSI presents even greater opportunities for monitoring and protecting cultural heritage objects. This technology enables the extraction of intricate pattern information from cultural relics [15], removal of stains from old artwork [16], and identification of the optimal combinations of mineral pigments for restoring the original colors of paintings [17]. The HR-HSI of Thangka images is not only crucial for preserving the accurate information to appreciate the art, but also serves as a vital digital resource for art protection and restoration.

Despite the numerous advantages of high-resolution hyperspectral imaging (HR-HSI) in cultural heritage preservation, the application of this technology is limited compared to that of standard RGB, due to factors such as its high cost and limitations in improving imaging equipment [18]. HR-HSI cameras are typically based on push-broom scanning technology that has substantial registration errors and is both time-consuming and challenging for capturing large-scale images compared to area scanning technology. Achieving a satisfactory signal-to-noise ratio (SNR) often requires a larger instantaneous field of view (IFOV), which can result in a lower spatial resolution. There is an inherent trade-off between spatial and spectral resolution in image capturing. As the spectral resolution increases, the spatial resolution tends to decrease, and vice versa. HR-HSI provides a high spectral resolution but a lower spatial resolution, while RGB offers a better spatial resolution but fewer spectral bands, limiting its ability to differentiate between different spectral features. To address these challenges, several methods have been developed to combine data with different spatial and spectral resolutions, aiming to obtain images with a higher spatial and spectral resolution at a lower cost [19]. While hardware-based approaches are one strategy for improving hyperspectral image resolution, they are not the focus of the present study. The other strategy involves algorithmic-based image super-resolution (SR) technology, which entails fusing HR-HSI with a high spectral resolution but low spatial resolution and RGB with a low spectral resolution but high spatial resolution using the same scene. This fusion aims to obtain detailed high-resolution hyperspectral images, which are crucial for the preservation of Thangka and other cultural artifacts. In recent decades, numerous low-resolution HSI super-resolution methods have been successfully applied to reconstruct HR-HSI [20].

Image super-resolution (SR) suffers from severe problems, as there is no unique solution for reconstructing a high-resolution (HR) image from one or multiple low-resolution (LR) images. It should be noted that, before the proliferation of SR methods, the research focus was primarily on single-image SR (SISR) methods, which suffer from limitations in recovering HR images from multiple LR images [21,22]. Traditional HSI SR methods can be broadly categorized into interpolation-based and reconstruction-based approaches. Interpolation-based methods establish a mapping relationship between LR HSI and HR HSI, using interpolation algorithms such as bilinear and bicubic interpolation [23,24]. While these methods are computationally efficient, they often struggle to restore high-frequency detail information, particularly edges and textures. On the other hand, reconstruction-based methods rely on prior knowledge of the input image as a constraint in the super-resolution reconstruction process [25,26]. These methods typically require higher computational costs compared to interpolation-based methods. However, manually designed priors may not always yield satisfactory results, and there is a lack of spatial constraints to ensure spatial consistency when the scene changes.

In recent years, the development of machine learning (ML) has led to the emergence of learning-based super-resolution (SR) algorithms that utilize deep neural networks to establish implicit mapping from low-resolution (LR) images to their corresponding high-resolution (HR) counterparts. In 2014, Dong et al. introduced the application of a convolutional neural network (CNN)-based SRCNN to SR, marking a significant milestone [27]. Subsequently, scholars have developed various variations of SR methods, including Faster-SRCNN (FSRCNN) [28] and deeply recursive convolutional networks (DRCN) [29]. The deep residual network (ResNet) has also been widely employed in image SR, with researchers increasing the number of network layers to enhance the performance of residual learning (Jiwon Kim et al., 2016 [29]). To improve the fusion of the spatial and spectral information within the network structure, several approaches have been proposed. These approaches include the utilization of generative adversarial networks (GANs) [30], intensity hue saturation transforms [31], spatial attention mechanisms [32], and channel attention modules [33]. These techniques have demonstrated a superior performance in exploiting the mapping relationship between LR hyperspectral images and HR RGB images.

Although deep learning (DL) methods have been applied to enhance image super-resolution (SR), they often overlook the relationship between the spectral frequency of hyperspectral imaging (HSI) and the spatial features of RGB, resulting in checkerboard-like artifacts that degrade the quality of the reconstructed images [34]. To address this issue, a novel approach called a High-Resolution Dual domain Network (HDNet) has been proposed, which integrates a spatial–spectral domain and frequency domain attention mechanism to capture the influence of long-range pixels [35]. However, HDNet lacks the ability to effectively map the high-frequency edge information from low-resolution (LR) HSI, which can lead to artifacts and ambiguous structural textures in the reconstructed images. Recently, Transformer models, originally developed for natural language processing (NLP), have been adopted in computer vision tasks and have demonstrated superiority over traditional convolutional neural network (CNN) models in image reconstruction [36]. The Multi-head Self-Attention (MSA) module within the Transformer model excels at capturing non-local similarities and long-range interactions, making it a promising approach for remote sensing image restoration, including hyperspectral imaging [18]. However, the original Transformer design struggles to capture long-range inter-spectral dependencies and non-local self-similarity, posing challenges in hyperspectral image reconstruction. To overcome these challenges, we propose a novel spatial–spectral integration network (SSINet) specifically designed to reconstruct sharp spatial details. This network includes three key components: the Spatial–Spectral Integration (SSI) block, the Spatial–Spectral Recovery (SSR) block, and the Frequency Multi-head Self-Attention (F-MSA) module. These components work together to effectively integrate the spatial and spectral information and capture the long-range dependencies, resulting in improved hyperspectral image reconstruction. Firstly, to sufficiently capture the spatial–spectral features, Spatial–Spectral Integration (SSI) and Spatial–Spectral Recovery (SSR) blocks are proposed. The SSI block combines the channel attention and spatial attention modules, enabling the capture of local-level and global-level correlations between the spatial and spectral domains. This integration aims to effectively represent the spatial–spectral features while minimizing the computational complexity. Next, the SSR block decomposes the fused features into frequencies and incorporates the Frequency Multi-head Self-Attention (F-MSA) module. This module enables the capture of local and long-range dependencies among the frequency features, further enhancing the restoration process. By explicitly modeling frequency information, SSINet exhibits an improved performance in handling hyperspectral images and mitigating issues such as striping and mixed-noise artifacts. Extensive experiments were conducted on a new Thangka dataset specifically designed for image spectral restoration. The results demonstrated that SSINet can achieve a state-of-the-art performance, particularly in reconstructing sharp spatial details. Notably, SSINet implicitly extracts the textures and edge information from the feature maps through the F-MSA module, effectively suppressing striping and mixed-noise artifacts.

This paper proposes a method that effectively obtains high-spatial-resolution and hyperspectral reconstructed images of Thangka by fusing high-spatial-resolution RGB images with low-spatial-resolution hyperspectral images, while sacrificing the internal resolution balance between the texture details and high spectral information. This method contributes significantly to the research and protection of Thangka cultural heritage.

The main contributions of this work are summarized below:

• Our proposed method, SSINet, employs an encoder–decoder Transformer architecture to enable spatial–spectral multi-domain representation learning for HSI spectral super-resolution on HS-RGB data. By leveraging Transformers, SSINet effectively captures and integrates the spatial and spectral information, leading to improved reconstruction results.
• A notable contribution of our work is the introduction of the F-MSA self-attention module, which is designed to capture the inter-similarity and dependencies across high, medium, and low frequency domains. This module enhances the modeling of frequency information, enabling SSINet to restore spatial details and suppress artifacts more effectively.
• To evaluate the performance and effectiveness of SSINet, we curated Thangka datasets with varying spatial and spectral resolutions. These datasets serve as valuable resources for experimentation, enabling comprehensive assessments of SSINet under different conditions and facilitating comparisons with existing methods.

2. Methodology

This section provides an overview of the overall network architecture and then provides details on the Spatial–spectral Integration (SSI) and Spatial–spectral Recovery (SSR) components. Finally, a comprehensive description of the Frequency Multi-head Self-Attention (F-MSA) module is presented.

2.1. Overall Network Architecture

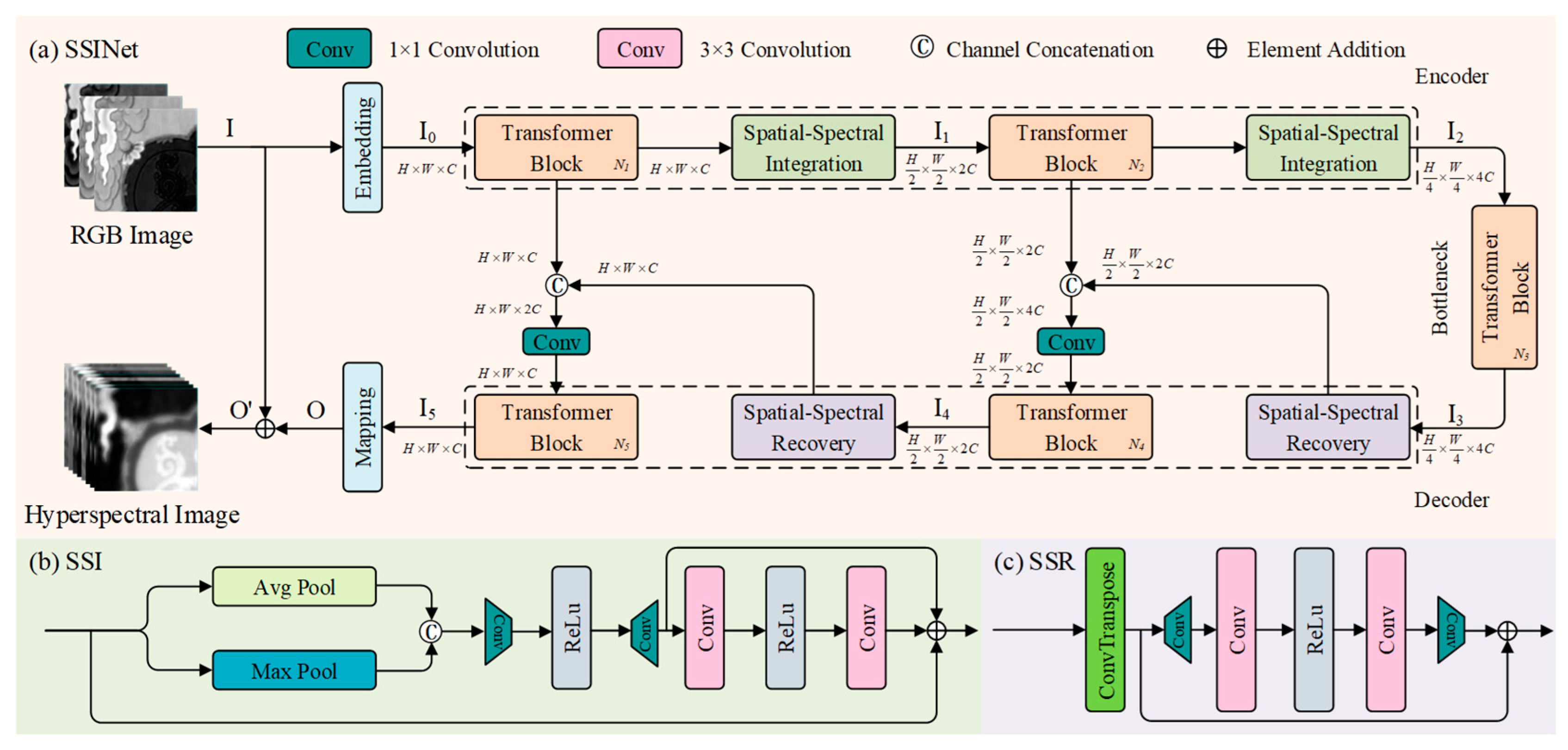
In this section, we present an overview of the network architecture utilized in our SSINet. The overall framework of SSINet is illustrated in Figure 1, which follows a U-shaped structure as the baseline. The architecture includes an encoder, a bottleneck, and a decoder, thereby facilitating effective information flow and feature extraction.

The encoder component of SSINet captures and encodes the input HS-RGB data, extracting the meaningful spatial and spectral features. The bottleneck serves as a bridge between the encoder and decoder, facilitating the flow of information while reducing the dimensionality of the feature representations.

The decoder component of SSINet reconstructs high-resolution spectral details based on the encoded features. By leveraging the spatial–spectral recovery blocks and F-MSA module, the decoder effectively combines and refines the encoded features to generate high-quality, super-resolved hyperspectral images.

We trained the proposed model with the L1 loss function. Given HR RGB $I_{HR}$ and the corresponding LR HSI reference $I_{LR}$, the loss function can be obtained as follows:

$$L\left(\theta \right)=\frac{1}{N}\sum _{i=1}^N{‖I_{LR}^{\left(i\right)}-G_{\theta }\left(I_{HR}^{\left(i\right)}\right)‖}_1$$

where $G_{\theta }$ is the proposed model with parameters $\theta$ and the reconstructed image $G_{\theta }\left(I_{HR}^{\left(i\right)}\right)$ and $N$ is the number of training images.

2.2. Spatial–Spectral Integration and Spatial–Spectral Recovery Block

The SSINet model takes a high-resolution RGB image $\mathrm{I}$ as an input, with dimensions of $\mathrm{I}\in {\mathbb{R}}^{H\times W\times 3}$. The input image first passes through a convolutional layer ($conv3\times 3$) to obtain low-level feature embedding ${\mathrm{I}}_0$, with dimensions of ${\mathrm{I}}_0\in {\mathbb{R}}^{H\times W\times C}$, where $H\times W$ represents the spatial dimensions and $C$ is the number of channels. These feature embeddings ${\mathrm{I}}_0$ are then processed through a series of blocks in the SSINet framework. The blocks consist of an ${\mathrm{N}}_1$ Transformer block, a Spatial–Spectral Integration (SSI) block, ${\mathrm{N}}_2$ Transformer block, another SSI block, ${\mathrm{N}}_3$ Transformer blocks in the bottleneck layer, ${\mathrm{N}}_4$ Transformer block, SSR block, ${\mathrm{N}}_5$ Transformer block, and another SSR block.

In the SSI block, max pooling and average pooling operations are applied along the spectral axis, and convolutional layers ($conv1\times 1$) are applied along the spatial axis. This process helps to extract multi-dimensional features from the input. The feature embedding ${\mathrm{I}}_2$, obtained from the SSI block, is then passed through the bottleneck layer, which includes the ${\mathrm{N}}_3$ Transformer blocks. The decoder part of the network takes the potential feature embedding ${\mathrm{I}}_3\in {\mathbb{R}}^{\frac{H}{4}\times \frac{W}{4}\times 4C}$ from the SSR block and passes it through the ${\mathrm{N}}_4$ Transformer blocks, Spatial–Spectral Recovery block, ${\mathrm{N}}_5$ Transformer blocks, and another SSR block.

The SSR block utilizes a deconvolutional layer with a kernel size of $1\times 1$ and employs residual learning to increase the spatial dimensions while reducing the spectral capacity. The decoder refines the features using a convolutional layer ($conv3\times 3$), resulting in the reconstructed HSI $\mathrm{O}\in {\mathbb{R}}^{H\times W\times C}$.

Finally, the reconstructed HSI ${\mathrm{O}}^{\prime }\in {\mathbb{R}}^{H\times W\times C}$ is obtained by adding the input RGB image $\mathrm{I}$ and reconstructed HSI $\mathrm{O}$, i.e., ${\mathrm{O}}^{\prime }=\mathrm{I}+\mathrm{O}$. Skip connections are used to aggregate the features between the encoder and decoder parts of the network, helping to alleviate the information loss during the Spatial–Spectral Integration operations.

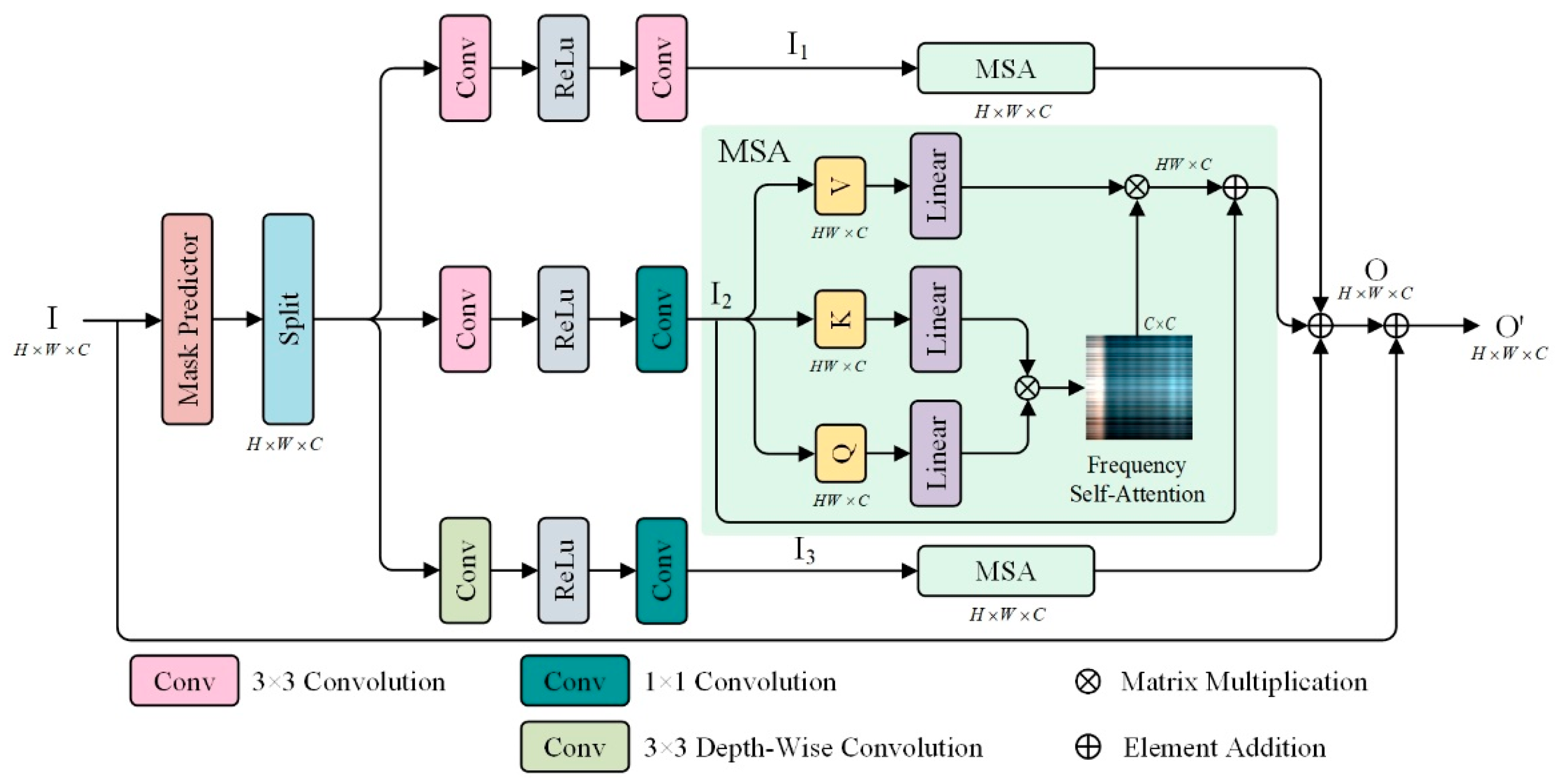
2.3. Frequency-Aware Transformer Block

The Transformer model has garnered significant attention in spectral super-resolution tasks due to its ability to capture long-range spectral dependencies through self-attention mechanisms [18]. This paper introduces a novel method called F-MSA (Frequency Multi-head Self-Attention) to address the limitations of the Transformer model in capturing spatial dependencies and effectively enhancing hyperspectral imaging (HSI). F-MSA leverages the inherent spatial and spectral self-similarity in HSI representations by fusing the spatial and spectral information. To extract the spatial–spectral fusion features, F-MSA employs a frequency domain transformation. This transformation converts the spatial–spectral domain features into the frequency domain. By operating in the frequency domain, F-MSA enables the application of self-attention calculations across multiple frequency branches, including high, medium, and low frequencies.

The use of frequency domain self-attention allows F-MSA to capture the spatial–spectral dependencies at different frequency levels. This comprehensive feature fusion approach enhances the model’s ability to capture long-range dependencies in both the spatial and spectral dimensions, thereby overcoming the limitations of the Transformer model in areas with limited spatial fidelity information. By incorporating the F-MSA module into the SSINet framework, the proposed method effectively combines spatial–spectral fusion and multi-head feature self-attention mechanisms. This situation enables the model to capture both the local and long-range interactions between high-resolution RGB images and low-resolution HSI, leading to an improved hyperspectral image reconstruction performance.

In this paper, to decompose a frequency feature, the discrete cosine transforms (DCTs) operate separately on each feature of the high-frequency, medium-frequency, and low-frequency parts [37]. Figure 2 shows the F-MSA, where the input $\mathrm{I}\in {\mathbb{R}}^{H\times W\times C}$ is partitioned based on frequency masks of varying frequencies and separated into distinct branches via frequency ${\mathrm{I}}_{1-3}\in {\mathbb{R}}^{H\times W\times C}$. Then, ${\mathrm{I}}_1\in {\mathbb{R}}^{H\times W\times C}$ is reshaped into tokens ${\mathrm{I}}_1\in {\mathbb{R}}^{HW\times C}$. Subsequently, ${\mathrm{I}}_1$ is linearly projected into query $Q\in {\mathbb{R}}^{HW\times C}$, key $K\in {\mathbb{R}}^{HW\times C}$, and value $V\in {\mathbb{R}}^{HW\times C}$.

$$Q=P^Q\left(I_1\right),K=P^K\left(I_1\right), V={ P}^V\left(I_1\right)$$

where $P^Q$, $P^K$, and $P^V$ are learnable parameters of the linear projection. Next, we further split the $Q$, $K$, and $V$ into $N$ heads along the frequency dimension, and their dot-product interaction generates the frequency self-attention map $A\in {\mathbb{R}}^{C\times C}$. Overall, the F-MSA process is defined as

$$\begin{gathered} O^{\prime }=Attention(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)+I \\ Attention(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{d}})V \end{gathered}$$

where $\mathrm{I}$ and ${\mathrm{O}}^{\prime }$ are the input and output feature maps; $W_i^Q$, $W_i^K$, and $W_i^V$ present parameters in different projections; and $\sqrt{d}$ is a learning scaling parameter.

3. Experiment and Results

In this section, we present a comprehensive evaluation of the performance of our proposed model, including both quantitative and qualitative analyses. We begin by introducing the creation of the Thangka dataset and providing the necessary implementation details. This dataset serves as the foundation for our evaluation, ensuring the relevance and accuracy of our results. Next, we discuss the evaluation metrics and comparison methods employed to assess the performance of our proposed model. These metrics and methods enable us to objectively measure the effectiveness of our approach and compare it against the state-of-the-art algorithms in the field. To further demonstrate the efficacy of our network blocks, we conduct ablation experiments. These experiments involve systematically removing or modifying the specific components of our proposed model to evaluate their individual contributions. Through these experiments, we can assess the effectiveness of each network block and validate their importance in achieving superior results. Finally, we compare the performance of our proposed method with state-of-the-art algorithms in the field. This comparison allows us to highlight the advancements and improvements achieved by our approach in hyperspectral super-resolution. By showcasing the strengths and advantages of our proposed method over existing techniques, we establish our method’s superiority and applicability in the field.

3.1. Experimental Data and Pre-Processing

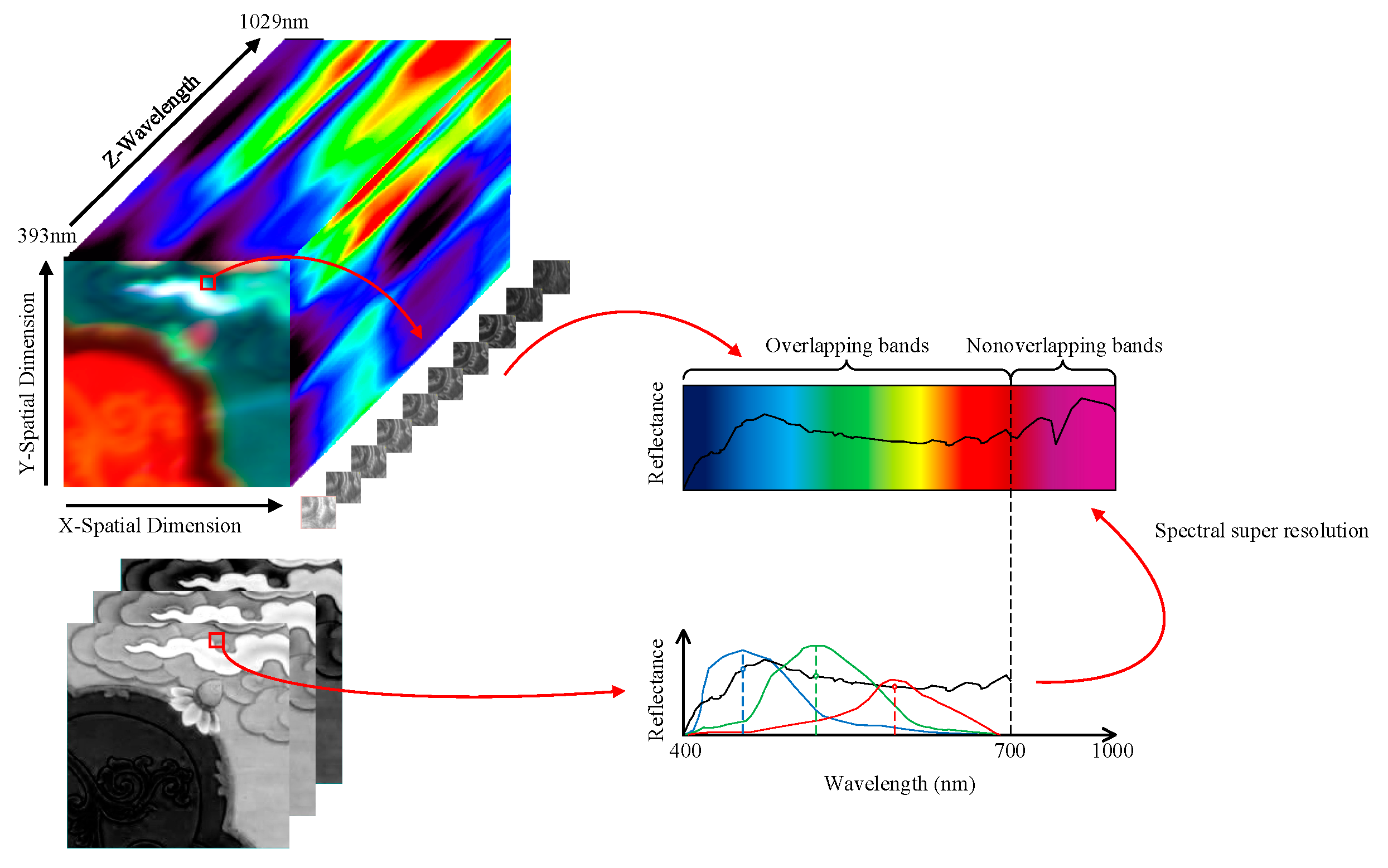
For data gathering, high-resolution images were captured using a Canon 5DSR camera under natural light. This camera can capture a wide range of visible colors in the RGB spectrum. To ensure accuracy in the testing reconstruction results of the Thangka, only one digital snapshot was taken. Here, each Thangka image is digitally represented such that each pixel corresponds to an approximate spatial extent of 0.03 mm. The dataset contains RGB images with a spatial resolution of 1798 × 1225 pixels, and 1 pixel of the digital image covers about 0.8 mm in the painting, consisting of three spectral bands, as depicted in Figure 3a. These RGB images serve as the input data for the subsequent stages of our proposed method.

The LR-HSI data acquisition was carried out using a hyperspectral imaging camera, specifically the Pika L Hyperspectral Imaging camera, as depicted in Figure 3d. This camera is equipped with visible and near-infrared hyperspectral sensors that can capture map images and provide the spectral information essential for a pigment analysis. The hyperspectral sensor used in our experiment has a spectral range from 400 nm to 1000 nm, with a spectral resolution of 3.3 nm and a spectral bandwidth of 2.1 nm for 281 channels. The acquired LR-HSI has a size of approximately 616 × 431 pixels, where each pixel covers an area of approximately 2.4 mm on the painting. This coverage is nearly three times larger than that of an RGB image in spatial resolution. Although the hyperspectral data contain hundreds of bands that can provide comprehensive information for depicting the Thangka, our focus in this paper is primarily on reconstructing RGB images with a high spectral resolution. The data collection was conducted on 30 May 2022, from 12:00 to 14:00, under clear weather and constant lighting conditions. The camera was positioned 2 m away from the Thangka and radiometric calibration was performed using standard whiteboard data during each scanning period. The collected data include a series of RGB and hyperspectral data from the same scene and were accurately registered. The region of interest for reconstruction testing is indicated by the red dashed box in Figure 1b,c, encompassing various colors and intricate spatial details. The acquired data are 3D data cubes, in which the two-dimensional spatial image is combined with the wavelength band as the third dimension, as illustrated in Figure 4.

To reduce the severe impact of the uneven light source intensity distribution and dark current noise in the HSIs, radiometric correction was performed. This correction converts the pixel digital number (ND) to standard whiteboard and dark current data using the following method:

$$R=\frac{R_{raw}-R_{dark}}{R_{white}-R_{dark}}\times 100\%$$

where $R$ represents the calibrated image, $R_{raw}$ indicates the original HSI, $R_{dark}$ is the black reference image, and $R_{white}$ is the standard whiteboard image. For the experimental dataset, a range from 400 nm to 800 nm was selected after meticulous band filtering and calibration. This range includes a total of 196 bands. The subsequent bands were excluded as they predominantly contained noise.

The high-resolution RGB image and low-resolution HSI of the Thangka were resampled to have the RGB spatial resolution and were then used in the training and testing phases individually to evaluate our proposed methods. The HSI and RGB were then cropped into cubic patches with dimensions of 200 × 200 × 196 and 200 × 200 × 3, respectively. Around 80% of these patches were randomly selected for the training set, while the remaining patches were used for the testing set. Each image was sliced into 20 patches with overlapping regions.

3.2. Experimental Setting

Based on the MST configuration in [36], we used 196 wavelengths ranging from 393 to 800 nm for the HIS through spectral interpolation manipulation. In our evaluation, we compared the performance of SSINet with several state-of-the-art spectral reconstruction techniques, including HSCNN [38], HSCNN+ [39], EDSR [40], HINet [41], Restormer [42], and MST++ [36]. These models were trained and optimized on the Thangka dataset to achieve the best results. During the training process, we utilized the Adam optimizer with an initial learning rate of 0.0004 over 200 epochs. The learning rate was halved every 50 epochs to ensure a stable convergence. The training procedure aimed to optimize the hyperparameters of each model and improve their performance on the Thangka dataset. The proposed SSINet was implemented using Python 3.9 and the PyTorch 1.9 framework. The experiments were conducted on an Nvidia GeForce RTX 2080ti GPU with 64 GB of memory to leverage the computational power and accelerate the training process.

3.3. Evaluation Metrics

In this paper, six quantitative image quality indices were employed to assess the quality of the spectral super-resolution (SR) reconstruction results. These indices provide objective measures for various aspects of the reconstructed images, allowing for a comprehensive evaluation. The following section describes the six indices used in this study. Root Mean Square Error (RMSE): This index measures the average difference between the reconstructed SR image and the reference image. It quantifies the spectral fidelity of the reconstruction, indicating how close the reconstructed image is to the ground truth. Dimensionless Global Relative Error of Synthesis (ERGAS): ERGAS evaluates the global relative error of the reconstructed image in terms of the spatial–spectral information. This index provides a measure of the overall quality of the reconstructed image, considering both the spatial and spectral characteristics. Spectral Angle Mapper (SAM): SAM quantifies the spectral similarity between the reference image and the reconstructed image by measuring the angle between their spectral vectors. A lower SAM value indicates a higher degree of similarity in terms of the spectral content. Universal Image Quality Index (UIQI): UIQI measures the overall similarity between the reference image and the reconstructed image, reflecting brightness and contrast distortions. This index provides a comprehensive assessment of the similarity between the two images [43]. Peak Signal-to-Noise Ratio (PSNR): PSNR represents the ratio between the maximum possible power of the reference image and the power of the difference between the reference and reconstructed images. PSNR is a widely used index for measuring the fidelity of image reconstruction, with higher values indicating a better reconstruction quality [44]. Structural Similarity (SSIM): SSIM evaluates the structural similarity between the reference and reconstructed images, considering the luminance, contrast, and structural components. This index provides a measure of how well the structures and textures in the reconstructed image match those in the reference image [45].

The aforementioned metrics, including UIQI, PSNR, SSIM, RMSE, ERGAS, and SAM, provide quantitative measures for the quality of the recovered hyperspectral images. Higher values of UIQI, PSNR, and SSIM represent better recovery results, indicating a higher similarity and fidelity between the reconstructed images and the ground truth. Conversely, lower values of RMSE, ERGAS, and SAM correspond to better recovery results, indicating lower errors and discrepancies between the reconstructed and ground truth images. The error maps visualize the discrepancies between the true spectral values and the reconstructed values in an image. These maps are created by computing the pixel-wise differences between the reconstructed image and ground truth image. In these maps, darker areas represent regions where the reconstruction closely matches the ground truth, indicating a better accuracy. Conversely, brighter spots indicate larger deviations or errors between the reconstructed and ground truth values.

3.4. Comparison with Other Methods

In this section, we present an analysis of the experimental results obtained from our simulated experiments on the Thangka dataset, aiming to evaluate the effectiveness of the proposed SSINet in achieving a super-resolution reconstruction. The evaluation results, encompassing various image quality indices, are summarized in

Table 1. Quantitative results on the Thangka dataset. Results in bold are the best and those underlined are the second best.

	HSCNN	HSCNN+	EDSR	HINet	Restormer	MST++	SSINet
RMSE	15.3730	15.2221	29.3646	14.5156	12.7500	14.0767	11.9773
ERGAS	20.1375	19.9285	48.0325	20.0000	18.3242	18.8177	15.8489
SAM	4.7342	4.5390	17.3205	5.8034	5.7635	5.7523	3.9851
UIQI	0.5028	0.5180	0.3123	0.5200	0.5767	0.6081	0.6387
PSNR	25.2837	25.3818	19.1752	25.5317	26.4004	25.9618	27.4166
SSIM	0.8340	0.8459	0.5677	0.8554	0.8672	0.8940	0.9057

, where the best performance is indicated in bold and the second-best performance is underlined. These metrics serve as quantitative measures for assessing the quality and fidelity of the reconstructed images. The results presented in Table 1 offer valuable insights into the performance of our proposed SSINet, showcasing its superiority over other methods in terms of the image quality and reconstruction accuracy.

Table 1 shows that SSINet achieves the lowest values for RMSE, ERGAS, and SAM, indicating a superior performance in terms of spectral fidelity. Additionally, SSINet corresponds to the highest values for UIQI, PSNR, and SSIM, indicating better recovery results in terms of brightness distortion, contrast distortion, and structural similarity. Comparing the results of HSCNN, HSCNN+, and EDSR, we find that a deeper and more complex network architecture does not necessarily lead to improved results. Although HSCNN+ performs well in terms of SAM, its ability to reconstruct spectral details is relatively poor. While ResNet-based methods can achieve good results, they tend to consume significant computational resources due to their complex residual network connections. On the other hand, Restormer and MST++ models, which combine Transformers with CNNs, demonstrate a promising performance in spectral super-resolution, indicating that spectral interpolation can effectively capture both local and non-local interactions to better preserve spectral features.

The proposed SSINet method in this paper combines frequency division, Transformers, and CNNs to effectively reduce the sensitivity to noise in spectral reconstruction and integrate both local and global spatial information. This integration was found to offer a superior performance in terms of the image quality indices compared to the evaluated benchmark methods.

Figure 3c and Figure 5 provide a visual comparison of the error maps between the reconstructed results generated by different models and the ground truth from 0 to 1. A randomly selected image from the test set is used as an example, and magnified views within the red box in Figure 3a are provided to facilitate this comparison. By examining these maps, several interesting conclusions can be drawn. Firstly, the color regions in the different spectral bands exhibit variations in the reconstruction, indicating the diversity of the spectral curves in the Thangka dataset. Secondly, although HSCNN and HSCNN+ were found to achieve a better restoration of spatial information, they exhibit higher spectral errors in all the spectral bands except for the 400 nm band. EDSR did not successfully learn the mapping of HR-RGB to LR-HSI. This result suggests that these models struggle to effectively learn the complete mapping from the RGB domain to the hyperspectral domain. Furthermore, the results of other models show higher spectral errors in complex-shaped areas, indicating difficulties in accurately reconstructing the spectral information in these regions. In contrast, SSINet demonstrates an almost perfect recovery of the spectrum compared to the ground truth, with minimal errors observed in the 500 nm band, highlighting the powerful mapping ability of SSINet in maintaining a balance between high spatial and spectral resolutions. This result further emphasizes the excellent performance of SSINet in both the spatial and spectral domains.

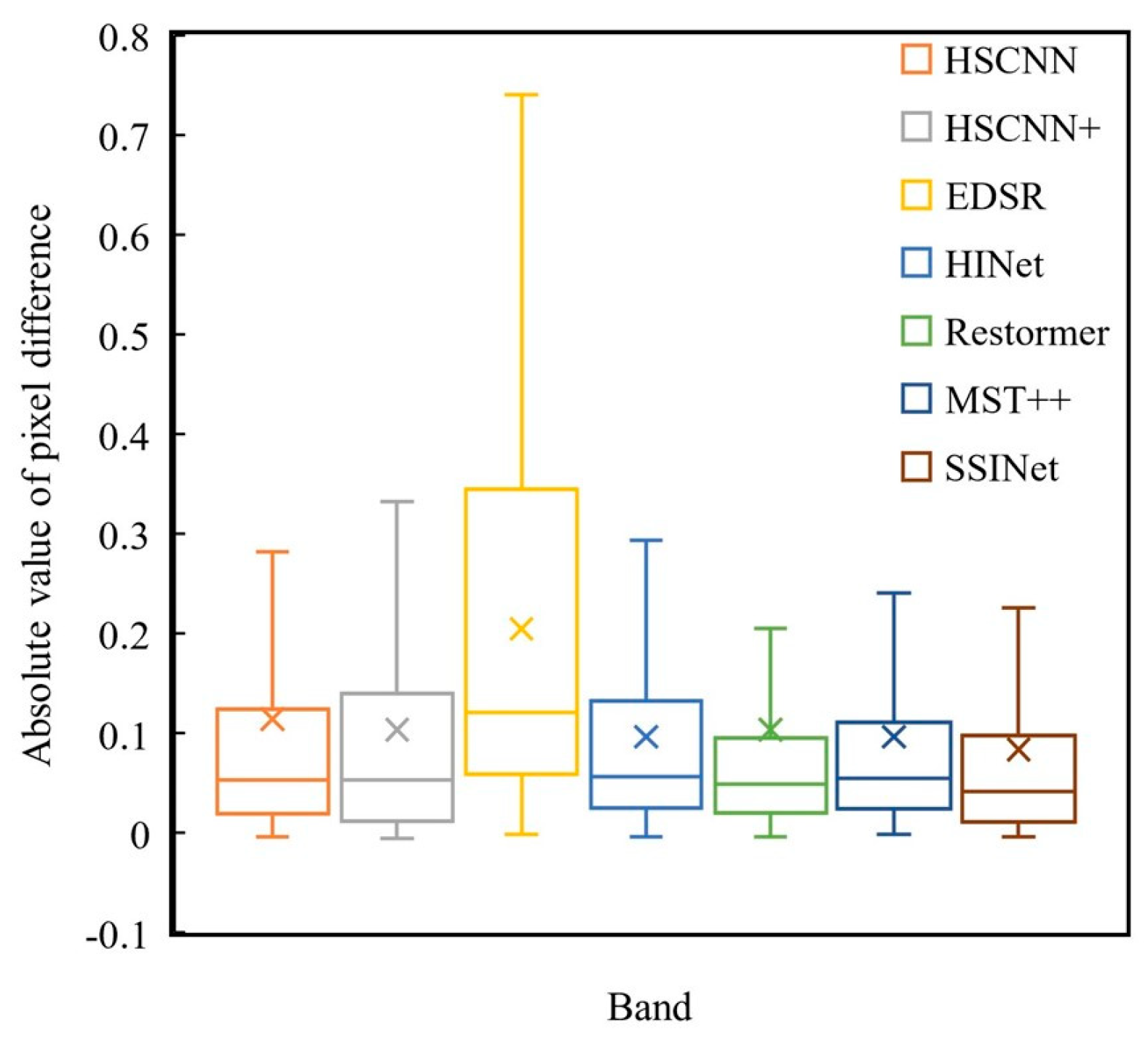
To further analyze the accuracy of the super-resolution (SR) results, we present boxplots depicting the absolute pixel differences between the reconstructed results and the ground truth in all the spectral bands (Figure 6). The boxplots provide indicators such as the median, mean, and range from the 25th to the 75th percentile, as well as the 1st and 99th percentile values. These indicators clearly demonstrate that the proposed SSINet method achieves the highest accuracy across all the bands. These findings highlight that the SR results obtained by SSINet closely match the ground truth, indicating the superior performance of our proposed method in accurately reconstructing hyperspectral images.

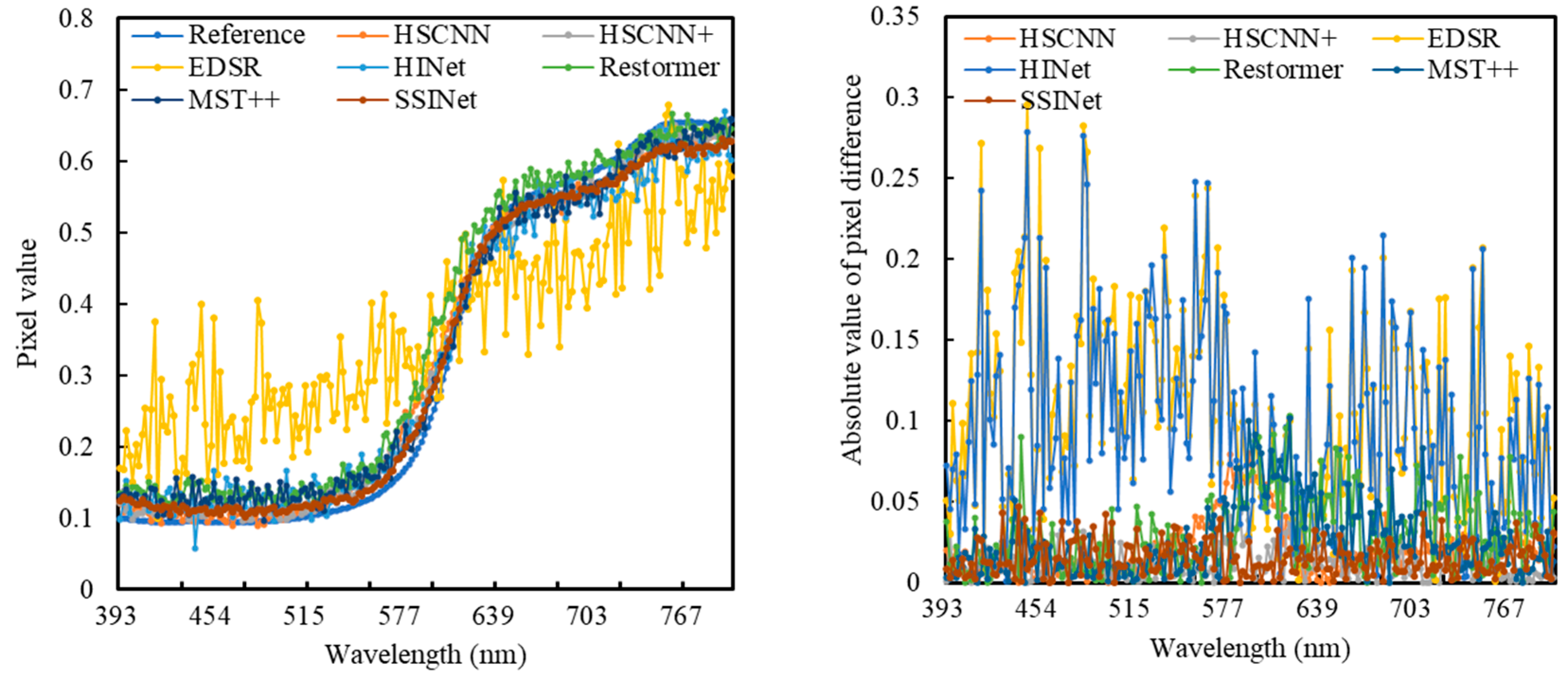
In addition to the error maps presented in Figure 5, we also conducted a comparison of the spectral curves by randomly selecting pixels from the Thangka dataset (Figure 7). The results of this comparison align with the quantitative evaluation. Although the spectral reflectance curves of the six competing methods exhibit similar trends for the representative pixels, their ability to restore the spectral reflectance values across different wavelength bands varies. Here, Restormer and MST++ were found to retain more spectral details compared to HSCNN. On the other hand, HINet and HSCNN+ performed better in reconstructing subtle spectral variations. However, our proposed SSINet outperformed all the CNN-based models by closely matching the subtle spectral fluctuations in the ground truth and preserving the overall trend. This demonstrates the superiority of our method in retaining the spectral information and accurately capturing the spectral variations in the Thangka dataset. The comparison of the spectral curves further supports these findings, as SSINet achieved a better reconstruction of the spectral reflectance values, effectively capturing subtle variations and preserving the overall trend in the spectral information.

4. Discussion

4.1. Ablation Study

In this subsection, we report on a series of ablation experiments performed to analyze the individual contributions of the key components in SSINet, namely SSI (Spatial–spectral Integration), SSR (Spatial–spectral Recovery), and F-MSA (Frequency Multi-head Self-Attention). The quantitative results of these ablation studies conducted on the Thangka image are presented in Figure 8 and

Table 2. Ablation study results of the proposed elaborate designs in the proposed SSINet. Results in bold are the best and those underlined are the second best.

Model	Baseline	Model 1	Model 2	Model 3	Model 4	SSINet
SSI	×	×	✓	✓	×	✓
SSR	×	✓	×	✓	×	✓
F-MSA	×	✓	✓	×	✓	✓
RMSE	15.6191	36.6485	33.1223	12.8843	30.2657	11.9773
ERGAS	19.3564	46.6416	46.7124	17.5920	39.4191	15.8489
SAM	4.7740	12.5387	18.3812	4.7307	12.4032	3.9851
UIQI	0.5133	0.3841	0.3313	0.6182	0.4043	0.6387
PSNR	25.6360	18.6504	19.0243	26.6145	20.1283	27.4166
SSIM	0.8763	0.6180	0.5797	0.8917	0.6724	0.9057

.

The baseline model was created by removing all three components (SSI, SSR, and F-MSA) from the standard SSINet. Comparing Model 1, Model 2, and Model 4 shows that using the SSI and SSR components individually does not lead to significant improvements in the quality of the hyperspectral image reconstruction. This lack of improvement can be attributed to the difficulty of the neural network structure in effectively extracting the features from the spatial and spectral fusion information, which is necessary for enhancing the spectral super-resolution performance. Furthermore, comparing Model 3, Model 4, and the complete SSINet, we can see that reconstructing hyperspectral information by incorporating spatial–spectral feature fusion and the multi-head feature self-attention mechanism (F-MSA) can greatly enhance the quality of the recovery. This finding indicates that F-MSA plays a crucial role in improving the hyperspectral super-resolution performance by capturing spectral features.

The ablation experiments demonstrate that the individual usage of the SSI and SSR components does not lead to substantial improvements, but when combined with F-MSA in the complete SSINet architecture, the spatial–spectral feature fusion and multi-head feature self-attention mechanisms work synergistically to significantly enhance the hyperspectral super-resolution reconstruction quality. This result highlights the importance of capturing spatial–spectral correlations and frequency dependencies to achieve state-of-the-art results in hyperspectral image reconstruction.

Our quantitative analysis is further supported by the reconstruction images presented in Figure 8. These images visually demonstrate the impact of incorporating the different components in the SSINet architecture. When using the SSI and SSR components individually, the reconstructed hyperspectral images exhibit distorted textures and fuzzy artifacts. This outcome indicates that these components alone are insufficient for capturing both spatial and spectral features accurately. However, when Model 3 incorporates both SSI and SSR, the resulting images show significant improvements in terms of their sharpness and similarity to the real image in terms of the spectral information. This result demonstrates that a combination of SSI and SSR effectively enhances the reconstruction performance. Comparing our proposed SSINet with Model 3, which includes SSI and SSR, the inclusion of the F-MSA component further improves the results. The images reconstructed by SSINet with F-MSA exhibit higher PSNR and SSIM values, as well as smaller SAM values. This result indicates that the network, when combined with F-MSA, can efficiently extract the spatial features and enhance the spatial fidelity of the reconstructed images. Moreover, the F-MSA component significantly optimizes the spectral information, resulting in hyperspectral images with higher PSNR values, suggesting that the incorporation of F-MSA improves the reconstruction of spectral details.

A combination of SSI, SSR, and F-MSA in the SSINet architecture effectively fuses the spatial and spectral features, enhances the spatial fidelity, and optimizes the spectral information. This comprehensive approach results in a superior hyperspectral image reconstruction performance compared to using the SSI, SSR, and F-MSA components individually.

4.2. Computational Speed Analysis

In this section, we present a comparison of the model complexity and computational speed of different deep learning methods using FLOPs (Floating Point Operations), Params (number of parameters), training convergence, and the test times in

Table 3. Computational speed analysis of deep-learning-based methods on the Thangeka dataset.

Method	HSCNN	HSCNN+	EDSR	HINet	Restormer	MST++	SSINet
FLOPs(G)	0.723	5.211	10.284	83.739	5.934	55.706	96.903
Params(M)	0.670	4.825	2.515	208.569	15.236	62.922	132.304
Training(s)	28	235	95	970	300	645	642
Test(s)	1.736	2.917	1.709	7.497	4.836	6.981	8.302

. The results are summarized in the subsequent table. When comparing CNN-based models with Transformer-based models, it is commonly observed that Transformer-based models tend to have more parameters. Similarly, in our method (SSINet), the number of parameters is relatively high, mainly because our network integrates the spatial and spectral dimensions and utilizes a frequency attention mechanism to capture long-range interaction spectral features, which increases its computational complexity. Although SSINet may require more computation time due to its complex architecture, it maintains a good balance between accuracy and computation speed. While SSINet does not exhibit a significant advantage in terms of its running time compared to CNN-based models, SSINet delivers an improved accuracy in spectral recovery tasks. Therefore, the additional computation time is justified by the enhanced performance and accuracy achieved by SSINet. SSINet strikes a balance between model complexity and computation speed, ensuring an improved accuracy in spectral recovery while still maintaining a reasonable runtime. The increased computational requirements of SSINet are justified by its superior performance, making it a promising choice for hyperspectral image reconstruction tasks.

4.3. Limitations of the Cross-Sensor Unpaired Images

In this section, we discuss the generalization performance and limitations of the proposed cross-sensor unpaired SR framework. One key aspect is the difference between multispectral area scan cameras and hyperspectral line scan cameras in terms of their image capture. Multispectral cameras capture an entire image in a single frame, while hyperspectral cameras build a high-resolution image line by line. However, the actual line frequency of hyperspectral cameras may deviate from the ideal line frequency, resulting in distortion in the line scan image. HSI SR refers to the task of reconstructing high-resolution hyperspectral images from high-resolution multispectral images while preserving high spectral information. Even if we have access to pairs of multispectral and hyperspectral images, geometric registration errors between different sensors can pose challenges and affect the accuracy of the reconstruction algorithm. SSINet addresses this issue by using spatial–spectral fusion features to reduce the impact of these image registration errors. The trained model can bridge the gap between training and testing data through domain-gap aware training and domain-distance weight supervision strategies.

Another approach is to exploit the data distribution learning with a GAN-based framework for unpaired image SR [46]. The CinCGAN [47] is an early attempt in this direction, which combines two CycleGAN structures to train both low-resolution (LR) to clean LR and clean LR to target high-resolution (HR) mappings. However, GAN-based frameworks rely on the image content for degradation, which may not hold true in all applications. While the proposed framework demonstrates promising results, there are potential limitations that need to be addressed. Geometric registration errors have a significant impact on the quality and quantity of training data, and a lower registration accuracy can lead to blurred images. Therefore, further improvements are necessary to develop an adaptive strategy for the SR of real-world cross-sensor unpaired images, considering the challenges of these geometric registration errors.

Addressing these limitations will require continued research and development to enhance the robustness and effectiveness of GAN-based frameworks for unpaired image SR. It is crucial to explore adaptive techniques and novel approaches that can handle the complexities introduced by real-world scenarios and address the challenges associated with geometric registration errors. By doing so, we can further advance the field and improve the performance of SR algorithms in practical applications.

5. Conclusions

The paper introduced a novel framework called the Spatial–spectral Integrated Network (SSINet), which focuses on accurately reconstructing high-resolution hyperspectral images (HSI) using a Transformer-based approach. SSINet incorporates various components, including feature extractors, spatial–spectral feature fusion, frequency decomposition, and a multi-head feature self-attention mechanism. These components enable the effective extraction and restoration of both spatial and spectral features, while addressing challenges such as image registration errors. By utilizing multiple frequency branches, SSINet learns powerful spectral representations to reduce the influence of these registration errors.

The effectiveness of SSINet was evaluated through quantitative experiments, providing visually satisfactory results for HSI reconstruction. This result highlights the potential of the proposed framework for enhancing the preservation and analysis of cultural artifacts, thereby contributing to the advancement of digital heritage research.