Aboveground Biomass Prediction of Arid Shrub-Dominated Community Based on Airborne LiDAR through Parametric and Nonparametric Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition and Preprocessing
2.2.1. Field Survey
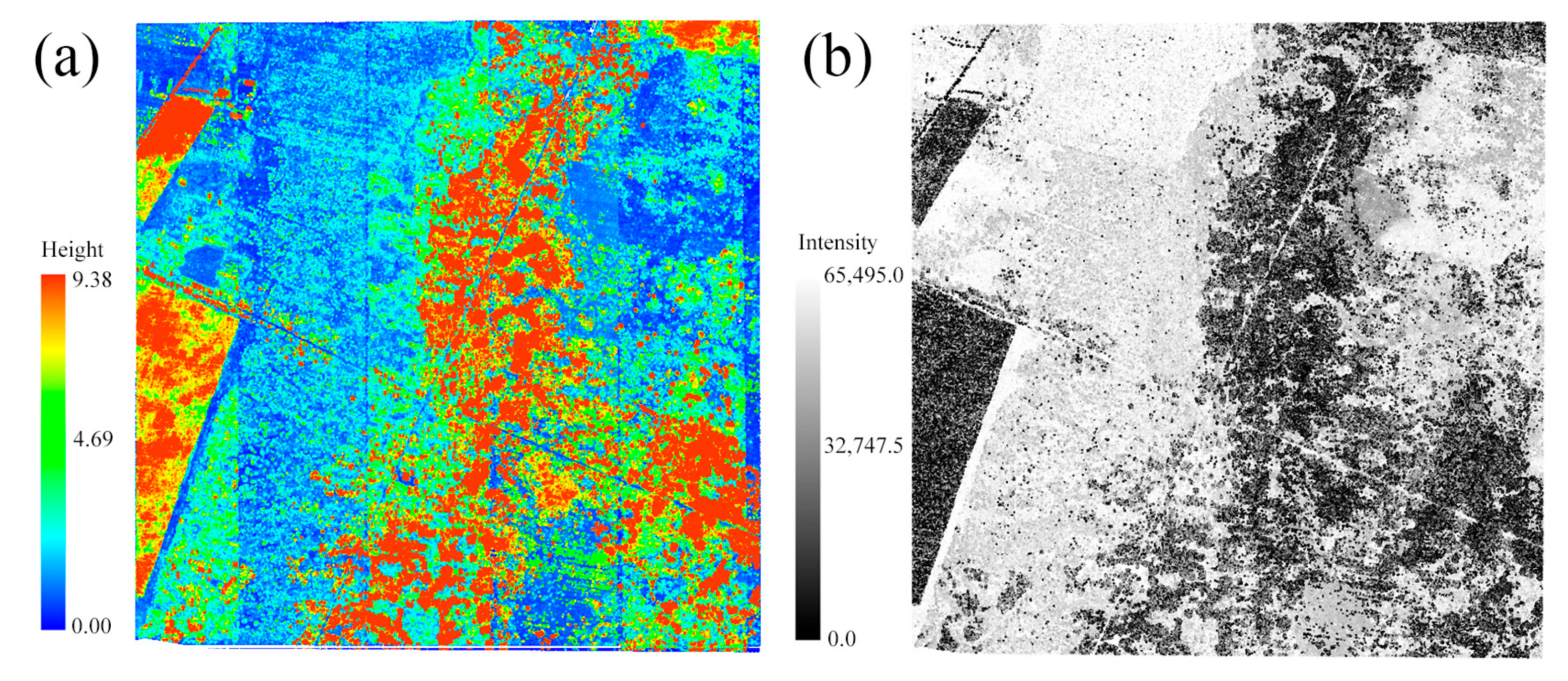
2.2.2. LiDAR Data and Preprocessing
2.3. Parametric Regression Models
2.3.1. Base Model
2.3.2. Nonlinear Mixed-Effects Model
2.4. Machine Learning Algorithms
2.4.1. Random Forest
2.4.2. Support Vector Machine
2.4.3. K-Nearest-Neighbor
2.4.4. Gradient Boosting Machine
2.4.5. Multivariate Adaptive Regression Splines Model
2.5. Model Evaluation
3. Results
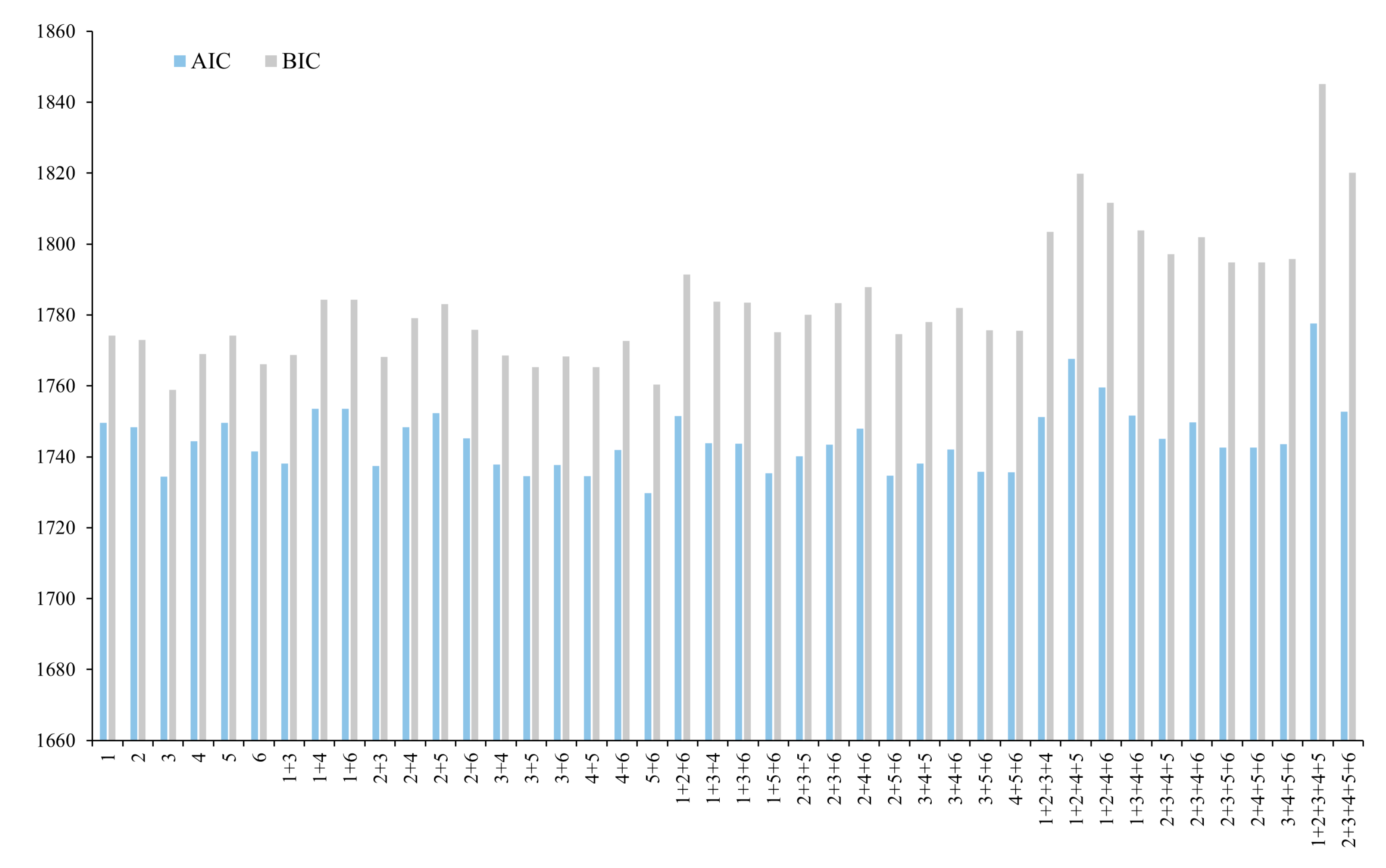
3.1. Parametric Regression Models
3.1.1. Base Models
3.1.2. NLME Models
3.1.3. Parameter Estimates
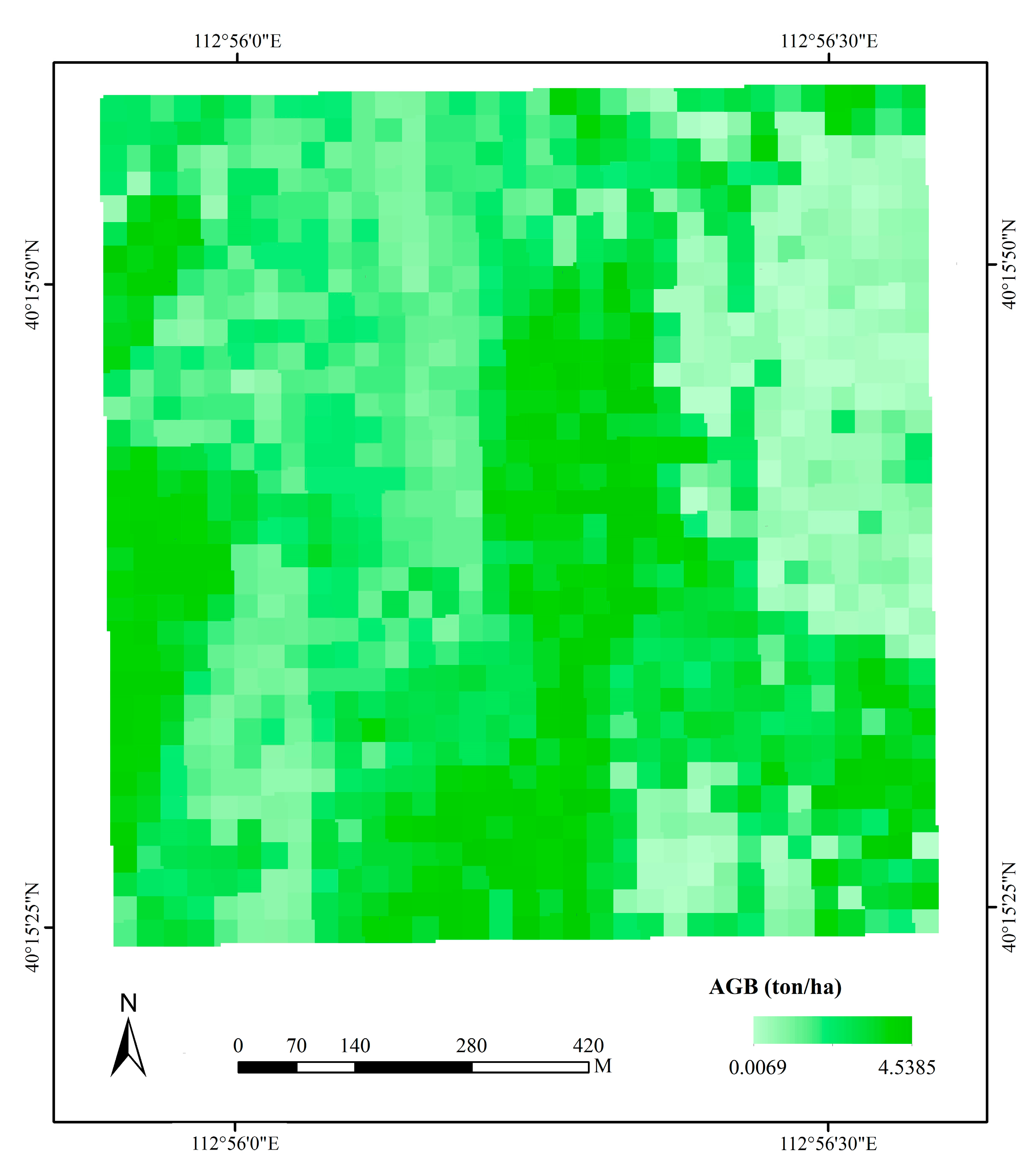
3.2. Machine Learning
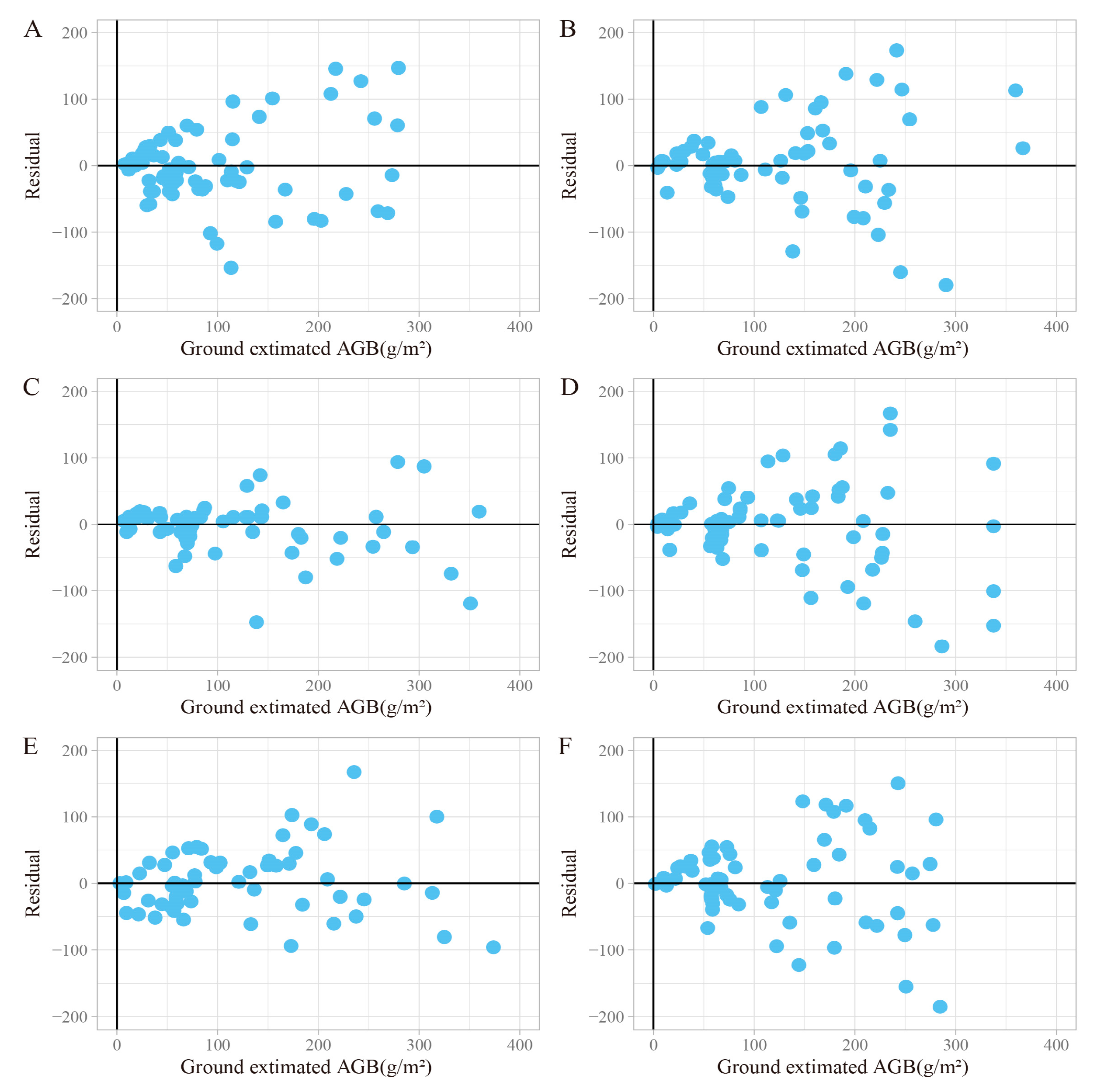
3.3. Model Evaluation
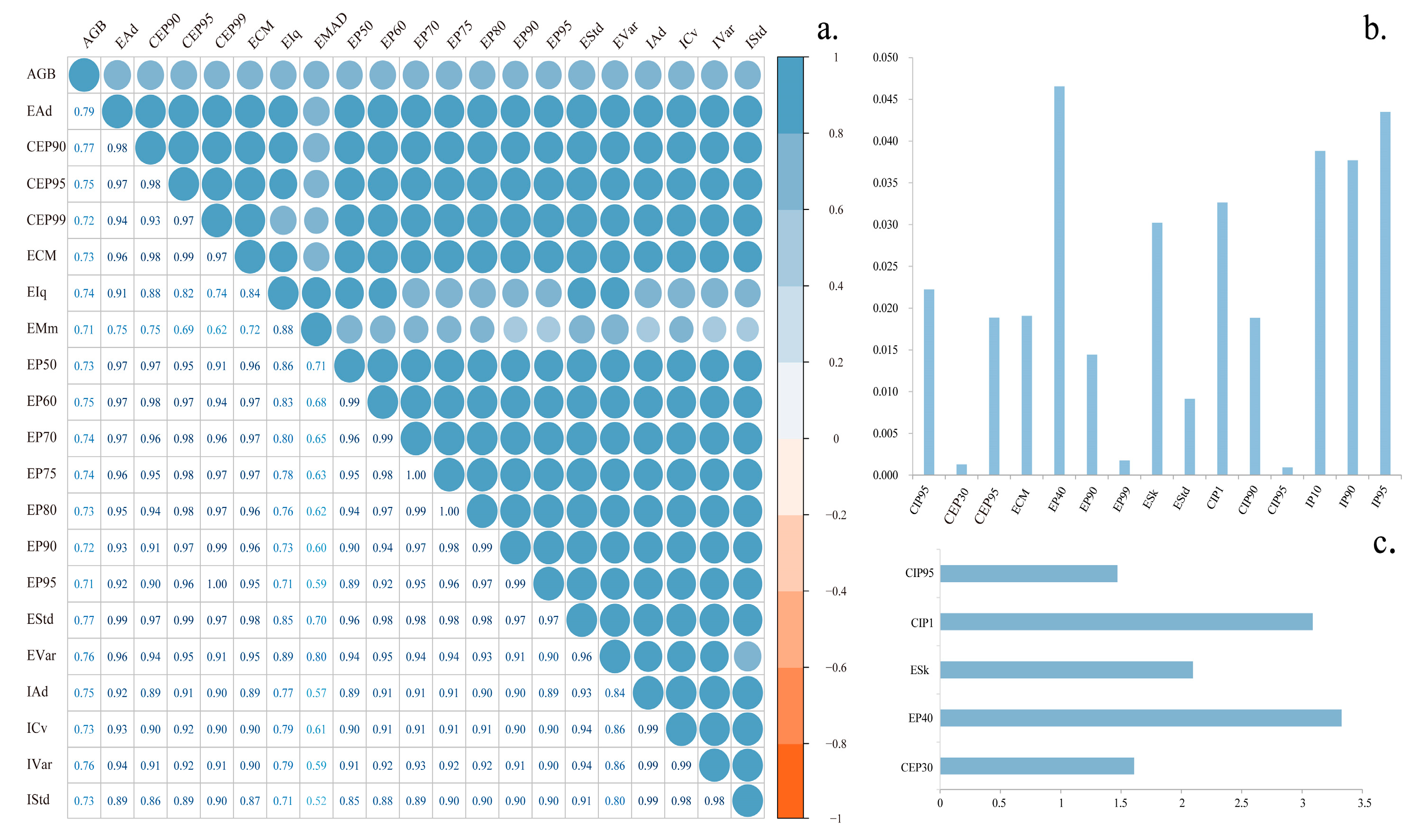
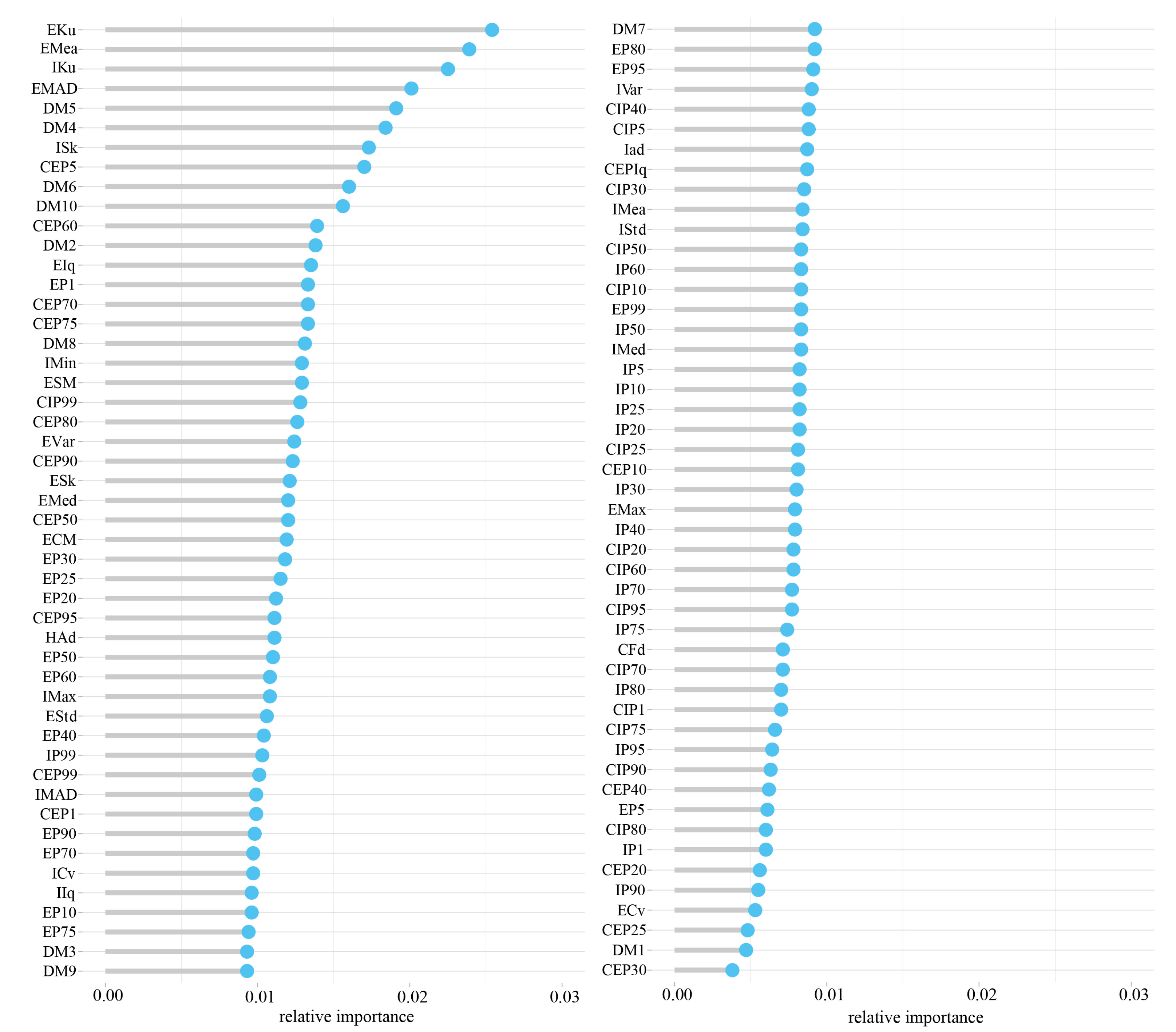
3.4. Variables Importance
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grainger, A. The Threatening Desert: Controlling Desertification; Routledge: London, UK, 2013. [Google Scholar]
- Mao, P.; Ding, J.; Jiang, B.; Qin, L.; Qiu, G.Y. How can UAV bridge the gap between ground and satellite observations for quantifying the biomass of desert shrub community? ISPRS J. Photogramm. Remote Sens. 2022, 192, 361–376. [Google Scholar] [CrossRef]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhang, Q.; Huang, H.; Huang, Y.; Tao, J.; Zhou, G.; Zhang, Y.; Yang, Y.; Lin, J. Aboveground Biomass of Typical Invasive Mangroves and Its Distribution Patterns Using UAV-LiDAR Data in a Subtropical Estuary: Maoling River Estuary, Guangxi, China. Ecol. Indic. 2022, 136, p. 108694. Available online: https://www.sciencedirect.com/science/article/pii/S1470160X22001650 (accessed on 11 December 2022).
- Perez-Quezada, J.; Delpiano, C.; Snyder, K.; Johnson, D.; Franck, N. Carbon pools in an arid shrubland in Chile under natural and afforested conditions. J. Arid Environ. 2011, 75, 29–37. [Google Scholar] [CrossRef]
- Ahlström, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, W.; Zhou, G.; Bai, Y.; Li, J.; Tang, X.; Chen, D.; Liu, Q.; Ma, W.; Xiong, G. Patterns of plant carbon, nitrogen, and phosphorus concentration in relation to productivity in China’s terrestrial ecosystems. Proc. Natl. Acad. Sci. USA 2018, 115, 4033–4038. [Google Scholar] [CrossRef]
- Tian, S.; Liu, X.; Jin, B.; Zhao, X. Contribution of Fine Roots to Soil Organic Carbon Accumulation in Different Desert Communities in the Sangong River Basin. Int. J. Environ. Res. Public Health 2022, 19, 10936. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Xie, L.; Nie, X.; Wang, Z.; Du, Z.; Yue, T. Remote sensing inversion of grassland aboveground biomass based on high accuracy surface modeling. Ecol. Indic. 2021, 121, 107215. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Fassnacht, F.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Dalponte, M.; Frizzera, L.; Ørka, H.O.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting stem diameters and aboveground biomass of individual trees using remote sensing data. Ecol. Indic. 2018, 85, 367–376. [Google Scholar] [CrossRef]
- Ahamed, T.; Tian, L.; Zhang, Y.; Ting, K. A review of remote sensing methods for biomass feedstock production. Biomass Bioenergy 2011, 35, 2455–2469. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- John, R.; Chen, J.; Giannico, V.; Park, H.; Xiao, J.; Shirkey, G.; Ouyang, Z.; Shao, C.; Lafortezza, R.; Qi, J. Grassland canopy cover and aboveground biomass in Mongolia and Inner Mongolia: Spatiotemporal estimates and controlling factors. Remote Sens. Environ. 2018, 213, 34–48. [Google Scholar] [CrossRef]
- Zandler, H.; Brenning, A.; Samimi, C. Quantifying dwarf shrub biomass in an arid environment: Comparing empirical methods in a high dimensional setting. Remote Sens. Environ. 2015, 158, 140–155. [Google Scholar] [CrossRef]
- Forkuor, G.; Zoungrana, J.-B.B.; Dimobe, K.; Ouattara, B.; Vadrevu, K.P.; Tondoh, J.E. Above-ground biomass mapping in West African dryland forest using Sentinel-1 and 2 datasets—A case study. Remote Sens. Environ. 2020, 236, 111496. [Google Scholar] [CrossRef]
- Li, S.; Su, P.; Zhang, H.; Zhou, Z.; Xie, T.; Shi, R.; Gou, W. Distribution Patterns of Desert Plant Diversity and Relationship to Soil Properties in the Heihe River Basin, China. Ecosphere 2018, 9, e02355. Available online: https://esajournals.onlinelibrary.wiley.com/doi/pdfdirect/10.1002/ecs2.2355 (accessed on 11 December 2022).
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and limitations of Landsat and land cover data for aboveground woody biomass estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, L.; Wang, G.; Li, S.; Hu, K. Improving Estimation of Forest Canopy Cover by Introducing Loss Ratio of Laser Pulses Using Airborne LiDAR. IEEE Trans. Geosci. Remote Sens. 2019, 58, 567–585. [Google Scholar] [CrossRef]
- Zhou, L.; Meng, R.; Tan, Y.; Lv, Z.; Zhao, Y.; Xu, B.; Zhao, F. Comparison of UAV-based LiDAR and digital aerial photogrammetry for measuring crown-level canopy height in the urban environment. Urban For. Urban Green. 2022, 69, 127489. [Google Scholar] [CrossRef]
- Luo, S.; Chen, J.M.; Wang, C.; Gonsamo, A.; Xi, X.; Lin, Y.; Qian, M.; Peng, D.; Nie, S.; Qin, H. Comparative Performances of Airborne LiDAR Height and Intensity Data for Leaf Area Index Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 300–310. [Google Scholar] [CrossRef]
- Donoghue, D.N.; Watt, P.J.; Cox, N.J.; Wilson, J. Remote sensing of species mixtures in conifer plantations using LiDAR height and intensity data. Remote Sens. Environ. 2007, 110, 509–522. [Google Scholar] [CrossRef]
- Antonarakis, A.; Richards, K.S.; Brasington, J. Object-based land cover classification using airborne LiDAR. Remote Sens. Environ. 2008, 112, 2988–2998. [Google Scholar] [CrossRef]
- Yunfei, B.; Guoping, L.; Chunxiang, C.; Xiaowen, L.; Hao, Z.; Qisheng, H.; Linyan, B.; Chaoyi, C. Classification of LIDAR point cloud and generation of DTM from LIDAR height and intensity data in forested area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 313–318. [Google Scholar] [CrossRef]
- Senthil Kumar, A.; Sudheer, K.; Jain, S.; Agarwal, P. Rainfall-runoff modelling using artificial neural networks: Comparison of network types. Hydrol. Process. Int. J. 2005, 19, 1277–1291. [Google Scholar] [CrossRef]
- Horowitz, J.L. Semiparametric and Nonparametric Methods in Econometrics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 12. [Google Scholar] [CrossRef]
- Zang, H.; Lei, X.; Zeng, W. Height–diameter equations for larch plantations in northern and northeastern China: A comparison of the mixed-effects, quantile regression and generalized additive models. For. Int. J. For. Res. 2016, 89, 434–445. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Rocha, A.V.; Calvin, K.; Holmes, B.; Wang, C.; Goulden, M.L. Disturbance legacies and climate jointly drive tree growth and mortality in an intensively studied boreal forest. Glob. Chang. Biol. 2014, 20, 216–227. [Google Scholar] [CrossRef]
- Kilham, P.; Hartebrodt, C.; Kändler, G. Generating tree-level harvest predictions from forest inventories with random forests. Forests 2018, 10, 20. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Crookston, N.L.; Radtke, P.J. Linking climate, gross primary productivity, and site index across forests of the western United States. Can. J. For. Res. 2011, 41, 1710–1721. [Google Scholar] [CrossRef]
- Mitsopoulos, I.; Xanthopoulos, G. Effect of stand, topographic, and climatic factors on the fuel complex characteristics of Aleppo (Pinus halepensis Mill.) and Calabrian (Pinus brutia Ten.) pine forests of Greece. For. Ecol. Manag. 2016, 360, 110–121. [Google Scholar] [CrossRef]
- Ye, J.; Wu, B.; Liu, M.; Gao, Y.; Gao, J.; Lei, Y. Estimation of aboveground biomass of vegetation in the desert-oasis ecotone onthe northeastern edge of the Ulan Buh Desert. Acta Ecol. Sin. 2018, 38, 1216–1225. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Team, R.C. Linear and nonlinear mixed effects models. R Package Version 2007, 3, 1–89. [Google Scholar]
- Fu, L.; Tang, S. A general formulation of nonlinear mixed effect models and its application. Sci. Sin. Math 2020, 50, 15–30. [Google Scholar] [CrossRef]
- Arnold, T.W. Uninformative parameters and model selection using Akaike’s Information Criterion. J. Wildl. Manag. 2010, 74, 1175–1178. [Google Scholar] [CrossRef]
- Fredensborg Hansen, R.M.; Rinne, E.; Skourup, H. Classification of Sea Ice Types in the Arctic by Radar Echoes from SARAL/AltiKa. Remote Sens. 2021, 13, 3183. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M.J.R.N. Classification and Regression by random. Forest 2002, 23, 18–22. [Google Scholar]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Shah-Hosseini, R.; Homayouni, S.; Safari, A. A hybrid kernel-based change detection method for remotely sensed data in a similarity space. Remote Sens. 2015, 7, 12829–12858. [Google Scholar] [CrossRef]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R Package Version 2015. Available online: https://cran.r-project.org/web//packages/e1071 (accessed on 11 December 2022).
- Shu, S.; Zhou, X.H.; Shen, X.Y.; Liu, Z.C.; Tang, Q.H.; Li, H.L.; Ke, C.Q.; Li, J. Discrimination of different sea ice types from CryoSat-2 satellite data using an Object-based Random Forest (ORF). Mar. Geod. 2020, 43, 213–233. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef]
- Greenwell, B.; Cunningham, B.B.; Developers, G. gbm: Generalized Boosted Regression Models; R Package Version 2.1.8.1. 2022. Available online: https://CRAN.R-project.org/package=gbm (accessed on 11 December 2022).
- Kuhn, M. caret: Classification and Regression Training; R Package Version 6.0-93. 2022. Available online: https://CRAN.R-project.org/package=caret (accessed on 11 December 2022).
- Liang, T.; Yang, S.; Feng, Q.; Liu, B.; Zhang, R.; Huang, X.; Xie, H. Multi-factor modeling of above-ground biomass in alpine grassland: A case study in the Three-River Headwaters Region, China. Remote Sens. Environ. 2016, 186, 164–172. [Google Scholar] [CrossRef]
- Lyu, X.; Li, X.; Gong, J.; Li, S.; Dou, H.; Dang, D.; Xuan, X.; Wang, H. Remote-sensing inversion method for aboveground biomass of typical steppe in Inner Mongolia, China. Ecol. Indic. 2021, 120, 106883. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, D.; Chen, X.; Zhang, Y.; Maisupova, B.; Tao, Y. The spatiotemporal patterns of vegetation coverage and biomass of the temperate deserts in Central Asia and their relationships with climate controls. Remote Sens. Environ. 2016, 175, 271–281. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, X.; Qiu, J.; Li, J.; Gao, T.; Wu, Q.; Zhao, F.; Ma, H.; Yu, H.; Xu, B. Remote sensing-based biomass estimation and its spatio-temporal variations in temperate grassland, Northern China. Remote Sens. 2014, 6, 1496–1513. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Spangenberg, G.; Kant, S. Fusion of spectral and structural information from aerial images for improved biomass estimation. Remote Sens. 2020, 12, 3164. [Google Scholar] [CrossRef]
- Grüner, E.; Astor, T.; Wachendorf, M. Biomass prediction of heterogeneous temperate grasslands using an SfM approach based on UAV imaging. Agronomy 2019, 9, 54. [Google Scholar] [CrossRef]
- Li, A.; Dhakal, S.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K. Lidar aboveground vegetation biomass estimates in shrublands: Prediction, uncertainties and application to coarser scales. Remote Sens. 2017, 9, 903. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.; Madonsela, S.; Van De Kerchove, R.; Kaszta, Z.; Wolff, E. Monitoring grass nutrients and biomass as indicators of rangeland quality and quantity using random forest modelling and WorldView-2 data. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 43–54. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, G.; Deng, L.; Tang, Z.; Wang, K.; Sun, W.; Shangguan, Z. Prediction of aboveground grassland biomass on the Loess Plateau, China, using a random forest algorithm. Sci. Rep. 2017, 7, 6940. [Google Scholar] [CrossRef]
- Salehnasab, A.; Bayat, M.; Namiranian, M.; Khaleghi, B.; Omid, M.; Masood Awan, H.U.; Al-Ansari, N.; Jaafari, A. Machine learning for the estimation of diameter increment in mixed and uneven-aged forests. Sustainability 2022, 14, 3386. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, S.; Zhao, F.; Tian, L.; Zhao, Z. Comparison of machine learning algorithms for forest parameter estimations and application for forest quality assessments. For. Ecol. Manag. 2019, 434, 224–234. [Google Scholar] [CrossRef]
- Mahesh, B. Machine learning algorithms—A review. Int. J. Sci. Res. 2020, 9, 381–386. [Google Scholar] [CrossRef]
- Adamec, Z.; Drápela, K. Comparison of parametric and nonparametric methods for modeling height-diameter relationships. IForest 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Ray, S. A quick review of machine learning algorithms. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 35–39. [Google Scholar] [CrossRef]
- Rudin, C.; Radin, J. Why are we using black box models in AI when we don’t need to? A lesson from an explainable AI competition. Harv. Data Sci. Rev. 2019, 1, 2. [Google Scholar] [CrossRef]
- Xiangdong, L. Applications of machine learning algorithms in forest growth and yield prediction. J. Beijing For. Univ. 2019, 41, 23–36. (In Chinese) [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Thessen, A. Adoption of machine learning techniques in ecology and earth science. One Ecosyst. 2016, 1, e8621. [Google Scholar] [CrossRef]
- Fielding, A.H. Cluster and Classification Techniques for the Biosciences; Cambridge University Press: London, UK, 2006. [Google Scholar] [CrossRef]
- Miao, X.; Heaton, J.S.; Zheng, S.; Charlet, D.A.; Liu, H. Applying tree-based ensemble algorithms to the classification of ecological zones using multi-temporal multi-source remote-sensing data. Int. J. Remote Sens. 2012, 33, 1823–1849. [Google Scholar] [CrossRef]
- Baccarini, L.M.R.; e Silva, V.V.R.; de Menezes, B.R.; Caminhas, W.M. SVM practical industrial application for mechanical faults diagnostic. Expert Syst. Appl. 2011, 38, 6980–6984. [Google Scholar] [CrossRef]
- Safari, A.; Sohrabi, H.; Powell, S.L. Comparison of satellite-based estimates of aboveground biomass in coppice oak forests using parametric, semiparametric, and nonparametric modeling methods. J. Appl. Remote Sens. 2018, 12, 046026. [Google Scholar] [CrossRef]
- Zeng, N.; Ren, X.; He, H.; Zhang, L.; Li, P.; Niu, Z. Estimating the grassland aboveground biomass in the Three-River Headwater Region of China using machine learning and Bayesian model averaging. Environ. Res. Lett. 2021, 16, 114020. [Google Scholar] [CrossRef]
- Cao, L.; Pan, J.; Li, R.; Li, J.; Li, Z. Integrating airborne LiDAR and optical data to estimate forest aboveground biomass in arid and semi-arid regions of China. Remote Sens. 2018, 10, 532. [Google Scholar] [CrossRef]
- Książek, W.; Gandor, M.; Pławiak, P. Comparison of various approaches to combine logistic regression with genetic algorithms in survival prediction of hepatocellular carcinoma. Comput. Biol. Med. 2021, 134, 104431. [Google Scholar] [CrossRef] [PubMed]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. Estimating aboveground biomass and leaf area of low-stature Arctic shrubs with terrestrial LiDAR. Remote Sens. Environ. 2015, 164, 26–35. [Google Scholar] [CrossRef]
- Olsoy, P.J.; Glenn, N.F.; Clark, P.E.; Derryberry, D.R. Aboveground total and green biomass of dryland shrub derived from terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 88, 166–173. [Google Scholar] [CrossRef]
- Ni-Meister, W.; Lee, S.; Strahler, A.H.; Woodcock, C.E.; Schaaf, C.; Yao, T.; Ranson, K.J.; Sun, G.; Blair, J.B. Assessing general relationships between aboveground biomass and vegetation structure parameters for improved carbon estimate from lidar remote sensing. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Kim, S.; McGaughey, R.J.; Andersen, H.-E.; Schreuder, G. Tree species differentiation using intensity data derived from leaf-on and leaf-off airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1575–1586. [Google Scholar] [CrossRef]
- Zhang, K.; Hu, B. Individual urban tree species classification using very high spatial resolution airborne multi-spectral imagery using longitudinal profiles. Remote Sens. 2012, 4, 1741–1757. [Google Scholar] [CrossRef]
| Plant Species | Formula | Allometric Exponent |
|---|---|---|
| Artemisia desertorum | 1.135 | |
| Nitraria tangutorum | 0.945 | |
| Haloxylon ammodendron | 1.007 | |
| Caragana korshinskii | 1.014 | |
| Hedysarum scoparium | 0.816 | |
| Tamarix ramosissima | 0.869 | |
| Elaeagnus angustifolia | 1.071 |
| Variables | Description | Variables | Description |
|---|---|---|---|
| CEP1, CEP5, CEP10, …, CEP90, CEP95, CEP99 | Cumulative elevation percentile of 15 different statistical units | EMax, EMean, EMed, EStd, EVar, IMax, IMin, IMean, IMed, IStd, IVar | Maximum, Minimum, Mean, Median, Standard Deviation and Variance of Elevation and Intensity |
| CIP1, CIP5, CIP10, …, CIP90, CIP95, CIP99 | Cumulative intensity percentile of 15 different statistical units | EP1, EP5, EP10…, EP95, EP99 | Elevation percentile of 15 different statistical units |
| IP1, IP5, IP10, …, IP90, IP95, IP99 | Intensity percentile of 15 different statistical units | DM1, DM2…, DM10 | Point cloud density of 10 different statistical units |
| CEPIq, EIq, IIq | Percentile quartile spacing of Cumulative Elevation, Elevation and Intensity | EMAD, IMAD | Median absolute deviation of the median Elevation and Intensity |
| ECM, ESM | Mean elevation of Cube and Sqrt | HAd, IAd | Average absolute deviation of Elevation and Intensity |
| ECv, ICv | Coefficient of variation of Elevation and Intensity | CFd | Canopy fluctuation rate |
| EKu, IKu | Elevation kurtosis and intensity kurtosis | ESk, ISk | Elevation Skewness and Intensity Skewness |
| Model | Number of Parameters | Training Data | Validation Data | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | TRE | AIC | BIC | RMSE | R2 | TRE | ||
| Linear | 6 | 60.9266 | 0.6362 | 20.2317 | 1771.09 | 1792.58 | 79.8046 | 0.5467 | 25.7699 |
| Richards | 6 | 57.2373 | 0.6789 | 17.4414 | 1751.23 | 1772.71 | 85.4208 | 0.4807 | 25.1191 |
| Logistic | 7 | 55.9541 | 0.6931 | 16.5402 | 1746.02 | 1770.57 | 74.8961 | 0.6006 | 23.2180 |
| Exponential | 6 | 56.5880 | 0.6861 | 16.9811 | 1747.60 | 1769.09 | 73.3495 | 0.6169 | 22.7290 |
| Parameter | Variables | Liner | Logistic | Richards | Exponential | NLME |
|---|---|---|---|---|---|---|
| β1 | / | −60.340 | −182.121 | −20.556 | 26.834 | 24.436 |
| β2 | CEP30 | −29.370 | −3.922 | −0.336 | −0.361 | −0.106 |
| β3 | EP40 | 270.500 | 0.188 | −1.059 | −0.843 | −0.928 |
| β4 | Eske | 86.700 | 0.206 | −0.834 | −0.247 | −0.462 |
| β5 | CIP30 | −144.790 | −0.102 | 1.901 | 2.555 | 2.197 |
| β6 | CIP95 | 192.47 | −1.572 | −2.327 | −2.434 | −2.272 |
| β7 | / | / | 1.117 | / | / | / |
| μ5i | / | / | / | / | / | 1.062 |
| μ6i | / | / | / | / | / | 0.586 |
| Model | Training Data | Validation Data | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | TRE | RMSE | R2 | TRE (g m−2) | |
| RF | 49.7021 | 0.7579 | 13.0055 | 62.8252 | 0.7191 | 14.4489 |
| SVM | 26.8635 | 0.9293 | 3.5050 | 38.1919 | 0.8962 | 5.4063 |
| KNN | 46.4816 | 0.7882 | 11.3961 | 63.5297 | 0.7128 | 16.5406 |
| MARS | 32.0995 | 0.8990 | 4.8997 | 60.8154 | 0.7367 | 10.4576 |
| GBM | 48.8357 | 0.7662 | 13.5585 | 74.0015 | 0.6103 | 23.2776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, D.; Huang, H.; Feng, L.; Sharma, R.P.; Chen, Q.; Liu, Q.; Fu, L. Aboveground Biomass Prediction of Arid Shrub-Dominated Community Based on Airborne LiDAR through Parametric and Nonparametric Methods. Remote Sens. 2023, 15, 3344. https://doi.org/10.3390/rs15133344
Xie D, Huang H, Feng L, Sharma RP, Chen Q, Liu Q, Fu L. Aboveground Biomass Prediction of Arid Shrub-Dominated Community Based on Airborne LiDAR through Parametric and Nonparametric Methods. Remote Sensing. 2023; 15(13):3344. https://doi.org/10.3390/rs15133344
Chicago/Turabian StyleXie, Dongbo, Hongchao Huang, Linyan Feng, Ram P. Sharma, Qiao Chen, Qingwang Liu, and Liyong Fu. 2023. "Aboveground Biomass Prediction of Arid Shrub-Dominated Community Based on Airborne LiDAR through Parametric and Nonparametric Methods" Remote Sensing 15, no. 13: 3344. https://doi.org/10.3390/rs15133344
APA StyleXie, D., Huang, H., Feng, L., Sharma, R. P., Chen, Q., Liu, Q., & Fu, L. (2023). Aboveground Biomass Prediction of Arid Shrub-Dominated Community Based on Airborne LiDAR through Parametric and Nonparametric Methods. Remote Sensing, 15(13), 3344. https://doi.org/10.3390/rs15133344








