Evaluation of Arctic Sea Ice Thickness from a Parameter-Optimized Arctic Sea Ice–Ocean Model
Abstract
1. Introduction
2. Data and Methods
2.1. SIT from NAOSIM
2.2. SIT from CS2SMOS
2.3. SIT from In Situ Observations
2.4. Data Processing and Methods
3. Results
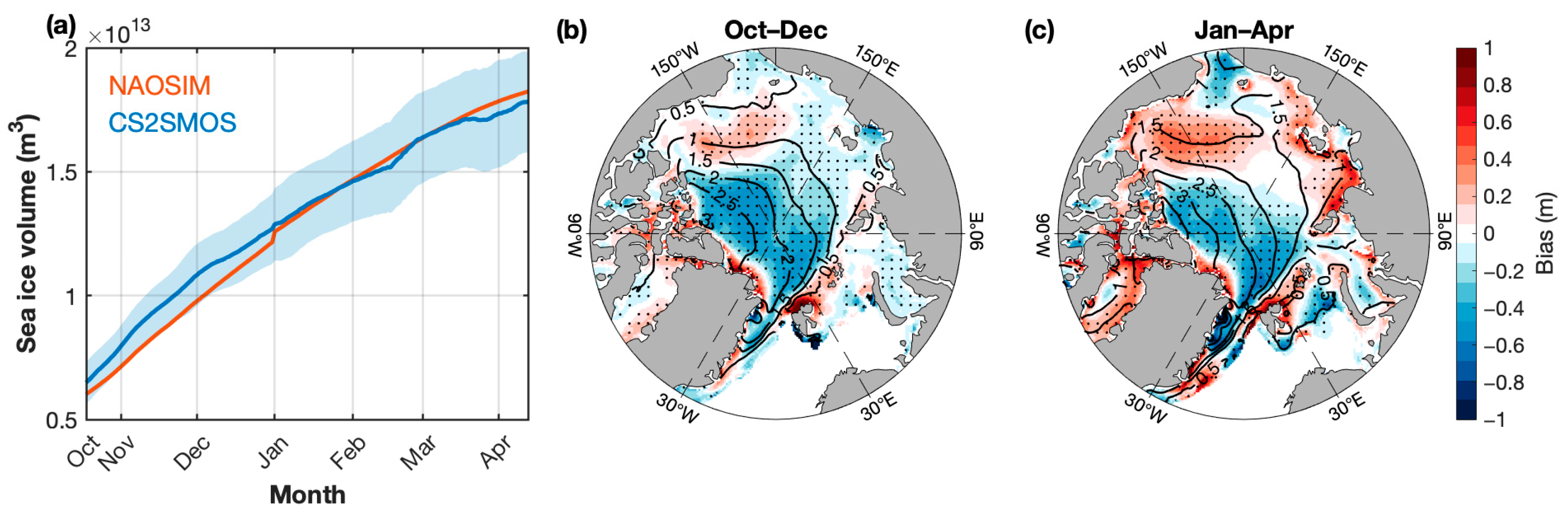
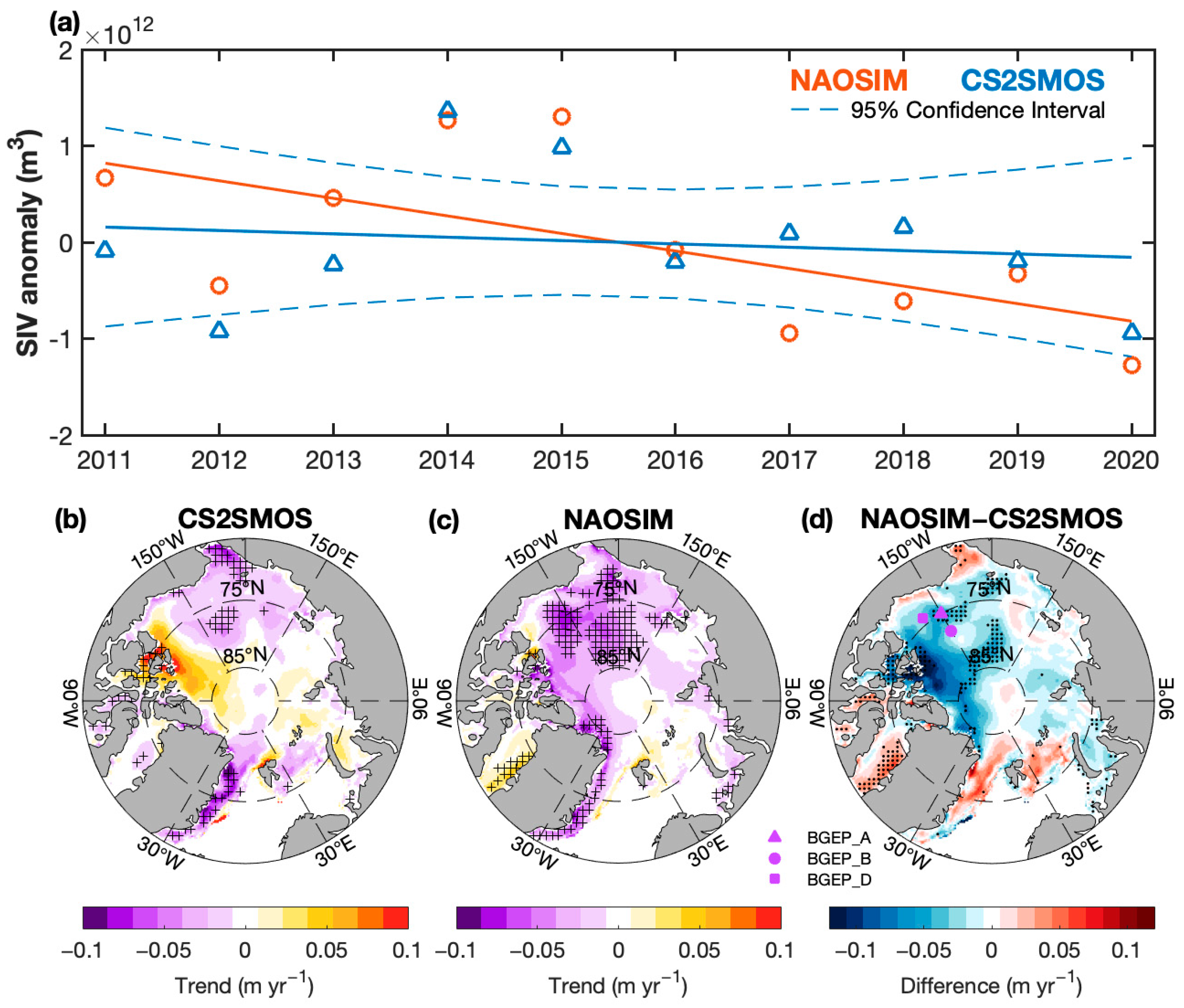
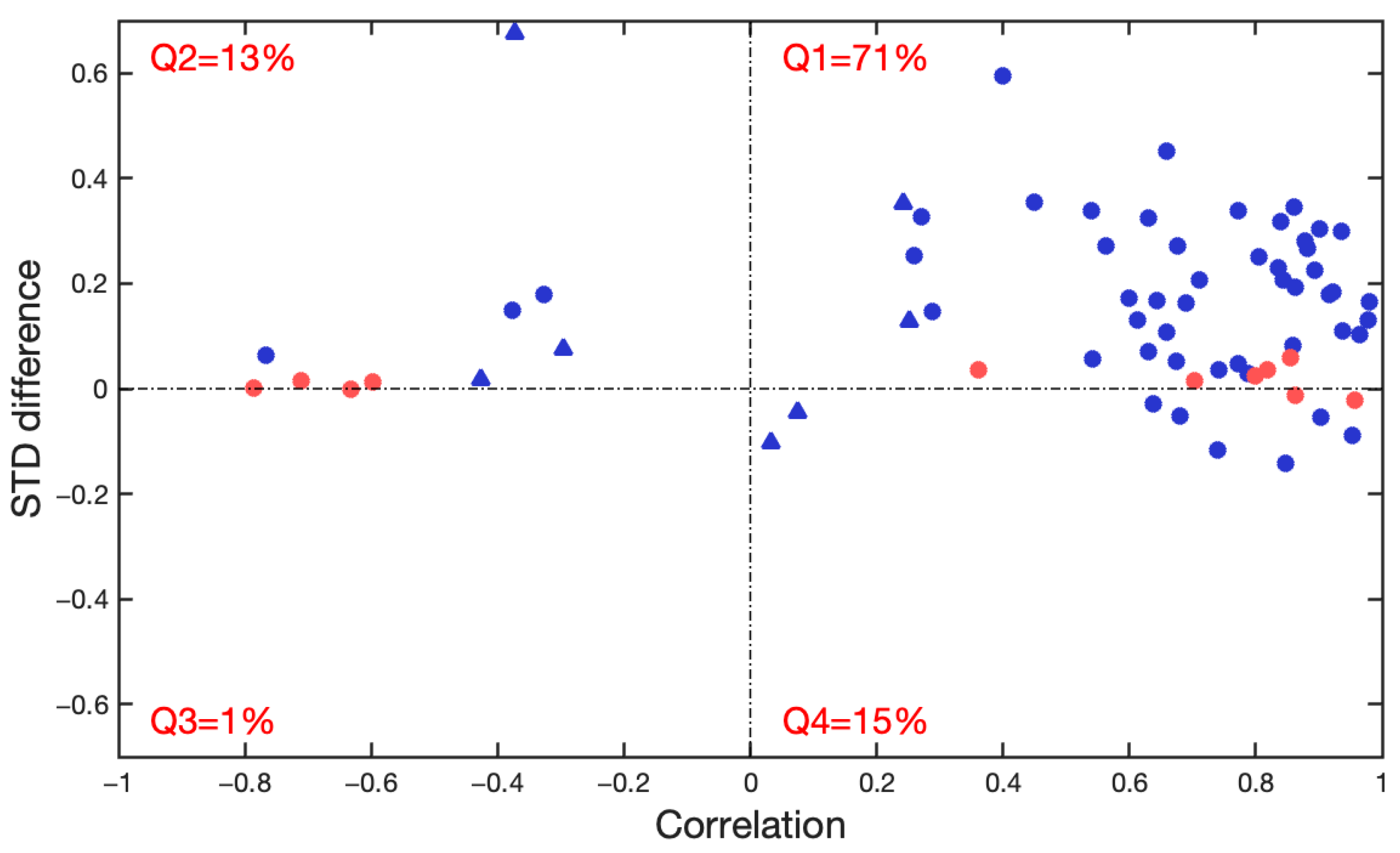
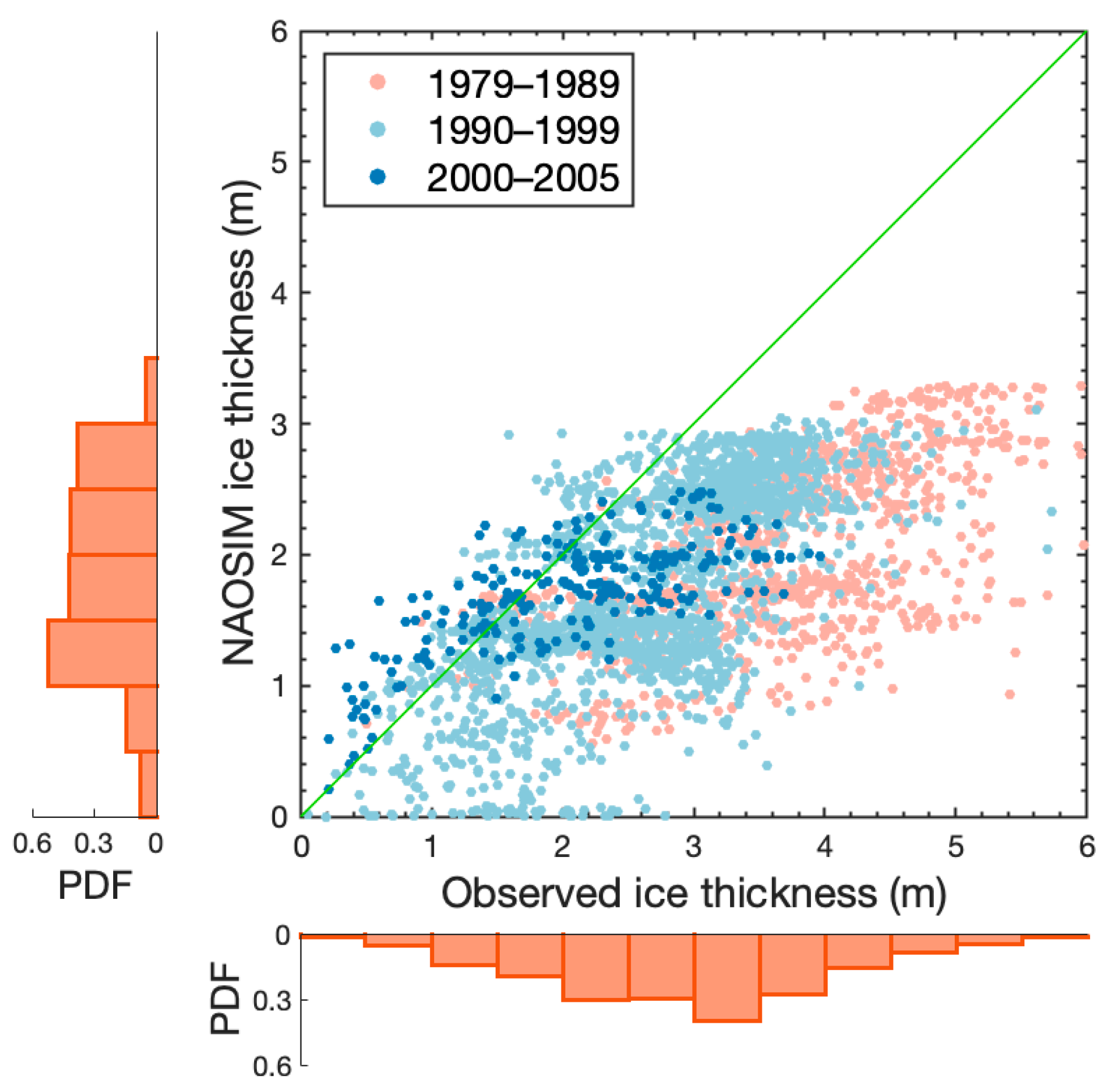
3.1. Comparison to CS2SMOS
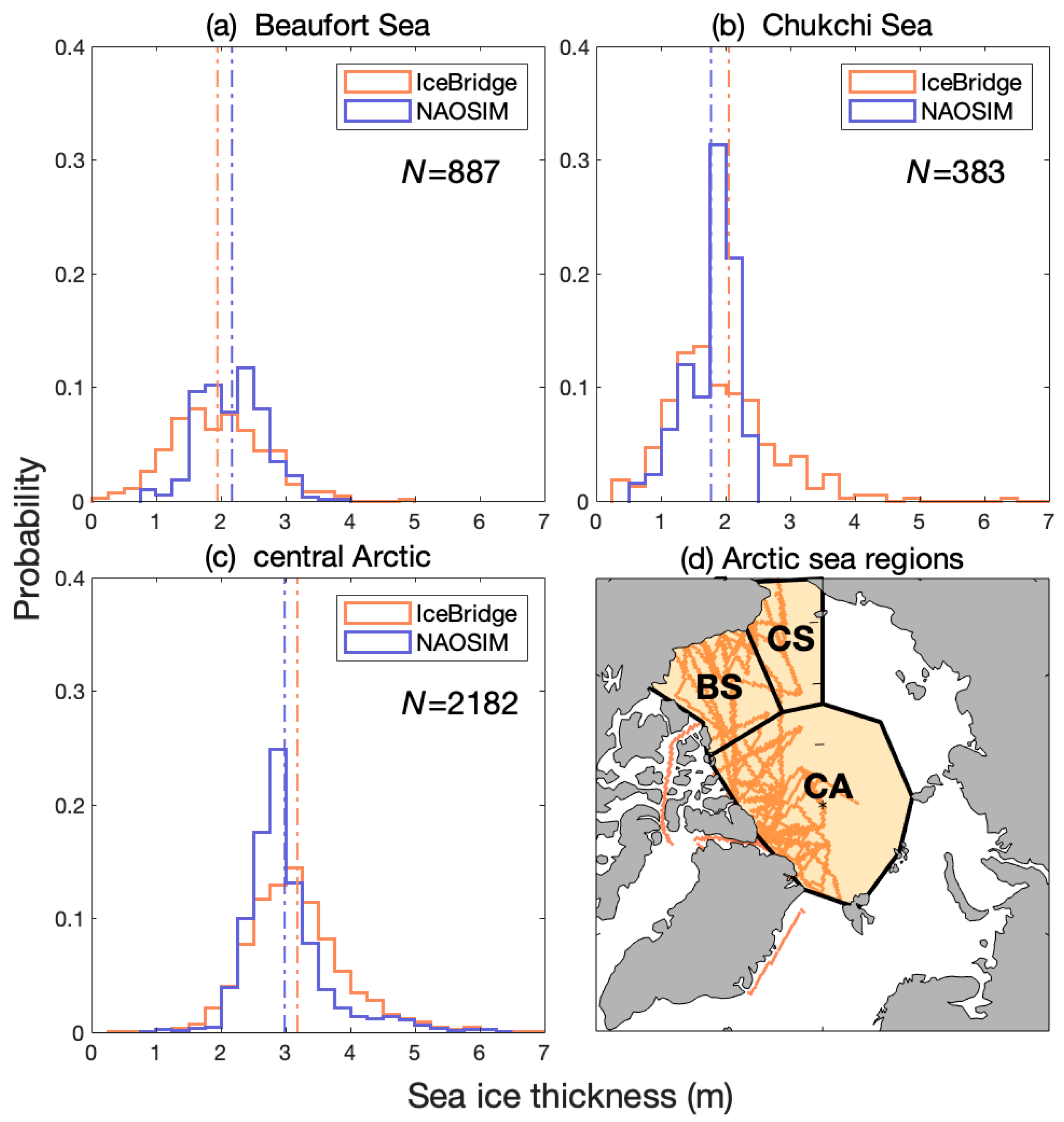
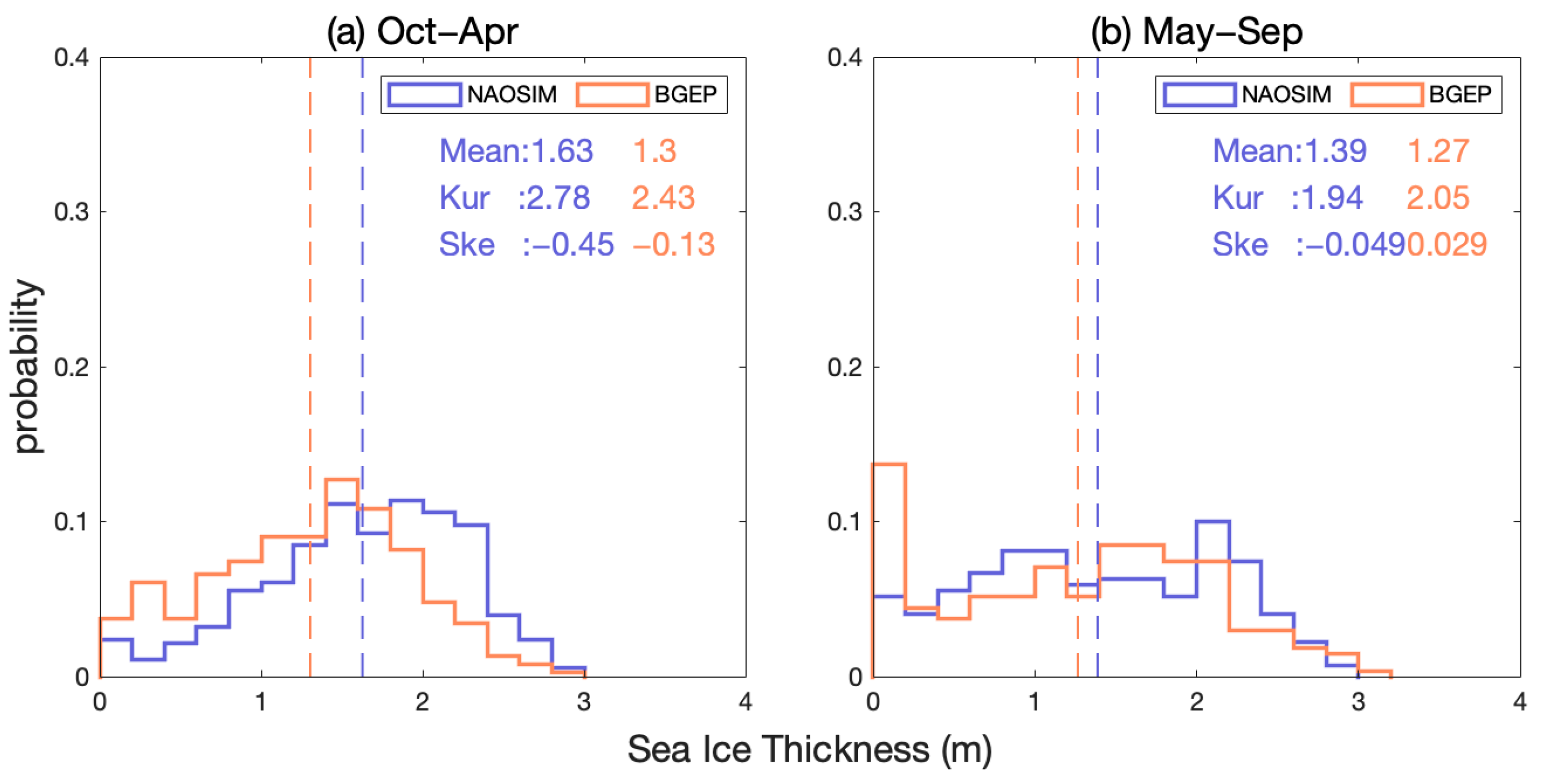
3.2. Comparison to In Situ Observations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serreze, M.C.; Meier, W.N. The Arctic’s sea ice cover: Trends, variability, predictability, and comparisons to the Antarctic. Ann. N. Y. Acad. Sci. 2019, 1436, 36–53. [Google Scholar] [CrossRef] [PubMed]
- Kwok, R. Arctic sea ice thickness, volume, and multiyear ice coverage: Losses and coupled variability (1958–2018). Environ. Res. Lett. 2018, 13, 105005. [Google Scholar] [CrossRef]
- Meier, W.N.; Hovelsrud, G.K.; van Oort, B.E.H.; Key, J.R.; Kovacs, K.M.; Michel, C.; Haas, C.; Granskog, M.A.; Gerland, S.; Perovich, D.K.; et al. Arctic sea ice in transformation: A review of recent observed changes and impacts on biology and human activity. Rev. Geophys. 2014, 52, 185–217. [Google Scholar] [CrossRef]
- Melia, N.; Haines, K.; Hawkins, E.; Day, J.J. Towards seasonal Arctic shipping route predictions. Environ. Res. Lett. 2017, 12, 084005. [Google Scholar] [CrossRef]
- Min, C.; Yang, Q.; Chen, D.; Yang, Y.; Zhou, X.; Shu, Q.; Liu, J. The Emerging Arctic Shipping Corridors. Geophys. Res. Lett. 2022, 49, e2022GL099157. [Google Scholar] [CrossRef]
- Min, C.; Zhou, X.; Luo, H.; Yang, Y.; Wang, Y.; Zhang, J.; Yang, Q. Toward Quantifying the Increasing Accessibility of the Arctic Northeast Passage in the Past Four Decades. Adv. Atmos. Sci. 2023. [Google Scholar] [CrossRef]
- Kurtz, N.T.; Markus, T.; Farrell, S.L.; Worthen, D.L.; Boisvert, L.N. Observations of recent Arctic sea ice volume loss and its impact on ocean-atmosphere energy exchange and ice production. J. Geophys. Res. Ocean. 2011, 116, C04015. [Google Scholar] [CrossRef]
- Rothrock, D.A.; Yu, Y.; Maykut, G.A. Thinning of the Arctic sea-ice cover. Geophys. Res. Lett. 1999, 26, 3469–3472. [Google Scholar] [CrossRef]
- Rothrock, D.A.; Percival, D.B.; Wensnahan, M. The decline in arctic sea-ice thickness: Separating the spatial, annual, and interannual variability in a quarter century of submarine data. J. Geophys. Res. 2008, 113, C05003. [Google Scholar] [CrossRef]
- Melling, H.; Riedel, D.A.; Gedalof, Z.E. Trends in the draft and extent of seasonal pack ice, Canadian Beaufort Sea. Geophys. Res. Lett. 2005, 32, L24501. [Google Scholar] [CrossRef]
- Kurtz, N.T.; Farrell, S.L.; Studinger, M.; Galin, N.; Harbeck, J.P.; Lindsay, R.; Onana, V.D.; Panzer, B.; Sonntag, J.G. Sea ice thickness, freeboard, and snow depth products from Operation IceBridge airborne data. Cryosphere 2013, 7, 1035–1056. [Google Scholar] [CrossRef]
- Haas, C.; Lobach, J.; Hendricks, S.; Rabenstein, L.; Pfaffling, A. Helicopter-borne measurements of sea ice thickness, using a small and lightweight, digital EM system. J. Appl. Geophys. 2009, 67, 234–241. [Google Scholar] [CrossRef]
- Polashenski, C.; Perovich, D.; Richter-Menge, J.; Elder, B. Seasonal ice mass-balance buoys: Adapting tools to the changing Arctic. Ann. Glaciol. 2011, 52, 18–26. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F. ICESat over Arctic sea ice: Estimation of snow depth and ice thickness. J. Geophys. Res. Ocean. 2008, 113, C08010. [Google Scholar] [CrossRef]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C.; et al. CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Zhang, S.; Xuan, Y.; Li, J.; Geng, T.; Li, X.; Xiao, F. Arctic Sea Ice Freeboard Retrieval from Envisat Altimetry Data. Remote Sens. 2021, 13, 1414. [Google Scholar] [CrossRef]
- Laxon, S.; Peacock, N.; Smith, D. High interannual variability of sea ice thickness in the Arctic region. Nature 2003, 425, 947–950. [Google Scholar] [CrossRef] [PubMed]
- Tian-Kunze, X.; Kaleschke, L.; Maaß, N.; Mäkynen, M.; Serra, N.; Drusch, M.; Krumpen, T. SMOS-derived thin sea ice thickness: Algorithm baseline, product specifications and initial verification. Cryosphere 2014, 8, 997–1018. [Google Scholar] [CrossRef]
- Landy, J.C.; Dawson, G.J.; Tsamados, M.; Bushuk, M.; Stroeve, J.C.; Howell, S.E.L.; Krumpen, T.; Babb, D.G.; Komarov, A.S.; Heorton, H.; et al. A year-round satellite sea-ice thickness record from CryoSat-2. Nature 2022, 609, 517–522. [Google Scholar] [CrossRef]
- Zheng, F.; Sun, Y.; Yang, Q.; Mu, L. Evaluation of Arctic Sea-ice Cover and Thickness Simulated by MITgcm. Adv. Atmos. Sci. 2021, 38, 29–48. [Google Scholar] [CrossRef]
- Chen, L.; Wu, R.; Shu, Q.; Min, C.; Yang, Q.; Han, B. The Arctic Sea Ice Thickness Change in CMIP6′s Historical Simulations. Adv. Atmos. Sci. 2023, 1–3. [Google Scholar] [CrossRef]
- Schweiger, A.; Lindsay, R.; Zhang, J.; Steele, M.; Stern, H.; Kwok, R. Uncertainty in modeled Arctic sea ice volume. J. Geophys. Res. 2011, 116, C00D06. [Google Scholar] [CrossRef]
- Sumata, H.; Kauker, F.; Karcher, M.; Gerdes, R. Covariance of Optimal Parameters of an Arctic Sea Ice–Ocean Model. Mon. Weather. Rev. 2019, 147, 2579–2602. [Google Scholar] [CrossRef]
- Kim, J.G.; Hunke, E.C.; Lipscomb, W.H. Sensitivity analysis and parameter tuning scheme for global sea-ice modeling. Ocean. Model. 2006, 14, 61–80. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Menemenlis, D.; Kwok, R. Arctic ice-ocean simulation with optimized model parameters: Approach and assessment. J. Geophys. Res. Ocean. 2011, 116, C04025. [Google Scholar] [CrossRef]
- Sumata, H.; Kauker, F.; Gerdes, R.; Köberle, C.; Karcher, M. A comparison between gradient descent and stochastic approaches for parameter optimization of a sea ice model. Ocean. Sci. 2013, 9, 609–630. [Google Scholar] [CrossRef]
- Sumata, H.; Kauker, F.; Karcher, M.; Gerdes, R. Simultaneous Parameter Optimization of an Arctic Sea Ice–Ocean Model by a Genetic Algorithm. Mon. Weather. Rev. 2019, 147, 1899–1926. [Google Scholar] [CrossRef]
- Ricker, R.; Kauker, F.; Schweiger, A.; Hendricks, S.; Zhang, J.; Paul, S. Evidence for an increasing role of ocean heat in Arctic winter sea ice growth. J. Clim. 2021, 34, 5215–5227. [Google Scholar] [CrossRef]
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Lindsay, R.; Schweiger, A. Arctic sea ice thickness loss determined using subsurface, aircraft, and satellite observations. Cryosphere 2015, 9, 269–283. [Google Scholar] [CrossRef]
- Min, C.; Yang, Q.; Mu, L.; Kauker, F.; Ricker, R. Ensemble-based estimation of sea-ice volume variations in the Baffin Bay. Cryosphere 2021, 15, 169–181. [Google Scholar] [CrossRef]
- Yang, Y.; Min, C.; Luo, H.; Kauker, F.; Ricker, R.; Yang, Q. The evolution of the Fram Strait sea ice volume export decomposed by age: Estimating with parameter-optimized sea ice-ocean model outputs. Environ. Res. Lett. 2022, 18, 014029. [Google Scholar] [CrossRef]
- Hibler, W.D. A Dynamic Thermodynamic Sea Ice Model. J. Phys. Oceanogr. 1979, 9, 815–846. [Google Scholar] [CrossRef]
- Pacanowski, R.C. Documentation user’s guide and reference manual (MOM2, Version 2). GFDL Ocean. Tech. Rep. 1996, 329. [Google Scholar]
- Hibler, W.D.; Bryan, K. A Diagnostic Ice–Ocean Model. J. Phys. Oceanogr. 1987, 17, 987–1015. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Eastwood, S.; Jenssen, M.; Lavergne, T.; Sørensen, A.M.; Tonboe, R. Global Sea Ice Concentration Reprocessing: Product User Manual. Product OSI-409, OSI-409-a, OSI-430. Available online: http://osisaf.met.no/docs/osisaf_cdop3_ss2_pum_sea-ice-conc-reproc_v2p5.pdf (accessed on 15 February 2023).
- Lavergne, T.; Eastwood, S.; Teffah, Z.; Schyberg, H.; Breivik, L.-A. Sea ice motion from low-resolution satellite sensors: An alternative method and its validation in the Arctic. J. Geophys. Res. Ocean. 2010, 115, C10032. [Google Scholar] [CrossRef]
- Kimura, N.; Nishimura, A.; Tanaka, Y.; Yamaguchi, H. Influence of winter sea-ice motion on summer ice cover in the Arctic. Polar Res. 2013, 32, 20193. [Google Scholar] [CrossRef]
- Fowler, C.; Maslanik, J.; Emery, W.; Tschudi, M. Polar Pathfinder Daily 25 km EASE-Grid Sea Ice Motion Vectors, Version 2; National Snow and Ice Data Center: Boulder, CL, USA, 2013. [Google Scholar] [CrossRef]
- Tschudi, M.; Fowler, C.; Maslanik, J.; Stroeve, J. Tracking the Movement and Changing Surface Characteristics of Arctic Sea Ice. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 536–540. [Google Scholar] [CrossRef]
- Ricker, R.; Hendricks, S.; Kaleschke, L.; Tian-Kunze, X.; King, J.; Haas, C. A weekly Arctic sea-ice thickness data record from merged CryoSat-2 and SMOS satellite data. Cryosphere 2017, 11, 1607–1623. [Google Scholar] [CrossRef]
- Ricker, R. CryoSat-2/SMOS Merged Product Description Document (PDD). Available online: https://spaces.awi.de/download/attachments/297634429/AWI_ESA_CS2SMOS_PDD_v1.2.pdf (accessed on 15 February 2023).
- Hendricks, S. CryoSat-2/SMOS Merged Product Description Document (PDD). Available online: https://earth.esa.int/eogateway/documents/20142/37627/CryoSat-2-SMOS-Merged-Product-Description-Document-PDD.pdf (accessed on 15 February 2023).
- Kurtz, N.; Studinger, M.; Harbeck, J.; Onana, V.; Yi, D. IceBridge L4 Sea Ice Freeboard, Snow Depth, and Thickness, Version 1; NASA DAAC at the National Snow and Ice Data Center: Boulder, CL, USA, 2015. [CrossRef]
- Richter-Menge, J.A.; Perovich, D.K.; Elder, B.C.; Claffey, K.; Rigor, I.; Ortmeyer, M. Ice mass-balance buoys: A tool for measuring and attributing changes in the thickness of the Arctic sea-ice cover. Ann. Glaciol. 2006, 44, 205–210. [Google Scholar] [CrossRef]
- Perovich, D.; Richter-Menge, J.A. From points to Poles: Extrapolating point measurements of sea-ice mass balance. Ann. Glaciol. 2017, 44, 188–192. [Google Scholar] [CrossRef]
- Melling, H.; Johnston, P.H.; Riedel, D.A. Measurements of the Underside Topography of Sea Ice by Moored Subsea Sonar. J. Atmos. Ocean. Technol. 1995, 12, 589–602. [Google Scholar] [CrossRef]
- Wensnahan, M.; Rothrock, D.A. Sea-ice draft from submarine-based sonar: Establishing a consistent record from analog and digitally recorded data. Geophys. Res. Lett. 2005, 32, L11502. [Google Scholar] [CrossRef]
- Wensnahan, M.; Rothrock, D.A. The Accuracy of Sea Ice Drafts Measured from U.S. Navy Submarines. J. Atmos. Ocean. Technol. 2007, 24, 1936–1949. [Google Scholar] [CrossRef]
- Kwok, R. Sea ice convergence along the Arctic coasts of Greenland and the Canadian Arctic Archipelago: Variability and extremes (1992–2014). Geophys. Res. Lett. 2015, 42, 7598–7605. [Google Scholar] [CrossRef]
- Kwok, R. Outflow of Arctic Ocean Sea Ice into the Greenland and Barents Seas: 1979–2007. J. Clim. 2009, 22, 2438–2457. [Google Scholar] [CrossRef]
- Zhang, S.; Geng, T.; Zhu, C.; Li, J.; Li, X.; Zhu, B.; Liu, L.; Xiao, F. Arctic Sea Ice Freeboard Estimation and Variations from Operation IceBridge. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Ogawa, F.; Keenlyside, N.; Gao, Y.; Koenigk, T.; Yang, S.; Suo, L.; Wang, T.; Gastineau, G.; Nakamura, T.; Cheung, H.N.; et al. Evaluating Impacts of Recent Arctic Sea Ice Loss on the Northern Hemisphere Winter Climate Change. Geophys. Res. Lett. 2018, 45, 3255–3263. [Google Scholar] [CrossRef]

| Mooring | Trend in CS2SMOS Period | Trend in ULS Period |
|---|---|---|
| BGEP_A | −0.043 ± 0.030 | −0.045 ± 0.018 |
| CS2SMOS_A | −0.016 | |
| NAOSIM_A | −0.075 | −0.044 |
| BGEP_B | −0.051 ± 0.034 | −0.062 ± 0.018 |
| CS2SMOS_B | −0.029 | |
| NAOSIM_B | −0.046 | −0.047 |
| BGEP_D | −0.076 ± 0.044 | −0.059 ± 0.028 |
| CS2SMOS_D | −0.017 | |
| NAOSIM_D | −0.050 | −0.040 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Luo, H.; Min, C.; Xiu, Y.; Shi, Q.; Yang, Q. Evaluation of Arctic Sea Ice Thickness from a Parameter-Optimized Arctic Sea Ice–Ocean Model. Remote Sens. 2023, 15, 2537. https://doi.org/10.3390/rs15102537
Zhang Q, Luo H, Min C, Xiu Y, Shi Q, Yang Q. Evaluation of Arctic Sea Ice Thickness from a Parameter-Optimized Arctic Sea Ice–Ocean Model. Remote Sensing. 2023; 15(10):2537. https://doi.org/10.3390/rs15102537
Chicago/Turabian StyleZhang, Qiaoqiao, Hao Luo, Chao Min, Yongwu Xiu, Qian Shi, and Qinghua Yang. 2023. "Evaluation of Arctic Sea Ice Thickness from a Parameter-Optimized Arctic Sea Ice–Ocean Model" Remote Sensing 15, no. 10: 2537. https://doi.org/10.3390/rs15102537
APA StyleZhang, Q., Luo, H., Min, C., Xiu, Y., Shi, Q., & Yang, Q. (2023). Evaluation of Arctic Sea Ice Thickness from a Parameter-Optimized Arctic Sea Ice–Ocean Model. Remote Sensing, 15(10), 2537. https://doi.org/10.3390/rs15102537






