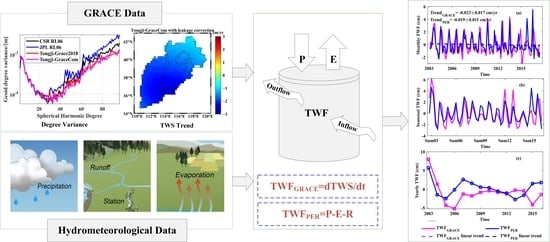
Evaluation of Terrestrial Water Storage and Flux in North China by Using GRACE Combined Gravity Field Solutions and Hydrometeorological Models
Abstract
1. Introduction
2. Data and Methodology
2.1. Data Analysis
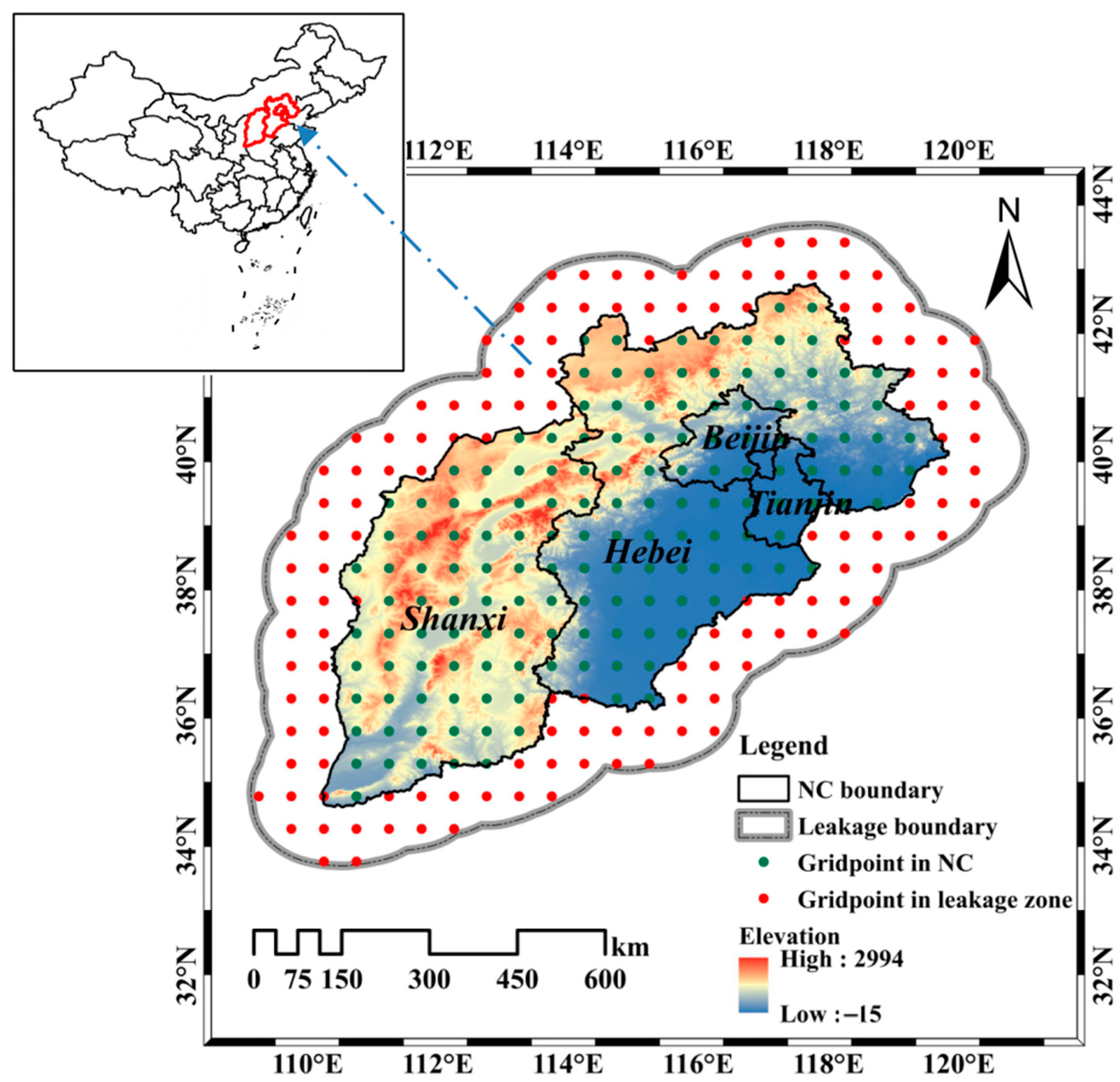
2.1.1. GRACE Data
2.1.2. Hydrometeorological Data
2.1.3. Statistical Data
2.2. Methodology
2.2.1. TWSA Inversion with Signal-Leakage Correction
2.2.2. Water Budget Estimates
2.2.3. Evaluation Metrics
3. Results
3.1. TWSA Estimation in North China
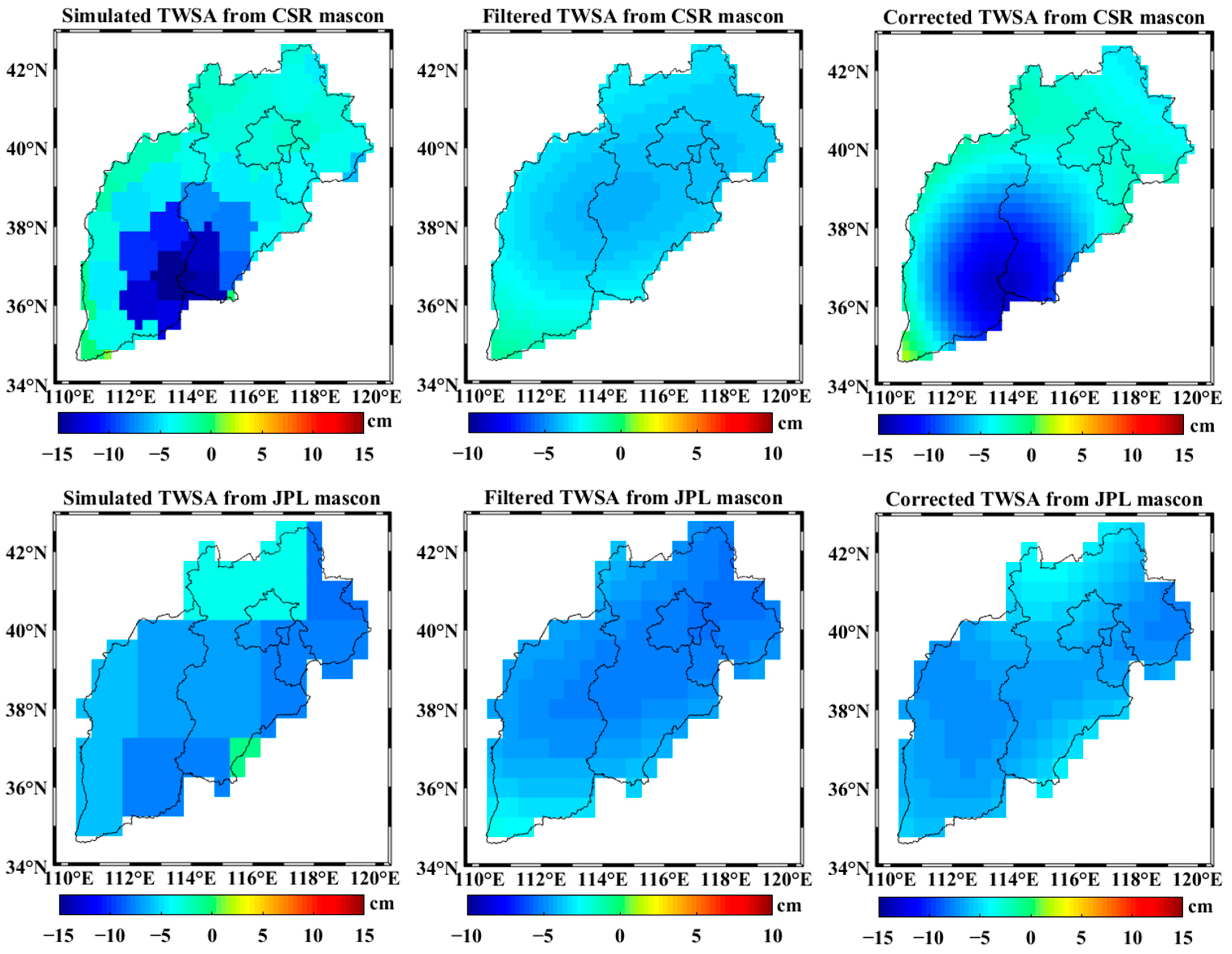
3.1.1. Applicability Test of Signal-Leakage-Correction Method in North China
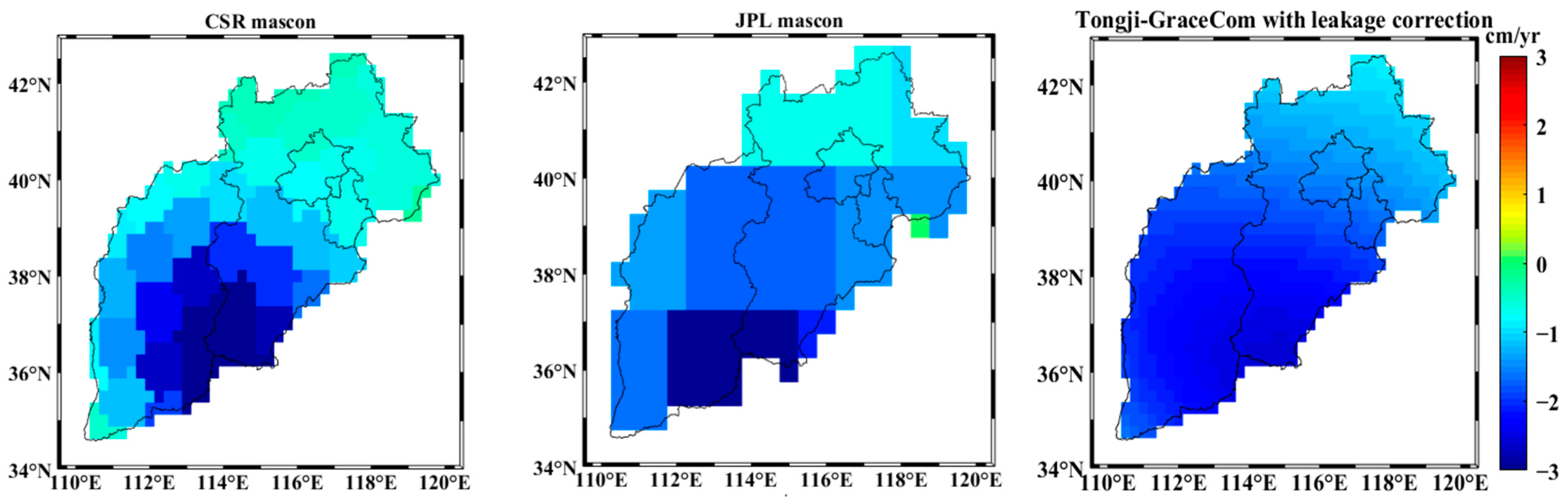
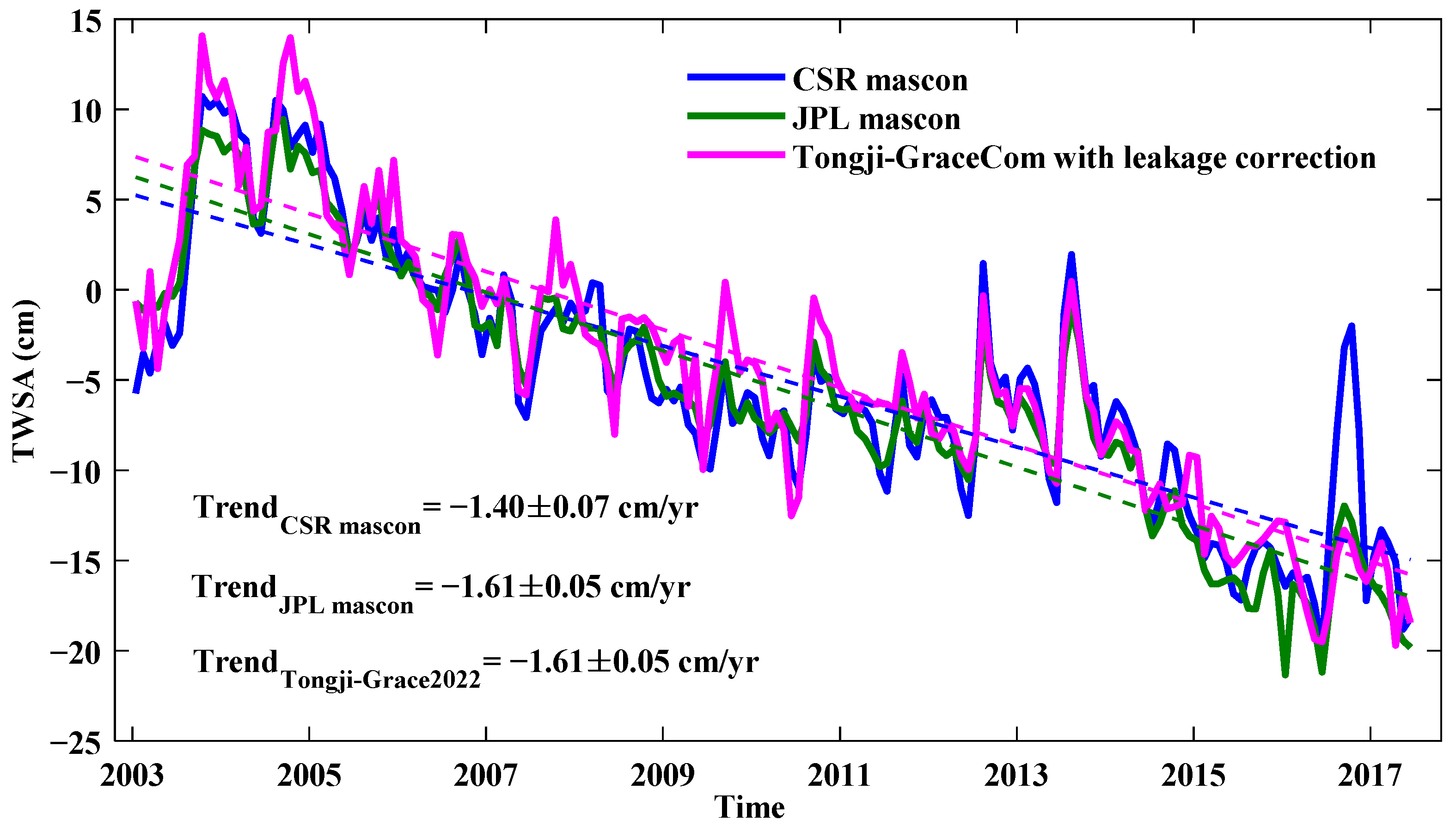
3.1.2. Spatiotemporal Pattern of TWSA in North China
3.2. Evaluation of TWF Based on the Water Budget Equation
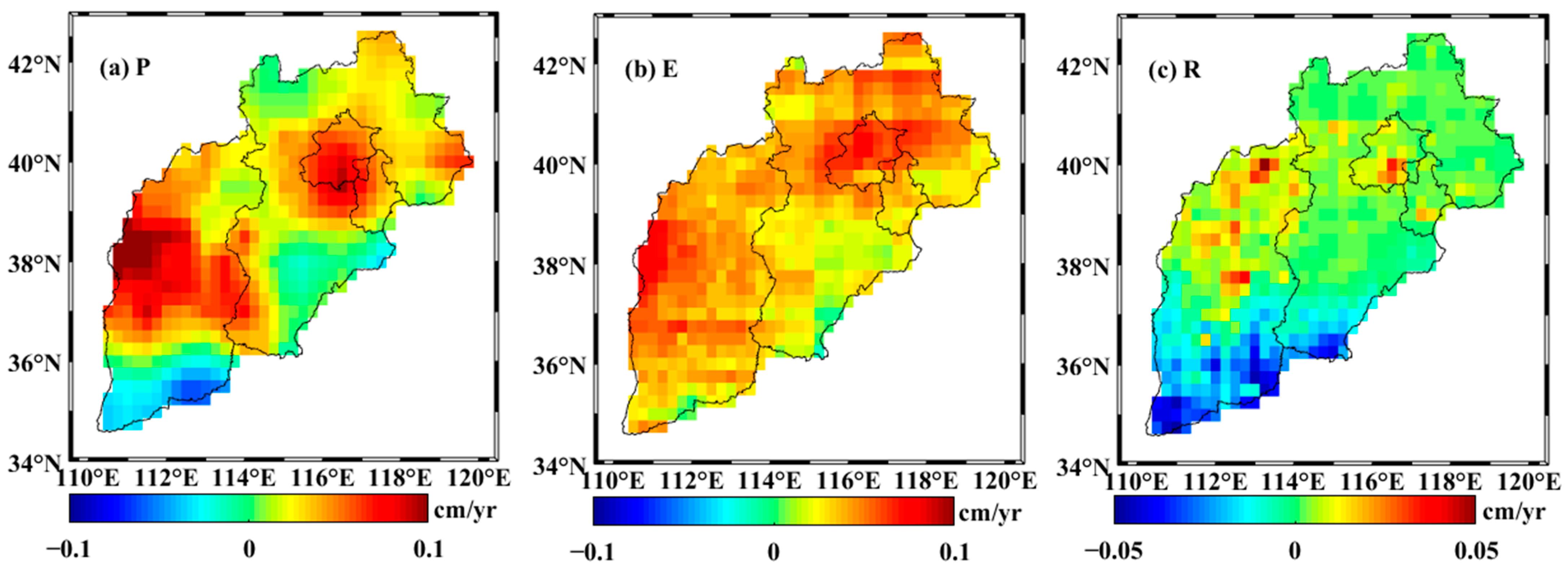
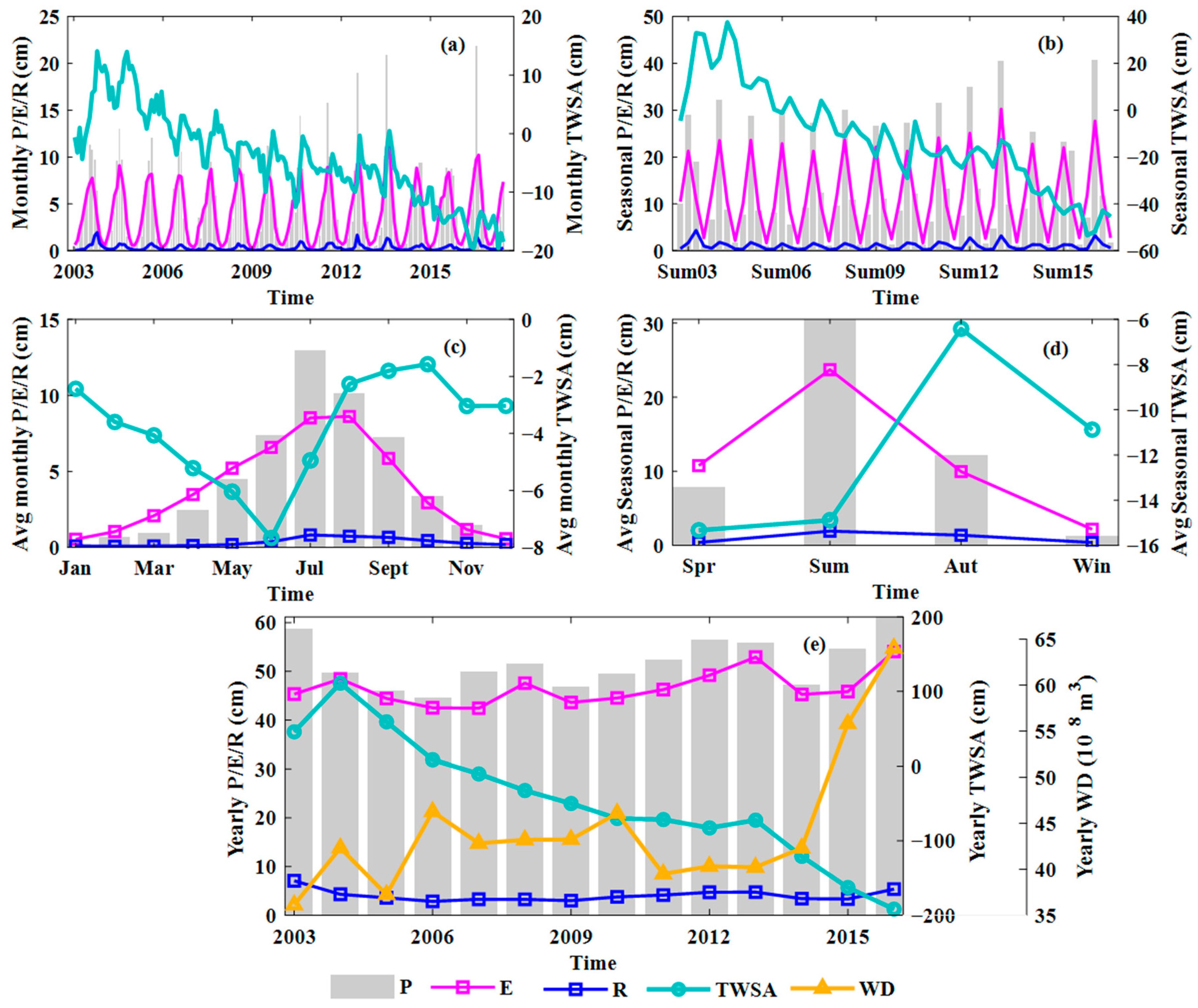
3.2.1. Budget Components
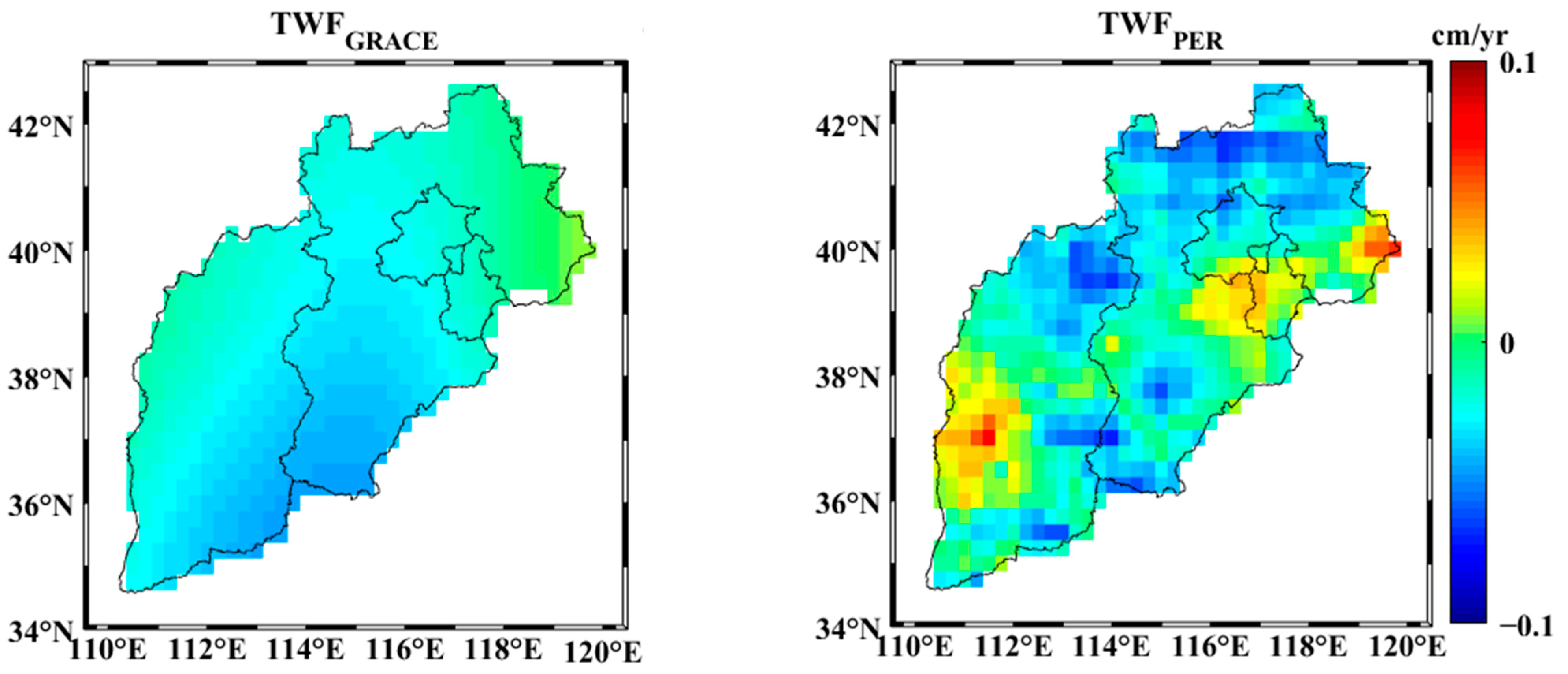
3.2.2. Spatiotemporal Pattern of TWF
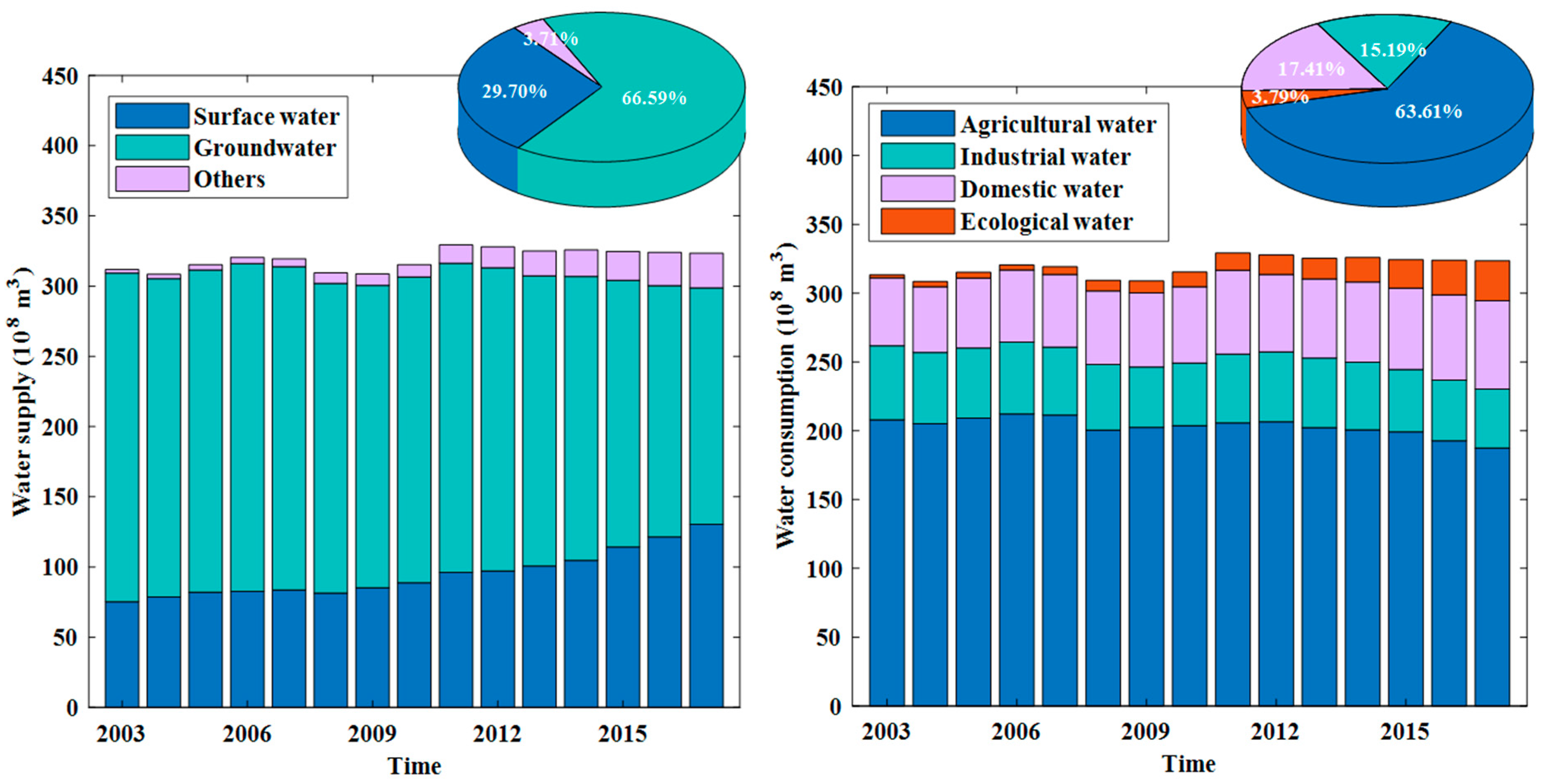
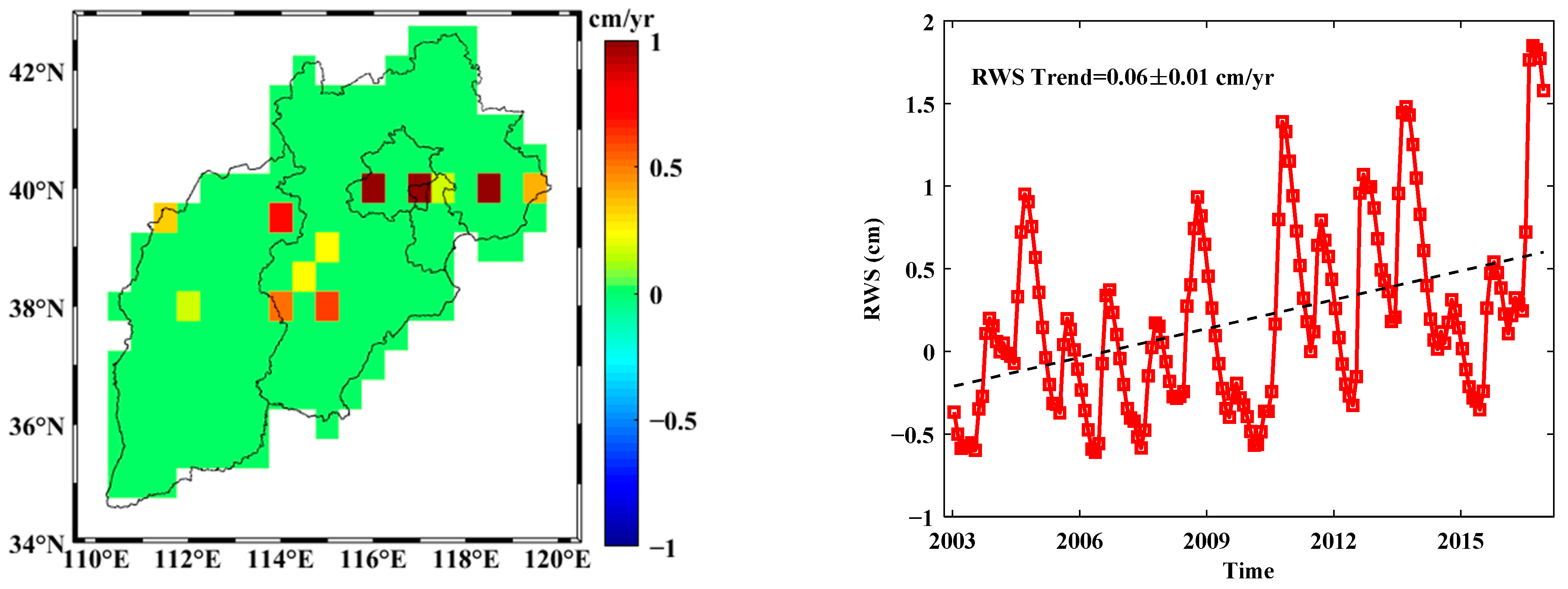
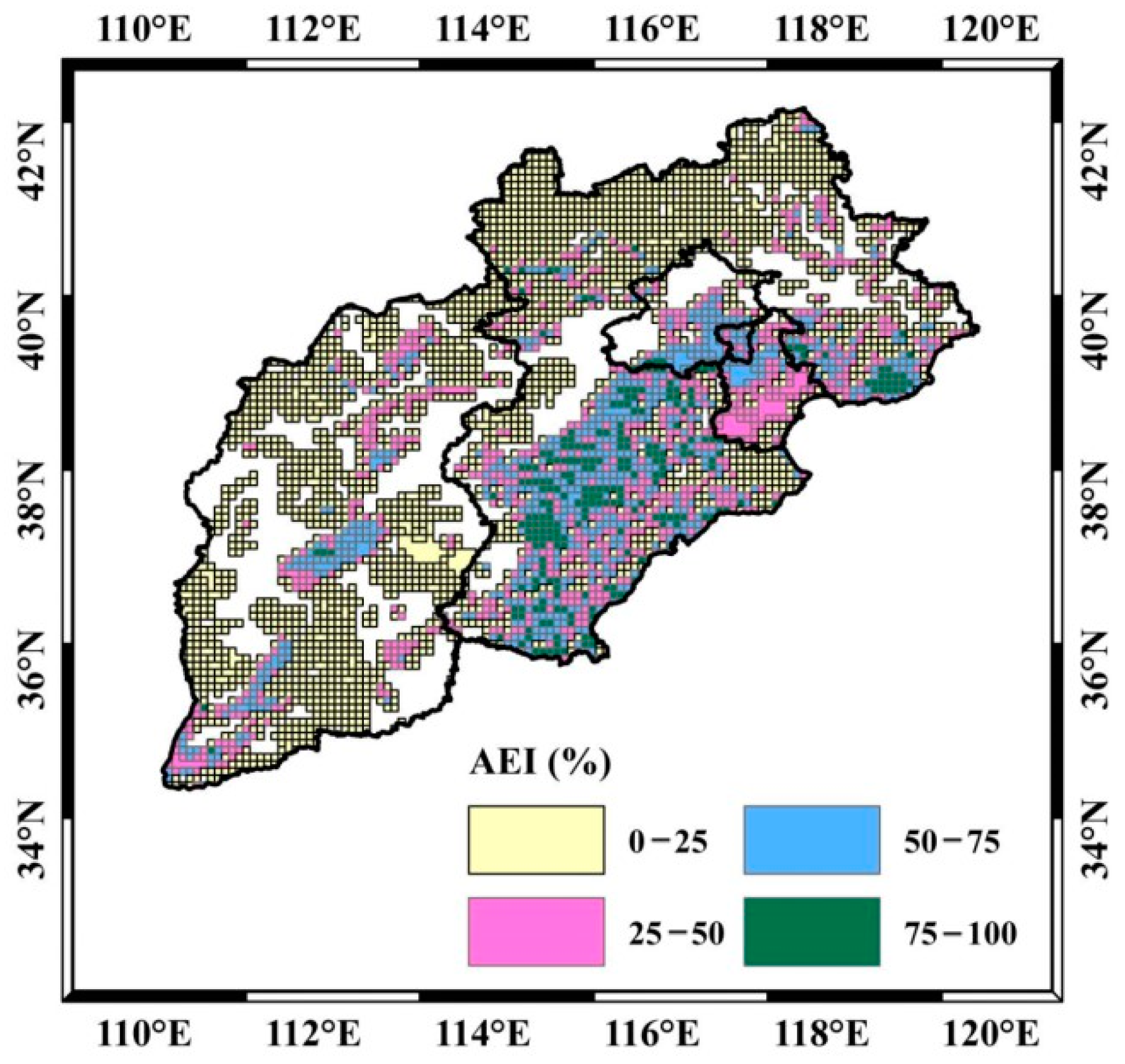
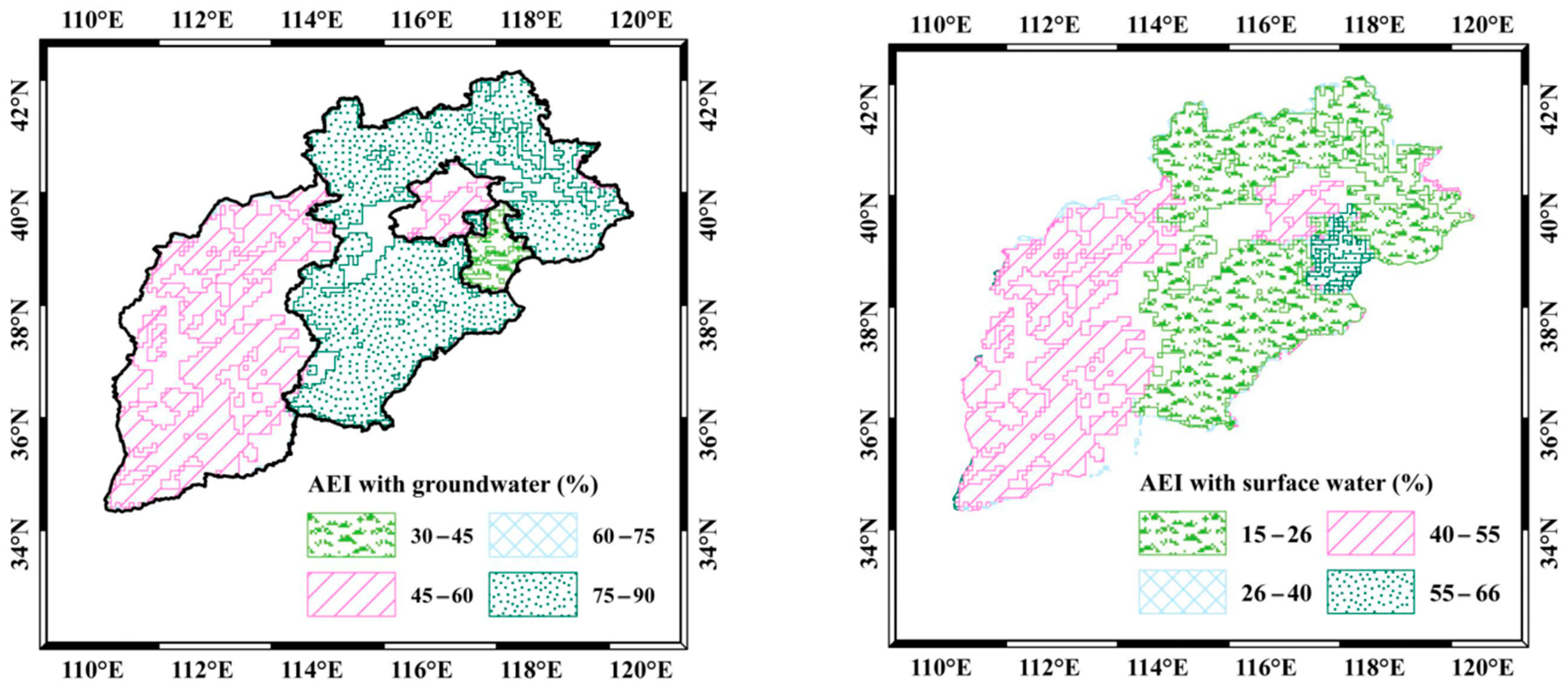
3.3. Attributions of Water Resources Depletion
4. Discussion
4.1. Comparison of TWSA and TWF Estimates with Previous Studies
4.2. Challenges for the Leakage-Correction Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moiwo, J.P.; Tao, F.; Lu, W. Analysis of satellite-based and in situ hydro-climatic data depicts water storage depletion in North China Region. Hydrol. Process. 2013, 27, 1011–1020. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the gravity recovery and climate experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Wang, L.; Chao, C.; Du, J.; Wang, T. Detecting seasonal and long-term vertical displacement in the North China Plain using GRACE and GPS. Hydrol. Earth Syst. Sci. 2017, 21, 2905–2922. [Google Scholar] [CrossRef]
- Qiu, J. China faces up to groundwater crisis. Nature 2010, 466, 308. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, B.R.; Fakhreddine, S.; Rateb, A.; De Graaf, I.; Famiglietti, J.; Gleeson, T.; Grafton, R.Q.; Jobbagy, E.; Kebede, S.; Kolusu, S.R.; et al. Global water resources and the role of groundwater in a resilient water future. Nat. Rev. Earth Environ. 2023, 4, 87–101. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, Z.; Cheng, G.; Li, W.; Li, T.; Jiao, J. Groundwater-derived land subsidence in the North China Plain. Environ. Earth Sci. 2015, 74, 1415–1427. [Google Scholar] [CrossRef]
- Liu, R.; Zou, R.; Li, J.; Zhang, C.; Zhao, B.; Zhang, Y. Vertical displacements driven by groundwater storage changes in the North China Plain detected by GPS observations. Remote Sens. 2018, 10, 259. [Google Scholar] [CrossRef]
- Willmott, C.J.; Rowe, C.M.; Mintz, Y. Climatology of the terrestrial seasonal water cycle. J. Climatol. 1985, 5, 589–606. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.; Chen, J.; Seneviratne, S.; Viterbo, P.; Holl, S.; Wilson, C. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31, L20504. [Google Scholar] [CrossRef]
- Sheffield, J.; Ferguson, C.R.; Troy, T.J.; Wood, E.F.; McCabe, M.F. Closing the terrestrial water budget from satellite remote sensing. Geophys. Res. Lett. 2009, 36, L07403. [Google Scholar] [CrossRef]
- Forootan, E.; Schumacher, M.; Mostafaie, A. Large-scale total water storage and water flux changes over the arid and semiarid parts of the Middle East from GRACE and reanalysis products. Surv. Geophys. 2017, 38, 591–615. [Google Scholar] [CrossRef]
- Zhang, C.; Long, D.; Zhang, Y.; Anderson, M.C.; Kustas, W.P.; Yang, Y. A decadal (2008–2017) daily evapotranspiration data set of 1 km spatial resolution and spatial completeness across the North China Plain using TSEB and data fusion. Remote Sens. Environ. 2021, 262, 112519. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Guntner, A.; Ngo-Duc, T.; Cazenave, A.; Laval, K. Time variations of the regional evapotranspiration rate from Gravity Recovery and Climate Experiment (GRACE) satellite gravimetry. Water Resour. Res. 2006, 42, W10403. [Google Scholar] [CrossRef]
- Mousavi, R.; Nasseri, M.; Abbasi, S.; Taheri, M.; Anboohi, M. Global gridded products efficiency in closing water balance models: Various modeling scenarios for behavioral assessments. Acta Geophys. 2022, 1–22. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Vargas Godoy, M.R.; Markonis, Y.; Hanel, M.; Kyselý, J.; Papalexiou, S.M. The global water cycle budget: A chronological review. Surv. Geophys. 2021, 42, 1075–1107. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Bates, P.; Sneeuw, N.; Westaway, R.; Bamber, J. Re-assessing global water storage trends from GRACE time series. Environ. Res. Lett. 2021, 16, 1–9. [Google Scholar] [CrossRef]
- Asoka, A.; Mishra, V. Anthropogenic and climate contributions on the changes in terrestrial water storage in India. J. Geophys. Res. Atmos. 2020, 125, e2020JD032470. [Google Scholar] [CrossRef]
- Xiong, J.; Yin, J.; Guo, S.; Slater, L. Continuity of terrestrial water storage variability and trends across mainland China monitored by the GRACE and GRACE-Follow on satellites. J. Hydrol. 2021, 599, 126308. [Google Scholar] [CrossRef]
- Feng, W.; Wang, C.; Mu, D.; Zhong, M.; Zhong, Y.L.; Xu, H.Z. Groundwater storage variations in the North China Plain from GRACE with spatial constraints. Chin. J. Geophys. 2017, 60, 1630–1642. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.F.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophs. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, C.; Gong, H.; Yeh, P.J.F.; Shen, Y.; Guo, Y.; Huang, Z.; Li, X. Detection of human-induced evapotranspiration using GRACE satellite observations in the Haihe River basin of China. Geophs. Res. Lett. 2017, 44, 190–199. [Google Scholar] [CrossRef]
- Long, D.; Yang, W.; Scanlon, B.R.; Zhao, J.; Liu, D.; Burek, P.; Pan, Y.; You, L.; Wada, Y. South-to-North water diversion stabilizing Beijing’s groundwater levels. Nat. Commun. 2020, 11, 3665. [Google Scholar] [CrossRef]
- Zhang, C.; Duan, Q.; Yeh, P.; Pan, Y. Sub-regional groundwater storage recovery in North China Plain after the South-to-North water diversion project. J. Hydrol. 2021, 597, 126156. [Google Scholar] [CrossRef]
- Pang, Y.; Wu, B.; Cao, Y.; Jia, X. Spatiotemporal changes in terrestrial water storage in the Beijing-Tianjin sandstorm source region from GRACE satellites. Int. Soil Water Conserv. Res. 2020, 8, 295–307. [Google Scholar] [CrossRef]
- Feng, T.; Shen, Y.; Chen, Q.; Wang, F.; Zhang, X. Groundwater storage change and driving factor analysis in North China using independent component decomposition. J. Hydrol. 2022, 609, 127708. [Google Scholar] [CrossRef]
- Feng, T.; Shen, Y.; Chen, Q.; Wang, F. Seasonal driving sources and hydrological-induced secular trend of the vertical displacement in North China. J. Hydrol. Reg. Stud. 2022, 41, 101091. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Z.; Shen, Y.; Chen, W.; Zhang, X. Tongji-Grace2022: New Global Temporal Earth’s Gravity Field Models Derived from K-Band and LRI Inter-Satellite Rang-Rate Data. In Proceedings of the 28th IUGG General Assembly, Berlin, Germany, 11–20 July 2023. [Google Scholar]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Wiese, D.N.; Landerer, F.W.; Luthcke, S.B. Replacing GRACE/GRACE-FO C30 with satellite laser ranging: Impacts on Antarctic Ice Sheet mass change. Geophs. Res. Lett. 2020, 47, e2019GL085488. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Comment on “An assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Blankenship, D.; Tapley, B.D. Accelerated Antarctic ice loss from satellite gravity measurements. Nat. Geosci. 2009, 2, 859–862. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Chen, W.; Zhang, X.; Hsu, H. An improved GRACE monthly gravity field solution by modelling the non-conservative acceleration and attitude observation errors. J. Geod. 2015, 90, 503–523. [Google Scholar] [CrossRef]
- Mu, D.; Yan, H.; Feng, W.; Peng, P. GRACE leakage error correction with regularization technique: Case studies in Greenland and Antarctica. Geophys. J. Int. 2017, 208, 1775–1786. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Zhong, Y.; Feng, W.; Humphrey, V.; Zhong, M. Human-induced and climate-driven contributions to water storage variations in the Haihe River Basin, China. Remote Sens. 2019, 11, 3050. [Google Scholar] [CrossRef]
- Feng, T.; Shen, Y.; Wang, F.; Chen, Q.; Ji, K. Spatiotemporal variability and driving factors of the shallow soil moisture in North China during the past 31 years. J. Hydrol. 2023, 619, 129331. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.G.; Lievens, H. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, F. Abrupt change of runoff and its major driving factors in Haihe River Catchment, China. J. Hydrol. 2009, 374, 373–383. [Google Scholar] [CrossRef]
- Schmied, H.M.; Cáceres, D.; Eisner, S.; Flrke, M.; Doell, P. The global water resources and use model WaterGAP v2.2d: Model description and evaluation. Geosci. Model Dev. 2020, 14, 1037–1079. [Google Scholar] [CrossRef]
- Siebert, S.; Döll, P.; Hoogeveen, J.; Faures, J.M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- Tang, J.; Cheng, H.; Liu, L. Using nonlinear programming to correct leakage and estimate mass change from GRACE observation and its application to Antarctica. J. Geophys. Res. Solid Earth 2012, 117, B11410. [Google Scholar] [CrossRef]
- Yi, S.; Sun, W. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models. J. Geophys. Res. Solid Earth 2014, 119, 2504–2517. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Regularization of ill-posed problems. Dokl. Akad. Nauk SSSR 1963, 151, 49–52. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, P.; Li, B. Bias-corrected regularized solution to inverse ill-posed models. J. Geod. 2012, 86, 597–608. [Google Scholar] [CrossRef]
- Deus, D.; Gloaguen, R.; Krause, P. Water balance modeling in a semi-arid environment with limited in situ data using remote sensing in Lake Manyara, East African Rift, Tanzania. Remote Sens. 2013, 5, 1651–1680. [Google Scholar] [CrossRef]
- Li, Q.; Liu, X.; Zhong, Y.; Wang, M.; Zhu, S. Estimation of Terrestrial water storage changes at small basin scales based on multi-source data. Remote Sens. 2021, 13, 3304. [Google Scholar] [CrossRef]
- Sun, A.Y.; Green, R.; Rodell, M.; Swenson, S. Inferring aquifer storage parameters using satellite and in situ measurements: Estimation under uncertainty. Geophs. Res. Lett. 2010, 37, L10401. [Google Scholar] [CrossRef]
- Tian, L.; Zhang, B.; Chen, S.; Wang, X.; Ma, X.; Pan, B. Large-scale afforestation enhances precipitation by intensifying the atmospheric water cycle over the Chinese Loess Plateau. J. Geophys. Res. Atmos. 2022, 127, e2022JD036738. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Z.; Li, J.; Liu, J.; Wu, G. How to measure the strength of the east Asian summer monsoon. J. Clim. 2008, 21, 4449–4463. [Google Scholar] [CrossRef]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraër, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar] [CrossRef]
- Zhong, Y.; Bai, H.; Feng, W.; Lu, J.; Humphrey, V. Separating the precipitation- and non-precipitation driven water storage trends in China. Water Resour. Res. 2023, 59, e2022WR033261. [Google Scholar] [CrossRef]
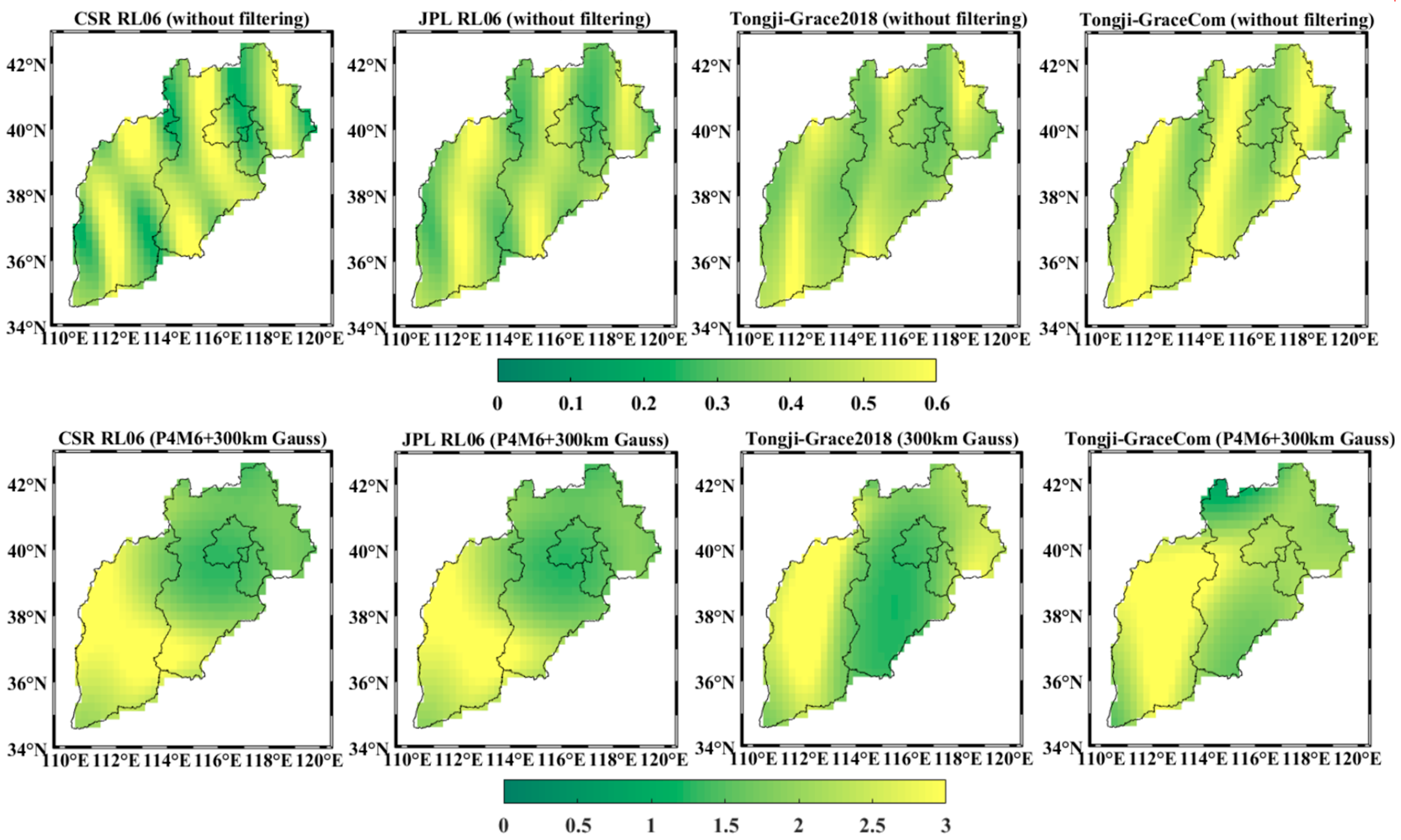

| Models | Mean SNR | |
|---|---|---|
| Without Filtering | Filtered with P4M6 and 300 km Gaussian Smoothing | |
| CSR RL06 | 0.44 | 2.14 |
| JPL RL06 | 0.42 | 2.11 |
| Tongji-Grace2018 | 0.43 | 2.14 |
| Tongji-GraceCom | 0.50 | 2.37 |
| Model | Simulated Mass | Filtered Mass | Corrected Mass |
|---|---|---|---|
| CSR mascon | −22.04 | −13.14 | −21.18 |
| JPL mascon | −25.72 | −19.14 | −25.82 |
| Region | Area (km2) | Period | GRACE Model | Trend (cm/yr) | Reference |
|---|---|---|---|---|---|
| North China | 3.7 × 105 | 2003–2017 | Tongji-GraceCom | −1.61 ± 0.05 | This work |
| North China | 3.7 × 105 | 2003–2012 | CSR RL05 SH | −1.23 ± 0.23 | Wang et al. [3] |
| North China | 3.7 × 105 | 2004–2015 | Tongji-Grace2019 | −1.00 ± 0.06 | Feng et al. [28] |
| Haihe River Basin | 3.2 × 105 | 2005–2012 | RL05 SH of CSR, GFZ, JPL | −1.27 ± 1.4 | Pan et al. [24] |
| Haihe River Basin | 3.2 × 105 | 2003–2013 | CSR mascon | −0.86 ± 0.08 | Zhong et al. [39] |
| North China Plain | 1.4 × 105 | 2003–2018 | JPL mascon | −2.61 | Zhang et al. [26] |
| North China | 2.1 × 106 | 2002–2009 | CSR RL04 | −1.68 | Moiwo et al. [1] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, T.; Shen, Y.; Chen, Q.; Wang, F.; Ji, K. Evaluation of Terrestrial Water Storage and Flux in North China by Using GRACE Combined Gravity Field Solutions and Hydrometeorological Models. Remote Sens. 2023, 15, 2536. https://doi.org/10.3390/rs15102536
Feng T, Shen Y, Chen Q, Wang F, Ji K. Evaluation of Terrestrial Water Storage and Flux in North China by Using GRACE Combined Gravity Field Solutions and Hydrometeorological Models. Remote Sensing. 2023; 15(10):2536. https://doi.org/10.3390/rs15102536
Chicago/Turabian StyleFeng, Tengfei, Yunzhong Shen, Qiujie Chen, Fengwei Wang, and Kunpu Ji. 2023. "Evaluation of Terrestrial Water Storage and Flux in North China by Using GRACE Combined Gravity Field Solutions and Hydrometeorological Models" Remote Sensing 15, no. 10: 2536. https://doi.org/10.3390/rs15102536
APA StyleFeng, T., Shen, Y., Chen, Q., Wang, F., & Ji, K. (2023). Evaluation of Terrestrial Water Storage and Flux in North China by Using GRACE Combined Gravity Field Solutions and Hydrometeorological Models. Remote Sensing, 15(10), 2536. https://doi.org/10.3390/rs15102536