Abstract
Floods have always threatened the survival and development of human beings. To reduce the adverse effects of floods, it is very important to understand the influencing factors of floods and their formation mechanisms. In our study, we integrated the Gravity Recovery and Climate Experiment and its Follow-On and Swarm solutions to estimate an uninterrupted 19-year flood potential index (FPI) time series, discussed the spatiotemporal distribution characteristics of the FPI and monitored major floods in the Volga River basin (VRB) from 2003 to 2021. Finally, we analyzed the relationship between the FPI and hydrometeorological factors to comprehend the flood formation mechanism. The results show that data fusion has reduced the uncertainty of terrestrial water storage change (TWSC), and the TWSC from the combined satellite gravity observations has a good consistency with that from the Global Land Data Assimilation System model (correlation coefficient = 0.92). During the study period, two major floods (June 2005 and May 2018) occurred in the VRB. The FPI has a significant seasonal change characteristic, and shows a high flood risk in spring and a low one in autumn. With regards to spatial distribution, the flood risk is increasing in the north (increasing rate = 0.1) and decreasing in the south (decreasing rate = 0.39). Snow water equivalent (SWE, correlation coefficient = 0.75) has a stronger correlation with the FPI than precipitation (PPT, correlation coefficient = 0.46), which is attributed to the recharge of SWE on water resources greater than that of PPT. The rising surface temperature (ST) speeds up snow melt, resulting in excessive groundwater and soil moisture, and the flood risk greatly increases at this time. The process lasts about three months. Therefore, except for PPT, ST is also a climatic factor leading to the floods in the VRB. Our study provides a reference for flood research in high-latitude regions.
1. Introduction
Floods are a natural disaster with great destructive power, which bring property loss, casualties and ecological disasters [1,2]. With the increasing frequency of human activities, carbon dioxide in the atmosphere is rising, resulting in the continuous increase of the global temperature and the frequent occurrence of extreme disasters [3,4]. The sixth assessment report of the Intergovernment Panel on Climate Change indicated that the global surface temperature increased by 0.99 °C during 2001 and 2020 compared with 1850–1900, and it is expected to rise by 1.5 °C or more in 2021–2040 [5]. According to the Global Disaster Database, a total of 3302 floods occurred worldwide from 2001 to 2020, an increase of 199% compared with 1981 to 2000. Current forecast results based on climate models show that the severity and frequency of global floods tend to increase against the background of climate warming [6,7,8]. Therefore, it is of great significance for regional flood risk assessment to understand flood formation mechanisms and realize the early warning of floods.
Many scholars have studied floods and their causes [9,10,11]. Dahri et al. [12] indicated that the flood risk depends not only on precipitation (PPT) intensity, but also on land use, urban development and other anthropogenic settings. Groundwater (GW) is also an important factor affecting floods [13]. In Pakistan, heavy PPT and snow and glacier melt are the main factors causing the summer floods [14]. SM also has a certain impact on floods. Zhong et al. [15] pointed out that the combined effect of PPT and SM caused the floods in Arizona, United States. However, the studies on floods were mainly based on ground station and satellite remote sensing in previous studies. Although ground stations can provide direct and timely hydrometeorological observations, their sparse and uneven distribution make it difficult to plot a complete spatial distribution map of floods [16]. Although satellite remote sensing technology can achieve all-weather and full-coverage continuous observation, it cannot directly monitor PPT, evapotranspiration (ET), runoff, lake water, etc. [17,18,19]. Therefore, there are great uncertainties in the flood studies using satellite remote sensing.
The appearance of the Gravity Recovery and Climate Experiment (GRACE) and its Follow-On (GRACE-FO) missions have brought a revolutionary approach to detecting global or regional terrestrial water storage change (TWSC), whose components include surface and root zone SM, snow, ice, lake water, GW, etc. [20,21]. Therefore, GRACE TWSC data have an incomparable advantage in detecting large-scale floods [22]. Several scholars have applied GRACE TWSC to detect floods in multiple regions, for example, Europe [23], the Yangtze River basin [24,25], the Nile River basin [26], the Niger River basin [27], and the Liao River basin [28]. However, the GRACE and GRACE-FO missions have an 11-month data gap period, which led to the interruption of observations and bring great inconvenience to flood research [29,30]. Due to the fact that the mission period of Swarm satellites exactly covers this gap, some scholars have tried to join GRACE, Swarm and GRACE-FO observations for terrestrial hydrological research. Cui et al. [31] integrated GRACE, Swarm and GRACE-FO observations to monitor the droughts over the Amazon River basin from 2003 to 2020. The study results have been validated by previous studies. Zhang et al. [32] calculated the long-term change trend of the ice sheet in West Antarctica during 2003 and 2020 by combining GRACE, Swarm and GRACE-FO solutions. The results show that the ice sheet mass in West Antarctica maintained a rapid ablation trend (161.5 ± 48.4 Gt/a) during the GRACE intermission data gap.
The flood potential index (FPI) is an index that can quantitatively evaluate the difference between regional incoming water and local maximum water storage, and realize the evaluation of flood risk by measuring this difference. Reager et al. [33] firstly defined the FPI in 2009 and validated its reliability on a global scale. Subsequently, many scholars have applied the FPI to flood detection around the world. Molodtsova et al. [34] found that the FPI has good agreement with local flood observations in the continental United States. Sun et al. [35] used the three GRACE solutions to estimate the FPI, and applied the FPI to monitor the floods in the Yangtze River basin from 2003 to 2014. The FPI successfully caught the signal of the 2010 catastrophic flood, and PPT and runoff were 37.95% and 19.44% higher than normal averages, respectively. The flood-monitoring capabilities of the FPI have also been validated in the Mississippi River basin and Peninsular Indian River basins [36,37]. The FPI has become a powerful tool for monitoring large-scale regional floods. The FPI has more advantages in monitoring large floods than small and medium floods [38]. Gupta et al. [37] applied the FPI to flood monitoring in the Peninsular Indian River basins. Xiong et al. [39] used the FPI to detect three severe floods in 2010, 2015 and 2016 in the Yangtze River basin. However, the above study only used GRACE solutions, so the time span is only around 16 years. For hydrological research, the longer the observation time series is, the higher are the reliability of the results.
The Volga River is situated in southwestern Russia, with a total length of 3692 km, and is the longest inland river with the widest basin in the world [40]. Since records began, there have been 20 floods in the Volga River basin (VRB) (the water level was 11–13 m higher than the average water level in many years) [41]. The floods mainly occurred in spring in the VRB, and brought great suffering to the people along the bank [42]. However, as far as we know, there is very little literature on floods in the VRB. Therefore, it is necessary to study the floods in the VRB. To construct a long-term continuous observation time series, we combined GRACE, Swarm and GRACE-FO solutions to estimate the FPI time series for 19 consecutive years for the first time, and applied the FPI results to study the extreme floods in the VRB, and, finally, discussed the formation mechanism of extreme floods.
2. Study Areas
The VRB (Figure 1), approximately at 45–61°N and 32–60°E, covers an area of 1.38 million km2, and extends from the Valdai Hills and Central Russian Highlands in the west to the Ural Mountains in the east, and narrows abruptly in the south at Saratov. In the VRB, the crystalline rock base is completely covered by sedimentary rocks, and the lowlands, with an altitude below 200 m in the basin, account for about 65%, and the hills account for 25%. The average annual discharge of the estuary is about 8000 m3/s, and the annual runoff is 254 billion m3 [43]. The VRB is mainly affected by the continental climate, and is cold and snowy in winters and warm and humid in summers. The upper, middle and right bank of the lower reaches have a forest climate, the left bank of the lower reaches has a steppe climate and semi-desert climate, and the Caspian Sea lowland has a desert climate [40]. Annual PPT is 635 mm in the northwest and 305 mm in the southeast. The temperature is the highest and PPT is the largest in July in the west of the VRB. The average monthly temperature in winter in the east of the basin is much lower than in the western region, while the summer temperature is higher.

Figure 1.
The topographic map of the VRB.
3. Data and Methods
3.1. Data
3.1.1. GRACE/GRACE-FO Data
In this study, GRACE/GRACE-FO spherical harmonic (SH) solutions were applied to estimate monthly 1° × 1° TWSC gridded data from 2003 to 2021 based on the SH coefficient method. The specific expression is [44]:
where and are the co-latitude and longitude of the calculation point, respectively; is the Earth’s mean radius; is the Earth’s mean density; is the water density; and are degree and order, respectively; is the normalized Legendre function; is the Love number; and and are the variations of the SH coefficient.
GRACE/GRACE-FO SH solutions were from the Center for Space Research at the University of Texas at Austin (CSR), the Helmholtz-Centre Potsdam-German Research Centre for Geosciences (GFZ), Jet Propulsion Laboratory (JPL) and Institute of Geodesy at Graz University of Technology (ITSG). We performed a series of preprocessing work on SH solutions to reduce the uncertainty of TWSC, such as coefficient replacement, filtering, scale restoration and ice rebound correction [45]. In addition, Mascon solutions, from CSR and JPL, can directly provide TWSC data without any data processing. Due to the poor quality of GRACE/GRACE-FO observations in some months, the corresponding months of observations are missing. To ensure the continuity of GRACE/GRACE-FO observations, our study used the cubic spline interpolation approach to fill the missing months’ data. GRACE/GRACE-FO are abbreviated as GRACE, and the four SH and two Mascon solutions are abbreviated as CSR-SH, GFZ-SH, JPL-SH, ITSG-SH, CSR-M and JPL-M.
3.1.2. Swarm Solution
The Swarm SH solution was provided by the International Combination Service for Time-variable Gravity (COST-G), which was used to estimate the monthly TWSC gridded data with a spatial resolution 1° × 1° in the VRB from 2014 to 2021 based on the SH coefficient method. The calculation method and data preprocessing process are basically the same as GRACE, only the filter setting is different. GRACE uses a 300 km Gaussian filter and Swarm uses a 1000 km Fan filter [26]. The Swarm SH solution is a combination solution estimated using variance component estimation, fusing four solutions provided by the Astronomical Institute at the Czech Academy of Sciences, the University of Bern, the Institute of Geodesy at the Graz University of Technology and Ohio State University [46].
3.1.3. PPT Data
The monthly 0.5° × 0.5° PPT gridded data during 1979 and 2021 can be extracted from the Global Land Surface Reanalysis Products (CMA-RA/Land) provided by the China Meteorological Administration. The data were estimated by the set assimilation approach, data fusion and the surface parameter optimization algorithm [47]. In our study, the PPT gridded data are from 2003 to 2021.
3.1.4. ET Data
The 0.25° × 0.25° monthly ET gridded data from 2003 to 2021 were from the Global Land Evaporation Amsterdam Model (GLEAM) 3.7a [48]. The surface net radiation and near-surface air temperature observations were applied to calculate the potential evaporation, then the potential evaporation results of bare soil and canopy were transformed into actual ET based on a multiplicative evaporative stress factor according to microwave vegetative optical depth and root-zone SM observations [49]. ET gridded data can be read directly from the A model without any processing. In this study, we resampled the ET data to ensure the same spatial resolution as the TWSC data.
3.1.5. Other Hydrometeorological Data
The monthly SM and GW gridded data with a spatial resolution 0.25° × 0.25° during 2003 and 2021 were provided by the Global Land Data Assimilation System (GLDAS) 2.1 model. The GLDAS 2.1 model was from the National Centers for Environmental Prediction at the National Oceanic and Atmospheric and the Goddard Space Flight Center at National Aeronautics and Space Administration. The SM is the sum of four layers of SM (0–0.1 m, 0.1–0.4 m, 0.4–1.0 m and 1.0–2.0 m), and the GW data were estimated by subtracting SM, canopy water and snow water equivalent (SWE) from terrestrial water storage [50].
The monthly 0.5° × 0.5° runoff, SWE and surface temperature (ST) gridded data from 2003 to 2021 were collected from the CMA-RA/Land to study the causes of floods in the VRB. The same as ET, we resampled SM, GW and SWE data to ensure the consistency of the spatial resolution of the data.
3.2. Method
3.2.1. Data Fusion
Discrepancies in the methods and mathematical models used by different institutions when processing GRACE data lead to a discrepancy between TWSCs estimated by different GRACE solutions. This discrepancy can cause inaccuracy in our results. The uncertainty is an indicator used to measure the degree of this inaccuracy. A small uncertainty means high accuracy, and vice versa. To reduce the uncertainty of our study, the TWSCs from six GRACE solutions were fused. First of all, we calculated the uncertainties of six TWSCs using the generalized three-cornered hat method. Then, the weight of each TWSC was determined based on the uncertainties results. Finally, the six TWSCs were integrated using the least square approach. The technical details can be found in Refs. [51,52].
3.2.2. FPI Calculation
GRACE TWSC and PPT data were used to estimate the FPI. The expression is as follow [39]:
where is the discrepancy between incoming water and the maximum water storage of the ith year and jth month, which is the flood amount. A larger FPA means a higher probability of flood occurrence and greater flood severity. is the PPT of the ith year and jth month. and are the maximum value of the TWSC in the study period and the TWSC of the previous month. The FPA was normalized to calculate the FPI, and the expression is as follows:
where represents the maximum FPA during the study period. The FPI cannot be greater than 1, and the closer the FPI is to 1, the higher the probability of floods. In our study, the major floods occurred in the VRB when the FPI was greater than 0 [35].
3.2.3. Time Series Analysis
The observations time series contains information on the different time scales, such as the long-term change trend, acceleration, and annual and semi-annual changes. The extraction methods of different time scale components are as follows [53,54]:
where represents the TWSC time series; and represents the time and the residual signal, respectively; , , , , and represent the parameters to be requested; represents a constant, represents the long-term change trend, and represent annual changes; and and represent semi-annual changes.
3.2.4. Partial Least Square Regression Model (PLSR)
Under the condition that there is a correlation between different independent variables, the PLSR can accurately estimate the relationship between dependent and multiple independent variables [55]. In this study, we take the FPI as the dependent variable and PPT, ET, SM, runoff and GW data as the independent variables. The variable importance of projection (VIP) can quantify the correlation between the FPI and different hydrometeorological factors in the PLSR. If the VIP is larger than 0.8, it means the hydrometeorological factor has a significant impact on the FPI [56]. The specific expression of the VIP is as follows [57]:
where n is the number of hydrometeorological factors, is the VIP value of the jth hydrometeorological factor, represents the m principal components of Y, Y represents the FPI, represents the weight of each element in the matrix after the matrix X is standardized, X represents a matrix composed of the observations of n hydrometeorological factors, and and are the correlation coefficients between Y and , respectively.
3.2.5. Correlation Coefficient and Delay Months
Assuming and are the two independent observation time series, their correlation coefficient is expressed as [58]:
where and represents correlation coefficient and delay months, respectively, and are the variance of and , respectively, and is the covariance of and . When reaches the maximum (), is the corresponding delay months ().
4. Results
4.1. Construction of Combined TWSC Observation
Due to the different mathematical models and calculation approaches, the GRACE solutions provided by different institutions have some discrepancies, which increase the uncertainty of our results. To reduce the uncertainty, six TWSCs from GRACE solutions were fused. Figure 2 shows that the same peaks, troughs and change trend appear in the seven time series. The fused TWSC and six single solutions have a strong correlation (all the correlation coefficients are larger than 0.94). This shows that the fused TWSC has a good consistency with the six single solution results. The uncertainty level of the fused result (0.76 cm) has been significantly reduced, and is smaller than the uncertainty level of any single solution (CSR-SH, 1.58 cm; GFZ-SH, 3.35 cm; JPL-SH, 1.51 cm; ITSG-SH, 1.68 cm; CSR-M, 2.43 cm; JPL-M, 2.27 cm). Therefore, we used the fused TWSC as the GRACE TWSC in the follow-up research.
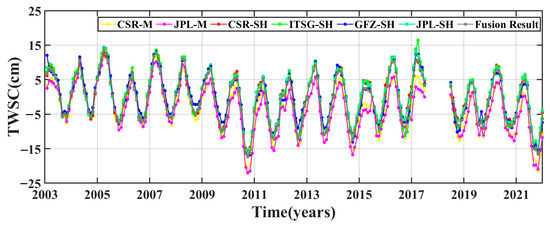
Figure 2.
The TWSC time series from six GRACE solutions and the fused result in the VRB from 2003 to 2021.
From Figure 2, we found that the GRACE TWSCs have a period of data gap (from July 2017 to May 2018). In this study, we applied the Swarm TWSC to fill the gap. The time series of GRACE and Swarm TWSCs in the VRB were compared from 2014 to 2021 (Figure 3). These two TWSCs have the same peaks and troughs (Figure 3a) and a strong correlation (Figure 3b). Table 1 shows that the two TWSCs show a decreasing trend in the VRB, and their annual amplitudes and annual phases are very close. The long-term change trend of the Swarm TWSC is smaller than the one of GRACE, which is due to the larger error and low spatial resolution of the Swarm solution. Overall, the Swarm TWSC has almost the same performance as the GRACE one in the VRB.
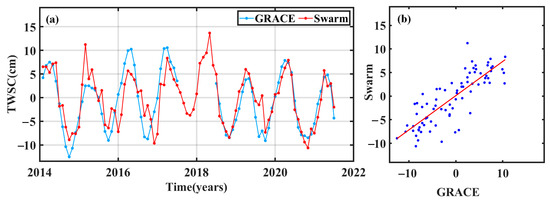
Figure 3.
The GRACE and Swarm TWSC time series (a) and scatter plots (b) in the VRB from 2014 to 2021.

Table 1.
Long-term changes trend and seasonal variation of GRACE and Swarm TWSCs in the VRB.
Figure 4 shows the two spatial distribution maps of uncertainties of the GRACE and Swarm TWSCs. The GRACE TWSC has smaller uncertainties than the Swarm one. The uncertainties of the GRACE TWSC are smaller than 0.6 cm in most regions, and are higher only in the delta (the maximum is 1.8 cm). The uncertainties of the Swarm TWSC are greater than 0.9 cm, and the central and delta regions have the largest uncertainties (2.1~2.7 cm), while the uncertainties in Northwest and Southeast are smaller (0.9~1.2 cm).
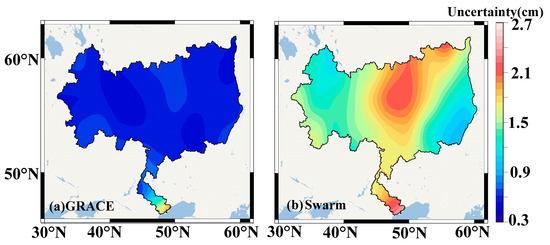
Figure 4.
The spatial distribution of uncertainties of the GRACE and Swarm TWSCs during 2014 and 2021.
In view of the good performance of the Swarm TWSC, we combined the GRACE and Swarm TWSCs to form the complete TWSC observations (GRACE/Swarm TWSC) for 19 consecutive years in the VRB. We used the GLDAS TWSC to evaluate the quality of the GRACE/Swarm one (Figure 5). The GRACE/Swarm and GLDAS TWSCs have the same peaks and troughs (Figure 5a), and their correlation coefficient reaches 0.92 (Figure 5b). Table 2 shows that their long-term trend changes are negative and numerically close, and their annual phases are also almost the same. Although their annual amplitudes are positive, they are numerically different. This is because the GLDAS TWSC is the sum of SM, SWE and plant canopy water, and it does not include groundwater, lake water, reservoir storage, etc. The GRACE TWSC includes all the terrestrial water components. Therefore, these TWSCs have a numerical difference. Overall, the GRACE/Swarm TWSC has a good performance compared with the GLDAS one in the VRB.
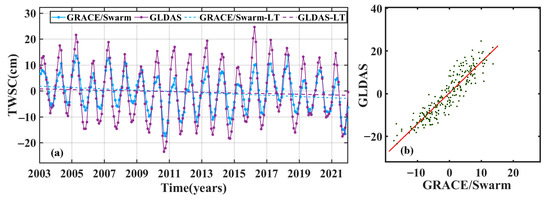
Figure 5.
The GRACE/Swarm and GLDAS TWSCs (a) and comparison scatter plots (b) in the VRB from 2003 to 2021.

Table 2.
Long-term change trend and seasonal variation of the GRACE/Swarm and GLDAS TWSCs in the VRB.
4.2. Spatial and Temporal Characteristics of the FPI
Figure 6 shows that the time series of TWSC, PPT and the FPI have a significant periodicity. TWSC and the FPI have similar peaks and troughs, and the FPI has a one-month delay relative to TWSC. And the long-term change trends of TWSC and the FPI show decreasing trends, which are −2.48 ± 1.57 mm/a and −0.10 ± 0.14, respectively. However, the long-term change trend of PPT is 0.18 ± 0.45 mm, and the fluctuation range of TWSC (−17~14 cm) is about twice that of PPT (−4~6 cm). This demonstrates that PPT is not the main reason for TWSC and FPI changes. Oltchev et al. [59] indicate that PPT accounts for only 17% of the water resources in the VRB. According to the definition of the FPI, two extreme floods (June 2005 and May 2018) occurred in the VRB during the study period, which have been verified [60,61].
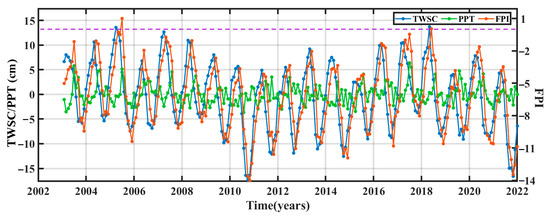
Figure 6.
The time series of TWSC, PPT and the FPI in the VRB during 2003 and 2021. Purple dotted line: FPI = 0.
We plotted the seasonal distribution map of the FPI, TWSC and PPT in the VRB (Figure 7). Figure 7a shows that spring is the season most prone to floods, and two extreme floods occurred in the VRB during 2003 and 2021 (dark red regions, FPI greater than 0). The seasonal distribution of PPT is the same as that of the FPI (Figure 7a,b). The positive TWSCs mainly are concentrated in spring and winter, while the negative ones are mainly concentrated in summer and autumn. Figure 7c reveals that the most concentrated time of PPT is mainly at the turn of spring and summer. The maximum PPT (6 cm) appeared in June 2018, which is consistent with the 2018 major flood defined by the FPI. This suggests that PPT may be the main cause of the 2018 major flood.
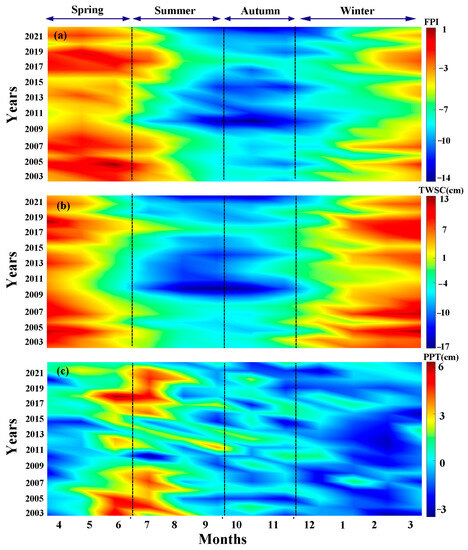
Figure 7.
The seasonal variance of TWSC, PPT and the FPI in the VRB during 2003 and 2021. (a) FPI; (b) TWSC; (c) PPT.
From Figure 8, TWSC and the FPI have the same spatial distribution of long-term change trends, that is, the north is dominated by growth, and the south is dominated by decline. The maximum increasing rates of TWSC (0.4 cm/a) and the FPI (0.2) occur in the north, while the maximum decreasing rates (−0.4 cm/a and −0.6) appear in the delta region. This demonstrates that the flood risk is increasing in the north and decreasing in the south. This change trend of flood risk is consistent with that of TWSC, which indicates that the TWSC changes the local maximum water storage capacity, and leads to the changes in the size of PPT that can be accommodated. The spatial distribution of the long-term change trend of PPT is different, that is, a decrease in the north and an increase in the south. The maximum increasing rate (1.5 mm/a) appears in the south, and the maximum decreasing rate (−0.5 mm/a) occurs in the east. This indicates that TWSC has a greater impact on the FPI than PPT.
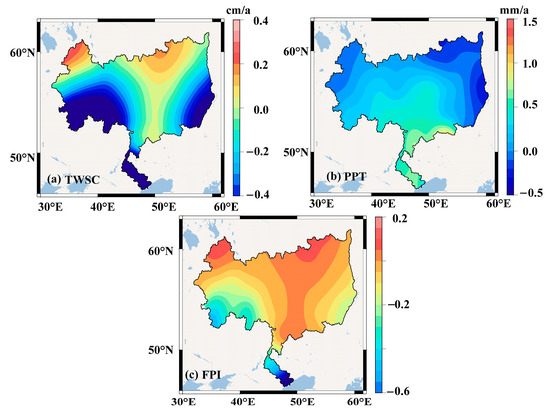
Figure 8.
The spatial distribution of the long-term change trend of TWSC, PPT and FPI.
4.3. Influencing Factors on the FPI
To discover the mechanism of flood formation, we used the two quantitative indicators (correlation coefficient and VIP) to evaluate the relationship between the FPI and seven hydrometeorological factors (PPT, ET, SM, GW, runoff, SWE and ST). In Table 3, the correlation coefficients between FPI and SM and GW are greater than 0.7 (0.76 and 0.77), their VIPs are also larger than 0.8 (1.77 and 1.85), and their correlation coefficients and VIPs are the largest. This demonstrates that SM and GW are the two factors most associated with the FPI among these hydrometeorological factors. PPT and ST are the two main factors reflecting climate change, but their correlation with the FPI is not significant. Figure 9 show that, regardless of the correlation coefficient and VIP, the dominant factors of the FPI are consistent in spatial distribution, that is, the dominant factor in most regions is SM, and GW is only in parts of the south. In the northwest, the influencing scopes of GW derived from the two results are slightly different.

Table 3.
Correlation coefficients and VIPs between the FPI and PPT, ET, SM, GW, runoff, SWE and ST in the VRB.
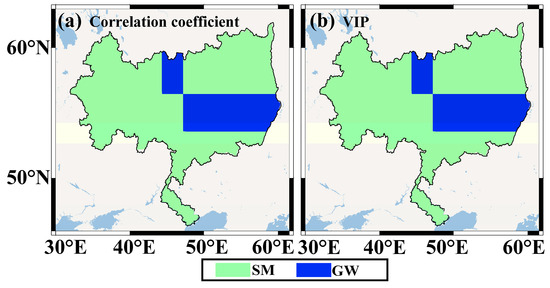
Figure 9.
The spatial distribution of dominant influencing factors based on the correlation coefficient (a) and VIP (b) results in the VRB.
The spatial distribution maps of correlation coefficients and VIPs between the FPI and SM and GW are shown in Figure 10. The correlation coefficients between the FPI and SM are larger than 0.5 in most regions, while the VIPs are all greater than 1 (Figure 10a,b). GW also exhibits a similar spatial distribution to SM (Figure 10c,d). This demonstrates that the two factors have a significant correlation with the FPI in most regions. The strongest correlations between the FPI and SM are concentrated in parts of the north and south, and the maximum correlation coefficient and VIP are 0.70 and 2.00, respectively. The minimum correlation coefficient and VIP are 0.40 and 1.00, respectively, which are located in the southeast. On the spatial scale, the correlations between the FPI and GW present a distribution characteristic of low in the north and high in the south, and the FPI and GW have a strong correlation in most regions (Figure 10c,d). The maximum correlation coefficient and VIP in the delta region are 0.90 and 3.00, respectively, while the minimum correlation coefficient and VIP in the northwest are 0.40 and 1.00, respectively.
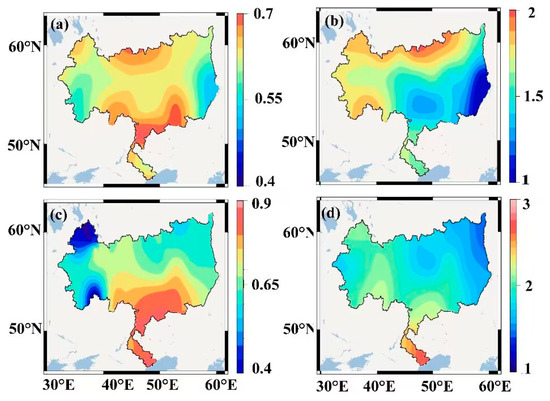
Figure 10.
The spatial distributions of correlation coefficients and VIPs between the FPI and SM, GW. (a) Correlation coefficient with the FPI vs. SM; (b) VIP with the FPI vs. SM; (c) Correlation coefficient with the FPI vs. GW; (d) VIP with the FPI vs. GW.
To discover the impact path of climate variability on extreme floods, we calculated the correlation coefficients and VIPs between seven hydrometeorological factors. It can be seen from Figure 11 that SM and GW have a strong correlation (correlation coefficient, 0.86; VIP, 4). This indicates that SM and GW have very close water exchange activity. Except for GW, runoff has a strong correlation with SM (correlation coefficient, 0.53; VIP, 2.97), and their correlation is much higher than the one between SM and SWE and PPT (correlation coefficient, 0.23 and 0.09, respectively; VIP, 0.22 and 0.14, respectively). This shows that the recharge effect of GW on SM is the largest, followed by runoff and SWE, and PPT is at the end. GW, SWE and PPT have a positive correlation with runoff. The correlation between runoff and GW is the strongest (correlation coefficient, 0.40; VIP, 1.70), followed by SWE (correlation coefficient, 0.29; VIP, 0.34) and PPT (correlation coefficient, −0.15; VIP, 0.24). This shows that GW has the largest replenishment effect on runoff, followed by SWE and PPT. SWE has a significant negative correlation with ST and ET (correlation efficient, −0.79 and −0.64, respectively; VIP, 1.94 and 1.65, respectively). ET itself is a reflection of ST changes, so SWE is mainly influenced by ST.

Figure 11.
The correlation coefficients and VIPs between seven hydrometeorological factors in the VRB.
Taking into account the response delay, we calculated the maximum correlation coefficients and delay months between the FPI and SM, GW, PPT and SWE (Figure 12a). The results show that SM (0.86), GW (0.78) and SWE (0.75) have the strong correlation with the FPI. This demonstrates that the above three terrestrial hydrological components have a very significant impact on the FPI. The FPI responds significantly faster to SM and GW (both one month) than SWE (three months). Although the correlation coefficient between PPT and the FPI reaches 0.46, it is much smaller than that between PPT and SM, GW and SWE. This indicates that PPT has a smaller impact on flood risk than SM, GW and SWE in the VRB. To explore the mechanism of flood formation, we estimated the correlation between SM, GW, SWE and the corresponding hydrometeorological factors. Figure 12b shows that SM has a strong correlation with GW (0.86), SWE (0.76) and runoff (0.62). It can be seen that the main source of supply for SM is GW, followed by SWE and runoff. From the perspective of response time, GW has the shortest (0 month), followed by runoff (1 month), SWE (2 months) and PPT (3 months). From Figure 12c, it can be seen that SWE (0.77), PPT (0.55) and GW (0.51) have a significant relationship with runoff. This shows that SWE has the largest rechange effect on runoff among the three factors, and PPT rechanges runoff slightly more than GW. Comparing Figure 12b,c, SM has a stronger correlation with GW than runoff, and the response time of SM to GW is 0 month, and the response time of runoff is −1 month. Figure 12d shows that SWE has a strong negative correlation with ST (−0.86) and ET (−0.74), and the response time of SWE to ET and ST is 1 month. Both ST and ET reflect the energy change trend, demonstrating that temperature is the main factor affecting SWE.
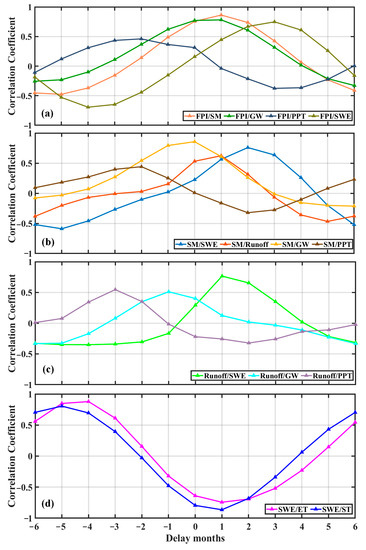
Figure 12.
The maximum correlation coefficients and delay months between hydrometeorological factors in the VRB. (a) FPI vs. SM, FPI vs. GW, FPI vs. PPT and FPI vs. SWE; (b) SM vs. SWE, SM vs. runoff, SM vs. GW and SM vs. PPT; (c) runoff vs. SWE, runoff vs. GW and runoff vs. PPT; (d) SWE vs. ET and SWE vs. ST.
5. Discussion
5.1. Path of Flood Formation
The main sources of river recharge in the basin are PPT, GW, glacier melt, snow melt and lake water [62]. Since the VRB is located in the middle and high latitude region, its water source comes from snowmelt (60%), GW (30%) and PPT (10%) [40]. Figure 12a shows that the correlations between SWE, GW and the FPI are much stronger than the ones between PPT and the FPI. According to the results in Figure 12, we can roughly describe the formation process of the floods in the VRB. ST has a strong effect on SWE (−0.86, Figure 12c). Ma et al. [63] indicated that the decline in snow depth was driven by temperature rise, and the continued decline in snow depth could increase the frequency of floods. Snow melts faster when the ST is usually high, and the process takes one month (the delay month is one, Figure 12c). Part of the water flow formed by melting snow flows into the river, and the other part enters the soil through osmosis and is stored in the form of SM. Loukas et al. [64] showed that snowmelt runoff is the dominant component of peak flows in the spring and summer floods in the inland basin of Illecillewaet, Canada. Duan et al. [65] pointed out that snowmelt has a significant correlation with the normalized difference vegetation index. Figure 12b,c show that the correlation coefficients between SWE and SM and runoff are 0.76 and 0.77, respectively, which is much greater than the ones between PPT and SM and runoff (0.44 and 0.55, respectively). This verifies that SWE’s replenishment effect on SM and runoff is greater than that of PPT. The response time of SM (2 months) to SWE is greater than the response time of runoff (1 month). The correlation coefficient between SM and runoff is 0.62, and the response time of SM to runoff is 1 month. This demonstrates that runoff has a replenishing effect on SM. The correlation coefficient between runoff and GW is 0.51, and the response time of runoff to GW is −1 month. This suggests that runoff is also one of the recharge sources for GW. There is also strong recharge activity between GW and SM (0.86). The water storage capacity of GW and SM is limited. When the water in GW and SM exceeds their water storage capacity, the excess water will overflow the surface and cause floods. Wasko et al. [66] indicate that floods are closely related to SM before floods, and SM changes must be taken into account when predicting floods due to climate change. Previous studies [67,68] show that a high GW level leads to floods. Figure 12a shows that GW and SM have a strong correlation with the FPI (0.78 and 0.86, respectively), and the response time of the FPI to SM and GW is 1 month. This demonstrates that SM and GW show abnormal changes before floods. SWE also has a strong correlation with the FPI (0.75), and the correlation is much greater than that of PPT (0.46) and slightly lower than that of SM and GW. This due to the fact that the recharge source of water resources in the VRB is mainly SWE. Yan et al. [69] point out that sharply rising temperature may accelerated the snow melting and increase the floods risk in the Manas River basin in spring.
5.2. Uncertainty of the FPI
The uncertainty of observations has an important impact on the reliability of our results. In our study, data fusion was used to decrease the uncertainty of the TWSC results. Compared with a single solution, the uncertainty level of the fused result has been reduced by nearly five times (from 3.35 cm to 0.76 cm). We used the Swarm TWSC result to complete the gap of GRACE/GRACE-FO data. Although the uncertainty of the Swarm TWSC results is greater than that of the GRACE TWSC results, it is completely reliable to use the Swarm solution for TWSC monitoring in the VRB. Wang et al. [70] have also conducted research on the hydrological application potential of the Swarm solution in the VRB. The results show that the Swarm solution demonstrates excellent performance in TWSC monitoring, and can replace the GRACE solution to detect TWSC in the VRB. The spatial distribution of the residuals in the FPI in the VRB is shown in Figure 13. In most regions, the RMSs are less than 1.2. The greater RMSs are mainly located in parts of the south, as well as in the delta.
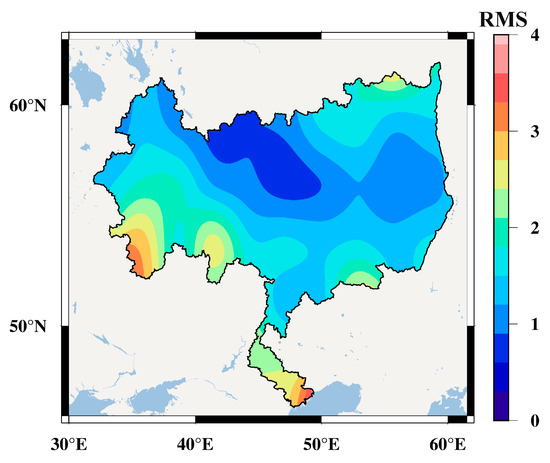
Figure 13.
The spatial distribution of RMSs of the residuals in the FPI.
5.3. Future Direction
Although the observation time series in our study has been reached 19 years, it is still not enough to study the long-term change pattern of regional floods. Therefore, in the next step of research, we will focus on how to obtain long-term observation data. And human activities also have a certain impact on regional floods, but our study only focuses on the impact of natural factors. Therefore, it is also the content that needs to be focused on in the next research step. Our results provide a certain scientific reference for flood research in middle- and high-latitude basins, and the scientific data support for local government and management departments to formulate relevant measures.
6. Conclusions
We applied the FPI based on the combined satellite gravity observations to detect the extreme floods in the VRB during 2003 and 2021, and analyzed the spatio-temporal distribution of the FPI. Subsequently, the relationship between the FPI and hydrometeorological factors are estimated by using the Pearson correlation coefficient and PLSR model to discuss the formation mechanism of floods. The primary conclusion are as follows:
- (1)
- The uncertainty of the fused TWSC results (0.76 cm) is much lower than the uncertainty of any single solution (the average is 2.14 cm), and the Swarm TWSC results have a good consistency with the GRACE results (correlation coefficient is 0.82) in the VRB. The TWSC time series estimated by combining the fused result and Swarm solution has the same performance as the ones from the GLDAS model.
- (2)
- On the seasonal scale, spring and autumn are the seasons with the greatest and smallest FPI, respectively. With regards to spatial distribution, the FPI is rising in the north and falling in the south, so the north is more prone to floods than the south. In the study period, there were two extreme floods detected by the FPI in the VRB.
- (3)
- Since SWE is an important source of recharge for water resources in the VRB, it has a strong correlation with the FPI. SWE is vulnerable to ST. Snow melts faster when the ST rises. And more water in runoff and SM comes from SWE than PPT. Therefore, the abnormal changes in SWE have a very important impact on the floods in the VRB, and the effect of SWE on the floods is greater than that of PPT.
Our study reveals the formation pathways of floods in the VRB, which is of great significance for comprehensive understand of floods occurrence and development, especially in high-latitude regions.
Author Contributions
Conceptualization, L.C. and Z.Z.; methodology, L.C. and C.Y.; software, C.X. and C.Z.; investigation, Z.Z.; resources, C.X. and L.C.; data curation, Y.L. and M.Y.; writing—original draft preparation, Z.Z. and L.C.; writing—review and editing, Z.Z., C.Y. and L.C.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Fund of Wuhan, Gravitation and Solid Earth Tides, National Observation and Research Station (WHYWZ202102, WHYWZ202103); the National Natural Science Foundation of China (41931074, 41974014, 42074172, 42004013, 42274004); the Science for Earthquake Resilience (XH21021); the Max Planck Society and the Chinese Academy of Sciences within the LEGACY (“Low-Frequency Gravitational Wave Astronomy in Space”) collaboration (M.IF.A.QOP18098); Guangdong Basic and Applied Basic Research Foundation (2022A1515010469).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
GRACE RL06 data from CSR, GFZ, JPL, and ITSG: http://icgem.gfz-potsdam.de/series (accessed on 31 May 2023); Swarm solution from COST-G: http://icgem.gfz-potsdam.de/home (accessed on 31 May 2023); PPT, runoff, SWE and ST gridded data: http://data.cma.cn (accessed on 31 May 2023); ET gridded data: sftp://hydras.ugent.be (accessed on 31 May 2023); SM and GW gridded data from GLDAS model: https://disc.gsfc.nasa.gov/datasets (accessed on 31 May 2023).
Acknowledgments
We are grateful to CSR, GFZ, JPL and ITSG for providing GRACE solution; the COST-G for providing Swarm solution; the China National Meteorological Science Data Center for providing PPT, SWE, ST and runoff data; the Global Land Evaporation Amsterdam Model for providing ET data; and the Goddard Space Flight Center for providing GLDAS-2.1 data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hall, J.; Arherimer, B.; Borga, M.; Brázdil, R.; Claps, P.; Kiss, A.; Kjeldsen, T.; Kriaučiūniene, J.; Kundzewica, Z.; Lang, M.; et al. Understanding flood regime changes in Europe: A state-of-the-art assessment. Hydol. Earth Syst. Sci. 2014, 18, 2735–2772. [Google Scholar]
- Cui, L.; He, M.; Zou, Z.; Yao, C.; Wang, S.; An, J.; Wang, X. The influence of climate change on droughts and floods in the Yangtze River basin from 2003 to 2020. Sensors 2022, 22, 8178. [Google Scholar] [PubMed]
- Fang, J.; Kong, F.; Fang, J.; Zhao, L. Observed changes in hydrological extreme and flood disaster in Yangtze River Basin: Spatial-temporal variability and climate change impacts. Nat. Hazards 2018, 93, 89–107. [Google Scholar]
- Zhao, Q.; Ding, Y.; Wang, J.; Gao, H.; Zhang, S.; Zhao, C.; Xu, J.; Han, H.; Shangguan, D. Projecting climate change impacts on hydrological processes on the Tibetan Plateau with model calibration against the glacier inventory data and observed streamflow. J. Hydrol. 2019, 573, 60–81. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816–821. [Google Scholar]
- Arnell, N.; Gosling, S. The impacts of climate change on river flood risk at the global scale. Clim. Chang. 2016, 134, 387–401. [Google Scholar]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar]
- Khalequzzaman, M. Recent Floods in Bangladesh-possible causes and solutions. Nat. Hazards 1994, 9, 65–80. [Google Scholar]
- Persoons, E.; Vanclooster, M.; Desmed, A. Flood hazard causes and flood protection recommendations for Belgian river basins. Water Int. 2002, 27, 202–207. [Google Scholar]
- Marengo, J.; Espinoza, J. Extreme seasonal drought and floods in Amazonia: Causes, trends and Impacts. Int. J. Climatol. 2016, 36, 1033–1050. [Google Scholar]
- Dahri, N.; Abida, H. Causes and impacts of flash floods: Case of Gabes City, Southern Tunisia. Arab. J. Geosci. 2020, 13, 176. [Google Scholar]
- Hughes, A.; Vounaki, T.; Peach, D.; Ireson, A.; Jackson, C.; Butler, A.; Bloomfield, J.; Finch, J.; Wheater, H. Flood risk from groundwater: Examples from a Chalk catchment in southern England. J. Flood Risk Manag. 2011, 4, 143–155. [Google Scholar]
- Att-ur, R.; Amir, N. Analysis of flood causes and associated socio-economic damage in the Hindukush region. Nat. Hazards 2011, 59, 1239–1260. [Google Scholar] [CrossRef]
- Zhong, M.; Zeng, T.; Jiang, T.; Wu, H.; Chen, X.; Hong, Y. A copula-based multivariate probability analysis for flash flood risk under the compound effect of soil moisture and rainfall. Water Res. Manag. 2021, 35, 83–98. [Google Scholar] [CrossRef]
- Hagen, E.; Lu, X. Let us create flood hazard maps for developing countries. Nat. Hazards 2011, 58, 841–843. [Google Scholar] [CrossRef]
- Hossain, F.; Lettenmaier, D. Flood prediction in the future: Recognizing hydrologic issues in anticipation of the Global Precipitation Measurement mission. Water Resour. Res. 2006, 42, W11301. [Google Scholar]
- Clark, M.; Fan, Y.; Lawrence, D.; Adam, J.; Bolster, D.; Gochis, D.; Hooper, R.; Kumar, M.; Leung, L.; Mackay, D.; et al. Improving the representation of hydrologic processes in Earth System Models. Water Resour. Res. 2015, 51, 5929–5956. [Google Scholar]
- Wang, Y.; Chen, A.; Fu, G.; Djordjevic, S.; Zhang, C.; Savic, D. An integrated framework for high-resolution urban flood modelling considering multiple information sources and urban features. Environ. Model. Softw. 2018, 107, 85–95. [Google Scholar]
- Girotto, M.; Rodell, M. Chapter Two-Terrestrial water storage. In Extreme Hydro-Climatic Events and Multivariate Hazards in a Changing Environment; Maggioni, V., Massari, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 41–46. [Google Scholar]
- Mohamed, A.; Faye, C.; Othman, A.; Abdelrady, A. Hydro-geophysical evaluation of the regional variability of Senegal’s terrestrial water storage using time-variable gravity data. Remote Sens. 2022, 14, 4059. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.; Tapley, B. The 2009 exceptional Amazon flood and inter annual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46, W12526. [Google Scholar]
- Li, B.; Rodell, M.; Zaitchik, B.; Reichle, R.; Koster, R.; Dam, T. Assilation of GRACE terrestrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe. J. Hydrol. 2012, 446–447, 103–105. [Google Scholar]
- Wang, L.; Peng, Z.; Ma, X.; Zheng, Y.; Chen, C. Multiscale gravity measurements to characterize 2020 flodd events and their spatio-temporal evolution in Yangtze River of China. J. Hydrol. 2021, 603, 127176. [Google Scholar]
- Yan, X.; Zhang, B.; Yao, Y.; Yin, J.; Wang, H.; Ran, Q. Jointly using the GLDAS2.2 model and GRACE to study the severe Yangtze flooding of 2020. J. Hydrol. 2022, 610, 127927. [Google Scholar]
- Nigatu, Z.; Fan, D.; You, W.; Melesse, A. Hydroclimatic extremes evaluation using GRACE/GRACE-FO and multidecadal climatic variables over the Nile River basin. Remote Sens. 2021, 13, 651. [Google Scholar]
- Idowu, D.; Zhou, W. Performance evaluation of a potential component of an early flood warning system—A case study of the 2012 flood, lower Niger River basin, Nigeria. Remote Sens. 2019, 11, 1970. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, J.; Li, H. Drought and flood monitoring of the Liao River basin in northeast China using extended GRACE data. Remote Sens. 2018, 10, 1168. [Google Scholar]
- Cui, L.; Song, Z.; Luo, Z.; Zhong, B.; Wang, X.; Zou, Z. Comparison of terrestrial water storage changes derived from GRACE/GRACE-FO and Swarm: A case study in the Amazon River Basin. Water 2020, 12, 3128. [Google Scholar]
- Da Encarnação, T.; Visser, P.; Arnold, D.; Bezdek, A.; Doornbos, E.; Ellmer, M.; Guo, J.; van den IJssel, J.; Iorfida, E.; Jäggi, A.; et al. Description of the multi-approach gravity field models from Swarm GPS data. Earth Syst. Sci. Data 2020, 12, 1385–1417. [Google Scholar]
- Cui, L.; Yin, M.; Huang, Z.; Yao, C.; Wang, X.; Lin, X. The drought events over the Amazon River basin from 2003 to 2020 detected by GRACE/GRACE-FO and Swarm satellites. Remote Sens. 2022, 14, 2887. [Google Scholar]
- Zhang, C.; Shum, C.; Bezdĕk, A.; Bevis, M.; Da Encarnação, T.; Tapley, B. Rapid mass loss in West Antarctica revealed by Swarm gravimetry in the absence of GRACE. Geophys. Res. Letts 2021, 48, e2021GL095141. [Google Scholar]
- Reager, J.; Famigietti, J. Global terrestrial water storage capacity and flood potential using GRACE. Geophys. Res. Lett. 2009, 36, L23402. [Google Scholar]
- Molodtsova, T.; Molodtsov, S.; Kirilenko, A.; Zhang, X.; Vanlooy, J. Evaluating flood potential with GRACE in the United States. Nat. Hazards Earth Syst. Sci. 2016, 16, 1011–1018. [Google Scholar]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J. Assessing terrestrial water storage and flood potential using GRACE data in the Yangzte River basin, China. Remote Sens. 2017, 9, 1011. [Google Scholar]
- Idowu, D.; Zhou, W. Spatiotemporal evaluation of flood potential indices for watershed flood prediction in the Mississippi River basin, USA. Environ. Eng. Geosci. 2021, 27, 319–330. [Google Scholar]
- Gupta, D.; Dhanya, C. The potential of GRACE in assessing the flood potential of Peninsular Indian River basin. Int. J. Remote Sens. 2020, 41, 9009–9038. [Google Scholar] [CrossRef]
- Abelen, S.; Seitz, F.; Abarca-del-Rio, R.; Huentner, A. Droughts and floods in the La Plata basin in soil moisture data and GRACE. Remote Sens. 2015, 7, 7324–7349. [Google Scholar]
- Xiong, J.; Yin, J.; Guo, S.; Gu, L.; Xiong, F.; Li, N. Integrated flood potential index for flood monitoring in the GRACE era. J. Hydrol. 2021, 603, 127115. [Google Scholar]
- Kalugin, A. Hydrological and meteorological variability in the Volga River basin under global warming by 1.5 and 2 degrees. Climate 2022, 10, 107. [Google Scholar]
- Volga River. Available online: http://xxfb.mwr.cn/slbk/zh/zyhl/202004/t20200409_1466531.html (accessed on 9 August 2023).
- Buber, A.; Bolgov, M.; Buber, V. Statistical and water management assessment of the impact of climate change in the reservoir basin of the Volga-Kama cascade on the environment safety of the lower Volga ecosystem. Appl. Sci. 2023, 13, 4768. [Google Scholar] [CrossRef]
- Georgievskii, V.; Grek, E.A.; Grek, E.N.; Lobanova, A.; Molchanova, T. Spatiotemporal changes in extreme runoff characteristics for the Volga basin rivers. Russ. Meteorol. Hydrol. 2018, 43, 633–638. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible using GRACE. J. Geophys. Res. Soild Earth 1998, 103, 30205–30229. [Google Scholar]
- Cui, L.; Zhang, C.; Yao, C.; Luo, Z.; Wang, X.; Li, Q. Analysis of the influencing factors of drought events based on GRACE data under different climatic conditions: A case study in Mainland China. Water 2021, 13, 2575. [Google Scholar]
- Jean, Y.; Meyer, U.; Jäggi, A. Combination of GRACE monthly gravity field solutions from different processing strategies. J. Geod. 2018, 92, 1313–1328. [Google Scholar]
- National Weather Information Center. Global Atmospheric/Land Surface Reanalysis Products of China Meteorological Administration, 1st ed.; National Weather Information Center: Beijing, China, 2011; pp. 43–49. [Google Scholar]
- Miralles, D.G.; Holmes, T.R.H.; de Jeu, R.A.M.; Gash, H.; Meesters, A.G.C.A.; Dolman, A.J. Global land surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Martens, B.D.G.; Miralles, H.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Férnandez-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar]
- Rodell, M.; Houser, P.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Long, D.; Pan, Y.; Zhou, J.; Chen, Y.; Hou, X.; Hong, Y.; Scanlon, B.; Longuevergne, L. Global analysis of spatiotemporal variability in merged total water storage changes using multiple GRACE products and global hydrological models. Remote Sens. Environ. 2017, 192, 198–216. [Google Scholar]
- Cui, L.; Zhu, C.; Wu, Y.; Yao, C.; Wang, X.; An, J.; Wei, P. Natural- and human-induced influences on terrestrial water storage change in Sichuan, Southwest China from 2003 to 2020. Remote Sens. 2022, 14, 1369. [Google Scholar]
- Bai, H.; Ming, Z.; Zhong, Y.; Zhong, M.; Kong, D.; Ji, B. Evaluation of evapotranspiration for exorheic basins in China using an improved estimate of terrestrial water storage change. J. Hydrol. 2022, 610, 127885. [Google Scholar]
- Cui, L.; Luo, C.; Yao, C.; Zou, Z.; Wu, G.; Li, Q.; Wang, X. The influence of climate change on forest fires in Yunnan province, Southwest China detected by GRACE satellites. Remote Sens. 2022, 14, 712. [Google Scholar]
- Yan, B.; Fang, N.; Zhang, P.C.; Shi, Z. Impacts of land use change on watershed streamflow and sediment yield: An assessment using hydrologic modelling and partial least squares regression. J. Hydrol. 2013, 484, 26–37. [Google Scholar]
- Woldesenbet, T.A.; Elagib, N.A.; Ribbe, L.; Heinrich, J. Hydrological responses to land use/cover changes in the source region of the Upper Blue Nile Basin, Ethiopia. Sci. Total Environ. 2017, 575, 724–741. [Google Scholar] [PubMed]
- Cui, L.; Chen, X.; An, J.; Yao, C.; Su, Y.; Zhu, C.; Li, Y. Spatiotemporal Variation Characteristics of Droughts and Its Connection to Climate Variability and Human Activities in the Pearl River Basin, South China. Water 2023, 15, 1720. [Google Scholar] [CrossRef]
- Cui, L.; Zhu, C.; Zou, Z.; Yao, C.; Zhang, C.; Li, Y. The spatiotemporal characteristics of wildfires across Australia and their connection to extreme climate based on a combined hydrological drought index. Fire 2023, 6, 42. [Google Scholar]
- Oltchev, A.; Cermak, J.; Gurtz, J.; Tishenko, A.; Kiely, G.; Nadezhdine, N.; Zappa, M.; Lebedeva, N.; Vitvar, T.; Albertson, J.; et al. The response of the water fluxes of the boreal forest region at the Vloga’s source area to climatic and land-use changes. Phys. Chemis. Earth 2002, 27, 675–690. [Google Scholar] [CrossRef]
- Springtime Floods in Southern Russia. Available online: https://earthobservatory.nasa.gov/images/14928/springtime-floods-in-southern-russia (accessed on 30 June 2023).
- Gorelits, O.; Ermakova, G.; Terskii, P. Hydrological regime of the lower Volga River under modern conditions. Russ. Meteorol. Hydrol. 2018, 43, 646–654. [Google Scholar] [CrossRef]
- Rivard, C.; Lefebvre, R.; Paradis, D. Regional recharge estimation using multiple methods: An application in the Annapolis Valley, Nova Scotia (Canada). Environ. Earth Sci. 2014, 71, 1389–1408. [Google Scholar]
- Ma, Q.; Keyimu, M.; Li, X.; Wu, S.; Zeng, F.; Lin, L. Climate and elevation control snow depth and snow phenology on the Tibetan Plateau. J. Hydrol. 2023, 617, 128938. [Google Scholar]
- Loukas, A.; Vasiliades, L.; Dalezios, N. Flood Producing mechanisms identification in southern British Columbia, Canada. J. Hydrol. 2000, 227, 218–235. [Google Scholar]
- Duan, Y.; Liu, T.; Meng, F.; Yuan, Y.; Luo, M.; Huang, Y.; Xing, W.; Nzabarinda, V.; de Maeyer, P. Accurate simulation of ice and snow runoff for the mountainous terrain of the Kunlun Mountains, China. Remote Sens. 2020, 12, 179. [Google Scholar]
- Wasko, C.; Nathan, R. Influence of changes in rainfall and soil moisture on trends in flooding. J. Hydrol. 2019, 575, 432–441. [Google Scholar]
- Kreibich, H.; Thieken, A. Assessment of damage caused by high groundwater inundation. Water Resour. Res. 2008, 44, W09409. [Google Scholar]
- Czajkowski, J.; Engel, V.; Martinez, C.; Mirchi, A.; Watkins, D.; Sukop, M.; Hughes, J. Economic impacts of urban flooding in Soth Florida: Potential consequences of managing groundwater to prevent salt water intrusion. Sci. Total Environ. 2018, 621, 465–478. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Lu, X.; Zhang, L.; Li, Y.; Ji, C.; Wang, N.; Zhang, J. Quantifying rain, snow and glacier meltwater in river discharge during flood events in the Manas River basin, China. Nat. Hazards 2021, 108, 1137–1158. [Google Scholar]
- Wang, Z.; Tian, K.; Li, F.; Xiong, S.; Gao, Y.; Wang, L.; Zhang, B. Using Swarm to detect total water storage changes in 26 global basins (taking the Amazon Basin, Volga Basin and Zamibezi Basin as examples). Remote Sens. 2021, 13, 2659. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).