Dual-Branch Fusion of Convolutional Neural Network and Graph Convolutional Network for PolSAR Image Classification
Abstract
1. Introduction
- (1)
- Considering different PolSAR image characteristics, we attempt to derive network-specific features by dividing them into spatial and polarimetric categories. Hence, Pauli RGB and Yamaguchi decomposition of the PolSAR image present spatial feature channels, and six roll-invariant and hidden polarimetric features are polarimetric features channels.
- (2)
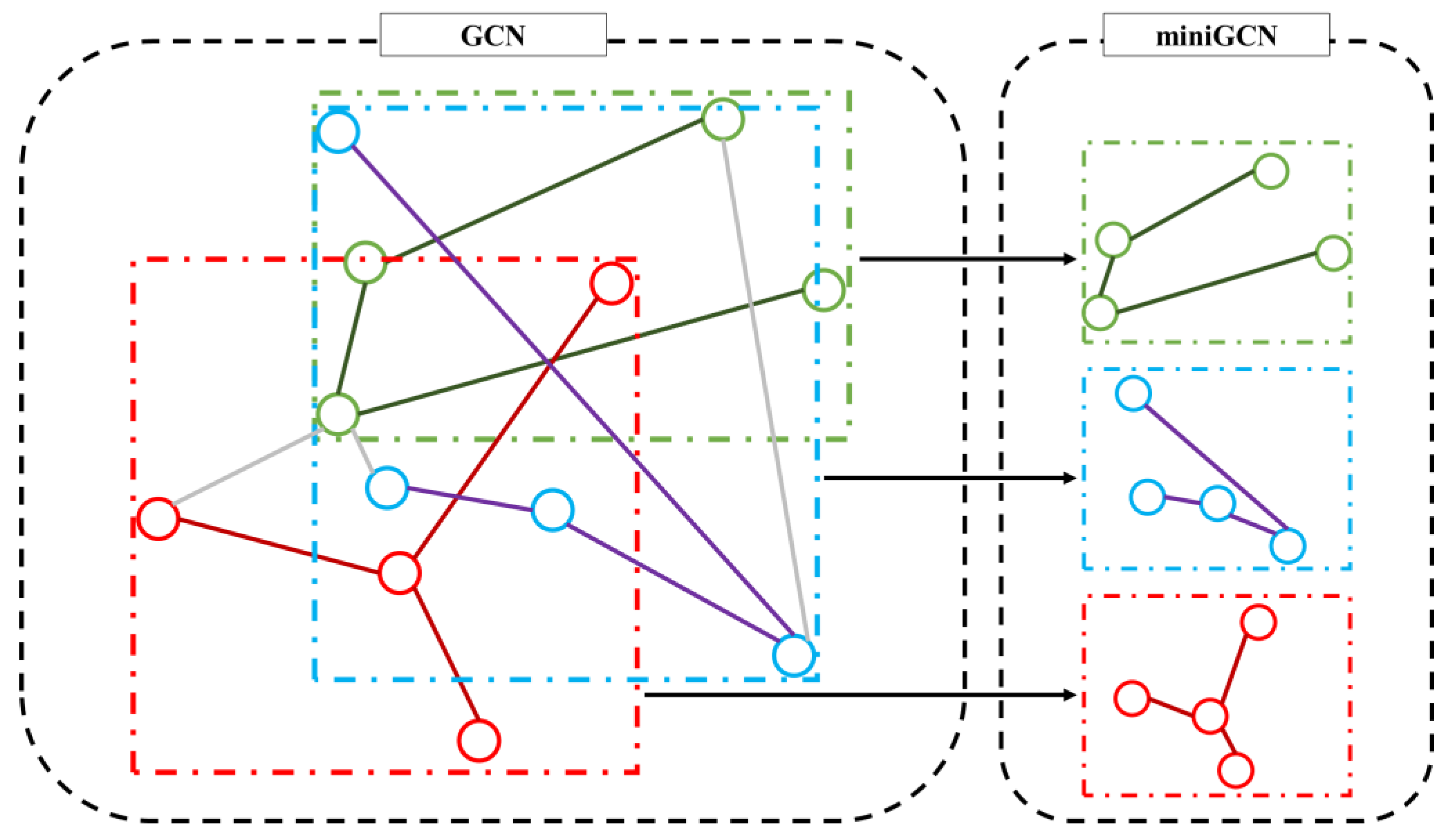
- The novel method of supervised batchwise version of GCN, known as miniGCN, is investigated as a classifier for PolSAR image classification.
- (3)
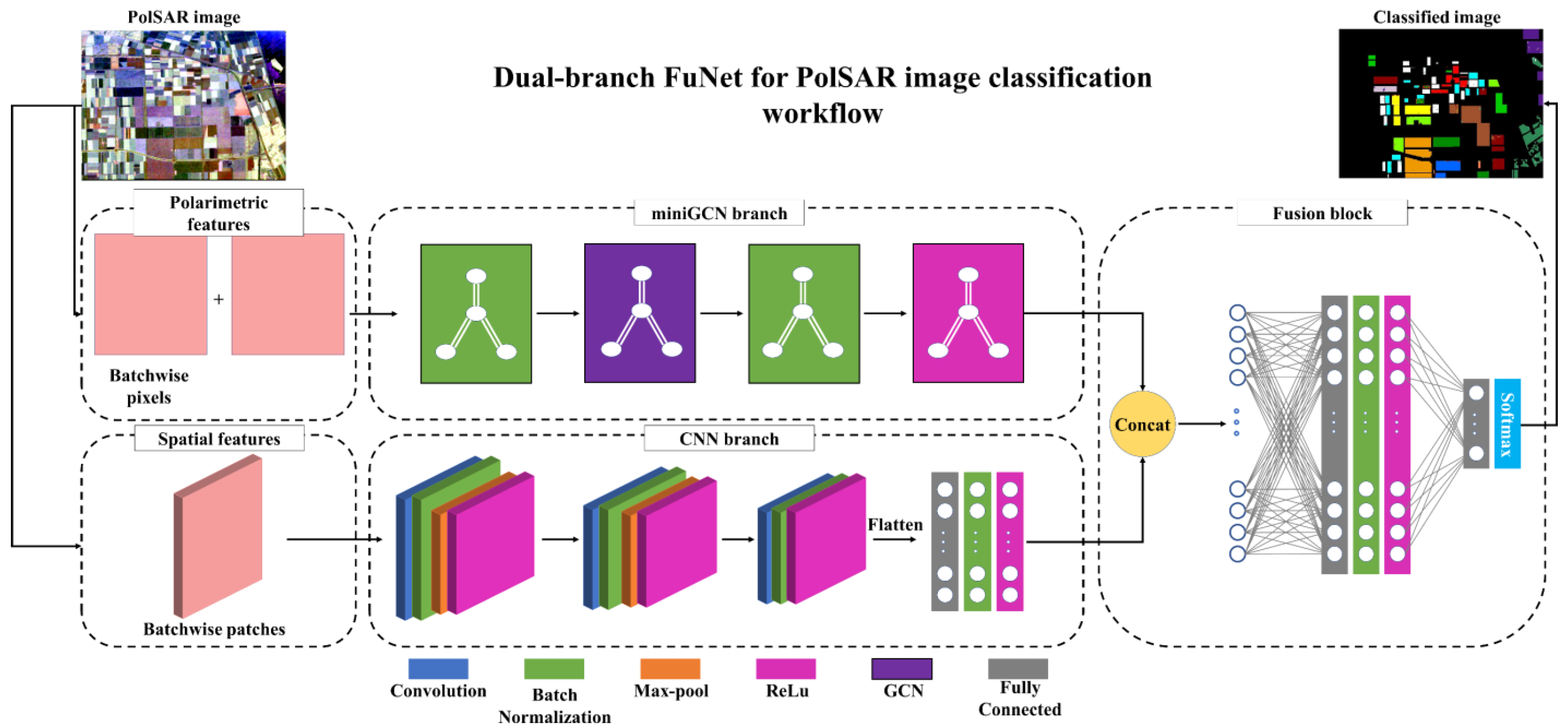
- Dual-branch fusion of miniGCN and CNN is proposed as a PolSAR classifier. Thus, each miniGCN and CNN is fed by the features with specific characteristics corresponding to its structure. Particularly, miniGCN and CNN extract spatial and polarimetric features, respectively. Subsequently, their integrated features are followed by two FC layers to determine PolSAR image classes.
2. Theory and Basics of CNN and miniGCN
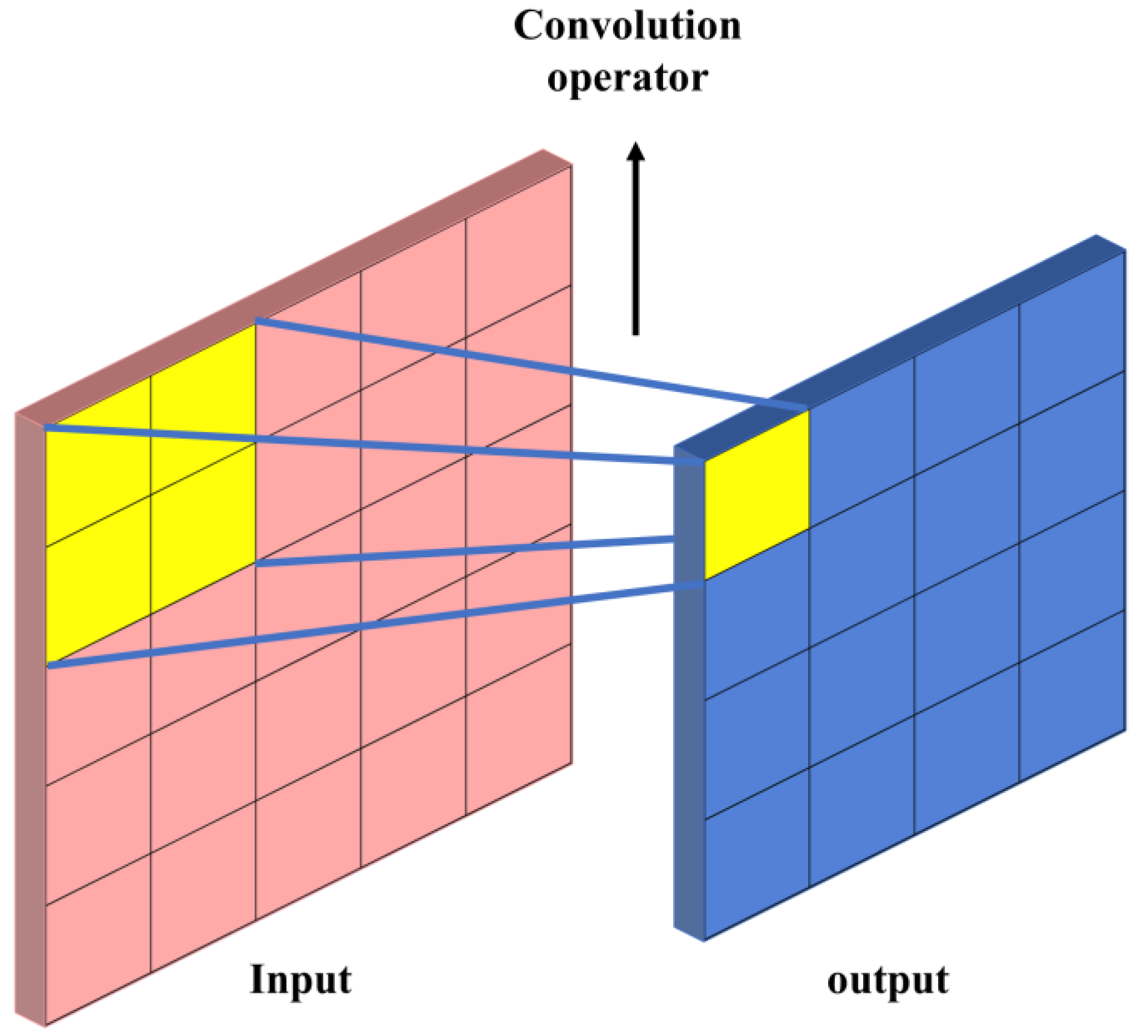
2.1. CNNs Basics and Overview
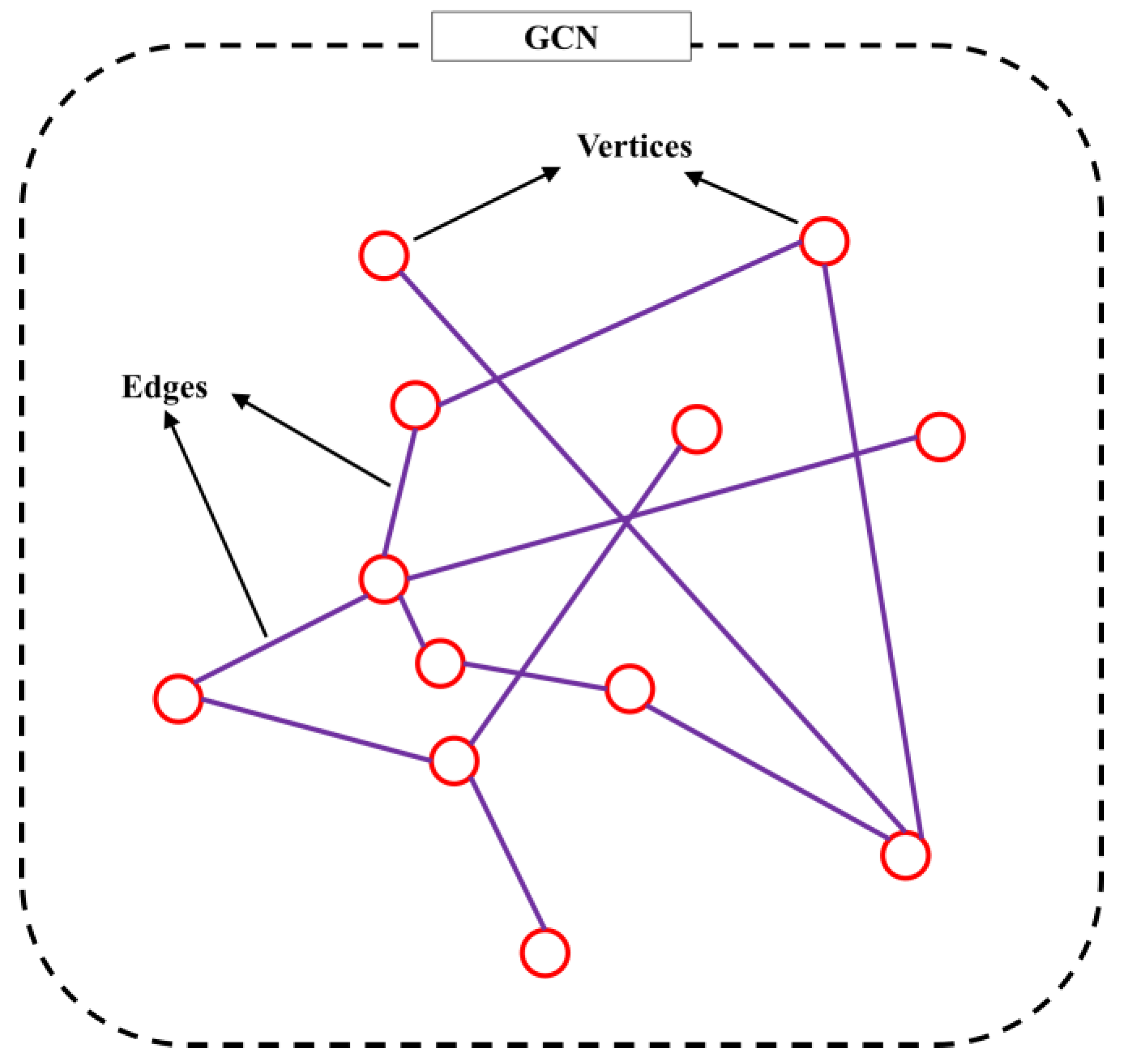
2.2. Graph and miniGCN
3. The Proposed Method
3.1. PolSAR Feature Extraction
3.2. Dual-Branch FuNet Architecture
4. Experiments
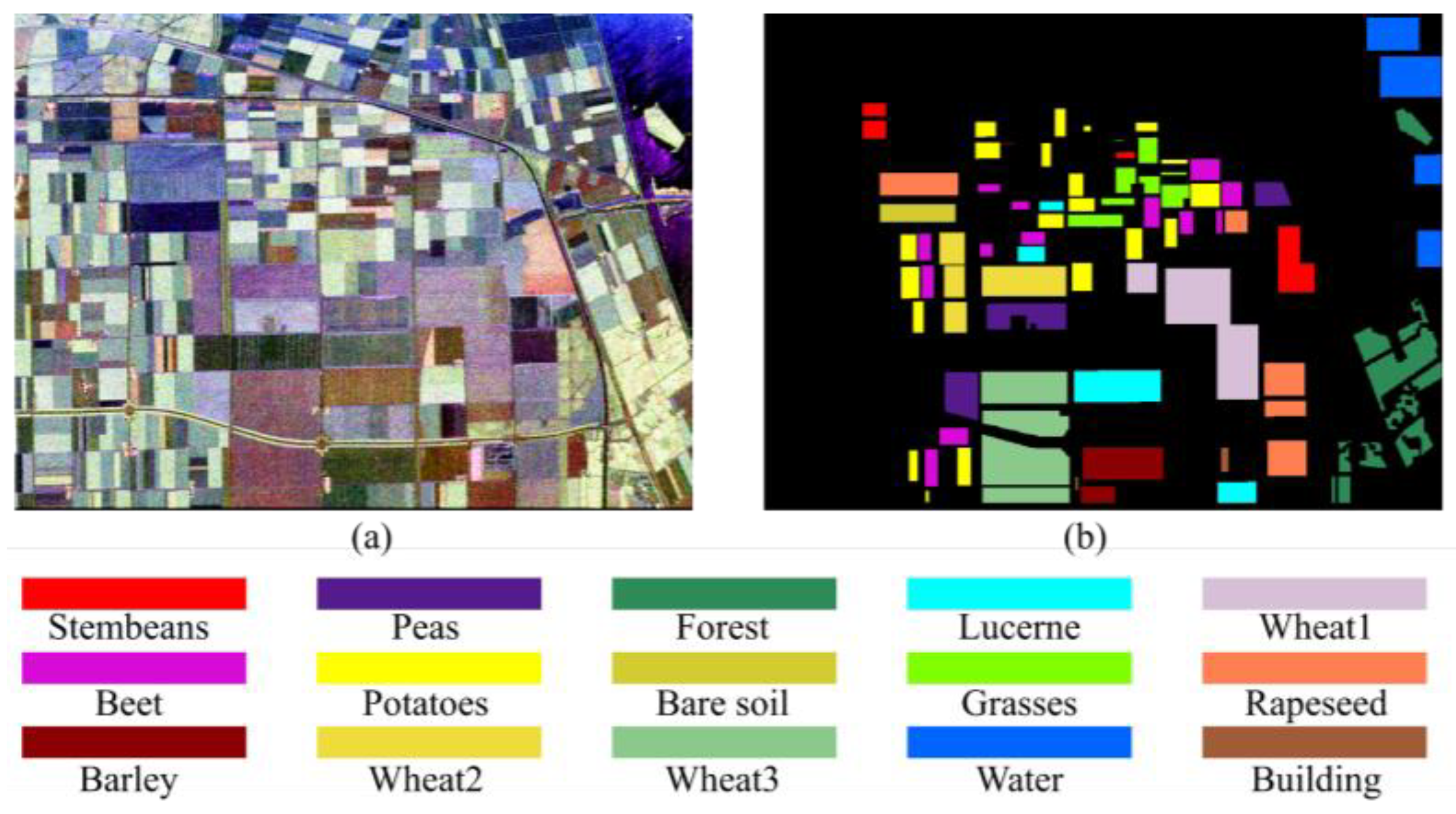
4.1. Data Description
4.2. Experimental Design
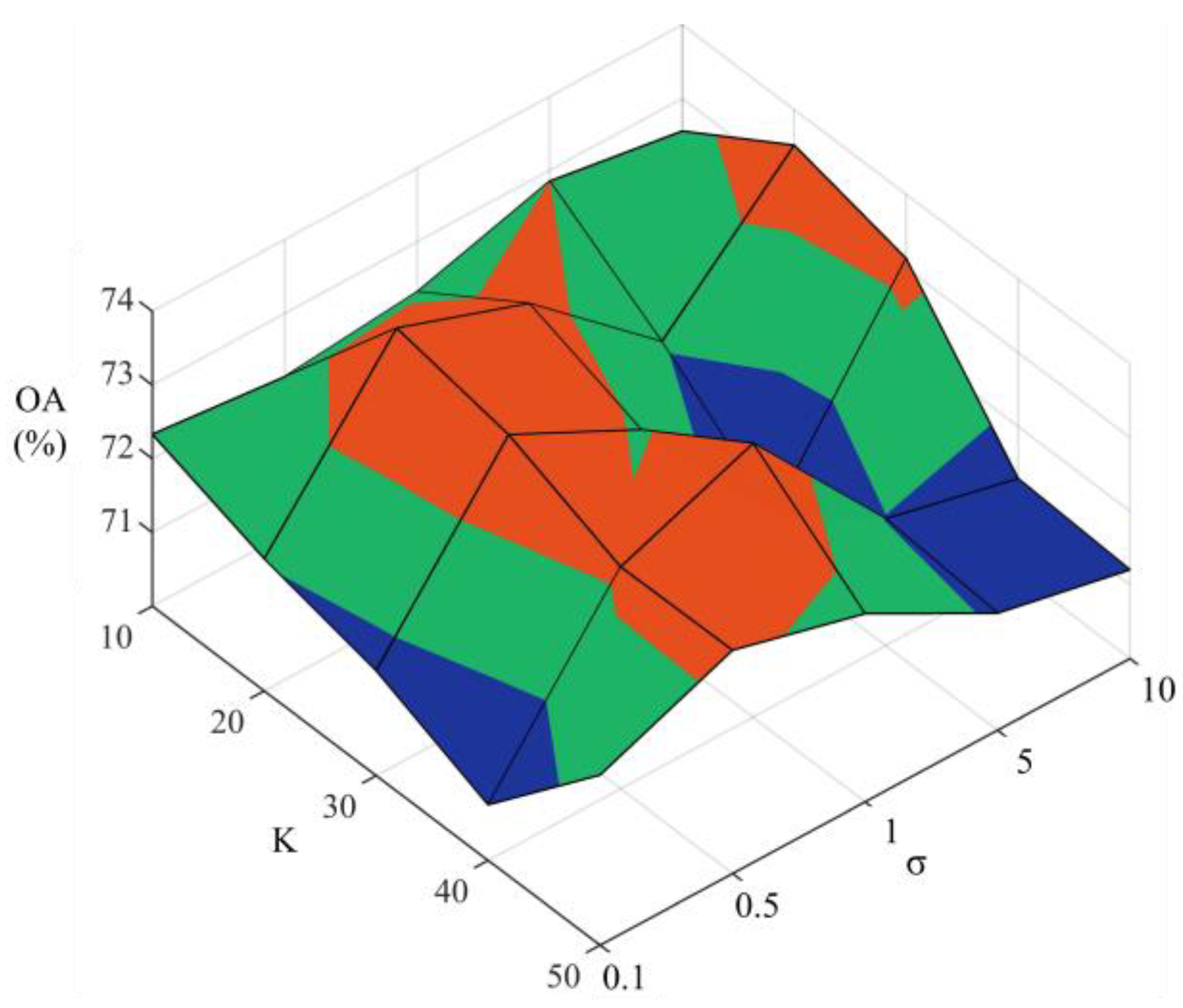
4.3. Parameter Setting, Adjacency Matrix
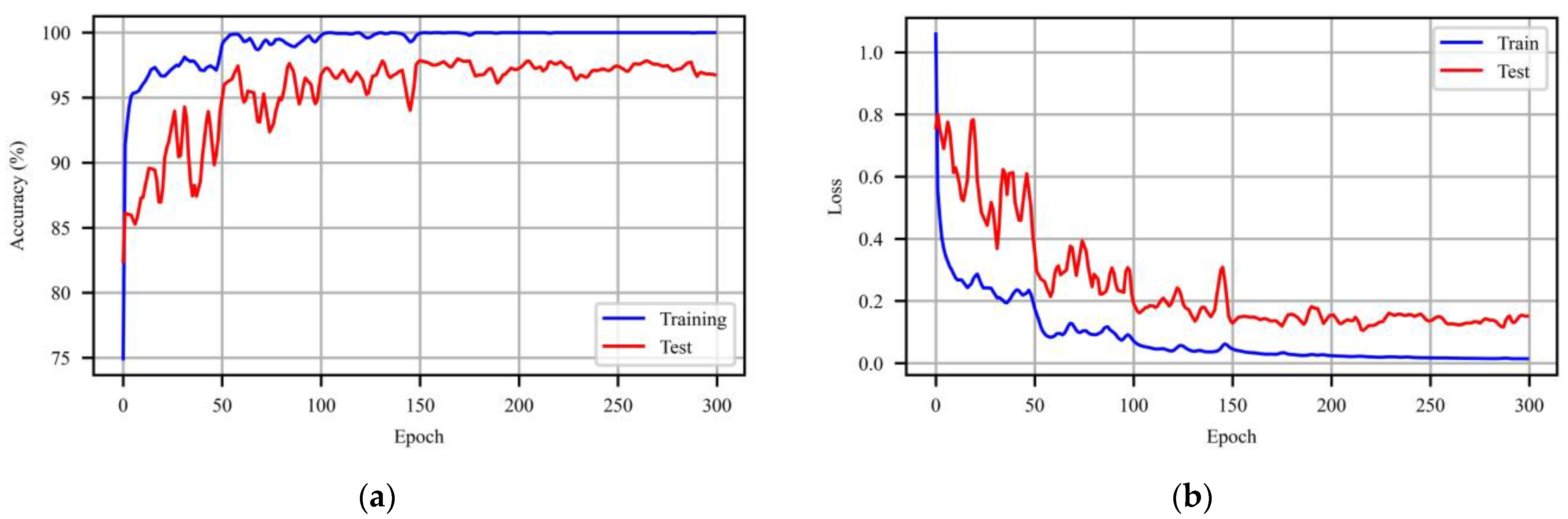
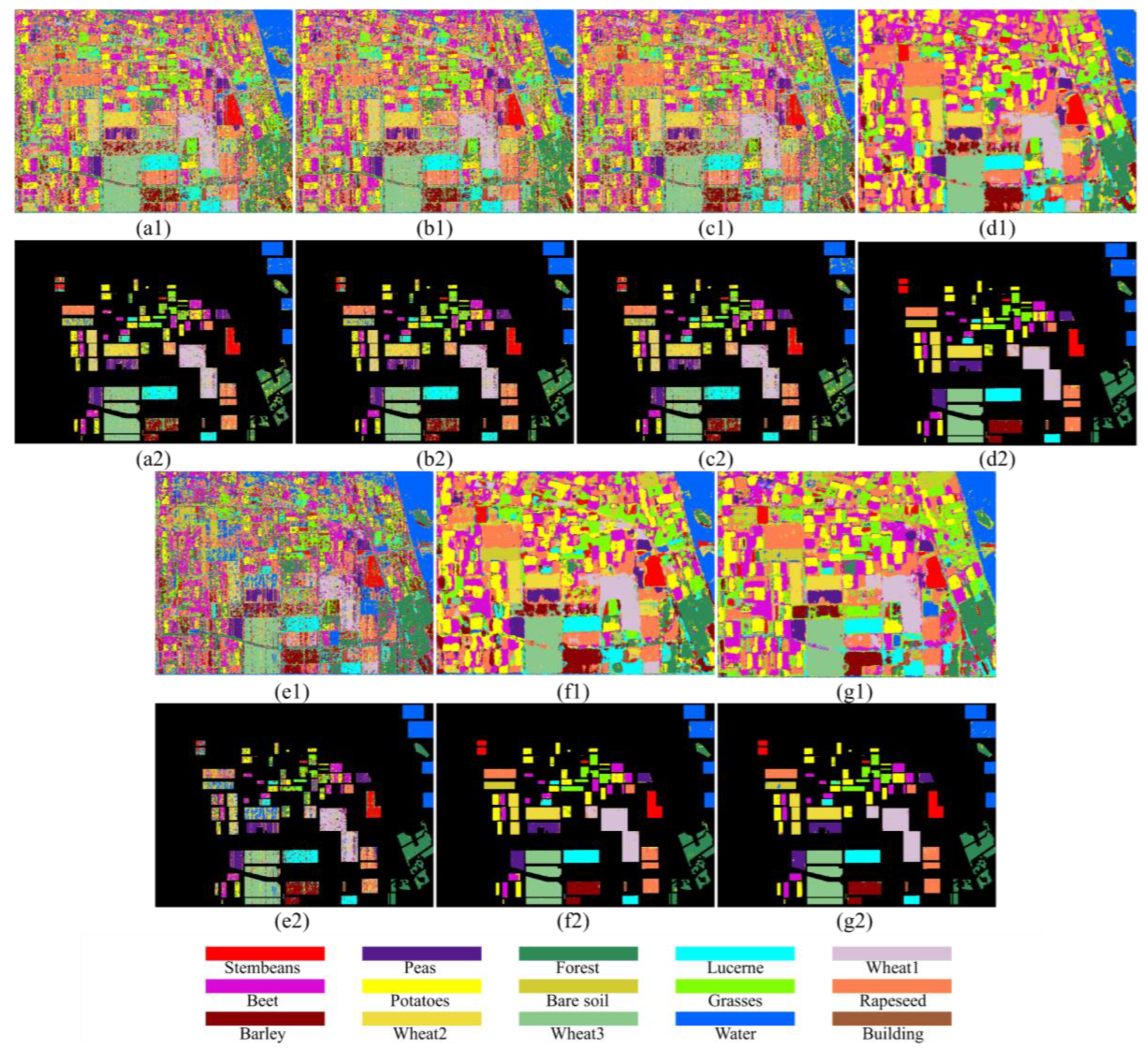
4.4. Effectiveness Evaluation
4.5. Experiments on AIRSAR Datasets
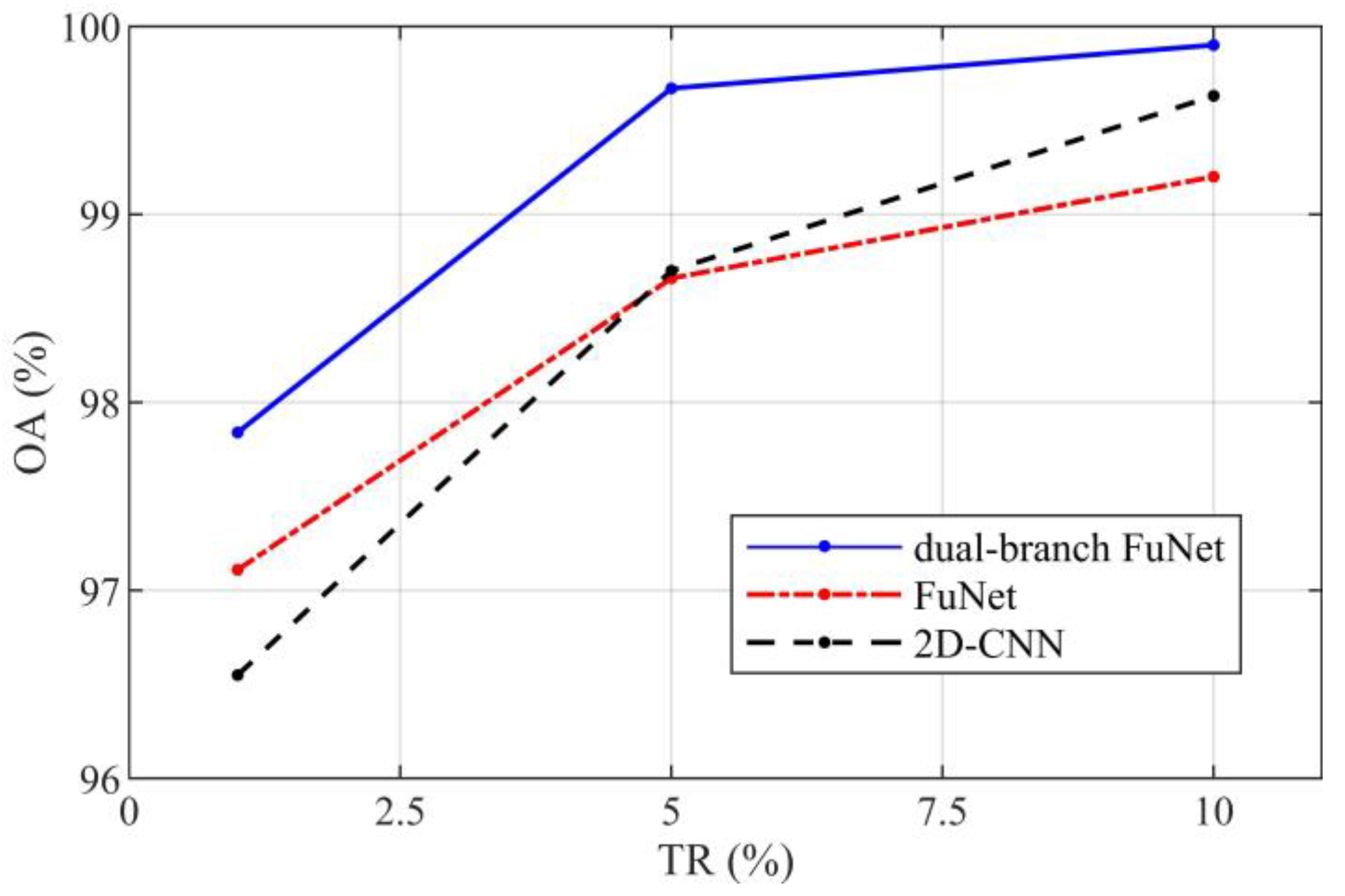
4.6. Performance Analyses with Different Training Sampling Rates
4.7. Comparison with Other Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, B.; Hou, B.; Zhao, J.; Jiao, L. Sparse subspace clustering-based feature extraction for PolSAR imagery classification. Remote Sens. 2018, 10, 391. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, X.; Xiang, D.; Sun, M. Supervised PolSAR Image Classification with Multiple Features and Locally Linear Embedding. Sensors 2018, 18, 3054. [Google Scholar] [CrossRef]
- Zhong, N.; Yang, W.; Cherian, A.; Yang, X.; Xia, G.-S.; Liao, M. Unsupervised classification of polarimetric SAR images via Riemannian sparse coding. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5381–5390. [Google Scholar] [CrossRef]
- Doulgeris, A.P.; Anfinsen, S.N.; Eltoft, T. Automated non-Gaussian clustering of polarimetric synthetic aperture radar images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3665–3676. [Google Scholar] [CrossRef]
- Yin, J.; Liu, X.; Yang, J.; Chu, C.-Y.; Chang, Y.-L. PolSAR image classification based on statistical distribution and MRF. Remote Sens. 2020, 12, 1027. [Google Scholar] [CrossRef]
- Jafari, M.; Maghsoudi, Y.; Zoej, M.J.V. A new method for land cover characterization and classification of polarimetric SAR data using polarimetric signatures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3595–3607. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Krogager, E. New decomposition of the radar target scattering matrix. Electron. Lett. 1990, 26, 1525–1527. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wang, X.; Zhao, J.; Liu, X. Incremental wishart broad learning system for fast PolSAR image classification. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1854–1858. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Chaudhari, N.; Mitra, S.K.; Mandal, S.; Chirakkal, S.; Putrevu, D.; Misra, A. Edge-Preserving classification of polarimetric SAR images using Wishart distribution and conditional random field. Int. J. Remote Sens. 2022, 43, 2134–2155. [Google Scholar] [CrossRef]
- Khosravi, I.; Safari, A.; Homayouni, S.; McNairn, H. Enhanced decision tree ensembles for land-cover mapping from fully polarimetric SAR data. Int. J. Remote Sens. 2017, 38, 7138–7160. [Google Scholar] [CrossRef]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Lin, Z. A novel algorithm for land use and land cover classification using RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2012, 118, 21–39. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, B.; Zhang, J.; Zhang, Y. Classification of polarimetric SAR image based on support vector machine using multiple-component scattering model and texture features. EURASIP J. Adv. Signal Process. 2009, 2010, 1–9. [Google Scholar] [CrossRef]
- Tao, C.; Chen, S.; Li, Y.; Xiao, S. PolSAR land cover classification based on roll-invariant and selected hidden polarimetric features in the rotation domain. Remote Sens. 2017, 9, 660. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.-Q. Polarimetric SAR image classification using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, W.; Zhang, D. Stacked sparse autoencoder in PolSAR data classification using local spatial information. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1359–1363. [Google Scholar] [CrossRef]
- Chen, Y.; Jiao, L.; Li, Y.; Zhao, J. Multilayer projective dictionary pair learning and sparse autoencoder for PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6683–6694. [Google Scholar] [CrossRef]
- Lv, Q.; Dou, Y.; Niu, X.; Xu, J.; Li, B. Classification of Land Cover Based on Deep Belief Networks Using Polarimetric RADARSAT-2 Data. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4679–4682. [Google Scholar]
- Jamali, A.; Mahdianpari, M.; Mohammadimanesh, F.; Bhattacharya, A.; Homayouni, S. PolSAR image classification based on deep convolutional neural networks using wavelet transformation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4510105. [Google Scholar] [CrossRef]
- Xie, W.; Jiao, L.; Hua, W. Complex-Valued Multi-Scale Fully Convolutional Network with Stacked-Dilated Convolution for PolSAR Image Classification. Remote Sens. 2022, 14, 3737. [Google Scholar] [CrossRef]
- Hua, W.; Xie, W.; Jin, X. Three-Channel Convolutional Neural Network for Polarimetric SAR Images Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4895–4907. [Google Scholar] [CrossRef]
- Wang, H.; Xing, C.; Yin, J.; Yang, J. Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sens. 2022, 14, 4656. [Google Scholar] [CrossRef]
- Chen, S.-W.; Tao, C.-S. PolSAR image classification using polarimetric-feature-driven deep convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 627–631. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.-Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Gao, F.; Huang, T.; Wang, J.; Sun, J.; Hussain, A.; Yang, E. Dual-branch deep convolution neural network for polarimetric SAR image classification. Appl. Sci. 2017, 7, 447. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, J.; Zhou, Y.; Zhang, F.; Yin, Q. A Multichannel Fusion Convolutional Neural Network Based on Scattering Mechanism for PolSAR Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4007805. [Google Scholar] [CrossRef]
- Shang, R.; Wang, J.; Jiao, L.; Yang, X.; Li, Y. Spatial feature-based convolutional neural network for PolSAR image classification. Appl. Soft Comput. 2022, 123, 108922. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y.Y. Spectral–spatial graph convolutional networks for semisupervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 241–245. [Google Scholar] [CrossRef]
- Wan, S.; Gong, C.; Zhong, P.; Pan, S.; Li, G.; Yang, J. Hyperspectral image classification with context-aware dynamic graph convolutional network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 597–612. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Yao, D.; Zhi-li, Z.; Xiao-feng, Z.; Wei, C.; Fang, H.; Yao-ming, C.; Cai, W.-W. Deep hybrid: Multi-graph neural network collaboration for hyperspectral image classification. Def. Technol. 2022, in press. [CrossRef]
- He, X.; Chen, Y.; Ghamisi, P. Dual Graph Convolutional Network for Hyperspectral Image Classification with Limited Training Samples. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5502418. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- Cai, W.; Wei, Z. Remote sensing image classification based on a cross-attention mechanism and graph convolution. IEEE Geosci. Remote Sens. Lett. 2020, 19, 8002005. [Google Scholar] [CrossRef]
- Du, X.; Zheng, X.; Lu, X.; Doudkin, A.A. Multisource remote sensing data classification with graph fusion network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10062–10072. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.-M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Ge, N.; Chanussot, J.; Zhu, X.X. Learnable manifold alignment (LeMA): A semi-supervised cross-modality learning framework for land cover and land use classification. ISPRS J. Photogramm. Remote Sens. 2019, 147, 193–205. [Google Scholar] [CrossRef]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Uhlmann, S.; Kiranyaz, S. Integrating color features in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2197–2216. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Sato, M. Uniform polarimetric matrix rotation theory and its applications. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4756–4770. [Google Scholar] [CrossRef]
- Liu, X.; Jiao, L.; Liu, F. PolSF: PolSAR Image Dataset on San Francisco. arXiv 2019, arXiv:1912.07259. [Google Scholar]
- Lee, J.-S.; Grunes, M.R.; De Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Ren, S.; Zhou, F. Semi-Supervised Classification for PolSAR Data with Multi-Scale Evolving Weighted Graph Convolutional Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2911–2927. [Google Scholar] [CrossRef]


| Class Number | Class Name | Train Number | Sample Number | TR (%) |
|---|---|---|---|---|
| 1 | Stem beans | 62 | 6103 | 1.015894 |
| 2 | Peas | 92 | 9111 | 1.009768 |
| 3 | Forest | 150 | 14,944 | 1.003747 |
| 4 | Lucerne | 95 | 9477 | 1.002427 |
| 5 | Wheat | 173 | 17,283 | 1.000984 |
| 6 | Beet | 101 | 10,050 | 1.004975 |
| 7 | Potatoes | 153 | 15,292 | 1.000523 |
| 8 | Bare soil | 31 | 3078 | 1.007147 |
| 9 | Grass | 63 | 6269 | 1.004945 |
| 10 | Rapeseed | 127 | 12,690 | 1.000788 |
| 11 | Barley | 72 | 7156 | 1.006149 |
| 12 | Wheat2 | 106 | 10,591 | 1.00085 |
| 13 | Wheat3 | 214 | 21,300 | 1.004695 |
| 14 | Water | 135 | 13,476 | 1.001781 |
| 15 | Buildings | 5 | 476 | 1.05042 |
| All | 1579 | 157,296 | 1.00384 |
| Class Number | Class Name | Train Number | Sample Number | TR (%) |
|---|---|---|---|---|
| 1 | Bare soil | 138 | 13,701 | 1.007226 |
| 2 | Mountain | 628 | 62,731 | 1.0011 |
| 3 | Water | 3296 | 329,566 | 1.000103 |
| 4 | Urban | 3428 | 342,795 | 1.000015 |
| 5 | Vegetation | 536 | 53,509 | 1.001701 |
| All | 8026 | 802,302 | 1.000371 |
| Layer | CNN | miniGCN |
|---|---|---|
| Input | 15 × 15 × 7 (Spatial feature) | 6 Polarimetric feature |
| Block 1 | 2 × 2 Conv | BN |
| BN | Graph Conv | |
| 2 × 2 Maxpool | BN | |
| ReLU | ReLU | |
| Output size | 8 × 8 × 30 | 120 |
| Block 2 | 2 × 2 Conv | - |
| BN | - | |
| 2 × 2 Maxpool | - | |
| ReLU | - | |
| Output size | 4 × 4 × 60 | - |
| Block 3 | 2 × 2 Conv | - |
| BN | - | |
| ReLU | - | |
| Output size | 4 × 4 × 120 | - |
| Fully connected | FC Encoder | - |
| BN | - | |
| ReLU | - | |
| Output size | 120 | - |
| Fusion | FC Encoder | |
| BN | ||
| ReLU | ||
| Output size | 240 | |
| Output | FC Encoder | |
| Softmax | ||
| Output size | Number of classes | |
| Classes | Models | ||||||
|---|---|---|---|---|---|---|---|
| Name | SVM | RF | 1D-CNN | 2D-CNN | miniGCN | FuNet | Dual-Branch FuNet |
| Stem beans | 80.95 | 80.90 | 79.59 | 99.47 | 66.33 | 99.47 | 99.35 |
| Peas | 77.26 | 76.22 | 77.78 | 97.54 | 83.14 | 96.74 | 97.62 |
| Forest | 77.13 | 85.36 | 76.65 | 96.69 | 96.62 | 96.43 | 98.33 |
| Lucerne | 83.23 | 84.56 | 81.28 | 97.11 | 81.12 | 97.35 | 94.54 |
| Wheat | 71.07 | 72.36 | 73.70 | 93.12 | 63.76 | 95.20 | 98.85 |
| Beet | 77.80 | 79.85 | 83.08 | 94.34 | 71.39 | 94.18 | 98.05 |
| Potatoes | 72.42 | 72.06 | 76.19 | 93.34 | 49.38 | 97.03 | 97.02 |
| Bare soil | 66.26 | 68.00 | 81.29 | 100.00 | 56.58 | 100.00 | 94.58 |
| Grass | 69.34 | 70.38 | 71.87 | 96.46 | 65.19 | 95.97 | 94.25 |
| Rapeseed | 74.82 | 71.69 | 74.31 | 94.98 | 58.13 | 95.52 | 97.48 |
| Barley | 70.99 | 76.96 | 78.67 | 98.09 | 83.54 | 98.90 | 97.52 |
| Wheat2 | 71.11 | 69.38 | 71.71 | 96.73 | 42.84 | 97.15 | 97.47 |
| Wheat3 | 90.18 | 89.64 | 89.86 | 99.67 | 78.32 | 99.21 | 99.75 |
| Water | 96.45 | 96.78 | 92.93 | 99.00 | 99.91 | 99.03 | 98.94 |
| Buildings | 65.82 | 68.79 | 77.28 | 80.68 | 83.86 | 86.20 | 91.93 |
| OA (%) | 78.57 | 79.55 | 79.81 | 96.54 | 72.32 | 97.11 | 97.84 |
| K (%) | 76.57 | 77.64 | 77.94 | 96.22 | 69.86 | 96.84 | 97.64 |
| Classes | Models | ||||||
|---|---|---|---|---|---|---|---|
| Name | SVM | RF | 1D-CNN | 2D-CNN | miniGCN | FuNet | Dual-Branch FuNet |
| Bare soil | 40.87 | 45.60 | 44.21 | 74.09 | 50.66 | 76.21 | 88.76 |
| Mountain | 73.10 | 76.32 | 73.92 | 96.25 | 82.98 | 95.92 | 97.38 |
| Water | 98.98 | 98.90 | 98.95 | 99.39 | 99.06 | 99.49 | 99.40 |
| Urban | 94.88 | 94.46 | 94.92 | 94.93 | 48.36 | 96.80 | 98.68 |
| Vegetation | 55.84 | 57.53 | 57.45 | 78.07 | 63.74 | 78.53 | 89.36 |
| OA (%) | 91.33 | 91.57 | 91.57 | 95.39 | 72.95 | 96.27 | 98.09 |
| K (%) | 86.22 | 86.65 | 86.62 | 92.79 | 62.05 | 94.14 | 97.00 |
| Training Ratio (%) | SVM | RF | 1D-CNN | 2D-CNN | miniGCN | FuNet | Dual-Branch FuNet | |
|---|---|---|---|---|---|---|---|---|
| OA (%) | 1 | 78.57 | 79.55 | 79.81 | 96.54 | 72.32 | 97.11 | 97.84 |
| 5 | 81.95 | 83.43 | 82.59 | 98.7 | 75.52 | 98.66 | 99.67 | |
| 10 | 83.16 | 84.45 | 83.1 | 99.63 | 76.94 | 99.2 | 99.9 |
| Training Ratio % | CV-CNN | Dual-Branch | 2D-CNN | MCFCNN | MEWGCN | Proposed | |
|---|---|---|---|---|---|---|---|
| OA (%) | 1 | 62 | 98.53 (75% TR) | 97.57 | 95.83 | - | 97.84 |
| 5 | 94 | 98.83 | - | 99.39 | 99.67 | ||
| 10 | 96.2 | 99.3 | - | - | 99.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radman, A.; Mahdianpari, M.; Brisco, B.; Salehi, B.; Mohammadimanesh, F. Dual-Branch Fusion of Convolutional Neural Network and Graph Convolutional Network for PolSAR Image Classification. Remote Sens. 2023, 15, 75. https://doi.org/10.3390/rs15010075
Radman A, Mahdianpari M, Brisco B, Salehi B, Mohammadimanesh F. Dual-Branch Fusion of Convolutional Neural Network and Graph Convolutional Network for PolSAR Image Classification. Remote Sensing. 2023; 15(1):75. https://doi.org/10.3390/rs15010075
Chicago/Turabian StyleRadman, Ali, Masoud Mahdianpari, Brian Brisco, Bahram Salehi, and Fariba Mohammadimanesh. 2023. "Dual-Branch Fusion of Convolutional Neural Network and Graph Convolutional Network for PolSAR Image Classification" Remote Sensing 15, no. 1: 75. https://doi.org/10.3390/rs15010075
APA StyleRadman, A., Mahdianpari, M., Brisco, B., Salehi, B., & Mohammadimanesh, F. (2023). Dual-Branch Fusion of Convolutional Neural Network and Graph Convolutional Network for PolSAR Image Classification. Remote Sensing, 15(1), 75. https://doi.org/10.3390/rs15010075










