Abstract
Infrared maritime target detection is a key technology in the field of maritime search and rescue, which usually requires high detection accuracy. Despite the promising progress of principal component analysis methods, it is still challenging to detect small targets of unknown polarity (bright or dark) with strong edge interference. Using the partial sum of tubal nuclear norm to estimate low-rank background components and weighted norm to estimate sparse components is an effective method for target extraction. In order to suppress the strong edge interference, considering that the uniformity of the target scattering field is significantly higher than that of the background scattering field in the eigenvalue of the structure tensor, a prior weight based on the multidirectional uniformity of structure tensor eigenvalue was proposed and applied to the optimization model. In order to detect targets with unknown polarity, the images with opposite polarity were substituted into the optimization model, respectively, and the sparse-weight similarity is used to judge the polarity of the target. In order to make the method more efficient, the polarity judgment is made in the second iteration, and then, the false iteration will stop. The proposed method is compared with nine advanced baseline methods on 14 datasets and shows significant strong robustness, which is beneficial to engineering applications.
1. Introduction
Infrared maritime target detection technology is widely used in maritime monitoring, military warning, rescue and other fields [1]. However, it is a challenging problem to achieve accurate detection due to the following two major problems: On the one hand, due to the influence of light or low temperature, the grayscale of infrared maritime target is not always higher than the background, which leads to the misdetection of methods using the prior condition that the grayscale of the target is higher than the background [2,3]. On the other hand, there is complex interference information in infrared maritime images, such as islands, clouds and strong waves. These interferences are easy to be detected incorrectly because they have similar characteristics to the target [4,5]. All these problems seriously affect the accuracy of target detection. Therefore, it is crucial to improve the accuracy of the target detection method.
1.1. Related Work
In the past few decades, researchers have proposed various methods according to different application scenes and made progress, which can be divided into two broad categories: multi-frame detection methods and single-frame detection methods. Multi-frame detection methods utilize spatial–temporal information and perform well for static background given some prior knowledge on targets. Classical methods include particle filter [6], Markov random field [7], pipeline filtering [8] and dynamic programming [9], etc. However, when the image scene changes rapidly, the performance of the multi-frame detection method is greatly degraded, which makes it limited in some practical application scenarios [10]. Single-frame detection methods are more suitable for real-time engineering demand. According to diverse theoretical methods, the existing single-frame detection methods can be roughly divided into the following several categories: methods based on background estimation filtering, local features, deep learning, principal component analysis, etc.
The method based on background estimation filtering aims to process infrared images by designing the filter in the spatial or transformed domain to suppress background and enhance the signal to noise ratio (SNR). Representative methods are: least mean square filtering [11], top-hat transformation [12] and Robinson guard filter [13], which belong to the spatial domain method. Wavelet transform [14] and phase spectrum of quaternion Fourier transform [15] belong to the transformed domain method. This kind of method has the advantages of low complexity and real time, but the detection results are easily affected by high-frequency interference [16].
The method based on local features can effectively detect weak targets. The representative methods are: local contrast method (LCM) [17], multiscale patch-based contrast measure (MPCM) [18] for adaptive contrast and relative LCM (RLCM) [19] for multiscale target detection. In addition, the methods based on the visual attention model [20,21] and local entropy method [22,23] achieve target detection according to their own theories. Since there may be other highlighted areas in the infrared image, some of these methods may cause false detection [24].
The method based on deep learning has been relatively novel in recent years, which has certain adaptive ability in different scenes. Different from traditional methods, deep learning methods do not need to artificially introduce image features, but they acquire features from the process of learning data [25]. Representative methods include convolutional neural networks (CNNs) [26], region CNNs (R-CNNs) [27], You Only Look Once (YOLO) [28], etc. In addition, the transformer networks, which were first used in natural language processing, have been applied to the field of computer vision in recent years and have made good progress [29], such as end-to-end object detection with transformers [30] and deformable transformers for end-to-end object detection [31]. This kind of method is affected by the rare data samples of the current infrared maritime image, so the detection accuracy cannot be guaranteed temporarily [5].
The method based on principal component analysis has attracted much attention recently, which assumes that the background belongs to the low-rank component and targets are considered as sparse components [32]. The infrared patch-image (IPI) [33] model is one of the most representative models, which generalizes the traditional infrared image model to an infrared patch-image model using partial patch construction. Since the small target occupies only a small part of the whole image, the sparse assumption for the target patch-image is applicable to a wide range of scenes. It is neither constrained by the shape of the target nor requires a predefined target dictionary [34]. However, the IPI model preserves the strong edges in the target component and is time-consuming [35]. Many improved methods have been proposed based on the IPI model, including the weighted infrared patch-image (WIPI) model [36], total variation regularization and principal component pursuit (TV-PCP) model [37], nonconvex rank approximation minimization (NRAM) [35], nonconvex optimization with -norm (NOLC) [38], etc. In addition, many researchers assume that the background comes from multiple subspaces and proposed methods based on a target dictionary, such as the low-rank representation (LRR) model [39], multisub-space learning (SMSL) method [40], self-regularization weighted sparse (SRWS) model [41], etc. However, the projection onto a dictionary and reconstruction is applied to every overlapped patch, which costs the whole method time and restricts their appliances in real scenes [34].
The reweighted infrared patch tensor (RIPT) [42] model successfully converts the two-dimensional matrix model into a three-dimensional patch tensor model, which makes better use of non-local spatial information and improves the solving speed. Many improvement methods have been proposed successively including partial sum of the tensor nuclear norm (PSTNN) [43], nonconvex tensor rank surrogate combined with local contrast energy (NTRS) [44], nonconvex tensor fibered rank approximation (NTFRA) [24], etc.
1.2. Motivation
Many methods employ structure tensor and its improved methods to obtain prior weight and achieve ideal results [24,42,43,44]. However, some islands and waves in infrared maritime images have strong corner characteristics similar to small targets, which can easily cause false alarms. Therefore, how to suppress the strong interference in the prior weight is a critical problem.
In order to meet the high efficiency of rapid maritime search and real-time monitoring in engineering, the model with a faster solution speed should be selected, such as the PSTNN model, even though the tensor singular value decomposition (t-SVD) it defines is a tensor singular value decomposition model of a single mode, and the tensor rank cannot be accurately approximated [24], which can be improved by designing more reasonable local prior weights.
Most infrared target detection methods default that the grayscale of the target is larger than the local background, which leads to some targets whose grayscale is lower than the background unable to be detected when interfered by light and temperature. Therefore, the design of a method that can detect both bright and dark targets will have a wider application space.
The contributions of this article are mainly three-fold:
- A method of multidirectional uniformity of eigenvalue based on structure tensor is proposed to construct prior weight, which can suppress strong edge interference.
- The polarity of the target is judged by substituting images with opposite polarities and calculating sparse-weight similarity, respectively.
- The flow of the proposed method is designed, the polarity is judged and the false iteration is stopped after two iterations to improve the efficiency of the method.
The remainder of this paper is organized as follows: In Section 2, the method based on the multidirectional uniformity of eigenvalue of the structure tensor is proposed to suppress strong edge interference. In Section 3, the proposed method based on sparse-weight similarity joint prior weight in Section 2 is introduced. In Section 4, the selection of parameters in the proposed method is discussed, and the baseline methods are compared. In Section 5 and Section 6, all the works in this paper are discussed and summarized.
2. Local Prior Weight Based on Multidirectional Uniformity
Using the principal component analysis method to detect an infrared target often needs to introduce prior weight. On the one hand, it can make the optimization problem have fast convergence; on the other hand, it can ensure the detection accuracy. The structure tensor [45] is a common method to construct the weight. Let the original image matrix be D; then, the structure tensor can be obtained by:
where represents the Gaussian kernel function with a variance of , * is the convolution operator symbol, represents the Gaussian kernel function with a variance of , ⊗ represents the Kronecker product symbol, ∇ represents the gradient operator, and represent the gradient of along the x and y directions, respectively. Then, two eigenvalue matrices and of can be obtained:
Let the two eigenvalues of a pixel in D be and , respectively, where . When , it indicates that the grayscale of D around the pixel changes very little, which belongs to the flat area; when , it indicates that the grayscale of the D around this pixel changes sharply, which can be regarded as the corner; when , it indicates that there is a grayscale change distance in the direction near this pixel, and the grayscale change in the direction perpendicular to it is very small, which can be regarded as the edge. Therefore, the possible corner points in the image can be extracted from the flat background area and the edge area by using the eigenvalue. Brown et al. [46] proposed a “corner strength” function to find the interest points:
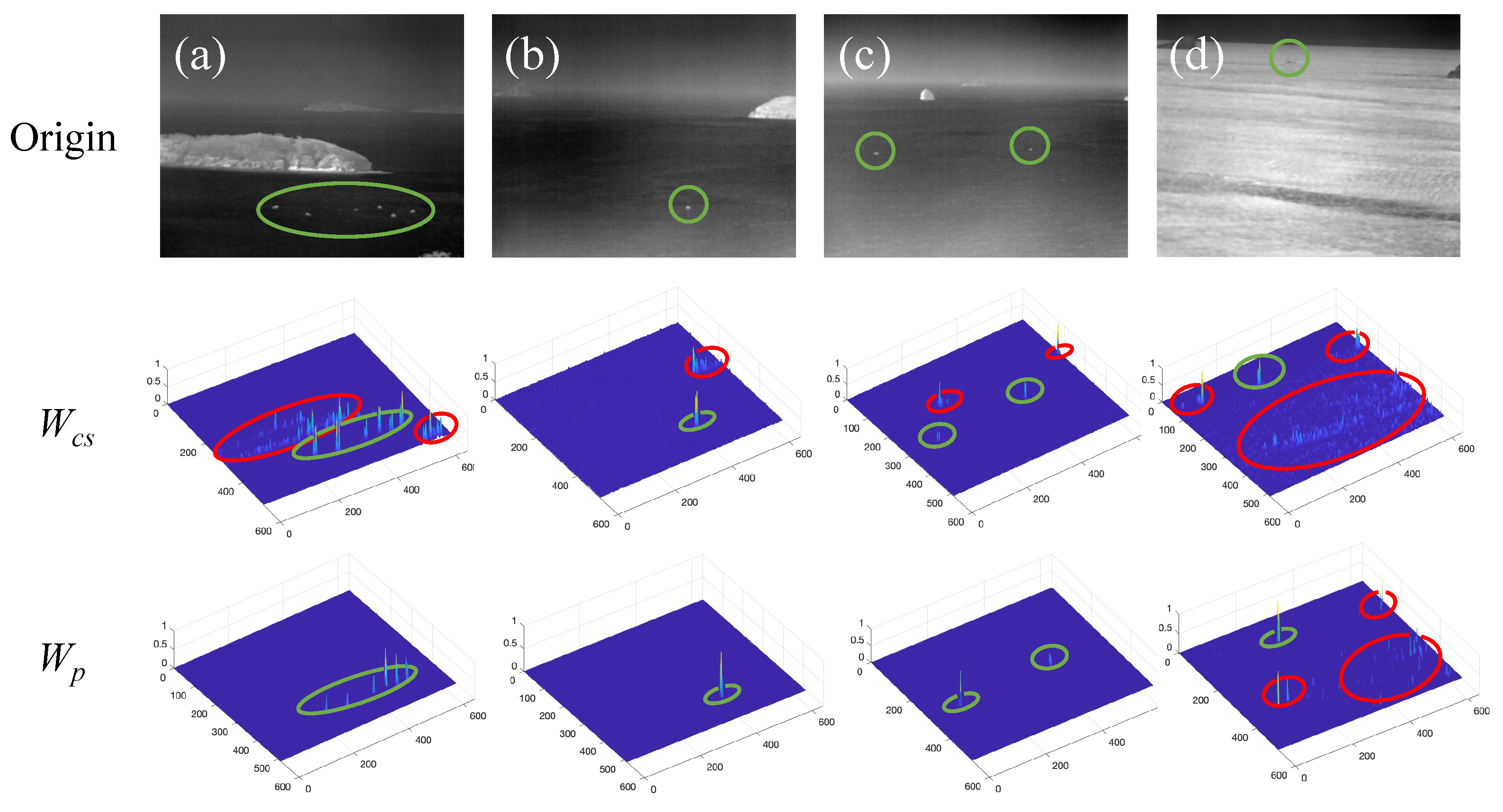
We selected four kinds of infrared maritime images with strong edge interference and calculated their corner strength maps by Equation (3). The results are shown in the second row of Figure 1. The target is circled in green, and the strong edge clutter is circled in red.
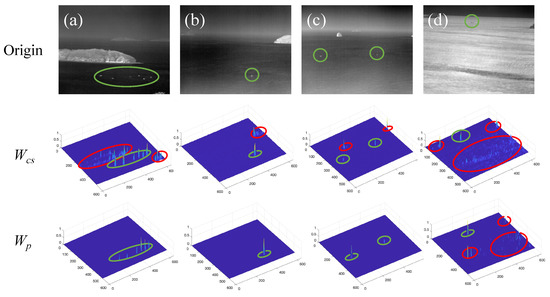
Figure 1.
Corner strength maps and the proposed improved method of four typical strong edge scenes. (a–d) represent four different scenes with strong edge interference, respectively.
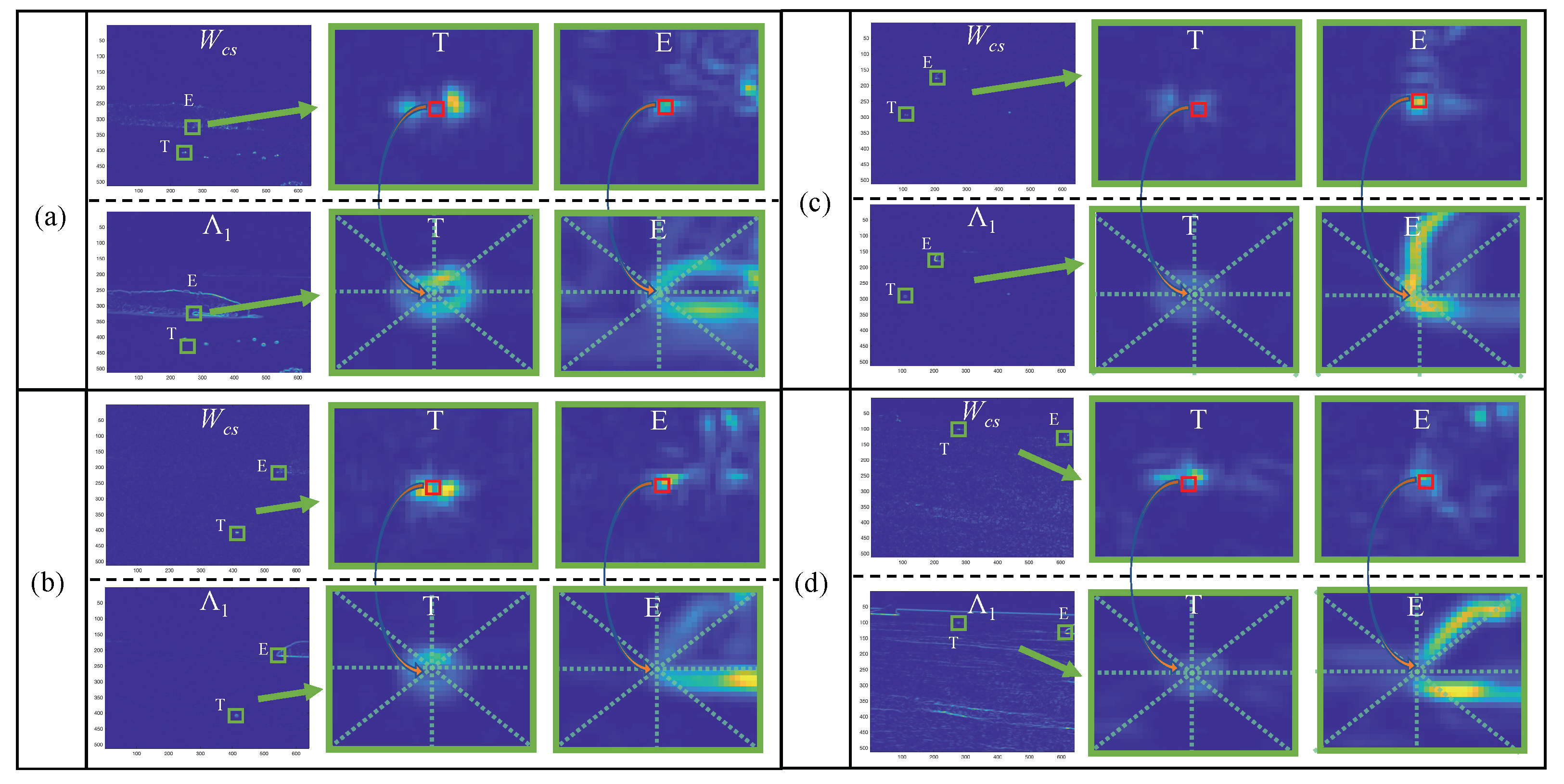
Obviously, the corner strength method can effectively extract the corner area. Although most of the edges are suppressed, the partial edge of the islands and the strong waves still cannot be effectively restrained. The prior weight with strong edge residue will seriously affect the detection result and cause many false alarms. Due to the obvious edge characteristic in eigenvalue , to further suppress these unnecessary interferences, we analyze the relationship between and the corner strength map in Figure 1, as shown in Figure 2.
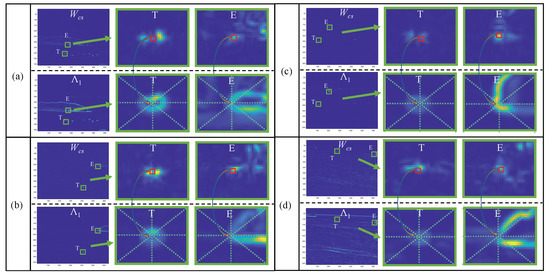
Figure 2.
The relationship between corner strength map and the eigenvalue of the structure tensor. (a–d) are the results of four different typical scenes corresponding to Figure 1 in the process of the multidirectional uniformity.
We selected a target region “T” and an edge interference region “E” in with higher intensity in each scene. It can be clearly seen that the prominent target area in tends to present a relatively uniform annular in the position of , while other edge interference areas prominent in tend to present irregular shapes in the position of , with large intensity only in a few directions. Therefore, we use the multidirectional uniformity of the target and the non-uniformity of the edge in to suppress the strong edge corner interference. Firstly, since the intensity of the target is very obvious in , a simple threshold segmentation can be used to obtain the region of interest:
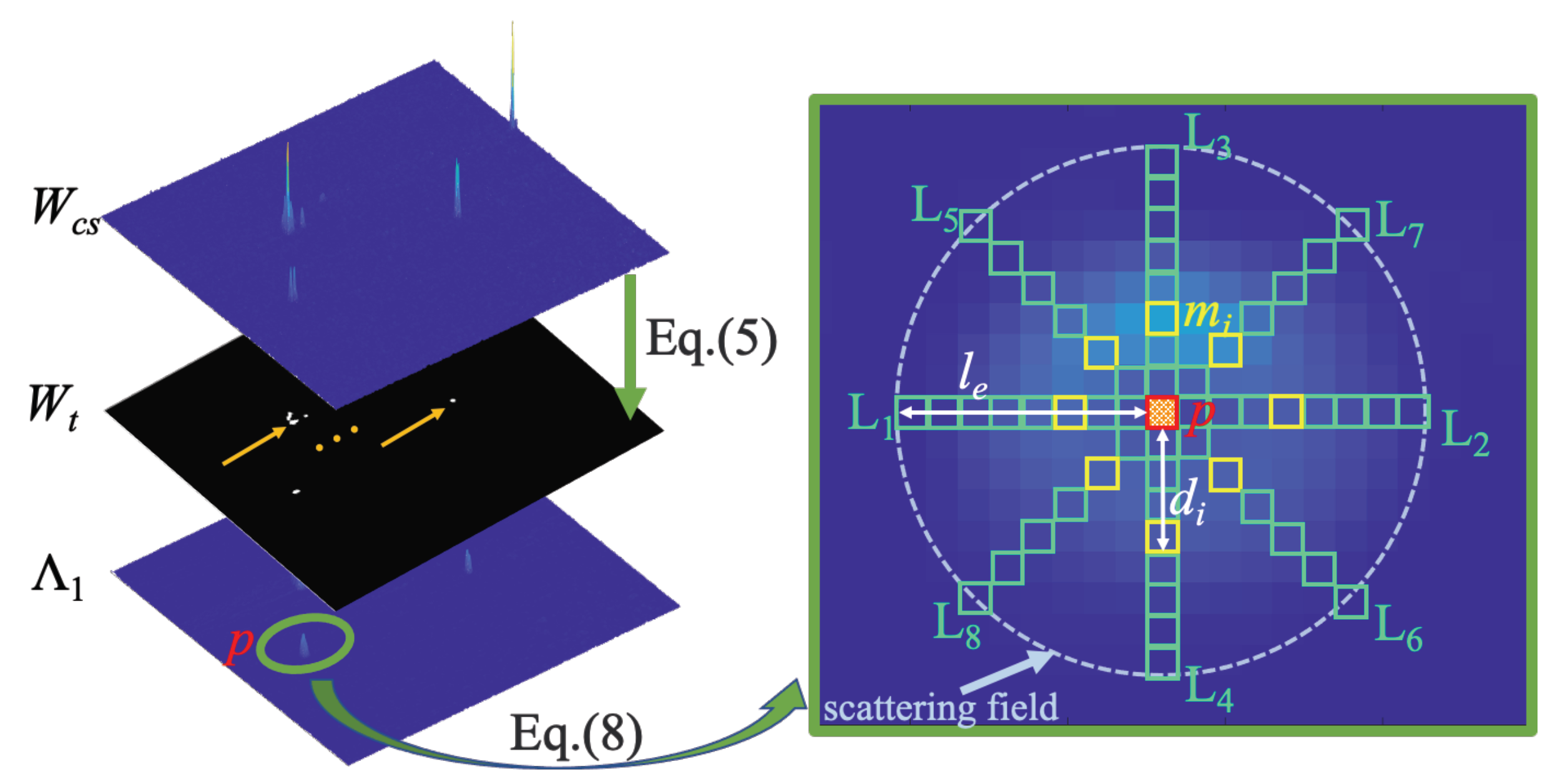
where indicates the mean value of , indicates the standard deviation of , indicates the segmentation threshold, and indicates the result of the segmentation. Performing a nonzero pixel operation on saves a lot of time compared to . By traversing the nonzero elements in , a scattering field of the corresponding pixel in is constructed, and then, the multidirectional uniformity of that pixel is calculated to suppress the background and highlight the target. The schematic diagram is shown in Figure 3. After obtaining , the location information is mapped into by traversing every nonzero element in . Suppose that the current traversal is at the mapping point p marked in the red box in , and let the intensity value of p be . Taking p as the center pixel, the vectors with length are extended in the horizontal and vertical directions, and the vectors with length are extended in the other four directions in the scattering field. Calculate and obtain the difference vector between the multidirectional vector and the center pixel by:
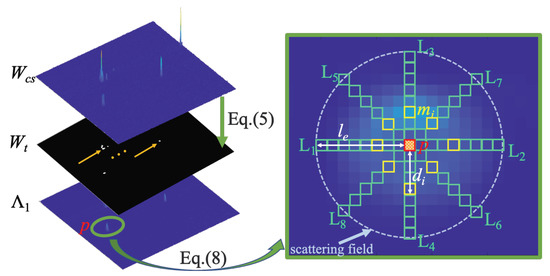
Figure 3.
Schematic diagram of multidirectional uniformity of eigenvalue .
Then, calculate the element of with the largest absolute value and its distance from the center pixel:
Let the vector formed by calculated in eight directions be called and the vector formed by be called . c is a decimal that prevents the denominator from being zero, which is set to 0.001 in this paper; then, the multidirectional uniformity calculation result of any pixel in can be obtained by:
We set the map calculated by Equations (6)–(8) is the prior weight map . The third columns in Figure 1 show the effect of the proposed improved method. It can be seen that although the target is shrunk to a certain extent, the interference of high corner strength is obviously suppressed; that is, under the premise of losing certain morphological characteristics of the target, the target is not missed, and the number of false alarms is greatly reduced.
3. Proposed Method
After determining the prior weight, how to solve the unknown polarity of target detection needs to be further considered. We use the efficient PSTNN to estimate the rank of the background and use the sparse-weight similarity to judge the polarity of the target in the process of solving the ADMM, and we realize the detection of the unknown polarity target. In order to clearly represent the difference of the local grayscale of the target, the concept of polarity of the target is defined according to [47]. In this paper, we set targets with grayscales higher than the local background to have positive polarity, and we set targets with grayscales higher than the local background to have negative polarity. Suppose the variable related to the positive polarity target is X; then, the variable with the opposite polarity of X is .
3.1. Infrared Patch-Tensor Model
The infrared patch-tensor (IPT) model was proposed by Dai et al. [42]. The patch-tensor is constructed by sliding rectangular patches of the same size on the original image and finally stacking the patches into a three-dimensional tensor cube, as shown in Figure 4. The original expression of the IPT model is as
where denotes the patch-tensor constructed from the original image; denotes the low-rank background patch-tensor; denotes the sparse target patch-tensor; and denotes the random noise patch-tensor. Then, a tensor robust principle component analysis (TRPCA) [48] problem can be obtained as follows:
where indicates the rank of a matrix or tensor, is a compromising parameter, and represents the -norm. Since solving the -norm of a patch-tensor is an NP-hard problem, the -norm is used to approximate the -norm convexly.
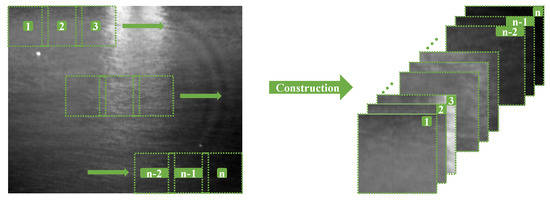
Figure 4.
The construction of patch-tensor.
3.2. IPT Model Based on PSTNN
Unlike matrices, the rank of patch-tensor is not uniquely defined. It is important to select a suitable tensor rank with a tight convex relaxation to ensure the speed and accuracy of the solution. Partial sum of the tubal nuclear norm [49] is selected to estimate the rank of patch-tensor. The definition is as follows:
where represents the estimate of the patch-tensor rank, and n represents the number of patches shown in Figure 4. denotes the matrix obtained by Fourier transformation of the i-th frontal slice of the tensor , denotes the partial sum of singular values (PSSV) [50]. In order to obtain the ideal N value, is decomposed into a matrix along the frontal slice, and we calculate the singular values and set the number of singular values greater than 10% of the maximum singular value to N value [49].
Thus, the low-rank and sparse infrared small target detection model based on PSTNN joint -norm is defined as:
where ⊙ indicates the Hadamard product, is the final weight tensor, which can be obtained by Equation (13), is the tensor obtained by inverting the elements in , sparse weight is a reweighted scheme [51], which is used to improve the accuracy and speed of solving the -norm minimization problem and can be calculated by Equation (14), where c is generally set to 1, is a small number to to prevent the denominator from being zero, and k denotes the number of iterations.
3.3. Solution of the Proposed Model
As a convex optimization problem-solving method, the alternating direction method of multipliers (ADMM) [52] is currently one of the most efficient methods, so it is applied in this paper to solve the problem in Equation (12). The augmented Langrangian function of Equation (12) can be represented as:
where is the Lagrange multiplier, denotes the inner product, is the Frobenius norm, and is a penalty factor.
Then, the problem in Equation (15) can be solved by the following several subproblems, and at step iteration is computed as follows:
The subproblem (16) is solved via soft thresholding operator [53]:
The subproblem (17) is solved via a partial singular value thresholding operator (PSVT) [50] through Fourier fast t-SVD computation, as shown in Algorithm 1 [54]. Then, Y and are updated by:
| Algorithm 1: Solve Equation using PSVT |
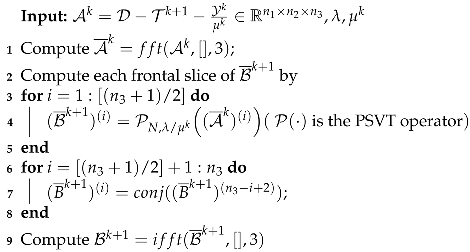 |
The k-th iteration flow of ADMM is shown in Algorithm 2. After the calculation of Algorithm 1, compared with , the smaller singular values of are suppressed, which inhibits more sparse components and causes more details loss. So, compared with , the grayscale of sparse components whose grayscale values are higher than local background will descend, yet the grayscale of sparse components whose grayscale values are lower than local background will ascend in . Therefore, in Equation (18), there will be some pixels with values less than zero in , which are discarded by the soft thresholding operator that only considers positive elements and default the grayscale of the target as higher than the local background. However, as we have discussed above, the grayscale of the target is not always higher than the local background. The dark targets will be missed by Equation (18). Unfortunately, we can not directly take the absolute value of the result of , because in most cases, targets in the infrared maritime image have uniform polarity. If the absolute value is taken directly, it is bound to introduce some interference with the opposite polarity to the target and then affect the false alarm rate. Therefore, determining the polarity of the target in a certain scene is the key to ensure a low miss rate and false alarm rate.
| Algorithm 2: The k-th iteration flow of ADMM |
|
We set the maximum grayscale of D to be 255, and the image of D with its polarity reversed () is defined as . If the polarity of the target in D is negative, substituting into Equation (12) can ensure that the dark target is not missed. We find that the prior weight is always significant at the target location, regardless of the polarity of the target positive or negative. Therefore, and can be substituted into Equation (12) to calculate the sparse components with different polarities, and the polarity of the target can be judged by comparing the similarity with . However, if and are iterated to convergence using ADMM and then judged for similarity to , this will double the computation time.
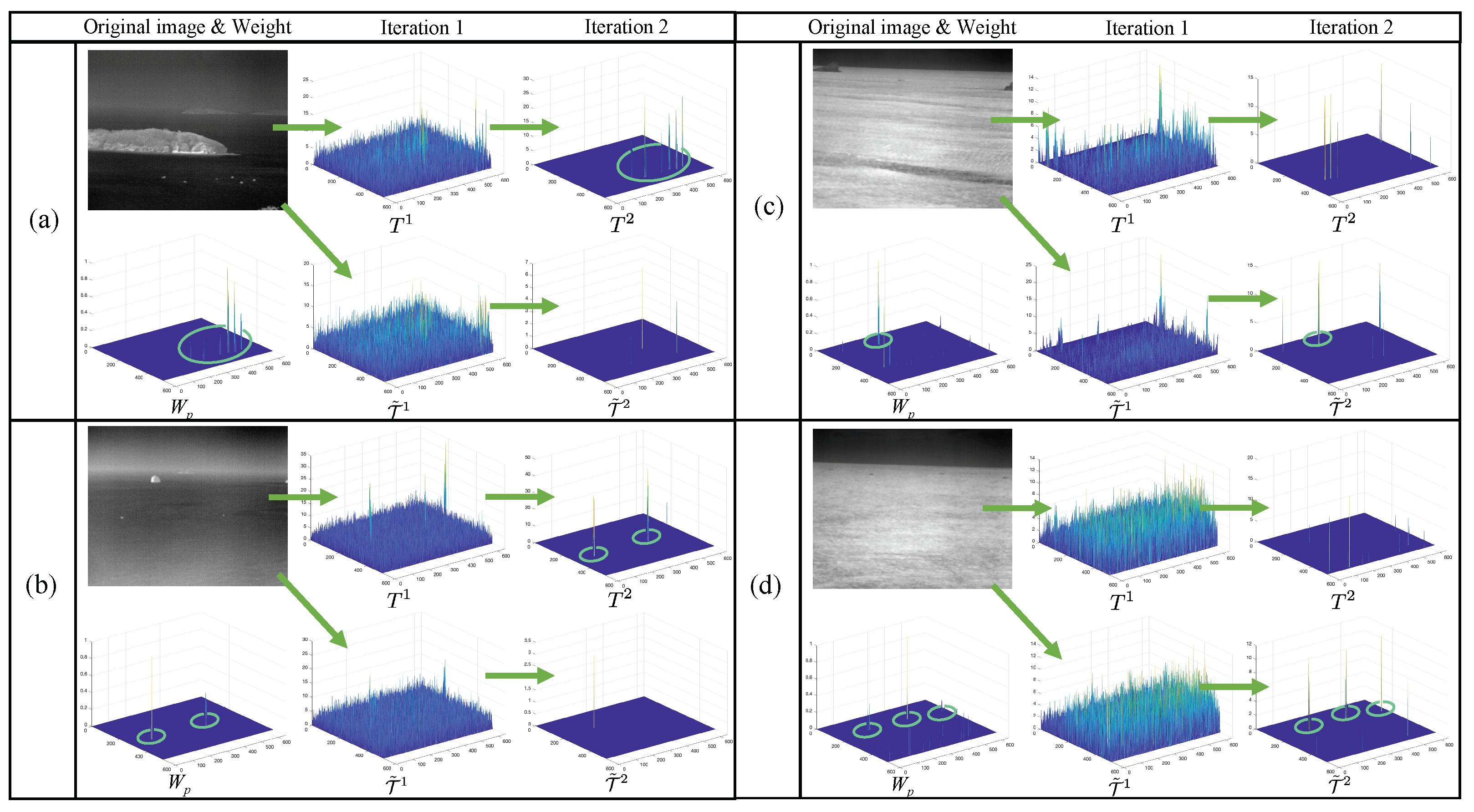
We notice that in the iterative process, when , the sparse component or is sufficiently separated from or . There is a significant difference between and . Therefore, we only need to determine the polarity when , which can effectively shorten the running time.
Figure 5 shows the comparison of the sparse components , , , and for the scene with different polarity targets. It can be seen that after the first iteration, the similarity of and to is not well resolved. After the second iteration, in both Figure 5a,b, is clearly more similar to , since the targets are of positive polarity; in both Figure 5c,d, is clearly more similar to , since the targets are of negative polarity. Features whose prior weight is clearly similar to the sparse component or are highlighted in the figure.
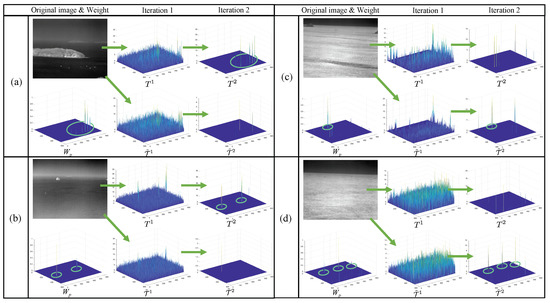
Figure 5.
Comparison of sparse components with opposite polarities in the first two iterations and the prior weight for target polarity judgment. (a–d) are the results of four different typical scenes corresponding to Figure 1 in the process of iterations.
Since the sparse component with the correct polarity or has a higher intensity value at the same position as the prior weight , we propose the concept of sparse-weight similarity . The sparse components and are obtained by iterating the original image and its grayscale inversion image twice through ADMM. Then, the polarity of the target is determined by comparing their similarity with :
Table 1 shows the values of and for each scene of Figure 5. Apparently, when , the polarity of the target is positive; when , the polarity of the target is negative. After judging the target polarity, the branch with higher sparse-weight similarity continues to iterate, and the other branch stops iteration, which can save a lot of computing time.

Table 1.
The values of and .
Since the -norm of the target patch-tensor will stop changing after several iterations, in order to reduce the running time of the method, the iteration will be stopped when the -norm of the target patch-tensor of the two adjacent iterations is equal or the relative error () is less than a certain threshold, as shown in Algorithm 3. The overall flow of the proposed PSTNN-based and ADMM methods with target polarity judgement is shown in Algorithm 4.
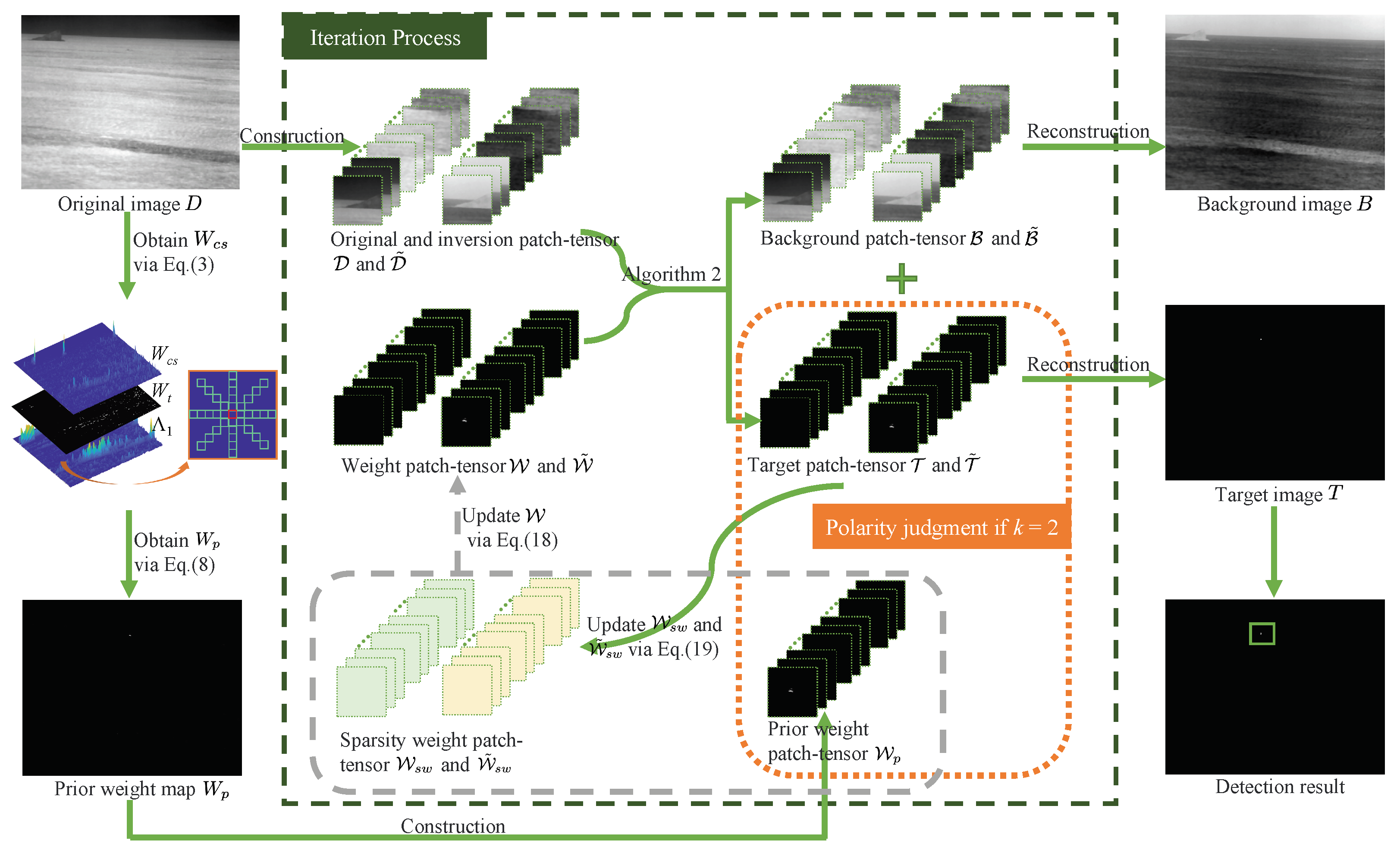
3.4. The Overall Procedure of the Proposed Method
Figure 6 shows the overall procedure of the proposed method, which can be described in the following steps:
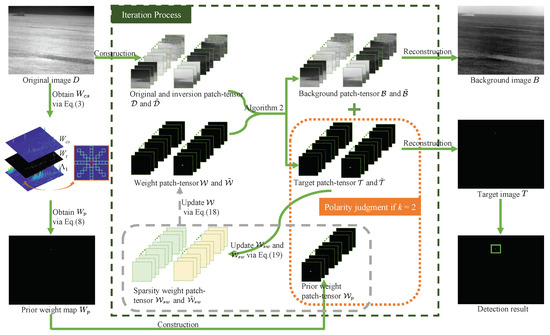
Figure 6.
The overall procedure of the proposed method. denotes the second iteration.
- Prior weight extraction. The prior weight map is extracted by Equations (3)–(8) using structure tensor and multidirectional uniformity.
- Patch-tensor construction. The patch-tensors of the original image D and its polarity reversed and prior weight are constructed by the illustration of Figure 4.
- Target-background separation and polarity judgment. The input patch-tensor and are decomposed into low-rank patch-tensors , and sparse patch-tensors , by Algorithm 2. The polarity of target is judged by comparing the similarity of the sparse components and with after two iterations.
- Image reconstruction and target extraction. When the iterative process meets the convergence condition in Algorithm 3, the background component B and target component T are reconstructed from the low-rank patch-tensor and sparse patch-tensor . The construction and reconstruction are opposite processes. Finally, the target we need to detect is obtained.
| Algorithm 3: Iteration stop judgment |
 |
| Algorithm 4: The proposed method |
 |
4. Experiments and Analysis
In this section, the experimental setup, including the dataset employed in this paper, quantitative evaluation indicators and baseline methods are introduced. Then, the parameters of the proposed method are determined by experiments. The proposed method is compared with baseline methods qualitatively and quantitatively. Finally, the running time of each method is compared.
4.1. Experimental Setup
4.1.1. The Data Set
In this paper, 14 groups of infrared maritime images of different scenes are selected to verify the effectiveness and robustness of the proposed methods. Each image sequence contains 100 frames. The size of each frame in sequence (a) is 284 × 236 and in sequence (b) to (l) is 640 × 512. Typical images in each sequence are shown in Figure 7. Among them, (a) to (e) are the scenes without island and with bright targets. (f) to (i) are the scenes with island, and (i) to (l) are the scenes with dark targets. Table 2 shows the target sizes and local mean contrast (LMC) in each sequence. LMC can be calculated by Equation (22), where represents the average grayscale of the target area, represents the average grayscale of the local background area, and the local background area is obtained by extending the target boundary by 20 pixels.

Figure 7.
Typical single frame images of 14 different scenes. (a–n) represents the image of a certain type of scene respectively.

Table 2.
Detail information contained in 14 different scenes.
4.1.2. Evaluation Metrics
In target detection, MAR, FAR, BSF and SCRG are used as evaluation indexes to evaluate the effect of the method. MAR (Missing Alarm Rate) represents the ratio between the number of missed targets calculated by the method and the number of real targets. FAR (False Alarm Rate) represents the ratio between the number of false targets detected by the method and the number of all detected targets, BSF (Background Suppression Factor) is used to represent the residual degree of background clutter in the image and to characterize the effect of background noise suppression before and after detection. SCRG (Signal-to-Clutter Ratio Gain) is used to evaluate signal-enhanced performance. MAR and FAR can be expressed by the following equations:
where MT represents the missed target, DT represents the detected real target, and FT represents the detected false target. BSF and SCRG can be represented by:
where in BSF represents the standard deviation of the hole image except for the target area, in and out represent input and output images, respectively, SCR represents the signal-to-clutter ratio of input or output signals, represents the average intensity of the target or background area, t represents the target, b represents the background, and in SCR represents the standard deviation of the local background of target. We set the size of the background in SCR as the area obtained by extending the target area boundary by 20 pixels. c is a small positive constant, which is set as 0.001 in this paper, to avoid the denominator becoming zero [55]. The larger the standard deviation of the image is, the more complex the image is, and the small and weak target is more likely to be submerged in the image with large standard deviation; otherwise, the target will be salient in the image. Therefore, the higher the BSF value of the image, the more obvious the background suppression, and the easier it is to detect the target. The larger the SCRG, the greater the saliency of the target relative to the background, indicating that the target is easier to be detected.
4.1.3. Baseline Method
We selected nine public typical baseline methods and compared them with the methods proposed in this paper to verify the effectiveness of our method, including: YOLOv5 (https://github.com/ultralytics/yolov5 (accessed on 20 July 2022 )), GST [56], FKRW [57], RLCM [19], NRAM [35], NOLC [38], PSTNN [43], SRWS [41], NTFRA [24]. Among them, YOLOv5 is a deep learning method, GST is based on structural tensor, FKRW is based on facet kernel and random walk, RLCM is based on local contrast, NRAM, NOLC, PSTNN, SRWS and NTFRA are based on principal component analysis.
In the comparison test, the parameter settings of each traditional baseline method are shown in Table 3. The parameters of baseline methods are the same as the default parameters in their open-source code except SRWS due to slower speed and non-ideal results.

Table 3.
Parameter settings for the eight baseline methods.
4.2. Analysis of Parameters
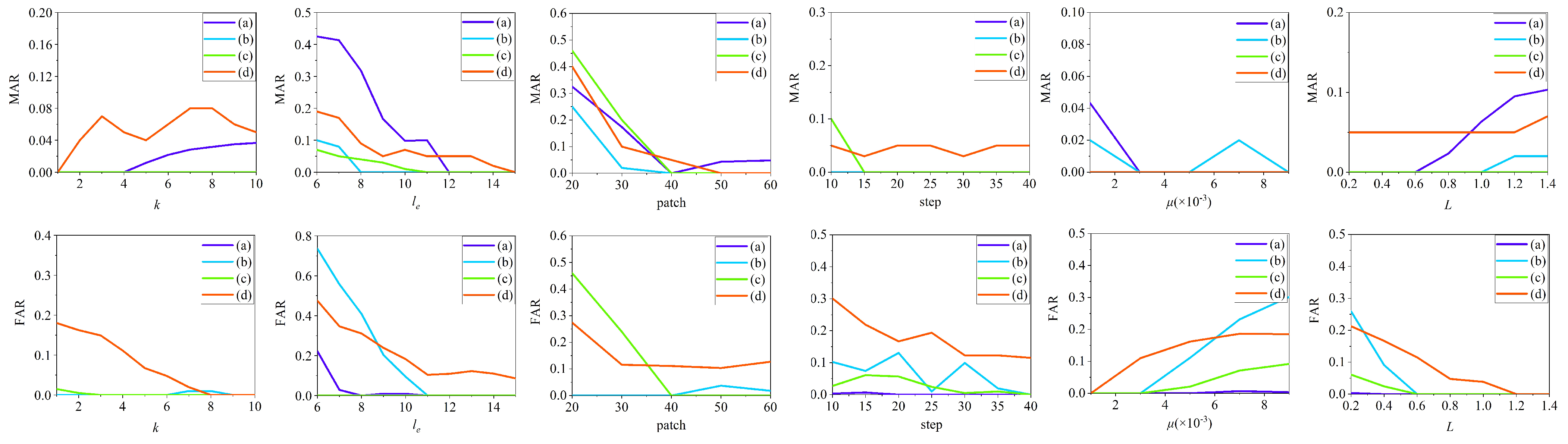
Four different scenes in Figure 1 are selected to discuss the influence of the values of each parameter in the proposed methods on detection results so as to provide a basis for the selection of parameters and obtain the best parameters to achieve the best detection results. Figure 8 shows the impact of six key parameters on the MAR and FAR.
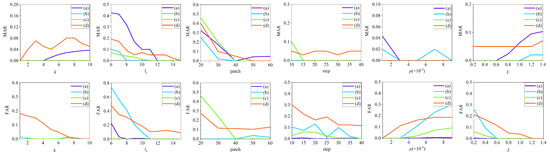
Figure 8.
Relationship between key parameters of the proposed method and FAR and MAR.
(a) Segmentation threshold k.
In the multidirectional uniformity method proposed in this paper, in order to reduce the running time, a simple adaptive threshold segmentation is first carried out. If the value of k is too large, the target with weak corner strength will be missed, and if it is too small, the running time of the method will be increased. By comparing the curves related to k in Figure 8, it can be seen that a larger value of k increases MAR and a smaller value of k increases FAR, so is taken in this paper to trade off FAR and MAR.
(b) Extended length of multidirectional uniformity .
It is necessary to determine the extended length when constructing the element-wise local multidirectional vectors. If the value of is too small to cover the size of the target, the target will be missed; if the value of is too large, other edge interference may be introduced when constructing multidirection vectors centered on the target, which will lead to missed detection. By comparing the curves related to in Figure 8, when , both the FAR and the MAR are relatively low. Considering that the value of should not be too large, is chosen as the final value in this paper
(c) Patch size.
The size of the patch in Figure 4 affects the accuracy and complexity of the method. When the patch size is large, the target has better sparsity and is easier to be separated from the background. When the patch size is small, the complexity of singular value decomposition of each patch will be reduced. By comparing the curves related to patch size in Figure 8, the ideal effect is achieved when the patch size=40, so the patch size is set as 40 in this paper.
(d) Sliding step.
The sliding step in the construction of patch-tensor should not be too small. A too small sliding step will result in insufficient sparsity of the target and increase the running time. Meanwhile, the distance should not be larger than the patch size to ensure that all information in the image is not lost. By comparing the curves related to the sliding step in Figure 8, the ideal effect is achieved when the sliding step = 40, so the sliding step is set as 40 in this paper.
(e) Penalty Factor .
controls the tradeoff between the low-rank and sparse tensors. If the value of is too small, more sparse components will remain in the low-rank background, resulting in an increase in MAR. If the value of is too large, the more background interference will be extracted into the sparse component, leading to an increase in FAR. By comparing the curves related to in Figure 8, the ideal effect is achieved when , so is set as in this paper.
(f) Compromising Parameter .
also controls the tradeoff between the low-rank and sparse tensors, which is set as with reference to [48] (, and denote the length, width and number of patches, respectively). By comparing the curves related to L in Figure 8, it can be seen that when L increases, MAR tends to increase, and when L decreases, FAR tends to increase. Therefore, is set as in this paper.
4.3. Accuracy of Polarity Judgment
The sparse-weight similarity to judge the polarity of the target proposed in this paper is not completely accurate, especially in some scenes with obvious sparse interference opposite to the polarity of the target. We counted the polarity judgment error rates for the 14 sequences in Figure 7, as shown in Table 4. Combined with Figure 7, it can be seen that there are a large number of negative polarity wave clutter in sequences (d) and (e), and a large number of positive polarity wave clutter in (i)–(l), leading to a certain amount of wrong judgments.

Table 4.
The polarity judgment error rates of 14 sequences.
4.4. The Qualitative Comparison
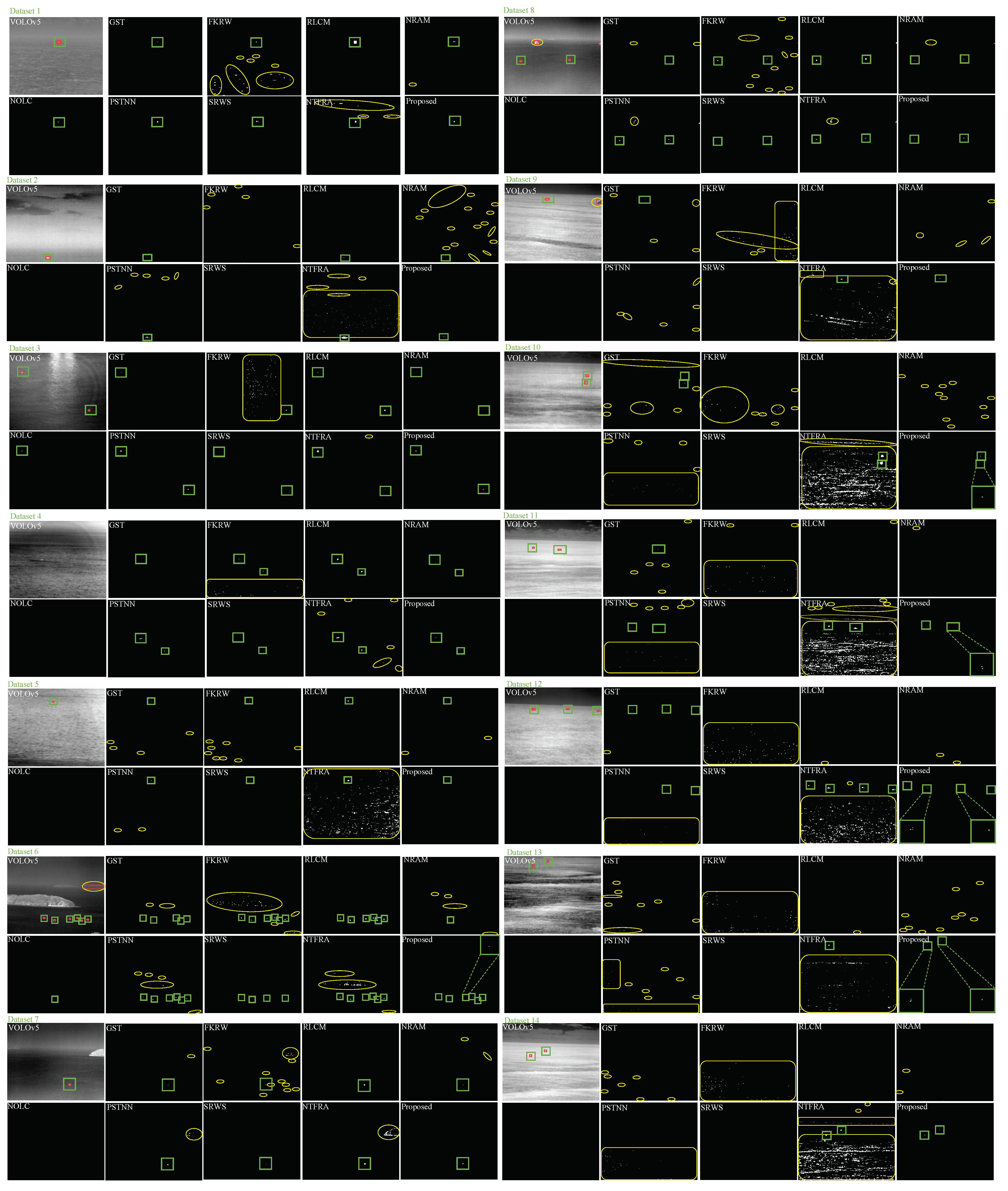
After determining the values of the parameters of the proposed method, we compared the detection results of nine baseline methods and the proposed method in 14 different sequences in Figure 7 and show representative single frame results in Figure 9. It can be seen in traditional methods that FKRW and NTFRA have higher FAR and are easily disturbed by wave clutter, while NOLC and SRWS have higher MAR. When detecting sequences with strong island edges, RLCM and the proposed method have a high suppression effect, while GST, FKRW, NRAM, PSTNN, NTFRA have a relatively poor suppression effect. Although RLCM has a good effect in detecting targets with positive polarity, the morphology of the targets is lost. When detecting sequences with negative polarity targets, GST, PSTNN, NTFRA can detect part of negative polarity targets, but they are accompanied by a large number of false alarms. VOLOv5 has a significant effect on background clutter suppression, and the main source of false alarm is misjudging islands as targets. At the same time, the phenomenon of missing detection appears in a few scenes. Due to the low multidirectional uniformity at the edge of the target, the proposed method will cause the target to shrink to a certain extent. In summary, the proposed method achieves strong robust detection for scenes with strong island edge and targets with different polarities at the cost of shrinking the detected target size.
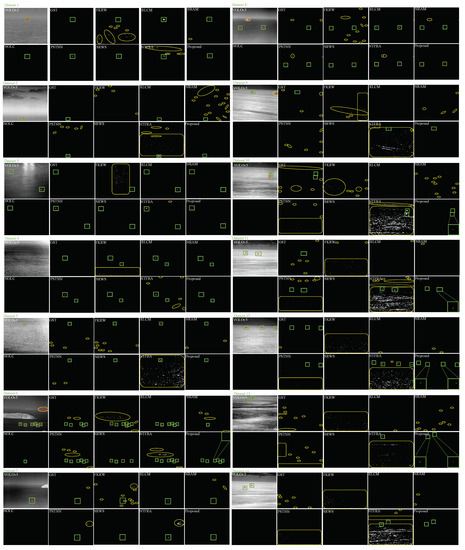
Figure 9.
Qualitative comparison of detection results of baseline methods. The red mark indicates the target detected by VOLOv5; The green marks indicate the correct targets detected by different methods; The yellow marks indicate false targets detected by different methods.
4.5. The Quantitative Comparison
In this paper, MAR, FAR, BSF and SCRG are used to measure the detection effect of the baseline methods and the proposed method. Table 5, Table 6, Table 7 and Table 8, respectively, show the comparison of average values of MAR, FAR, BSF and SCRG calculated by different baseline methods and proposed methods for 14 different sequence scenes. Each sequence contains 100 frames. For BSF and SCRG, the input image is the original image, and the output image is the image of the final result after normalization and before binarization.

Table 5.
Comparison of average MAR between the proposed method and 9 baseline methods in 14 sequence scenes.

Table 6.
Comparison of average FAR between the proposed method and 9 baseline methods in 14 sequence scenes.

Table 7.
Comparison of average BSF between the proposed method and 8 traditional baseline methods in 14 sequence scenes.

Table 8.
Comparison of average SCRG between the proposed method and 8 traditional baseline methods in 14 sequence scenes.
From the calculation results of the four parameters of MAR, FAR, BSF and SCRG, it can be seen that FKRW and NTFRA have high FAR in most scenes, NOLC and SRWS have high MAR in most scenes, and RLCM shows better detection results in scenes with positive polarity targets. Most of the methods do not have the ability to detect negative polarity targets. Although GST, RLCM and PSTNN can detect some negative polarity targets, they are accompanied by a large number of false alarms. VOLOv5 shows excellent results on many datasets and is not affected by the polarity of the target but shows high MAR and FAR on some specific datasets. Compared with other methods, the detection effect of the proposed method for negative polarity target is significant. However, compared with RLCM and PSTNN which have a better detection effect on positive polarity target, the proposed method causes some false and misalarm when detecting the positive polarity target in some cases. There are strong interferences of opposite polarity to the target in the corresponding datasets, which causes the wrong judgment of the polarity of the target. From the calculation results of BSF, it can be seen that YOLOv5 shows significant background suppression ability, although some islands are wrongly targeted. The suppression ability of the proposed method to the background interference is stronger than most traditional baseline methods. In order to suppress the strong edge islands, the multidirection uniformity method causes the target result to shrink, which leads to the proposed method having no obvious advantage compared with other methods in SCRG results. Although the results of the proposed method are not the best on some sequences when measuring either BSF or SCRG separately, the proposed method is still a better choice compared to other baseline methods when considering both BSF and SCRG parameters, which are underlined in the table. Combining the four parameters of FAR, MAR, BSF and SCRG, it can be concluded that the proposed method is more robust, can adapt to more complex scenes and has a wider range of application compared with traditional baseline methods.
4.6. Runtime Comparison
All experiments in this paper are run on a MAC computer with 2 GHz quad-core Intel Core I5 CPU and 16 GB memory. The codes of the traditional methods are implemented in MATLAB 2022a. The codes of VOLOv5 are implemented in PyCharm 2022.2. The average runtimes of the proposed method and nine other baseline methods for sequences (a) to (n) are calculated and shown in Table 9. It can be seen that the runtime of the proposed method is relatively short. Let the size of the input image be , the size of the patch-tensor be , the size of the sliding window in multidirectional uniformity be l, and x be the number of nonzero elements in Equation (5), which is a small number compared with . In the calculation of multidirectional uniformity, a sliding window is used to traverse every nonzero element in the whole image, which needs an cost. The main consumption in PSTNN lies in SVD and FFT, which requires cost, so the total computation cost of the proposed model is . Methods based on component analysis can greatly reduce the running time by GPU accelerated methods [58]. We implemented the proposed method on VS2015 by GPU acceleration technology on the server equipped with an infrared detection system in the laboratory. After acceleration, the average processing time of each frame of 14 sequential scenes is 0.047 s, which can meet the requirements of real-time monitoring in engineering.

Table 9.
Comparison of average runtime between the proposed method and 8 baseline methods in 14 sequence scenes.
5. Discussion
There is still room to improve the accuracy of infrared maritime target detection. The biggest challenge lies in the unexpected complex background and strong interference. The method based on background estimation filtering and the method based on local features make use of the global information and local information of the image, respectively, which have certain deficiencies. The optimization method based on local feature weight and structure tensors takes full account of global and local information and shows strong robustness. Some islands in infrared maritime images often cause a lot of false alarms because of their obvious edges. It is critical to reduce these interferences without affecting the intensity of the target. Therefore, we take advantage of the characteristic that the eigenvalue of the structure tensor has obvious edges features and propose the multidirectional uniformity to suppress the strong edges. Although the size of the target is shrunk to a certain extent, the detection accuracy is greatly improved. In addition, most of the methods neglect the case that the target grayscale is lower than the background, which leads to the lack of robustness in practical applications. Therefore, it is particularly important to achieve target detection with unknown polarity. The strategy of substituting images of opposite polarities into the optimization algorithm, respectively, and making polarity judgment in the second iteration and stopping the wrong polarity iteration is adopted, which can accurately judge polarity and ensure the effectiveness. After comparing with the advanced baseline methods on a large number of datasets, it can be concluded that the proposed method is more robust, although there are a small number of cases of polarity judgment errors. Deep learning-based methods also show excellent results, although the current infrared maritime datasets are still insufficient. In the future, our research focus will fall on more accurate polarity judgment and control the missed detection rate and false alarm rate in a lower range. In addition, we will consider the use of deep learning methods to obtain stronger robustness while expanding the dataset.
6. Conclusions
In this paper, an infrared maritime target detection method based on multidirectional uniformity and sparse-weight similarity is proposed. In order to detect targets of unknown polarity in infrared maritime images with strong edge interference, firstly, the problem of small infrared target detection is transformed into solving sparse and low-rank components by the TRPCA model. Due to the weak ability of suppressing strong edge interference by the prior weight obtained based on the structure tensor, the strong edge interference in the corner strength map is suppressed by constructing the elementwise scattering filed in eigenvalue and calculating the multidirectional uniformity. PSTNN is used to estimate the rank of the background patch-tensor, and ADMM with target polarity judgment based on sparse-weight similarity is used to solve the optimization model by substituting in images of opposite polarities simultaneously. In order to reduce the complexity of the method, only the polarity of the target is judged in the second step of the iterative process, and the whole method process is designed. By comparing with nine advanced methods on 14 different datasets, the proposed method shows strong robustness, which has a wide range of engineering application value.
Author Contributions
Conceptualization, E.Z.; Formal analysis, H.D.; Funding acquisition, L.D.; Investigation, E.Z.; Methodology, E.Z.; Resources, L.D.; Software, E.Z.; Supervision, L.D.; Validation, H.D.; Writing—original draft, E.Z.; Writing—review and editing, L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Fundamental Research Funds for the Central Universities of China under Grant 3132019340 and 3132019200. This paper was funded in part by high-tech ship research project from ministry of industry and information technology of the people’s republic of China under Grant MC-201902-C01.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prasad, D.K.; Rajan, D.; Rachmawati, L.; Rajabally, E.; Quek, C. Video processing from electro-optical sensors for object detection and tracking in a maritime environment: A survey. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1993–2016. [Google Scholar] [CrossRef]
- Wang, B.; Motai, Y.; Dong, L.; Xu, W. Detecting infrared maritime targets overwhelmed in sun glitters by antijitter spatiotemporal saliency. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5159–5173. [Google Scholar] [CrossRef]
- Yang, P.; Dong, L.; Xu, H.; Dai, H.; Xu, W. Robust Infrared Maritime Target Detection via Anti-Jitter Spatial–Temporal Trajectory Consistency. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7506105. [Google Scholar] [CrossRef]
- Eysa, R.; Hamdulla, A. Issues on infrared dim small target detection and tracking. In Proceedings of the 2019 International Conference on Smart Grid and Electrical Automation (ICSGEA), Xiangtan, China, 10–11 August 2019; pp. 452–456. [Google Scholar]
- Liu, D.; Cao, L.; Li, Z.; Liu, T.; Che, P. Infrared small target detection based on flux density and direction diversity in gradient vector field. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2528–2554. [Google Scholar] [CrossRef]
- Pak, J. Visual odometry particle filter for improving accuracy of visual object trackers. Electron. Lett. 2020, 56, 884–887. [Google Scholar] [CrossRef]
- Lin, G.; Fan, W. Unsupervised video object segmentation based on mixture models and saliency detection. Neural Process. Lett. 2020, 51, 657–674. [Google Scholar] [CrossRef]
- Li, B.; Zhiyong, X.; Zhang, J.; Wang, X.; Fan, X. Dim-Small Target Detection Based on Adaptive Pipeline Filtering. Math. Probl. Eng. 2020, 2020, 8234349. [Google Scholar] [CrossRef]
- Fu, J.; Zhang, H.; Luo, W.; Gao, X. Dynamic Programming Ring for Point Target Detection. Appl. Sci. 2022, 12, 1151. [Google Scholar] [CrossRef]
- Liu, J.; He, Z.; Chen, Z.; Shao, L. Tiny and dim infrared target detection based on weighted local contrast. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1780–1784. [Google Scholar] [CrossRef]
- Lv, P.Y.; Sun, S.L.; Lin, C.Q.; Liu, G.R. Space moving target detection and tracking method in complex background. Infrared Phys. Technol. 2018, 91, 107–118. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L. Multidirectional ring top-hat transformation for infrared small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8077–8088. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, X.; Wang, M. Background Suppression Algorithm for Infrared Images Based on Robinson Guard Filter. In Proceedings of the 2017 2nd International Conference on Multimedia and Image Processing (ICMIP), Wuhan, China, 17–19 March 2017; pp. 250–254. [Google Scholar]
- Wang, H.; Xin, Y. Wavelet-based contourlet transform and kurtosis map for infrared small target detection in complex background. Sensors 2020, 20, 755. [Google Scholar] [CrossRef]
- Ren, K.; Song, C.; Miao, X.; Wan, M.; Xiao, J.; Gu, G.; Chen, Q. Infrared small target detection based on non-subsampled shearlet transform and phase spectrum of quaternion Fourier transform. Opt. Quantum Electron. 2020, 52, 1–15. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, L.; Zheng, H.; Xu, W. Infrared maritime small target detection based on edge and local intensity features. Infrared Phys. Technol. 2021, 119, 103940. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared small target detection based on the weighted strengthened local contrast measure. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1670–1674. [Google Scholar] [CrossRef]
- Dong, L.; Wang, B.; Zhao, M.; Xu, W. Robust infrared maritime target detection based on visual attention and spatiotemporal filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3037–3050. [Google Scholar] [CrossRef]
- Chen, Y.; Song, B.; Wang, D.; Guo, L. An effective infrared small target detection method based on the human visual attention. Infrared Phys. Technol. 2018, 95, 128–135. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, H.; Wang, Z.; Zheng, H. The small target detection based on local directional contrast associated with directional entropy. In Proceedings of the Eleventh International Conference on Digital Image Processing (ICDIP 2019), Guangzhou, China, 10–13 May 2019; Volume 11179, pp. 609–617. [Google Scholar]
- Zhang, H.; Zhou, Z. Small target detection based on automatic ROI extraction and local directional gray&entropy contrast map. Infrared Phys. Technol. 2020, 107, 103290. [Google Scholar]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared small target detection via nonconvex tensor fibered rank approximation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–21. [Google Scholar] [CrossRef]
- Zhao, M.; Li, W.; Li, L.; Hu, J.; Ma, P.; Tao, R. Single-frame infrared small-target detection: A survey. IEEE Geosci. Remote. Sens. Mag. 2022, 10, 87–119. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 213–229. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai J F, D.D. Deformable transformers for end-to-end object detection. In Proceedings of the 9th International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar]
- Sun, Y.; Yang, J.; Long, Y.; An, W. Infrared small target detection via spatial-temporal total variation regularization and weighted tensor nuclear norm. IEEE Access 2019, 7, 56667–56682. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared patch-image model for small target detection in a single image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y.; Guo, J. Non-negative infrared patch-image model: Robust target-background separation via partial sum minimization of singular values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared small target detection via non-convex rank approximation minimization joint l 2, 1 norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y. Infrared small target and background separation via column-wise weighted robust principal component analysis. Infrared Phys. Technol. 2016, 77, 421–430. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; Zhang, P.; He, Y. Infrared dim target detection based on total variation regularization and principal component pursuit. Image Vis. Comput. 2017, 63, 1–9. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared small target detection based on non-convex optimization with Lp-norm constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef]
- Li, M.; He, Y.J.; Zhang, J. Small infrared target detection based on low-rank representation. In Image and Graphics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 393–401. [Google Scholar]
- Wang, X.; Peng, Z.; Kong, D.; He, Y. Infrared dim and small target detection based on stable multisubspace learning in heterogeneous scene. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5481–5493. [Google Scholar] [CrossRef]
- Zhang, T.; Peng, Z.; Wu, H.; He, Y.; Li, C.; Yang, C. Infrared small target detection via self-regularized weighted sparse model. Neurocomputing 2021, 420, 124–148. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted infrared patch-tensor model with both nonlocal and local priors for single-frame small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, L.; Huang, S.; Peng, Z. Infrared small target detection via non-convex tensor rank surrogate joint local contrast energy. Remote Sens. 2020, 12, 1520. [Google Scholar] [CrossRef]
- Bigün, J.; Granlund, G.H.; Wiklund, J. Multidimensional orientation estimation with applications to texture analysis and optical flow. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 775–790. [Google Scholar] [CrossRef]
- Brown, M.; Szeliski, R.; Winder, S. Multi-image matching using multi-scale oriented patches. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 510–517. [Google Scholar]
- Li, Y.; Li, Z.; Xu, B.; Dang, C.; Deng, J. Low-Contrast Infrared Target Detection Based on Multiscale Dual Morphological Reconstruction. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7001905. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Jiang, T.X.; Huang, T.Z.; Zhao, X.L.; Deng, L.J. Multi-dimensional imaging data recovery via minimizing the partial sum of tubal nuclear norm. J. Comput. Appl. Math. 2020, 372, 112680. [Google Scholar] [CrossRef]
- Oh, T.H.; Tai, Y.W.; Bazin, J.C.; Kim, H.; Kweon, I.S. Partial sum minimization of singular values in robust PCA: Algorithm and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 744–758. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted l 1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Hale, E.T.; Yin, W.; Zhang, Y. Fixed-point continuation for l_1-minimization: Methodology and convergence. SIAM J. Optim. 2008, 19, 1107–1130. [Google Scholar] [CrossRef]
- Jiang, T.X.; Huang, T.Z.; Zhao, X.L.; Deng, L.J. A novel nonconvex approach to recover the low-tubal-rank tensor data: When t-SVD meets PSSV. arXiv 2017, arXiv:1712.05870. [Google Scholar]
- Li, Y.; Li, Z.; Zhang, C.; Luo, Z.; Zhu, Y.; Ding, Z.; Qin, T. Infrared maritime dim small target detection based on spatiotemporal cues and directional morphological filtering. Infrared Phys. Technol. 2021, 115, 103657. [Google Scholar] [CrossRef]
- Gao, C.Q.; Tian, J.W.; Wang, P. Generalised-structure-tensor-based infrared small target detection. Electron. Lett. 2008, 44, 1. [Google Scholar] [CrossRef]
- Qin, Y.; Bruzzone, L.; Gao, C.; Li, B. Infrared small target detection based on facet kernel and random walker. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7104–7118. [Google Scholar] [CrossRef]
- Cui, J.; Yang, J.; Graves, E.; Levin, C.S. GPU-enabled PET motion compensation using sparse and low-rank decomposition. In Proceedings of the 2012 IEEE Nuclear Science Symposium and Medical Imaging Conference Record (NSS/MIC), Anaheim, CA, USA, 27 October–3 November 2012; pp. 3367–3370. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).