Abstract
Integration of the Global Navigation Satellite System (GNSS), with Inertial Measurement Unit (IMU) sensors to improve navigation performance, is widely used in many land-based applications. However, further application, especially in urban areas, is limited by the quality (due mainly to multipath effects) and availability of GNSS measurements, with a significant impact on performance, especially from low grade integration. To maximize the potential of GNSS measurements, this paper proposes a dual w-test-based quality control algorithm for integrated IMU/GNSS navigation in urban areas. Quality control is achieved through fault detection and exclusion (FDE) with the capability to detect simultaneous multiple faults in measurements from different satellites. The remaining fault-free GNSS measurements are fused with IMU sensor measurements to obtain the final improved state solution. The effectiveness of the algorithm is validated in a deep urban field test. Compared to the cases without fault exclusion, the results show improvements of about 24% and 30% in horizontal and vertical positioning components, respectively.
1. Introduction
The emerging mission-critical applications in urban areas are placing more stringent requirements on the underpinning positioning, navigation, and timing (PNT) systems [1]. Due to complementary characteristics, GNSS and Inertial Measurement Unit (IMU) sensors are commonly used in an integrated architecture to support location-based services. However, in urban areas, GNSS signals are susceptible to attenuation and blockage in the built environment, resulting in multipath effects and non-line of sight (NLOS) reception. The satellite faults, defined in this paper, describe corresponding measurements that have acceptable errors, irrespective of the source and type of failure. These errors in the measurements will affect the accuracy and reliability of positioning from integrated IMU/GNSS systems. Therefore, it is particularly important to develop an effective fault detection scheme that can be applied to GNSS measurements so as to ensure quality control of integrated IMU/GNSS systems.
Fault Detection and Exclusion (FDE)-based GNSS measurements quality control has been investigated for many years. The basic FDE methods include: (1) range and position comparison [2]; (2) minimum least squares residuals [3]; (3) parity space [4]; (4) maximum slope (MS) [5]. The four methods have been shown to be largely equivalent.
The performance of FDE algorithms is related to GNSS signal quality and the number of visible satellites. With the increase in constellations beyond GPS, there are more visible satellites and better signal design, greatly improving positioning quality, and promoting the development of FDE algorithms. Some new FDE algorithms have appeared, such as: GPS Integrity Channel (GIC), which is a hybrid between the GIC approach and the maximum solution separation RAIM technique [6]; Novel Integrity Optimized RAIM [7]; Optimally Weighted Average Solution [8]. Given that the probability of multiple faults in a single constellation is relatively small, the above FDE algorithms assume a single fault at a time.
In medium to high density built environments coupled with the increase in the number of constellations, the probability of simultaneous multiple faults increases. Therefore, increasing research effort is dedicated to developing algorithms for simultaneous multiple FDE. These methods include the use of statistics, calculated based on the w-test, to detect and identify outlier faults [9]. A theoretical analysis of the principle of double satellites faults in 2009, as well as their successful elimination through experiments, is presented in [10]. The Solution Separation (SS) algorithm was also applied to Advanced RAIM (ARAIM) research [11]. A point to note is that, for 4-D positioning and geometry permitting, there must be at least five visible satellites for fault detection and at least six visible satellites for fault exclusion in a single constellation. When the number of satellites is insufficient, these FDE algorithms are unavailable, thus affecting the quality of GNSS positioning with potential safety risks.
To address the problem of GNSS measurement quality, additional sensors are also used to aid GNSS FDE by considering the various error characteristics of each sensor [12].
Comparison of FDE performance, based on loosely-coupled and tightly-coupled IMU/GPS integration modes, is also analyzed in some literature [13,14]. A multiple fault detection and elimination algorithm, based on pseudorange comparison, is proposed and used for vehicle GNSS/IMU integrated navigation and positioning [15], but it needs initial database generation. In real situations, multipath effects and poor user-satellite geometry result in excessive positioning errors in urban areas, and the methods above cannot verify the correctness or reliability of the FDE algorithms. In addition, the a priori parameters of the measurement covariance matrix cannot be determined in these urban areas. This increases the probability of incorrect fault detection resulting in excessive final positioning errors. A series of adaptive Kalman filters (AKF) have been developed to overcome the limitation of using a priori statistics to model errors that have time-varying characteristics [16,17,18]. The adaptive indicators may take on a range of roles, including an adjustment of the covariance matrix of the state estimation vector, the covariance matrix of the process vector, and the covariance matrix of measurement vector [19,20,21]. None of the adaptive indicators in the above fusion methods, however, have been adjusted specifically for the errors caused by multipath signals and NLOS that are common in urban areas.
In recent years, with the continuous emergence of multi-sensors, the integrated navigation system of multi-source fusion has also ushered in a vigorous development. Altimeter, wheel odometer, magnetometer, etc., improve the accuracy and reliability of navigation information by providing additional information such as position, speed, and altitude to the GNSS/IMU integration system. From the perspective of technology integration, the research on the integration of GNSS, INS, and emerging visual navigation technology is extremely hot. Li developed a semi-tightly coupled GNSS PPP/S-VINS integration framework for better navigation performance in urban environments [22]. On this basis, Li further studied GNSS/LiDAR/INS tightly coupled integrated navigation [23]. However, the above method is in the theoretical research stage, and the high cost of the sensor is not conducive to popularization.
Another idea for quality control is to assign appropriate weights to the GNSS measurements to mitigate the effects of multipath/NLOS signals. The commonly used method is to determine weight based on the quality of GNSS signals. This usually involves the use of one or more characteristics of GNSS signals (e.g., satellite elevation angle, C/N0, or a combination of the two) to assign corresponding weights to GNSS measurements. Other weighting-based quality control methods include Huber [24], Bifactor reduction model [25], Robust estimation based on M-estimation principle [26], Robust Bayesian estimation [27], and Danish [28]. However, application of appropriate weighting, in different scenarios in urban environments, is difficult. Given the limitations of the state-of-the-art methods above, this paper proposes a dual w-test-based quality control algorithm for integrated IMU/GNSS navigation in urban environments. The contributions are summarized below.
(1) A dual w-test is proposed, which achieves multiple fault detection from the observation domain, thus solving the problem of false alarms in the traditional w-test.
(2) A range detection is proposed to detect the subsets generated after dual w-test, and a scoring strategy is proposed to select the optimal subset. Starting from the location domain, the proposed algorithm is able to reduce the miss detection rate and, therefore, ensure the quality of the output position.
2. Algorithm Design
The proposed tightly-coupled algorithm is illustrated in Figure 1 and comprises two parts. In the first part, a dual w-test-based FDE model is designed for multiple failure detection in urban areas. In the second part, a scoring strategy is used to exclude faulty measurements. The remaining satellites are then fused with IMU sensor measurements to compute the final state.
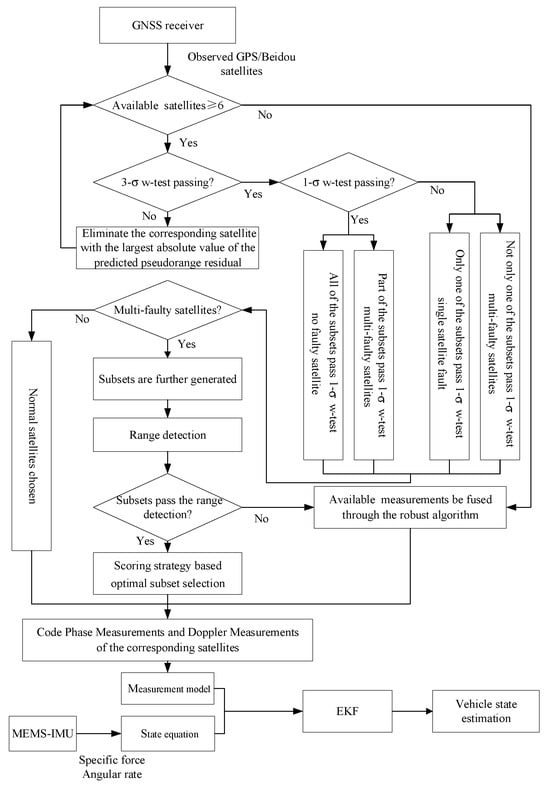
Figure 1.
System Framework.
2.1. Dual w-Test
2.1.1. Traditional w-Test
Due to the non-linear relationship between the GNSS pseudorange observation and state variables [29], the linearized pseudorange observation equation can be written as (1).
Here, is the difference between the observed pseudorange and computed pseudorange from the initial state, is the measurement matrix, is the user’s state vector, and is the observation error vector. The weighted least squares solution for the state vector is (2).
where, is the weighting matrix. With , based on Equation (2), the residual vector is derived as:
After obtaining the residual vector , the sum of the squares of the residual or error (SSE) vector is used as the statistics for GNSS fault detection, which is defined as (4)
Based on weighted least squares residuals, GNSS pseudorange measurements with significant errors are detected and eliminated by overall and local inspection methods. The overall test assumes that when observations do not contain gross errors, the observation errors follow the Gaussian distribution. Hence, the statistic SSE follows the chi-square distribution with degrees of freedom (n − m), where n is the total number of satellites observed, and m is the dimension of the state. When the test statistic exceeds the global threshold, there is at least one faulty satellite. The global test threshold is:
where is the probability of false alarm, which is selected according to specific application scenarios, and denotes the probability density of the chi-square distribution. When the statistic exceeds the global threshold, it is necessary to find the failing measurement or gross error in observations, using the traditional w-test. The test normalizes the residual as a new statistic. The specific expression is (6):
where is the unit vector whose i-th element is 1. When the i-th observation has no error, the variance of the corresponding observation noise is , with following the normal distribution . is then compared with the w-test threshold . If exceeds the threshold, it is considered that the corresponding observation contains gross error. Then, the traditional w-test eliminates the corresponding satellite. The expression of the w-test threshold is:
The traditional w-test only identifies one faulty satellite at a time, and the corresponding satellite is eliminated. At the same time, in order to confirm whether there are any faulty satellites in the remaining satellites, all the remaining satellites after w-test are regarded as a new corpus again, and a new round of fault detection is performed. Therefore, the w-test method is suitable for the case of highly redundant observation data, and it is assumed that only one failure occurs at a time. In urban environments, however, this condition may not be met. Therefore, this paper adopts and w-test double w-test, as shown in the following subsection.
2.1.2. and Dual w-Test
Different from the traditional w-test, this paper firstly adopts w-test. The first w-test is to prevent the observation noise variance from being too small, as well as too strict, for the corresponding w-test threshold. At the same time, in the w-test, the method of excluding satellites is not to eliminate the corresponding satellite, but it is to eliminate the corresponding satellite with the largest absolute value of the predicted pseudorange residual when the exceeds the threshold. The predicted pseudorange residual is calculated as (8):
where, is the observed pseudorange, is the pseudorange predicted by IMU, is the geometric range between the observed satellite and the user position estimated by IMU. and are the receiver and satellite clock errors, respectively, and are tropospheric and ionospheric corrections, respectively. The can be calculated as (9):
is the satellite position at epoch , is user positions estimated using IMU data at epoch . However, due to the complexity of urban environments, it is impossible to ensure correct detection using the w-test. Therefore, the positions calculated before and after each w-test are saved until either no faulty satellite measurements are detected or the number of remaining observed satellites is insufficient. Then, in order to ensure that multiple faults can be detected, this paper takes each subset obtained after the w-test, removing a satellite each time, and performing the w-test on each subset. The results can be one of four cases:
- The universal set and all subsets pass the w-test.
- The universal set and some subsets pass the w-test.
- The universal set does not pass the w-test, and only one of the subsets passes the w-test.
- The universal set does not pass the w-test, with more than one subset passing the w-test.
The fault conditions at a given epoch can be determined by considering the test results in these four cases. In case 1, we consider that there is no faulty satellite at this epoch, as the universal set and all subsets have passed the w-test. In case 2, the high correlation of each satellite will result in the universal set passing the test, while the low correlation of the faulty satellite in the subset, after one satellite exclusion, can result in the subset not passing the test. Therefore, in this case, we consider that there are multiple faults. In case 3, as a single satellite fault can lead to the universal set not passing the w-test, the subset can only pass the w-test in the case that the faulty satellite is excluded. Therefore, a single fault case is considered in this case. In case 4, faulty satellites in the universal set and subsets can lead to the failure to pass the w-test for a part or all of the subsets. Therefore, the existence of multiple faults is considered in this case. Satellite selection is then made according to the fault conditions. In case 1, all of the satellites at this epoch are selected for a further GNSS/IMU integration. In case 3, the satellites in the subset, which passed the w-test, are selected for further fusion. Considering cases 2 and 4 with multiple faults, the subsets are further generated, which are then subjected to range detection. The range is calculated by the difference between the predicted position estimated by the IMU data and the position calculated by the selected subset in the proposed algorithm. The expression for range detection is:
where and are, respectively, the latitude and longitude corresponding to the predicted position. and , respectively, are the coordinates of the calculated position and the predicted position in the WGS-84 coordinate system. Then,,, and are compared with the range threshold. Here, the threshold of the range value is set as 17 m, as the city speed limit is around 60 km/h (i.e., 17 m/s). Only the subsets that pass the range detection test are used further for the optimal subset selection.
2.2. Scoring Strategy Based Optimal Subset Selection
After range detection, the subsets that pass the test are selected. The optimal subset within these selected subsets is chosen, and the corresponding measurements in the optimal subset are used to integrate with the IMU data to calculate position. The strategy uses a scoring mechanism to subtract the positions calculated using the selected subsets from the predicted position at the current epoch. The predicted position can be obtained from that of the previous epoch combined with inertial navigation information. The difference in position is then scored according to the following formula, based on a weighting method, in which the smaller the the higher the score. Finally, the satellites corresponding to the position difference with the highest score are selected to be combined with the inertial navigation. The is calculated as:
Here, are the maximum values of longitude, latitude, and height difference among all the position differences. , and are the minimum values of longitude, latitude, and height difference among all the position differences. are all the longitude, latitude, and height difference among all the position differences.
2.3. IMU/GNSS Integration
In this section, an Extended Kalman Filter (EKF), based on linearization of nonlinear models, is used as the data fusion algorithm [30]. The state vector for the EKF is:
where, , , and are the three-axis error vectors of IMU position, velocity, altitude in the ECEF framework ; , , , and are the three-axis acceleration and gyroscope bias and scale factor error; and are the receiver clock error and drift rate of GPS satellite; and are the clock error and drift rate of Beidou satellite. The system model is then formed as a first-order state equation in (13):
where is the first derivative of . is the dynamic transition matrix, is the noise driven matrix, and is the system noise. The measurement model is given by:
where is the measurements vector, is the measurement mapping matrix, and represents the measurement noise. In this paper, if the number of visible satellites is , the pseudorange error and the Doppler measurement error are used to form measurement vector as:
where and denote IMU-derived GNSS pseudorange and Doppler measurements respectively. Based on the derivations in [30], and refer to pseudorange and Doppler measurements decoded from GNSS observation data, respectively. and refer to the number of GPS and BDS visible satellites. After discretization of (13) and (14), the discrete form of the Kalman filtering procedure can be split into two stages, as follows:
Prediction stage:
Update stage:
where, is the system state vector estimates at time epoch ; is the system transition matrix at time epoch ; is the error covariance matrix at time epoch ; is the system noise covariance matrix at time epoch ; is the measurement noise covariance matrix at time epoch ; is the measurement matrix at time epoch ; is the Kalman gain matrix at time epoch ; is the matrix/vector propagation from time epoch to .Table 1 has illustrated the parameters and their value or initial value used for the EKF. The setting of the system noise covariance matrix is based on experience. The means that the matrix is a diagonal matrix and the values in the bracket are the diagonal elements. The initial value of error covariance matrix of the state vector , noted as , is calculated by the historical data collected from the IMU and GNSS receiver. The covariance matrix of the measurement noise is set based on the statistical data collected from GNSS receiver.

Table 1.
The parameters used for the EKF.
If positions calculated by all subsets do not pass the range detection test or the number of satellites cannot meet the condition of the w-test, then all the satellite measurements and the inertial navigation output information are fused through the robust algorithm. The robust algorithm introduces a fault detection factor to scale . is given as:
is the innovation sequence, which exhibits a white Gaussian sequence of mean zero and covariance where . is a constant value, which is valued according to the specific scenario. Then, the elements in are given as:
3. Test and Validation
3.1. Simulation
Faults are simulated and added to data from UAV flight tests to test the proposed quality control algorithm. The UAV flight data were collected in Nantou City, Taiwan, shown in Figure 2. The UAV used in the test is AXH-E230 from AVIX Technology (Toronto, ON, Canada), and it was flown semi-automatically with a smart power control module to perform autonomous intelligent navigation flight mission. The onboard equipment setup included: (1) a dual-frequency GNSS receiver, Trimble BD 982 (Sunnyvale, CA, USA), with a sampling rate of 10 Hz for the raw pseudorange measurements collection; (2) a STIM-300 IMU (Sensonor, Horten, Norway), with a sampling rate of 100 Hz for UAV acceleration and angular rate collection; (3) an on-board VLP-16 Velodyne Lidar (San Jose, CA, USA) to provide centimeter-level positioning accuracy for the reference trajectory generation in the experiment. The speed of UAV was less than 10 m/s during the flight, and the height was about 60 m AGL (with the ground elevation around 120 m). The fault scenarios in Table 2 were specified in order to compare the proposed algorithm with the traditional IMU/GNSS tightly-coupled (TC) without fault exclusion, the TC with traditional w-test quality control (FDE TC), and the TC with Robust filter (AKF TC) in [31].
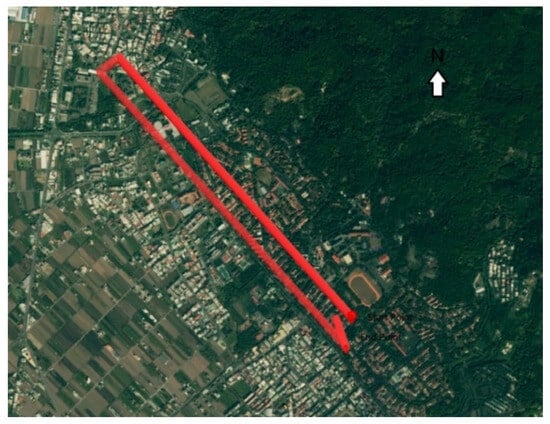
Figure 2.
Unmanned aerial vehicle (UAV) flight trajectory.

Table 2.
The defined scenarios.
In the different scenarios above, for each selected satellite, an error of 10 m, 30 m, or 50 m was injected into the pseudo-range observation of the satellite during the corresponding fault duration. Based on the derivations in [32], UAV flight in the urban environment is subjected to multipath interference to produce similar errors, with error magnitudes less than 10 m having little impact on the satellite navigation and positioning results, and is hence ignored as constituting failure. At the same time, considering the characteristics of UAV in urban low-altitude areas, fault duration is selected as 30 s. In order to verify the validity of the algorithm, in terms of accuracy, this paper uses the Root Mean Square Error (RMSE) metric to compare the performance of the TC, FDE TC, AKF TC, and the proposed methods. The errors of the position, calculated from the candidate algorithms, are shown in Figure 3. The RMSE of the positions for the candidate algorithms are represented in Table 3.
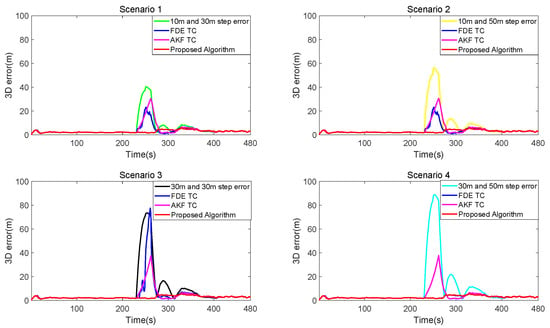
Figure 3.
The positioning error of TC, FDE TC, AKF TC, and the proposed algorithm in the four fault scenarios.

Table 3.
Comparison of algorithm performance between TC, FDE TC, AKF TC, and the proposed algorithm in the different fault scenarios.
It can be seen, in Figure 3, that TC position error increases rapidly after pseudorange errors are introduced in the four scenarios. This indicates that, without FDE, the IMU/GNSS integrated navigation positioning quality is seriously degraded and results in divergence in the filter estimated results. Therefore, quality control of the GNSS measurement is essential. Meanwhile, by observing the position errors of the FDE TC in different scenarios, it can be seen that, in most cases, when two satellites simultaneously fail, the performance of FDE TC is poor. Only when one satellite has a 30 m step error, and one satellite has a 50 m step error, does FDE TC correctly identify the two faulty satellites in all epochs and eliminate them.
In the other three scenarios, however, the corresponding faulty satellites could not be correctly detected and excluded in all epochs by FDE TC, resulting in a large positioning error. In scenario 3, the maximum positioning error of the FDE TC method even exceeds that of the traditional TC. This is mainly because, in scenario 3, the two satellites add the same step error. As a result, the test statistics of other satellites are strongly correlated with the two faulty satellites, resulting in the maximum test statistics exceeding the traditional w-test threshold. When the satellite with the maximum test statistics exceeding the threshold is eliminated based on a traditional w-test, the redundancy of the observation data is further reduced, so the remaining faulty satellite cannot be detected in the subsequent traditional w-test. The satellite faults still exist in the GNSS measurements, so the positioning performance of the FDE TC is comparable to that of the traditional TC without FDE. It can be seen from Table 3 that the FDE TC, in the above four different scenarios, has similar accuracy to the traditional TC in some cases. However, in scenarios 1 and 2, the FDE TC can still eliminate all faulty satellites in some epochs, but the faulty satellites cannot be correctly eliminated all the time by FDE TC. As a result, the positioning performance of FDE TC is improved by 49% and 62% compared with the traditional TC, respectively. On the other hand, although AKF TC cannot eliminate faults, it reduces the weight of fault observations, thus ensuring the navigation performance to a certain extent. The positioning performance of AKF TC is improved by 35%, 52%, 61%, and 67% compared with the traditional TC, respectively.
However, compared with the above algorithm, the proposed algorithm significantly improves positioning accuracy. This also shows that the proposed algorithm can correctly detect the satellites with the step errors in the above four different cases. The 3D positioning RMSE of the algorithm proposed in this paper, in four different fault scenarios, is 2.98 m. Compared with 9.62 m, 13.04 m, 17.36 m, and 20.73 m of the traditional TC, the accuracy is improved by 69.07%, 77.17%, 82.85%, and 85.64%, respectively. In summary, the above results show that the algorithm proposed in this paper can correctly detect the faulty satellites in the real-data field scenarios with the simulated step errors. Compared with the traditional TC, FDE TC, and AKF TC, it is able to provide a significant improvement in the position solutions.
3.2. Field Test
In order to further validate the performance of the proposed algorithm in an urban environment, a field test was carried out in a deep urban environment in Taipei. The experimental data acquisition equipment contained a low-cost IMU Stim-300 and a GNSS receiver Trimble BD 982, with a sampling rate of 250 Hz and 1 Hz, respectively. The reference trajectory was obtained by an integrated high-grade GNSS receiver and iNAV-RQH IMU with the commercial software NovAtel Inertial Explorer. The experimental test environment is shown in Figure 4, and the reference trajectory is shown in Figure 5. PDOP values during the test are always very high, with the highest value above 16, exhibiting the characteristics of the deep urban environment, as seen in Figure 6. The number of visible satellites is shown in Figure 7.

Figure 4.
Environments of field test.
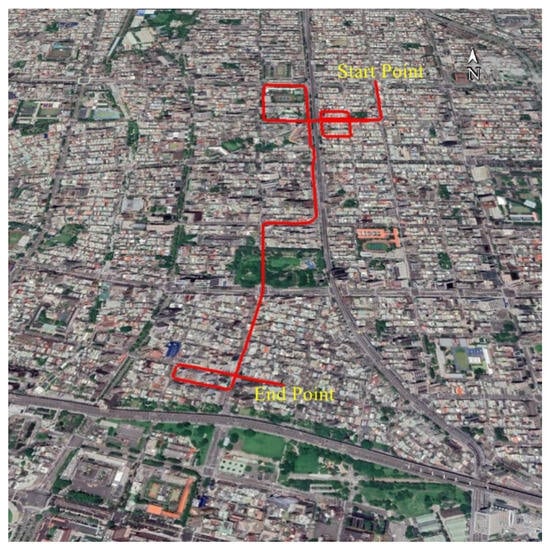
Figure 5.
Vehicle trajectory in field test.
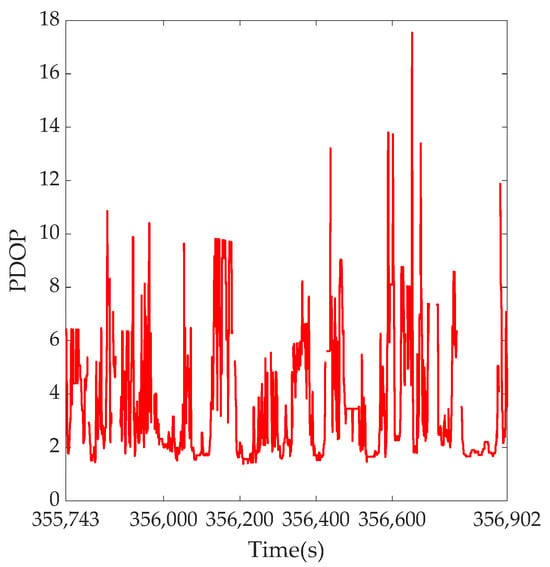
Figure 6.
PDOP in field test.
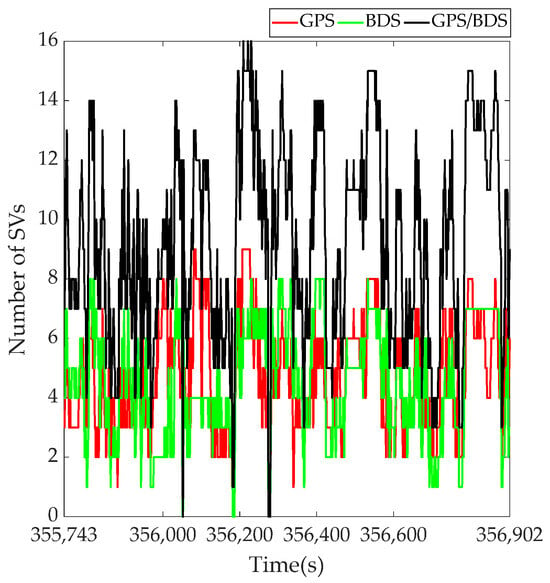
Figure 7.
Visible satellite number in field test.
In order to evaluate the performance of the proposed algorithm, the results of the proposed algorithm are compared with those of the traditional TC, FDE TC, and AKF TC. The errors in position, velocity, and altitude, calculated from the algorithms, are shown in Figure 8, Figure 9 and Figure 10. The accuracies (RMSE) of the position, velocity, and altitude for the algorithms are given in Table 3, Table 4, Table 5 and Table 6.
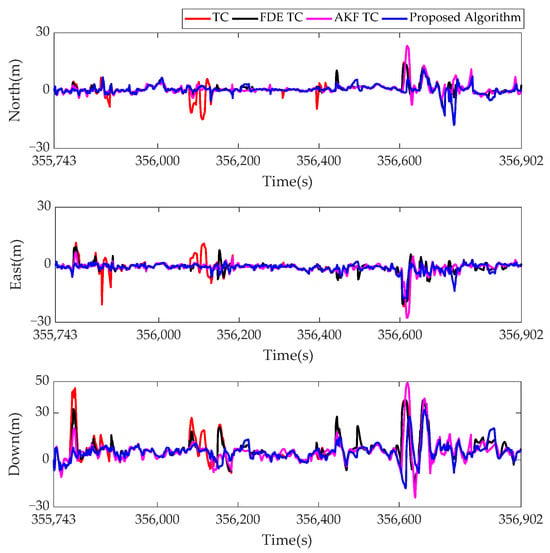
Figure 8.
The position error of TC, FDE TC, AKF TC, and the proposed algorithm in field test.

Figure 9.
The velocity error of TC, FDE TC, AKF TC, and the proposed algorithm in field test.
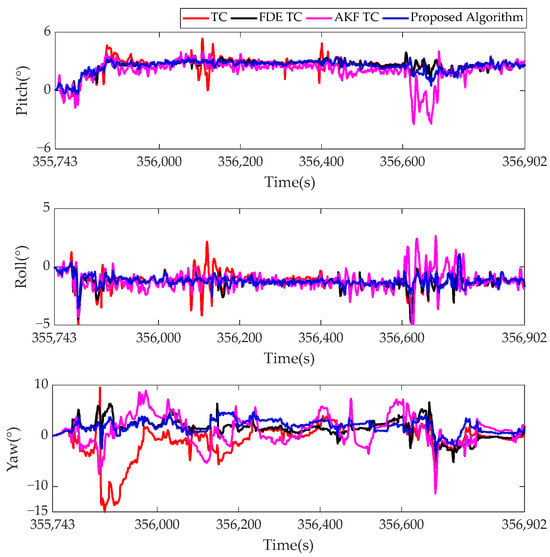
Figure 10.
The altitude error of TC, FDE TC, AKF TC, and the proposed algorithm in field test.

Table 4.
The position RMSE of TC, FDE TC, AKF TC, and the proposed algorithm in field test.

Table 5.
The velocity RMSE of TC, FDE TC, AKF TC, and the proposed algorithm in field test.

Table 6.
The altitude RMSE of TC, FDE TC, AKF TC, and the proposed algorithm in field test.
From Figure 8 and Table 3, the AKF TC position RMSE is 4.40 m in the horizontal direction and 8.94 m in the vertical direction (Down), which is an improvement of 11.65% and 17.15% compared to the 4.98 m and 10.79 m of the TC. The FDE TC vertical position RMSE is 9.66 m, whose performance is not as good as AKF TC, but the performance is better in the horizontal direction. However, neither is as much improved as the algorithm proposed in this paper. The position RMSE of the algorithm proposed is 3.79 m and 7.51 m in the horizontal and vertical directions. The results represent improvements of 23.90% and 30.40% compared to TC without FDE, 7.79% and 22.26% over FDE TC, as well as 13.86% and 15.88% over AKF TC, respectively. As shown in Figure 11, the algorithm proposed in this paper has a better performance in urban environments in the horizontal directions.
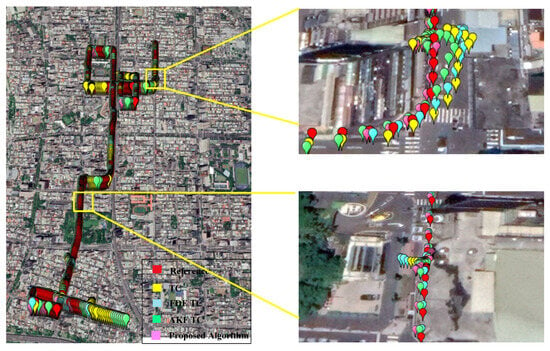
Figure 11.
Trajectory comparison for TC, FDE LC, AKF TC, and the proposed algorithm in field test.
It can be seen from Figure 9 and Table 5 that the horizontal and vertical velocity RMSE of the traditional TC scheme without FDE are 0.98 m/s and 1.07 m/s, with the corresponding values, from the proposed algorithm, of 0.59 m/s and 0.72 m/s. These correspond to improvements of 40% and 33%, respectively. While the AKF TC gives an RMSE for horizontal velocity of 0.89 m/s, the performance in the vertical direction deteriorates by 13.08% due to its inability to be accurately adjusted, specifically, for the errors caused by multipath signals and NLOS that are common in urban areas. Compared with the 0.73 m/s and 0.93 m/s of FDE TC, the proposed algorithm in this paper improves by 19% and 23%. This shows that correct fault detection and elimination is effective for quality control.
For the performance of altitude determination in Figure 10 and Table 6, pitch, roll, and yaw RMSE of the traditional TC scheme without FDE are 2.70°, 1.39°, and 3.43°, with the corresponding values from the FDE TC of 2.62°, 1.38°, and 2.28°. These correspond to improvements of 2.96%, 0.72%, and 33.53%, respectively. It is worth noting that the correction of yaw information has always been a difficult problem in the GNSS/IMU integrated navigation algorithm, and the yaw RMSE of FDE TC has dropped by 27.6%. This further illustrates the importance of quality control. While the AKF TC gives an RMSE for pitch angle of 2.33°, the performance in the roll angle deteriorates by 2.88%, and there is less improvement in the yaw angle. The proposed algorithm has improved the estimation results of pitch angle, roll angle, and yaw angle by 2%, 8%, and 1% compared with FDE TC, respectively. Although the performance of the proposed algorithm in this paper is not good in the pitch angle, compared with AKF TC, the overall performance of the proposed algorithm in this paper is better, which improves by 11.19% and 27.60% in roll and yaw angles.
4. Conclusions
This paper has developed a dual w-test-based quality control algorithm for IMU/GNSS integrated navigation in urban areas. Simulation and field test results show that the proposed algorithm is capable of achieving quality control for integrated IMU/GNSS navigation. The experimental results in deep urban environments show that the proposed integration algorithm can improve positioning accuracy compared to the cases without fault exclusion by about 24% and 30%, compared to FDE TC by about 8% and 22%, and compared to AKF TC by about 14% and 16% in the horizontal and vertical directions, respectively. However, the current work does not suit for the case of insufficient visible satellites, as the dual w-test cannot be carried out without enough of a degree of freedom in the statistic SSE. In future work, we will continue to develop more advanced quality control methods, including seeking a better robust algorithm when the number of satellites is insufficient and designing a corresponding failure detection algorithm according to the failure mechanisms of different sensors, such as inertial sensors, vision sensors, and lidar.
Author Contributions
Conceptualization, M.Q. and R.S.; Data curation, F.L.; Formal analysis, M.Q.; Methodology, M.Q. and R.S.; Software, F.L.; Supervision, Z.W. and W.Y.O.; Writing—original draft, M.Q.; Writing—review & editing, R.S. and W.Y.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the sponsorship of the National Natural Science Foundation of China under Grant 71731001, U1933130, 41974033, 42174025, in part by Natural Science Foundation of Jiangsu Province under Grant BK20211569 and in part by Zhe Jiang Key laboratory of General Aviation Operation technology (General Aviation Institute of Zhejiang JianDe) under Grant JDGA2020-11.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
References
- Du, Y.; Wang, J.; Rizos, C.; El-Mowafy, A. Vulnerabilities and integrity of precise point positioning for intelligent transport systems: Overview and analysis. Satell. Navig. 2021, 2, 3. [Google Scholar] [CrossRef]
- Lee, Y.C. Analysis of range and position comparison methods as a means to provide GPS integrity in the user receiver. In Proceedings of the The User Recver Us Institute of Navigation Annual Meeting, Seattle, WA, USA, 24–26 June 1986; Volume 42, pp. 1–4. [Google Scholar]
- Parkinson, B.W.; Axelrad, P. A basis for the development of operational algorithms for simplified GPS integrity checking. In Proceedings of the Satellite Division’s First Technical Meeting, Colorado Spring, CO, USA, 21–25 September 1987. [Google Scholar]
- Sturza, M.A. Navigation system integrity monitoring using redundant measurements. Navigation 1988, 35, 483–501. [Google Scholar] [CrossRef]
- Brown, R.G.; Mcburney, P.W. Self-Contained GPS integrity check using maximum solution separation. Navigation 1988, 35, 41–53. [Google Scholar] [CrossRef]
- Virball, V.G.; Michalson, W.R. A GPS integrity channel based fault detection and exclusion algorithm using maximum solution separation. In Proceedings of the Position Location and Navigation Symposium, IEEE, Las Vegas, NV, USA, 11–15 April 1994. [Google Scholar]
- Hwang, P.Y.; Brown, R.G. RAIM-FDE revisited: A new breakthrough in availability performance with NIORAIM (novel integrity-optimized RAIM). Navigation 2006, 53, 41–52. [Google Scholar] [CrossRef]
- Lee, Y.C.; Fernow, J.P.; McLaughlin, M.P. GPS and Galileo with RAIM or WAAS for vertically guided approaches. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; pp. 302–326. [Google Scholar]
- Hewitson, S.; Wang, J. GNSS Receiver Autonomous Integrity Monitoring (RAIM) for multiple outliers. Eur. J. Navig. 2006, 4, 47–57. [Google Scholar]
- Knight, N.L.; Wang, J.; Rizos, C. GNSS integrity monitoring for two satellite faults. In Proceedings of the International Global Navigation Satellite Systems Society IGNSS Symposium 2009, Surfers Paradise, Australia, 1–3 December 2009. [Google Scholar]
- Joerger, M.; Stevanovic, S.; Chan, F.C.; Langel, S.; Pervan, B. Integrity risk and continuity risk for fault detection and exclusion using solution separation ARAIM. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Bruggemann, T.S. GPS fault detection with IMU and aircraft dynamics. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 305–316. [Google Scholar] [CrossRef]
- Petovello, M.G. Real-Time Integration of a Tactical-Grade IMU and GPS for High-Accuracy Positioning and Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2003. [Google Scholar]
- Hewitson, S.; Wang, J. GNSS receiver autonomous integrity monitoring with a dynamic model. J. Navig. 2007, 60, 247–263. [Google Scholar] [CrossRef]
- Sun, R.; Wang, J.; Cheng, Q.; Mao, Y.; Ochieng, W.Y. A new IMU-aided multiple GNSS fault detection and exclusion algorithm for integrated navigation in urban environments. GPS Solut. 2021, 25, 147. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive kalman filtering for INS/GPS. J. Geodesy. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Hide, C.; Moore, T.; Smith, M. Adaptive kalman filtering for lowc ost INS/GPS. J. Navig. 2003, 56, 143–152. [Google Scholar] [CrossRef]
- Xiao, Z.; Zhao, P.; Li, S. Adaptive fuzzy Kalman filter based on INS/GPS integrated navigation system. J. Chin. Inert. Technol. 2010, 18, 203. [Google Scholar]
- Xian, Z.; Hu, X.; Lian, J. Robust innovation-based adaptive Kalman filter for INS/GPS land navigation. In Proceedings of the Chinese Automation Congress, Changsha, China, 7–8 November 2013; pp. 374–379. [Google Scholar]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive Kalman filter for integrated INS/GPS navigation of autonomous vehicles. Mech. Syst. Signal Process 2018, 100, 605–616. [Google Scholar] [CrossRef]
- Yan, F.; Li, S.; Zhang, E.; Chen, Q. An intelligent adaptive Kalman filter for integrated navigation systems. IEEE Access 2020, 8, 213306–213317. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Liao, J.; Li, X.; Lyu, H. Semi-tightly coupled integration of multi-GNSS PPP and S-VINS for precise positioning in GNSS-challenged environments. Satell. Navig. 2021, 2, 1. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Li, S.; Feng, S.; Wang, X.; Liao, J. GIL:a tightly coupled GNSS PPP/INS/LiDAR method for precise vehicle navigation. Satell. Navig. 2021, 2, 17. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Zhang, W.; Zuo, J.; Wang, H. Derivative-free huber-kalman smoothing based on alternating minimization. Signal Process 2019, 163, 115–122. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geodesy 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, M.K.; Shum, C.K.; Tapley, B.D. Robust estimation of systematic errors of satellite laser range. J. Geodesy 1999, 73, 345–349. [Google Scholar] [CrossRef]
- Yang, Y. Robust bayesian estimation. J. Geodesy 1991, 65, 145–150. [Google Scholar]
- Kuusniemi, H.; Wieser, A.; Lachapelle, G.; Takala, J. User-level reliability monitoring in urban personal satellite-navigation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1305–1318. [Google Scholar] [CrossRef]
- Teunissen, P. Quality control and GPS, chapter 7. In GPS for Geodesy, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Sun, R.; Zhang, W.; Zheng, J.; Ochieng, W.Y. GNSS/INS integration with integrity monitoring for UAV No-fly zone management. Remote Sens. 2020, 12, 524. [Google Scholar] [CrossRef]
- Wu, F.; Nie, J.; He, Z. Classified adaptive filtering to GPS/INS integrated navigation based on predicted residuals and selecting weight filtering. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 261–264. [Google Scholar]
- Cheng, Q.; Chen, P.; Sun, R.; Wang, J.; Mao, Y.; Ochieng, W.Y. A new faulty GNSS measurement detection and exclusion algorithm for urban vehicle positioning. Remote Sens. 2021, 13, 2117. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).