Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Signal Model
2.2. Proposed Method
2.2.1. Cyclic Minimization
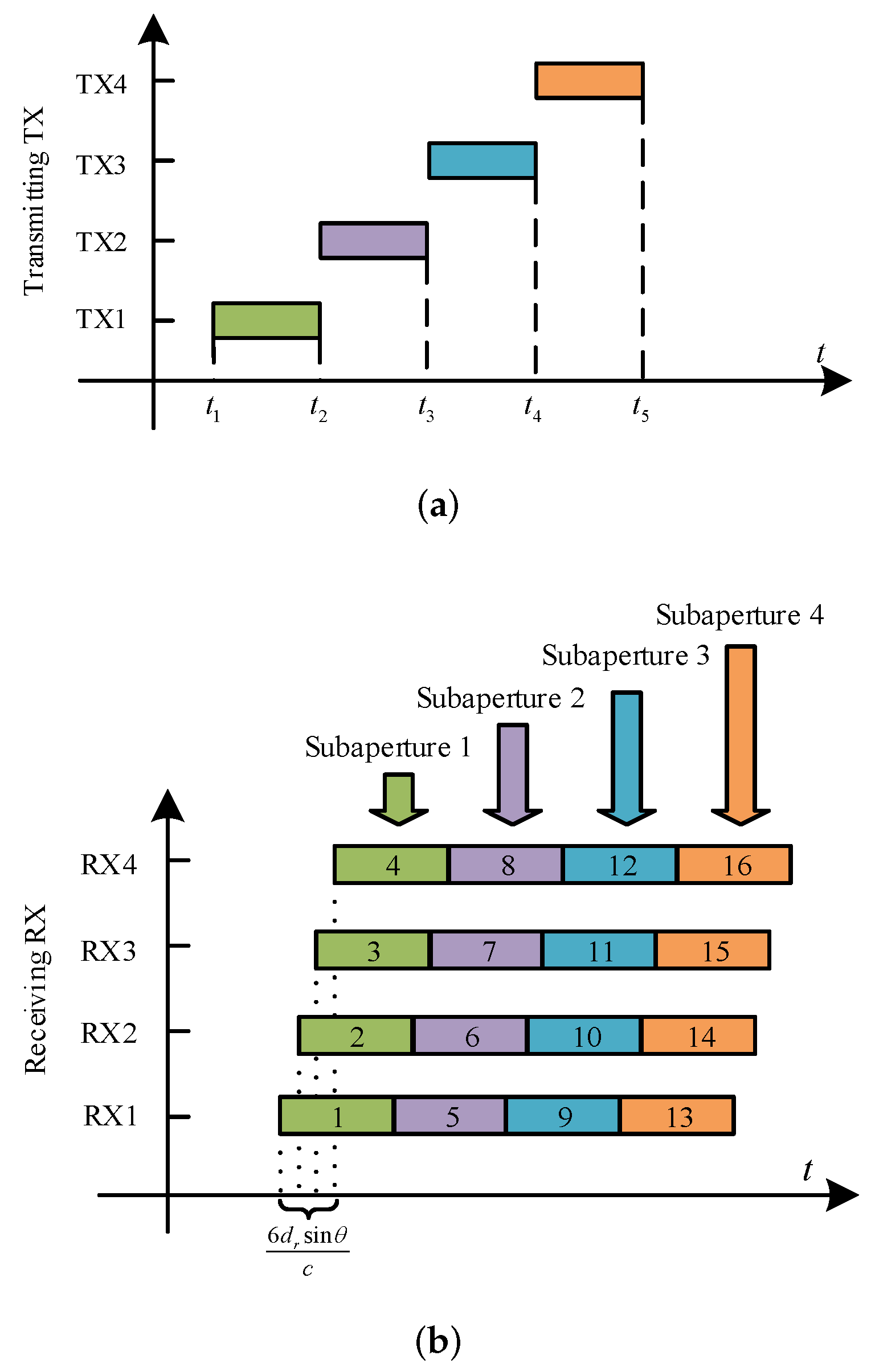
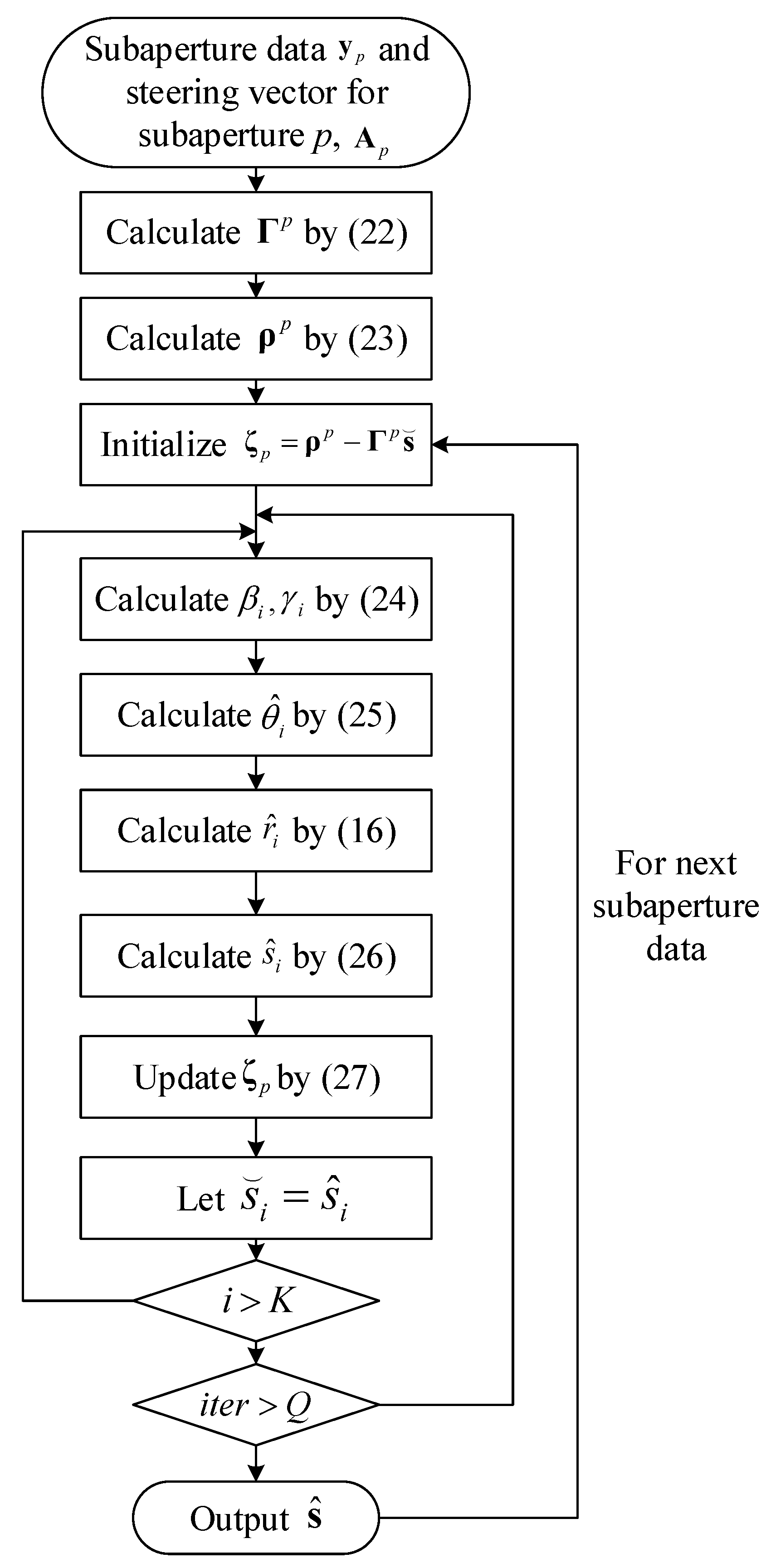
2.2.2. Proposed Online Strategy
2.2.3. Computational Complexity Analysis
3. Results
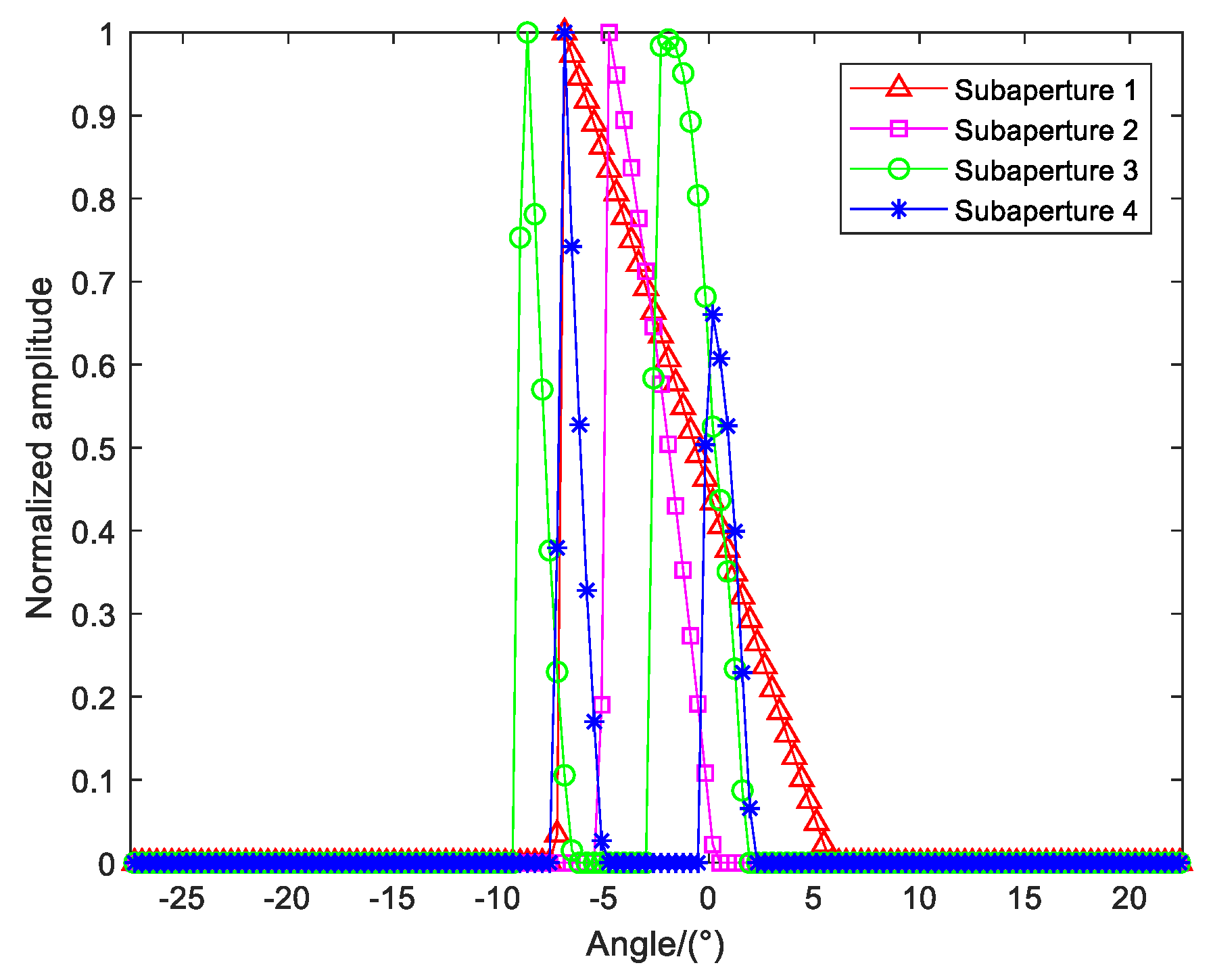
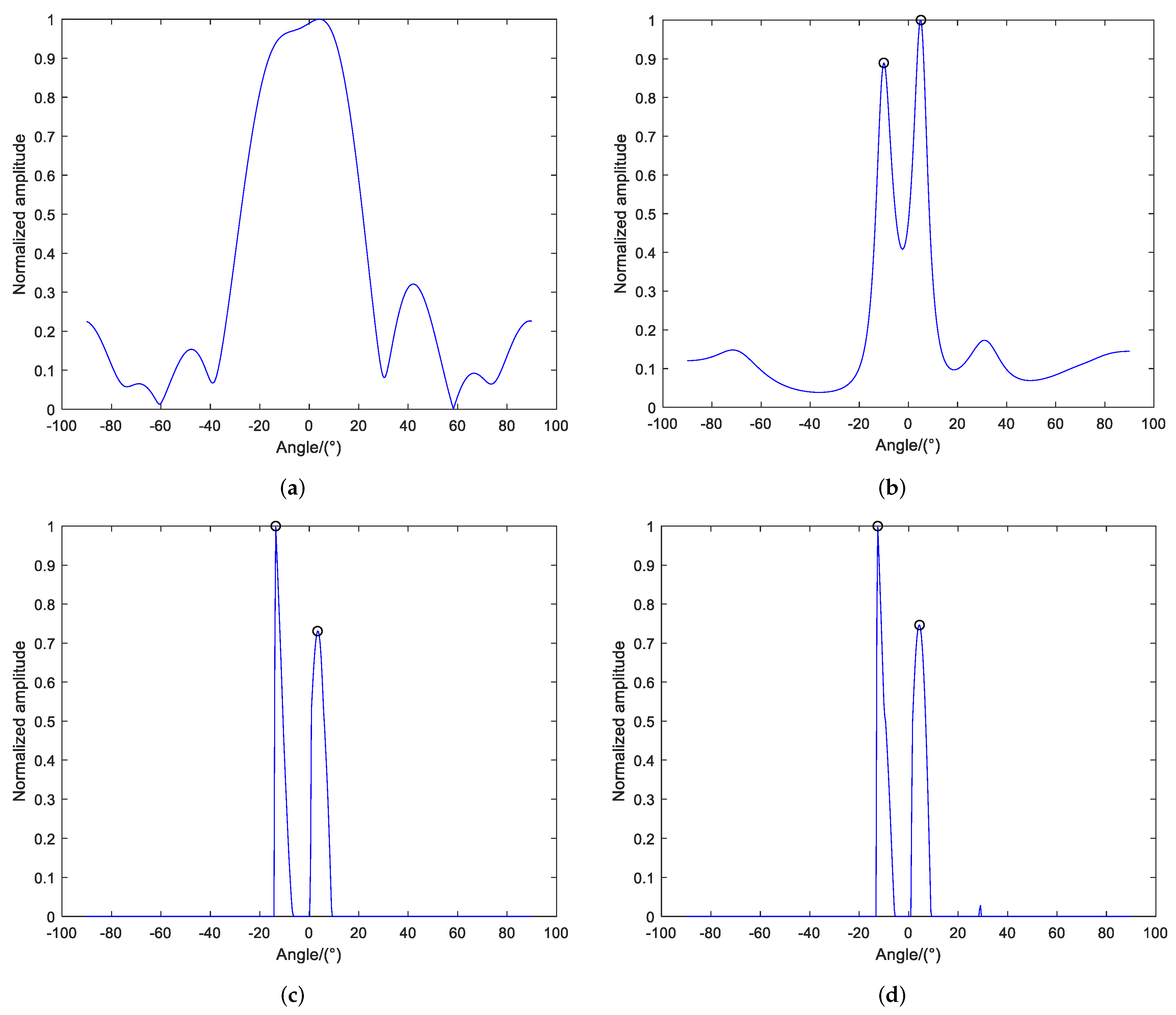
3.1. Simulation Results
3.2. Measurement Results
3.2.1. One–Dimensional Point Target Experiment
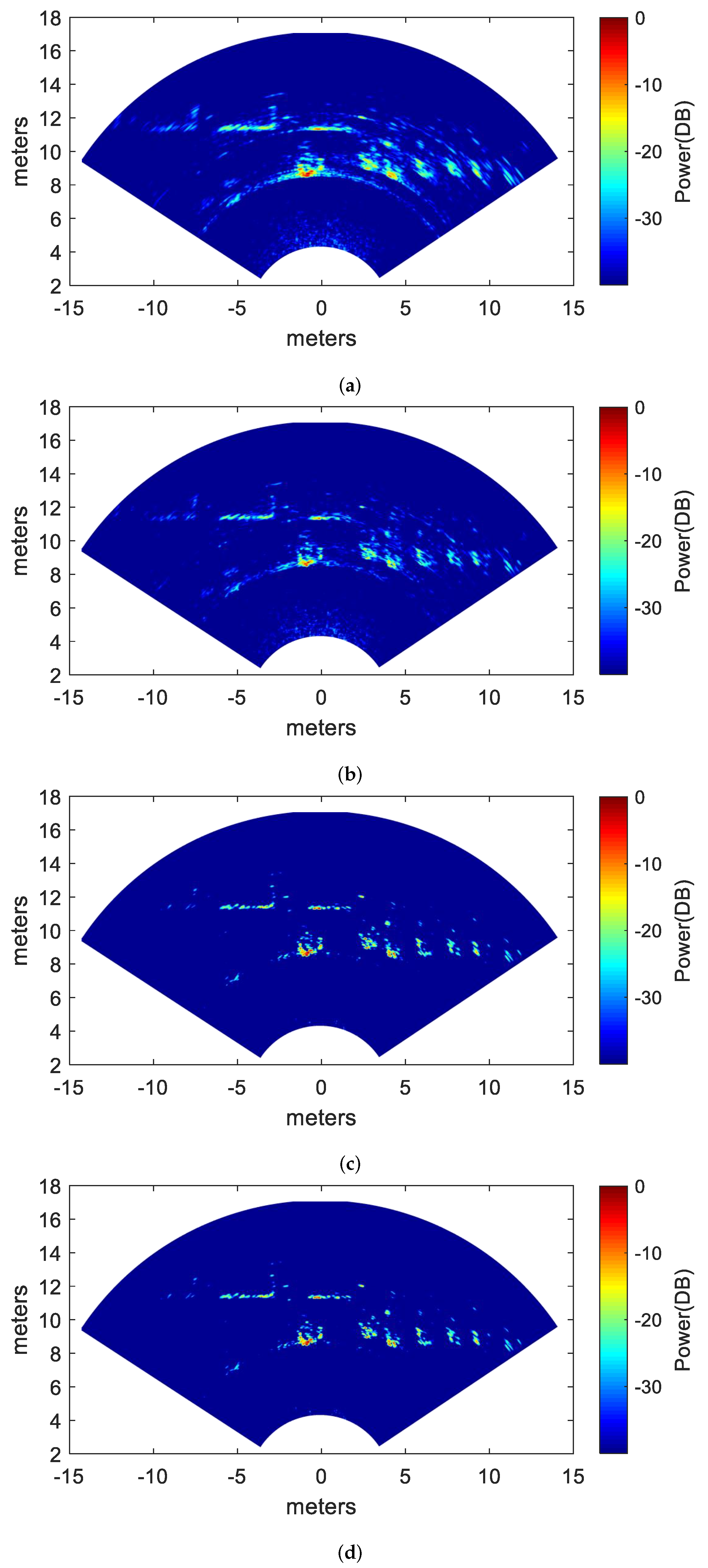
3.2.2. Two–Dimensional Surface Target Experiment
4. Discussion
4.1. Results Analysis
4.2. Extension to Optical Communication
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TDM | time–division multiplexing |
| MIMO | multiple–input multiple–output |
| DOA | direction–of–arrival |
| LASSO | least absolute shrinkage and selection operator |
| IAA | iterative adaptive approach |
| FMCW | frequency–modulated continuous wave |
| DAS | delay and sum |
| CRB | Cramer–Rao bound |
| SVD | singular value decomposition |
| ULA | uniform linear array |
| SIMO | single–input multiple–output |
| RMSE | root mean square error |
| SNR | signal–to–noise ratio |
References
- Roberts, W.; Stoica, P.; Li, J.; Yardibi, T.; Sadjadi, F.A. Iterative adaptive approaches to MIMO radar imaging. IEEE J. Sel. Top. Signal Process. 2010, 4, 5–20. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Chen, Q.; Han, F.; Liu, Q.H. Reverse-time migration and full waveform inversion applied to a stationary MIMO GPR system. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7446–7449. [Google Scholar]
- Hasan, S.M.A.; Ahmed, S.; Islam, A.N. Simulation of A Massive MIMO FSO System Under Atmospheric Turbulence. In Proceedings of the 2021 5th International Conference on Electrical Engineering and Information & Communication Technology (ICEEICT), Dhaka, Bangladesh, 18–20 November 2021; pp. 1–6. [Google Scholar]
- Li, J.; Stoica, P. MIMO radar with colocated antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Li, Z.; Ye, H.; Liu, Z.; Sun, Z.; An, H.; Wu, J.; Yang, J. Bistatic SAR Clutter-Ridge Matched STAP Method for Non-stationary Clutter Suppression. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- Hajjarian, Z.; Fadlullah, J.M.; Kavehrad, M. MIMO free space optical communications in turbid and turbulent atmosphere. J. Commun. 2009, 4, 524–532. [Google Scholar] [CrossRef]
- Miao, M.; Li, X. Parameter estimation of MIMO FSO systems using saddlepoint approximation. J. Mod. Opt. 2022, 69, 450–461. [Google Scholar] [CrossRef]
- Feger, R.; Wagner, C.; Schuster, S.; Scheiblhofer, S.; Jager, H.; Stelzer, A. A 77-GHz FMCW MIMO radar based on an SiGe single-chip transceiver. IEEE Trans. Microw. Theory Tech. 2009, 57, 1020–1035. [Google Scholar] [CrossRef]
- Hasch, J.; Topak, E.; Schnabel, R.; Zwick, T.; Weigel, R.; Waldschmidt, C. Millimeter-wave technology for automotive radar sensors in the 77 GHz frequency band. IEEE Trans. Microw. Theory Tech. 2012, 60, 845–860. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Liu, Z.; Yang, H.; Wu, J.; Yang, J. Bistatic forward-looking SAR MP-DPCA method for space–time extension clutter suppression. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6565–6579. [Google Scholar] [CrossRef]
- Hassanien, A.; Vorobyov, S.A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas. IEEE Trans. Signal Process. 2011, 59, 2669–2682. [Google Scholar] [CrossRef] [Green Version]
- Duofang, C.; Baixiao, C.; Guodong, Q. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 770–771. [Google Scholar] [CrossRef]
- Jinli, C.; Hong, G.; Weimin, S. Angle estimation using ESPRIT without pairing in MIMO radar. Electron. Lett. 2008, 44, 1422–1423. [Google Scholar] [CrossRef]
- Nion, D.; Sidiropoulos, N.D. A PARAFAC-based technique for detection and localization of multiple targets in a MIMO radar system. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 2077–2080. [Google Scholar]
- Liu, F.; Wang, J. AD-MUSIC for jointly DOA and DOD estimation in bistatic MIMO radar system. In Proceedings of the 2010 International Conference on Computer Design and Applications, Qinhuangdao, China, 25–27 June 2010; Volume 4, p. V4-455. [Google Scholar]
- Zhang, X.; Huang, Y.; Chen, C.; Li, J.; Xu, D. Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple-input multiple-output radar. IET Radar Sonar Navig. 2012, 6, 796–801. [Google Scholar] [CrossRef]
- Rambach, K.; Yang, B. Direction of arrival estimation of two moving targets using a time division multiplexed colocated MIMO radar. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1118–1123. [Google Scholar]
- Chen, T.; Wu, H.; Liu, L. A joint Doppler frequency shift and DOA estimation algorithm based on sparse representations for colocated TDM-MIMO radar. J. Appl. Math. 2014, 2014, 421391. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Zhang, L.; Long, J.; Liang, C.; Liu, J.; Wang, Y. High-resolution velocity-azimuth joint estimation for random-time-division-multiplexing multiple-input-multiple-output automotive radar using matrix completion. IET Radar Sonar Navig. 2021, 15, 1281–1296. [Google Scholar] [CrossRef]
- Yardibi, T.; Li, J.; Stoica, P.; Xue, M.; Baggeroer, A.B. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 425–443. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Jakobsson, A.; Zhang, Y.; Huang, Y.; Yang, J. Wideband sparse reconstruction for scanning radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6055–6068. [Google Scholar] [CrossRef]
- Panahi, A.; Viberg, M. On the resolution of the LASSO-based DOA estimation method. In Proceedings of the 2011 International ITG Workshop on Smart Antennas, Aachen, Germany, 24–25 February 2011; pp. 1–5. [Google Scholar]
- Stoica, P.; Babu, P.; Li, J. New method of sparse parameter estimation in separable models and its use for spectral analysis of irregularly sampled data. IEEE Trans. Signal Process. 2010, 59, 35–47. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. SPICE: A sparse covariance-based estimation method for array processing. IEEE Trans. Signal Process. 2010, 59, 629–638. [Google Scholar] [CrossRef]
- Zachariah, D.; Stoica, P. Online hyperparameter-free sparse estimation method. IEEE Trans. Signal Process. 2015, 63, 3348–3359. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Li, B.; Liang, P. On the matrix inversion approximation based on Neumann series in massive MIMO systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1763–1769. [Google Scholar]
- Albreem, M.A. Approximate matrix inversion methods for massive mimo detectors. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 87–92. [Google Scholar]
- Burger, M.; Kaltenbacher, B.; Neubauer, A. Iterative solution methods. In Handbook of Mathematical Methods in Imaging; Springer Science & Business Media: Vienna, Austria, 2015. [Google Scholar]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 2012, 30, 40–60. [Google Scholar] [CrossRef] [Green Version]
- Prabhu, H.; Rodrigues, J.; Edfors, O.; Rusek, F. Approximative matrix inverse computations for very-large MIMO and applications to linear pre-coding systems. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2710–2715. [Google Scholar]
- Wu, M.; Yin, B.; Wang, G.; Dick, C.; Cavallaro, J.R.; Studer, C. Large-scale MIMO detection for 3GPP LTE: Algorithms and FPGA implementations. IEEE J. Sel. Top. Signal Process. 2014, 8, 916–929. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Chen, X.; Wang, L.; Lu, X. Joint conjugate gradient and Jacobi iteration based low complexity precoding for massive MIMO systems. In Proceedings of the 2016 IEEE/CIC International Conference on Communications in China (ICCC), Chengdu, China, 27–29 July 2016; pp. 1–5. [Google Scholar]
- Mao, D.; Yang, J.; Zhang, Y.; Huo, W.; Luo, J.; Pei, J.; Zhang, Y.; Huang, Y. Angular Superresolution of Real Aperture Radar Using Online Detect-Before-Reconstruct Framework. IEEE Trans. Geosci. Remote Sens. 2021, 60. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Li, M.; Zhang, Y.; Luo, J.; Huang, Y.; Yang, J.; Jakobsson, A. Online Sparse Reconstruction for Scanning Radar Using Beam-Updating q-SPICE. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3869–3872. [Google Scholar]
- Fu, W.J. Penalized regressions: The bridge versus the lasso. J. Comput. Graph. Stat. 1998, 7, 397–416. [Google Scholar]
- Friedman, J.; Hastie, T.; Höfling, H.; Tibshirani, R. Pathwise coordinate optimization. Ann. Appl. Stat. 2007, 1, 302–332. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Super-resolution surface mapping for scanning radar: Inverse filtering based on the fast iterative adaptive approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 127–144. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Stoica, P. MIMO Radar Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Schmid, C.M.; Pfeffer, C.; Feger, R.; Stelzer, A. An FMCW MIMO radar calibration and mutual coupling compensation approach. In Proceedings of the 2013 European Radar Conference, Nuremberg, Germany, 9–11 October 2013; pp. 13–16. [Google Scholar]
- Jianxiong, Z.; Rongqiang, Z.; Haorun, L. Mutual Coupling Compensation for Compact MIMO Radar. IEEE Trans. Antennas Propag. 2022, 1. [Google Scholar] [CrossRef]
- Gu, F.F.; Zhang, Q.; Chi, L.; Chen, Y.A.; Li, S. A novel motion compensating method for MIMO-SAR imaging based on compressed sensing. IEEE Sens. J. 2014, 15, 2157–2165. [Google Scholar] [CrossRef]
- Bechter, J.; Roos, F.; Waldschmidt, C. Compensation of motion-induced phase errors in TDM MIMO radars. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 1164–1166. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Luo, J.; Li, J.; Mao, D.; Zhang, Y.; Huang, Y.; Yang, J. Fast Inverse-Scattering Reconstruction for Airborne High-Squint Radar Imagery Based on Doppler Centroid Compensation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Pang, X.; Ozolins, O.; Zhang, L.; Schatz, R.; Udalcovs, A.; Yu, X.; Jacobsen, G.; Popov, S.; Chen, J.; Lourdudoss, S. Free-Space Communications Enabled by Quantum Cascade Lasers. Phys. Status Solidi (a) 2021, 218, 2000407. [Google Scholar] [CrossRef]
- Spitz, O.; Herdt, A.; Wu, J.; Maisons, G.; Carras, M.; Wong, C.W.; Elsäßer, W.; Grillot, F. Private communication with quantum cascade laser photonic chaos. Nat. Commun. 2021, 12, 3327. [Google Scholar] [CrossRef]
- Gajić, A.; Radovanović, J.; Vuković, N.; Milanović, V.; Boiko, D.L. Theoretical approach to quantum cascade micro-laser broadband multimode emission in strong magnetic fields. Phys. Lett. A 2021, 387, 127007. [Google Scholar] [CrossRef]
- Garlinska, M.; Pregowska, A.; Gutowska, I.; Osial, M.; Szczepanski, J. Experimental Study of the Free Space Optics Communication System Operating in the 8–12 μm Spectral Range. Electronics 2021, 10, 875. [Google Scholar] [CrossRef]
- Lionis, A.; Peppas, K.; Nistazakis, H.E.; Tsigopoulos, A.D.; Cohn, K. Experimental performance analysis of an optical communication channel over maritime environment. Electronics 2020, 9, 1109. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Li, D.; Wang, R.; Jin, C.; Yin, X.; Gao, S.; Mu, Q.; Xuan, L.; Cao, Z. Performance analysis of an adaptive optics system for free-space optics communication through atmospheric turbulence. Sci. Rep. 2018, 8, 1124. [Google Scholar] [CrossRef] [PubMed]
- Savojbolaghchi, H.; Sadough, S.; Dabiri, M.; Ansari, I. Generalized channel estimation and data detection for MIMO multiplexing FSO parallel channels over limited space. Opt. Commun. 2019, 452, 158–168. [Google Scholar] [CrossRef]
- Agheli, P.; Emadi, M.J.; Beyranvand, H. Designing cost-and energy-efficient cell-free massive MIMO network with fiber and FSO fronthaul links. arXiv 2020, arXiv:2011.08511. [Google Scholar]
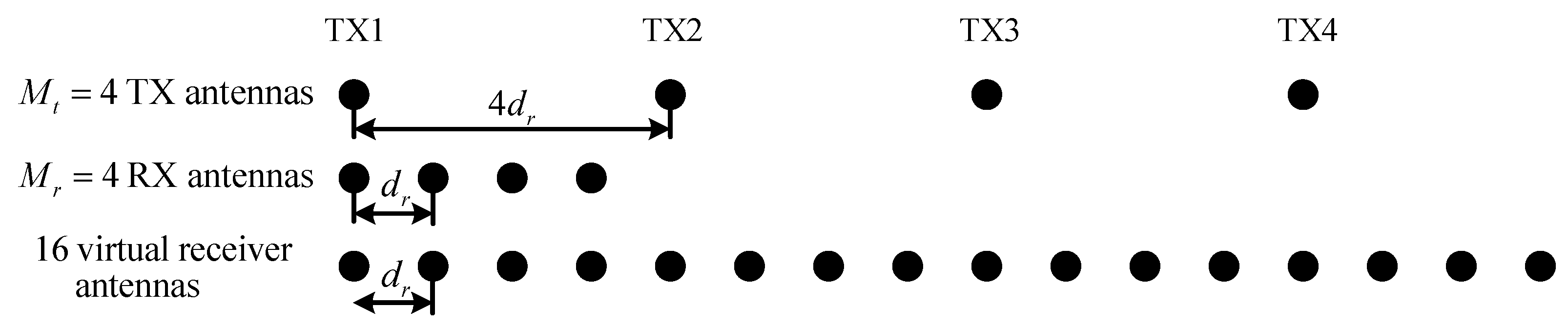




| Method | Calculation Times of Multiplication and Division | Computational Complexity |
|---|---|---|
| DAS | ||
| IAA [1] (per iteration) | (per iteration) | |
| LASSO [43] | ||
| Proposed method (per recursion) |
| Method | DAS (second) | IAA (second) | LASSO (second) | Proposed Method (second) | Speedup Ratio (vs. LASSO) |
|---|---|---|---|---|---|
| 10 | 0.0147 | 1.9863 | |||
| 100 | 0.3034 | 2.4910 | 0.1501 | 16.5956 | |
| 200 | 1.0196 | 14.8635 | 0.3952 | 37.6100 | |
| 500 | 12.0597 | 168.3409 | 1.7596 | 95.6699 | |
| 1000 | 195.6235 | 5.2865 | 194.3440 | ||
| 3000 | 40.2179 | 243.4488 |
| Parameter | Value |
|---|---|
| Carrier frequency | 77 GHz |
| Bandwidth | 3.75 GHz |
| Beam width | 1.4 |
| Pulse width | 1 ms |
| Pulse repetition interval (PRI) | 512 s |
| Number of transmitters | 12 |
| Number of receivers | 16 |
| Range samples | 261 |
| Methods | IE |
|---|---|
| DAS | 4.0273 |
| IAA | 3.7029 |
| LASSO | 1.1087 |
| Proposed method | 1.1122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Zhang, Y.; Yang, J.; Zhang, D.; Zhang, Y.; Zhang, Y.; Huang, Y.; Jakobsson, A. Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar. Remote Sens. 2022, 14, 2133. https://doi.org/10.3390/rs14092133
Luo J, Zhang Y, Yang J, Zhang D, Zhang Y, Zhang Y, Huang Y, Jakobsson A. Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar. Remote Sensing. 2022; 14(9):2133. https://doi.org/10.3390/rs14092133
Chicago/Turabian StyleLuo, Jiawei, Yongwei Zhang, Jianyu Yang, Donghui Zhang, Yongchao Zhang, Yin Zhang, Yulin Huang, and Andreas Jakobsson. 2022. "Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar" Remote Sensing 14, no. 9: 2133. https://doi.org/10.3390/rs14092133
APA StyleLuo, J., Zhang, Y., Yang, J., Zhang, D., Zhang, Y., Zhang, Y., Huang, Y., & Jakobsson, A. (2022). Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar. Remote Sensing, 14(9), 2133. https://doi.org/10.3390/rs14092133








