Integration of DInSAR Time Series and GNSS Data for Continuous Volcanic Deformation Monitoring and Eruption Early Warning Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
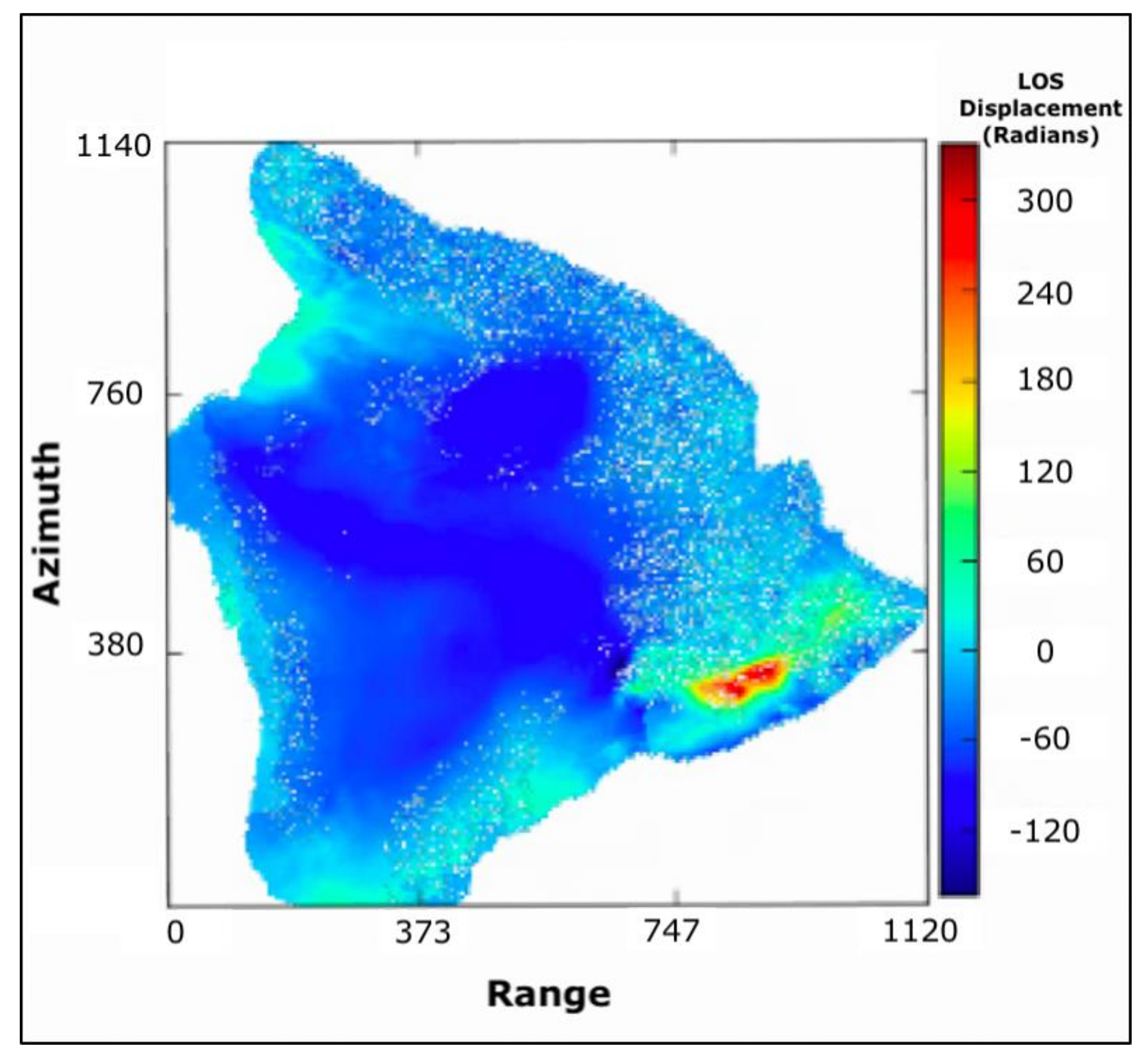
2.2. Building Interferograms
2.3. DInSAR Time Series Generation
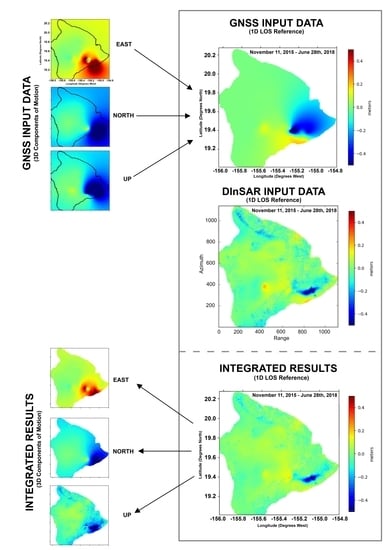
2.4. Integration of Geodetic Datasets
3. Results
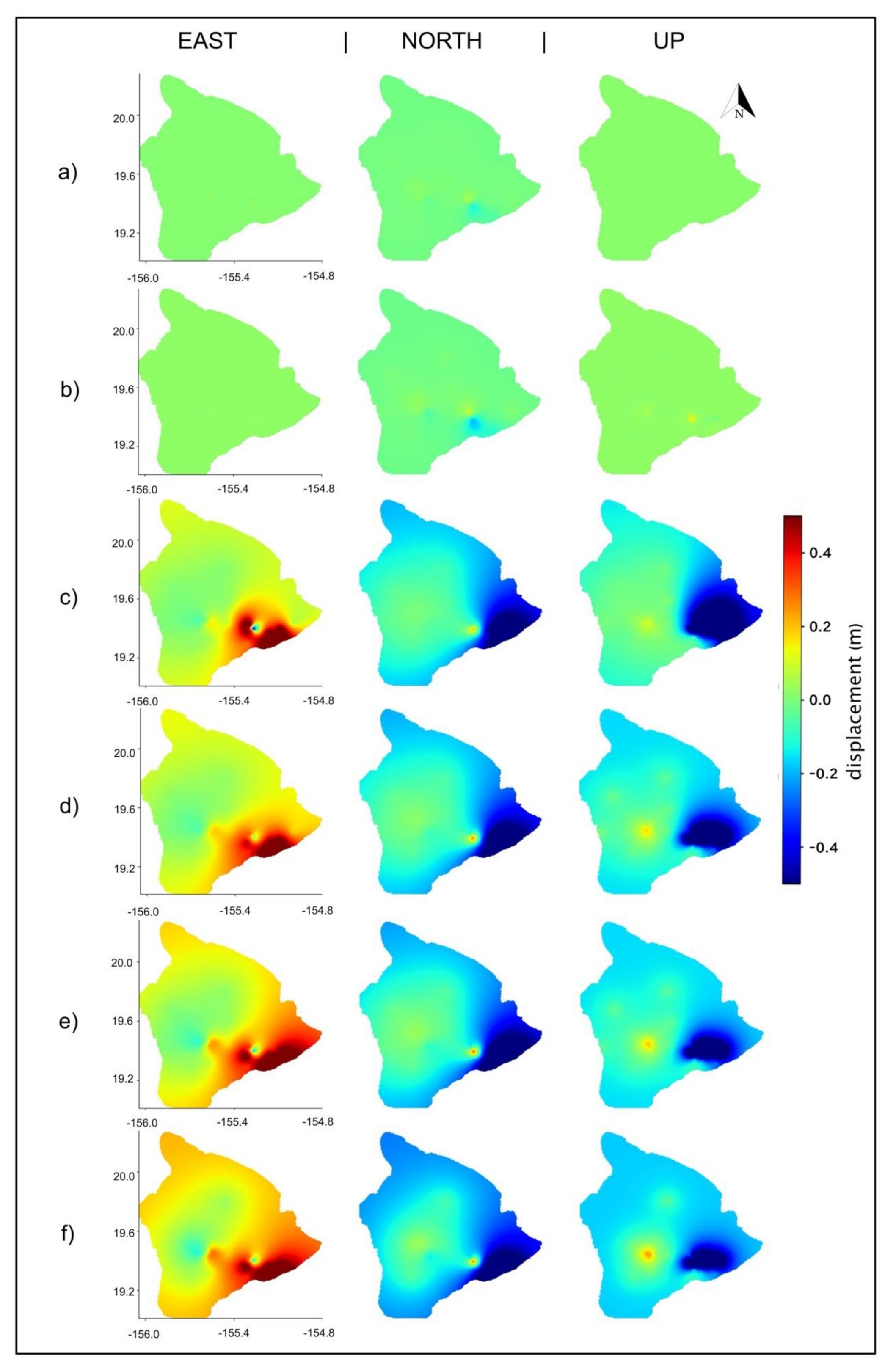
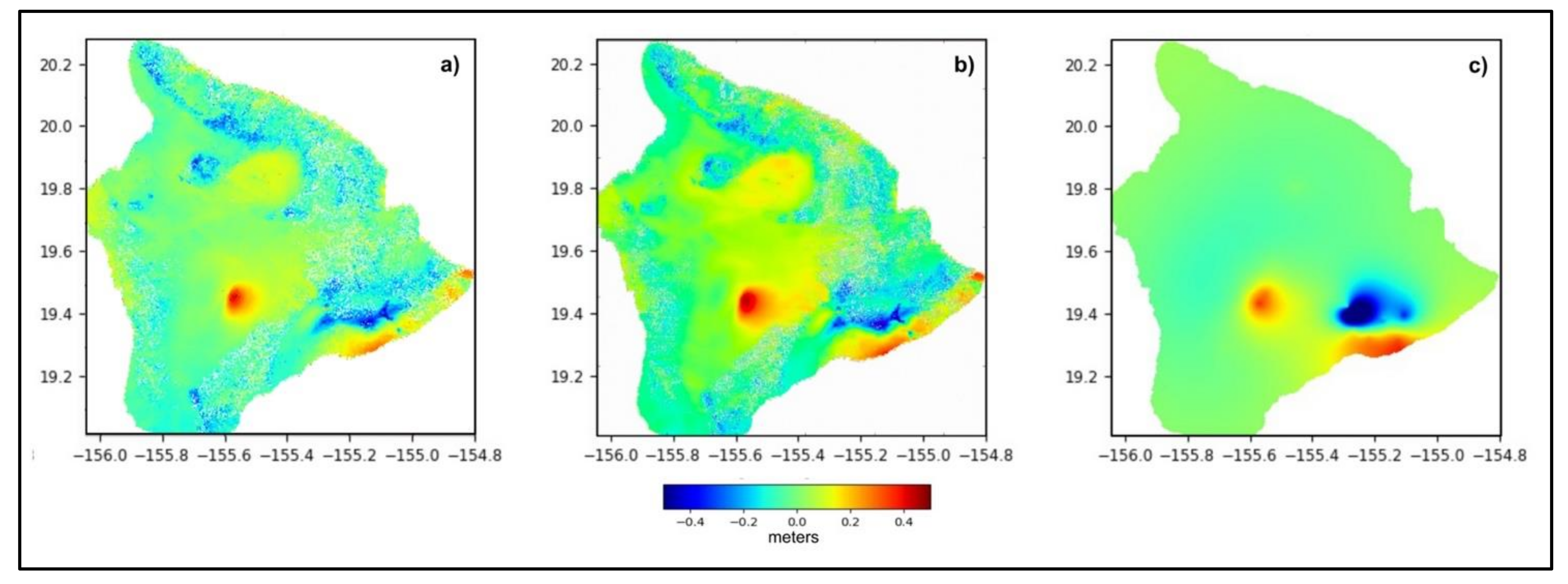
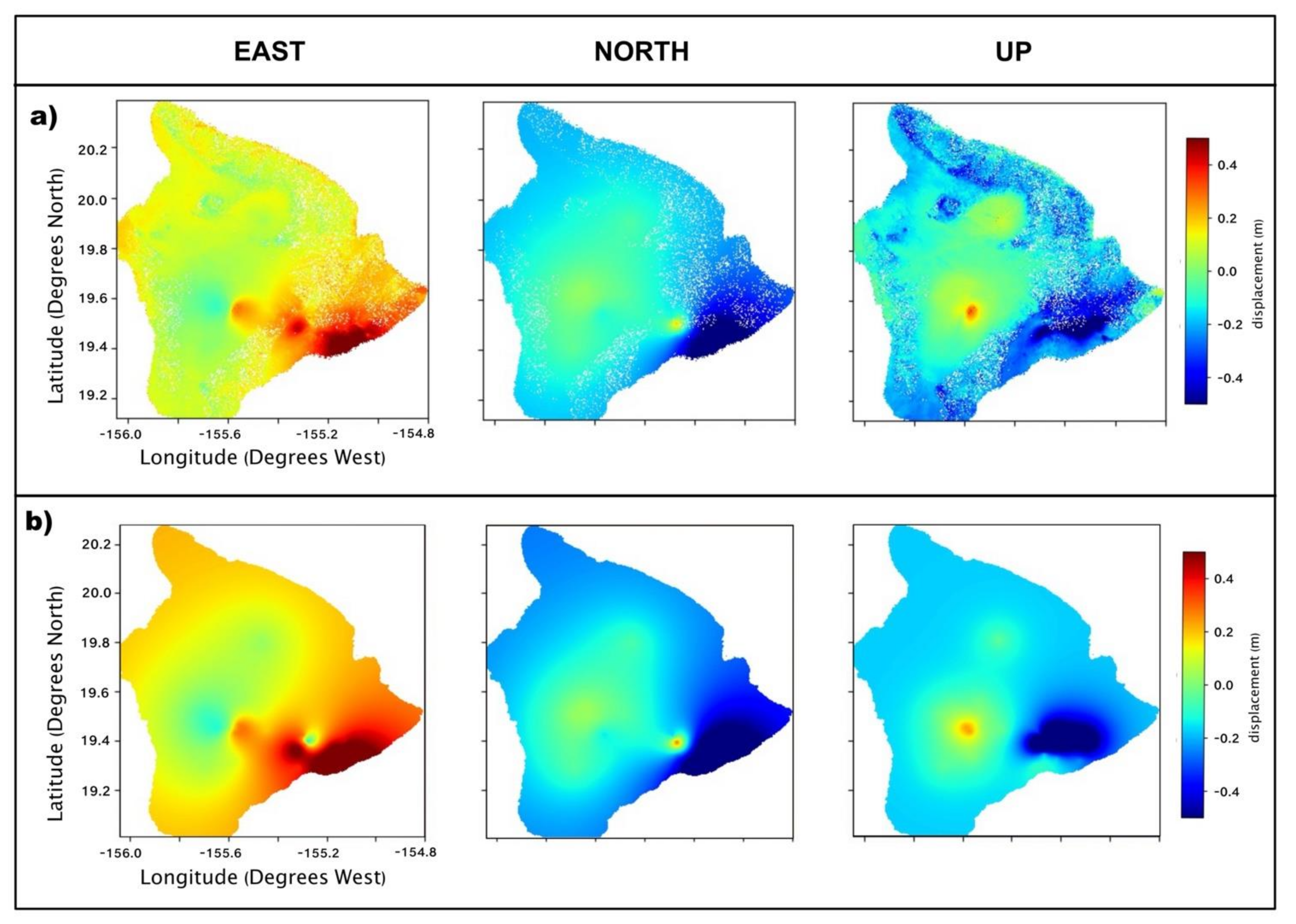
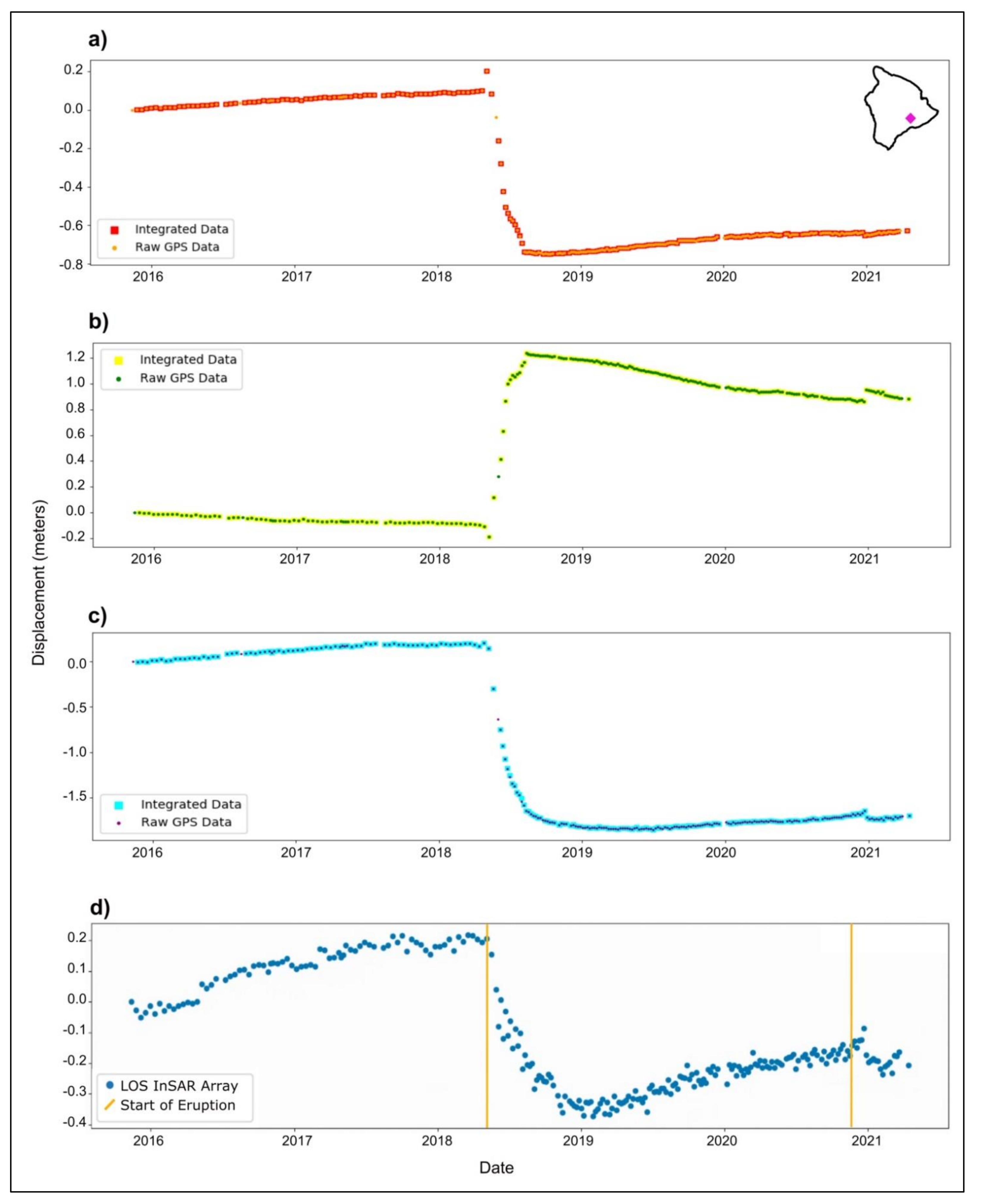
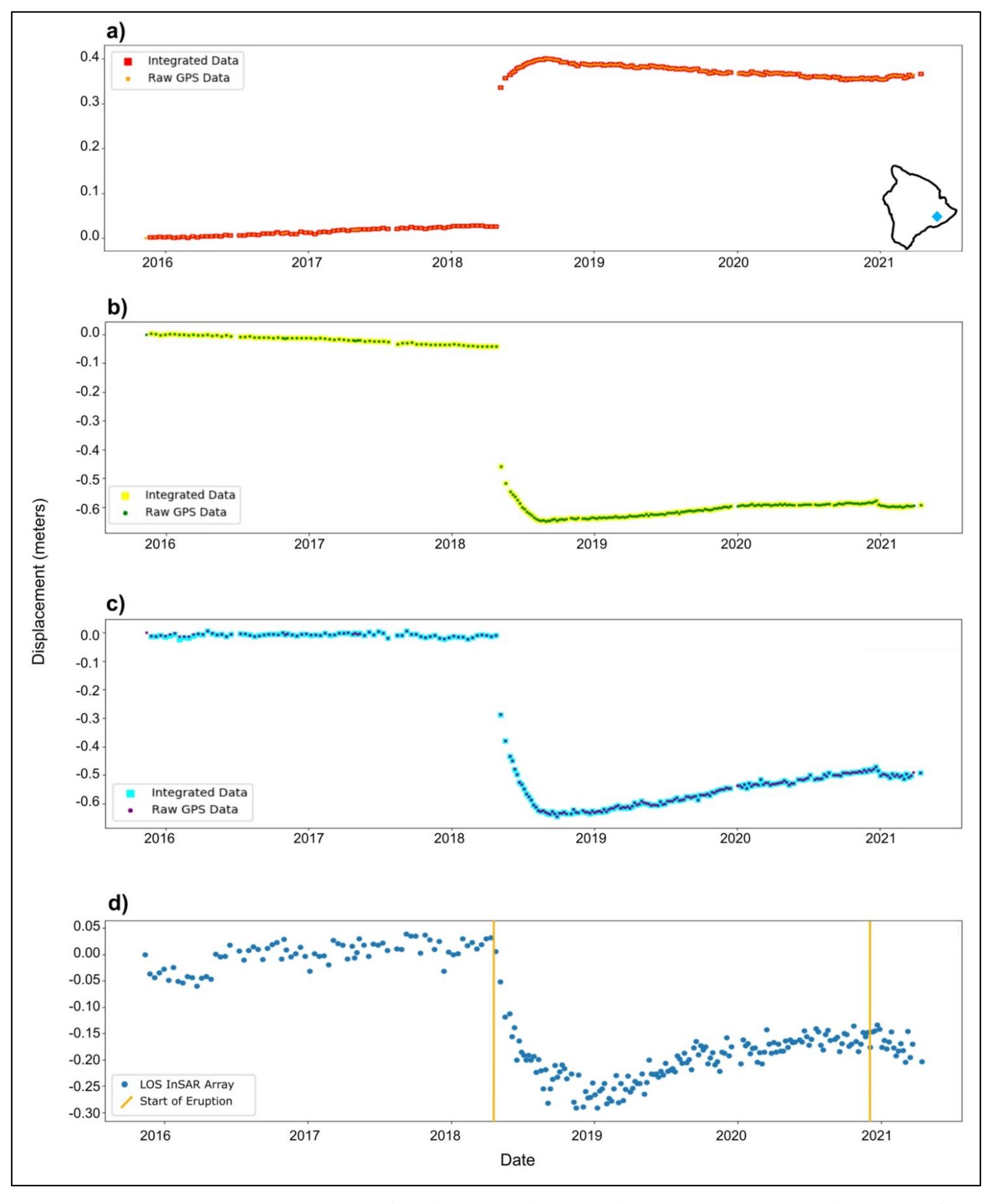
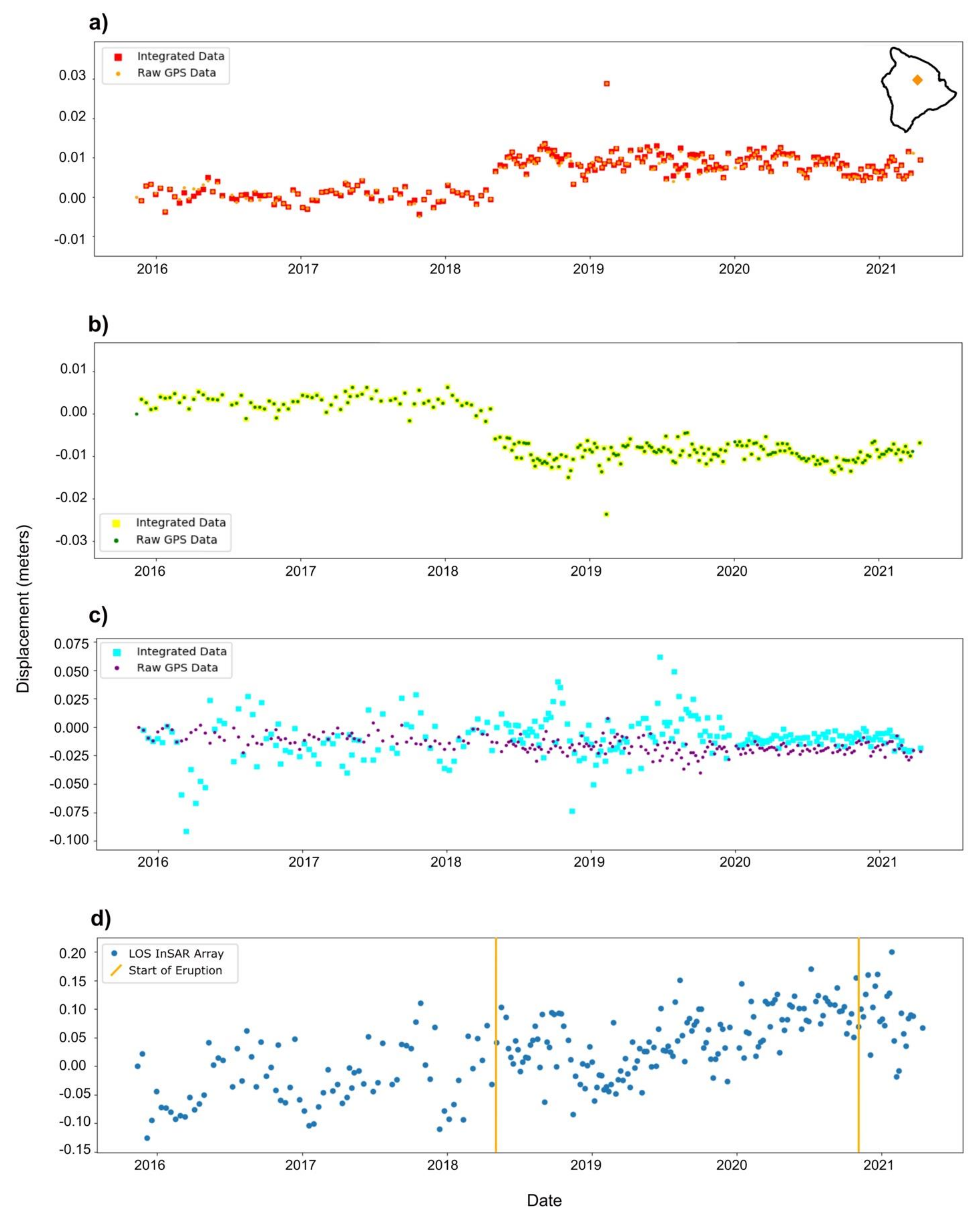
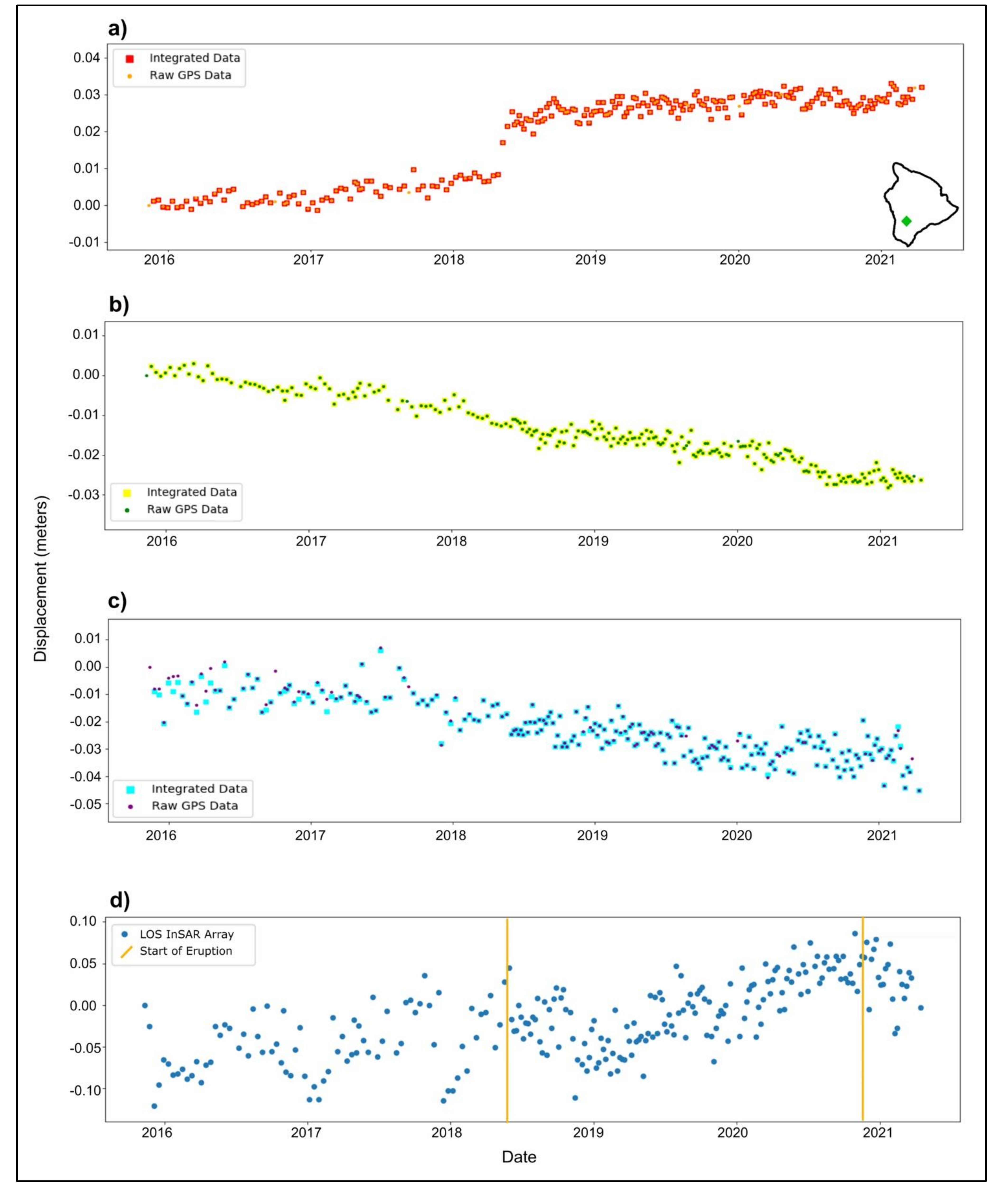
3.1. Cumulative Deformation Maps
3.2. Plotted Time Series
4. Discussion
5. Conclusions and Upcoming Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aiuppa, A.; Moretti, R.; Cinzia, F.; Giudice, G.; Gurrieri, S.; Liuzzo, M.; Papale, P.; Shinohara, H.; Valenza, M. Forecasting Etna eruptions by real-time observation of volcanic gas composition. Geology 2007, 35, 1115–1118. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Hill, P.; Bull, D. Application of machine learning to classification of volcanic deformation in routinely generated InSAR data. J. Geophys. Res. Solid Earth 2018, 123, 6592–6606. [Google Scholar] [CrossRef] [Green Version]
- Bebbington, M.S. Long-term forecasting of volcanic explosivity. Geophys. J. Int. 2014, 197, 1500–1515. [Google Scholar] [CrossRef]
- Marzocchi, W.; Bebbington, M.S. Probabilistic eruption forecasting at short- and long-time scales. Bull. Volcanol. 2012, 74, 1777–1805. [Google Scholar] [CrossRef]
- Phillipson, G.; Sobradelo, R.; Gottsmann, J. Global volcanic unrest in the 21st century: An analysis of the first decade. J. Volcanol. Geotherm. Res. 2013, 264, 183–196. [Google Scholar] [CrossRef]
- Potter, S.H.; Scott, B.J.; Fearnley, C.J.; Leonard, G.S.; Gregg, C.E. Challenges and benefits of standardising early warning system. In Observing the Volcano World; Fearnley, C.J., Bird, D.K., Haynes, K., McGuire, W.J., Jolly, G., Eds.; Advances in Volcanology (An Official Book Series of the International Association of Volcanology and Chemistry of the Earth’s Interior). Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef] [Green Version]
- Rouwet, D.; Sandri, L.; Marzocchi, W.; Gottsmann, J.; Selva, J.; Tonini, R.; Papale, P. Recognizing and tracking volcanic hazards related to non-magmatic unrest: A review. J. Appl. Volcanol. 2014, 3, 17. [Google Scholar] [CrossRef] [Green Version]
- Stix, J. Understanding fast and slow unrest at volcanoes and implications for eruption forecasting. Front. Earth Sci. 2018, 6, 2018. [Google Scholar] [CrossRef] [Green Version]
- Kelevitz, K.; Tiampo, K.F.; Corsa, B.D. Improved real-time natural hazard monitoring automated DInSAR time series. Remote Sens. 2021, 13, 867. [Google Scholar] [CrossRef]
- Chen, K.; Smith, J.D.; Avouac, J.-P.; Liu, Z.; Song, Y.T.; Gualandi, A. Triggering of the Mw 7.2 Hawaii earthquake of 4 May 2018 by a dike intrusion. Geophys. Res. Lett. 2019, 46, 2503–2510. [Google Scholar] [CrossRef]
- Derauw, D.; d’Oreye, N.; Jaspard, M.; Caselli, A.; Samsonov, S. Ongoing automated ground deformation monitoring of Domuyo—Laguna del Maule area (Argentina) using Sentinel-1 MSBAS time series: Methodology description and first observations for the period 2015–2020. J. South Am. Earth Sci. 2020, 104, 102850. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K. Analytical optimization of DInSAR and GPS dataset for derivation of three-dimensional surface motion. IEEE Geosci. Remote Sens. Lett. 2006, 3, 107–111. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Feng, W.; Fialko, Y. Subsidence at cerro prieto geothermal field and postseismic slip along the indiviso fault from 2011 to 2016 RADARSAT-2 DInSAR time series analysis. Geophys. Res. Lett. 2017, 44, 2716–2724. [Google Scholar] [CrossRef]
- Tilling, R.I. Volcanic hazards and early warning. In Encyclopedia of Complexity and Systems Science; Meyers, R., Ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Valade, S.; Ley, A.; Massimetti, F.; D’Hondt, O.; Laiolo, M.; Coppola, D.; Loibl, D.; Hellwich, O.; Walter, T.R. Towards global volcano monitoring using multisensor sentinel missions and artificial intelligence: The MOUNTS monitoring system. Remote Sens. 2019, 11, 1528. [Google Scholar] [CrossRef] [Green Version]
- Lundgren, P.; Girona, T.; Bato, M.G.; Realmut, V.J.; Samsonov, S.; Cardona, C.; Franco, L.; Gurrola, E.; Aivazis, M. The dynamics of large silicic systems from satellite remote sensing observations: The intriguing case of Domuyo volcano, Argentina. Sci. Rep. 2020, 10, 11642. [Google Scholar] [CrossRef]
- Ji, P.; Lv, X.; Yao, J.; Sun, G. A new method to obtain 3-D surface deformations from InSAR and GNSS data with genetic algorithm and support vector machine. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K.; Rundle, J.; Li, Z. Application of DInSAR-GPS optimization for derivation of fine scale surface motion maps of southern California. IEEE Trans. Geosci. Remote Sens. 2007, 45, 512–522. [Google Scholar] [CrossRef] [Green Version]
- Samsonov, S.; Tiampo, K.; Rundle, J. Application of DInSAR-GPS optimization for derivation of three-dimensional surface motion of southern California region along the San Andreas fault. Comput. Geosci. 2008, 34, 503–514. [Google Scholar] [CrossRef]
- Vollrath, A.; Zucca, F.; Bekaert, D.; Bonforte, A.; Guglielmino, F.; Hooper, A.J.; Stramondo, S. Decomposing DInSAR time-series into 3-D in combination with GPS in the case of low strain rates: An application to the Hyblean Plateau, Sicily, Italy. Remote Sens. 2017, 9, 33. [Google Scholar] [CrossRef] [Green Version]
- Copernicus Sentinel-1 data 2015–2021, retrieved from ASF DAAC 23-04-2021, processed by ESA. Available online: https://asf.alaska (accessed on 15 April 2021).
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99, 485. [Google Scholar] [CrossRef]
- Miklius, A. Hawaii GPS Network-CNPK-Cone Peak P.S. The GAGE Facility operated by UNAVCO, Inc., GPS/GNSS Observations Dataset. 2008. Available online: https://doi.org/10.7283/T5N014RM (accessed on 5 October 2021). [CrossRef]
- USGS.gov. December 2020–May 2021 Eruption. Available online: https://www.usgs.gov/volcanoes/kilauea/december-2020-may-2021-eruption?qt-science_support_page_related_con=0#qt-science_support_page_related_con (accessed on 5 October 2021).
- USGS.gov. Available online: https://volcanoes.usgs.gov/volcanoes/Kilauea/ (accessed on 5 October 2021).
- Patrick, M.R.; Houghton, B.F.; Anderson, K.R.; Poland, M.P.; Montgomery-Brown, E.; Johanson, I.; Thelen, W.; Elias, T. The cascading origin of the 2018 Kīlauea eruption and implications for future forecasting. Nat. Commun. 2020, 11, 5646. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. Eos Trans. AGU 2011, 92, 234. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. GMTSAR: An InSAR Processing System Based on Generic Mapping Tools; UC San Diego Scripps Institution of Oceanography: La Jolla, CA, USA, 2011; Available online: http://escholarship.org/uc/item/8zq2c02m (accessed on 1 October 2021).
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Doin, M.P.; Guillaso, S.; Jolivet, R.; Lasserre, C.; Lodge, F.; Ducret, G. Presentation of the small baseline NSBAS processing chain on a case example: The Etna deformation monitoring from 2003 to 2010 using Envisat data. In Proceedings of the ESA FRINGE 2011 Conference, Frascati, Italy, 19–23 September 2011. [Google Scholar]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An experimental comparison of ordinary and universal kriging and inverse distance weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Moussouris, J. Gibbs and Markov random systems with constraints. J. Stat. Phys. 1974, 10, 11–33. [Google Scholar] [CrossRef]
- Johnson, C.W.; Lau, N.; Borsa, A. An assessment of GPS velocity uncertainty in California. Earth Space Sci. 2020, 8, e2020EA001345. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Li, J.; Chen, J.; Hu, X.-G. Uncertainty assessments of load deformation from different GPS time series products, GRACE estimates and model predictions: A case study over Europe. Remote Sens. 2021, 13, 2765. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network model. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef] [Green Version]
- Agram, P.; Jolivet, R.; Riel, B.-V.; Simons, M.; Doin, M.; Lasserre, C.; Hetland, E.-A. GIAnT—Generic InSAR Analysis Toolbox, American Geophysical Union, Fall Meeting 2012, abstract id. G43A-0897. Available online: https://ui.adsabs.harvard.edu/abs/2012AGUFM.G43A0897A (accessed on 1 December 2021).
- Yu, C.; Penna, N.T.; Li, Z. Generation of real-time mode high-resolution water vapor fields from GPS observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for Interferometric Synthetic Aperture Radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Triggered afterslip on the southern Hikurangi subduction interface following the 2016 Kaikōura earthquake from InSAR time series with atmospheric corrections. Remote Sens. Environ. 2020, 251, 112097. [Google Scholar] [CrossRef]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new framework for the IGS Products. In Proceedings of the American Geophysical Union Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Samsonov, S.; Dille, A.; Dewitte, O.; Kervyn, F.; d’Oreye, N. Satellite interferometry for mapping surface deformation time series in one, two and three dimensions: A new method illustrated on a slow-moving landslide. Eng. Geol. 2020, 266, 105471. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for spatial data. In Wiley Series in Probability and Statistics; John Wiley and Sons, Inc.: New York, NY, USA, 1991; p. 900. [Google Scholar]
- Kitanidis, P.K. Introduction to Geostatistcs: Applications in Hydrogeology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Lin, G.; Shearer, P.M.; Matoza, R.S.; Okubo, P.G.; Amelung, F. Three-dimensional seismic velocity structure of Mauna Loa and Kilauea volcanoes in Hawaii from local seismic tomography. J. Geophys. Res. Solid Earth 2014, 119, 4377–4392. [Google Scholar] [CrossRef] [Green Version]
- Miklius, A.; Cervelli, P. Interaction between Kilauea and Mauna Loa. Nature 2003, 421, 229. [Google Scholar] [CrossRef]
- Neal, C.A.; Brantley, S.R.; Antolik, L.; Babb, J.L.; Burgess, M.; Calles, K.; Cappos, M.; Chang, J.C.; Conway, S.; Desmither, L.; et al. The 2018 rift eruption and summit collapse of Kīlauea Volcano. Science 2019, 363, 367–374. [Google Scholar] [CrossRef] [PubMed]
- USGS HVO Overview of Kīlauea Volcano’s 2018 Lower East Rift Zone Eruption and Summit Collapse. 2019. Available online: https://volcanoes.usgs.gov/vsc/file_mngr/file-224/OVERVIEW_Kil2018_LERZ-Summit_June%202019.pdf, (accessed on 12 December 2021).
- Wang, T.; Zheng, Y.; Pulvirenti, F.; Segall, P. Post-2018 caldera collapse re-inflation uniquely constrains Kīlauea’s magmatic system. J. Geophys. Res. Solid Earth 2020, 126, e2021JB021803. [Google Scholar] [CrossRef]
- Lundgren, P.R.; Bagnardi, M.; Dietterich, H. Topographic changes during the 2018 Kīlauea eruption from single-pass airborne InSAR. Geophys. Res. Lett. 2019, 46, 9554–9562. [Google Scholar] [CrossRef]
- Smith-Konter, B.; Ward, L.; Burkhard, L.; Foster, J.; Xa, X.; Sandwell, D. 2018 Kilauea Eruption and MW 6.9 Leilani Estates Earthquake: Line of Sight Displacement Revealed by Sentinel-1 Interferometry. 2018 Kilauea InSAR. Available online: http://pgf.soest.hawaii.edu/Kilauea_insar/ (accessed on 12 December 2021).
- Smittarello, D.; Cayol, V.; Pinel, V.; Peltier, A.; Froger, J.-L.; Ferrazzini, V. Magma propagation at Piton de la Fournaise from joint inversion of InSAR and GNSS. J. Geophys. Res. Solid Earth 2019, 124, 1361–1387. [Google Scholar] [CrossRef]
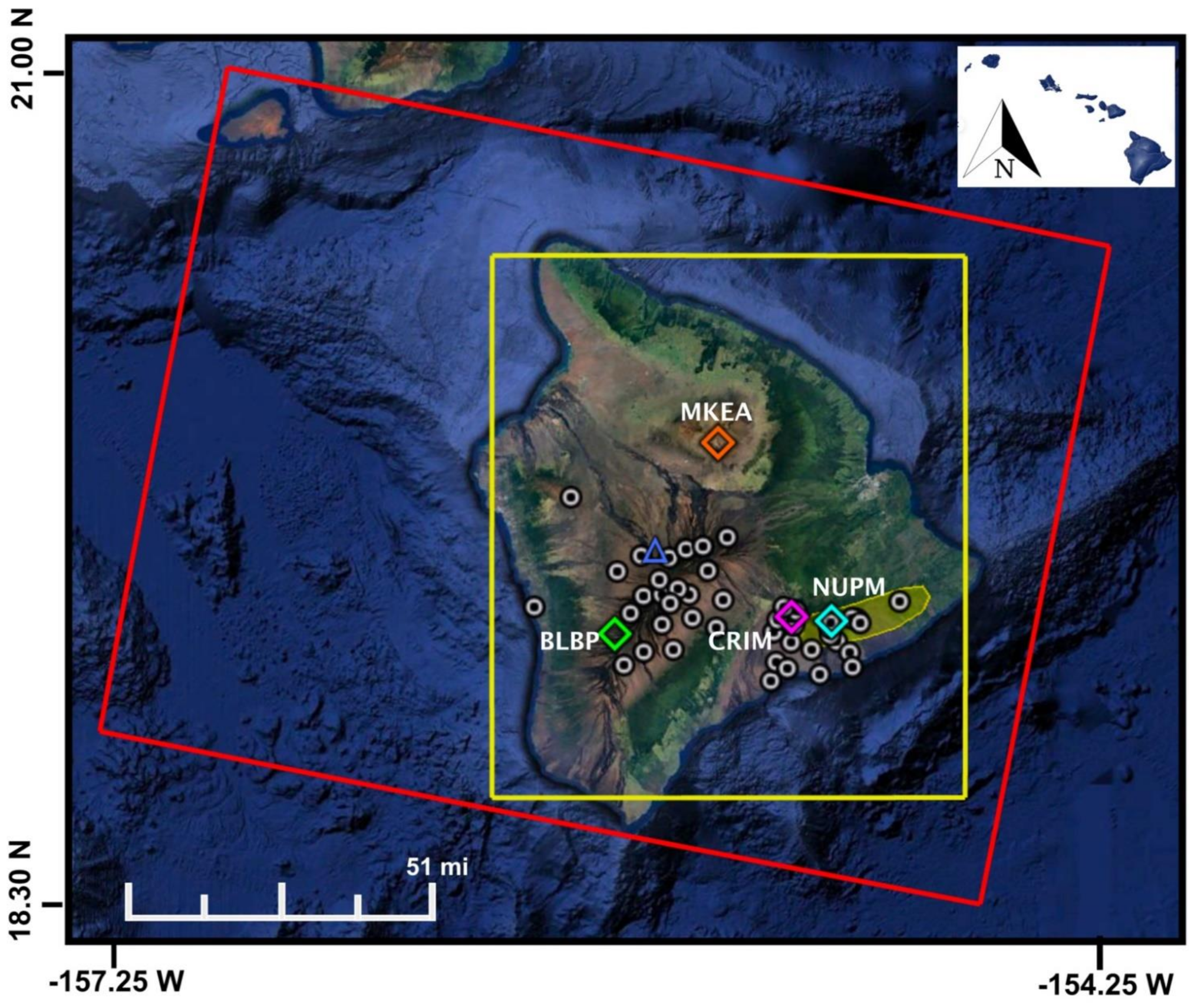
| Station Name: | Latitude (°N) | Longitude (°W) | Elevation (m) | Station Name: | Latitude (°N) | Longitude (°W) | Elevation (m) |
|---|---|---|---|---|---|---|---|
| AHUP | 19.379 | −155.266 | 1104.881 | KULE | 19.249 | −155.323 | 57.839 |
| AINP | 19.373 | −155.458 | 1567.881 | MANE | 19.339 | −155.273 | 996.466 |
| ALAL | 19.381 | −155.592 | 3203.593 | MKAI | 19.356 | −155.176 | 892.897 |
| ALEP | 19.541 | −155.644 | 2922.262 | MKEA | 19.801 | −155.456 | 3754.657 |
| ANIP | 19.396 | −155.517 | 2599.215 | MLCC | 19.563 | −155.491 | 2886.947 |
| APNT | 19.264 | −155.202 | 42.009 | MLES | 19.464 | −155.553 | 3841.48 |
| BLBP | 19.355 | −155.711 | 2664.265 | MLRD | 19.556 | −155.533 | 3082.687 |
| BYRL | 19.412 | −155.26 | 1099.085 | MLSP | 19.451 | −155.592 | 4078.4 |
| CNPK | 19.392 | −155.306 | 1123.818 | MMAU | 19.374 | −155.178 | 949.575 |
| CRIM | 19.395 | −155.274 | 1147.6 | MOKP | 19.485 | −155.599 | 4132.709 |
| ELEP | 19.45 | −155.525 | 3378.14 | NPOC | 19.393 | −155.11 | 809.836 |
| GOPM | 19.322 | −155.222 | 759.313 | NUPM | 19.385 | −155.175 | 933.27 |
| HLNA | 19.293 | −155.31 | 698.278 | OUTL | 19.387 | −155.281 | 1103.498 |
| HOLE | 19.315 | −155.128 | 408.431 | PAT3 | 19.43 | −155.572 | 3831.48 |
| JCUZ | 19.384 | −155.102 | 826.863 | PHAN | 19.447 | −155.638 | 3700.613 |
| JOKA | 19.434 | −155.004 | 482.625 | PIIK | 19.322 | −155.564 | 2308.363 |
| KAEP | 19.281 | −155.121 | 38.147 | PMAU | 19.677 | −155.818 | 2033.189 |
| KAMO | 19.395 | −155.122 | 781.432 | PUH2 | 19.421 | −155.908 | 50.715 |
| KAON | 19.278 | −155.282 | 288.305 | PUKA | 19.506 | −155.479 | 3026.304 |
| KFAP | 19.438 | −155.441 | 2073.534 | RADF | 19.584 | −155.431 | 2414.046 |
| KHKU | 19.317 | −155.637 | 2641.483 | SLPC | 19.407 | −155.67 | 3141.234 |
| KNNE | 19.286 | −155.686 | 2468.357 | STEP | 19.536 | −155.575 | 3419.067 |
| KOSM | 19.363 | −155.316 | 990.363 | TOUO | 19.504 | −155.703 | 2535.406 |
| KTPM | 19.341 | −155.16 | 783.049 | UWEV | 19.421 | −155.291 | 1257.633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corsa, B.; Barba-Sevilla, M.; Tiampo, K.; Meertens, C. Integration of DInSAR Time Series and GNSS Data for Continuous Volcanic Deformation Monitoring and Eruption Early Warning Applications. Remote Sens. 2022, 14, 784. https://doi.org/10.3390/rs14030784
Corsa B, Barba-Sevilla M, Tiampo K, Meertens C. Integration of DInSAR Time Series and GNSS Data for Continuous Volcanic Deformation Monitoring and Eruption Early Warning Applications. Remote Sensing. 2022; 14(3):784. https://doi.org/10.3390/rs14030784
Chicago/Turabian StyleCorsa, Brianna, Magali Barba-Sevilla, Kristy Tiampo, and Charles Meertens. 2022. "Integration of DInSAR Time Series and GNSS Data for Continuous Volcanic Deformation Monitoring and Eruption Early Warning Applications" Remote Sensing 14, no. 3: 784. https://doi.org/10.3390/rs14030784
APA StyleCorsa, B., Barba-Sevilla, M., Tiampo, K., & Meertens, C. (2022). Integration of DInSAR Time Series and GNSS Data for Continuous Volcanic Deformation Monitoring and Eruption Early Warning Applications. Remote Sensing, 14(3), 784. https://doi.org/10.3390/rs14030784