Next Article in Journal
Supervised Machine Learning Approaches on Multispectral Remote Sensing Data for a Combined Detection of Fire and Burned Area
Next Article in Special Issue
Assessment of Three Long-Term Satellite-Based Precipitation Estimates against Ground Observations for Drought Characterization in Northwestern China
Previous Article in Journal
Spatially Downscaling a Global Evapotranspiration Product for End User Using a Deep Neural Network: A Case Study with the GLEAM Product
Previous Article in Special Issue
Satellite Remote Sensing of Water Quality Variation in a Semi-Enclosed Bay (Yueqing Bay) under Strong Anthropogenic Impact
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 3
10.3390/rs14030659
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Interannual Variability of Water Level in Two Largest Lakes of Europe

by
Andrey G. Kostianoy
1,2,3,*,
Sergey A. Lebedev
3,4,5,
Evgeniia A. Kostianaia
1,3 and
Yaan A. Prokofiev
5
1
P.P. Shirshov Institute of Oceanology, Russian Academy of Sciences, Nakhimovsky pr. 36, 117997 Moscow, Russia
2
Laboratory of Integrated Research of Water Resources, S.Yu. Witte Moscow University, Second Kozhukhovsky pr. 12, Build. 1, 115432 Moscow, Russia
3
Geophysical Center, Russian Academy of Sciences, Molodezhnaya Str. 3, 119296 Moscow, Russia
4
Laboratory of Geoinformatics and Rational Nature Management, Maykop State Technological University, Pervomayskaya Str. 191, 385000 Maykop, Russia
5
Department of Higher Mathematics N1, National Research University “MIET”, Shokina Place 1, Zelenograd, 124498 Moscow, Russia
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(3), 659; https://doi.org/10.3390/rs14030659
Submission received: 28 December 2021 / Revised: 25 January 2022 / Accepted: 27 January 2022 / Published: 29 January 2022
(This article belongs to the Special Issue Remote Sensing for Water Resources and Environmental Management)
Browse Figures
Review Reports Versions Notes

Abstract

:
Regional climate change affects the state of inland water bodies and their water balance, which is determined by a number of hydrometeorological and hydrogeological factors. An integral characteristic of changes in the water balance is the behavior of the level of lakes and reservoirs, which not only largely determines the physical and ecological state of water bodies, but also significantly affects the coastal infrastructure and socio-economic development of the region. This paper investigates the interannual variability of the level of the Ladoga and Onega lakes, the largest lakes in Europe located in the northwest of Russia, according to satellite altimetry data for 1993–2020. For this purpose, we used three specialized altimetry databases: DAHITI, G-REALM, and HYDROWEB. Water level data from these altimetry databases were compared with in-situ records at water level gauge stations. Information on air temperature (1945–2019) and precipitation (1966–2019) acquired at three meteostations located at Ladoga and Onega lakes was used to investigate interannual trends in the regional climate change. Finally, we discuss the potential impact of the lake level rise and regional climate warming on the infrastructure and operability of railways in this region.

1. Introduction

The state of lakes, water reservoirs, and inland seas is an important indicator of ongoing regional climate change, including extreme climate events. Changes in climatic or long-term weather conditions affect the state and variability of natural parameters of inland water bodies: water level, water temperature, water salinity, vertical stratification of waters, currents, frontal zones, upwellings, eddies and gyres, ice cover and ice thickness, water turbidity, ecosystems, biodiversity, vegetation, algal bloom, etc. All over the world, many lakes are under the threat of drying up and even disappearing [1,2,3,4,5,6,7,8,9,10,11,12,13,14].
Lakes are included in the list of 54 essential climate variables (ECVs) of the Global Climate Observing System (GCOS), which make a decisive contribution to the characterization of the Earth’s climate [15]. Water level, lake area, lake surface temperature, ice area and thickness, and lake water color are key parameters of the WMO Global Terrestrial Network of Lakes [16], which focuses on biodiversity, climate change, and sustainable development. The most important physical characteristic of the state of lakes is the water level, which is measured in-situ at level gauges and remotely using satellite altimetry [17,18,19,20,21]. The water level in the lakes must be measured daily and with an accuracy of at least 3 cm [15].
The subarctic zone of Russia is particularly vulnerable to climate change, as the permafrost zone contains infrastructure worth hundreds of billions of dollars. At the same time, according to observational data since the mid-1970s, the average temperatures here have been growing 2.5 times faster than the rest of the planet. If the frozen stratum thaws, then due to the significant ice content in them the average subsidence of the soil can be 10 m or more. The hydrological regime of numerous small rivers and lakes can change, as well as groundwater level and flux, river runoff, floods, etc. The railway infrastructure in the subarctic regions is operated in extremely difficult engineering-geological and landscape-climatic conditions, being continuously exposed to various external influences, leading to deformations of the track and artificial structures [22]. Among them are coastal abrasion, mudflows, floods, water and thermal erosion, landslides and debris, karst sinkholes, suffusion subsidence, thermokarst, solifluction (mass wasting), bursting deformations, frost heaving, avalanches, etc. [22,23].
Island permafrost zones (or sporadic permafrost zones, SPZ) are located on the Kola Peninsula [22,23], situated northward of the White Sea (Figure 1). The infrastructure of Russian railways in this region is especially vulnerable to the negative factors of regional climate change, since the main problem of the Volkhovstroy–Murmansk section is the fact that out of 1320 km of its length, more than 340 km are single-track sections, which limits its throughput and makes it vulnerable. In this regard, the study of climate change in the Murmansk Region, the Republic of Karelia, and the Arkhangelsk Region is extremely important for the Russian railways (RZhD). This study is a continuation of the research started in [22,24,25,26,27].
Ladoga and Onega lakes are the two largest lakes in Europe, which are located in the northwest of Russia (Figure 1), based on their surface, volume, and watershed area (Table 1). There is a dense network of Russian railways in the area of these lakes, which surrounds Ladoga Lake from all sides and goes along the western coast of Lake Onega (Figure 2). Both lakes have been the focus of research and monitoring since the first expeditions led by Russian Captain-Lieutenant D. Selyaninov in 1763–1765 and Colonel A.P. Andreev in 1858–1866 [28,29,30,31,32]. Since 1956, the Laboratory of Limnology (now the Institute of Limnology of the Russian Academy of Sciences) and dozens of research institutes of the Russian Academy of Sciences, Russian Hydrometeorological Service, and universities began carrying out complex limnological studies (hydrological, hydrochemical, and hydrobiological) of the Ladoga and Onega lakes [29,30,31,32].
Water balance, lake level, and regional climate change are among the main directions of scientific research and monitoring of the Ladoga and Onega lakes [29,30,31,32,33,34,35]. Traditionally, this research was done based on the data provided by meteostations located along the coasts of the lakes and in the surrounding regions. The first studies of these lakes (water level and ice cover) using satellite altimetry were carried out in [36,37,38,39,40]. According to the results obtained by Lebedev et al. [38,39], the temporal variability of the levels of the lakes Ilmen’, Ladoga, and Pskovsko-Chudskoe (Peipus or Peipsi) is characterized by a wave with a period of four–five years, and the level of Lake Onega is characterized by a wave with a period of 15 years. In the period from 1993 to 2011, the level of Lake Ilmen’ rose at a rate of 1.17 ± 0.95 cm/year, Lake Ladoga at 0.24 ± 0.10 cm/year, Lake Peipus at 1.39 ± 0.18 cm/year, and Lake Onega at 0.18 ± 0.09 cm/year.
The aim of this paper is to investigate interannual variability of the level of Ladoga and Onega lakes using altimeters installed in different years on the satellites Topex/Poseidon, Jason-1, Jason-2, Jason-3, GFO-1, ENVISAT, SARAL, and Sentinel-3A for the period from 1993 to 2020. For this purpose, we used three specialized altimetry databases: DAHITI, G-REALM, and HYDROWEB. Water level data from these altimetry databases were compared with in-situ records at water level gauge stations. Information on air temperature (1945–2019) and precipitation (1966–2019) acquired at three meteostations located at Ladoga and Onega lakes was used to investigate interannual trends in the regional climate change. Finally, we discuss the potential impact of the lake level rise and regional climate warming on the infrastructure and operability of railways in this region.

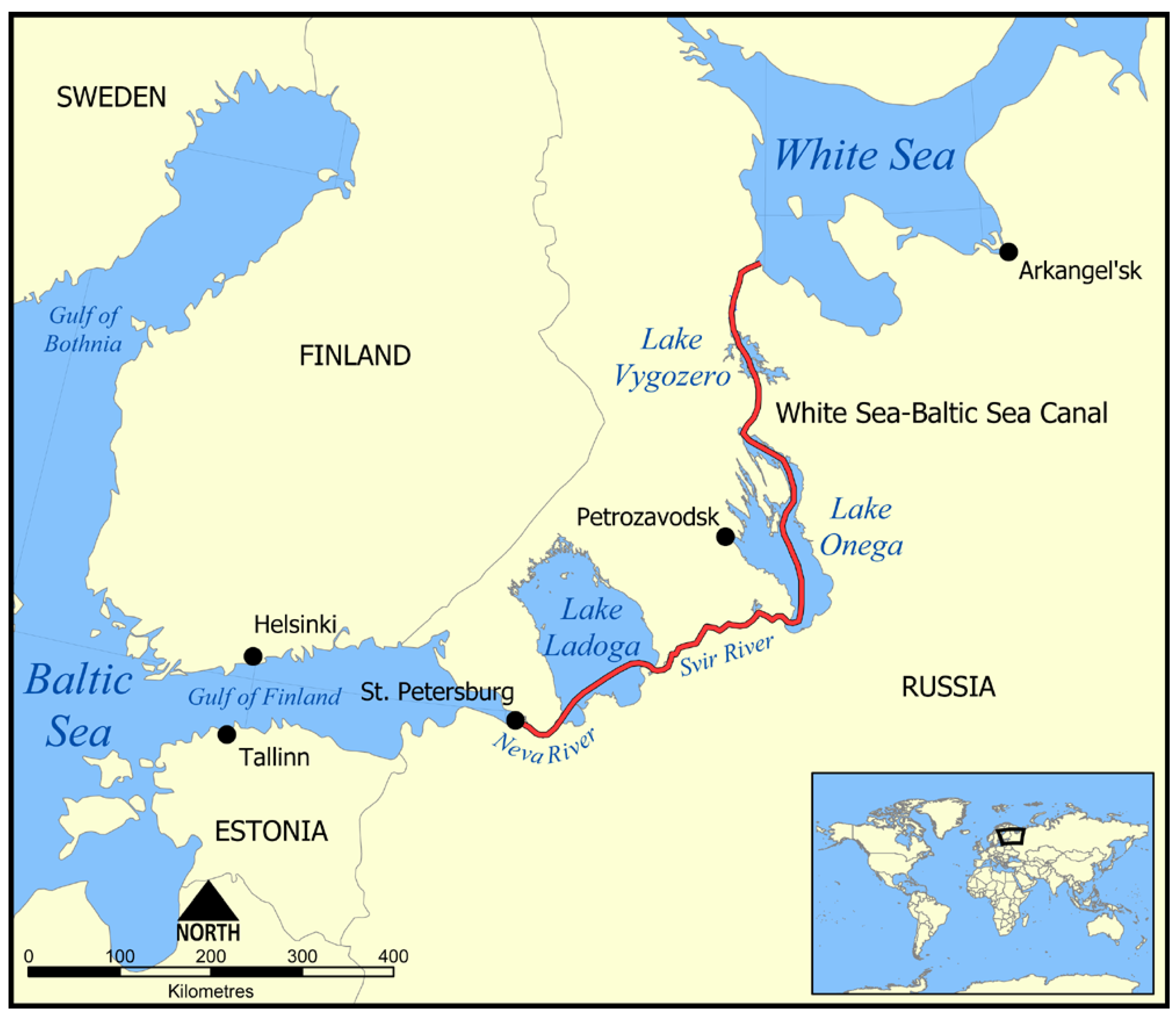
2. Study Area

Lake Ladoga (Figure 1) is the largest lake in Europe, with a surface area of 17,870 km2, a volume of 838 km3, and a maximum depth of 230 m. The length of the lake from south to north is 219 km, the greatest width is 138 km, and the average height above sea level is 4.84 m. The main flowing rivers are the Svir, Volkhov, Vuoksa, Syas’, Naziya, and Morye (35 rivers in total); the outflowing river is the Neva, which flows into the Gulf of Finland. The catchment area is 276,000 km2. Ladoga is located in the Republic of Karelia and the Leningrad Region and belongs to the Baltic Sea Basin [29,30,31,32].
The average air temperature in the area of Lake Ladoga is +3.2 °C. The average temperature of the coldest month (February) is −8.8 °C, the warmest (July) +16.3 °C. Average annual precipitation is 475 mm. The smallest monthly amount of precipitation falls in February–March (24 mm), the highest in September (58 mm). Approximately 85% (3820 mm) of the incoming part of the water balance gives the inflow of river water, 13% (610 mm) atmospheric precipitation, and 2% (90 mm) the inflow of groundwater. About 92% (4170 mm) of the expenditure part of the water balance goes to the Neva runoff and 8% (350 mm) to evaporation from the water surface. Seasonal and interannual variability of the water balance leads to significant variability in the level of Lake Ladoga [41].
Lake Onega is located in close proximity to Lake Ladoga (Figure 1), but the interannual variability of its level is absolutely different from the variability of the Ladoga level [41]. Lake Onega is the second largest lake after Lake Ladoga in Europe, with a surface area of 9720 km2, a volume of 285 km3, and a maximum depth of 127 m. About fifty rivers run to Lake Onega, and only the Svir flows out of the lake. The catchment area is 66,284 km2. Lake Onega is located in the Republic of Karelia, Leningrad, and Vologda regions of Russia and belongs to the Baltic Sea Basin [31,34,35].
Approximately 74% of the incoming part of the lake’s water balance (15.6 km3/year) belongs to the river runoff. More than 1000 watercourses flow into the lake, of which 52 rivers are more than 10 km long and eight rivers are more than 100 km long. The largest of them are the Vodla and the Suna. About 25% of the incoming part of the water balance belongs to precipitation and about 1% to groundwater. About 84% of the expenditure part of the water balance belongs to the runoff from the lake along with the Svir River (on average 17.6 km3/year) and 16% to evaporation from the water surface. Besides, the flow from the lake is regulated by the Verkhne-Svirskaya hydroelectric power station (HPP). The hydrological regime of Lake Onega is characterized by a spring rise of water which lasts 1.5–2 months, with annual fluctuations in the water level up to 0.9–1 m. The highest water levels in the lake are observed in June–August and the lowest in March–April [41].

3. Data and Methods

Satellite altimetry data have been successfully used to study the hydrological regime of lakes and rivers in South America, Africa, and Siberia [42,43,44,45]; water levels in the lower reaches of the Volga River [46]; the cascade of the Volga water reservoirs [47,48,49,50]; Lake Peipus located at the border between Russia and Estonia [38,39,41,51,52]; and Lake Ilmen’ [38,39,51] located not far from Lake Ladoga; and other inland water bodies [53]. For an overview of satellite altimetry applications for inland water monitoring, see [18,54,55,56].
In our recent publication [41] we analyzed the level of the Ladoga, Onega, Peipus, and Ilmen’ lakes based on the satellite altimetry data from the Topex/Poseidon (August 1992–January 2006), Jason-1 (December 2001–July 2013), Jason-2 (June 2008–October 2019), and Jason-3 (January 2016–present), whose ground tracks pass over these lakes (Figure 3). This continuity in the satellite measurements allowed for obtaining a continuous series of data on the lake level along the same tracks from September 1992 to the present with a time step of 10 days. In the abovementioned study, the observation period was selected from 1 January 1993 to 31 December 2020 [41]. Data were obtained from the HYDROWEB database of the French Space Agency (CNES) and the Laboratory for the Study of Geophysics and Satellite Oceanography (LEGOS) [37].
In the present research, we used three specialized databases, DAHITI, G-REALM, and HYDROWEB—all focused on the water level of lakes, water reservoirs, and rivers—which contain data from almost all altimetry satellites operated between October 1992 and December 2020 (Table 2). These databases were used to investigate interannual variability of the water level in Lakes Ladoga and Onega, to compare the databases between themselves, and to compare the databases with in-situ records at water level gauge stations in both lakes.
The Database for Hydrological Time Series of Inland Waters (DAHITI) was developed by the Deutsches Geodätisches Forschungsinstitut der Technischen Universität München, Germany (DGFI-TUM) in 2013. DAHITI provides a variety of hydrological information on 5507 lakes, reservoirs, rivers, and wetlands derived from satellite data over all continents from multi-mission satellite altimetry and optical remote sensing imagery [57]. G-REALM (www.pecad.fas.usda.gov/cropexplorer, accessed on 6 December 2021) was developed by the United States Department of Agriculture (USDA) and is focused on lake and reservoir level variations using the TOPEX/Poseidon, Jason-1, Jason-2, and Envisat satellites. It produces and distributes archived and NRT water level parameters on a network of more than 200 lakes worldwide [6,45]. Hydroweb (https://hydroweb.theia-land.fr, accessed on 6 December 2021) was developed at LEGOS (France). It produces and delivers river level data from satellite altimetry on more than 12,548 virtual stations spread over the largest river basins worldwide. It also provides lake level, surface extent, and volume variations for 310 lakes. Some of the products are delivered in the near real-time (NRT) mode [18,37].
Daily lake level data from water level gauge stations Petrokrepost, Novaya Sviritsa, Syas’skye Ryadki at Lake Ladoga, and Voznesenye, Petrozavodsk, Kondopoga at Lake Onega for the period from 1 January 2001 to 31 December 2020 were used for verification of three satellite altimetry databases (Figure 3). Data on daily water level values were taken from the Information System on Water Resources and Water Management of the Russian River Basins at the Center of Register and Cadastre of the Russian Federation (http://gis.vodinfo.ru, accessed on 22 November 2021). Geographic coordinates and “zero” levels of these gauge stations are listed in Table 3.
We have to note here that in the past two decades there has been a development of alternative in-situ methods of measurements of the water level in water reservoirs based on the geomatic methods and time-lapse photography, which is a very accurate and low-cost methodology [58,59]. These new methods can be applied in the case of a lack of water level gauge stations, expensive infrastructure, administrative barriers, etc. Satellite altimetry, remote, indirect, and different in-situ methods of water level measurements have their own advantages and disadvantages. For example, remote sensing has a global coverage and unified system of measurements for the World Ocean, inland seas, lakes, water reservoirs, and rivers, but it has a set of known disadvantages related to processing of data (a set of different corrections and retracking should be applied) and measurements in the coastal zone and in the narrow water bodies. Moreover, measurements are done along the fixed ground tracks which may cross the water body too close to the shoreline, and repetition of measurements is of 10 days or more. On the other hand, in-situ measurements allow to measure the water level with a frequency starting from minutes with much higher accuracy, but their location at coasts leads to the impact of specific local currents, winds, waves, orography effects, etc. Gauge stations also cannot be installed at remotely located water bodies with a lack of coastal infrastructure. There are many examples of this in deserts of Central Asia or in the mountains of South America. We can conclude briefly that every method has its own advantages and disadvantages which can be specific for every water body, and only a combination of different methods can provide the best result.
Regional climate change is a critical factor for changes in the hydrological regime, water balance, and water level of the Ladoga and Onega lakes [29,30,31,32,33,34,35]. To clarify the rates of warming of the atmosphere and precipitation namely at Ladoga and Onega lakes, we calculated interannual trends in air temperature and precipitation recorded at three coastal meteostations (Figure 3, Table 4). To reveal general cyclicality in the interannual variability of the water level, air temperature, and precipitation over Ladoga and Onega lakes, we performed wavelet analysis (the Ricker wavelet transform) of these data after preliminary exclusion the linear trends from these time series.
We used data on monthly average air temperature for the meteostation Sortavala (WMO Station N 22802) at Lake Ladoga for 1945–2019, and at Lake Onega for meteostations Petrozavodsk (22820) for 1949–2019 and Vytegra (22837) for 1945–2019 to calculate interannual trends in air temperature change (Figure 3, Table 4). Monthly averaged sum of precipitation for the meteostation Sortavala (WMO station N 22802) at Lake Ladoga for 1966–2019, and at Lake Onega for the meteostations Petrozavodsk (22820) for 1966–2019 and Vytegra (22837) for 1966–2019 was used to calculate interannual trends in atmospheric precipitation.
The standard method of least squares, which is a common approach in regression analysis, was used to estimate linear trends in temporal variability of the water level, air temperature, and precipitation on Lakes Ladoga and Onega, as well as relationships between satellite altimetry databases and in-situ records at water level gauge stations.
Seasonality was not removed before estimating the linear trend because the seasonal cycles in the water level in these lakes are not stable. Moreover, for Lake Onega a seasonal cycle is modulated by the runoff through the hydropower station which is determined by the needs in the amount of electricity production. In such specific cases, removal of the “standard” seasonal trend leads to introduction of artificial errors in the time series.
To show the relationship between altimetry and in-situ datasets we drew scatterplots, which is a common procedure for such kinds of tasks. Correlation coefficient R and coefficient of determination R2 were used to show the correlational relationships. The values of Nash-Sutcliffe model efficiency coefficient (NSE) as an additional characteristic for relationships between all three databases and in-situ records at gauge stations, and Percent bias (PBIAS), which is a characteristic of the systematic error, were calculated.

4. Results

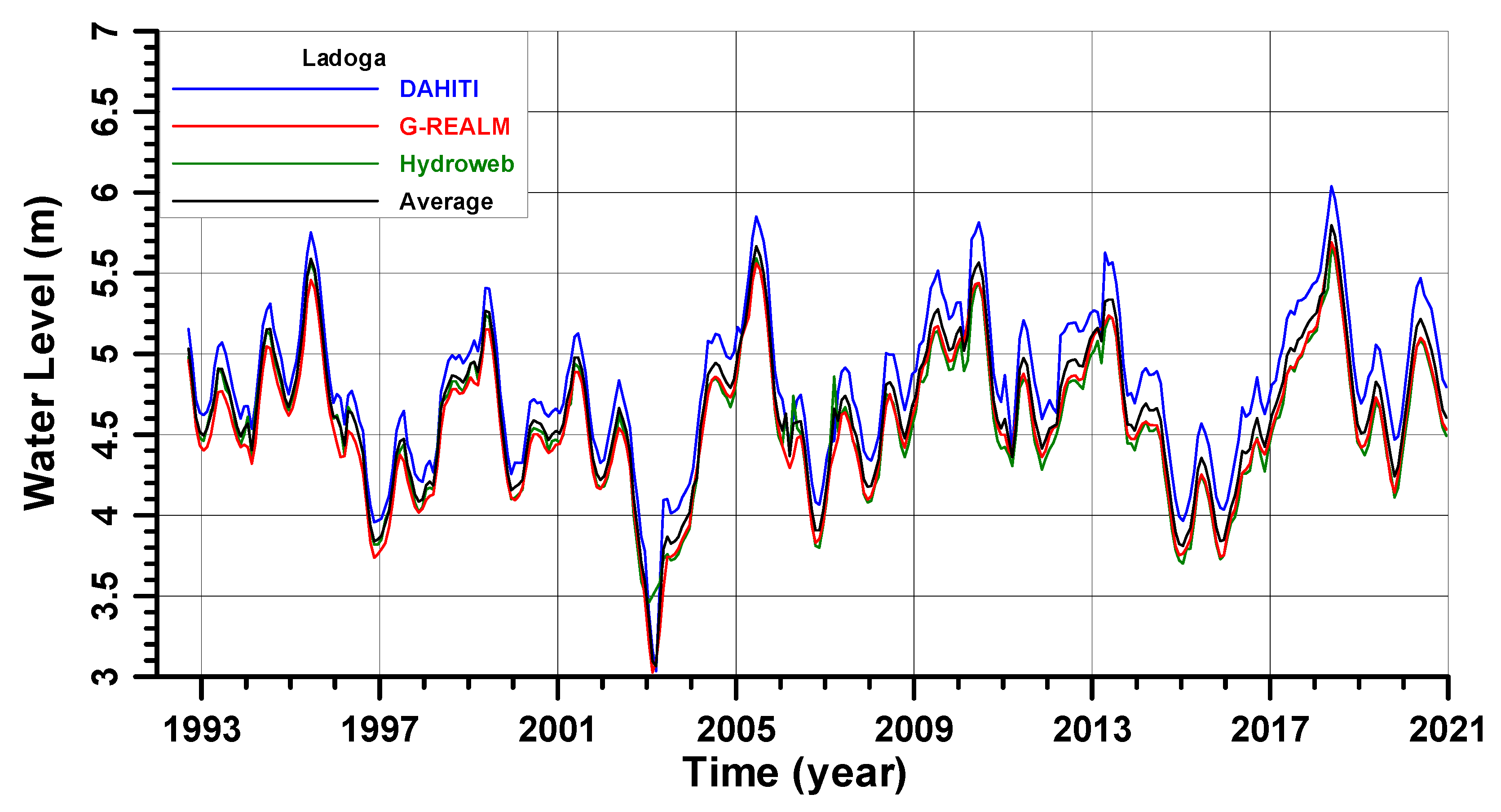
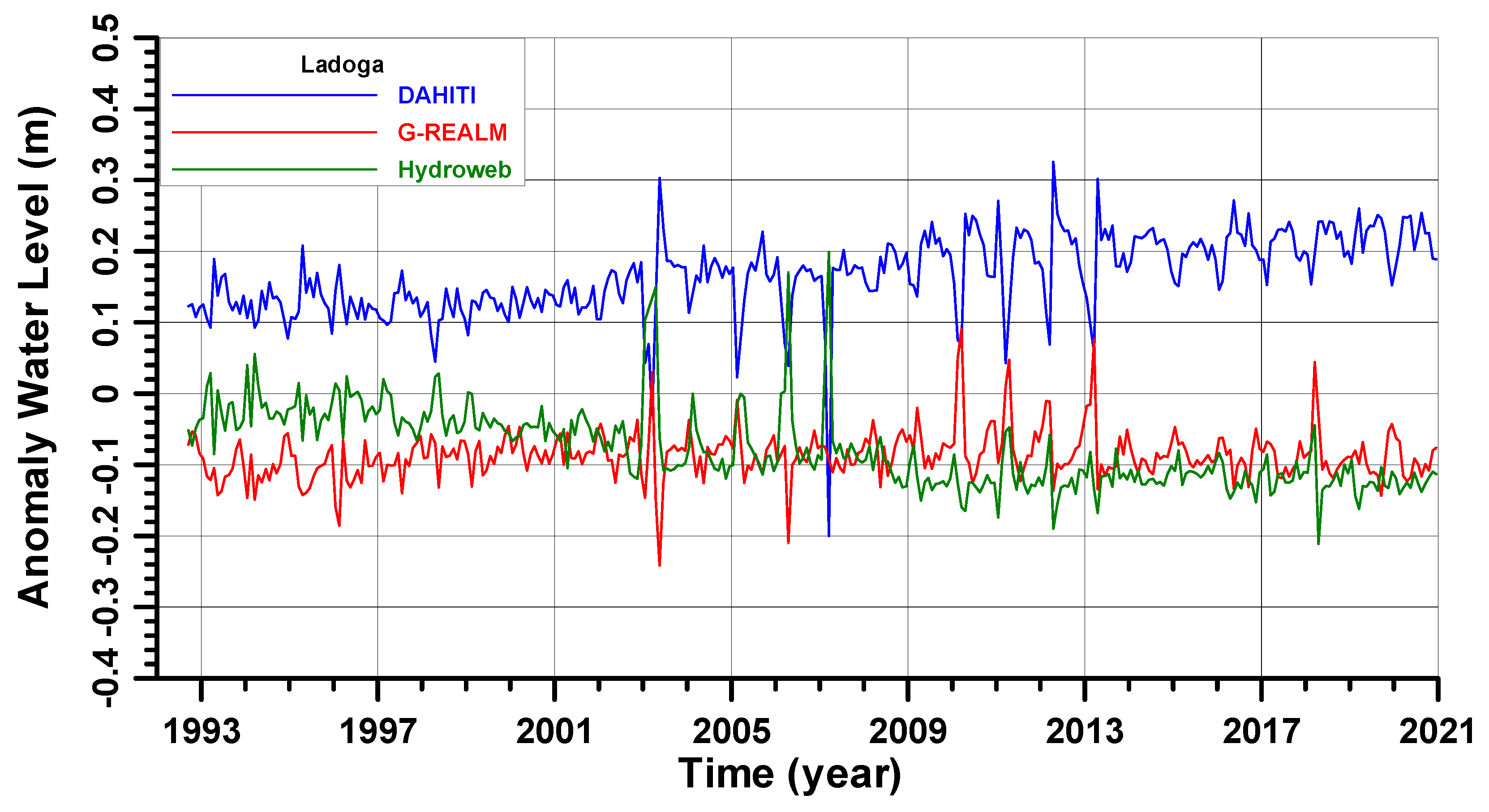
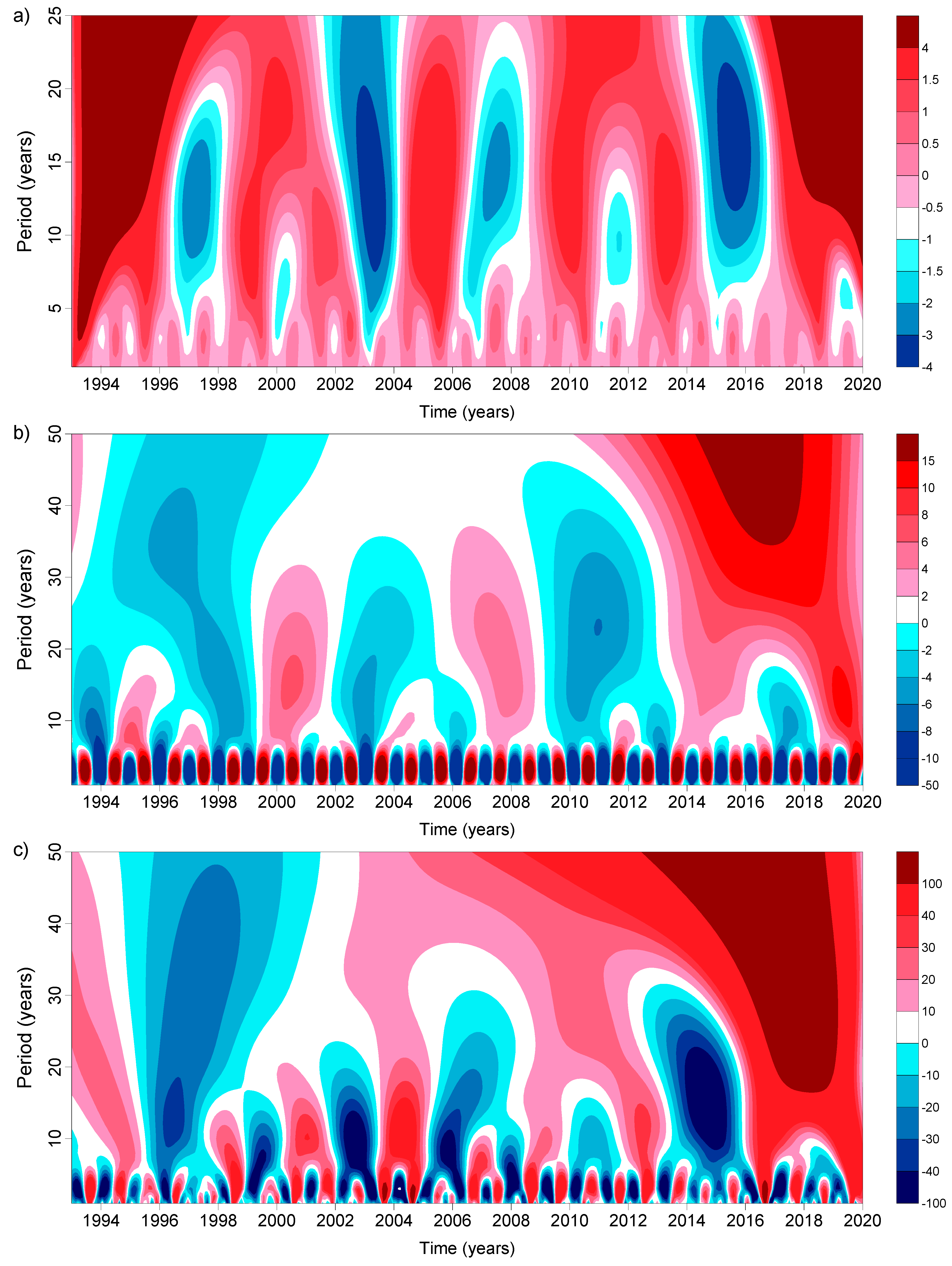
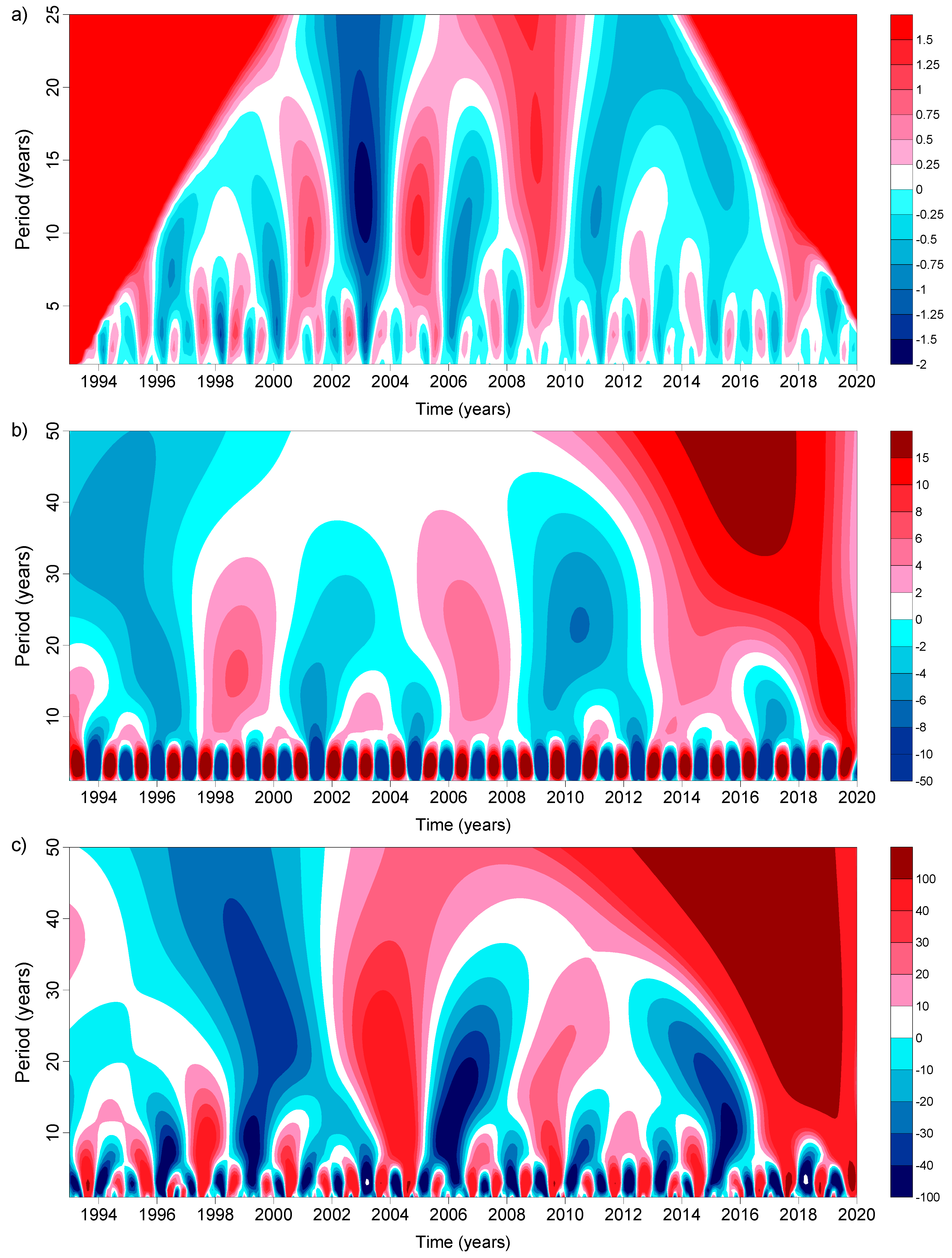
4.1. Lake Ladoga

Figure 4 shows seasonal and interannual variability of the Lake Ladoga level from October 1992 to December 2020 derived from the satellite altimetry data. The gaps in the satellite altimetry databases during wintertime when the lakes were covered with ice were filled by data derived from the appropriate regressions obtained by calibration/validation of remote sensing data by in-situ measurements (see Section 4.3 Validation and calibration of altimetry data). The lowest level is observed in winter, the highest in summer, which corresponds to the seasonal variability of precipitation in the drainage basin. The range of seasonal fluctuations varies within 0.5–1.6 m, with the greatest values of the amplitude of level fluctuations observed during sharp interannual changes in the water balance. Over the entire observation period from October 1992 to December 2020, there were three maxima of the water level in the lake, which exceeded the mark of 5.5 m based on the HYDROWEB data. This occurred on 16 June 1995 (5.56 m), 17 June 2005 (5.59 m), and 15 May 2018 (5.74 m). DAHITI data, which give the highest water level values, show two additional maxima in June 2010 of about 5.8 m and June 2013 of 5.6 m (Figure 4). During the same time, based on the HYDROWEB data there were two minima of the water level which were below the 3.6 m mark—on 17 January 2003 (3.46 m) and 7 March 2015 (3.6 m). The maximum range of lake level fluctuations for 28 years was 2.28 m as recorded in the HYDROWEB database.
According to Figure 4, the DAHITI data show larger values than those from G-REALM and HYDROWEB, which are close to each other. To show the difference between all three databases, we calculated an averaged (arithmetic mean) value of the water level based on all three databases (see the black line in Figure 4) and calculated the difference between data from every database and their average value (Figure 5). Thus, the DAHITI data are 0.1–0.25 m larger than the average value with a steady increase from the beginning of the 1990s to the end of 2020. The G-REALM and HYDROWEB data are lower than the average and are better correlated with each other. In interannual variability, the G-REALM data seem to be much more stable (around −0.1 m) with no drift, while the HYDROWEB data show a negative drift from −0.02 m in the beginning of the 1990s to −0.12 m by the end of 2020 (Figure 5).
It looks like both maximum and minimum levels occur with a cycle of 10–13 years. A characteristic feature of the interannual variability of the Lake Ladoga level is a sharp rise in the level by about 2 m to the maximum levels in two–three years after the lowest values, and the subsequent rather sharp drop by about 1.5–2 m in about two years to the next minimum values (Figure 4). For example, after the interim maximum of 1995 there was an irregular decrease of the water level until the minimum of 2003. Then, a sharp rise of the water level was observed until 2005, followed by a subsequent irregular decrease of the water level by 2015. Then, we observe again a sharp rise of the water level until 2018, and again followed by a general decrease of the water level. If the observed periodicity (regularity) continues, then in the next five–six years, we can expect a further decrease in the level of Lake Ladoga by less than one meter relative to the level observed at the end of December 2020.
We summarized the main characteristics of the Lake Ladoga level derived from all three altimetry databases in Table 5. The mean lake level lies in the range between 4.55 m and 4.81 m ASL and the standard deviation (SD) of data is of 0.2 m. The main differences between the DAHITI, G-REALM, and HYDROWEB databases arise in the determination of the minimum and maximum absolute values, as well as in the amplitude of lake level variability. The difference between the databases in the extreme states of the lake level reaches almost 0.5 m. This leads to a large difference in the observed amplitude of lake level variability, being the highest for DAHITI (3.15 m) and lowest for HYDROWEB (2.28 m) (Table 5). There is a notable difference in the linear trends of the Lake Ladoga level change between three databases for the period from October 1992 to December 2020 (Table 4). DAHITI gives +1.17 cm/year, G-REALM +0.81 cm/year, and HYDROWEB +0.27 cm/year. For the averaged values of the lake level, it will be +0.75 cm/year.

4.2. Lake Onega

Figure 6 shows the seasonal and interannual variability of the Lake Onega level from October 1992 to December 2020 derived from the satellite altimetry data. The lowest level was observed in spring, the highest in summer. The range of seasonal fluctuations varied within 0.4–1.0 m, with the greatest values of the amplitude of level fluctuations observed during sharp interannual changes in the water balance. Since the flow from the lake is regulated by the Verkhne-Svirskaya HPP (the maximum discharge is 47 km3/year), the interannual variability of the Lake Onega level does not correspond to the neighboring Lake Ladoga (see Figure 4). According to the HYDROWEB data, for the observation period from October 1992 to December 2020, there were two maxima of the water level, which exceeded the mark of 34.1 m–on 20 June 1995 (34.22 m) and on 14 December 2008 (34.14 m). During the same period, there were two minima of the water level in the lake, which were below 32.8 m–on 8 March 2011 (32.76 m) and on 17 March 2019 (32.73 m). The maximum range of lake level fluctuations for 28 years was 1.49 m (Figure 6).
According to Figure 7, the HYDROWEB data show larger values than those from DAHITI, which corresponds well to the average values from all three databases, and G-REALM, which show lower values. To show the difference between all three databases, we calculated an averaged value of the water level based on all three databases (see the black line in Figure 6) and calculated the difference between data from every database and their average value (Figure 7). On average, the HYDROWEB data are up to 0.1–0.2 m larger than the average value with a steady decrease from the beginning of the 1990s to the end of 2020. The DAHITI data fluctuate around zero value of the anomaly. G-REALM data seem to be a mirror of the HYDROWEB data in terms of the anomalies because they show lower values than the average. In the interannual variability, the G-REALM data differences drift from −0.1 to −0.2 m in the beginning of the 1990s to −0.1 m by the end of 2020 (Figure 7). It looks like there are no evident cycles in the interannual variability of the Lake Onega level, which is explained by the regulation of its water balance by the Verkhne-Svirskaya HPP.
We summarized the main characteristics of the Lake Onega level derived from all three altimetry databases in Table 6. The mean lake level lies in the range between 33.35 m and 33.58 m ASL, and the dispersion of data is of 0.06 m. The main differences between the DAHITI, G-REALM, and HYDROWEB databases arise in the determination of the minimum and maximum absolute values, as well as in the amplitude of lake level variability. The difference between the databases in the extreme states of the lake level reaches 0.65 m for a minimum level and 0.27 m for a maximum level of the lake. This highest amplitude of the lake level change was recorded for G-REALM (1.87 m) and the lowest one for HYDROWEB (1.49 m) (Table 6). There is a notable difference in the linear trends of the Lake Onega level change among three databases for the period from October 1992 to December 2020 (Table 6). DAHITI gives +0.41 cm/year, G-REALM +0.62 cm/year, and HYDROWEB gives a negative trend of −0.27 cm/year. The averaged values of the lake level will be +0.47 cm/year, which is 37% less than for Lake Ladoga. Again, this can be explained by the regulation of its water level by the Verkhne-Svirskaya HPP.

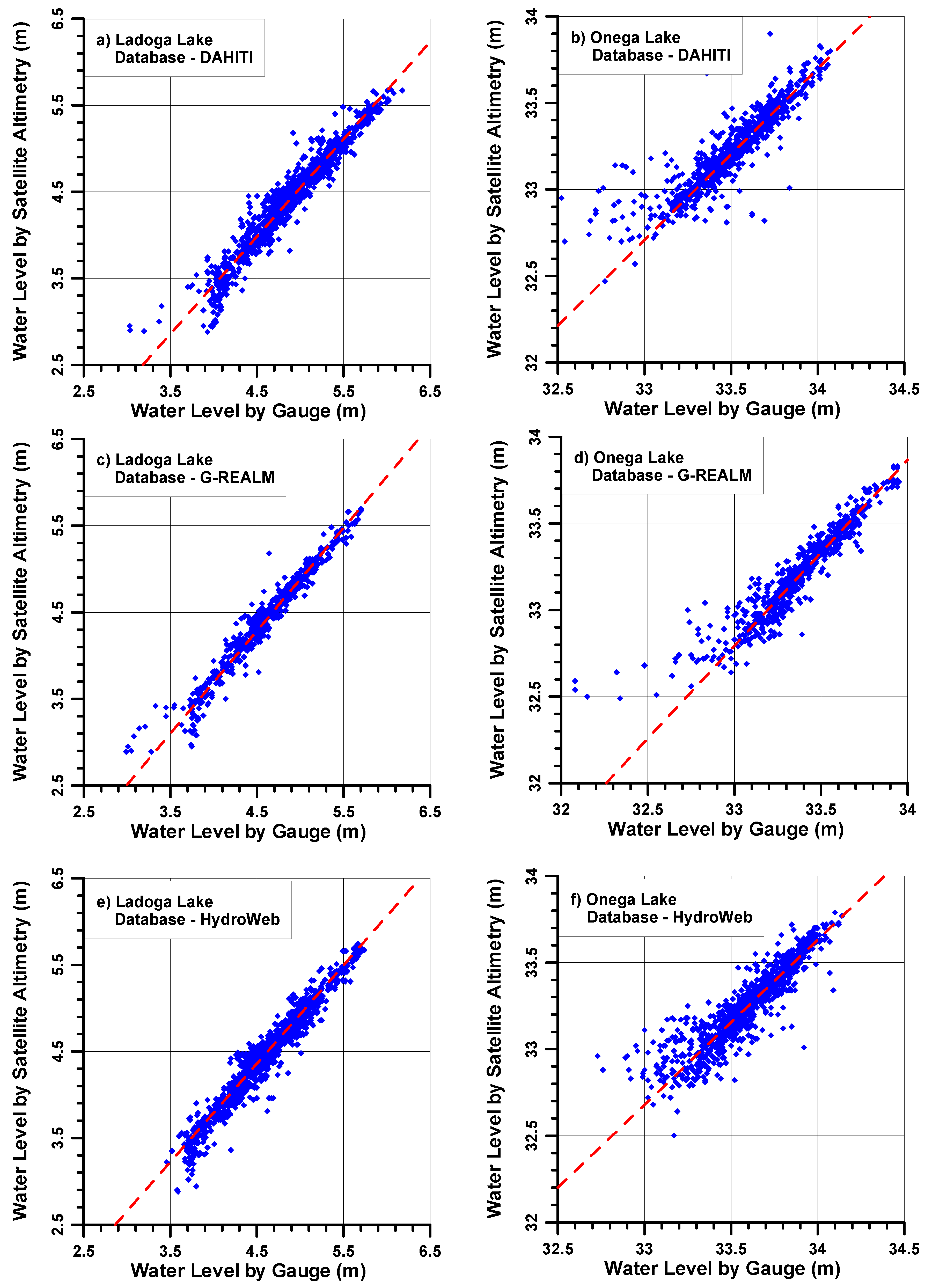
4.3. Validation and Calibration of Altimetry Data

To verify satellite altimetry data, daily data from three gauge stations at Lake Ladoga and three gauge stations at Lake Onega were used for the period from 1 January 2001 to 31 December 2020. Data on daily water level values were taken from the Information System on Water Resources and Water Management of the Russian River Basins at the Center of Register and Cadastre of the Russian Federation (http://gis.vodinfo.ru, accessed on 22 November 2021). Examples of temporal variability of the water level at the Petrokrepost (Lake Ladoga) and Voznesenye (Lake Onega) gauge stations for the period from 1 January 2015 to 31 December 2019 are shown in Figure 8. To show the discrepancy between in-situ data and satellite altimetry products, as well as the difference between all three databases, we plotted over the appropriate data from the DAHITI, G-REALM, and HYDROWEB databases.
Figure 8a clearly shows that the data from the DAHITI database for Lake Ladoga exceed the in-situ data from the Petrokrepost gauge station by an average of 0.4 m. The maximum deviation was observed in autumn 2015 at 0.8 m. Data from the G-REALM and HYDROWEB databases exceed in-situ measurements by 0.3 m and 0.15 m, respectively. Maximum deviation of 0.5 m was also observed in autumn 2015. From October 2016, the average difference between the G-REALM and HYDROWEB databases and in-situ records was of 0.15 and 0.10 m, respectively (Figure 8a). Therefore, both databases fit better in the in-situ measurements.
For Lake Onega, the DAHITI data exceed the in-situ measurements at the Voznesenye water level gauge station by an average of 0.3 m (Figure 8b). The maximum deviation of 0.57 m was observed in the spring of 2019. The data from the G-REALM and HYDROWEB databases on average exceed the in-situ measurements by 0.15 m and 0.3 m, respectively. The maximum deviations of 0.4 m and 0.7 m, respectively, were also observed in the spring of 2019. In general, for Lake Ladoga, the DAHITI and HYDROWEB data are close to each other, but the best fit with the in-situ records is G-REALM (Figure 8b).
It is interesting that all three databases show different behavior for the Ladoga and Onega lakes which are located close to each other. For example, for Lake Ladoga DAHITI shows larger values than those from G-REALM and HYDROWEB, and for Lake Onega HYDROWEB shows larger values than those from DAHITI and G-REALM (see Figure 5,7,8). But the abovementioned analysis could not answer the question: Which database better describes real variations of the water level in the lakes? To validate these databases, we built scatterplots and calculated linear regressions and correlations between the water level derived from the DAHITI, G-REALM, and HYDROWEB databases and all six in-situ water level gauge stations located at both lakes for the period from 1 January 2001 to 31 December 2020 (Table 7 and Table 8). Figure 9 shows two examples of this analysis for Lake Ladoga (Petrokrepost) and Lake Onega (Voznesenye).
For Lake Ladoga, for the Petrokrepost gauge station we have the correlation coefficient R in the range from 0.965 (DAHITI) to 0.976 (G-REALM), for Syas’skye Ryadki from 0.929 (HYDROWEB) to 0.984 (G-REALM), and for Novaya Sviritsa from 0.919 (HYDROWEB) to 0.927 (DAHITI) (Table 7). For every gauge station we have high, but different correlations for every database. The observed discrepancy can be explained by geographic peculiarities (coastline, depth, prevailed winds, etc.) at the gauge station locations. Thus, for Petrokrepost the best database is G-REALM with R = 0.976, for Syas’skye Ryadki G-REALM with R = 0.984, and for Novaya Sviritsa DAHITI with R = 0.927 (Table 7). Therefore, it looks like G-REALM better describes the Lake Ladoga level variability.
For all gauge stations at Lake Onega, the G-REALM database shows the highest correlation coefficient R: for Kondopoga (0.924), Petrozavodsk (0.928), and Voznesenye (0.937). HYDROWEB shows second rank correlations (R = 0.906–0.917) for all gauge stations. DAHITI shows the lowest R (0.893–0.896) for all gauge stations (Table 8). Thus, the best database for Lake Onega is also G-REALM.
There are several reasons to explain the different correlations among the three databases for every gauge station. First, DAHITI and G-REALM use TOPEX/Poseidon, Jason-1/2/3 satellites, while HYDROWEB additionally uses GFO-1, Envisat, SARAL, and Sentinel-3A (see Table 2). The NASA-built nadir pointing Radar Altimeter using C band (5.3 GHz) and Ku band (13.6 GHz) for measuring height above sea surface was operated on TOPEX/Poseidon. The same type of radar altimeters Poseidon-2 was installed onboard Jason-1, Poseidon-3 onboard Jason-2, and Poseidon-3B onboard Jason-3. Slightly different types of altimeters were installed onboard GFO-1, Envisat, SARAL, and Sentinel-3A satellites. Second, ground tracks for TOPEX/Poseidon and Jason-1/2/3 are the same, but they differ from ground tracks of other satellites. Thus, the distance between the ground tracks and gauge station as well as geographic orientation of ground tracks is different for different sets of satellites. Third, DAHITI, G-REALM, and HYDROWEB use different algorithms for processing altimetry data, in particular, corrections for wet and dry troposphere, ionosphere, solid Earth tide, Pole tide, range bias, and geoid. Finally, retracking of satellite altimetry data is done with the use of different algorithms.
It is evident that the specific location of gauge stations in Ladoga and Onega lakes may have an impact on the validation and calibration of individual altimeters as well as of altimetry databases. For instance, three gauge stations are located along the southeastern coast of Lake Ladoga. Moreover, the Petrokrepost gauge station is located in the entrance to the Neva River, Syas’skye Ryadki is located in the mouth of the Syas’ River which runs to the Volkhov Bay of Lake Ladoga, and Novaya Sviritsa is located in the mouth of the Svir’ River which runs to Lake Ladoga (Figure 3). The Kondopoga, Petrozavodsk, and Voznesenye gauge stations at Lake Onega are located at the western shore but in the narrow and long bays of the lake (Figure 3). The location of the gauge stations in the mouths of small rivers and in the bays may cause problems in correct validation and calibration of satellite altimetry data for these water bodies. In this respect, they are not representative for satellite altimetry, but there is no choice.
The DAHITI, G-REALM, and HYDROWEB databases can be additionally calibrated against these three gauge stations at Lake Ladoga and three gauge stations at Lake Onega based on the linear regression equations presented in Table 7 and Table 8. Moreover, in wintertime and in the presence of ice, the abovementioned equations can be used to fill the gaps in water level data in the satellite altimetry databases based on daily data records on water level at gauge stations.

5. Discussion

Regional climate change is a critical factor for changes in the hydrological regime and water balance of Ladoga and Onega lakes [29,30,31,32,33,34,35]. Since the early 2000s, several papers have been published on regional climate change in the study region, mainly in the drainage basin of the White Sea and Karelia. However, in most works the study period ended by 2000, therefore critical climate change in the first two decades of the 21st century was not reflected [27].
For example, in [60,61,62] it was shown that for the White Sea region since 1985 a period began which was characterized by positive anomalies of the eastern transport of air masses, while the frequency of occurrence of the western forms of transport was close to the multiyear average. Negative air temperature anomalies in the late 1980s changed to positive ones up to 2.0–2.5 °C, and atmospheric pressure anomalies changed their sign from positive to negative. A decrease in atmospheric pressure is explained by an increase in western transports, an increase in cyclonic activity, and an increase in air temperature is explained by the influx of warm air masses from the Atlantic. It is interesting to note that from 1930 to 2000, a weak negative trend in the air temperature was observed at almost all meteorological stations in the region [62]. The spectrum of fluctuations in surface air temperature in Arkhangelsk for 176 years revealed dominant fluctuations for a period of 4–5 and 11–13 years, which indicates the influence of large-scale climatic processes on the formation of long-term variability of hydrometeorological characteristics of the White Sea Region [62]. It is expected that the air temperature in the region by the middle of the 21st century will rise by 2.5–2.7 °C [62].
The temperature regime of the territory of Karelia in 1950–2011 is considered in [63,64]. It was shown that since 1989 only positive air temperature anomalies of the order of 1–2 °C have been observed, compared with the average value for 1961–1990. The greatest warming was observed in winter and in March from 0.3 °C to 0.6 °C/10 years. An increase in air temperature obviously leads to an increase in soil temperature. Analysis of observational data using soil temperature sensors at depths from 20 to 320 cm showed that during the 1990s and 2000s, the average annual soil temperature at various depths up to 320 cm in Karelia exceeded the climatic norm by 1.0–1.5 °C in the southern regions and by 0.5–1.0 °C in the northern regions of Karelia. It should be noted that in southern Karelia from December to mid-April the climatic norm of soil temperature was between −1.5 and −2.0 °C at a depth of 20 cm, however, during 1991–2011 soil freezing was not noted, while in the central and northern regions of Karelia it was still observed. At other depths the mean monthly temperature values were positive throughout the year. In [65], according to satellite data for 2002–2019, it was shown that the rate of growth of soil temperature in some areas of the Kola Peninsula can reach +0.1 °C/year.
In [66,67], to analyze the interannual variability of the thermal and ice regime of the lakes of Karelia, data on air temperature from adjacent meteorological stations were used. Analysis of these series for 1953–2011 showed an increasing trend in air temperature of 0.2–0.3 °C/10 years, and in 1976–2014 of 0.57–0.67 °C/10 years in the area between Lake Ladoga and the White Sea, and at the Valaam weather station (Lake Ladoga) up to +1.12 °C/10 years in July.
In [68], it was shown that for the Kola Peninsula air temperature from 1878 to 2013 increased at an average rate of 1 °C/100 years, while the growth rate was noticeably increasing in 1980–2009 by +0.55 °C/10 years. In 2000–2009, the maximum values of the average surface air temperature anomalies were observed in winter (+1.8 °C), and the minimum in summer (+0.75 °C). The authors pay attention to the significant heterogeneity of temperature changes on the Kola Peninsula. For example, on the Murmansk coast facing the Barents Sea, warming was noticeable and statistically significant, while on the Tersk and Kandalaksha shores of the White Sea the trend values were significantly less and practically insignificant. This testifies to the mosaic nature of microclimatic conditions, which for geomorphological processes in small basins of mountain rivers are more important than regional trends.
In [69,70], for the White Sea drainage basin it was shown that, based on the data of meteorological stations, the average air temperature values for 1991–2017 increased by 0.8–1.2 °C compared to the standard climatic period of 1961–1990. The observational data indicate an almost synchronous nature of the variability of the mean annual air temperature over the entire catchment area of the White Sea. As for different seasons of the year, the greatest increase in temperature was recorded for the winter months, especially for January (the average values for 1991–2017 exceeded the climatic norm by 1.7–2.5 °C).
In [71], for the drainage basin of Lake Onega it was shown that in the second half of the 21st century air temperature will increase by an average of 4.53 °C compared to the period 1951–2000, and the most significant warming is expected in winter. It is expected that the increase in average January temperatures in 2001–2050 will be of 5.6 °C, and in 2051–2100 of 8.6 °C.
Recently, Serykh et al. [27] investigated changes in near surface air temperature and vorticity of the wind speed field of the White Sea and the territory of the Murmansk and Arkhangelsk regions and the Republic of Karelia. They analyzed the monthly average NCEP/NCAR reanalysis data for the period 1950–2020. The average air temperature growth estimated using a linear trend was +0.24 °C/10 years. Against the background of this linear growth, significant interdecadal changes in air temperature were observed. The following periods are highlighted: strengthening of climate continentality (1950–1976), a more maritime climate (1977–1998), and the rapid growth of air temperature (1999–2020). The transition from a period of increasing climate continentality to a period of a more maritime climate is associated with an increase in the influence of the North Atlantic on the study region. A hypothesis has been put forward that the period of rapid growth of air temperature is caused by the transition of the climatic system of the western part of the Russian Arctic into a new phase state.
This study shows [27] that in the White Sea Region in the last two decades (1999–2020) there was a significant change in the regional climate, which was expressed in the warming of this region from +0.9 to + 1.5 °C compared to previous years (1977–1998), in a sharp increase of air temperature (+0.4–+ 1.0°C over 10 years), and to a shift of the +2 °C isotherm by 550 km northward up to the southern part of the White Sea and to the complete disappearance of average negative temperatures. The latter fact is extremely important, since it means a phase transition which will lead to thawing of permafrost soils throughout the territory of the Karelia, Murmansk, and Arkhangelsk regions. The thawing of permafrost soils and a significant increase in average temperatures will lead to a change in the water balance of numerous rivers and lakes in the study region, to an increase in geomorphological processes such as water-snow flows (a type of mudflows) and landslides [68] and may have a negative impact on the transport infrastructure [72], including the infrastructure and operability of Russian railways in the study region.
To clarify warming and precipitation rates namely at Ladoga and Onega lakes, we calculated interannual trends in air temperature for 1945–2019 and the sum of precipitation for 1966–2019 recorded at meteostations Sortavala (Lake Ladoga, WMO N 22802), Petrozavodsk (Lake Onega, WMO N 22820), and Vytegra (Lake Onega, WMO N 22837) (Table 9). Indeed, during the past 75 years there has been a warming at all meteostations, with an average rate in the range of +0.029–0.031 °C/year (Table 9). Since 1945, the average air temperature increased by about 2.5 °C from 2.0–2.5 °C to about 5.0 °C in 2019. We observed that since 2000 the monthly average air temperature during summer has reached 20 °C more often than in the previous period, but a general increase in summer temperatures is not significant. On the other hand, winter temperatures after 1987 have gotten warmer and warmer, and during the past 30 years have always been higher than −15 °C. This means that the winter period has shortened, which results in a decrease of time periods with negative temperatures, snowfalls, and ice cover, as well as a change of the hydrological regime of the watershed area of the lakes and water-air heat and mass transfer over Ladoga and Onega lakes.
Analysis of meteostations’ records shows a notable increase in precipitation with an average rate from +0.086 to +0.227 mm/month/year (Table 9) for the past 54 years depending on the meteostation location. This means that monthly mean precipitation increased from 4.6 to 12.3 mm/month or by 10–25% from 1966 to 2019, which is a significant value. We also observed that during the past 25 years heavy rains seem to occur more often because precipitation over 150 mm/month, which is triple the yearly average value, is registered more often. All these factors directly impact the water regime on the watershed area of the lakes, the water balance, and the level of Ladoga and Onega lakes.
To reveal general cyclicality in the interannual variability of the water level, air temperature, and precipitation over Ladoga and Onega lakes, we performed wavelet analysis of these data after preliminary exclusion the linear trends from these time series. As for the water level, we used averaged values obtained from the DAHITI, G-REALM, and HYDROWEB databases for 1993–2019. For air temperature and precipitation, we used records from the meteostations Sortavala at Lake Ladoga and Vytegra for Lake Onega for 1993–2019 to have the same time interval with altimetry data. The Ricker wavelet (or Mexican-hat wavelet) and Morlet wavelet are the most common tools for hydrometeorological applications [73,74,75,76,77].
The Ricker wavelet transform of the time series of the monthly average water level shows a powerful oscillation with a period of 12.5 ± 1.9 years for Lake Ladoga (Figure 10a) and 11.7 ± 2.4 for Lake Onega (Figure 11a). In some time intervals, weak fluctuations in the water level of Lake Ladoga were shown with a period of 2.98 ± 0.43 years (Figure 10a), and Lake Onega with a period of 2.96 ± 0.41 years (Figure 11a). The Ricker wavelet transform of the time series of the monthly average air temperature and precipitation at the Sortavala weather station (Lake Ladoga) (Figure 10b,c) and Vytegra weather station (Lake Onega) (Figure 11b,c) showed fluctuations with periods of two years and from 8 to 21 years; and from 5–7 to 18 years, respectively.
Thus, the wavelet analysis showed cyclicity in the water level on periods of 3 and 12 years, in air temperature on periods of 2 years and from 8 to 21 years, and in precipitation on periods from 5–7 to 18 years. Filatov et al. [34] showed oscillations in the water level and air temperature at Ladoga and Onega lakes for 1900–2014 with periods of 2, 5–7, and 30 years. The discrepancy can be explained by a much longer time period (115 years) used by Filatov et al. [34], as only 27 years were used in our analysis. It can also be explained by a hypothesis that has been put forward by Serykh et al. [27] that the period of rapid growth of air temperature (1999–2000) was caused by the transition of the climatic system of the western part of the Russian Arctic into a new phase state. Our period of investigation of 1993–2019 fits this new state of regional climate with new or not-yet-established oscillations. Finally, concerning the water level, we used satellite altimetry data and Filatov et al. [34] used in-situ data. As was already mentioned, these are a bit different data measured at different places (in the middle of the lake in case of altimetry and in river mouths or narrow bays for gauge stations) and with different frequency (daily at gauge stations and every 10 days in case of altimetry).

6. Conclusions

The conducted study of the interannual variability of the water level of Lake Ladoga for more than 28 years (October 1992–December 2020) showed that the change in the amplitude of interannual fluctuations of the level is in the range between 2.28 m (HYDROWEB) and 3.15 m (DAHITI). The linear interannual trend varies from +0.27 cm/year (HYDROWEB) to +1.17 cm/year (DAHITI). For Lake Onega the amplitude of water level variations changes from 1.49 m (HYDROWEB) to 1.87 m (G-REALM). The linear interannual trend varies from −0.27 cm/year (HYDROWEB) to +0.62 cm/year (G-REALM).
Bogdanov et al. [33] showed interannual variability of the Lake Ladoga level at the Valaam gauge station for 1859–2001 with a general decrease of the water level with a rate of −4.24 mm/year. Unfortunately, the periodicity in water level variations was not established. It is interesting that this general water level decrease corresponds exactly to the Earth crust rise of +3.3 mm/year measured in 1999–2009 at the Valaam and +4.2 mm/year at the Sortavala meteostations at Lake Ladoga with the help of high-resolution GPS receivers [78].
It seems that a long-term decreasing trend in water level variability has changed to an increasing one at the turn of the 20th and 21st centuries, simultaneously with a sharp change in the regional climate. The water level rise in both lakes seems to be related to a significant increase in precipitation over the lakes by 10–25% from 1966 to 2019. An increase in air temperature may have changed the hydrological regime of both lakes affecting snow/rain, ice cover, groundwater, and runoff of numerous small rivers. This may have led to an additional increase in the incoming part of water balance and, as a result, to a steady increase in the water level.
Such significant interannual fluctuations in the level of both lakes, as well as high trends in the water level rise, taking into account the expected changes in the regional climate (increase in air and soil temperature, and precipitation, change in snow and ice cover, hydrological regime and water balance), can lead to flooding of roads and railways and the corresponding infrastructure (bridges, embankments, power lines, etc.) located in the vicinity of Ladoga and Onega lakes [22,23,41].
Thawing of permafrost soils and a significant increase in average temperatures will lead to a change in the water balance of numerous rivers and lakes in the study region, to an increase in geomorphological processes such as water-snow flows (a type of mudflows) and landslides [68], and may have a negative impact on the transport infrastructure [72], including the infrastructure and operability of Russian railways in the study region.
In [72], it was shown that for the territory of the Kola Peninsula, which is characterized by high-temperature permafrost of a rare-island nature, infrastructure, whose base is formed by piles 5 m deep or less, is exposed to very high risks of decreasing functionality, down to the zero level. For example, with relatively small warming up to +1 °C, piles 5 m deep, as a rule, still provide functionality U = 0.65–0.85 (U = 1 corresponds to the maximum level of functionality for a basic, unchanged climate), which is considered as an average level of a climatic risk in relation to the object of transport infrastructure. Warming to +2 °C often already leads to a decrease in functionality to U < 0.5 (in the presence of soils with low humidity) and warming to + 3 °C for objects of this group can be considered catastrophic; functionality is reduced to the level U = 0–0.35, which corresponds to an unacceptably high level of climatic risks. An extremely important conclusion follows from the study: Objects on pile foundations with a depth of less than 6 m are under an increased risk even when the temperature is up to +2 °C, therefore, engineering protection of these objects should be carried out at a rate that outstrips regional climate warming [72].
Google Earth is a handy tool to search for critical areas in terms of potential impact of the water level rise in Ladoga and Onega lakes on the Russian railway infrastructure. Google Earth allows for checking the distance between the shoreline and railway tracks, as well as checking the height of the railway track over the water level. If both parameters are minimal, we consider this location to be a critical one. In this way, we checked the whole length of railways which encircle Lake Ladoga and a part of railways which passes along Lake Onega on its western shore (Figure 2). In the area of Lake Ladoga, one should pay attention to the northeastern coast of the lake near the settlements of Tuloksa, Vidlitsa, Salmi, Pitkyaranta, Sortavala, and Lake Karkumlampi. In the area of Lake Onega, such critical locations are situated in the northwestern part of its coast, near the settlements of Shuya, Yanishpole, Kondopoga, and Lake Kedr. Since the flow from Lake Onega is regulated by the Verkhne-Svirskaya HPP, its level can be maintained at a safe level with the help of this hydraulic structure. It is thanks to the hydroelectric power station that the range of interannual fluctuations of Lake Onega is only 1.49–1.87 m, while for Lake Ladoga this is between 2.28 m and 3.15 m.
It is necessary to conduct further studies of the level of Ladoga and Onega lakes, and other lakes in Karelia, to identify trends and cyclicality of its variability and assess its relationship with change in air and soil temperature, precipitation, and snow cover. Special attention should be paid to further validation and calibration of the DAHITI, G-REALM, and HYDROWEB satellite altimetry databases because they differ significantly among each other and from in-situ records at the local water level gauge stations. The obtained linear regressions between altimetry and in-situ data could help in recalculation of water level datasets specific for Ladoga and Onega lakes, as well as for filling the gaps in data related to ice cover during wintertime. All these efforts will make it possible to forecast sustainable development, management, and safe functioning of the railway transport infrastructure in the Karelia and the Murmansk region.

Author Contributions

Conceptualization, all authors; methodology, A.G.K. and S.A.L.; software, S.A.L. and Y.A.P.; validation, S.A.L. and Y.A.P.; formal analysis, A.G.K. and S.A.L.; investigation, all authors; data curation, S.A.L. and Y.A.P.; writing—original draft preparation, A.G.K. and E.A.K.; writing—review and editing, A.G.K. and E.A.K.; visualization, S.A.L. and Y.A.P.; supervision, A.G.K.; funding acquisition, A.G.K. and S.A.L. All authors have read and agreed to the published version of the manuscript.

Funding

The research was supported by the Russian Science Foundation (RNF) Grant N 21-77-30010 (2021–2024) “System analysis of geophysical process dynamics in the Russian Arctic and their impact on the development and operation of the railway infrastructure”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All freely available data are mentioned in section on Data and Methods.

Acknowledgments

The authors would like to thank Remote Sensing, MDPI and Geophysical Center, and Russian Academy of Sciences for coverage of the APC.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kostianoy, A.G.; Zavialov, P.O.; Lebedev, S.A. What do we know about dead, dying and endangered lakes and seas? In Dying and Dead Seas. Climatic versus Anthropic Causes; Nihoul, J.C.J., Zavialov, P.O., Micklin, P.P., Eds.; NATO ARW/ASI Series; Kluwer Acad. Publ.: Dordrecht, The Netherlands, 2004; pp. 1–48. [Google Scholar]
  2. Kostianoy, A.G. Dead and Dying Seas. In Encyclopedia of Water Science; Taylor & Francis: Abingdon, UK, 2007; pp. 1–3. [Google Scholar] [CrossRef]
  3. Adrn, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; VanDonk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
  4. Schindler, D.W. Lakes as sentinels and integrators for the effects of climate change on watersheds, airsheds, and landscapes. Limnol. Oceanogr. 2009, 54, 2349–2358. [Google Scholar] [CrossRef]
  5. Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and reservoirs as sentinels, integrators, and regulators of climate change. Limnol. Oceanogr. 2009, 54, 2273–2282. [Google Scholar] [CrossRef]
  6. Birkett, C.; Reynolds, C.; Beckley, B.; Doorn, B. From research to operations: The USDA global reservoir and lake monitor. In Coastal Altimetry; Springer: Berlin/Heidelberg, Germany, 2011; pp. 19–50. [Google Scholar]
  7. Kostianoy, A.G. Seas: Dead and Dying. In Encyclopedia of Water Science, 2nd ed.; Taylor & Francis: Abingdon, UK, 2011; pp. 1029–1031. [Google Scholar] [CrossRef]
  8. Kostianoy, A.G. Inland seas and lakes: Central Asia case study. In Encyclopedia of Environmental Management; Jorgensen, S.E., Ed.; Taylor & Francis: New York, NY, USA, 2013; Volume II, pp. 1460–1467. [Google Scholar]
  9. Williamson, C.E.; Brentrup, J.A.; Zhang, J.; Renwick, W.H.; Hargreaves, B.R.; Knoll, L.B.; Overholt, E.P.; Rose, K.C. Lakes as sensors in the landscape: Optical metrics as scalable sentinel responses to climate change. Limnol. Oceanogr. 2014, 59, 840–850. [Google Scholar] [CrossRef] [Green Version]
  10. Crétaux, J.-F.; Biancamaria, S.; Arsen, A.; Bergé-Nguyen, M.; Becker, M. Global surveys of reservoirs and lakes from satellites and regional application to the Syrdarya river basin. Environ. Res. Lett. 2015, 10, 015002. [Google Scholar] [CrossRef] [Green Version]
  11. Sulistioadi, Y.B.; Tseng, K.-H.; Shum, C.K.; Hidayat, H.; Sumaryono, M.; Suhardiman, A.; Setiawan, F.; Sunarso, S. Satellite radar altimetry for monitoring small rivers and lakes in Indonesia. Hydrol. Earth Syst. Sci. 2015, 19, 341–359. [Google Scholar] [CrossRef] [Green Version]
  12. Kostianoy, A.G. Inland Seas and Lakes: Central Asia Case Study. In Environmental Management Handbook, Second Edition, Volume 4: Managing Water Resources and Hydrological Systems; Fath, B.D., Jorgensen, S.E., Eds.; Taylor and Francis: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2020; pp. 337–348. [Google Scholar] [CrossRef]
  13. Tortini, R.; Noujdina, N.; Yeo, S.; Ricko, M.; Birkett, C.M.; Khandelwal, A.; Kumar, V.; Marlier, M.E.; Lettenmaier, D.P. Satellite-based remote sensing data set of global surface water storage change from 1992 to 2018. Earth Syst. Sci. Data 2020, 12, 1141–1151. [Google Scholar] [CrossRef]
  14. Pham-Duc, B.; Sylvestre, F.; Papa, F.; Frappart, F.; Bouchez, C.; Crétaux, J.F. The Lake Chad hydrology under current climate change. Sci. Rep. 2020, 10, 5498. [Google Scholar] [CrossRef] [Green Version]
  15. GOSIC. 2021. Available online: https://www.ncdc.noaa.gov/gosic (accessed on 14 November 2021).
  16. GTN-L. 2021. Available online: https://community.wmo.int/governance/commission-membership/executive-council/executive-council-members/global-climate-observing-system-gcos/gcos-steering-committee/terrestrial-observation-panel-climate/global-terrestrial-network-lakes (accessed on 14 November 2021).
  17. Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef] [Green Version]
  18. Crétaux, J.-F.; Nielsen, K.; Frappart, F.; Papa, F.; Calmant, S.; Benveniste, J. Hydrological applications of satellite altimetry: Rivers, lakes, man-made reservoirs, inundated areas. In Satellite Altimetry over Oceans and Land Surfaces; Earth Observation of Global Changes; Stammer, D., Cazenave, A., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 459–504. [Google Scholar]
  19. Shu, S.; Liu, H.; Beck, R.A.; Frappart, F.; Korhonen, J.; Lan, M.; Xu, M.; Yang, B.; Huang, Y. Evaluation of historic and operational satellite radar altimetry missions for constructing consistent long-term lake water level records. Hydrol. Earth Syst. Sci. 2021, 25, 1643–1670. [Google Scholar] [CrossRef]
  20. Bergé-Nguyen, M.; Cretaux, J.F.; Calmant, S.; Fleury, S.; Satylkanov, R.; Chontoev, D.; Bonnefond, P. Mapping mean lake surface from satellite altimetry and GPS kinematic surveys. Adv. Sp. Res. 2021, 67, 985–1001. [Google Scholar] [CrossRef]
  21. Frappart, F.; Blarel, F.; Fayad, I.; Bergé-Nguyen, M.; Crétaux, J.-F.; Shu, S.; Schregenberger, J.; Baghdadi, N. Evaluation of the Performances of Radar and Lidar Altimetry Missions for Water Level Retrievals in Mountainous Environment: The Case of the Swiss Lakes. Remote Sens. 2021, 13, 2196. [Google Scholar] [CrossRef]
  22. Kostianaia, E.A.; Kostianoy, A.G.; Scheglov, M.A.; Karelov, A.I.; Vasileisky, A.S. Impact of regional climate change on the infrastructure and operability of railway transport. Transp. Telecommun. 2021, 22, 183–195. [Google Scholar] [CrossRef]
  23. World Experience in the Construction, Maintenance and Repair of Railway Infrastructure Facilities in Permafrost Conditions; Center for Scientific and Technical Information and Libraries: Moscow, Russia, 2017; pp. 126p. (In Russian)
  24. Serykh, I.V.; Kostianoy, A.G. Seasonal and interannual variability of the Barents Sea temperature. Ecol. Montenegrina 2019, 25, 1–13. [Google Scholar] [CrossRef]
  25. Serykh, I.V.; Kostianoy, A.G. About the climatic changes in the temperature of the Baltic Sea. Fundam. Appl. Hydrophys. 2019, 12, 5–12. (In Russian) [Google Scholar] [CrossRef]
  26. Serykh, I.V.; Tolstikov, A.V. On the Reasons for the Long-Term Variability of the Near-Surface Air Temperature over the White Sea; Moscow University Bulletin; Series 5: Geography; Moscow University: Moscow, Russia, 2020; Volume 4, pp. 83–95. (In Russian) [Google Scholar]
  27. Serykh, I.V.; Kostianoy, A.G.; Lebedev, S.A.; Kostianaia, E.A. On the transition of temperature regime of the White Sea Region to a new phase state. Fundam. Appl. Hydrophys. 2022. in press (In Russian) [Google Scholar]
  28. Andreev, A.P. Lake Ladoga; Part 1–2; Publishing House of Maritime Department in the Main Admiralty: St. Petersburg, Russia, 1875; Part I, 263p, Part II, 135p. (In Russian) [Google Scholar]
  29. Filatov, N.N. (Ed.) Ladoga Lake; Petrozavodsk, Karelian Research Center, Russian Academy of Sciences: Petrozavodsk, Russia, 2000; 490p. (In Russian) [Google Scholar]
  30. Rumyantsev, V.A.; Drabkova, V.G. Ladoga Lake: Past, Present and Future; Publ. House “Nauka”: St. Petersburg, Russia, 2002; 327p. (In Russian) [Google Scholar]
  31. Rukhovets, L.; Filatov, N. (Eds.) Ladoga and Onego—Great European Lakes; Observations and Modelling; Springer: Berlin/Heidelberg, Germany; Praxis Publishing Ltd.: Chichester, UK, 2010; 315p. [Google Scholar]
  32. Rumyantsev, V.A.; Kondratyev, S.A. Ladoga; Publ. House of Institute of Limnology of Russian Academy of Sciences: St.-Petersburg, Russia, 2013; 568p. (In Russian) [Google Scholar]
  33. Bogdanov, V.I.; Kravchenkova, T.G.; Malova, T.I.; Marinich, M.A. Changes in the level of Lake Ladoga according to observations of 1859–2001 on Valaam. Doklady Akademii Nauk. 2002, 386, 672–675. (In Russian) [Google Scholar]
  34. Filatov, N.N.; Vyruchalkina, T.Y.; Diansky, N.A.; Nazarova, L.E.; Sinyukovich, V.N. Intracental variability of the level of the largest lakes in Russia. Doklady Akademii Nauk. 2016, 467, 589–593. (In Russian) [Google Scholar]
  35. Filatov, N.; Baklagin, V.; Efremova, T.; Nazarova, L.; Palshin, N. Climate change impacts on the watersheds of Lakes Onego and Ladoga from remote sensing and in situ data. Inland Waters 2019, 9, 130–141. [Google Scholar] [CrossRef]
  36. Kouraev, A.V.; Shimaraev, M.N.; Buharizin, P.I.; Naumenko, M.A.; Cretaux, J.F.; Mognard, N.; Legresy, B.; Remy, F. Ice and Snow Cover of Continental Water Bodies from Simultaneous Radar Altimetry and Radiometry Observations. Surv. Geophys. 2008, 29, 271–295. [Google Scholar] [CrossRef]
  37. Cretaux, J.-F.; Jelinski, V.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Abarco Del Rio, R.; Cazenave, A.; et al. SOLS, a lake database to monitor in near real time water level storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
  38. Lebedev, S.A.; Troitskaya, Y.I.; Rybushkina, G.V.; Dobrovolsky, M.N. Satellite altimetry of large lakes of the Baltic Basin. In Proceedings of the 2014 IEEE/OES Baltic International Symposium (BALTIC), Tallinn, Estonia, 27–29 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar] [CrossRef]
  39. Lebedev, S.A.; Troitskaya, Y.I.; Rybushkina, G.V.; Dobrovolsky, M.N. Interannual variability of the lake levels in northwest Russia based on satellite altimetry. In Complex Interfaces under Change: Sea—River—Groundwater—Lake, Proceedings of the HP2/HP3, IAHS-IAPSO-IASPEI Assembly, Gothenburg, Sweden, 22–26 July 2013; IAHS Publ.: Oxfordshire, UK, 2015; pp. 91–97. [Google Scholar] [CrossRef] [Green Version]
  40. Karetnikov, S.G.; Naumenko, M.A.; Guzivatiy, V.V.; Shimaraev, M.N.; Kouraev, A.V. Concordance of interannual variability in ice regime of Baikal and lake Ladoga. Geogr. Nat. Resour. 2016, 37, 135–143. [Google Scholar] [CrossRef]
  41. Kostianoy, A.G.; Kostianaia, E.A.; Lebedev, S.A.; Serykh, I.V.; Prokofiev, Y.A. Interannual variability in the level of lakes in northwestern Russia. In Proceedings of the VI International Scientific and Practical Conference “Fundamental and Applied Aspects of Geology, Geophysics and Geoecology Using Modern Information Technologies”, Maykop State Technological University, Maykop, Russia, 17–21 May 2021; Part 1. pp. 158–167. (In Russian). [Google Scholar]
  42. Campos, I.O.; Mercier, F.; Maheu, C.; Cochonneau, G.; Kosuth, P.; Blitzkow, D.; Cazenave, A. Temporal variations of river basin waters from Topex/Poseidon satellite altimetry. Application to the Amazon basin. Earth Planet. Sci. 2001, 333, 633–643. [Google Scholar] [CrossRef]
  43. Birkett, C.M.; Mertes, L.A.K.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: Application of satellite radar altimetry. J. Geophys. Res. 2002, 107, 8059. [Google Scholar] [CrossRef]
  44. Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef] [Green Version]
  45. Birkett, C.M.; Beckley, B. Investigating the performance of the Jason-2/OSTM radar altimeter over lakes and reservoirs. Mar. Geodesy 2010, 33, 204–238. [Google Scholar] [CrossRef]
  46. Lebedev, S.A.; Kostianoy, A.G. Satellite Altimetry of the Caspian Sea; Publ. House “Sea”: Moscow, Russia, 2005; 366p. (In Russian) [Google Scholar]
  47. Rybushkina, G.V.; Troitskaya, Y.I.; Soustova, I.A.; Balandina, G.N.; Lebedev, S.A.; Kostianoy, A.G. Satellite altimetry of inland water bodies. Tr. GOIN (Proc. Russ. State Oceanogr. Inst.) 2011, 213, 179–192. (In Russian) [Google Scholar]
  48. Troitskaya, Y.I.; Rybushkina, G.V.; Soustova, I.A.; Balandina, G.N.; Lebedev, S.A.; Kostianoy, A.G.; Panyutin, A.A.; Filina, L.V. Satellite altimetry of inland water bodies. Water Resour. 2012, 39, 184–199. [Google Scholar] [CrossRef]
  49. Troitskaya, Y.; Rybushkina, G.; Soustova, I.; Balandina, G.; Lebedev, S.; Kostianoy, A. Adaptive retracking of Jason-1 altimetry data for inland waters: The example of the Gorky Reservoir. Int. J. Remote Sens. 2012, 33, 7559–7578. [Google Scholar] [CrossRef]
  50. Troitskaya, Y.; Rybushkina, G.; Soustova, I.; Lebedev, S. Adaptive Retracking of Jason-1, 2 Satellite Altimetry Data for the Volga River Reservoirs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1603–1608. [Google Scholar] [CrossRef]
  51. Kostianoy, A.G.; Lebedev, S.A.; Kazmina, M.V.; Tsepelev VYu Varlashina, V.M.; Neschadimova, T.G. Satellite Monitoring of Transboundary Waters of Russia and Estonia; Publ. House “Signal”: Moscow, Russia, 2012; 16p, (In Russian and English). [Google Scholar]
  52. Liibusk, A.; Kall, T.; Rikka, S.; Uiboupin, R.; Suursaar, Ü.; Tseng, K.-H. Validation of Copernicus sea level altimetry products in the Baltic Sea and Estonian Lakes. Remote Sens. 2021, 12, 4062. [Google Scholar] [CrossRef]
  53. Berry, P.A.M.; Garlick, J.D.; Freeman, J.A.; Mathers, E.L. Global inland water monitoring from multimission altimetry. Geophys. Res. Lett. 2005, 32, L16401. [Google Scholar] [CrossRef]
  54. Calmant, S.; Seyler, F. Continental surface waters from satellite altimetry. C. R. Geosci. 2006, 338, 1113–1122. [Google Scholar] [CrossRef]
  55. Cretaux, J.-F.; Calmant, S.; Abarca del Rio, R.; Kouraev, A.; Berge-Nguyen, M.; Maisongrande, P. Lakes studies from satellite altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 509–534. [Google Scholar] [CrossRef]
  56. International Altimetry Team (358 Co-Authors). Altimetry for the Future: Building on 25 Years of Progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
  57. Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef] [Green Version]
  58. Molina, J.L.; Rodríguez-Gonzálvez, P.; Molina, M.C.; González-Aguilera, D.; Espejo, F. Geomatic methods at the service of water resource smodelling. J. Hydrol. 2014, 509, 105–162. [Google Scholar] [CrossRef]
  59. García-López, S.; Ruiz-Ortiz, V.; Muñoz-Pérez, J.J. Time-lapse photography for monitoring reservoir leakages (Montejaque dam, Andalusia, southern Spain). Hydrol. Res. 2018, 49, 281–290. [Google Scholar] [CrossRef]
  60. Filatov, N.N. (Ed.) Climate of Karelia: Variability and Impact on Water Bodies and Catchments; Karelian Research Center, Russian Academy of Sciences: Petrozavodsk, Russia, 2004; 224p. (In Russian) [Google Scholar]
  61. Filatov, N.; Johannessen, O.M.; Pozdnyakov, D.; Bobylev, L.P.; Pettersson, L. White Sea: Its Marine Environment and Ecosystem Dynamics Influenced by Global Change; Springer-Praxis: Chichester, UK, 2005; 530p. [Google Scholar]
  62. Filatov, N.N.; Terzhevik, A.Y. (Eds.) The White Sea and Its Catchment Area under the Influence of Climatic and Anthropogenic Factors; Institute of Northern Water Problems, Karelian Research Center, Russian Academy of Sciences: Petrozavodsk, Russia, 2007; 349p. (In Russian) [Google Scholar]
  63. Nazarova, L.E. Variability of mean long-term values of air temperature in Karelia. Izv. Russ. Geogr. Soc. 2014, 46, 27–33. (In Russian) [Google Scholar]
  64. Nazarova, L.E. Climate of the Republic of Karelia (Russia): Air temperature, variability and changes. Geopolit. Ecogeodyn. Reg. 2014, 10, 746–749. (In Russian) [Google Scholar]
  65. Tronin, A.A.; Gorny, V.I.; Kiselev, A.V.; Kritsuk, S.G.; Latypov, I.S. Satellite mapping of the thermal response of northern European ecosystems to climate change. In Proceedings of the All-Russian Scientific Conference with International Participation “Ecology and Space” to the Centenary of Academician of the Russian Academy of Sciences K.Ya. Kondratyev, St. Petersburg, Russia, 25–26 May 2020; pp. 72–78. (In Russian). [Google Scholar]
  66. Efremova, T.V.; Pal’shin, N.I. Influence of climate change on the thermal and ice regime of the lakes of Karelia according to the data of instrumental observations. In Ecological Problems of Northern Regions and Ways to Solve Them, Proceedings of the VI All-Russian Scientific Conference with International Participation Devoted to 120 Years Anniversary of G.M. Kreps and 110 Years An-niversary of O.I. Semenov-Tyan-Shanskiy, Apatity, Russia, 10–14 October 2016; Institute of North Industrial Ecology Problems of the North of the Kola Science Center of the Russian Academy of Sciences: Apatity, Russia, 2016; pp. 189–193. (In Russian) [Google Scholar]
  67. Efremova, T.V.; Pal’shin, N.I.; Belashev, B.Z. Water temperature of different types of lakes in Karelia under conditions of climate change (according to the data of instrumental measurements in 1953–2011). Water Resour. 2016, 43, 228–238. (In Russian) [Google Scholar] [CrossRef]
  68. Romanenko, F.A.; Shilovtseva, O.A. Geomorphological Processes in the Mountains of the Kola Peninsula and Climate Change; Vestnik Moscow University, Series 5 Geography; Moscow University: Moscow, Russia, 2016; Volume 6, pp. 78–86. (In Russian) [Google Scholar]
  69. Nazarova, L.E. Modern climatic conditions of the White Sea catchment area. Izv. Russ. Geogr. Soc. 2017, 149, 16–24. (In Russian) [Google Scholar]
  70. Filatov, N.N.; Nazarova, L.E.; Druzhinin, P.V. Influence of climatic and anthropogenic factors on the state of the “White Sea—Catchment” system. Trans. Karelian Res. Cent. Russ. Acad. Sci. 2019, 9, 30–50. (In Russian) [Google Scholar]
  71. Kondratyev, S.A.; Nazarova, L.E.; Shmakova, M.V.; Bovykin, I.V. Assessment of Runoff Changes in the Drainage Basin of Lake Onega as a Result of Possible Changes in Climatic Parameters (According to Mathematical Modeling); Institute of Limnology RAS, Institute of Water Problems of the North, Karelian Research Center, Russian Academy of Sciences: St. Petersburg, Russia, 2007; 30p. (In Russian) [Google Scholar]
  72. Yakubovich, A.N.; Yakubovich, I.A. Forecasting the impact of climatic changes on the functionality of the transport infrastructure of the permafrost zone in Russia. Intellect. Innov. Investig. 2019, 1, 104–110. (In Russian) [Google Scholar]
  73. Ricker, N. Further developments in the wavelet theory of seismogram structure. Bull. Seismol. Soc. Am. 1943, 33, 197–228. [Google Scholar] [CrossRef]
  74. Ricker, N. Wavelet functions and their polynomials. Geophysics 1944, 9, 314–323. [Google Scholar] [CrossRef]
  75. Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
  76. Astaf’eva, N.M. Wavelet analysis: Basic theory and some applications. Physics-Uspekhi 1996, 39, 1085–1108. [Google Scholar] [CrossRef]
  77. Mallat, S. Wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2009; 824p. [Google Scholar] [CrossRef]
  78. Galaganov, O.N.; Gorshkov, V.L.; Guseva, T.V.; Rosenberg, N.K.; Perederin, V.P.; Scherbakova, N.V. Recent crustal motion of Ladoga-Onega Region revealed from satellite and ground measurements. Curr. Probl. Remote Sens. Earth Space 2011, 8, 130–136. (In Russian) [Google Scholar]
Remotesensing 14 00659 g001 550
Figure 1. Map of Ladoga and Onega lakes with the route of the White Sea–Baltic Sea shipping canal (shown by the red line) (Courtesy: Norman Einstein, https://commons.wikimedia.org/wiki/File:White_Sea_Canal_map.png. (Accessed on 22 November 2021)).
Figure 1. Map of Ladoga and Onega lakes with the route of the White Sea–Baltic Sea shipping canal (shown by the red line) (Courtesy: Norman Einstein, https://commons.wikimedia.org/wiki/File:White_Sea_Canal_map.png. (Accessed on 22 November 2021)).
Remotesensing 14 00659 g001
Remotesensing 14 00659 g002 550
Figure 2. Network of Russian railways around Ladoga and Onega lakes (red lines) (modified from http://www.200stran.ru/maps_group26_item2118.html (Accessed on 22 November 2021)).
Figure 2. Network of Russian railways around Ladoga and Onega lakes (red lines) (modified from http://www.200stran.ru/maps_group26_item2118.html (Accessed on 22 November 2021)).
Remotesensing 14 00659 g002
Remotesensing 14 00659 g003 550
Figure 3. Watershed area of the Neva River (upper panel). Network of ground tracks of altimetry satellites TOPEX/Poseidon (T/P), Jason-1 (J1), Jason-2 (J2), and Jason-3 (J3) (lower panel). Locations of water level gauge stations and meteostations are shown on the map by black and red dots, respectively.
Figure 3. Watershed area of the Neva River (upper panel). Network of ground tracks of altimetry satellites TOPEX/Poseidon (T/P), Jason-1 (J1), Jason-2 (J2), and Jason-3 (J3) (lower panel). Locations of water level gauge stations and meteostations are shown on the map by black and red dots, respectively.
Remotesensing 14 00659 g003
Remotesensing 14 00659 g004 550
Figure 4. Interannual and seasonal variability of the Lake Ladoga level from October 1992 to December 2020 based on the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases. The black line shows average value calculated from all three databases.
Figure 4. Interannual and seasonal variability of the Lake Ladoga level from October 1992 to December 2020 based on the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases. The black line shows average value calculated from all three databases.
Remotesensing 14 00659 g004
Remotesensing 14 00659 g005 550
Figure 5. Interannual and seasonal variability of water level difference between the average value and the values from the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases for Lake Ladoga from October 1992 to December 2020.
Figure 5. Interannual and seasonal variability of water level difference between the average value and the values from the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases for Lake Ladoga from October 1992 to December 2020.
Remotesensing 14 00659 g005
Remotesensing 14 00659 g006 550
Figure 6. Interannual and seasonal variability of the Lake Onega level from October 1992 to December 2020 based on the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases. The black line shows average value calculated from all three databases.
Figure 6. Interannual and seasonal variability of the Lake Onega level from October 1992 to December 2020 based on the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases. The black line shows average value calculated from all three databases.
Remotesensing 14 00659 g006
Remotesensing 14 00659 g007 550
Figure 7. Interannual and seasonal variability of the water level difference between the average value and the values from the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases for Lake Onega from October 1992 to December 2020.
Figure 7. Interannual and seasonal variability of the water level difference between the average value and the values from the DAHITI (blue line), G-REALM (red line), and HYDROWEB (green line) databases for Lake Onega from October 1992 to December 2020.
Remotesensing 14 00659 g007
Remotesensing 14 00659 g008 550
Figure 8. Variability in the level of Lake Ladoga (a) and Lake Onega (b) according to the water level gauges stations Petrokrepost (a) and Voznesenye (b) (shown by the blue line), and data from the DAHITI (red diamonds), G-REALM (green circles), and HYDROWEB (purple triangles) databases for the period from 1 January 2015 to 31 December 2019.
Figure 8. Variability in the level of Lake Ladoga (a) and Lake Onega (b) according to the water level gauges stations Petrokrepost (a) and Voznesenye (b) (shown by the blue line), and data from the DAHITI (red diamonds), G-REALM (green circles), and HYDROWEB (purple triangles) databases for the period from 1 January 2015 to 31 December 2019.
Remotesensing 14 00659 g008
Remotesensing 14 00659 g009 550
Figure 9. Scatterplots between water levels derived from the DAHITI (a–b), G-REALM (c–d), and HYDROWEB (e–f) altimetry databases and in-situ water level gauge stations for Lake Ladoga (Petrokrepost) and Lake Onega (Voznesenye) from 1 January 2001 to 31 December 2020.
Figure 9. Scatterplots between water levels derived from the DAHITI (a–b), G-REALM (c–d), and HYDROWEB (e–f) altimetry databases and in-situ water level gauge stations for Lake Ladoga (Petrokrepost) and Lake Onega (Voznesenye) from 1 January 2001 to 31 December 2020.
Remotesensing 14 00659 g009
Remotesensing 14 00659 g010 550
Figure 10. The wavelet transform of the monthly average water level derived from satellite altimetry (a), air temperature, (b) and precipitation (c) at the Sortavala meteostation (Lake Ladoga) for 1993–2019.
Figure 10. The wavelet transform of the monthly average water level derived from satellite altimetry (a), air temperature, (b) and precipitation (c) at the Sortavala meteostation (Lake Ladoga) for 1993–2019.
Remotesensing 14 00659 g010
Remotesensing 14 00659 g011 550
Figure 11. The wavelet transform of the monthly average water level derived from satellite altimetry (a), air temperature, (b) and precipitation (c) at the Vytegra meteostation (Lake Onega) for 1993–2019.
Figure 11. The wavelet transform of the monthly average water level derived from satellite altimetry (a), air temperature, (b) and precipitation (c) at the Vytegra meteostation (Lake Onega) for 1993–2019.
Remotesensing 14 00659 g011
Table
Table 1. Physical characteristics of the five largest lakes in Europe.
Table 1. Physical characteristics of the five largest lakes in Europe.
ParameterLadoga
(Russia)		Onega
(Russia)		Vänern
(Sweden)		Saimaa
(Finland)		Peipus
(Estonia,
Russia)
Watershed area (km2)276,00066,28446,80061,05447,800
Max length (km)219245140190152
Max width (km)13891.6658547
Surface of the area (km2)17,8709720565043803555
Average depth (m)53027177.1
Max depth (m)2301271068215.3
Volume (km3)8382851533625
Table
Table 2. A list of satellites and their track numbers which cross Ladoga and Onega lakes included in the DAHITI, G-REALM, and HYDROWEB databases.
Table 2. A list of satellites and their track numbers which cross Ladoga and Onega lakes included in the DAHITI, G-REALM, and HYDROWEB databases.
LakeSatelliteTrack Number
Database for Hydrological Time Series of Inland Waters (DAHITI)
LadogaTOPEX/Poseidon, Jason-1/2/3066, 187
OnegaTOPEX/Poseidon, Jason-1/2/3009, 218
Global Reservoirs and Lakes Monitor (G-REALM)
LadogaTOPEX/Poseidon, Jason-1/2/3066
OnegaTOPEX/Poseidon, Jason-1/2/3218
HYDROWEB
LadogaTopex/Poseidon009, 066, 187, 244
Jason-1009, 066, 187
Jason-2/3009, 066, 187
GFO-1016, 139, 225, 332, 418
ENVISAT272, 358, 369, 455, 730, 816, 902, 913, 999
SARAL272, 358, 455, 730, 816, 902, 913, 999
Sentinel-3A100, 111, 214, 328, 756, 767
OnegaTopex/Poseidon009, 218
Jason-1/2/3009, 040, 187, 218
GFO-1016, 081, 102, 483
ENVISAT100, 186, 197, 558, 644, 655
SARAL100, 197, 558, 644, 655
Sentinel-3A442, 556, 567, 670, 681
Table
Table 3. A list of water level gauge stations at Ladoga and Onega lakes.
Table 3. A list of water level gauge stations at Ladoga and Onega lakes.
LakeWater Level Gauge Station“Zero” Level of the Gauge Station, m ASL *Latitude NLongitude E
LadogaPetrokrepost0.059.9531.03
Novaya Sviritsa0.060.4732.9
Syas’skye Ryadki0.060.1532.5
OnegaVoznesenye31.861.3635.35
Petrozavodsk31.861.7334.33
Kondopoga31.862.6134.43
* ASL is absolute sea level.
Table
Table 4. A list of meteostations at Ladoga and Onega lakes.
Table 4. A list of meteostations at Ladoga and Onega lakes.
LakeMeteostation (WMO N)Elevation,
m ASL		Latitude NLongitude E
LadogaSortavala  (N 22802)+19.061.7230.72
OnegaPetrozavodsk (N22820)+110.061.8234.27
Vytegra   (N 22837)+56.061.0236.45
Table
Table 5. The main characteristics of the Lake Ladoga level derived from the DAHITI, G-REALM, and HYDROWEB databases.
Table 5. The main characteristics of the Lake Ladoga level derived from the DAHITI, G-REALM, and HYDROWEB databases.
ParameterDAHITIG-REALMHYDROWEBAverage
Number of measurements1810107315361473
Mean lake level (m ASL)4.814.554.624.64
Standard deviation (m)0.210.190.190.21
Minimum (m ASL)3.012.993.463.07
Maximum (m ASL)6.185.705.745.79
Amplitude (m)3.152.712.282.73
Linear trend (cm/year)+1.17+0.81+0.27+0.75
Table
Table 6. The main characteristics of the Lake Onega level derived from the DAHITI, G-REALM, and HYDROWEB databases.
Table 6. The main characteristics of the Lake Onega level derived from the DAHITI, G-REALM, and HYDROWEB databases.
ParameterDAHITIG-REALMHYDROWEBAverage
Number of measurements1160103112501147
Mean lake level (m ASL)33.5033.3533.5833.44
Standard deviation (m)0.060.070.050.08
Minimum (m ASL)32.5232.0832.7332.11
Maximum (m ASL)34.1033.9534.2234.07
Amplitude (m)1.581.871.491.96
Linear trend (cm/year)+0.41+0.62−0.27+0.47
Table
Table 7. The main correlation characteristics between the Lake Ladoga water level derived from the DAHITI, G-REALM, and HYDROWEB altimetry databases, and in-situ water level gauge stations for the period from 1 January 2001 to 31 December 2020. Values in bold show the largest correlation coefficient.
Table 7. The main correlation characteristics between the Lake Ladoga water level derived from the DAHITI, G-REALM, and HYDROWEB altimetry databases, and in-situ water level gauge stations for the period from 1 January 2001 to 31 December 2020. Values in bold show the largest correlation coefficient.
Water Level Gauge StationParameterDAHITIG-REALMHYDROWEB
PetrokrepostCorrelation coefficient, R0.9660.9760.971
Arithmetical mean, AM (m)4.404.414.47
Standard deviation, SD (m)0.440.430.41
Coefficients in a linear regression equation (y = ax + b), where Y is water level (m) derived from altimetry data and X is water level (m) derived from in-situ gauge stations.a = +1.103
b = −0.97		a = +1.135
b = −0.80		a = +1.138
b = −0.79
Coefficient of determination, R20.9330.9530.942
Nash–Sutcliffe model efficiency coefficient (NSE)0.9330.9530.942
Percent bias (PBIAS)0.47%0.32%0.36%
Syas’skye RyadkiR0.9780.9840.929
AM (m)4.624.624.69
SD (m)0.370.360.38
Coefficients in a linear regressiona = +0.938
b = +0.08		a = +0.969
b = +0.21		a = +1.009
b = +0.04
R20.9570.9670.863
NSE0.9570.9670.863
PBIAS0.20%0.15%0.71%
Novaya SviritsaR0.9270.9240.919
AM (m)4.804.814.87
SD (m)0.360.350.36
Coefficients in a linear regressiona = +0.907
b = +0.41		a = +0.950
b = +0.47		a = +0.957
b = +0.46
R20.8600.8530.844
NSE0.85600.8530.844
PBIAS0.65%0.69%0.71%
Table
Table 8. The main correlation characteristics between the Lake Onega water level derived from the DAHITI, G-REALM, and HYDROWEB altimetry databases, and in-situ water level gauge stations for the period from 1 January 2001 to 31 December 2020. Values in bold show the largest correlation coefficient.
Table 8. The main correlation characteristics between the Lake Onega water level derived from the DAHITI, G-REALM, and HYDROWEB altimetry databases, and in-situ water level gauge stations for the period from 1 January 2001 to 31 December 2020. Values in bold show the largest correlation coefficient.
Water Level Gauge StationParameterDAHITIG-REALMHYDROWEB
KondopogaR0.8930.9240.907
AM (m)33.2233.1833.21
SD (m)0.180.20.18
Coefficients in a linear regressiona = +0.778a = +0.856a = +0.845
b = +7.15b = +4.63b = +4.83
R20.7970.8550.822
NSE0.7970.8550.822
PBIAS0.03%0.03%0.02%
PetrozavodskR0.8960.9280.917
AM (m)33.2233.1933.22
SD (m)0.180.190.18
Coefficients in a linear regressiona = +0.776a = +0.850a = +0.844
b = +7.22b = +4.82b = +4.89
R20.8040.8620.841
NSE0.8040.8620.841
PBIAS0.03%0.02%0.02%
VoznesenyeR0.8950.9370.906
AM (m)33.2333.2133.24
SD (m)0.180.20.18
Coefficients in a linear regressiona = +0.806a = +0.892a = +0.859
b = +6.24b = +3.46b = +4.40
R20.80.8770.821
NSE0.80.8770.821
PBIAS0.03%0.02%0.03%
Table
Table 9. Characteristics of linear regression trends in air temperature for 1945–2019 and precipitation for 1966–2019 at meteostations Sortavala (Lake Ladoga, WMO N 22802), Petrozavodsk (Lake Onega, WMO N 22820), and Vytegra (Lake Onega, WMO N 22837).
Table 9. Characteristics of linear regression trends in air temperature for 1945–2019 and precipitation for 1966–2019 at meteostations Sortavala (Lake Ladoga, WMO N 22802), Petrozavodsk (Lake Onega, WMO N 22820), and Vytegra (Lake Onega, WMO N 22837).
WMO Meteostation Number StationLakeTime PeriodY = aX + bCoefficient of Determination, R2
ab
Air Temperature Trend (°C/year)
22802SortavalaLadoga1945–2019+0.029−54.470.0046
22820PetrozavodskOnega1949–2019+0.030−57.410.0042
22837VytegraOnega1945–2019+0.031−57.720.0044
Sum of Precipitation Trend (mm/month/year)
22802SortavalaLadoga1966–2019+0.227−399.400.0119
22820PetrozavodskOnega1966–2019+0.086−122.790.0020
22837VytegraOnega1966–2019+0.114−170.540.0030
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Kostianoy, A.G.; Lebedev, S.A.; Kostianaia, E.A.; Prokofiev, Y.A. Interannual Variability of Water Level in Two Largest Lakes of Europe. Remote Sens. 2022, 14, 659. https://doi.org/10.3390/rs14030659

AMA Style

Kostianoy AG, Lebedev SA, Kostianaia EA, Prokofiev YA. Interannual Variability of Water Level in Two Largest Lakes of Europe. Remote Sensing. 2022; 14(3):659. https://doi.org/10.3390/rs14030659

Chicago/Turabian Style

Kostianoy, Andrey G., Sergey A. Lebedev, Evgeniia A. Kostianaia, and Yaan A. Prokofiev. 2022. "Interannual Variability of Water Level in Two Largest Lakes of Europe" Remote Sensing 14, no. 3: 659. https://doi.org/10.3390/rs14030659

APA Style

Kostianoy, A. G., Lebedev, S. A., Kostianaia, E. A., & Prokofiev, Y. A. (2022). Interannual Variability of Water Level in Two Largest Lakes of Europe. Remote Sensing, 14(3), 659. https://doi.org/10.3390/rs14030659

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop