An Algorithm to Assist the Robust Filter for Tightly Coupled RTK/INS Navigation System
Abstract
:1. Introduction
- (1)
- We improve our previous work to support GPS/BDS TC RTK/INS integration. Many related works introduce TC RTK/INS. However, most of them do not go into much detail about the implementation of the code. Although the TC RTK/INS integration is not rocket science, the implementation difficulties are easily underestimated, especially for the teams and labs just entering the field. This study introduces our implementations in detail and gives some derivations of key issues. We also open source our codes to facilitate the work of other researchers. Our codes are in C++ and are based on RTKLIB, PSINS, and GINAV. As mentioned above, GINAV is implemented in Matlab. We believe our C++ implementation can be more suitable for some engineering applications. Furthermore, GINAV aims to meet the researcher’s requirements for PPK. GINAV imports all the GNSS measurements and IMU data simultaneously when it comes to the input. We let the observations enter the integration sequentially by timestamp, approaching the real-time operation.
- (2)
- We propose a novel algorithm to improve RKF and test the improvement. We introduce the Cignal-to-Noise Ratio (CNR) to help detect outliers that should be discarded. We use CNR to decide whether a potential outlier should be maintained for a while to resist excessive robustness. The algorithm’s performance is tested on open-source datasets. The test shows that our algorithm’s positioning performance is improved compared to that of conventional RKF.
2. Materials and Methods
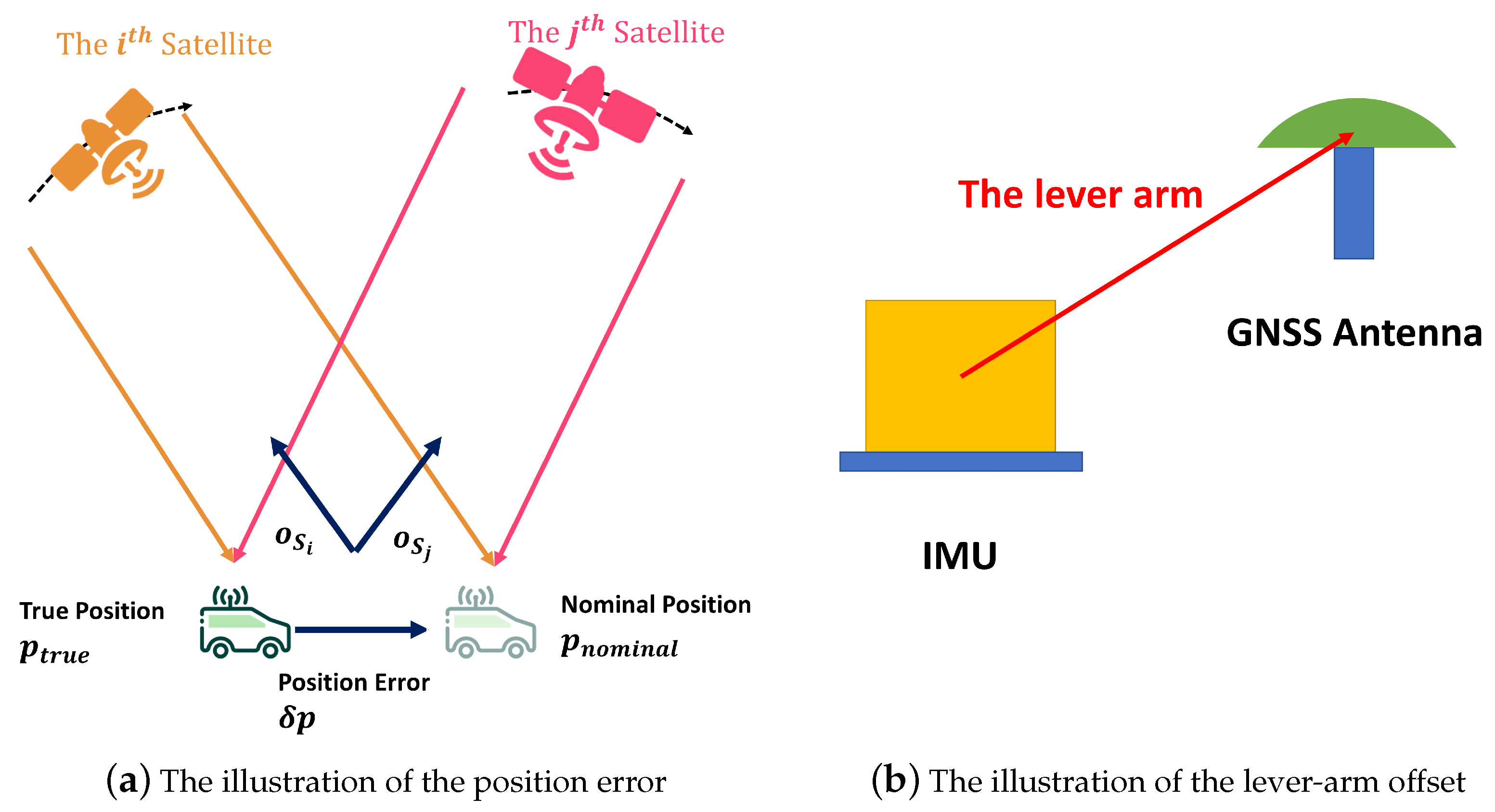
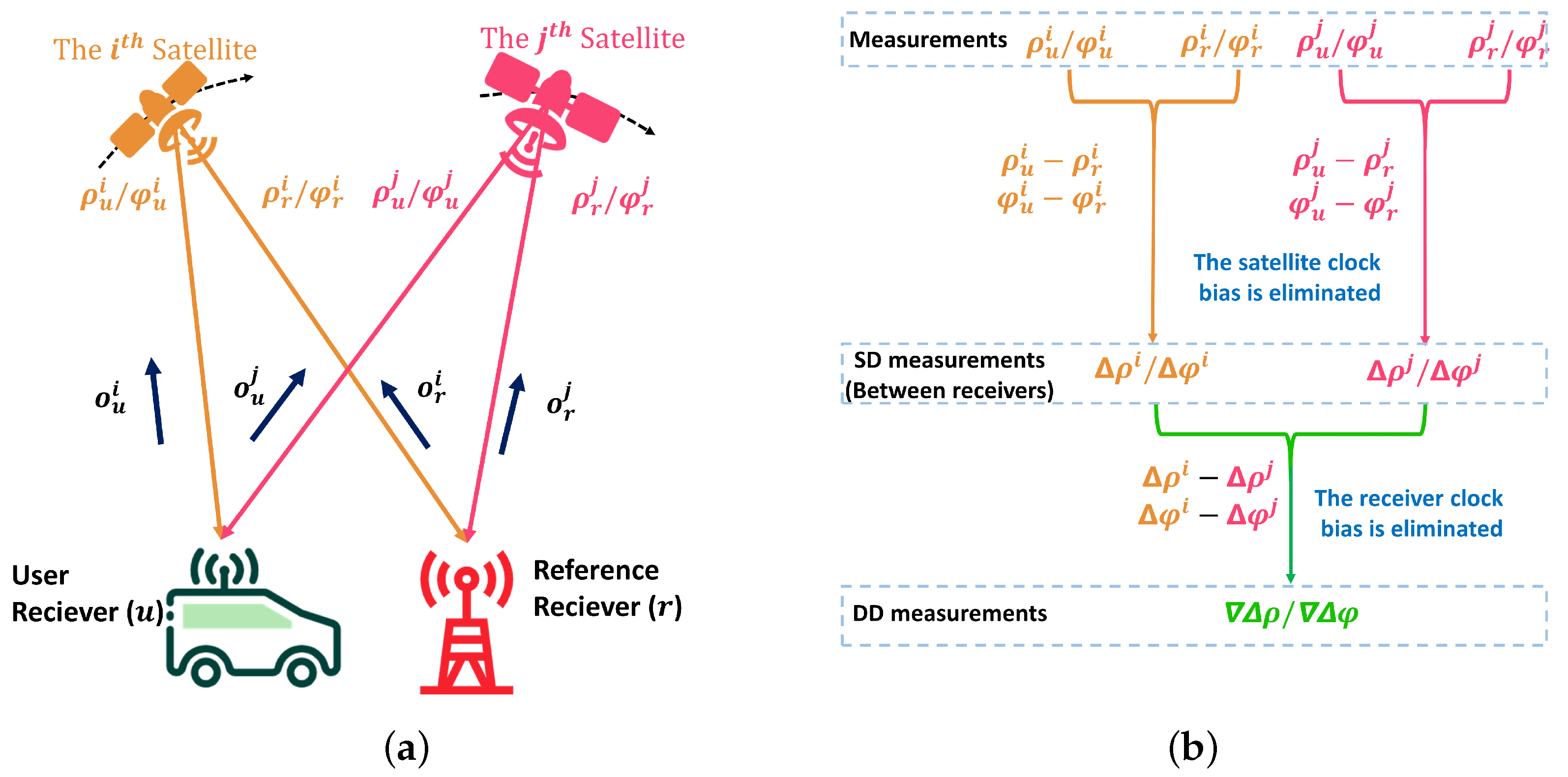
2.1. SD and DD
2.2. The Prediction Step of the TC RTK/INS Integration
2.2.1. The State Vector
2.2.2. The Covariance Matrix of the Process Noise
2.3. The Update Step of the TC RTK/INS Integration
2.3.1. The Measurement Vector and the Observation Matrix
2.3.2. The Covariance Matrix of the Observation Noise
2.3.3. The IGG-III Model
2.4. The Fixed Solution
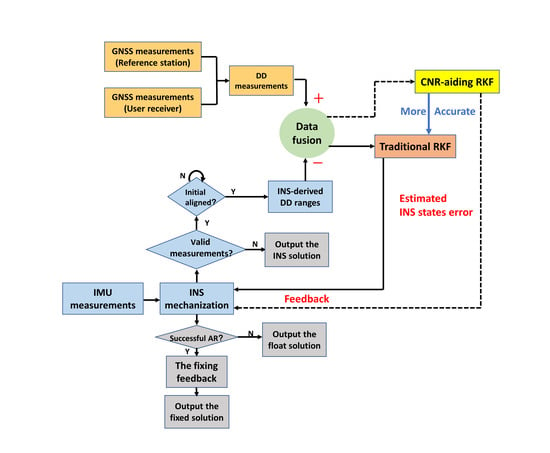
2.5. The TC RTK/INS Integration Architecture
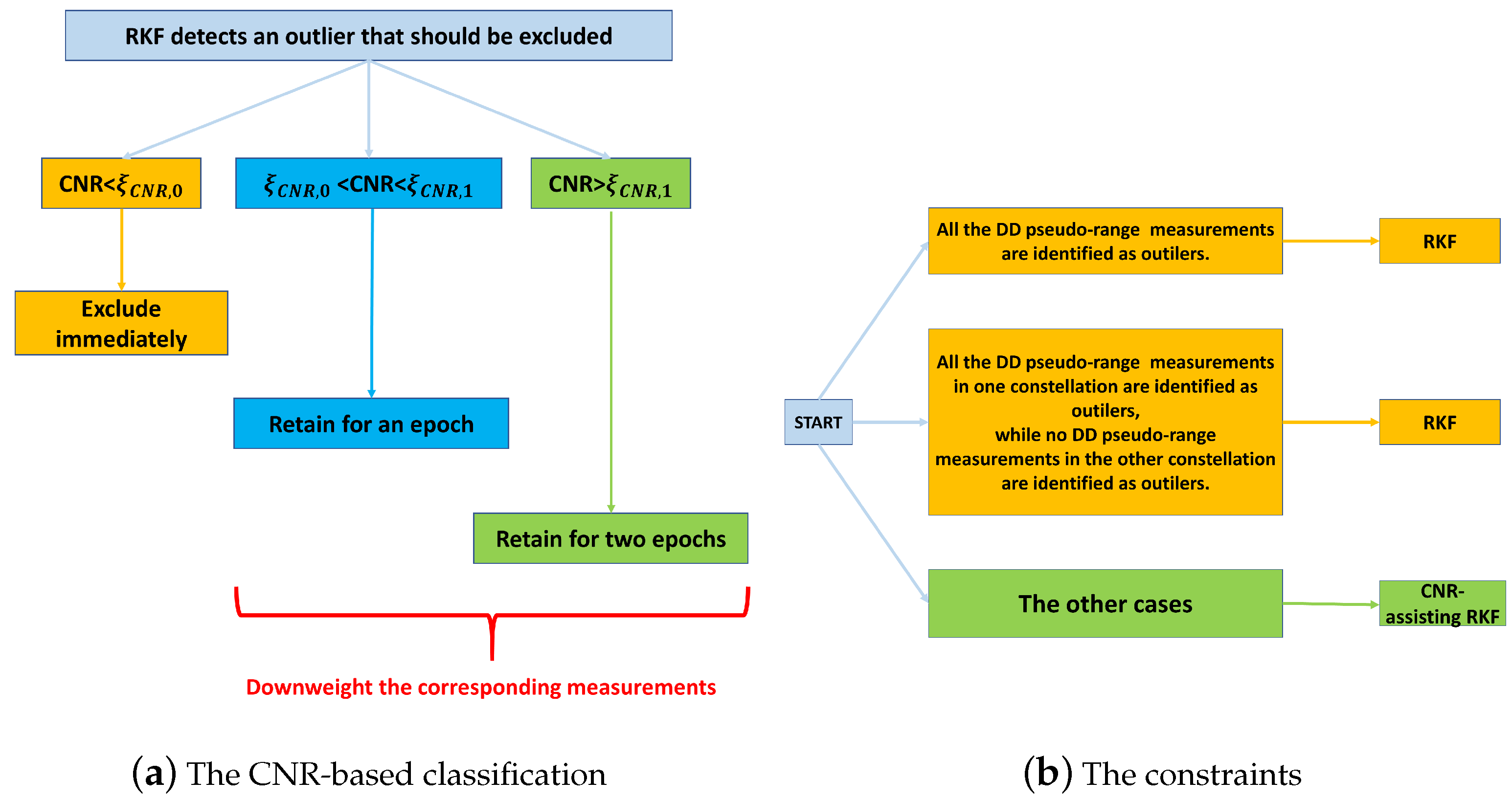
2.6. Modified RKF
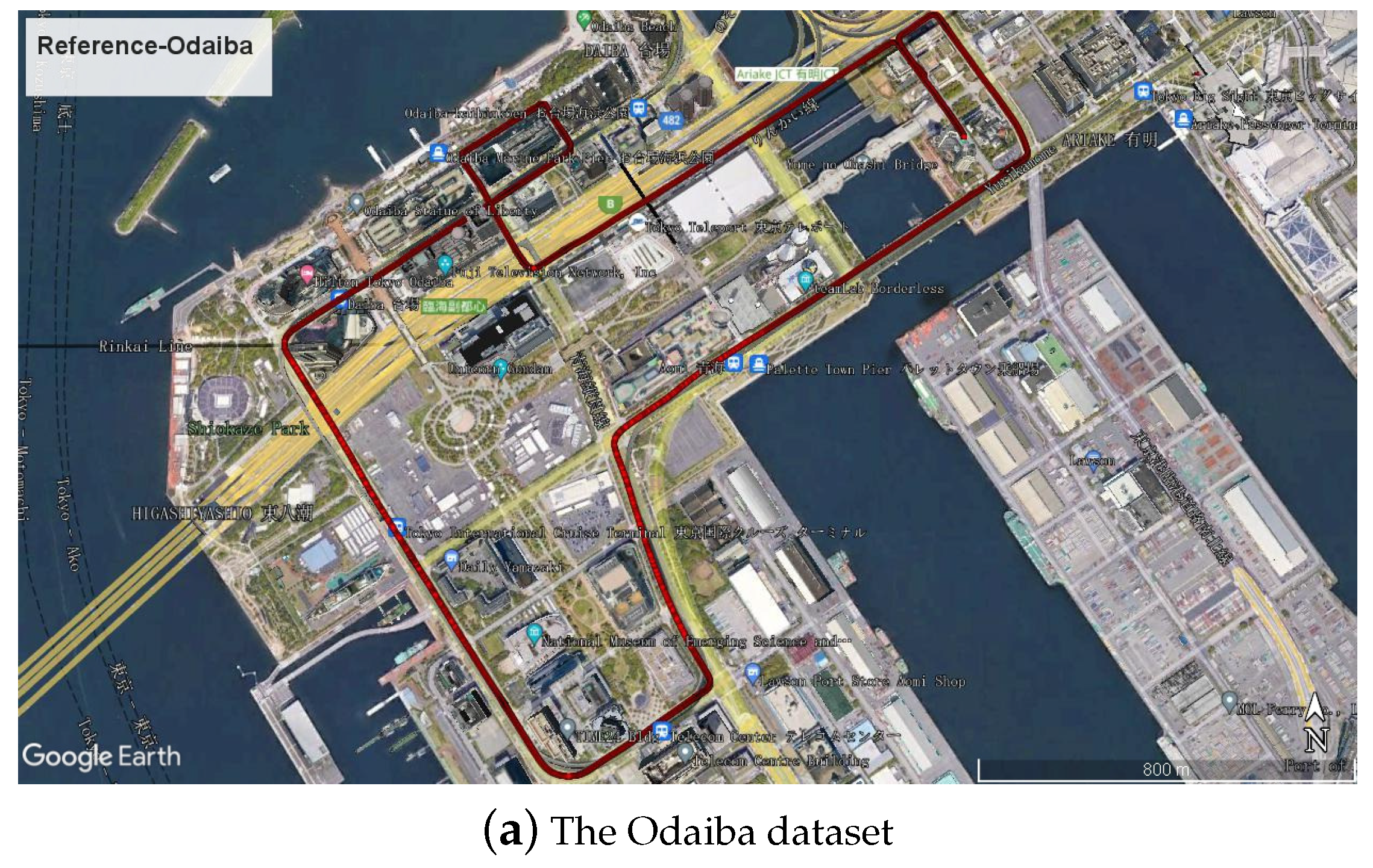
3. Description of the Datasets
4. Results
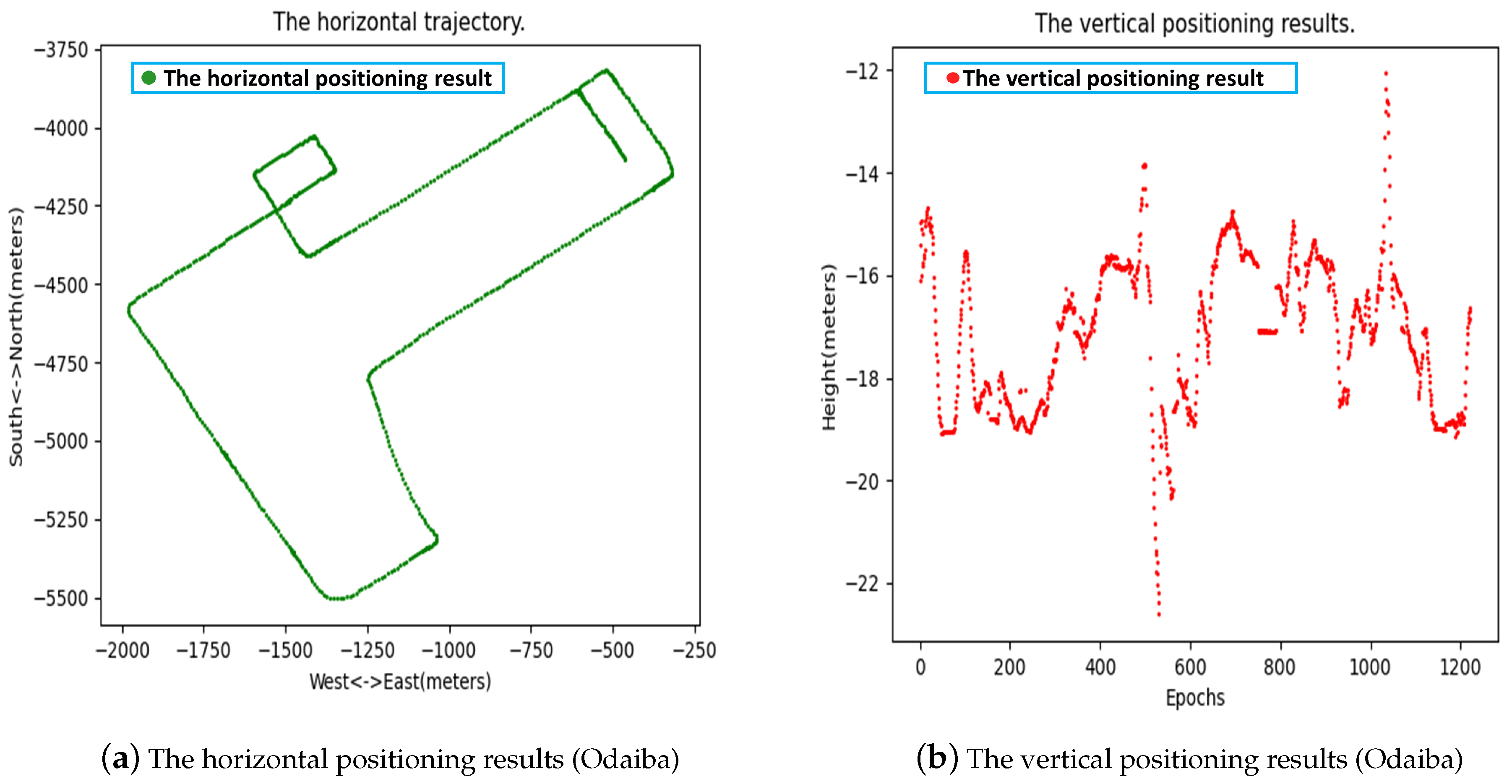
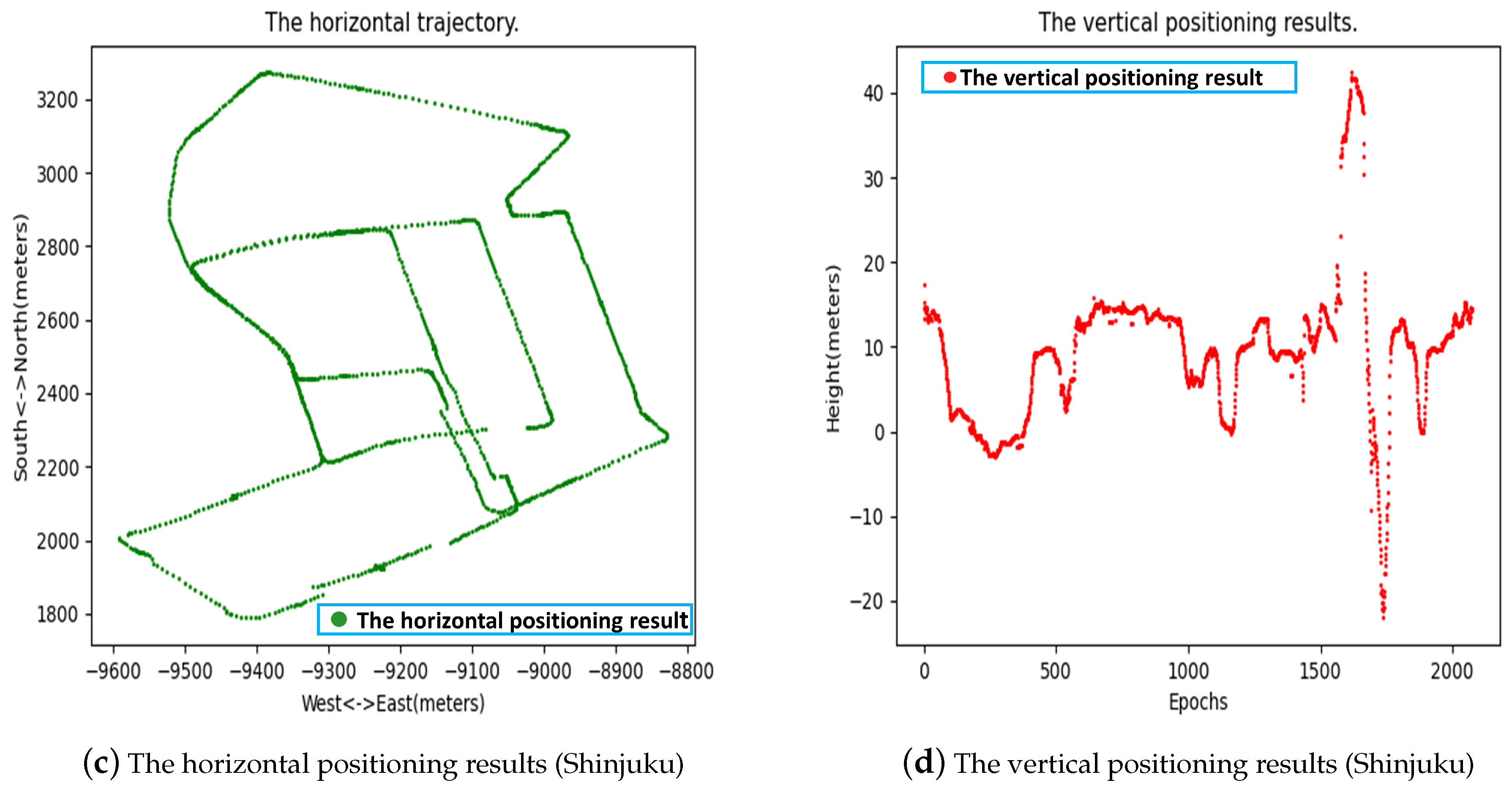
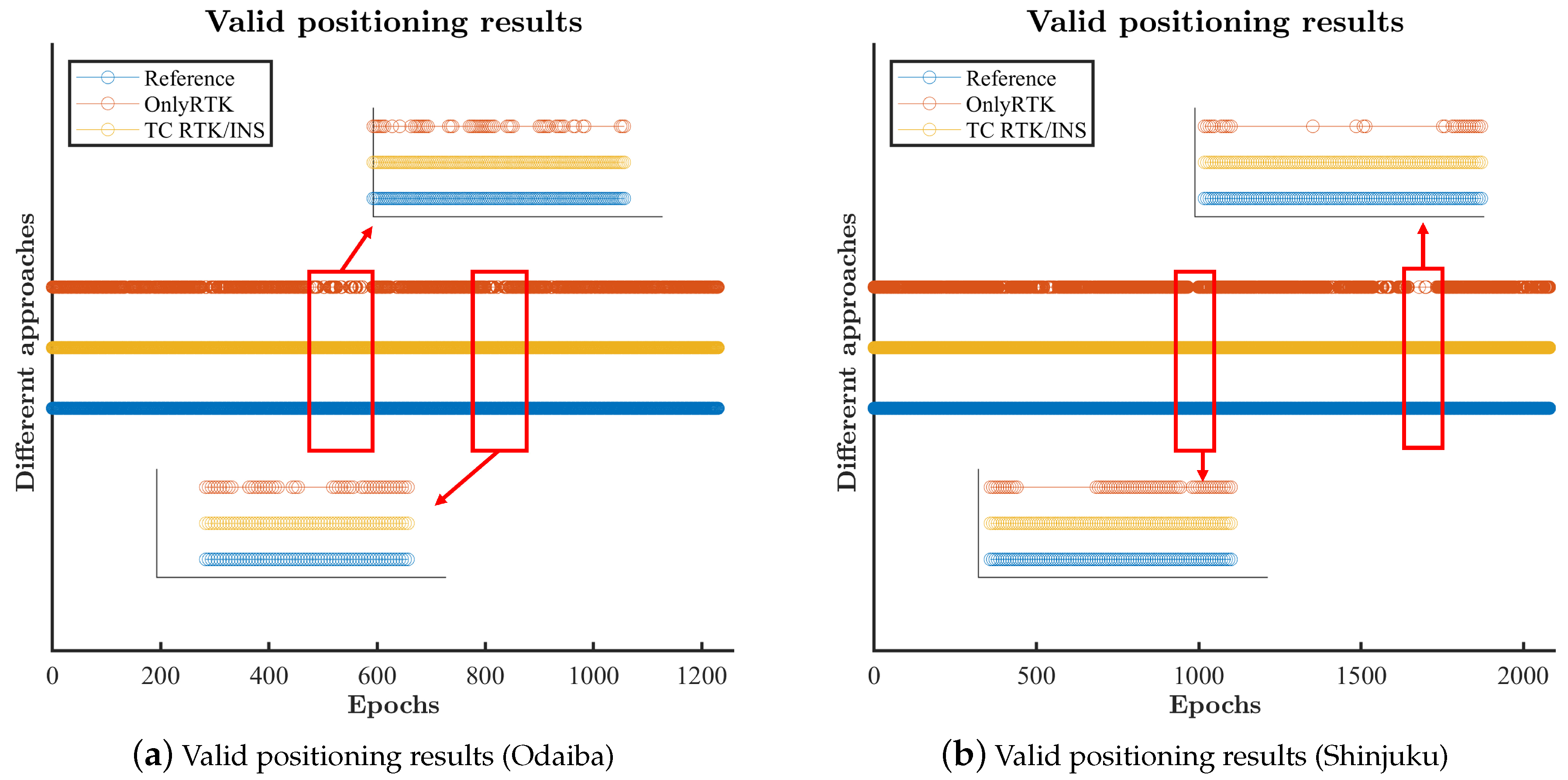
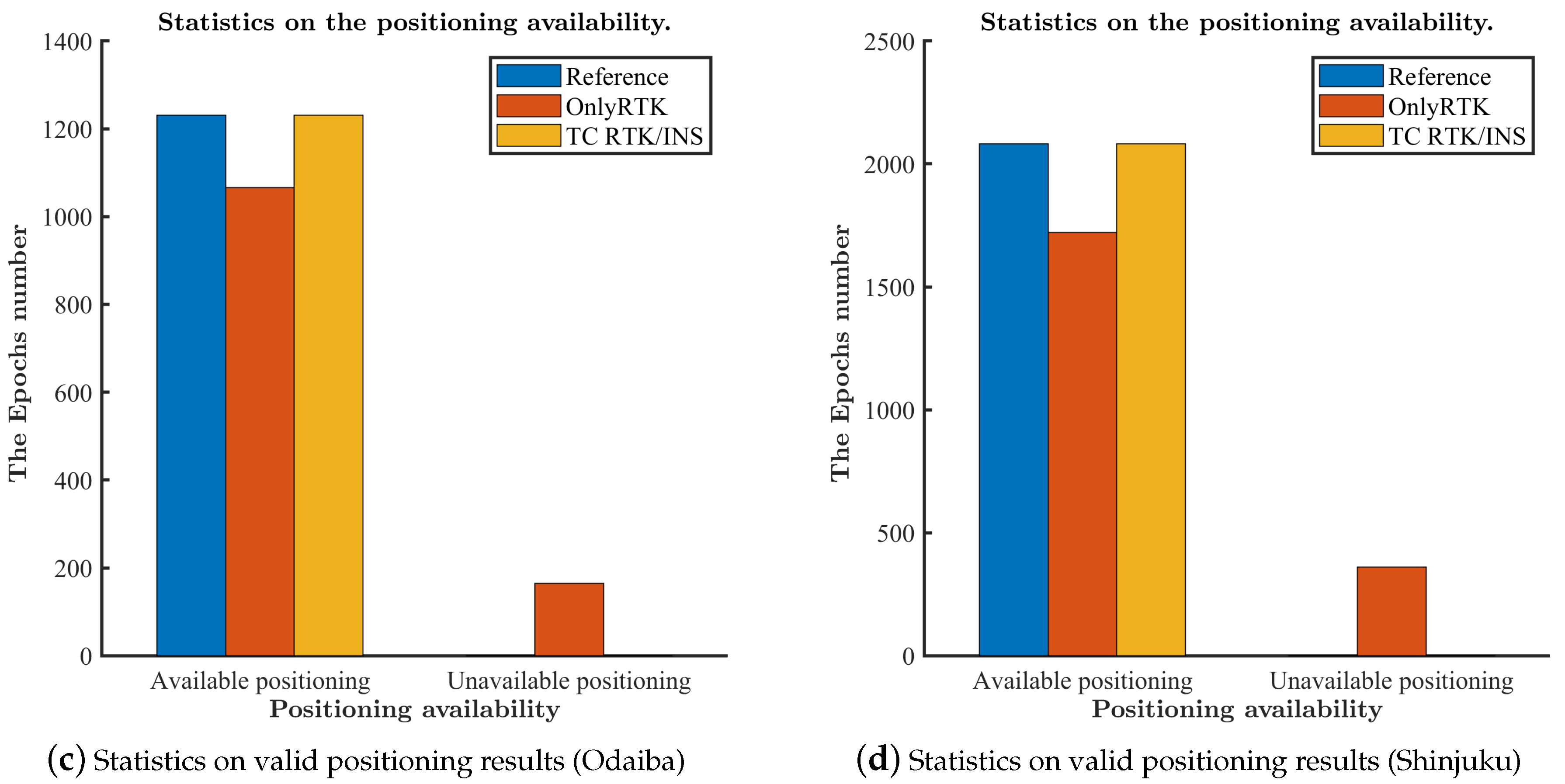
4.1. The Solution Visualization
4.2. The Performance of the TC RTK/INS Integration without the Outlier Resistance
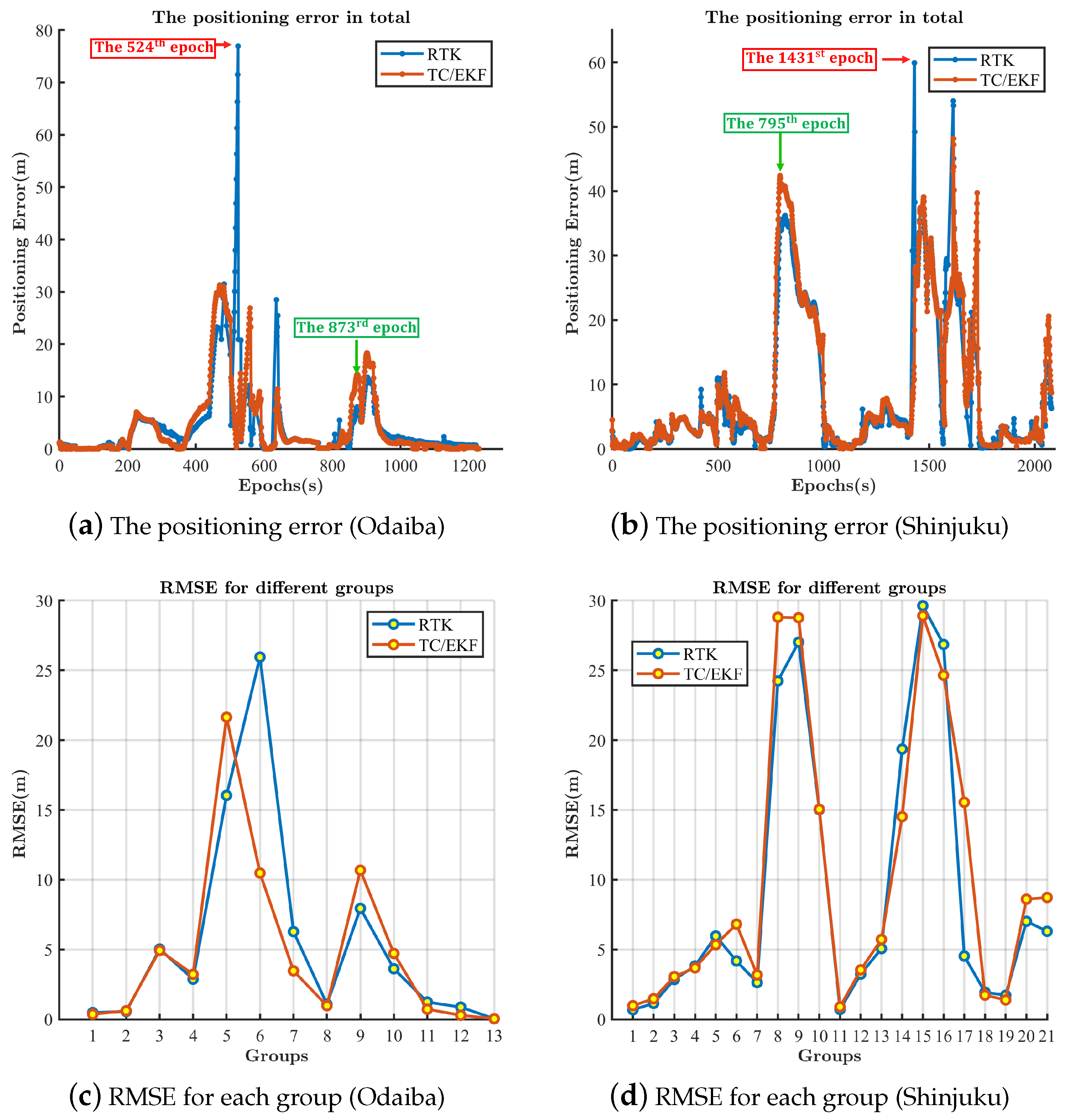
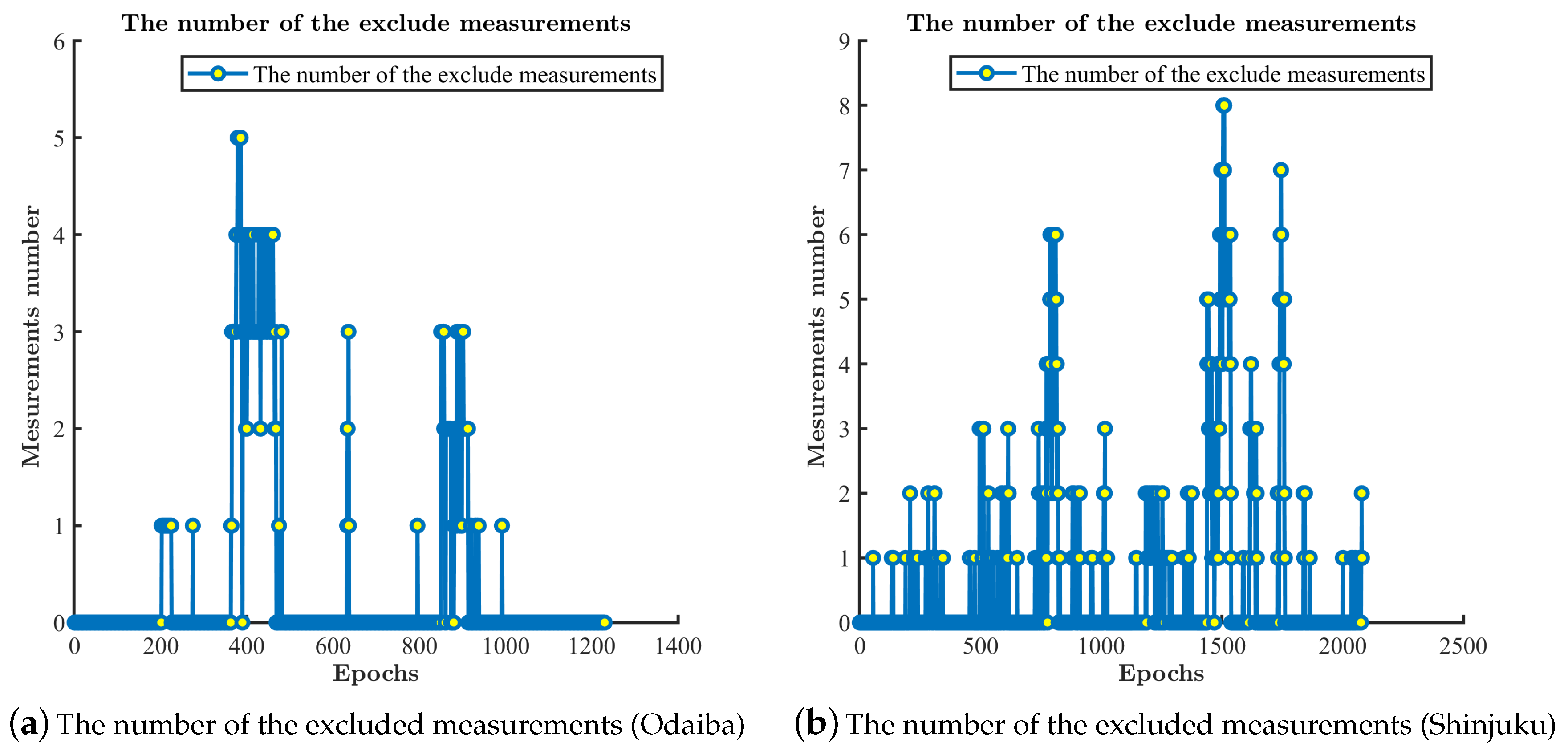
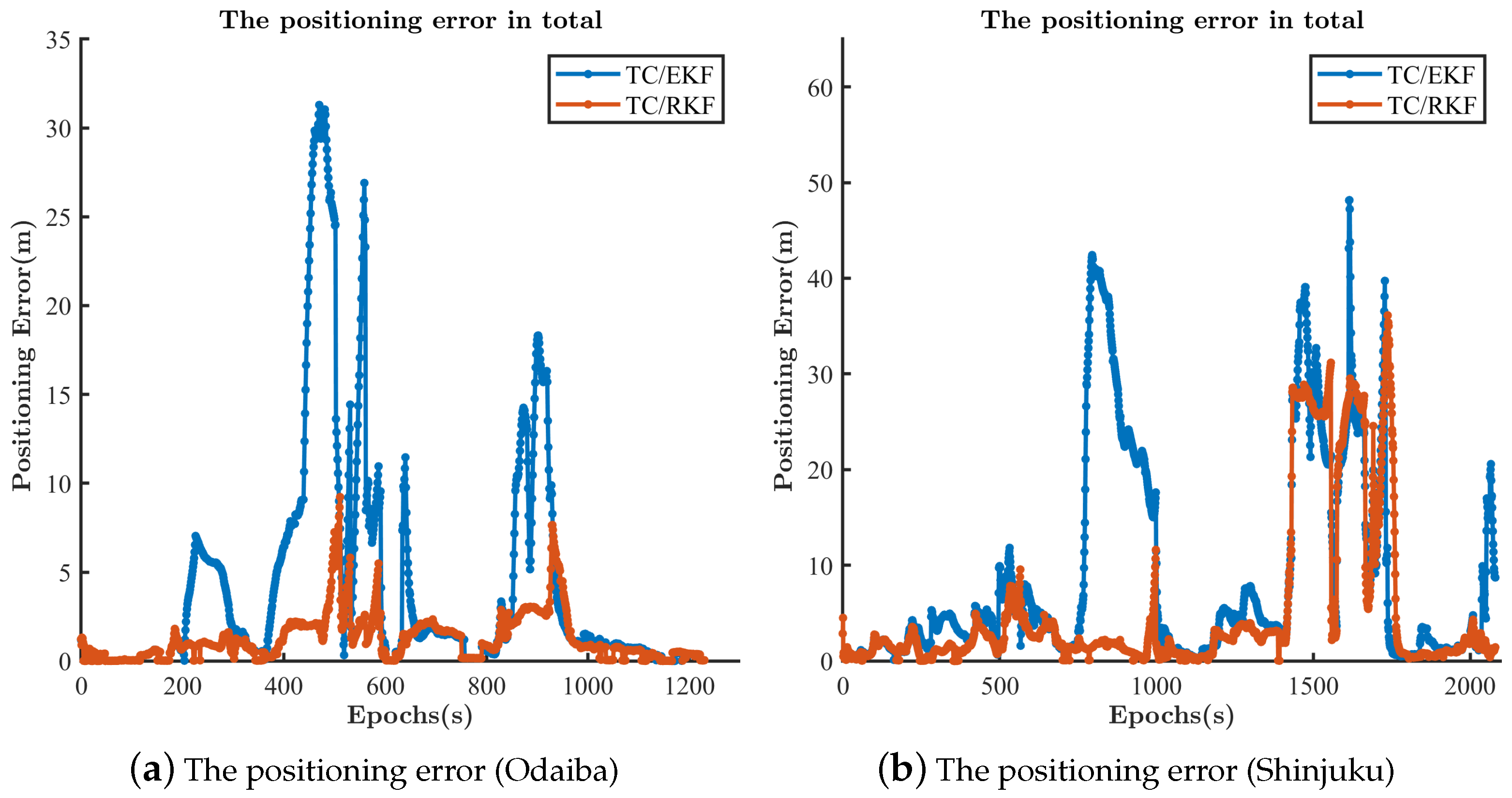
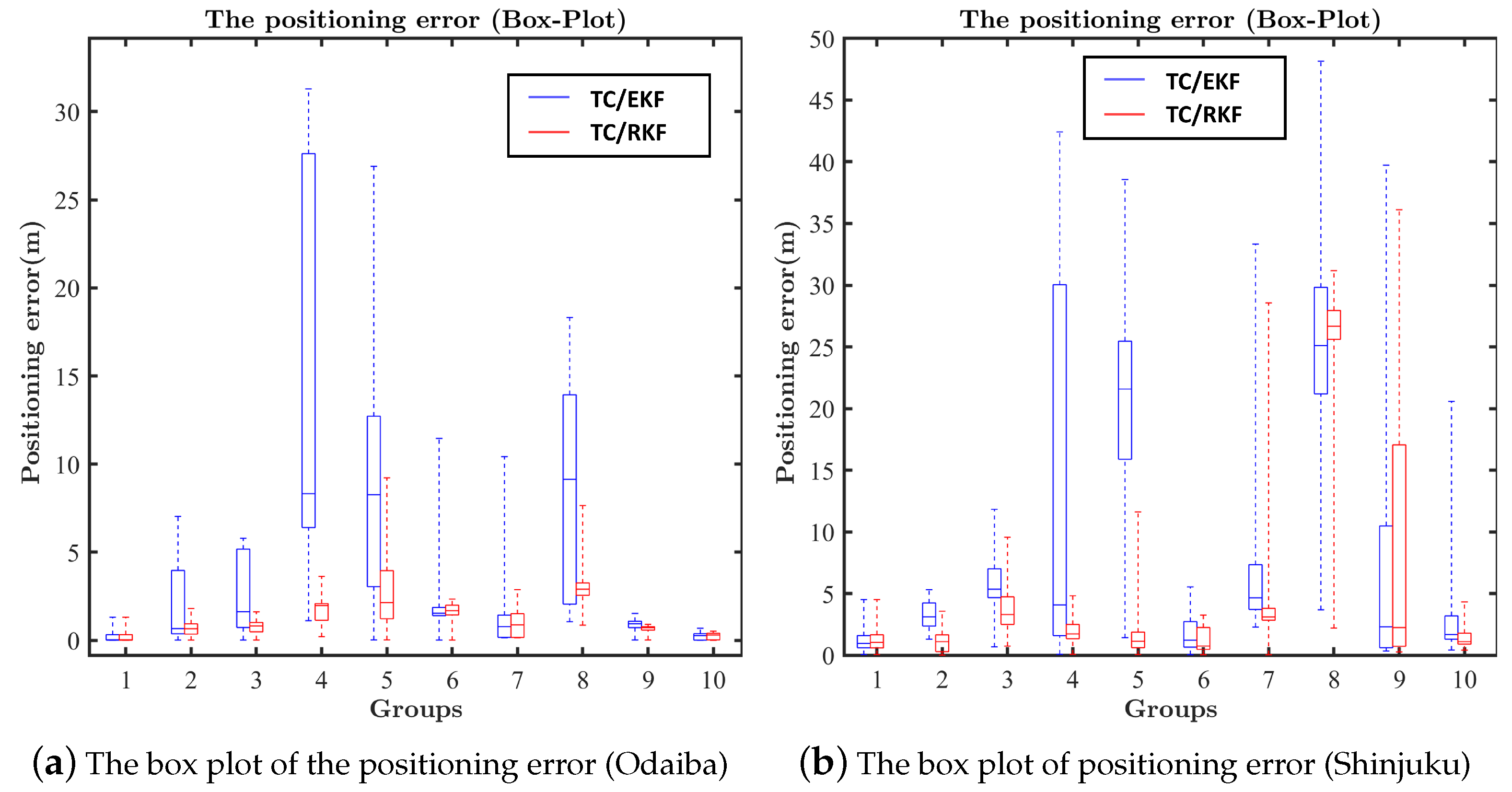
4.3. The Performance of the TC RTK/INS Integration with the Outlier Resistance
4.4. The Performance of the TC RTK/INS Integration with the Improved Outlier Resistance
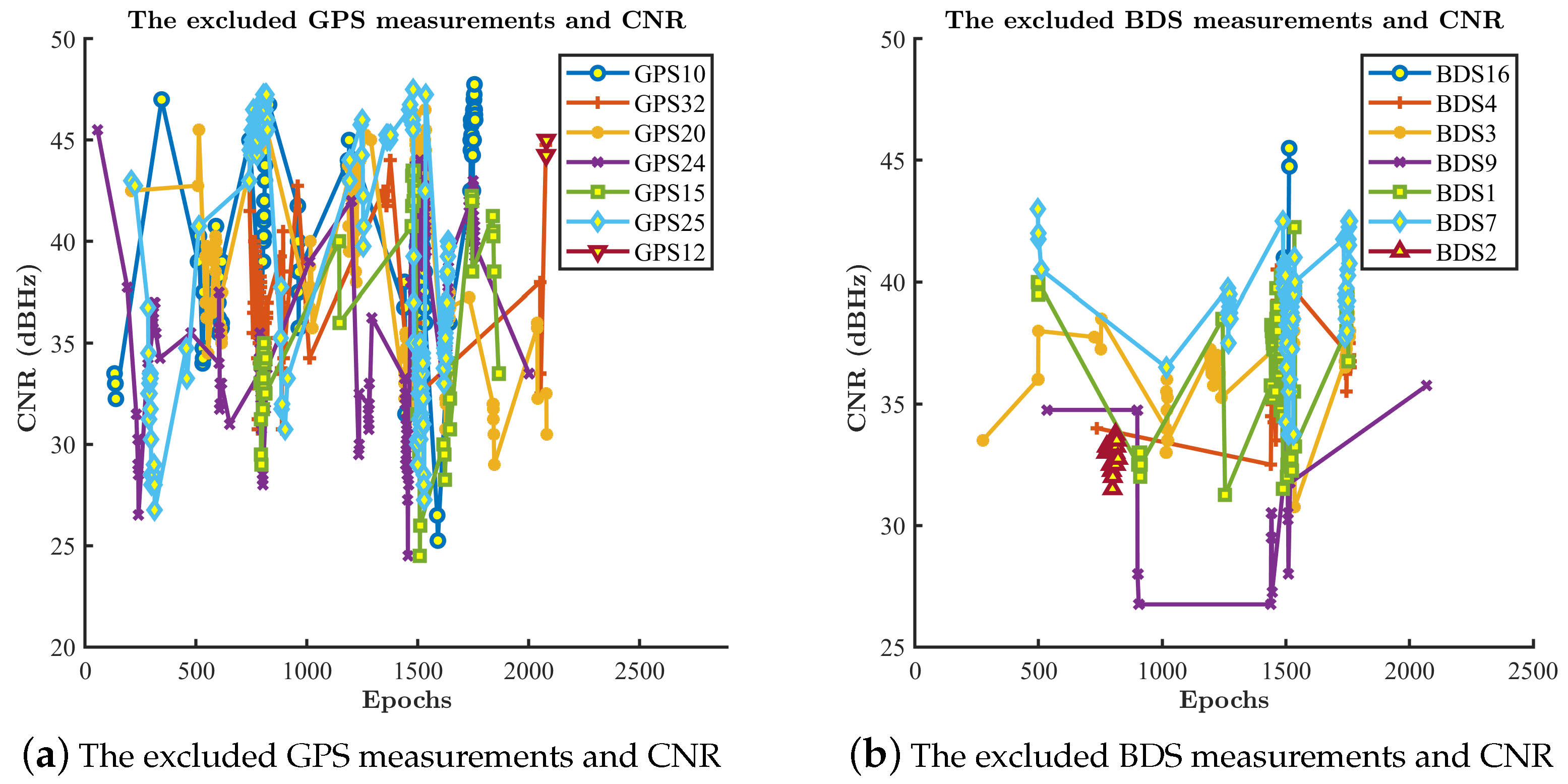
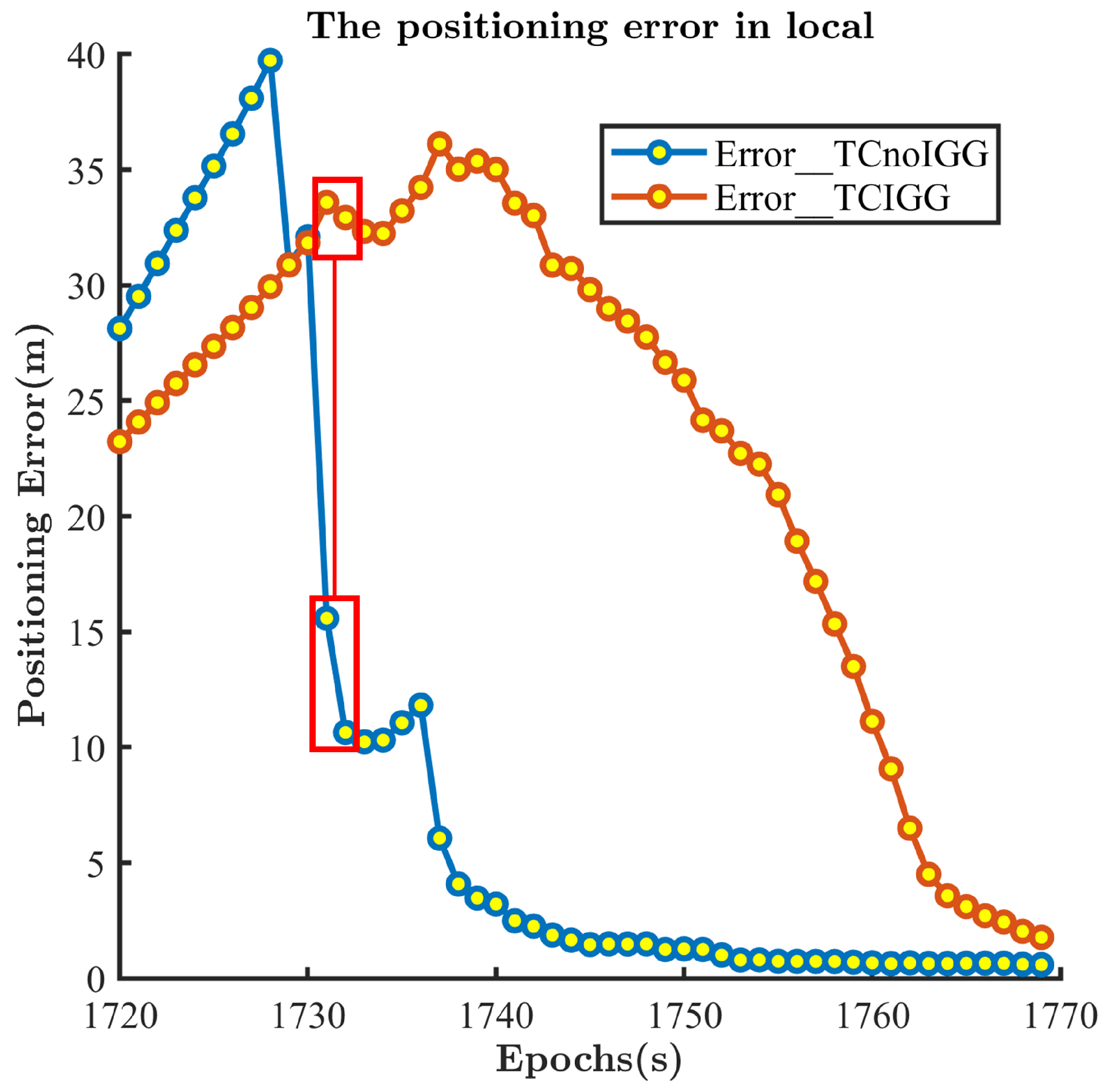
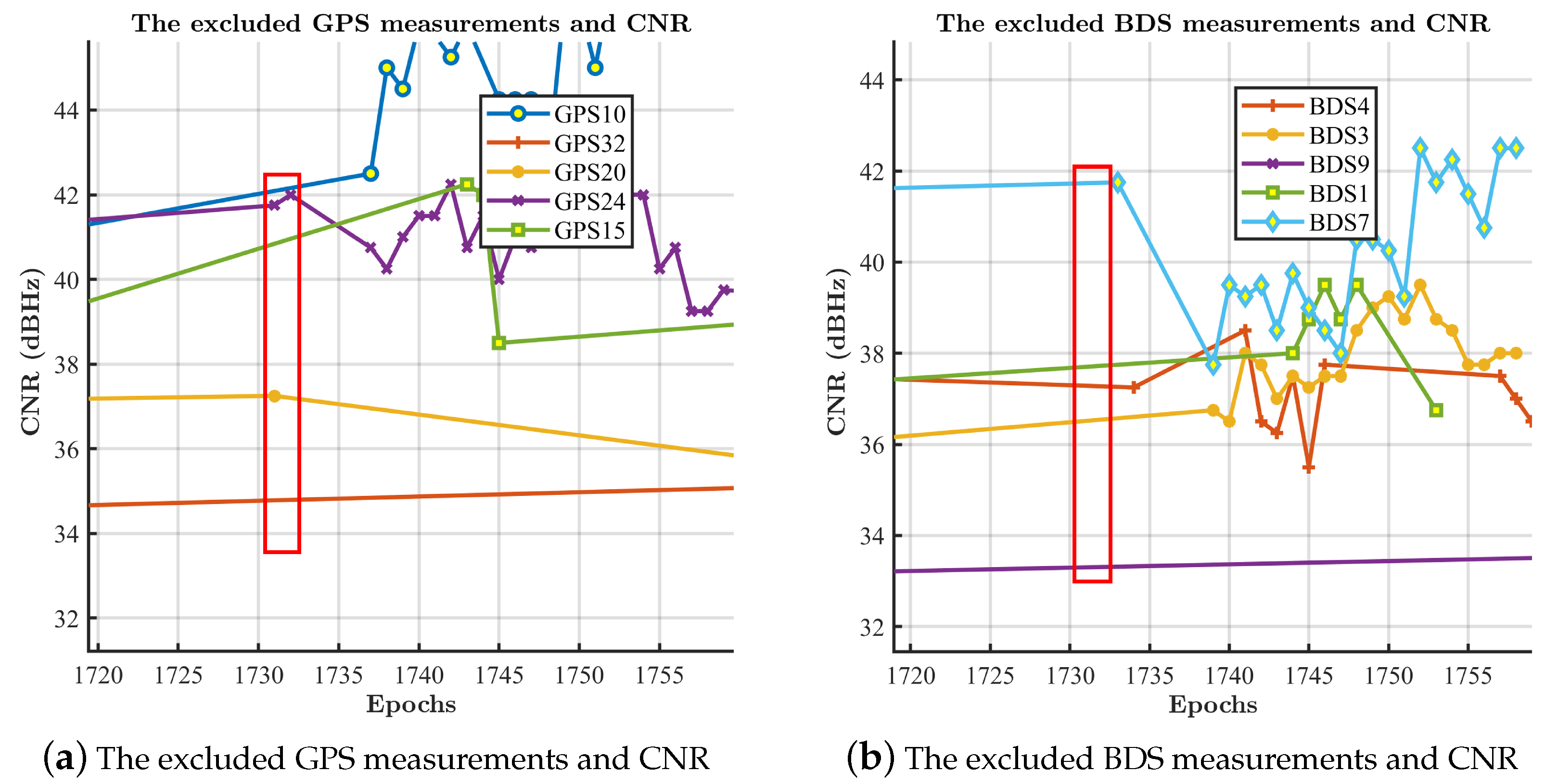
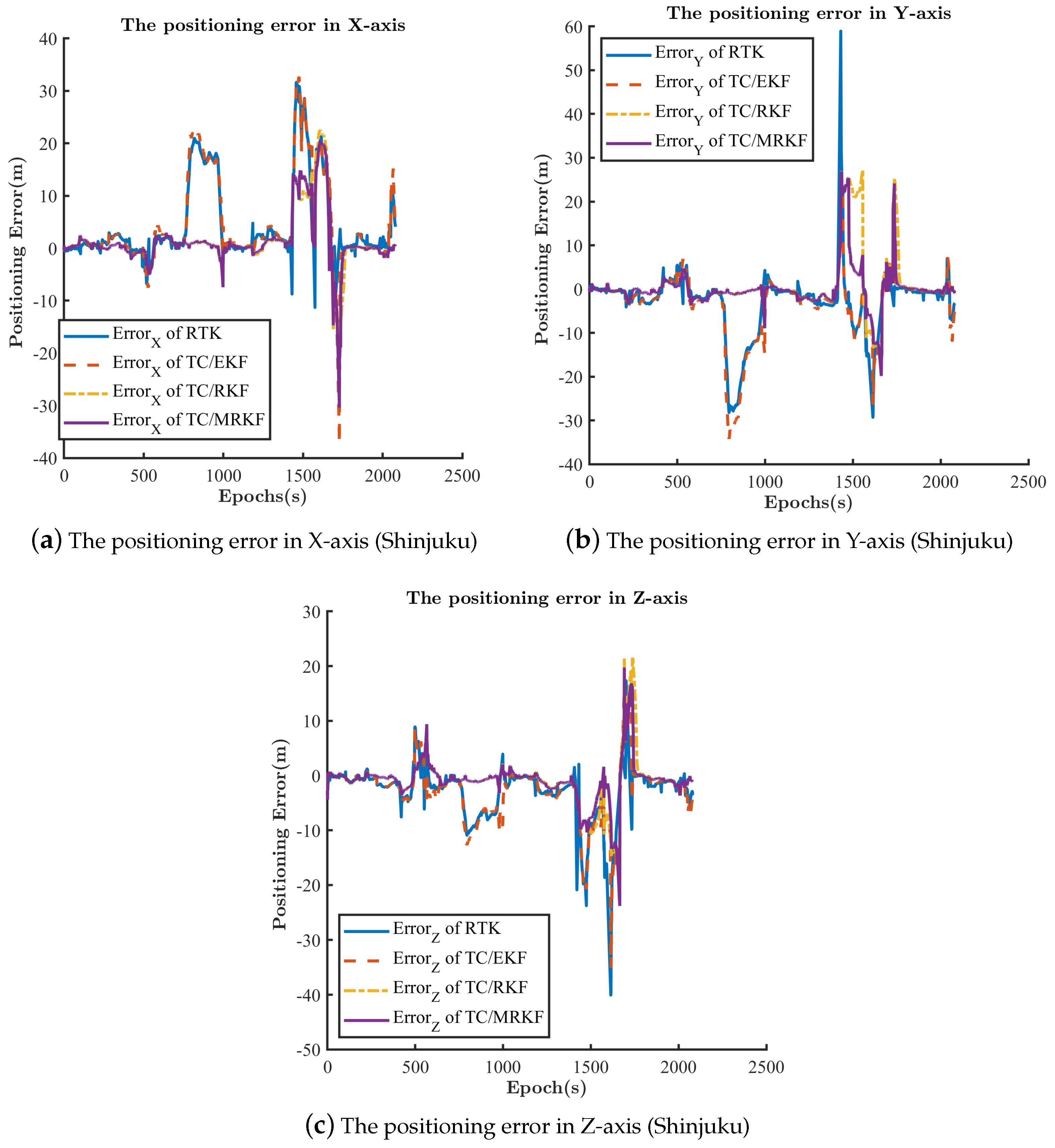
4.4.1. Further Analysis of the Shinjuku Dataset
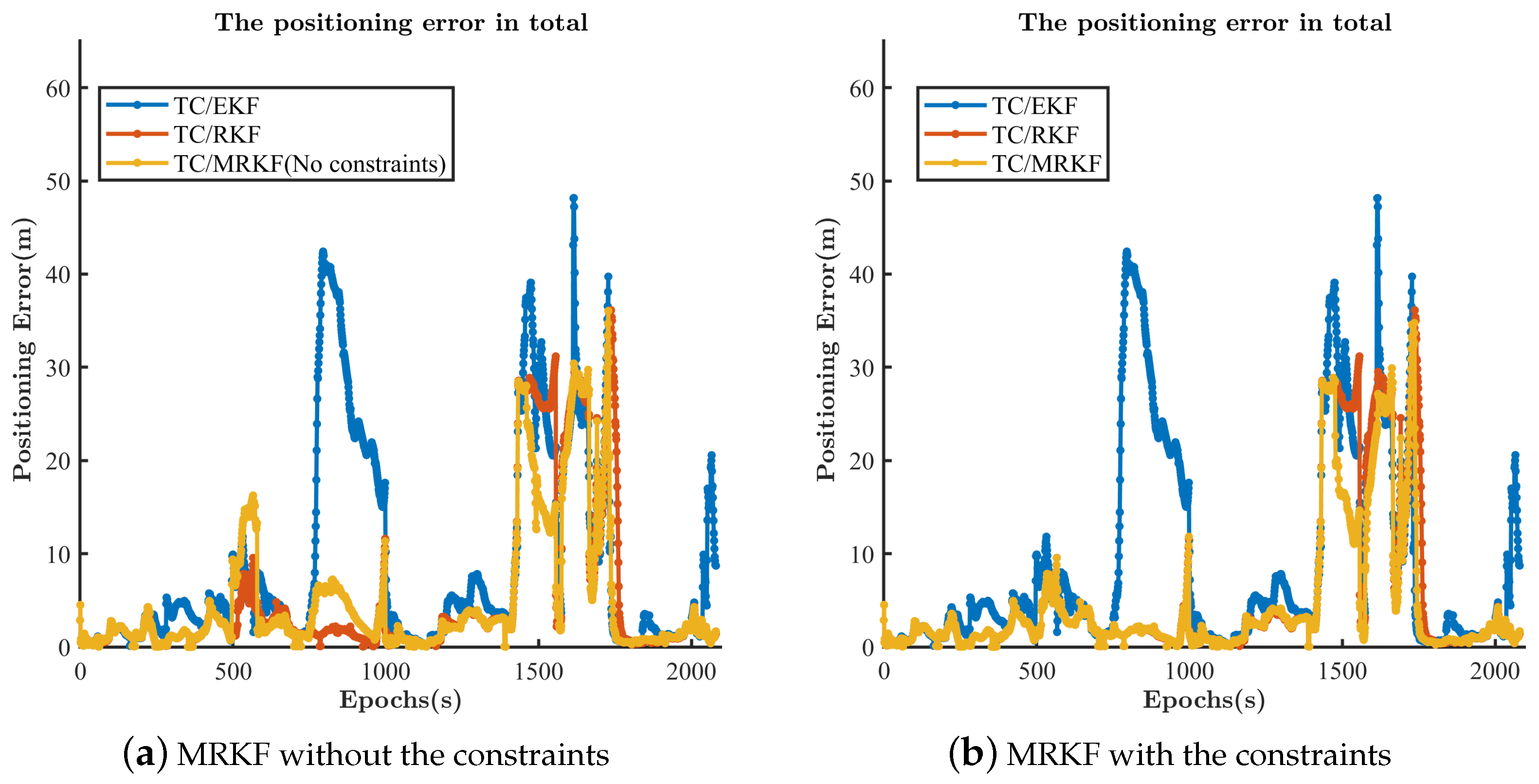
4.4.2. The Performance of MRKF
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Derivation of the Observation Matrix
References
- GNSS & Surveying 2017: The Year in Review. Available online: https://www.gpsworld.com/gnss-surveying-2017-the-year-in-review/ (accessed on 31 March 2022).
- The Almanac. Available online: https://www.gpsworld.com/the-almanac/ (accessed on 31 March 2022).
- Varbla, S.; Puust, R.; Ellmann, A. Accuracy assessment of RTK-GNSS equipped UAV conducted as-built surveys for construction site modelling. Survey Rev. 2020, 53, 477–492. [Google Scholar] [CrossRef]
- Rietdorf, A.; Daub, C.; Loef, P. Precise positioning in real-time using navigation satellites and telecommunication. In Proceedings of the 3rd Workshop on Positioning, Navigation and Communication (WPNC’06), Hannover, Germany, 16–19 March 2006; pp. 209–218. [Google Scholar]
- Takasu, T.; Kubo, N.; Yasuda, A. Development, evaluation and application of RTKLIB: A program library for RTK-GPS. In Proceedings of the 2007 GPS/GNSS Symposium, Tokyo, Japan, 20–22 November 2007. [Google Scholar]
- Teunissen, P.; Montenbruck, O. Basic observation equations. In Handbook of Global Navigation Satellite Systems, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-319-42926-7. [Google Scholar]
- Lee, I.S.; Ge, L. The performance of RTK-GPS for surveying under challenging environmental conditions. Earth Planets Sp. 2006, 58, 515–522. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Gao, C.F.; Pan, S.G.; Wang, D.H.; Wang, S.L. Single-epoch positioning method in network RTK with BDS triple-frequency widelane combinations. Acta Geod. Cartogr. Sin. 2015, 44, 641–648. Available online: http://xb.sinomaps.com/EN/10.11947/j.AGCS.2015.20140308 (accessed on 2 April 2022).
- Deng, C.L.; Tang, W.M.; Liu, J.N.; Shi, C. Reliable single-epoch ambiguity resolution for short baselines using combined GPS/BeiDou system. GPS Solut. 2014, 18, 375–386. [Google Scholar] [CrossRef]
- Gao, W.; Gao, C.F.; Pan, S.G.; Yu, G.R.; Hu, H.Q. Method and assessment of BDS triple-frequency ambiguity resolution for long-baseline network RTK. Adv. Space Res. 2017, 60, 2520–2532. [Google Scholar] [CrossRef]
- Carcanague, S.; Julien, O.; Vigneau, W.; Macabiau, C. Low-cost single-frequency GPS/GLONASS RTK for road users. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013; pp. 168–184. [Google Scholar]
- Li, T.; Zhang, H.P.; Niu, X.J.; Gao, Z.Z. Tightly-coupled integration of multi-GNSS single-Frequency RTK and MEMS-IMU for enhanced positioning performance. Sensors 2017, 17, 2462. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS) – achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: A low-cost and high-grade receivers GPS-BDS RTK analysis. J. Geod. 2016, 90, 1255–1278. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P. Characterization of between-receiver GPS-Galileo inter-system biases and their effect on mixed ambiguity resolution. GPS Solut. 2013, 17, 521–533. [Google Scholar] [CrossRef]
- Odolinski, R.; Odijk, D.; Teunissen, P. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2015, 19, 151–163. [Google Scholar] [CrossRef]
- Sinko, J.W. RTK performance in highway and racetrack experiments. J. Inst. Navig. 2003, 50, 265–276. [Google Scholar] [CrossRef]
- Yang, C.; Shi, W.; Chen, W. Correlational inference-based adaptive unscented Kalman filter with application in GNSS/IMU-integrated navigation. GPS Solut. 2018, 22, 1–14. [Google Scholar] [CrossRef]
- Kirkko-Jaakkola, M.; Ruotsalainen, L.; Bhuiyan, M.Z.H.; Söderholm, S.; Thombre, S.; Kuusniemi, H. Performance of a MEMS IMU deeply coupled with a GNSS receiver under jamming. 2014 Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS), Corpus Christi, TX, USA, 20–21 November 2014; pp. 64–70. [Google Scholar]
- Angrisano, A. GNSS/INS integration methods. Ph.D. Thesis, The Parthenope University of Naples, Naples, Italy, 2010. [Google Scholar]
- Li, T.; Zhang, H.P.; Gao, Z.Z.; Niu, X.J.; El-sheimy, N. Tight fusion of a monocular camera, MEMS-IMU, and single-frequency multi-GNSS RTK for precise navigation in GNSS-challenged environments. Remote. Sens. 2019, 11, 610. [Google Scholar] [CrossRef] [Green Version]
- Schütz, A.; Sánchez-Morales, D.E.; Pany, T. Precise positioning through a loosely-coupled sensor fusion of GNSS-RTK, INS and LiDAR for autonomous driving. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 219–225. [Google Scholar]
- El-Mowafy, A.; Kubo, N. Integrity monitoring for positioning of intelligent transport systems using integrated RTK-GNSS, IMU and vehicle odometer. IET Intell. Transp. Syst. 2018, 12, 901–908. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.R.; Tao, L.; Niu, Z.; Zhu, B.C. An improved adaptive unscented Kalman filter with application in the deeply integrated BDS/INS navigation system. IEEE Access 2020, 8, 95321–95332. [Google Scholar] [CrossRef]
- Wang, J.; Liu, D.; Jiang, W.; Lu, D.B. Evaluation on loosely and tightly coupled GNSS/INS vehicle navigation system. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 892–895. [Google Scholar]
- Jwo, D.J.; Yang, C.F.; Chuang, C.H.; Lin, K.C. A novel design for the ultra-tightly coupled GPS/INS navigation system. J. Navig. 2012, 65, 717–747. [Google Scholar] [CrossRef] [Green Version]
- Falco, G.; Pini, M.; Marucco, G. Loose and tight GNSS/INS integrations: Comparison of performance assessed in real urban scenarios. Sensors 2017, 17, 255. [Google Scholar] [CrossRef]
- Weiss, J.D.; Kee, D.S. A direct performance comparison between loosely coupled and tightly coupled GPS/INS integration techniques. In Proceedings of the 51st Annual Meeting of The Institute of Navigation, Colorado Springs, CO, USA, 5–7 June 1995; pp. 537–544. [Google Scholar]
- Sun, J.R.; Niu, Z.; Zhu, B.C. Fault detection and exclusion method for a deeply integrated BDS/INS system. Sensors 2020, 20, 1844. [Google Scholar] [CrossRef] [Green Version]
- Alban, S.; Akos, D.M.; Rock, S.M. Performance analysis and architectures for INS-aided GPS tracking loops. In Proceedings of the 2003 National Technical Meeting of The Institute of Navigation (NTM), Anaheim, CA, USA, 22–24 January 2003; pp. 611–622. [Google Scholar]
- Imparato, D.; Floch, J.J. INS/GNSS fusion. In Proceedings of the Airbus Defence and Space, Ottobrunn, Germany, 11 February 2019; Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5c206c883&appId=PPGMS (accessed on 2 April 2022).
- Dai, Z. MATLAB software for GPS cycle-slip processing. GPS Solut. 2012, 16, 267–272. [Google Scholar] [CrossRef] [Green Version]
- Takasu, T.; Yasuda, A. Cycle slip detection and fixing by MEMS-IMU/GPS integration for mobile environment RTK-GPS. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 64–71. [Google Scholar]
- Kim, Y.; Song, J.; Ho, Y.; Kee, C.; Park, B. Optimal selection of an inertial sensor for cycle slip detection considering single-frequency RTK/INS integrated navigation. Trans. Japan Soc. Aero. Space Sci. 2016, 59, 205–217. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Chang, G.B.; Chen, C.; Zhu, T. An improved TDCP-GNSS/INS integration scheme considering small cycle slip for low-cost land vehicular applications. Meas. Sci. Technol. 2021, 32, 055006. [Google Scholar] [CrossRef]
- Scherzinger, B.M. Robust positioning with single frequency inertially aided RTK. In Proceedings of the 2002 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 28–30 January 2002; pp. 911–917. [Google Scholar]
- Done, M.; Filwarny, J.O.; Wieser, M. Inertially-aided RTK based on tightly-coupled integration using low-cost GNSS receivers. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2002; pp. 186–197. [Google Scholar]
- Li, W.; Li, W.Y.; Cui, X.W.; Zhao, S.H.; Lu, M.Q. A tightly coupled RTK/INS algorithm with ambiguity resolution in the position domain for ground vehicles in harsh urban environments. Sensors 2018, 18, 2160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, T.; Zhang, H.P.; Gao, Z.Z.; Chen, Q.J.; Niu, X.J. High-accuracy positioning in urban environments using single-frequency multi-GNSS RTK/MEMS IMU integration. Remote. Sens. 2018, 10, 205. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.F.; Ai, L.; Xiao, J.P.; Hsu, L.T.; Kamijo, S.; Gu, Y.L. Tightly coupled RTK/MIMU using single frequency BDS/GPS/QZSS receiver for automatic driving vehicle. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 185–189. [Google Scholar]
- Zhu, S.; Li, S.H.; Liu, Y.; Fu, Q.W.; Kamijo, S.; Gu, Y.L. Low-cost MEMS-IMU/RTK tightly coupled vehicle navigation system with robust lane-level position accuracy. In Proceedings of the 2019 26th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 27–29 May 2019; pp. 1–4. [Google Scholar]
- Li, T.; Zhang, H.P.; Niu, X.J.; Zhang, Q. Performance analysis of tightly coupled RTK/INS algorithm in case of insufficient number of satellites. Remote. Sens. 2018, 43, 478–484. [Google Scholar] [CrossRef]
- Wang, D.J.; Dong, Y.; Li, Z.Y.; Li, Q.S.; Wu, J. Constrained MEMS-Based GNSS/INS tightly coupled system with robust Kalman filter for accurate land vehicular navigation. IEEE Trans. Ins. Meas. 2020, 69, 5138–5148. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.J.; Zhang, L.; Li, Q.S.; Wu, J. Tightly coupled GNSS/INS integration with robust sequential Kalman filter for accurate vehicular navigation. Sensors 2020, 20, 561. [Google Scholar] [CrossRef] [Green Version]
- De Jong, C.D.; Marel, H.V.; Jonkman, N.F. Real-time GPS and GLONASS integrity monitoring and reference station software. Phys. Chem. Earth Part Solid Earth Geod. 2001, 26, 545–549. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Quality control in integrated navigation systems. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20 March 1990; pp. 158–165. [Google Scholar]
- Gillissen, I.; Elema, I.A. Test results of DIA: A real-time adaptive integrity monitoring procedure, used in an integrated naviation system. Int. Hydrogr. Rev. 1996, 73, 75–100. [Google Scholar]
- Hewitson, S.; Wang, J.L. Extended receiver autonomous integrity monitoring (eRAIM) for GNSS/INS integration. J. Surveying Eng. 2010, 136, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Sage, A.P.; Husa, G.W. Adaptive filtering with unknown prior statistics. In Proceedings of the 10th Joint Automatic Control Conference, Boulder, CO, USA, 5–7 August 1969; pp. 760–769. [Google Scholar]
- Xu, S.Q.; Zhou, H.Y.; Wang, J.Q.; He, Z.M.; Wang, D.Y. SINS/CNS/GNSS integrated navigation based on an improved federated Sage–Husa adaptive filter. Sensors 2019, 19, 3812. [Google Scholar] [CrossRef] [Green Version]
- Koch, K.R.; Yang, Y. Robust Kalman filter for rank deficient observation models. J. Geod. 1998, 72, 436–441. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, S.B.; Li, H.; Li, Z. Performance evaluation of the flters with adaptive factor and fading factor for GNSS/INS integrated systems. GPS Solut. 2021, 25, 130–141. [Google Scholar] [CrossRef]
- Yang, Y.X.; Cui, X.Q. Adaptively robust filter with multi adaptive factors. Survey Rev. 2008, 40, 260–270. [Google Scholar] [CrossRef]
- Crespillo, O.G.; Medina, D.; Skaloud, J.; Meurer, M. Tightly coupled GNSS/INS integration based on robust M-estimators. 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1554–1561. [Google Scholar]
- Yang, Y.X.; Ren, X.; Xu, Y. Main progress of adaptively robust filter with applications in navigation. J. Navig. Pos. 2013, 1, 9–15. [Google Scholar] [CrossRef]
- Gao, B.B.; Hu, G.G.; Zhong, Y.M.; Zhu, X.H. Cubature Kalman filter with both adaptability and robustness for tightly-coupled GNSS/INS integration. IEEE Sensors J. 2021, 21, 14997–15011. [Google Scholar] [CrossRef]
- Yang, Z.H.; Li, Z.K.; Liu, Z.; Wang, C.C.; Sun, Y.W.; Shao, K.F. Improved robust and adaptive filter based on non-holonomic constraints for RTK/INS integrated navigation. Meas. Sci. Technol. 2021, 32, 105110. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Zhao, L.D.; Zhao, L. A two-step robust adaptive filtering algorithm for GNSS kinematic precise point positioning. Chinese J. Aero. 2021, 34, 210–219. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Zhao, L.; Zhou, J.H. Two-step robust adaptive filtering with application to PPP/INS integrated navigation. Navig. Pos. Timing 2020, 7. [Google Scholar] [CrossRef]
- Yue, Z.; Lian, B.W.; Tong, K.X.; Chen, S.H. Novel strong tracking square-root cubature Kalman filter for GNSS/INS integrated navigation system. IET Radar Sonar Navig. 2019, 13, 976–982. [Google Scholar] [CrossRef]
- Li, Z.K.; Gao, J.X.; Wang, J.; Yao, Y.F. PPP/INS tightly coupled navigation using adaptive federated filter. GPS Solut. 2017, 21, 137–148. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Jeju, Korea, 4–6 November 2009. [Google Scholar]
- Chen, C.; Chang, G.B. PPPLib: An open-source software for precise point positioning using GPS, BeiDou, Galileo, GLONASS, and QZSS with multi-frequency observations. GPS Solut. 2020, 25, 18. [Google Scholar] [CrossRef]
- Yan, G.M. PSINS. Available online: http://www.psins.org.cn/kydm (accessed on 31 March 2022).
- Chen, K.; Chang, G.B.; Chen, C. GINav: A MATLAB-based software for the data processing and analysis of a GNSS/INS integrated navigation system. GPS Solut. 2021, 25, 108. [Google Scholar] [CrossRef]
- i2Nav-WHU. OB-GINS. Available online: https://github.com/i2Nav-WHU/OB_GINS (accessed on 31 March 2022).
- Niu, Z.; Guo, F.G.; Shuai, Q.Q.; Li, G.C.; Zhu, B.C. The integration of GPS/BDS real-time kinematic positioning and visual–inertial odometry based on smartphones. ISPRS Int. J. Geo-Inf. 2021, 10, 699. [Google Scholar] [CrossRef]
- Terejanu, G.A. Extended Kalman filter tutorial. University at Buffalo. 2008. Available online: https://homes.cs.washington.edu/~todorov/courses/cseP590/readings/tutorialEKF.pdf (accessed on 2 April 2022).
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Xie, G. Precise positioning systems. In Principles of GPS and Receiver Design, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2017; Volume 7, pp. 166–171. ISBN 978-7-121-09077-6. [Google Scholar]
- Chen, K. GINAV Manual. Available online: https://github.com/kaichen686/GINav (accessed on 31 March 2022).
- IMU Noise Model. Available online: https://github.com/ethz-asl/kalibr/wiki/IMU-Noise-Model (accessed on 31 March 2022).
- El-Sheimy, N.; Hou, H.Y.; Niu, X.J. Analysis and modeling of inertial sensors using Allan Variance. IEEE Trans. Ins. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Takasu, T. RTKLIB ver. 2.4.2 Manual. Available online: http://www.rtklib.com/prog/manual_2.4.2.pdf (accessed on 31 March 2022).
- Li, T. Research on the tightly coupled singlefrequency multi-GNSS/INS/Vision integration for precise position and orientation estimation. Ph.D. Thesis, Wuhan University, Wuhan, China, 2019. [Google Scholar]
- Zhang, Q.Q.; Zhao, L.; Zhou, J.H. A novel weighting approach for variance component estimation in GPS/BDS PPP. IEEE Sensors J. 2019, 19, 3763–3771. [Google Scholar] [CrossRef]
- Yang, Y.X.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Han, H.Z.; Wang, J.; Du, M.Y. A fast SINS initial alignment method based on RTS forward and backward resolution. J. Sensors 2017, 2017. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J. Measurement errors and tracking thresholds. In Understanding GPS/GNSS Principles and Applications, 3rd ed.; Artech House: Norwood, MA, USA, 2017; ISBN 978-1-63081-058-0. [Google Scholar]
- Kennedy, S.; Hamilton, J.; Martell, H. Architecture and system performance of SPAN-NovAtel’s GPS/INS solution. In Proceedings of the 2006 IEEE/ION Position, Location, and Navigation Symposium, Coronado, CA, USA, 25–27 April 2006. [Google Scholar]
- Li-Ta, H.; Kubo, N.; Wen, W.S.; Chen, W.; Liu, Z.Z.; Suzuki, T.; Meguro, J. UrbanNav: An open-sourced multisensory dataset for benchmarking positioning algorithms designed for urban areas. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 22–25 September 2021. [Google Scholar]
- Matplotlib-cpp. Available online: https://github.com/lava/matplotlib-cpp (accessed on 31 March 2022).
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.S.; Wang, N.B.; Wang, Z.Y. Real-time GNSS precise point positioning for low-cost smart devices. GPS Solut. 2021, 25, 69. [Google Scholar] [CrossRef]






| Strategies | LC | TC | DC | |
|---|---|---|---|---|
| Characteristics | ||||
| EKF measurements | GNSS outputs (position and velocity) | Raw observations (pseudo range, phase, Doppler) | Loop parameters (code error, phase error) | |
| Minimum number of available satellites | Four | One | One | |
| Aiding receiver | No | No | Yes | |
| Acquisition and tracking performance improvement | No | No | Yes | |
| Disturbance resistance | No | No | Yes | |
| Cost and complexity | Low | High | Highest | |
| Possible to use INS to exclude outlying measurements | No | Yes | Yes | |
| characteristics | Field | Frame | Language | |
|---|---|---|---|---|
| Projects | ||||
| RTKLIB | GNSS (RTK and PPP) | EKF | C | |
| PPPLIB | GNSS (RTK and PPP) GNSS/INS (LC) | EKF | C/C++ | |
| PSINS | GNSS/INS (LC and range-based TC) | EKF | Matlab/C++ | |
| GINAV | GNSS/INS (LC, range-based TC, PPK TC, PPP TC) | EKF | Matlab | |
| OB-GINS | GNSS/INS (LC) | Optimization | C++ | |
| Situation | Valid GNSS Measurements | AR | Generation | |
|---|---|---|---|---|
| Outputs | ||||
| Fixed Solution | Yes | Yes | Feedback to the float solution | |
| Float Solution | Yes | No | EKF estimation and feedback to the INS solution | |
| INS Solution | No | No | The INS mechanization | |
| Techniques | RMSE (m) | Continuity | The Fixed Rate |
|---|---|---|---|
| RTK | 7.99 | 86% | 20% |
| TC RTK/INS (EKF) | 7.95 | 100% | 26% |
| TC RTK/INS (RKF) | 1.75 | 100% | 27% |
| Techniques | RMSE(m) | Continuity | The Fixed Rate |
|---|---|---|---|
| RTK | 13.21 | 82% | 10.0% |
| TC RTK/INS (EKF) | 14.17 | 100% | 12.8% |
| TC RTK/INS (RKF) | 10.01 | 100% | 13.1% |
| Techniques | RMSE-X (m) | RMSE-Y (m) | RMSE-Z (m) | Total RMSE (m) | Fixed Rate |
|---|---|---|---|---|---|
| RTK | 8.95 | 8.07 | 5.43 | 13.21 | 10.0% |
| TC RTK/INS (EKF) | 9.70 | 8.44 | 5.94 | 14.17 | 12.8% |
| TC RTK/INS (RKF) | 5.49 | 6.92 | 4.70 | 10.01 | 13.1% |
| TC RTK/INS (MRKF) | 5.44 | 4.83 | 3.91 | 8.26 | 13.8% |
| Techniques | RMSE-X (m) | RMSE-Y (m) | RMSE-Z (m) | Total RMSE (m) | Fixed Rate |
|---|---|---|---|---|---|
| RTK | 3.25 | 5.00 | 5.31 | 7.98 | 20.0% |
| TC RTK/INS (EKF) | 3.58 | 5.58 | 4.39 | 7.95 | 26.1% |
| TC RTK/INS (RKF) | 0.90 | 1.08 | 1.19 | 1.84 | 26.8% |
| TC RTK/INS (MRKF) | 0.88 | 1.08 | 1.14 | 1.80 | 26.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Z.; Li, G.; Guo, F.; Shuai, Q.; Zhu, B. An Algorithm to Assist the Robust Filter for Tightly Coupled RTK/INS Navigation System. Remote Sens. 2022, 14, 2449. https://doi.org/10.3390/rs14102449
Niu Z, Li G, Guo F, Shuai Q, Zhu B. An Algorithm to Assist the Robust Filter for Tightly Coupled RTK/INS Navigation System. Remote Sensing. 2022; 14(10):2449. https://doi.org/10.3390/rs14102449
Chicago/Turabian StyleNiu, Zun, Guangchen Li, Fugui Guo, Qiangqiang Shuai, and Bocheng Zhu. 2022. "An Algorithm to Assist the Robust Filter for Tightly Coupled RTK/INS Navigation System" Remote Sensing 14, no. 10: 2449. https://doi.org/10.3390/rs14102449
APA StyleNiu, Z., Li, G., Guo, F., Shuai, Q., & Zhu, B. (2022). An Algorithm to Assist the Robust Filter for Tightly Coupled RTK/INS Navigation System. Remote Sensing, 14(10), 2449. https://doi.org/10.3390/rs14102449