Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data
Abstract
:1. Introduction
2. Material & Methods
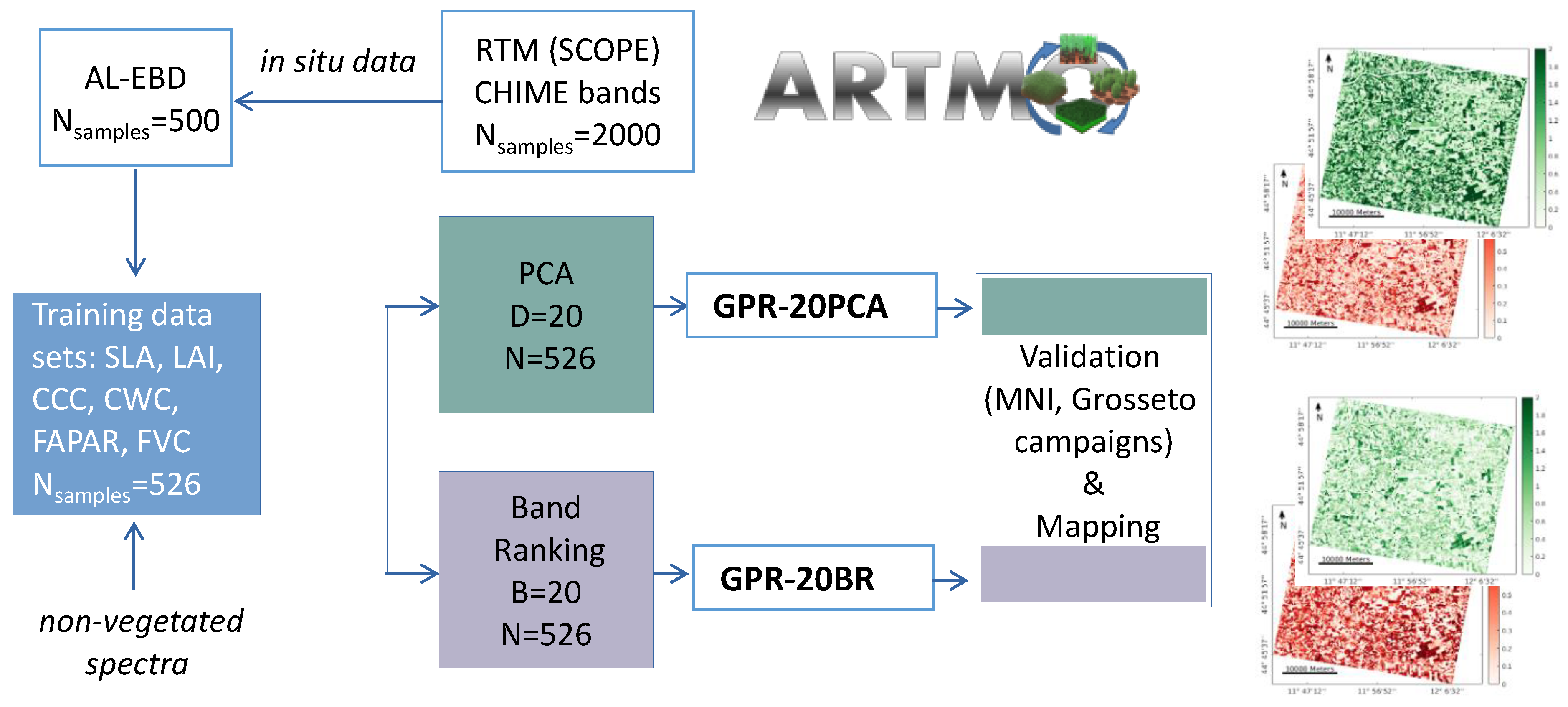
2.1. Study Design & Workflow
- Generating a training database with an RTM (see Section 2.2);
- Applying AL methods to reduce and optimize the training data sets for each variable (see Section 2.3);
- Training and validation using GPR (Section 2.4);
- Reducing dimensionality of simulated and measured spectra with: (i) PCA and (ii) an iterative band ranking (BR) procedure (see Section 2.5);
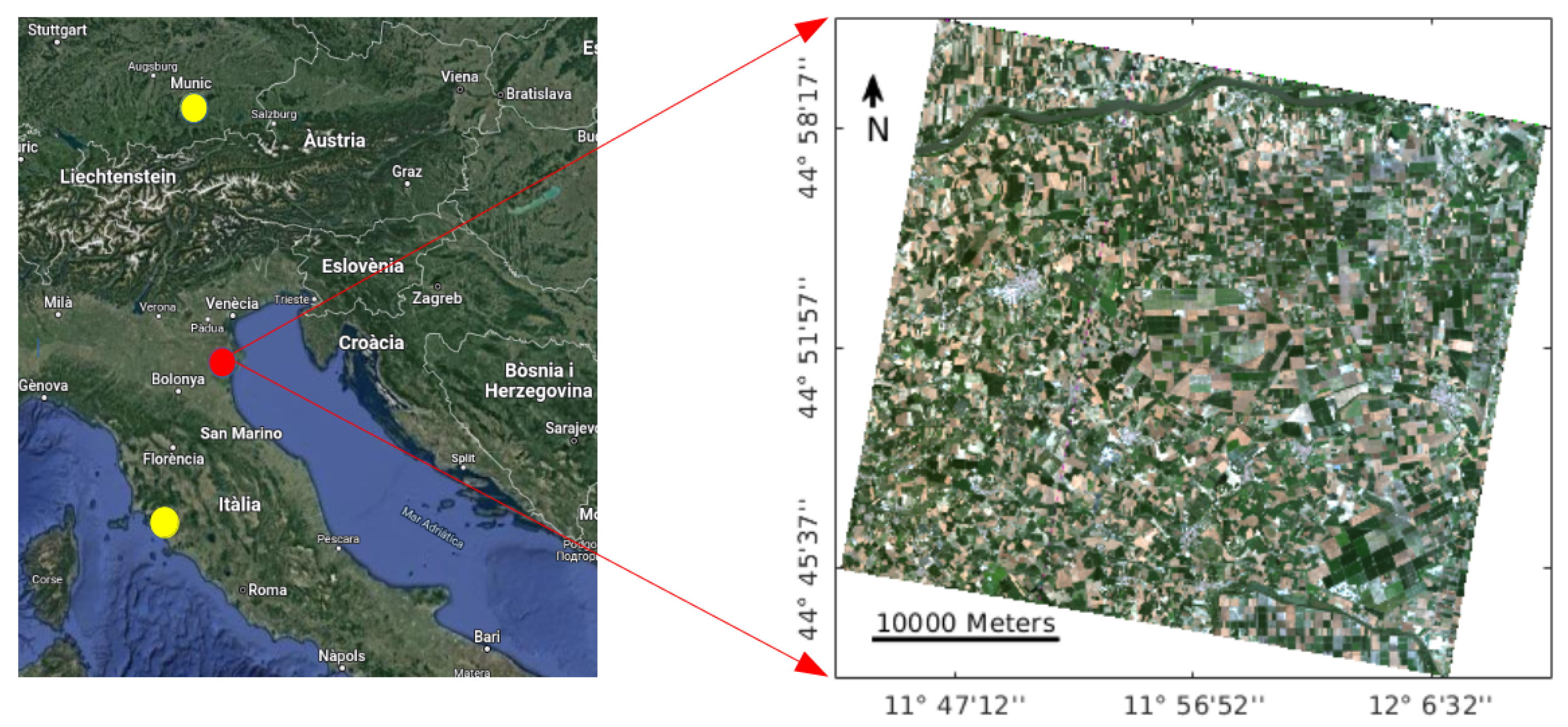
- Mapping using PRISMA scenes, resampled to CHIME, over cultivated areas of the agricultural site close to Jolanda di Savoia, Italy (data set description see Section 2.6).
2.2. Training Database Establishment
2.3. Sample Reduction: Active Learning
2.4. Gaussian Process Regression
2.5. Retrieval with Dimensionality Reduction Strategies
2.6. Experimental Sites
2.7. PRISMA Imagery Acquisition and Pre-Processing
3. Results
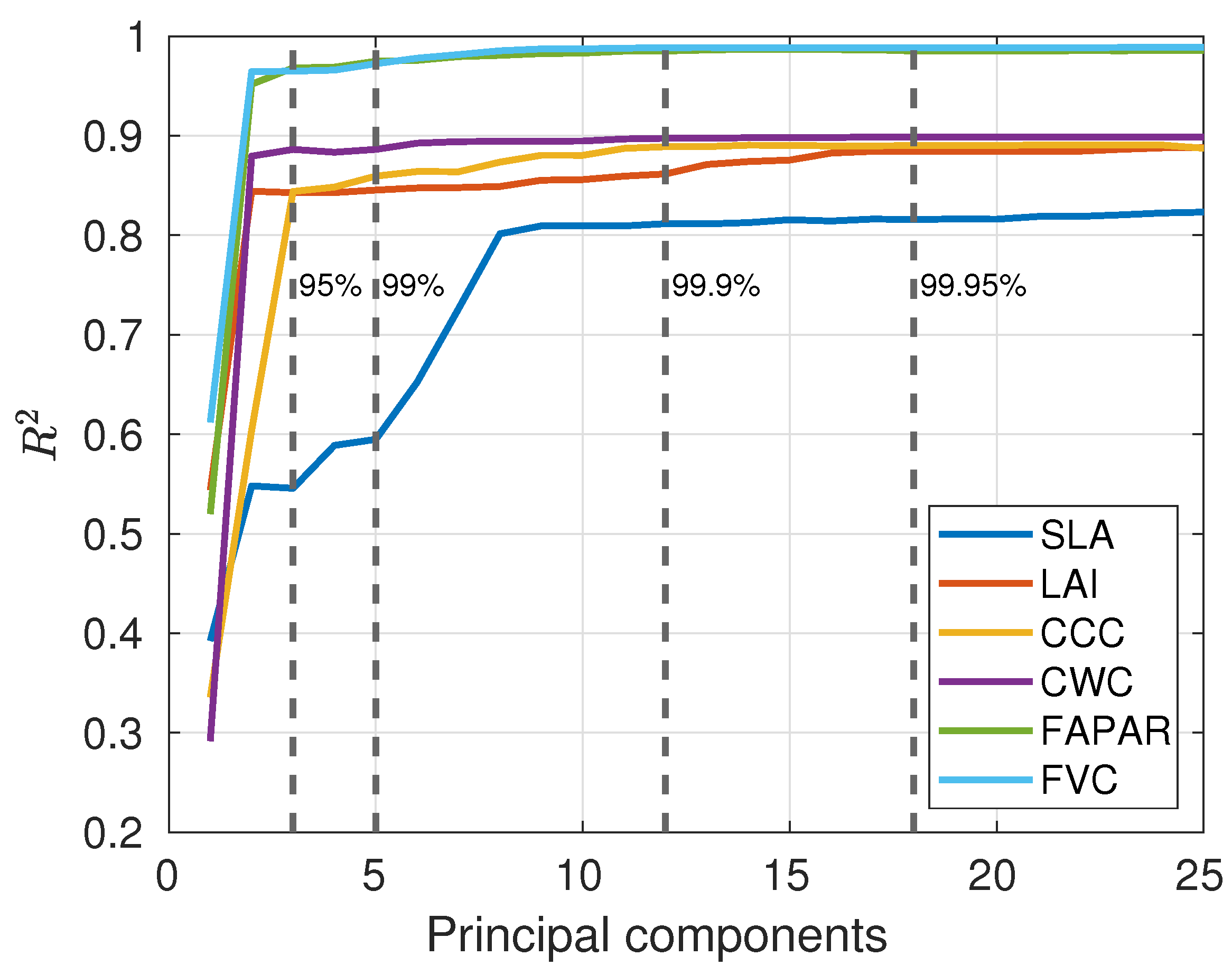
3.1. Active Learning Performance
3.2. Optimizing GPR-20PCA and GPR-20BR Retrieval Models
3.3. Validation of Crop Traits Models
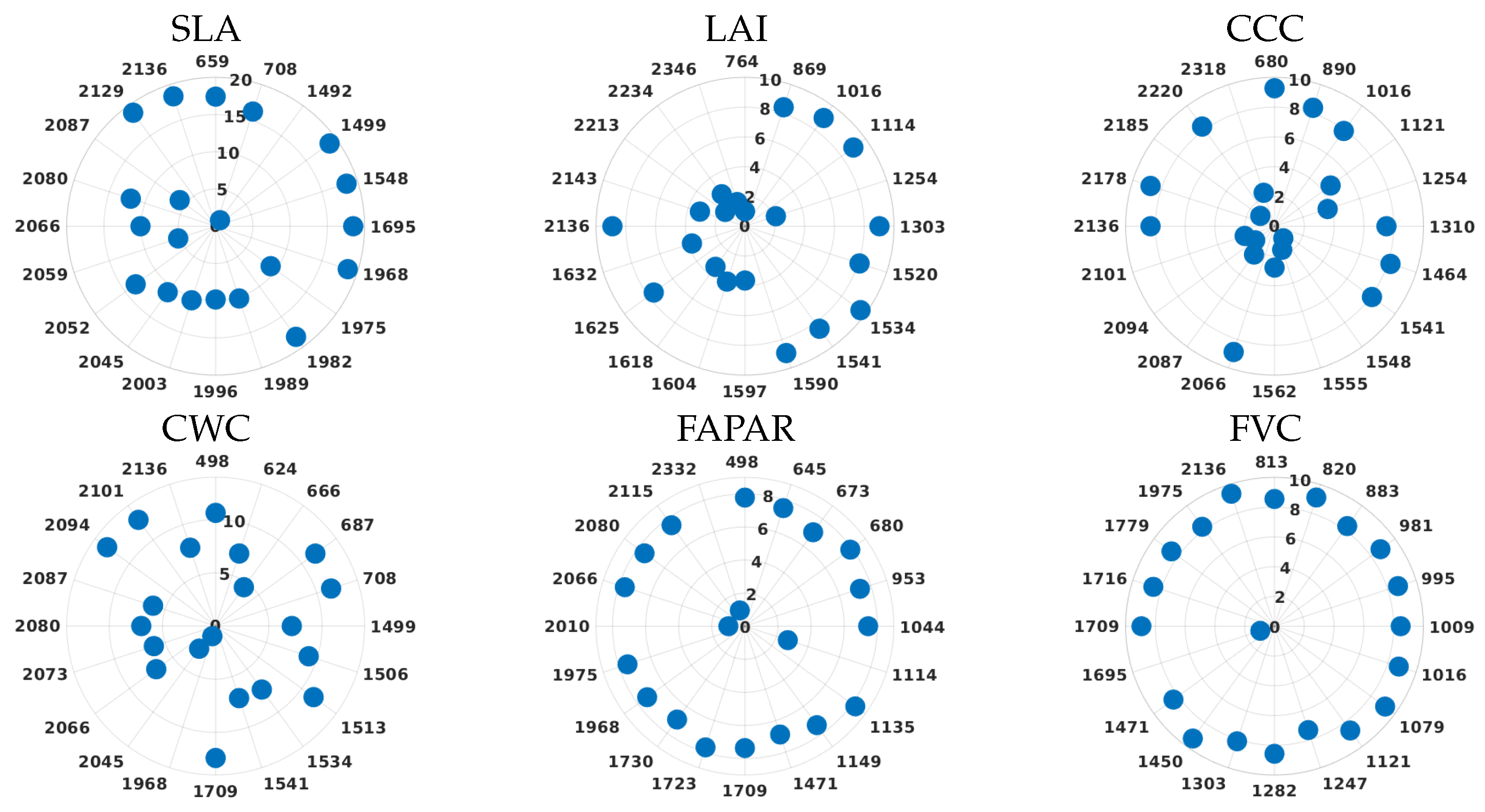
3.4. PCA vs. BR Analysis: Polar Plots
3.5. Mapping Crop Traits Using CHIME-like Imagery and Comparison
4. Discussion
4.1. Role of Active Learning in Optimizing Training Samples
4.2. Role of Dimensionality Reduction Strategies in Spectral Domain
4.3. Implications for the Preparation of CHIME
4.4. Challenges and Opportunities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | Optimal Number of Bands | RMSE | RRMSE | NRMSE | Train Time (s) | Test Time (s) | |
|---|---|---|---|---|---|---|---|
| SLA BR | 130 | 94.794 | 43.137 | 28.177 | 0.001 | 184.178 | 0.015 |
| LAI BR | 6 | 0.812 | 38.554 | 13.533 | 0.809 | 1.458 | 0.006 |
| CCC BR | 227 | 0.667 | 68.775 | 20.537 | 0,721 | 268.194 | 0.025 |
| CWC BR | 2 | 302.114 | 72.383 | 27.129 | 0.669 | 0.312 | 0.001 |
| FAPAR BR | 65 | 0.045 | 5.670 | 4.589 | 0.967 | 219.088 | 0.103 |
| FVC BR | 218 | 0.048 | 6.305 | 4.872 | 0.969 | 658.799 | 0.097 |
References
- Prosekov, A.Y.; Ivanova, S.A. Food security: The challenge of the present. Geoforum 2018, 91, 73–77. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in Remote Sensing of Agriculture: Context Description, Existing Operational Monitoring Systems and Major Information Needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef] [Green Version]
- Ustin, S.L.; Middleton, E.M. Current and near-term advances in Earth observation for ecological applications. Ecol. Process. 2021, 10, 1. [Google Scholar] [CrossRef] [PubMed]
- Loizzo, R.; Daraio, M.; Guarini, R.; Longo, F.; Lorusso, R.; Dini, L.; Lopinto, E. Prisma Mission Status and Perspective. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4503–4506. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP Spaceborne Imaging Spectroscopy Mission for Earth Observation. Remote Sens. 2015, 7, 8830. [Google Scholar] [CrossRef] [Green Version]
- Drusch, M.; Moreno, J.; Del Bello, U.; Franco, R.; Goulas, Y.; Huth, A.; Kraft, S.; Middleton, E.M.; Miglietta, F.; Mohammed, G.; et al. The FLuorescence EXplorer Mission Concept—ESA’s Earth Explorer 8. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1273–1284. [Google Scholar] [CrossRef]
- Board, S.S.; National Academies of Sciences, Engineering, and Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academies Press: Washington, DC, USA, 2018. [Google Scholar]
- Nieke, J.; Rast, M. Status: Copernicus Hyperspectral Imaging Mission For The Environment (CHIME). In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4609–4611. [Google Scholar]
- Rast, M.; Painter, T.H. Earth Observation Imaging Spectroscopy for Terrestrial Systems: An Overview of Its History, Techniques, and Applications of Its Missions. Surv. Geophys. 2019, 40, 303–331. [Google Scholar] [CrossRef]
- Buschkamp, P.; Sang, B.; Peacocke, P.; Pieraccini, S.; Geiss, M.J.; Roth, C.; Moreau, V.; Borguet, B.; Maresi, L.; Rast, M.; et al. CHIME’s hyperspectral imaging spectrometer design result from phase A/B1. In International Conference on Space Optics — ICSO 2020; SPIE: Bellingham, DC, USA, 2021; Volume 11852, pp. 1091–1105. [Google Scholar] [CrossRef]
- Rast, M.; Ananasso, C.; Bach, H.; Ben-Dor, E.; Chabrillat, S.; Colombo, R.; Del Bello, U.; Feret, J.; Giardino, C.; Green, R.O.; et al. Copernicus Hyperspectral Imaging Mission for the Environment: Mission Requirements Document; European Space Agency: Paris, France, 2019. [Google Scholar]
- Verrelst, J.; Rivera-Caicedo, J.P.; Reyes-Muñoz, P.; Morata, M.; Amin, E.; Tagliabue, G.; Panigada, C.; Hank, T.; Berger, K. Mapping landscape canopy nitrogen content from space using PRISMA data. ISPRS J. Photogramm. Remote Sens. 2021, 178, 382–395. [Google Scholar] [CrossRef]
- Verrelst, J.; De Grave, C.; Amin, E.; Reyes, P.; Morata, M.; Portales, E.; Belda, S.; Tagliabue, G.; Panigada, C.; Boschetti, M.; et al. Prototyping vegetation traits models in the context of the hyperspectral CHIME mission preparation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne imaging spectroscopy for sustainable agriculture: Contributions and challenges. Surv. Geophys. 2019, 40, 515–551. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz Marí, J.; Rivera, J.; Veroustraete, F.; Clevers, J.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovskỳ, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Vicent, J.; Rivera-Caicedo, J.P.; Lumbierres, M.; Morcillo-Pallarés, P.; Moreno, J. Global Sensitivity Analysis of Leaf-Canopy-Atmosphere RTMs: Implications for Biophysical Variables Retrieval from Top-of-Atmosphere Radiance Data. Remote Sens. 2019, 11, 1923. [Google Scholar] [CrossRef] [Green Version]
- Brede, B.; Verrelst, J.; Gastellu-Etchegorry, J.P.; Clevers, J.G.; Goudzwaard, L.; den Ouden, J.; Verbesselt, J.; Herold, M. Assessment of workflow feature selection on forest LAI prediction with sentinel-2A MSI, landsat 7 ETM+ and Landsat 8 OLI. Remote Sens. 2020, 12, 915. [Google Scholar] [CrossRef] [Green Version]
- Berger, K.; Verrelst, J.; Féret, J.B.; Hank, T.; Wocher, M.; Mauser, W.; Camps-Valls, G. Retrieval of aboveground crop nitrogen content with a hybrid machine learning method. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102174. [Google Scholar] [CrossRef]
- Berger, K.; Hank, T.; Halabuk, A.; Rivera-Caicedo, J.P.; Wocher, M.; Mojses, M.; Gerhátová, K.; Tagliabue, G.; Dolz, M.M.; Venteo, A.B.P.; et al. Assessing Non-Photosynthetic Cropland Biomass from Spaceborne Hyperspectral Imagery. Remote Sens. 2021, 13, 4711. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Efficient RTM-based training of machine learning regression algorithms to quantify biophysical & biochemical traits of agricultural crops. ISPRS J. Photogramm. Remote Sens. 2021, 173, 278–296. [Google Scholar] [CrossRef]
- De Grave, C.; Verrelst, J.; Morcillo-Pallarés, P.; Pipia, L.; Rivera-Caicedo, J.P.; Amin, E.; Belda, S.; Moreno, J. Quantifying vegetation biophysical variables from the Sentinel-3/FLEX tandem mission: Evaluation of the synergy of OLCI and FLORIS data sources. Remote Sens. Environ. 2020, 251, 112101. [Google Scholar] [CrossRef]
- Salinero-Delgado, M.; Estévez, J.; Pipia, L.; Belda, S.; Berger, K.; Paredes Gómez, V.; Verrelst, J. Monitoring Cropland Phenology on Google Earth Engine Using Gaussian Process Regression. Remote Sens. 2021, 14, 146. [Google Scholar] [CrossRef]
- Estévez, J.; Berger, K.; Vicent, J.; Rivera-Caicedo, J.P.; Wocher, M.; Verrelst, J. Top-of-Atmosphere Retrieval of Multiple Crop Traits Using Variational Heteroscedastic Gaussian Processes within a Hybrid Workflow. Remote Sens. 2021, 13, 1589. [Google Scholar] [CrossRef]
- de Sá, N.C.; Baratchi, M.; Hauser, L.T.; van Bodegom, P. Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data. Remote Sens. 2021, 13, 648. [Google Scholar] [CrossRef]
- Rivera-Caicedo, J.P.; Verrelst, J.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Hyperspectral dimensionality reduction for biophysical variable statistical retrieval. ISPRS J. Photogramm. Remote Sens. 2017, 132, 88–101. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise Reduction in Hyperspectral Imagery: Overview and Application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef] [Green Version]
- Morales, G.; Sheppard, J.W.; Logan, R.D.; Shaw, J.A. Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection. Remote Sens. 2021, 13, 3649. [Google Scholar] [CrossRef]
- Pasolli, E.; Melgani, F.; Alajlan, N.; Bazi, Y. Active Learning Methods for Biophysical Parameter Estimation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4071–4084. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Verrelst, J.; Berger, K.; Rivera-Caicedo, J.P. Intelligent Sampling for Vegetation Nitrogen Mapping Based on Hybrid Machine Learning Algorithms. IEEE Geosci. Remote Sens. Lett. 2020, 18, 2038–2042. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Muñoz-Marí, J. A survey of active learning algorithms for supervised remote sensingimage classification. IEEE J. Sel. Top. Signal Process. 2011, 4, 606–617. [Google Scholar] [CrossRef]
- Berger, K.; Rivera Caicedo, J.P.; Martino, L.; Wocher, M.; Hank, T.; Verrelst, J. A Survey of Active Learning for Quantifying Vegetation Traits from Terrestrial Earth Observation Data. Remote Sens. 2021, 13, 287. [Google Scholar] [CrossRef]
- Settles, B. Active Learning Literature Survey; University of Wisconsin-Madison, Department of Computer Sciences: Madison, WI, USA, 2009. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: New York, NY, USA, 2006. [Google Scholar]
- Camps-Valls, G.; Verrelst, J.; Munoz-Mari, J.; Laparra, V.; Mateo-Jimenez, F.; Gomez-Dans, J. A survey on Gaussian processes for earth-observation data analysis: A comprehensive investigation. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef] [Green Version]
- Verrelst, J.; Rivera, J.; Veroustraete, F.; Muñoz Marí, J.; Clevers, J.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Moreno, J.; Camps-Valls, G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef] [Green Version]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef] [Green Version]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote Estimation of Crop Chlorophyll Content Using Spectral Indices Derived From Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W. Beyond NDVI: Extraction of Biophysical Variables From Remote Sensing Imagery. In Land Use and Land Cover Mapping in Europe: Practices & Trends; Springer: Dordrecht, The Netherlands, 2014; pp. 363–381. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef] [Green Version]
- Atzberger, C.; Richter, K.; Vuolo, F.; Darvishzadeh, R.; Schlerf, M. Why confining to vegetation indices? Exploiting the potential of improved spectral observations using radiative transfer models. Remote. Sens. Agric. Ecosyst. Hydrol. XIII 2011, 8174, 81740Q. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sens. 2018, 10, 2063. [Google Scholar] [CrossRef] [Green Version]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Tagliabue, G.; Boschetti, M.; Bramati, G.; Candiani, G.; Colombo, R.; Nutini, F.; Pompilio, L.; Rivera-Caicedo, J.P.; Rossi, M.; Rossini, M.; et al. Hybrid retrieval of crop traits from multi-temporal PRISMA hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2022, 187, 362–377. [Google Scholar] [CrossRef]
- Candiani, G.; Tagliabue, G.; Panigada, C.; Verrelst, J.; Picchi, V.; Rivera Caicedo, J.P.; Boschetti, M. Evaluation of Hybrid Models to Estimate Chlorophyll and Nitrogen Content of Maize Crops in the Framework of the Future CHIME Mission. Remote Sens. 2022, 14, 1792. [Google Scholar] [CrossRef]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping Vegetation Density in a Heterogeneous River Floodplain Ecosystem Using Pointable CHRIS/PROBA Data. Remote Sens. 2012, 4, 2866–2889. [Google Scholar] [CrossRef] [Green Version]
- Van der Tol, C.; Berry, J.; Campbell, P.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar] [PubMed] [Green Version]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Vilfan, N.; van der Tol, C.; Muller, O.; Rascher, U.; Verhoef, W. Fluspect-B: A model for leaf fluorescence, reflectance and transmittance spectra. Remote Sens. Environ. 2016, 186, 596–615. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL model capabilities for future hyperspectral model environments: A review study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef] [Green Version]
- García-Haro, F.J.; Campos-Taberner, M.; Munoz-Mari, J.; Laparra, V.; Camacho, F.; Sanchez-Zapero, J.; Camps-Valls, G. Derivation of global vegetation biophysical parameters from EUMETSAT Polar System. ISPRS J. Photogramm. Remote Sens. 2018, 139, 57–74. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural network estimation of LAI, fAPAR, fCover and LAI×Cab, from top of canopy MERIS reflectance data: Principles and validation. Remote Sens. Environ. 2006, 105, 313–325. [Google Scholar] [CrossRef]
- Pacheco-Labrador, J.; El-Madany, T.S.; van der Tol, C.; Martin, M.P.; Gonzalez-Cascon, R.; Perez-Priego, O.; Guan, J.; Moreno, G.; Carrara, A.; Reichstein, M.; et al. senSCOPE: Modeling mixed canopies combining green and brown senesced leaves. Evaluation in a Mediterranean Grassland. Remote Sens. Environ. 2021, 257, 112352. [Google Scholar] [CrossRef]
- Verhoef, W.; van der Tol, C.; Middleton, E.M. Hyperspectral radiative transfer modeling to explore the combined retrieval of biophysical parameters and canopy fluorescence from FLEX – Sentinel-3 tandem mission multi-sensor data. Remote Sens. Environ. 2018, 204, 942–963. [Google Scholar] [CrossRef]
- Yang, P.; van der Tol, C.; Yin, T.; Verhoef, W. The SPART model: A soil-plant-atmosphere radiative transfer model for satellite measurements in the solar spectrum. Remote Sens. Environ. 2020, 247, 111870. [Google Scholar] [CrossRef]
- Verrelst, J.; Dethier, S.; Rivera, J.P.; Munoz-Mari, J.; Camps-Valls, G.; Moreno, J. Active Learning Methods for Efficient Hybrid Biophysical Variable Retrieval. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1012–1016. [Google Scholar] [CrossRef]
- Douak, F.; Melgani, F.; Benoudjit, N. Kernel ridge regression with active learning for wind speed prediction. Appl. Energy 2013, 103, 328–340. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Rivera Caicedo, J.; Moreno, J.; Camps-Valls, G. Gaussian Process Retrieval of Chlorophyll Content From Imaging Spectroscopy Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 867–874. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Sejdinovic, D.; Runge, J.; Reichstein, M. A Perspective on Gaussian Processes for Earth Observation. Natl. Sci. Rev. 2019, 6, 616–618. [Google Scholar] [CrossRef] [Green Version]
- Morata, M.; Siegmann, B.; Morcillo-Pallarés, P.; Rivera-Caicedo, J.P.; Verrelst, J. Emulation of Sun-Induced Fluorescence from Radiance Data Recorded by the HyPlant Airborne Imaging Spectrometer. Remote Sens. 2021, 13, 4368. [Google Scholar] [CrossRef]
- De Peppo, M.; Taramelli, A.; Boschetti, M.; Mantino, A.; Volpi, I.; Filipponi, F.; Tornato, A.; Valentini, E.; Ragaglini, G. Non-Parametric Statistical Approaches for Leaf Area Index Estimation from Sentinel-2 Data: A Multi-Crop Assessment. Remote Sens. 2021, 13, 2841. [Google Scholar] [CrossRef]
- Süß, A.; Danner, M.; Obster, C.; Locherer, M.; Hank, T.; Richter, K.; Consortium, E. Measuring Leaf Chlorophyll Content with the Konica Minolta SPAD-502Plus. GFZ Data Serv. 2015, 1–13. [Google Scholar] [CrossRef]
- Zhu, J.; Tremblay, N.; Liang, Y. Comparing SPAD and atLEAF values for chlorophyll assessment in crop species. Can. J. Soil Sci. 2012, 92, 645–648. [Google Scholar] [CrossRef]
- Siegmann, B.; Alonso, L.; Celesti, M.; Cogliati, S.; Colombo, R.; Damm, A.; Douglas, S.; Guanter, L.; Hanuš, J.; Kataja, K.; et al. The High-Performance Airborne Imaging Spectrometer HyPlant—From Raw Images to Top-of-Canopy Reflectance and Fluorescence Products: Introduction of an Automatized Processing Chain. Remote Sens. 2019, 11, 2760. [Google Scholar] [CrossRef] [Green Version]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Fitted PROSAIL parameterization of leaf inclinations, water content and brown pigment content for winter wheat and maize canopies. Remote Sens. 2019, 11, 1150. [Google Scholar] [CrossRef] [Green Version]
- Wocher, M.; Berger, K.; Danner, M.; Mauser, W.; Hank, T. Physically-based retrieval of canopy equivalent water thickness using hyperspectral data. Remote Sens. 2018, 10, 1924. [Google Scholar] [CrossRef] [Green Version]
- Lichtenthaler, H.K. Chlorophylls and carotenoids: Pigments of photosynthetic biomembranes. In Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1987; Volume 148, pp. 350–382. [Google Scholar]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy. Remote Sens. 2017, 9, 726. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Ryu, Y.; Nilson, T.; Kobayashi, H.; Sonnentag, O.; Law, B.E.; Baldocchi, D.D. On the correct estimation of effective leaf area index: Does it reveal information on clumping effects? Agric. For. Meteorol. 2010, 150, 463–472. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Chen, J.M.; Fernandes, R.; Deering, D.W.; Conley, A. Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agric. For. Meteorol. 2005, 129, 187–207. [Google Scholar] [CrossRef] [Green Version]
- Busetto, L.; Ranghetti, L. Prismaread: A Tool for Facilitating Access and Analysis of PRISMA L1/L2 Hyperspectral Imagery v1.0.0. Available online: https://irea-cnr-mi.github.io/prismaread/ (accessed on 25 April 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Wutzler, T.; Migliavacca, M.; Julitta, T. FieldSpectroscopyCC: R Package for Characterization and Calibration of Spectrometers; R Package Version 0.5.227; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Pipia, L.; Amin, E.; Belda, S.; Salinero-Delgado, M.; Verrelst, J. Green LAI Mapping and Cloud Gap-Filling Using Gaussian Process Regression in Google Earth Engine. Remote Sens. 2021, 13, 403. [Google Scholar] [CrossRef]
- Binh, N.A.; Hauser, L.T.; Viet Hoa, P.; Thi Phuong Thao, G.; An, N.N.; Nhut, H.S.; Phuong, T.A.; Verrelst, J. Quantifying mangrove leaf area index from Sentinel-2 imagery using hybrid models and active learning. Int. J. Remote Sens. 2022, 1–22. [Google Scholar] [CrossRef]
- Marshall, M.; Belgiu, M.; Boschetti, M.; Pepe, M.; Stein, A.; Nelson, A. Field-level crop yield estimation with PRISMA and Sentinel-2. ISPRS J. Photogramm. Remote Sens. 2022, 187, 191–210. [Google Scholar] [CrossRef]
- Liang, L.; Geng, D.; Yan, J.; Qiu, S.; Di, L.; Wang, S.; Xu, L.; Wang, L.; Kang, J.; Li, L. Estimating Crop LAI Using Spectral Feature Extraction and the Hybrid Inversion Method. Remote Sens. 2020, 12, 3534. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Mardashova, M.; Moreno, J. ARTMO’s Global Sensitivity Analysis (GSA) toolbox to quantify driving variables of leaf and canopy radiative transfer models. EARSeL eProc. Speical 2015, 2, 1–11. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global sensitivity analysis of the SCOPE model: What drives simulated canopy-leaving sun-induced fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
- Liu, L.; Song, B.; Zhang, S.; Liu, X. A Novel Principal Component Analysis Method for the Reconstruction of Leaf Reflectance Spectra and Retrieval of Leaf Biochemical Contents. Remote Sens. 2017, 9, 1113. [Google Scholar] [CrossRef] [Green Version]
- Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model. Remote Sens. 2015, 7, 10321–10346. [Google Scholar] [CrossRef] [Green Version]
- Sothe, C.; Gonsamo, A.; Arabian, J.; Snider, J. Large scale mapping of soil organic carbon concentration with 3D machine learning and satellite observations. Geoderma 2022, 405, 115402. [Google Scholar] [CrossRef]
- Ishibashi, H.; Hino, H. Stopping criterion for active learning based on deterministic generalization bounds. arXiv 2020, arXiv:2005.07402. [Google Scholar]




| Model Variables | Units | Range (Min-Max) | Distribution | |
|---|---|---|---|---|
| Leaf Variables | ||||
| N | Leaf structure parameter | unitless | 1.0–2.7 | Gaussian (: 1.5, SD: 0.5) |
| Leaf chlorophyll content | [μg/cm] | 0–80 | Gaussian (: 45, SD: 35) | |
| Leaf dry matter content | [g/cm] | 0.002–0.02 | Gaussian (: 0.0075, SD: 0.005) | |
| Leaf water content | [g/cm] | 0.005–0.035 | Gaussian (: 0.015, SD: 0.0075) | |
| Leaf carotenoid content | [μg/cm] | 0–20 | Uniform | |
| Canopy Variables | ||||
| LAI | Leaf area index | [m/m] | 0.1–8 | Uniform |
| LIDF | Leaf Inclination | rad | −1–1 | Uniform |
| Soil scaling factor | unitless | 0–1 | Uniform | |
| SZA | Sun zenith angle | [] | 0–80 | Uniform |
| OZA | Observer zenith angle | [] | 0–25 | Uniform |
| RAA | Relative azimuth angle | [] | 0–180 | Uniform |
| Soil variables | ||||
| Soil Moisture Content | [%] | 5–55 | Gaussian (: 25, SD: 12.5) | |
| BSM Brightness | [%] | 0–0.9 | Gaussian (: 0.5, SD: 0.25) | |
| BSM latitude | [] | 20–40 | Gaussian (: 25, SD: 12.5) | |
| BSM longitude | [] | 45–65 | Gaussian (: 50, SD: 10) | |
| Variable (Abr) | Unit | Mean (SD) | Range | No. of Samples |
|---|---|---|---|---|
| Specific Leaf Area (SLA) | cm/g | 219 (51.2) | 142–478 | 59 |
| Leaf Area Index (LAI) | m/m | 2.1 (1.6) | 0–6 | 115 |
| Canopy Chloropyll Content (CCC) | g/m | 0.97 (0.7) | 0–3.2 | 115 |
| Canopy Water Content (CWC) | g/m | 417 (271) | 0–1113 | 59 |
| #Bands | SD | Min | Max | Wavelengths (nm) | |
|---|---|---|---|---|---|
| 235 | 0.869 | 0.062 | 0.832 | 0.940 | All bands |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 20 | 0.879 | 0.071 | 0.825 | 0.960 | 680 890 1016 1121 1254 1310 1464 1541 1548 1555 1562 2066 2087 2094 2101 2136 2178 2185 2220 2318 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 15 | 0.879 | 0.071 | 0.825 | 0.960 | 680 890 1016 1121 1254 1310 1464 1541 1548 1555 1562 2136 2185 2220 2318 |
| 14 | 0.879 | 0.071 | 0.825 | 0.960 | 680 890 1016 1121 1254 1310 1464 1541 1548 1555 1562 2185 2220 2318 |
| 13 | 0.879 | 0.071 | 0.825 | 0.960 | 680 890 1016 1121 1254 1310 1464 1541 1555 1562 2185 2220 2318 |
| 12 | 0.879 | 0.071 | 0.825 | 0.960 | 680 890 1016 1121 1254 1310 1464 1541 1555 1562 2220 2318 |
| 11 | 0.883 | 0.069 | 0.825 | 0.960 | 680 890 1016 1121 1254 1310 1464 1541 1562 2220 2318 |
| 10 | 0.872 | 0.050 | 0.825 | 0.925 | 680 890 1016 1121 1254 1310 1464 1555 2220 2318 |
| 9 | 0.894 | 0.050 | 0.825 | 0.925 | 680 890 1016 1121 1254 1310 1464 2220 2318 |
| 8 | 0.874 | 0.050 | 0.825 | 0.925 | 680 890 1016 1121 1254 1310 1464 2318 |
| 7 | 0.873 | 0.049 | 0.825 | 0.924 | 680 890 1016 1121 1254 1310 1464 |
| 6 | 0.869 | 0.044 | 0.824 | 0.913 | 680 890 1016 1121 1310 1464 |
| 5 | 0.851 | 0.076 | 0.765 | 0.913 | 680 890 1016 1310 1464 |
| 4 | 0.850 | 0.087 | 0.757 | 0.913 | 680 890 1310 1464 |
| 3 | 0.808 | 0.091 | 0.747 | 0.913 | 680 890 1310 |
| 2 | 0.796 | 0.099 | 0.731 | 0.910 | 890 1310 |
| 1 | 0.237 | 0.193 | 0.069 | 0.449 | 1310 |
| #Variable | Wavelengths (nm) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SLA | 659 | 708 | 1492 | 1499 | 1548 | 1695 | 1968 | 1975 | 1982 | 1989 | 1996 | 2003 | 2045 | 2052 | 2059 | 2066 | 2080 | 2087 | 2129 | 2136 |
| LAI | 764 | 869 | 1016 | 1114 | 1254 | 1303 | 1520 | 1534 | 1541 | 1590 | 1597 | 1604 | 1618 | 1625 | 1632 | 2136 | 2143 | 2213 | 2234 | 2346 |
| CCC | 680 | 890 | 1016 | 1121 | 1254 | 1310 | 1464 | 1541 | 1548 | 1555 | 1562 | 2066 | 2087 | 2094 | 2101 | 2136 | 2178 | 2185 | 2220 | 2318 |
| CWC | 498 | 624 | 666 | 687 | 708 | 1499 | 1506 | 1513 | 1534 | 1541 | 1709 | 1968 | 2045 | 2066 | 2073 | 2080 | 2087 | 2094 | 2101 | 2136 |
| FAPAR | 498 | 645 | 673 | 680 | 953 | 1044 | 1114 | 1135 | 1149 | 1471 | 1709 | 1723 | 1730 | 1968 | 1975 | 2010 | 2066 | 2080 | 2115 | 2332 |
| FVC | 813 | 820 | 883 | 981 | 995 | 1009 | 1016 | 1079 | 1121 | 1247 | 1282 | 1303 | 1450 | 1471 | 1695 | 1709 | 1716 | 1779 | 1975 | 2136 |
| Variable | N Samples | RMSE | RRMSE | NRMSE | Train Time (s) | Test Time (s) | |
|---|---|---|---|---|---|---|---|
| SLA 20PCA | 526 | 57.553 | 26.190 | 17.107 | 0.113 | 8.978 | 0.005 |
| SLA 20BR | 526 | 97.988 | 44.590 | 29.127 | 0.016 | 6.175 | 0.009 |
| SLA all bands | 526 | 120.151 | 54.676 | 35.715 | 0.095 | 795.557 | 0.011 |
| LAI 20PCA | 526 | 1.121 | 53.235 | 18.686 | 0.814 | 7.393 | 0.003 |
| LAI 20BR | 526 | 1.394 | 66.184 | 23.231 | 0.765 | 5.602 | 0.009 |
| LAI all bands | 526 | 1.272 | 60.391 | 21.197 | 0.598 | 317.261 | 0.020 |
| CCC 20PCA | 409 | 0.725 | 74.676 | 22.299 | 0.651 | 3.831 | 0.003 |
| CCC 20BR | 409 | 0.778 | 80.166 | 23.939 | 0.491 | 21.394 | 0.023 |
| CCC all bands | 409 | 0.586 | 60.414 | 18.041 | 0.715 | 156.698 | 0.028 |
| CWC 20PCA | 526 | 155.224 | 37.189 | 13.939 | 0.785 | 6.730 | 0.005 |
| CWC 20BR | 526 | 217.953 | 52.219 | 19.572 | 0.704 | 5.895 | 0.003 |
| CWC all bands | 526 | 381.125 | 91.313 | 34.225 | 0.595 | 387.714 | 0.011 |
| FAPAR 20PCA | 1026 | 0.033 | 4.218 | 3.413 | 0.982 | 21.619 | 0.032 |
| FAPAR 20BR | 1026 | 0.042 | 5.329 | 4.313 | 0.970 | 13.205 | 0.014 |
| FAPAR all bands | 1026 | 0.056 | 7.168 | 5.801 | 0.948 | 1842 | 0.053 |
| FVC 20PCA | 1026 | 0.038 | 4.934 | 3.812 | 0.981 | 26.943 | 0.022 |
| FVC 20BR | 1026 | 0.044 | 5.700 | 4.404 | 0.974 | 12.709 | 0.010 |
| FVC all bands | 1026 | 0.039 | 5.113 | 3.951 | 0.979 | 1969 | 0.093 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascual-Venteo, A.B.; Portalés, E.; Berger, K.; Tagliabue, G.; Garcia, J.L.; Pérez-Suay, A.; Rivera-Caicedo, J.P.; Verrelst, J. Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data. Remote Sens. 2022, 14, 2448. https://doi.org/10.3390/rs14102448
Pascual-Venteo AB, Portalés E, Berger K, Tagliabue G, Garcia JL, Pérez-Suay A, Rivera-Caicedo JP, Verrelst J. Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data. Remote Sensing. 2022; 14(10):2448. https://doi.org/10.3390/rs14102448
Chicago/Turabian StylePascual-Venteo, Ana B., Enrique Portalés, Katja Berger, Giulia Tagliabue, Jose L. Garcia, Adrián Pérez-Suay, Juan Pablo Rivera-Caicedo, and Jochem Verrelst. 2022. "Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data" Remote Sensing 14, no. 10: 2448. https://doi.org/10.3390/rs14102448
APA StylePascual-Venteo, A. B., Portalés, E., Berger, K., Tagliabue, G., Garcia, J. L., Pérez-Suay, A., Rivera-Caicedo, J. P., & Verrelst, J. (2022). Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data. Remote Sensing, 14(10), 2448. https://doi.org/10.3390/rs14102448









