Abstract
The paper introduces an essentially new algorithm for calculating the GNSS position as an alternative to the least-square method. The proposed approach can be widely applied to any positioning method that uses multiple position lines for position calculation and is an example of how using a numerical solution can improve position accuracy without access to historical data. In essence, the method is based on the adaptation of the median filtering method widely used in the field of image processing, while at the same time applying a combinatorial approach and order statistics. The proposed solution makes it possible to improve on and assess the credibility of a single measurement. The article highlights the differences between the proposed and currently used approaches, as well as their advantages and disadvantages. The algorithm has been extensively tested under various environmental and weather conditions. The tests were carried out in typical and also in very demanding conditions, thus taking into account the real application context, i.e., pedestrian and car navigation in densely urbanized areas.
1. Introduction
The sensitivity of the Global Navigation Satellite Systems receivers is improving, which highlights the problem of reflected, non-line-of-sight (NLoS) or multipath signals, because the reflected signals can reach the receiver via very unexpected paths [1]. This leads to errors called outliers. Improvements due to augmentations, e.g., satellite based augmentation systems (SBAS), differential GNSS (DGNSS), and real-time kinematic (RTK), etc., are reducing many sources of error, but leave multipath as a significant contributor to overall error. These multipath and reflected signals are a major source of error for global navigation satellite system receivers. From the receiver’s point of view, it comes down to the simultaneous presence of line of sight and non-line of sight signals, which are reflected one or more times from nearby obstructions before reaching the receiver antenna. Although modern GNSS receivers provide high accuracy positioning in open air conditions, multipath and reflected signals still remain a major error source, especially in urbanized areas. The multipath and reflected signal lead, e.g., to incorrect ambiguity resolution affecting carrier phase positioning. If the multipath pseudorange error becomes large, the initial position solution may be highly biased, and the carrier phase ambiguity search space can be seriously enlarged or impossible to search efficiently.
The phenomenon of multipath, NLoS, can be mitigated in the three phases of signal processing in the GNSS receiver: antenna, signal processing (in this phase in the time, frequency, and spatial domains), and in a navigation phase. However, all of these mitigation methods consist of a rejecting or conditioning of the GNSS satellite signal by means of an electronic circuit or software that manipulates the signal in a way that prepares it for the next processing stage.
In the antenna array processing phase, a signal processing scheme that exploits the signal spatial features is proven to be effective in mitigating different types of interference. For instance, long-delay code multipath caused by distant reflectors can be mitigated using relatively old, but currently available, advanced correlator techniques, such as narrow correlator [2] and the strobe and edge correlator method which is presented in [3], while the general limitations of multipath closed-loop delay estimation are described in [4].
Moreover, the effectiveness of different beam forming techniques for GNSS applications was studied in [5,6,7]. Most distortion-free beamforming techniques are developed under the assumption that there is no correlation between the desired and interfering signals. However, these methods only partially eliminate multipath, as the performance of such beamforming techniques is degraded in the presence of reflected and multipath signals as there is a strong correlation between the desired and multipath signals and a relatively strong random change in signal polarity in a densely urbanized environment [5].
Thus, many modifications are used in this field, such as adaptive multipath compensation and context-aware compensation based on channel pattern recognition as presented in [8], and even artificial neural networks are used in this context where a new mitigation strategy has been proposed in the coordinate, spatial domain. In this case a convolutional neural network (CNN), based on the long short-term memory method is used to mine the deep NLoS or multipath features in GNSS coordinate series, so this is still a method based on historical data [9].
However, antenna array techniques are not suitable for complicated multipath environments, and they are usually not suitable for kinematic situations due to the cumbersome equipment they require, so some have investigated other methods, namely height aiding, C/N0 weighting and consistency checking to mitigate the effect of NLoS reception and multipath on navigation solutions [10], or attempting to mitigate NLoS using other techniques such as trend-surface analysis [11].
Various techniques can be used in the signal processing stage. The most common code multipath mitigation techniques include variants of the traditional delay lock loop (DLL) method, such as the double-delta correlator, strobecorrelator, and high-resolution correlator techniques, such as using multiple-input multiple-output and orthogonal frequency division multiplexing (MIMO-OFDM), equalization techniques, wavelet analysis, etc. They are typically divided into four categories: signal filtering, such as Kalman filtering [12]; multi-antenna solutions, based on auxiliary information that contains 3D maps; and time-domain techniques, such as sidereal filtering. Although these techniques are effective when the receiver is subjected to a few weak multipath reflections, their performance in severe multipath scenarios, such as in urban areas where reflections are numerous and often stronger than the line of sight (LoS) signals, is still limited [13].
For instance, sidereal filtering is derived from observing a multipath signal correlation for a repeating or similar satellite constellation. However, this approach can be applied to stationary measurements but generally not to moving objects in an urban environment, where the time domain approach may not be as effective. Of course this type of multipath mitigation method resulting from a similar satellite constellation can still be implemented in some specific dynamic environments where the main effect of the multi-path operation comes from, for example, the object itself [13].
Some additional hybrid techniques have also been implemented in this context, such as hybrid navigation systems that use the global positioning system (GPS) and dead reckoning sensors. Two main models were used in the investigation to detect the presence or absence of direct signals that consider variations in the mean and variance of the signal, as reported in [14].
Last but not least, some improvements have been observed using the vector tracking method of processing the GNSS position. As reported in [15], vector tracking may be a promising approach to minimizing the impact of multipath or NLoS interference. This method is used in place of the delay lock loop (DLL) used to trace the code phase. It also uses a Kalman filter to track GNSS signals and calculate the position of the GNSS receiver; however, in this case, by combining the tracking and positioning processes, the vector tracking can use the motion parameters of the GNSS receiver determined from well-conditioned GNSS signals to predict the code phase and track weaker signals. This makes vector tracking more resistant to signal interference and attenuation. This method can be simulated and tested using open source simulators [16]. In this report, the global positioning system (GPS) vector tracking (VT) method based on a software-defined radio is discussed, including in the context of urban areas. Excellent performance in tracking signals under high-dynamic applications is reported.
At the stage of calculating the navigation position, so at the stage of the GNSS navigation processor the fundamental theory of observation is involved. This is the theory of forward or inverse estimation, in which unknown parameters are determined on the basis of a set of observations. The processor for calculating the position of the GNSS receiver uses the inverse estimation method. The inverse problem is usually difficult, and the estimation serves, in this case, to determine, as accurately as possible, the real value of the unknown parameters, i.e., the position and time of the GNSS receiver [17,18]. That is especially true for overdetermined systems, where there are more observations, measurements, or methods than unknowns. At this point mathematical methods or models to obtain optimal estimation are applied [19].
Currently, the main approach to estimating the GNSS position, namely the Gauss least square method (LSQ), still dominates as the best linear unbiased estimation [20,21]. In this approach, the position estimate is usually calculated from redundant observations, i.e., overdetermined GNSS pseudo-ranging observations, because there are more observations than are necessary to determine a set of unknowns exactly. The estimate follows from [20]:
where is the estimation, ρ is measurement vector, is weight matrix, is a geometry matrix, and the operator , called a “hat matrix”, is the generalized relative geometry of the GNSS receiver and the satellites participating in the least square solution computation. This is the weighted version of the LSQ method (WLSQ or WLS).
Discussing the disadvantages of LSQ is beyond the scope of this article, but it is enough to pay attention to the geometric interpretation of the LSQ, as presented in Figure 1.
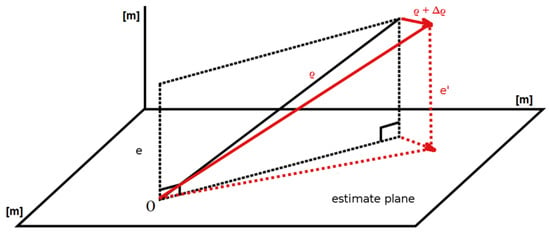
Figure 1.
3D geometric interpretation of least squares. The vector of observations is projected onto the solution plane.
In this geometric interpretation of a 3D LSQ overdetermined system, the estimate plane presented in Figure 1, stems from column vectors and is the plane of possible solutions, where ρ is the measurement vector. It is clear from Figure 1 that every disturbance of the measurement vector, e.g., ρ + Δρ, has a direct impact on an estimation with new error e’. It is therefore very unlikely that changing a single measurement from the measurement vector ρ will not affect the final solution. That is the reason that since the very beginning of global satellite systems, using subsets of satellites, all the way down to the minimum of four satellites, and using selection schemes and weights to determine the optimal number and spatial distribution of satellites, has been studied [20]. However, these approaches still fail in the context of multipath and reflected signals. WLSQ methods, like other least square methods, are also sensitive to outliers. If potential outliers are not handled properly, they will have a large negative impact on the position estimate, as further shown in Section 3.4.
However, this paper is not just another paper about satellite selection or satellite signal conditioning, which is typical for WLSQ [20] and other conditioning methods. On the contrary, this article proposes a different algorithm that makes it possible to use as many satellites as possible without any requiring selection and conditioning (of course proper conditioning can only improve the final position estimation). Instead of LSQ, this paper proposes using order statistics, e.g., a median filtering. Order statistics are important in estimation procedures in situations when classical parameters and their estimators cannot be used [22]. The median filter is one of the most widely used order statistics filters, as it is especially effective for certain specific types of noise, such as Gaussian, random, and salt and pepper noise [23]. It is employed extensively in such applications as speech, signal, and image processing. However, its disadvantage is that it is rather difficult to analyze the median filter effect analytically due to its nonlinearity.
Therefore, in Section 2 of this paper, the proposed algorithm is discussed in detail and a numerical example is given. Following this, due to the aforementioned nonlinear nature of the proposed method, Section 2.3 presents statistical simulations that confirm, e.g., the bounds of the proposed method, so that the algorithm does not introduce unexpected artifacts. Section 3 verifies the introduced algorithm using real data. The results provide only a 1 m accuracy, but it should be underlined that the phase measurements using RTK, i.e., centimeter accuracy, was not possible under these measurement conditions. The conclusions summarize the paper.
2. Material and Methods
2.1. New GNSS Position Calculation Algorithm Details
There are several steps in determining the GNSS position at the receiver, namely, receiving the satellite signal, correlating the signal with the receiver local reference oscillator (discriminator), and finally processing the navigation information, corrections, etc. The algorithm proposed in this paper is concerned with the last step of this processing chain, i.e., processing the navigational information, and can be treated as opposite to the widely used LSQ approach [20,21].
In his seminal, well-known paper, S. Bancroft proved analytically, using complex numbers, and discussed extensively in [24,25] (it will be given here to introduce further notations), that there is an analytical solution:
where is a final receiver position, stands for the satellite position, is a pseudo-range from a satellite, and denotes a set indexed with i (i = 1,2,3,4). It is significant that, even in that paper, [24] used the LSQ method as a solution to the overdetermined equations. However, there is also a different way; by using a non-linear median filter. So if we denote a set of as follows:
stands for a satellite number, so the set of combinations is the collection of all subsets of of size k, and P(S) denotes the set of all subsets of , and then we may introduce the set
Then also taking into account the algebraic solution that “performs better than an iterative solution in regions of poor GDOP” [24], this yields a set of receiver positions:
The final receiver position is the median of the set :
Now the estimate replaces estimate from Equation (1). A simplified representation of the proposed algorithm is presented in the form of pseudocode as Algorithm 1.
| Algorithm 1: Simplified Pseudocode Representation of the Proposed Algorithm. |
| Initialization xyzK, xyzKs, xyzMed sets calculate receiver position xyzK using 4 satellites save calculated receiver position to memory, xyzKs = [xyzKs xyzK] EndFor find xyzMed = median of xyzKs; end |
The computational complexity of the approach is O(n!) because and the number of combinations is , where n is the number of satellites observed by the receiver. So, the proposed method is straightforward but computationally expensive. In the proposed method, k = 4 and there are satellite combinations. For n = 18 satellites (GPS/GLONASS/Galileo/BeiDou) there are 3060 combinations, but potentially, for 30 satellites from all GNSS systems, there are 27,405 combinations available. The first combination consists of the position and pseudorange of the 1st, 2nd, 3rd and 4th satellite, the second combination consists of the position and pseudorange of the 1st, 2nd, 3rd and 5th satellite, and so on. The combinations of satellites were chosen to avoid LSQ, which is very prone to even small errors in estimating the position of even one satellite (ref. Figure 1). As mentioned above, a GNSS position calculation algorithm is usually an example of an LSQ approximate solution to an overdetermined linear equation system. This differs from the proposed algorithm, where the proposed algorithm is not only an example of a non–Gaussian least square approach to overdetermined linear system equations but is also a non-Newtonian or non-iterative approach, thanks to the Bancroft algebraic approach [24]; but of course, this is not an original input of this paper.
2.2. Numerical Example
All values are given in [m], according to actual measurements. Suppose the receiver receives signals from n = 6 satellites with the following coordinates in the ECEF system: xs, ys, zs, and pseudoranges ρ, as presented in Table 1. For n = 6 we get = 15 combinations. The satellite position is calculated from the GNSS almanac and its ephemeris, the precision of the numbers in the Table 1, therefore, significantly exceeds centimeters, but it is only an example of the navigation processing chain.

Table 1.
Satellite coordinates and pseudoranges.
The receiver coordinates for n = 6, thus for 15 different satellite combinations from Table 1, are calculated using Equation (2), with the results presented in Table 2.

Table 2.
Receiver coordinates for different satellite combinations.
Table 2 presents receiver positions for particular satellite combinations. The final receiver position is calculated from Equation (6) and equals = {xr, yr, zr} = {3,528,894.62913, 1,188,544.38338561, 5,161,007.42269604} [m]. Due to the method used, we avoided LSQ estimation, which is very sensitive to errors of pseudorange measurements, as presented in Section 3.4.
2.3. Algorithm Verification Using Simulation
Median filtering is a non-linear filtering technique. The disadvantage is that it is difficult to treat the effect of a median filter analytically. In order to illustrate the method, examine the nature of the process, and to finally answer the question of which conditions the method applies to, a simulation of the proposed method was performed. Taking into account the fixed position of the receiver , the exact distances from chosen satellites were calculated, which were then modified with additive Gaussian noise and then NLoS delay shifts were added randomly [26,27]. The final position can easily be compared with the expected, fixed position of the receiver .
The proposed simulation defines the environment in which the tests were carried out, i.e., the operating conditions of the GNSS receiver similar to NLoS conditions. The simulation consists of choosing any real satellite constellation, while the real distances in relation to the fixed position of the receiver are modified using the Gaussian distribution. The above-mentioned distances from the satellites were modified with additive noise from 10 to 100 m in the following way:
where and are random sequences, while and , which can be interpreted as a significant error, e.g., multipath, are defined to be Gaussian random variables, where of course µ is the mean, is the variance of the Gaussian noise, n is the number of satellites, and is the size of the random vector, which typically equals 1. The receiver position is calculated from and finally as the median , as in Equation (6). is a vector of zeros of size n, modified randomly with a permutation element as follows . Finally, it gives a binary (Hadamard) product with the Gaussian noise random vector responsible for a significant error, as in Equation (8). Algorithm 2 presents the pseudocode of the test procedure.
| Algorithm 2: Algorithm Test Pseudocode Representation. |
| Initialization of xyzLsqs, xyzMeds For i = number of iterations Initialization xyzLsq, xyzMed, recPos k = 8; number of available satellites n = 2; number of multipath satellites generate or choose satellites position add randomly multipath distance for n randomly chosen pseudoranges calculate receiver position xyzLsq using analytic or iteration method xyzLsqs = [xyzLsqs xyzLsq]; save calculated xyzLsq receiver position calculate receiver position xyzMed using Algorithm 1 save xyzMed, xyzMeds = [xyzMeds xyzMed] EndFor calculate standard error of xyzLsqs, xyzMeds to be compared |
In each simulated case, better results were observed (i.e., the standard deviation for the fixed position) compared to the estimation of from the LSQ method, Equation (1), with around 30% of satellites having signal quality degradation caused by multipath, as presented in Figure 2. The figure shows the ratio of the standard deviation of the proposed method to the standard deviation of LSQ, depending on the number of satellites degraded by NLoS.
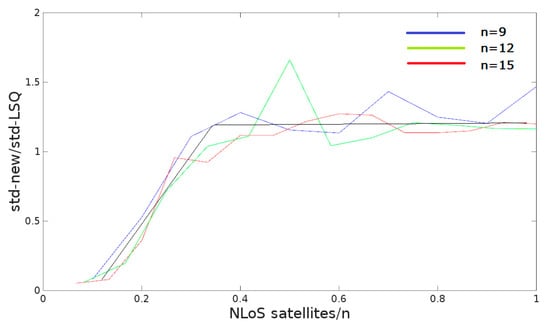
Figure 2.
Algorithm verification using simulation in relative values.
The following observation can be presented; namely, for a larger number of satellites in open area conditions, both methods are comparable, i.e., for the 30 hypothetically available satellites, the position variance for the proposed method is worse than LSQ by approx. 10–20% or comparable number (ref. Figure 2). However, the method is much better then LSQ, even for the 30% of satellites burdened with multipath or reflection effects, as presented in Figure 2, where n is the number of satellites available, in this case n = 9, 12, or 15 presented in blue, green, and red, respectively. The black line shows the trend. A simple statistical interpretation of the Figure 2 is as follows: for 1000 iterations (viz. Algorithm 2) and for a small number of pseudorange measurements disturbed mainly with NLoS, only a small number of positions calculated using the LSQ method will be better than when using the proposed method. For example, for 1 pseudorange disturbed by multipath (given the 10 satellites available), the position calculated with the proposed method is almost always better. The situation changes in favor of LSQ if the number of pseudo-range measurements disturbed with multipath or reflection exceed 30–40% of all available satellites; then the proportions change and for 1000 random cases the standard error of the calculated position is about 10–20% worse using the proposed method. It seems that this justifies the use of the proposed algorithm in highly urbanized areas.
3. Results
3.1. Algorithm Testing
The real testing of the proposed algorithm lasted over a year. Measurements, i.e., pseudoranges, in the Receiver Independent Exchange Format (RINEX) format were recorded using a high-end receiver and low–cost receiver as a comparison. They were a high-end CHC X91 geodetic GNSS receiver with RTK support, due to its GPS, GLONASS, and Galileo interoperability, and a common, cheap ublox 5 receiver. Both receivers are presented in Figure 3.

Figure 3.
GNSS receivers used for testing. A CHC x91 geodetic receiver (a) and an ublox receiver (b).
The X91 GNSS Receiver combines a dual-frequency GNSS receiver, GNSS antenna, Ultra High Frequency (UHF) datalink, and optional GPRS Module. The built-in Bluetooth® allows it to connect to a controller and the build in the GPRS Modem allows it to transmit phase corrections in Radio Technical Commission for Maritime Services (RTCM) format, optionally through a 1 W UHF internal transmitter for the base station. RTCM2.1, RTCM 2.3, RTCM 3.0, Compact Measurement Record (CMR), and CMR+ formats were accepted, so virtual RTCM corrections were used from the Active Geodetic Network European Positioning System (ASG-EUPOS), a geodetic reference system [28]. Multipath correction and minimum tracking thresholds were included, but no details are available [28]. The measurements were stored in the RINEX format, as an observation file (extension .obs) which consists of pseudoranges, phase cycles, etc., for all available satellites and as a navigation file (extension .nav.) which includes mostly ephemerides [28]. To be precise, all measurements were stored in the proprietary raw HCN format to be converted to RINEX. A full technical specification is available [29]. It should be mentioned here that according to the technical specification, the horizontal accuracy is + (10 mm + 1 ppm) RMS, and the vertical accuracy is + (20 mm + 1 ppm) RMS. However, such precision is not available for the environmental conditions in which the measurements were made.
The ublox EVK-5P Evaluation Kit is a low cost GNSS receiver of relatively good precision, including time evaluation. It is designed for vehicles, outdoor locations, and mobile devices [30].
In the field of geodesy, the RINEX [31] format is a data interchange format for raw satellite navigation system data. This allows the user to post-process the received data to produce a more accurate result—usually with other data unknown to the original receiver, such as better models of the atmospheric conditions at the time of measurement.
Along with the RINEX format, the well-known and well-tested RTKLib was used [32]. The software is versatile and was used for GNSS signal receiving to capture the position and for conversions. The source code is under an Open Source license [33].
The software is also available in terminal mode, in which it was mainly used to record ublox measurements and for further post-processing or data conversion to a more convenient format, used to verify the proposed algorithm.
3.2. Environment Conditions
Tests were carried out in the following environmental conditions: open, medium urbanized areas with high buildings, using a high–end and low–end receiver. For highly urbanized areas, research lasting 0.5 years was conducted. It should be underlined again that it was impossible to determine the position of the RTK quality using RTCM corrections in such conditions (the receiver in float mode). Only some more important results are presented below.
3.3. Algorithm Testing in Open Area in Static Conditions
First of all, the algorithm was tested in open area conditions; this means with line of sight (LoS) to satellites and using the high–end receiver. The data were collected multiple times over the year. The measurements usually lasted for about 6 h. To compare the results of the proposed algorithm, calculations were also carried out for the same data using the LSQ algorithm. According to the simulations carried out, the standard deviation and the mean value are almost identical for the Gaussian distribution data (such a distribution features the measurements collected in the open area). The calculated positions in the open area are presented in Figure 4, both for LSQ and the new, proposed algorithm using the high–end receiver. There were about 20 satellites available on average, and Table 3 presents errors of the ECEF coordinates.
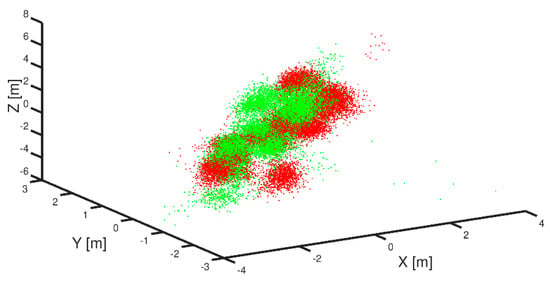
Figure 4.
GNSS position accuracy records for the static measurement receiver outputs in open area conditions (red—LSQ algorithm, green—proposed new algorithm).

Table 3.
Comparison of the results of LSQ vs. median filter method.
The median and mean values are close for the Gaussian distribution locations, as presents in Figure 4. The standard deviation for both methods (LSQ and the proposed method) differs by 15% in favor of the LSQ method. It is worth recalling that the simulations give similar results.
Figure 4 presents a 3D plot of records collected from the open area conditions (LoS). Calculated positions are presented in red for the LSQ method and in green for the proposed median filter method. All axes are in meters and all positions are in Earth-centered Earth-fixed coordinate system (ECEF).
Table 3 summarizes the standard deviation errors for the X, Y, Z coordinates in ECEF system.
3.4. Static Testing Results of the Proposed Method in an Urban Area
The results are different for the data collected in an urbanized area. The data were collected in relatively difficult conditions, namely relatively close to a building façade. The idea was that the multipath and NLoS effect should be large. The precise position (reference) was determined by other surveying methods.
Figure 5 presents the GNSS constellations for the urbanized area with a specific, limited sky view for the collected data. The figure represents the azimuth and altitude for all satellites available during the measurements, but some of the azimuths > 100 and <280 could not be observed at all through LoS, as shown in Figure 5b with a shaded orange zone, because they were obscured by buildings.
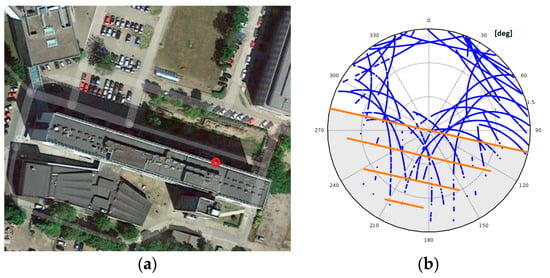
Figure 5.
Example of GNSS constellation for an obscured sky view (polar map) (b) for survey position (a).
Polar charts of the statistical distribution of azimuths and elevations for these measurements are presented in Figure 6.
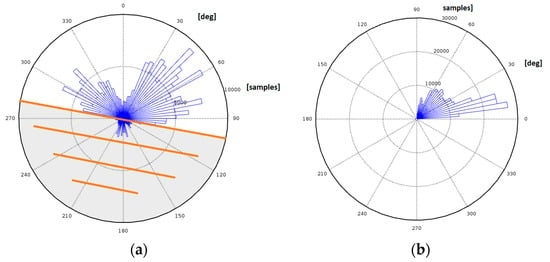
Figure 6.
Statistical distribution of azimuths (a) and elevations (b) for recorded GNSS measurements.
Most of the measurements were recorded at approx. 45 degrees for the azimuth and for most elevations at approx. 10 degrees. Figure 7a shows a histogram of the raw position records for the latitudes of the recorded positions (similarly for longitudes). A graphical method, a quantile–quantile plot of the records, is also presented in Figure 7b. The result is not a straight line for latitude distributions. It is obvious that the distributions are to some extent or even strongly non-Gaussian, as they should be. This is rather a Rayleigh or chi distribution. The results of the proposed algorithm are presented in green in Figure 8. The proposed method gives the better position evaluation than LSQ and, most importantly, it guarantees that a minimum of outliers is present.

Figure 7.
Histogram of raw position records in latitude (from the reference true position) (a) and the quantile–quantile plot as applied to raw position observation (b).
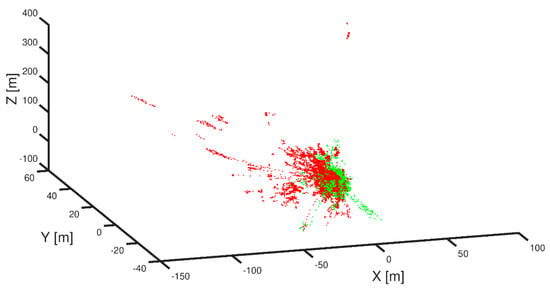
Figure 8.
Overlaid results of both LSQ and new combinatorial methods for static records in urbanized aresa (green for proposed method, red for LSQ).
Figure 8 presents a 3D plot of the measurements collected for dense urbanized conditions (NLoS satellites are present). The calculated positions are shown in red for the LSQ method and in green for the proposed median filter method. All axes are in meters and all positions are in the ECEF coordinate system.
Table 4 lists the standard deviation errors for the X, Y, Z coordinates in the ECEF system.

Table 4.
Comparison of results of both LSQ and median filter methods for static records in an urbanized area.
Constellations consisting of satellite distances degraded with multipath errors significantly affect the final positioning process, and sometimes they introduce outliers to a position evaluation, as shown in Figure 9, and are difficult to detect. The outliers are the real problem in GNSS position calculations, especially in urbanized areas, as they cause a sharp increase in position error, as presented in Figure 9. They occur relatively often, in about 10% of cases using LSQ. The proposed method significantly reduces their occurrence to about 1.5% in this case, as presented in Table 5, in a 6 h observation. The results of the proposed method are therefore promising.
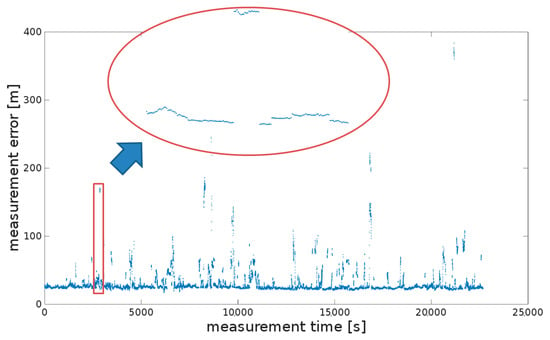
Figure 9.
GNSS position accuracy records for the static measurements.

Table 5.
Standard error and percentile evaluation of position processing using the proposed new approach.
3.5. Long-Term Static Verification Using Low-Cost Receiver
Long-term, i.e., semi-annual, tests were also carried out using the low-cost receiver. Long-term studies confirm the effectiveness of the introduced method. LSQ is presented in red, and the results for the new algorithm are presented in green in Figure 10. A summary of the result is presented in Table 6. The difference is huge.
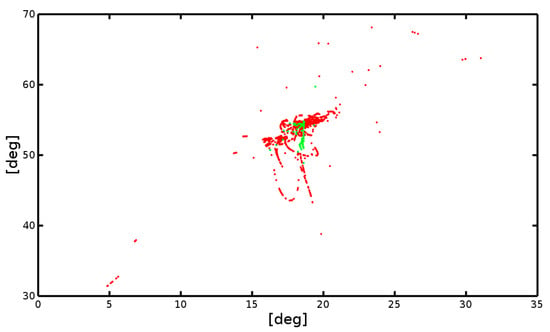
Figure 10.
GNSS position accuracy records for the static measurements.

Table 6.
Comparison the results of both the LSQ and median filter methods.
Figure 10 presents the measurements collected for a densely urbanized area using the ublox-5 GNSS receiver (NLoS satellites are present). The measurements were collected in the RINEX format for nearly half a year in the same position as the measurements collected with CHC x91 receiver. The calculated positions, as before, are shown in red for the LSQ method and in green for the proposed median filtration method. However, this time all axes are given in degrees and all positions are presented using the geographic coordinate system due to the large variation in coordinates of the recorded positions.
Table 6 lists the standard deviation errors for the X, Y, Z coordinates in the ECEF system for these measurements. The presented method of median filtration gives much better results. For the X, Y, Z axes of the ECEF system, the standard deviations are many times better. This is certainly determined by at least several factors: the quality of the antenna, the tracking/correlation algorithm, and the position calculation algorithm itself implemented in the RTKLib library. The algorithm implemented in the RTKLib library is not adapted to receiving signals in conditions of disturbances resulting from signal reflections. The same algorithms applied to the measurements collected with the CHC x91 receiver, in an identical position, give much better results. However, in both cases the conclusions are similar, i.e., the median filter is relatively better under the conditions of receiving strong reflected signals.
3.6. Application of New Method in Urbanized Area—Dynamic Measurements
Figure 11 presents, in red, the raw dynamic measurements obtained using the regular LSQ method with many position outliers observed. The black trajectory line shows a reference, true route. The measurements were carried out with the CHC x91 receiver.
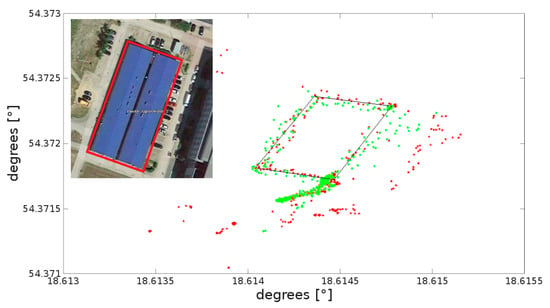
Figure 11.
Sample results of determining position coordinates for dynamic measurements in urbanized areas. In the insert the true trajectory is depicted on the photograph with a red line.
The results in red (LSQ) from Figure 11 may not be satisfactory, not only because of the reduced accuracy and an error, but also because of the outliers. The results for the proposed method are presented in green and are significantly improved. All positions are presented in geographic coordinates. An image presenting the true route is inserted in the upper left corner.
4. Discussion
As part of the tests, two algorithms were compared. The LSQ algorithm was used as a reference, because LSQ is commonly used in GNSS receivers, though that does not mean it is immune to multipath or reflected signal errors. Therefore, various modifications are used in this phase of GNSS receivers (navigation processors), e.g., WLSQ.
At the same time, as also shown by the research carried out in this project, even very good quality GNSS receivers are only to some extent immune to multipath interference or NLoS. The proposed algorithm gives good results for typical disturbances and very good results under the conditions of large disturbances caused by NLoS. It is significantly more immune to outliers, which are sometimes just artifacts. Due to its nonlinearity, the algorithm has been statistically tested, both through long-term field statistical studies and simulations. The simulations showed (this was not confirmed by the actual field tests) that under optimal conditions (good LoS), the LSQ method is slightly better, i.e., it reports a better precision, in the sense of RMS, by about 10–20%. However, the proposed algorithm returns a significantly better precision in urbanized areas with strong multipath disturbances. Simulation tests of the proposed algorithm are a very important element of the algorithm verification and seem very convincing. Thousands of random satellite constellations have been tested. The constellations evenly covered the entire sky. The test results differ slightly from the results obtained on the basis of actual measurements. Test results are presented in Figure 2.
The last question is that of the stability of the proposed algorithm. This is simply a question of whether the algorithm introduces artifacts. It is safe to say that no modifications to the process of position calculation were made at the stage of median filtering. In the context of NLoS signals, the advantage of the proposed method is the fact that, like the LSQ method, it is intuitively understandable.
There are at least several ways in which the proposed algorithm can be studied. For example, one could try to answer the question of what results it will give for different values of k. This is particularly important as the commonly used LSQ method was selected for comparison, i.e., the two methods were compared without the use of weights. It should be emphasized that the use of weights for observational measurements is also possible using the proposed method and may be the subject of future analyses. Another direction could be to test the heuristics for this algorithm in the context of a large number of combinations. The study of the satellite constellations for which LSQ gives better results than the proposed approach is yet another possibility. Obviously, as it shows very good results in the urban environment, the method can also be used in many other applications, e.g., as an anti-spoofing method.
5. Conclusions
This paper proposes a computationally expensive but effective method of GNSS position estimation as an alternative to the LSQ method. This is an essentially new and better approach to positioning, which is confirmed by tests, especially in high-density, urbanized areas, where routes approach building façades and satellite constellations may change quickly and in unexpected ways. The results of the real tests confirm the simulations, i.e., that under strong multipath and NLoS conditions, the GNSS position calculations using the proposed method are statistically significantly better in the vast majority of cases. Of course, the main disadvantage of the algorithm is that it is quite difficult to analyze the median filter effect analytically due to its nonlinearity but despite this, this non-linear technique also turned out to be a successful alternative in other research areas, e.g., image processing, etc. The longer computation time may be treated as a minor disadvantage of the proposed method, taking into account the current computational power possibilities. It should be emphasized that no historical filters such as the Kalman filter were used and the RTK method could not be used in the most of the studied environment conditions. However, the algorithm is generic, and its output can be used for further processing as input for RTK measurements and filtering. Considering all these factors, the proposed algorithm may prove to be a good alternative to the different variants of the weighted version of LSQ currently used in urban areas, as it does not use any weights. At the same time, it is slightly worse than the LSQ method for open areas, i.e., in the optimal conditions for receiving GNSS signals.
Funding
This research received no external funding.
Data Availability Statement
Detailed information of measurements regarding RTCM data collecting included in the paper. Measurements and Matlab source code available upon request.
Acknowledgments
I would like to thank the creators of satellite navigation systems and all those who share their knowledge, in particular the developers of the Open Source license software.
Conflicts of Interest
The author declares no conflict of interest.
References
- Lin, T.; Ma, M.; Broumandan, A.; Lachapelle, G. Demonstration of a High Sensitivity GNSS Software Receiver for Indoor Positioning. Adv. Space Res. 2013, 51, 1035–1045. [Google Scholar] [CrossRef]
- Dierendonck, A.J.V.; Fenton, P.; Ford, T. Theory and performance of narrow correlator spacing in a GPS receiver. J. Inst. Navig. 1992, 39, 265–283. [Google Scholar] [CrossRef]
- Garlin, L.; Van Digelen, F.; Rousseau, J.M. Strobe and edge correlator multipathmitigation for code. In Proceedings of the 9th International Technical Meeting of the Satellite Division of the Institute of Navigation, Kansas City, MO, USA, 17–20 September 1996. [Google Scholar]
- Van Nee, D.J.; Siereveld, J.; Fenton, P.C.; Townsend, B.R. The multipath estimating delay lock loop: Approaching theoretical accuracy limits. In Proceedings of the 1994 IEEE Position, Location and Navigation Symposium-PLANS’94, Las Vegas, NV, USA, 11–15 April 1994. [Google Scholar]
- Vagle, N.; Broumandan, A.; Jafarnia-Jahromi, A.; Lachapelle, G. Performance analysis of GNSS multipath mitigation using antenna arrays. J. Glob. Position. Syst. 2016, 14, 4. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Prades, C.; Closas, P.; Arribas, J. Eigenbeamforming for interferencemitigation in GNSS receivers. In Proceedings of the 1st International Conference on Localization and GNSS (ICLGNSS’11), Tampere, Finland, 29–30 June 2011; pp. 93–97. [Google Scholar]
- Gupta, I.J.; Weiss, I.M.; Morrison, A.W. Desired features of adaptive antennaarrays for GNSS receivers. Proc. IEEE 2016, 99, 1–12. [Google Scholar]
- Sokhandan, N.; Ziedan, N.; Broumandan, A.; Lachapelle, G. Context-Aware Adaptive Multipath Compensation Based on Channel Pattern Recognition for GNSS Receivers. J. Navig. 2017, 70, 944–962. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.; Liu, C.; Chen, T.; Zhao, X.; Liu, C.; Hu, H.; Zhou, T.; Xin, H. Real-Time Multipath Mitigation in Multi-GNSS Short Baseline Positioning via CNN-LSTM Method. Math. Probl. Eng. 2021, 2021, 6573230. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang ZSkelton, B.; Cross, P.A. Novel multipath mitigation methods using a dual-polarization antenna. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 140–151. [Google Scholar]
- Lu, R.; Chen, W.; Dong, D.; Wang, Z.; Zhang, C.; Peng, Y.; Yu, C. Multipath mitigation in GNSS precise point positioning based on trend-surface analysis and multipath hemispherical map. GPS Solut. 2021, 25, 119. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Filtering; Courier Corporation: Chelmsford, MA, USA, 2005. [Google Scholar]
- Wang, Z.; Chen, W.; Dong, D.; Wang, M.; Cai, M.; Yu, C.; Zheng, Z.; Liu, M. Multipath mitigation based on trend surface analysis applied to dual-antenna receiver with common clock. GPS Solut. 2019, 23, 104. [Google Scholar] [CrossRef]
- Spangenberg, M.; Tourneret, J.; Calmettes, V.; Duchateau, G. Detection of Variance Changes andMean Value Jumps in Measurement Noise for Multipath Mitigation in Urban Navigation. Navigation 2010, 57, 35–52. [Google Scholar] [CrossRef] [Green Version]
- Hsu, L.-T.; Jan, S.-S.; Groves, P.D.; Kubo, N. Multipath mitigation and NLOS detection using vector tracking in urban environments. GPS Solut. 2015, 19, 249–262. [Google Scholar] [CrossRef]
- Xu, B.; Hsu, L.-T. Open-source MATLAB code for GPS vector tracking on a software-defined receiver. GPS Solut. 2019, 23, 46. [Google Scholar] [CrossRef]
- Shultz Kenneth, S. Measurement Theory in Action; Taylor & Francis Ltd.: New York, NY, USA, 2020. [Google Scholar]
- Chikhi, S. Modelling and Implementation of Complex Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Branham, R.L., Jr. Scientific Data Analysis: An Introduction to Overdetermined Systems; Springer Science: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Leick, A.; Lapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2015; ISBN 978-1-118-67557-1. [Google Scholar]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS/GNSS Principles and Applications; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- David, H.A.; Nagaraja, H.N. Order Statistics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2003; ISBN 978-0-471-38926-2. [Google Scholar]
- Gonzalez, R.; Woods, R. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Bancroft, S. An Algebraic Solution of the GPS Equations. IEEE Trans. Aerosp. Electron. Syst. 1985, 1, 56–59. [Google Scholar] [CrossRef]
- Kleusberg, A. Analytical GPS Navigation Solution. In Geodesy-The Challenge of the 3rd Millennium; Springer: Berlin/Heidelberg, Germany, 2003; pp. 93–96. [Google Scholar]
- Abdolkarimi, E.S.; Mosavi, M.R. A low-cost integrated MEMS-based INS/GPS vehicle navigation system with challenging conditions based on an optimized IT2FNN in occluded environments. GPS Solut. 2020, 24, 108. [Google Scholar] [CrossRef]
- Demkowicz, J. MEMS Gyro in the Context of Inertial Positioning. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 247–251. [Google Scholar]
- ASG-EUPOS. EUPOS, System Description. 2013. Available online: http://www.asgeupos.pl/ (accessed on 1 February 2022).
- CHC X91 Manual. Available online: https://chcnav.es/es/productos/x91-gnss/chc-Manual-Gps-Centimetrico-X91-en.pdf (accessed on 1 February 2022).
- UBlox EVK-5 Evaluation Kit. Available online: https://www.u-blox.com (accessed on 1 February 2022).
- RINEX Format, International GNSS Service. Available online: https://kb.igs.org/hc/en-us/articles/201096516-IGS-Formats (accessed on 1 February 2022).
- RTKLib ver 2.4.2 Manual. Available online: http://www.rtklib.com/prog/manual_2.4.2.pdf (accessed on 1 February 2022).
- RTKLib Source Code. Available online: https://github.com/tomojitakasu/RTKLIB (accessed on 1 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).