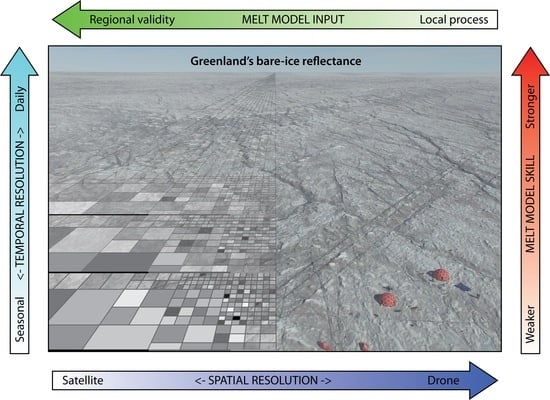
Temporal Variability of Surface Reflectance Supersedes Spatial Resolution in Defining Greenland’s Bare-Ice Albedo
Abstract
1. Introduction
2. Data, Methods, and Experimental Design
2.1. Study Site
2.2. Surface Reflectance Datasets
2.2.1. Satellite Reflectance Products
2.2.2. Field Spectroscopy Observations
2.2.3. Uncrewed Aerial Vehicle Imagery and Reflectance Measurements
2.3. Numerical Modelling of Ice Ablation
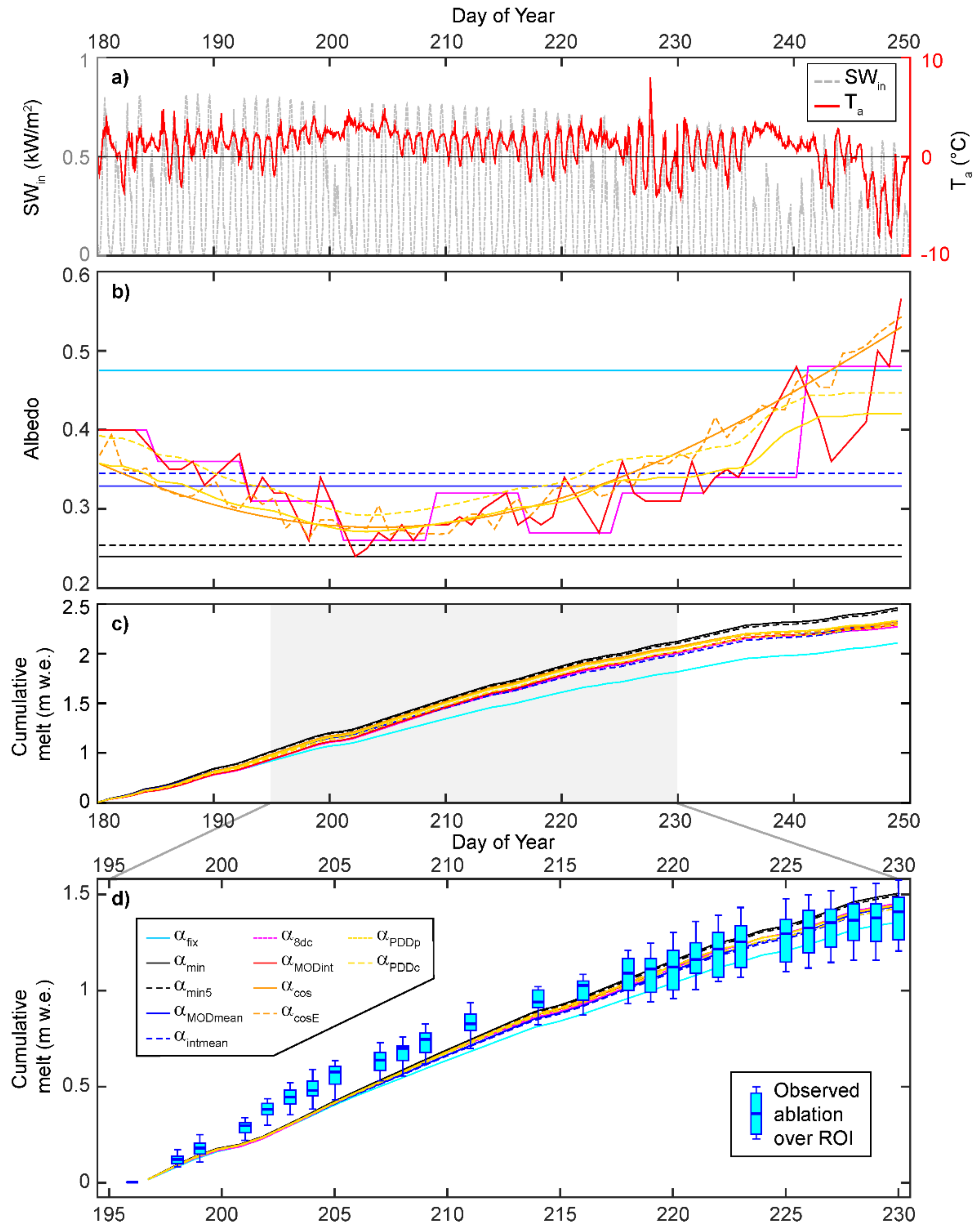
3. Results
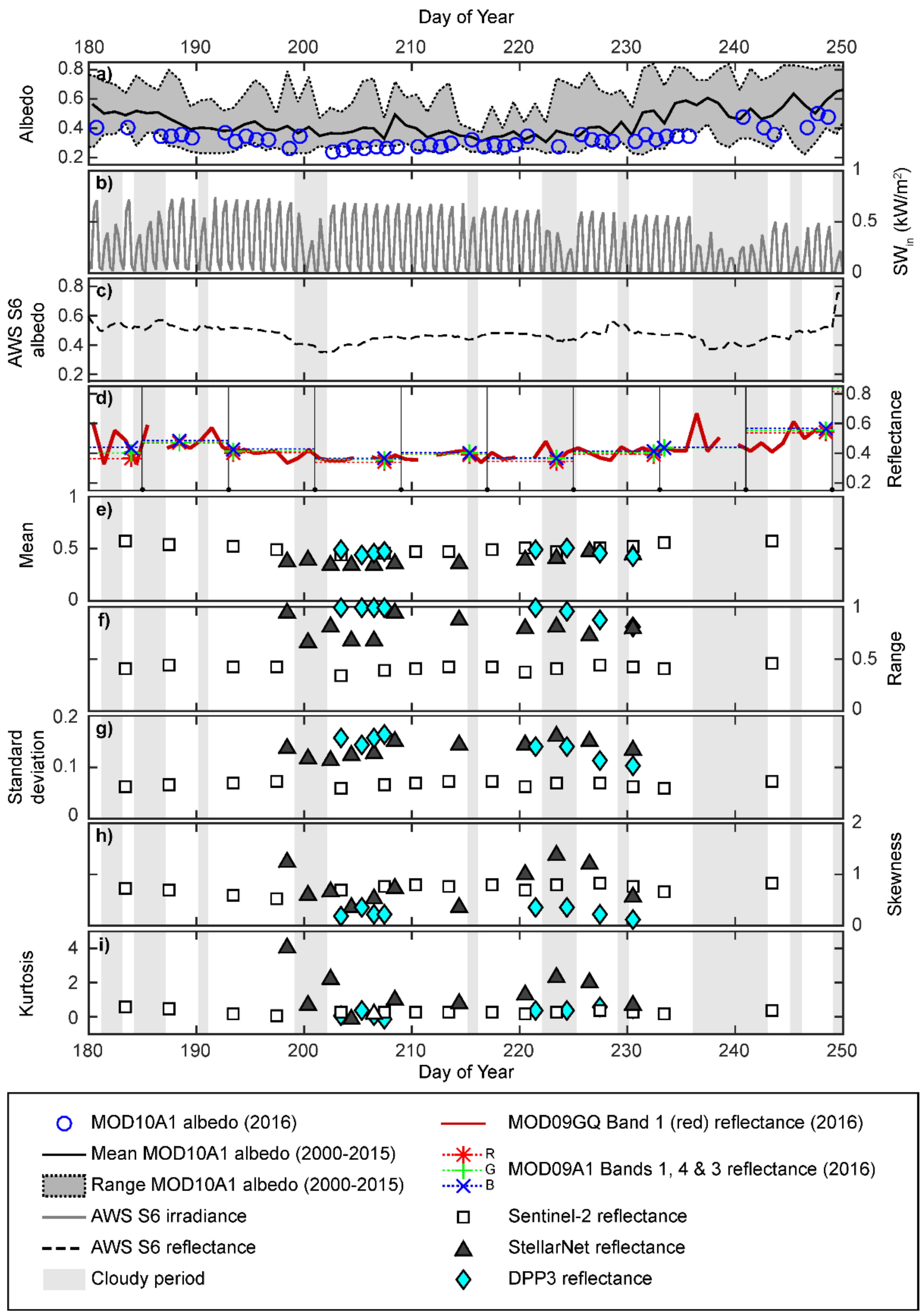
3.1. Bare-Ice Reflectance Variability
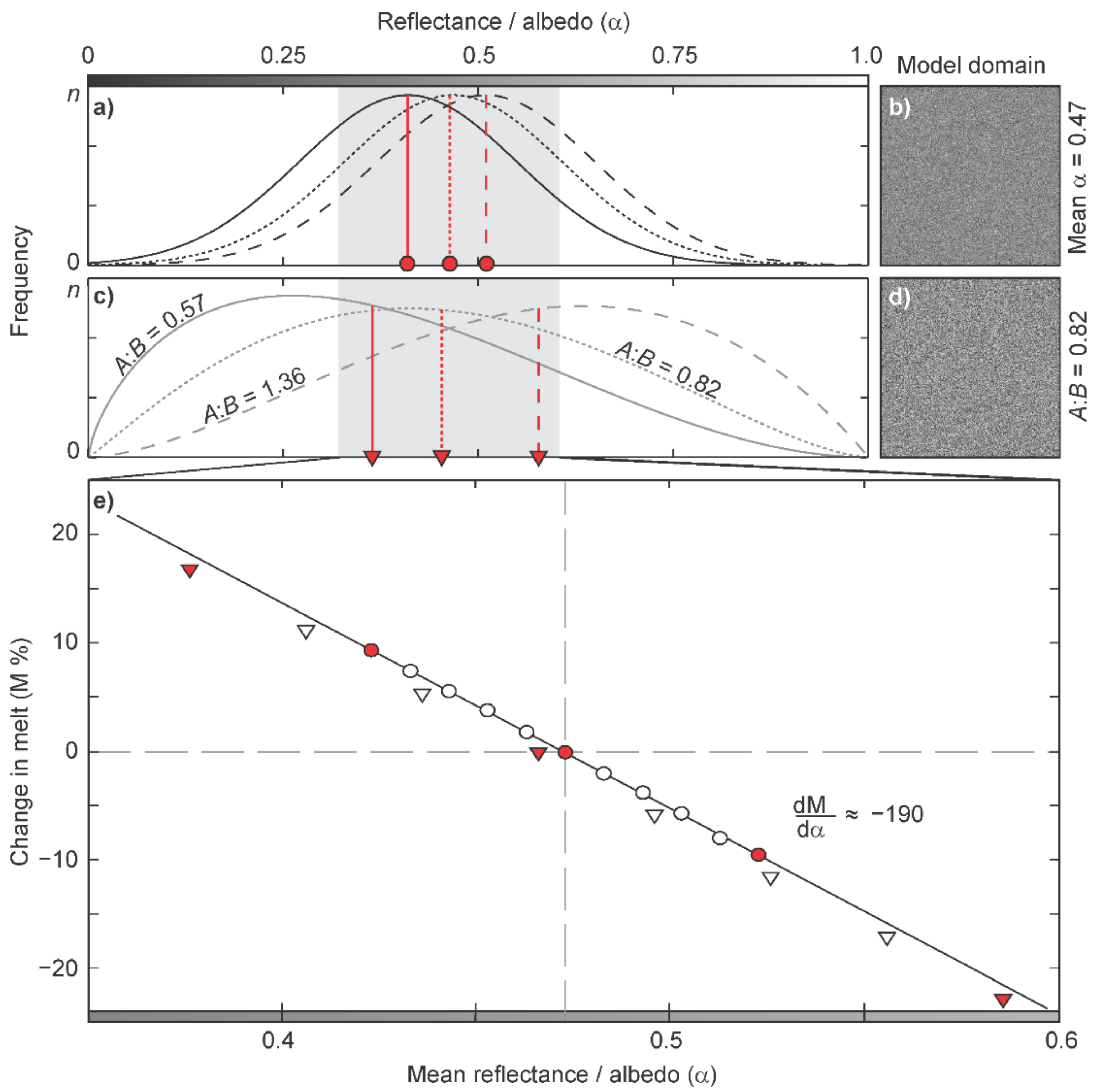
3.2. Reflectance Variability and Ablation
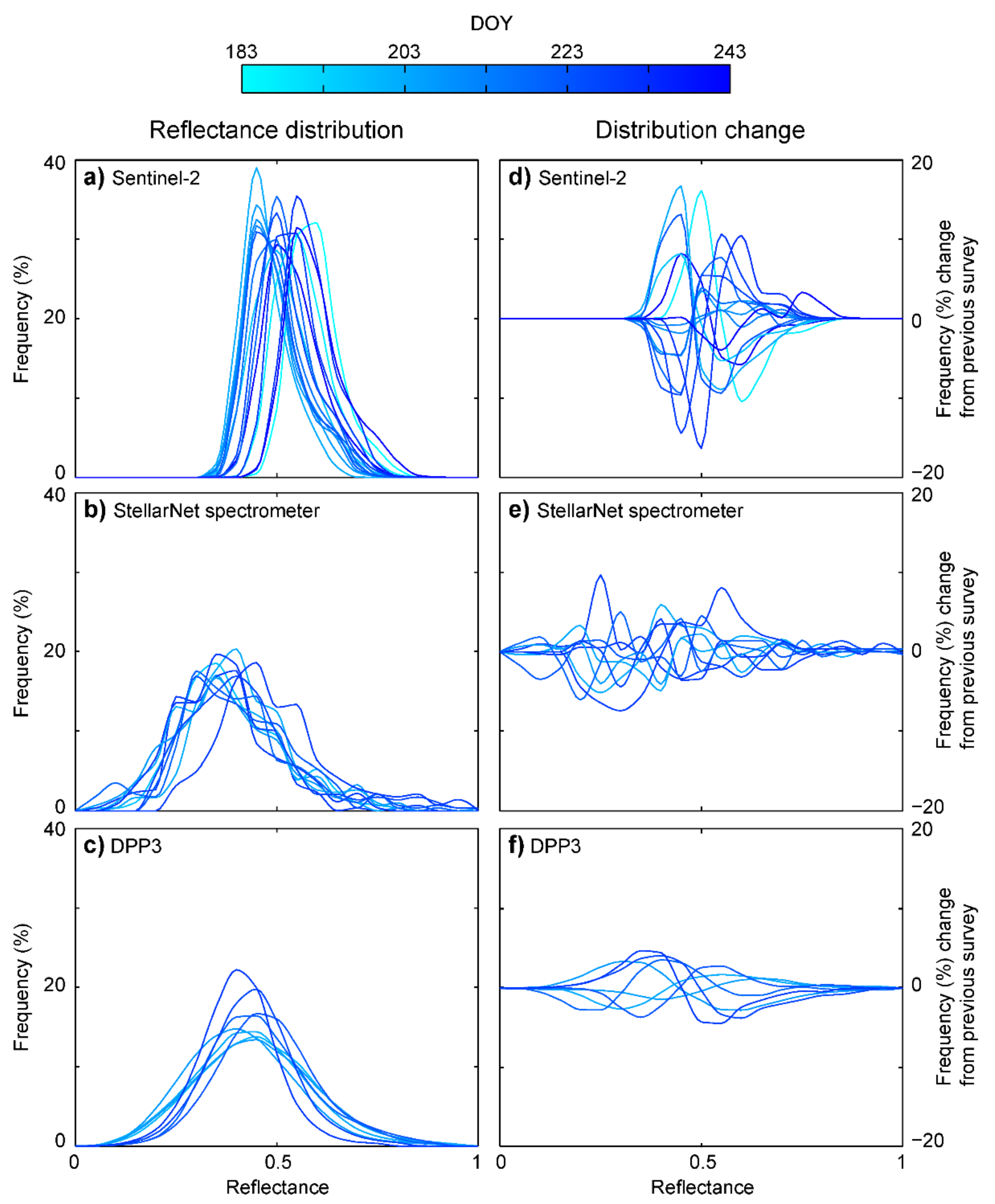
3.2.1. Spatial Variability
3.2.2. Temporal Variability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trusel, L.D.; Das, S.B.; Osman, M.B.; Evans, M.J.; Smith, B.; Fettweis, X.; McConnell, J.R.; Noel, B.P.Y.; van den Broeke, M.R. Nonlinear rise in Greenland runoff in response to post-industrial Arctic warming. Nature 2018, 564, 104–108. [Google Scholar] [CrossRef]
- Hanna, E.; Cappelen, J.; Fettweis, X.; Mernild, S.H.; Mote, T.L.; Mottram, R.; Steffen, K.; Ballinger, T.J.; Hall, R. Greenland surface air temperature changes from 1981 to 2019 and implications for ice-sheet melt and mass-balance change. Int. J. Climatol. 2021, 41, E1336–E1352. [Google Scholar] [CrossRef]
- Hofer, S.; Tedstone, A.J.; Fettweis, X.; Bamber, J.L. Decreasing cloud cover drives the recent mass loss on the Greenland Ice Sheet. Sci. Adv. 2017, 3, e1700584. [Google Scholar] [CrossRef]
- Hanna, E.; Cropper, T.E.; Hall, R.J.; Cappelen, J. Greenland Blocking Index 1851–2015: A regional climate change signal. Int. J. Climatol. 2016, 36, 4847–4861. [Google Scholar] [CrossRef]
- Doyle, S.H.; Hubbard, A.; van de Wal, R.S.W.; Box, J.E.; van As, D.; Scharrer, K.; Meierbachtol, T.W.; Smeets, P.C.J.P.; Harper, J.T.; Johansson, E.; et al. Amplified melt and flow of the Greenland ice sheet driven by late-summer cyclonic rainfall. Nat. Geosci. 2015, 8, 647–653. [Google Scholar] [CrossRef]
- Oltmanns, M.; Straneo, F.; Tedesco, M. Increased Greenland melt triggered by large-scale, year-round cyclonic moisture intrusions. Cryosphere 2019, 13, 815–825. [Google Scholar] [CrossRef]
- Fettweis, X.; Tedesco, M.; van den Broeke, M.; Ettema, J. Melting trends over the Greenland ice sheet (1958–2009) from spaceborne microwave data and regional climate models. Cryosphere 2011, 5, 359–375. [Google Scholar] [CrossRef]
- Noel, B.; van de Berg, W.J.; Lhermitte, S.; van den Broeke, M.R. Rapid ablation zone expansion amplifies north Greenland mass loss. Sci. Adv. 2019, 5, eaaw0123. [Google Scholar] [CrossRef]
- Ryan, J.C.; Smith, L.C.; van As, D.; Cooley, S.W.; Cooper, M.G.; Pitcher, L.H.; Hubbard, A. Greenland Ice Sheet surface melt amplified by snowline migration and bare ice exposure. Sci. Adv. 2019, 5, eaav3738. [Google Scholar] [CrossRef]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 2020, 579, 233–239. [Google Scholar] [CrossRef]
- Steger, C.R.; Reijmer, C.H.; van den Broeke, M.R. The modelled liquid water balance of the Greenland Ice Sheet. Cryosphere 2017, 11, 2507–2526. [Google Scholar] [CrossRef]
- Munneke, P.K.; Smeets, C.J.P.P.; Reijmer, C.H.; Oerlemans, J.; van de Wal, R.S.W.; van den Broeke, M.R. The K-transect on the western Greenland Ice Sheet: Surface energy balance (2003–2016). Arct. Antarct. Alp. Res. 2018, 50, e1420952. [Google Scholar] [CrossRef]
- Van den Broeke, M.; Smeets, P.; Ettema, J.; van der Veen, C.; van de Wal, R.; Oerlemans, J. Partitioning of melt energy and meltwater fluxes in the ablation zone of the west Greenland ice sheet. Cryosphere 2008, 2, 179–189. [Google Scholar] [CrossRef]
- Box, J.E.; Fettweis, X.; Stroeve, J.C.; Tedesco, M.; Hall, D.K.; Steffen, K. Greenland ice sheet albedo feedback: Thermodynamics and atmospheric drivers. Cryosphere 2012, 6, 821–839. [Google Scholar] [CrossRef]
- Helsen, M.M.; van de Wal, R.S.W.; Reerink, T.J.; Bintanja, R.; Madsen, M.S.; Yang, S.T.; Li, Q.; Zhang, Q. On the importance of the albedo parameterization for the mass balance of the Greenland ice sheet in EC-Earth. Cryosphere 2017, 11, 1949–1965. [Google Scholar] [CrossRef]
- He, T.; Liang, S.L.; Yu, Y.Y.; Wang, D.D.; Gao, F.; Liu, Q. Greenland surface albedo changes in July 1981–2012 from satellite observations. Environ. Res. Lett. 2013, 8, 044043. [Google Scholar] [CrossRef]
- Riihela, A.; King, M.D.; Anttila, K. The surface albedo of the Greenland Ice Sheet between 1982 and 2015 from the CLARA-A2 dataset and its relationship to the ice sheet’s surface mass balance. Cryosphere 2019, 13, 2597–2614. [Google Scholar] [CrossRef]
- Tedesco, M.; Doherty, S.; Fettweis, X.; Alexander, P.; Jeyaratnam, J.; Stroeve, J. The darkening of the Greenland ice sheet: Trends, drivers, and projections (1981–2100). Cryosphere 2016, 10, 477–496. [Google Scholar] [CrossRef]
- Shimada, R.; Takeuchi, N.; Aoki, T. Inter-annual and geographical variations in the extent of bare ice and dark ice on the Greenland Ice Sheet derived from MODIS satellite images. Front. Earth Sci. 2016, 4, 43. [Google Scholar] [CrossRef]
- Tedstone, A.J.; Bamber, J.L.; Cook, J.M.; Williamson, C.J.; Fettweis, X.; Hodson, A.J.; Tranter, M. Dark ice dynamics of the south-west Greenland Ice Sheet. Cryosphere 2017, 11, 2491–2506. [Google Scholar] [CrossRef]
- Van den Broeke, M.; Box, J.; Fettweis, X.; Hanna, E.; Noel, B.; Tedesco, M.; van As, D.; van de Berg, W.J.; van Kampenhout, L. Greenland Ice Sheet surface mass loss: Recent developments in observation and modeling. Curr. Clim. Change Rep. 2017, 3, 345–356. [Google Scholar] [CrossRef]
- Van de Berg, W.J.; van Meijgaard, E.; van Ulft, L.H. The added value of high resolution in estimating the surface mass balance in southern Greenland. Cryosphere 2020, 14, 1809–1827. [Google Scholar] [CrossRef]
- Boggild, C.E.; Brandt, R.E.; Brown, K.J.; Warren, S.G. The ablation zone in northeast Greenland: Ice types, albedos and impurities. J. Glaciol. 2010, 56, 101–113. [Google Scholar] [CrossRef]
- Goelles, T.; Boggild, C.E. Albedo reduction of ice caused by dust and black carbon accumulation: A model applied to the K-transect, West Greenland. J. Glaciol. 2017, 63, 1063–1076. [Google Scholar] [CrossRef]
- Stibal, M.; Box, J.E.; Cameron, K.A.; Langen, P.L.; Yallop, M.L.; Mottram, R.H.; Khan, A.L.; Molotch, N.P.; Chrismas, N.A.M.; Quaglia, F.C.; et al. Algae drive enhanced darkening of bare ice on the Greenland Ice Sheet. Geophys. Res. Lett. 2017, 44, 11463–11471. [Google Scholar] [CrossRef]
- Tedstone, A.J.; Cook, J.M.; Williamson, C.J.; Hofer, S.; McCutcheon, J.; Irvine-Fynn, T.; Gribbin, T.; Tranter, M. Algal growth and weathering crust state drive variability in western Greenland Ice Sheet ice albedo. Cryosphere 2020, 14, 521–538. [Google Scholar] [CrossRef]
- Williamson, C.J.; Anesio, A.M.; Cook, J.; Tedstone, A.; Poniecka, E.; Holland, A.; Fagan, D.; Tranter, M.; Yallop, M.L. Ice algal bloom development on the surface of the Greenland Ice Sheet. FEMS Microbiol. Ecol. 2018, 94, fiy025. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.; Ryan, J.; Holt, T.; Hubbard, A. Structural glaciology of Isunguata Sermia, West Greenland. J. Maps 2018, 14, 517–527. [Google Scholar] [CrossRef]
- Wientjes, I.G.M.; van de Wal, R.S.W.; Schwikowski, M.; Zapf, A.; Fahrni, S.; Wacker, L. Carbonaceous particles reveal that Late Holocene dust causes the dark region in the western ablation zone of the Greenland ice sheet. J. Glaciol. 2012, 58, 787–794. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.; Stibal, M.; Irvine-Fynn, T.D.; Cook, J.; Smith, L.C.; Cameron, K.; Box, J. Dark zone of the Greenland Ice Sheet controlled by distributed biologically-active impurities. Nat. Commun. 2018, 9, 1065. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.J.; Cook, J.; Tedstone, A.; Yallop, M.; McCutcheon, J.; Poniecka, E.; Campbell, D.; Irvine-Fynn, T.; McQuaid, J.; Tranter, M.; et al. Algal photophysiology drives darkening and melt of the Greenland Ice Sheet. Proc. Natl. Acad. Sci. USA 2020, 117, 5694–5705. [Google Scholar] [CrossRef] [PubMed]
- Janssens, I.; Huybrechts, P. The treatment of meltwater retention in mass-balance parameterizations of the Greenland ice sheet. Ann. Glaciol. 2000, 31, 133–140. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Meier, M.F.; Illangasekare, T.H. Retention of Greenland runoff by refreezing: Implications for projected future sea-level change. J. Geophys. Res. Oceans 1991, 96, 22117–22124. [Google Scholar] [CrossRef]
- Hodson, A.; Boggild, C.; Hanna, E.; Huybrechts, P.; Langford, H.; Cameron, K.; Houldsworth, A. The cryoconite ecosystem on the Greenland ice sheet. Ann. Glaciol. 2010, 51, 123–129. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.; Box, J.E.; Brough, S.; Cameron, K.; Cook, J.M.; Cooper, M.; Doyle, S.H.; Edwards, A.; Holt, T.; et al. Derivation of High Spatial Resolution Albedo from UAV Digital Imagery: Application over the Greenland Ice Sheet. Front. Earth Sci. 2017, 5, 40. [Google Scholar] [CrossRef]
- Wientjes, I.G.M.; Van de Wal, R.S.W.; Reichart, G.J.; Sluijs, A.; Oerlemans, J. Dust from the dark region in the western ablation zone of the Greenland ice sheet. Cryosphere 2011, 5, 589–601. [Google Scholar] [CrossRef]
- Cooper, M.G.; Smith, L.C.; Rennermalm, A.K.; Miege, C.; Pitcher, L.H.; Ryan, J.C.; Yang, K.; Cooley, S. Meltwater storage in low-density near-surface bare ice in the Greenland ice sheet ablation zone. Cryosphere 2018, 12, 955–970. [Google Scholar] [CrossRef]
- Greuell, W. Melt-water accumulation on the surface of the Greenland ice sheet: Effect on albedo and mass balance. Geogr. Ann. A 2000, 82, 489–498. [Google Scholar] [CrossRef]
- Zuo, Z.; Oerlemans, J. Modelling albedo and specific balance of the Greenland ice sheet: Calculations for the Sondre Stromfjord transect. J. Glaciol. 1996, 42, 305–317. [Google Scholar] [CrossRef]
- Yang, K.; Smith, L.C.; Cooper, M.G.; Pitcher, L.H.; van As, D.; Lu, Y.; Lu, X.; Li, M.C. Seasonal evolution of supraglacial lakes and rivers on the southwest Greenland Ice Sheet. J. Glaciol. 2021, 67, 592–602. [Google Scholar] [CrossRef]
- Chandler, D.M.; Alcock, J.D.; Wadham, J.L.; Mackie, S.L.; Telling, J. Seasonal changes of ice surface characteristics and productivity in the ablation zone of the Greenland Ice Sheet. Cryosphere 2015, 9, 487–504. [Google Scholar] [CrossRef]
- Cook, J.M.; Hodson, A.J.; Gardner, A.S.; Flanner, M.; Tedstone, A.J.; Williamson, C.; Irvine-Fynn, T.D.L.; Nilsson, J.; Bryant, R.; Tranter, M. Quantifying bioalbedo: A new physically based model and discussion of empirical methods for characterising biological influence on ice and snow albedo. Cryosphere 2017, 11, 2611–2632. [Google Scholar] [CrossRef]
- Takeuchi, N.; Sakaki, R.; Uetake, J.; Nagatsuka, N.; Shimada, R.; Niwano, M.; Aoki, T. Temporal variations of cryoconite holes and cryoconite coverage on the ablation ice surface of Qaanaaq Glacier in northwest Greenland. Ann. Glaciol. 2018, 59, 21–30. [Google Scholar] [CrossRef]
- Cook, J.M.; Tedstone, A.J.; Williamson, C.; McCutcheon, J.; Hodson, A.J.; Dayal, A.; Skiles, M.; Hofer, S.; Bryant, R.; McAree, O.; et al. Glacier algae accelerate melt rates on the south-western Greenland Ice Sheet. Cryosphere 2020, 14, 309–330. [Google Scholar] [CrossRef]
- Moustafa, S.E.; Rennermalm, A.K.; Roman, M.O.; Wang, Z.S.; Schaaf, C.B.; Smith, L.C.; Koenig, L.S.; Erb, A. Evaluation of satellite remote sensing albedo retrievals over the ablation area of the southwestern Greenland ice sheet. Remote Sens. Environ. 2017, 198, 115–125. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.; Irvine-Fynn, T.D.; Doyle, S.H.; Cook, J.M.; Stibal, M.; Box, J.E. How robust are in situ observations for validating satellite-derived albedo over the dark zone of the Greenland Ice Sheet? Geophys. Res. Lett. 2017, 44, 6218–6225. [Google Scholar] [CrossRef]
- Moustafa, S.E.; Rennermalm, A.K.; Smith, L.C.; Miller, M.A.; Mioduszewski, J.R.; Koenig, L.S.; Hom, M.G.; Shuman, C.A. Multi-modal albedo distributions in the ablation area of the southwestern Greenland Ice Sheet. Cryosphere 2015, 9, 905–923. [Google Scholar] [CrossRef]
- Cathles, L.M.; Abbot, D.S.; Bassis, J.N.; MacAyeal, D.R. Modeling surface-roughness/solar-ablation feedback: Application to small-scale surface channels and crevasses of the Greenland ice sheet. Ann. Glaciol. 2011, 52, 99–108. [Google Scholar] [CrossRef]
- Nolin, A.W.; Payne, M.C. Classification of glacier zones in western Greenland using albedo and surface roughness from the Multi-angle Imaging SpectroRadiometer (MISR). Remote Sens. Environ. 2007, 107, 264–275. [Google Scholar] [CrossRef]
- Knap, W.H.; Oerlemans, J. The surface albedo of the Greenland ice sheet: Satellite-derived and in situ measurements in the Sondre Stromfjord area during the 1991 melt season. J. Glaciol. 1996, 42, 364–374. [Google Scholar] [CrossRef]
- Greuell, W.; Reijmer, C.H.; Oerlemans, J. Narrowband-to-broadband albedo conversion for glacier ice and snow based on aircraft and near-surface measurements. Remote Sens. Environ. 2002, 82, 48–63. [Google Scholar] [CrossRef]
- Naegeli, K.; Damm, A.; Huss, M.; Wulf, H.; Schaepman, M.; Hoelzle, M. Cross-comparison of albedo products for glacier surfaces derived from airborne and satellite (Sentinel-2 and Landsat 8) optical data. Remote Sens. 2017, 9, 110. [Google Scholar] [CrossRef]
- Alexander, P.M.; LeGrande, A.N.; Fischer, E.; Tedesco, M.; Fettweis, X.; Kelley, M.; Nowicki, S.M.J.; Schmidt, G.A. Simulated Greenland surface mass balance in the GISS Model E2 GCM: Role of the ice sheet surface. J. Geophys. Res. Earth 2019, 124, 750–765. [Google Scholar] [CrossRef]
- Bougamont, M.; Bamber, J.L. A surface mass balance model for the Greenland ice sheet. J. Geophys. Res. Earth 2005, 110, F04018. [Google Scholar] [CrossRef]
- Rae, J.G.L.; Aoalgeirsdottir, G.; Edwards, T.L.; Fettweis, X.; Gregory, J.M.; Hewitt, H.T.; Lowe, J.A.; Lucas-Picher, P.; Mottram, R.H.; Payne, A.J.; et al. Greenland ice sheet surface mass balance: Evaluating simulations and making projections with regional climate models. Cryosphere 2012, 6, 1275–1294. [Google Scholar] [CrossRef]
- Noel, B.; van de Berg, W.J.; Machguth, H.; Lhermitte, S.; Howat, I.; Fettweis, X.; van den Broeke, M.R. A daily, 1 km resolution data set of downscaled Greenland ice sheet surface mass balance (1958–2015). Cryosphere 2016, 10, 2361–2377. [Google Scholar] [CrossRef]
- Navari, M.; Margulis, S.A.; Tedesco, M.; Fettweis, X.; Alexander, P.M. Improving Greenland surface mass balance estimates through the assimilation of MODIS albedo: A case study along the K-Transect. Geophys. Res. Lett. 2018, 45, 6549–6556. [Google Scholar] [CrossRef]
- Williamson, S.N.; Copland, L.; Thomson, L.; Burgess, D. Comparing simple albedo scaling methods for estimating Arctic glacier mass balance. Remote Sens. Environ. 2020, 246, 111858. [Google Scholar] [CrossRef]
- Dumont, M.; Gardelle, J.; Sirguey, P.; Guillot, A.; Six, D.; Rabatel, A.; Arnaud, Y. Linking glacier annual mass balance and glacier albedo retrieved from MODIS data. Cryosphere 2012, 6, 1527–1539. [Google Scholar] [CrossRef]
- Colgan, W.; Box, J.E.; Fausto, R.S.; van As, D.; Barletta, V.R.; Forsberg, R. Surface albedo as a proxy for the mass balance of Greenland’s terrestrial ice. Geol. Surv. Den. Greenl. 2014, 31, 91–94. [Google Scholar] [CrossRef][Green Version]
- Wilton, D.J.; Jowett, A.; Hanna, E.; Bigg, G.R.; van den Broeke, M.R.; Fettweis, X.; Huybrechts, P. High resolution (1 km) positive degree-day modelling of Greenland ice sheet surface mass balance, 1870–2012 using reanalysis data. J. Glaciol. 2017, 63, 176–193. [Google Scholar] [CrossRef][Green Version]
- Hubbard, B.; Glasser, N.F. Field Techniques in Glaciology and Glacial Geomorphology; John Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- Smeets, P.C.J.P.; Munneke, P.K.; van As, D.; van den Broeke, M.R.; Boot, W.; Oerlemans, H.; Snellen, H.; Reijmer, C.H.; van de Wal, R.S.W. The K-transect in west Greenland: Automatic weather station data (1993–2016). Arct. Antarct. Alp. Res. 2018, 50, e1420954. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Terra Snow Cover Daily L3 Global 0.05 Deg CMG, Version 6. 2019. Available online: https://nsidc.org/data/MOD10A1/versions/6 (accessed on 9 March 2021).
- Casey, K.A.; Polashenski, C.M.; Chen, J.; Tedesco, M. Impact of MODIS sensor calibration updates on Greenland Ice Sheet surface reflectance and albedo trends. Cryosphere 2017, 11, 1781–1795. [Google Scholar] [CrossRef]
- Vermote, E.F.; ElSaleous, N.; Justice, C.O.; Kaufman, Y.J.; Privette, J.L.; Remer, L.; Roger, J.C.; Tanre, D. Atmospheric correction of visible to middle-infrared EOS-MODIS data over land surfaces: Background, operational algorithm and validation. J. Geophys. Res. Atmos. 1997, 102, 17131–17141. [Google Scholar] [CrossRef]
- Bunting, P.; Clewley, D. Atmospheric and Radiometric Correction of Satellite Imagery (ARCSI). 2018. Available online: https://remotesensing.info/arcsi/ (accessed on 1 September 2021).
- Cutler, P.M.; Munro, D.S. Visible and near-infrared reflectivity during the ablation period on Peyto Glacier, Alberta, Canada. J. Glaciol. 1996, 42, 333–340. [Google Scholar] [CrossRef][Green Version]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing-definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.L.; Box, J.E.; Todd, J.; Christoffersen, P.; Carr, J.R.; Holt, T.O.; Snooke, N. UAV photogrammetry and structure from motion to assess calving dynamics at Store Glacier, a large outlet draining the Greenland ice sheet. Cryosphere 2015, 9, 1–11. [Google Scholar] [CrossRef]
- Moran, M.S.; Bryant, R.; Thome, K.; Ni, W.; Nouvellon, Y.; Gonzalez-Dugo, M.P.; Qi, J. A refined empirical line approach for reflectance factor retrieval from Landsat-5 TM and Landsat-7 ETM+. Remote Sens. Environ. 2001, 78, 71–82. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Boggs, T.P. Spectral Python (Spy): Python module for hyperspectral image processing. Available online: https://github.com/spectralpython/spectral (accessed on 25 September 2017).
- Liang, S.L. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Rippin, D.M.; Pomfret, A.; King, N. High resolution mapping of supra-glacial drainage pathways reveals link between micro-channel drainage density, surface roughness and surface reflectance. Earth Surf. Proc. Land. 2015, 40, 1279–1290. [Google Scholar] [CrossRef]
- Huss, M.; Zemp, M.; Joerg, P.C.; Salzmann, N. High uncertainty in 21st century runoff projections from glacierized basins. J. Hydrol. 2014, 510, 35–48. [Google Scholar] [CrossRef]
- Oerlemans, J. Glaciers and Climate Change; CRC Press—A.A. Balkema Publishers: Abingdon, UK, 2001. [Google Scholar]
- Reeh, N. Parameterization of melt rate and surface temperature in the Greenland ice sheet. Polarforschung 1991, 59, 113–128. [Google Scholar]
- Konzelmann, T.; Ohmura, A. Radiative fluxes and their impact on the energy-balance of the Greenland Ice-Sheet. J. Glaciol. 1995, 41, 490–502. [Google Scholar] [CrossRef][Green Version]
- Marshall, S.J.; Miller, K. Seasonal and interannual variability of melt-season albedo at Haig Glacier, Canadian Rocky Mountains. Cryosphere 2020, 14, 3249–3267. [Google Scholar] [CrossRef]
- Knap, W.H.; Brock, B.W.; Oerlemans, J.; Willis, I.C. Comparison of Landsat TM-derived and ground-based albedos of Haut Glacier d’Arolla, Switzerland. Int. J. Remote Sens. 1999, 20, 3293–3310. [Google Scholar] [CrossRef]
- Bartlett, J.S.; Ciotti, A.M.; Davis, R.F.; Cullen, J.J. The spectral effects of clouds on solar irradiance. J. Geophys. Res. Oceans 1998, 103, 31017–31031. [Google Scholar] [CrossRef]
- Müller, F.; Keeler, C.M. Errors in short-term ablation measurements on melting ice surfaces. J. Glaciol. 1969, 8, 91–105. [Google Scholar] [CrossRef]
- Cook, J.M.; Hodson, A.J.; Anesio, A.M.; Hanna, E.; Yallop, M.; Stibal, M.; Telling, J.; Huybrechts, P. An improved estimate of microbially mediated carbon fluxes from the Greenland ice sheet. J. Glaciol. 2012, 58, 1098–1108. [Google Scholar] [CrossRef]
- Burkhart, J.F.; Kylling, A.; Schaaf, C.B.; Wang, Z.S.; Bogren, W.; Storvold, R.; Solbo, S.; Pedersen, C.A.; Gerland, S. Unmanned aerial system nadir reflectance and MODIS nadir BRDF-adjusted surface reflectances intercompared over Greenland. Cryosphere 2017, 11, 1575–1589. [Google Scholar] [CrossRef]
- Naegeli, K.; Damm, A.; Huss, M.; Schaepman, M.; Hoelzle, M. Imaging spectroscopy to assess the composition of ice surface materials and their impact on glacier mass balance. Remote Sens. Environ. 2015, 168, 388–402. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995; Volume 289. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Wehrle, A.; Box, J.E.; Niwano, M.; Anesio, A.M.; Fausto, R.S. Greenland bare-ice albedo from PROMICE automatic weather station measurements and Sentinel-3 satellite observations. GEUS Bull. 2021, 47, 5284. [Google Scholar] [CrossRef]
- Stroeve, J.; Box, J.E.; Wang, Z.S.; Schaaf, C.; Barrett, A. Re-evaluation of MODIS MCD43 Greenland albedo accuracy and trends. Remote Sens. Environ. 2013, 138, 199–214. [Google Scholar] [CrossRef]
- Hartl, L.; Felbauer, L.; Schwaizer, G.; Fischer, A. Small-scale spatial variability in bare-ice reflectance at Jamtalferner, Austria. Cryosphere 2020, 14, 4063–4081. [Google Scholar] [CrossRef]
- Podgorny, I.; Lubin, D.; Perovich, D.K. Monte Carlo study of UAV-measurable albedo over Arctic sea ice. J. Atmos. Ocean. Tech. 2018, 35, 57–66. [Google Scholar] [CrossRef]
- Alexander, P.M.; Tedesco, M.; Fettweis, X.; van de Wal, R.S.W.; Smeets, C.J.P.P.; van den Broeke, M.R. Assessing spatio-temporal variability and trends in modelled and measured Greenland Ice Sheet albedo (2000–2013). Cryosphere 2014, 8, 2293–2312. [Google Scholar] [CrossRef]
- Delhasse, A.; Kittel, C.; Amory, C.; Hofer, S.; van As, D.; Fausto, R.S.; Fettweis, X. Brief communication: Evaluation of the near-surface climate in ERA5 over the Greenland Ice Sheet. Cryosphere 2020, 14, 957–965. [Google Scholar] [CrossRef]
- Hanna, E.; Hall, R.J.; Cropper, T.E.; Ballinger, T.J.; Wake, L.; Mote, T.; Cappelen, J. Greenland blocking index daily series 1851-2015: Analysis of changes in extremes and links with North Atlantic and UK climate variability and change. Int. J. Climatol. 2018, 38, 3546–3564. [Google Scholar] [CrossRef]

| Albedo Estimate | Albedo Parameterization | α Value in 2016 | c1 | c2 | NSE | d | MAE | RMSE |
|---|---|---|---|---|---|---|---|---|
| Fixed bare-ice albedo | 0.475 | 24.8 | −36.9 | |||||
| 0.936 | 0.984 | 0.092 | 0.106 | |||||
| (0.231) | (−0.343) | (0.0005) | (0.0006) | |||||
| MOD10A1 series minimum | 0.240 | 20.0 | −96.3 | |||||
| 0.956 | 0.990 | 0.069 | 0.087 | |||||
| (0.123) | (−0.320 | (0.0006) | (0.0005) | |||||
| MOD10A1 series lowest 10% values | 0.254 | 20.3 | −92.8 | |||||
| 0.957 | 0.990 | 0.069 | 0.006 | |||||
| (0.131) | (−0.323) | (0.0006) | (0.0007) | |||||
| MOD10A1 bare-ice series mean | 0.329 | 21.8 | −73.7 | |||||
| 0.956 | 0.990 | 0.073 | 0.033 | |||||
| (0.169) | (−0.330) | (0.0005) | (0.0007) | |||||
| Interpolated MOD10A1 bare-ice series mean | 0.345 | 18.9 | −80.0 | |||||
| 0.955 | 0.989 | 0.075 | 0.006 | |||||
| (0.175) | (−0.328) | (0.0005) | (0.0007) | |||||
| MOD10A1 interpolated daily series | 0.240–0.565 | 22.1 | −69.8 | |||||
| 0.960 | 0.991 | 0.068 | 0.020 | |||||
| (0.140) | (−0.300) | (0.0005) | (0.0006) | |||||
| Simulated MOD10A1 8-day composite | 0.260–0.48 | 17.4 | −78.7 | |||||
| 0.957 | 0.990 | 0.071 | 0.006 | |||||
| (0.116) | (−0.356) | (0.0006) | (0.0007) | |||||
| Cosine seasonal variation | 0.277–0.530 | 16.6 | −74.9 | |||||
| 0.961 | 0.991 | 0.067 | 0.009 | |||||
| (0.158) | (−0.290) | (0.0005) | (0.0007) | |||||
| Cosine seasonal variation inc. noise (E) | 0.262–0.542 | 17.1 | −75.9 | |||||
| 0.962 | 0.991 | 0.066 | 0.003 | |||||
| (0.166) | (−0.262) | (0.0005) | (0.0007) | |||||
| Physically related to ΣPDD | 0.292–0.447 | 17.1 | −76.5 | |||||
| 0.960 | 0.991 | 0.068 | 0.013 | |||||
| (0.171) | (−0.295) | (0.0005) | (0.0007) | |||||
| Physically related to ΣPDD | 0.271–0.420 | 17.2 | −70.9 | |||||
| 0.961 | 0.991 | 0.067 | 0.010 | |||||
| (0.162) | (−0.291) | (0.0005) | (0.0007) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irvine-Fynn, T.D.L.; Bunting, P.; Cook, J.M.; Hubbard, A.; Barrand, N.E.; Hanna, E.; Hardy, A.J.; Hodson, A.J.; Holt, T.O.; Huss, M.; et al. Temporal Variability of Surface Reflectance Supersedes Spatial Resolution in Defining Greenland’s Bare-Ice Albedo. Remote Sens. 2022, 14, 62. https://doi.org/10.3390/rs14010062
Irvine-Fynn TDL, Bunting P, Cook JM, Hubbard A, Barrand NE, Hanna E, Hardy AJ, Hodson AJ, Holt TO, Huss M, et al. Temporal Variability of Surface Reflectance Supersedes Spatial Resolution in Defining Greenland’s Bare-Ice Albedo. Remote Sensing. 2022; 14(1):62. https://doi.org/10.3390/rs14010062
Chicago/Turabian StyleIrvine-Fynn, Tristram D. L., Pete Bunting, Joseph M. Cook, Alun Hubbard, Nicholas E. Barrand, Edward Hanna, Andy J. Hardy, Andrew J. Hodson, Tom O. Holt, Matthias Huss, and et al. 2022. "Temporal Variability of Surface Reflectance Supersedes Spatial Resolution in Defining Greenland’s Bare-Ice Albedo" Remote Sensing 14, no. 1: 62. https://doi.org/10.3390/rs14010062
APA StyleIrvine-Fynn, T. D. L., Bunting, P., Cook, J. M., Hubbard, A., Barrand, N. E., Hanna, E., Hardy, A. J., Hodson, A. J., Holt, T. O., Huss, M., McQuaid, J. B., Nilsson, J., Naegeli, K., Roberts, O., Ryan, J. C., Tedstone, A. J., Tranter, M., & Williamson, C. J. (2022). Temporal Variability of Surface Reflectance Supersedes Spatial Resolution in Defining Greenland’s Bare-Ice Albedo. Remote Sensing, 14(1), 62. https://doi.org/10.3390/rs14010062