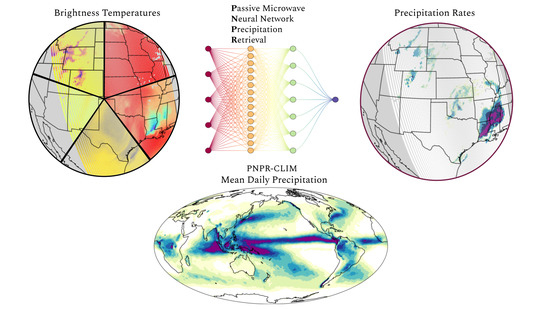
The Passive Microwave Neural Network Precipitation Retrieval Algorithm for Climate Applications (PNPR-CLIM): Design and Verification
Abstract
1. Introduction
2. Materials and Methods
2.1. Neural Networks
2.2. Input Data
2.3. GPM-CO Dual-Frequency Precipitation Radar
2.4. Datasets and Products for the Quality Assessment
2.4.1. MRMS
2.4.2. GPCP
2.4.3. GPROF
2.5. Regional and Global Verification Methodology
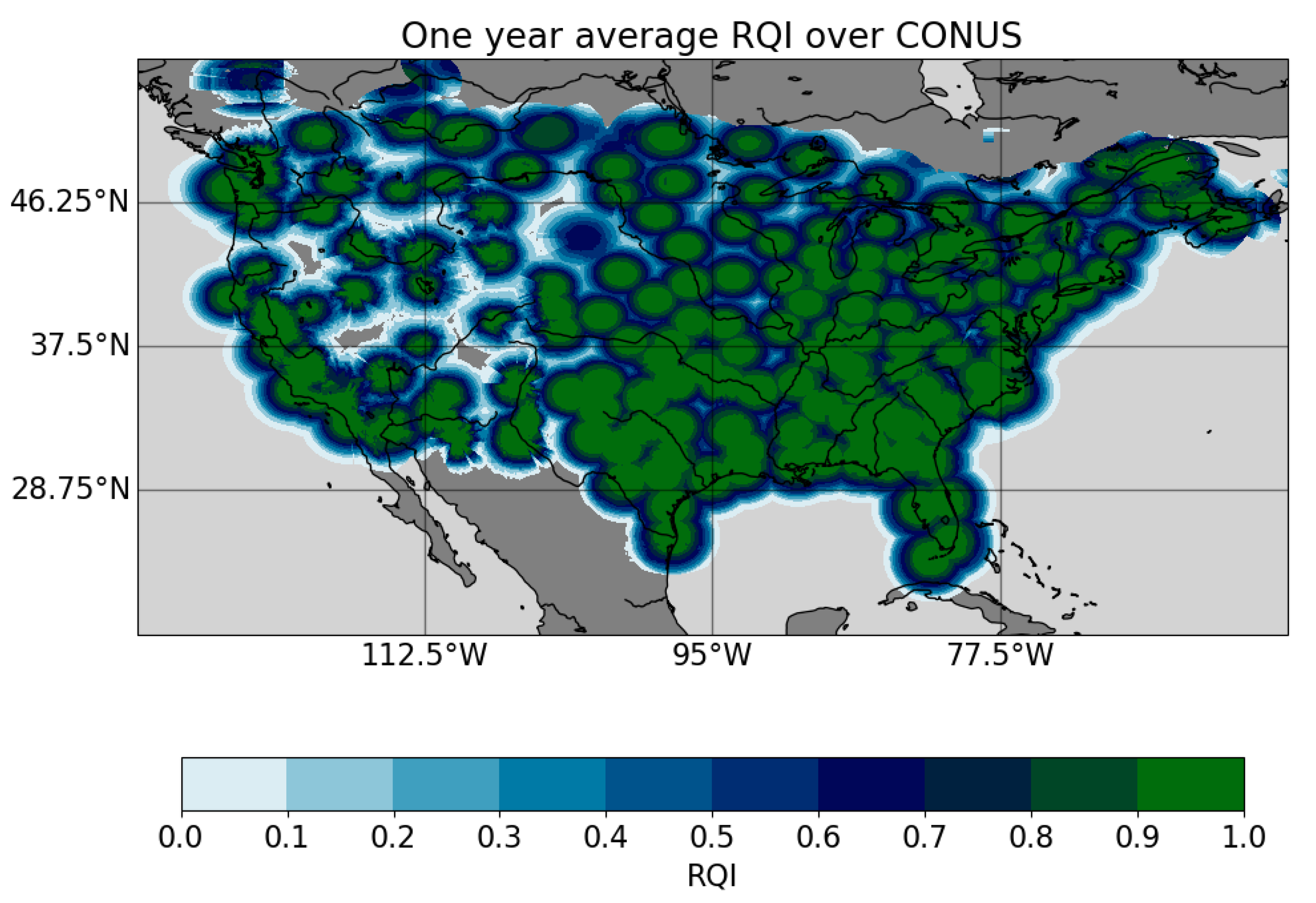
2.5.1. Regional Verification Methodology
2.5.2. Global Verification Methodology
2.6. Statistical Scores
3. Algorithm Description
3.1. The MHS-DPR Coincidence Dataset
PNPR-CLIM Design
4. Results and Discussion
4.1. Global Verification with DPR
4.1.1. PCM Performances
4.1.2. PEM Performances
4.2. Regional Verification over CONUS
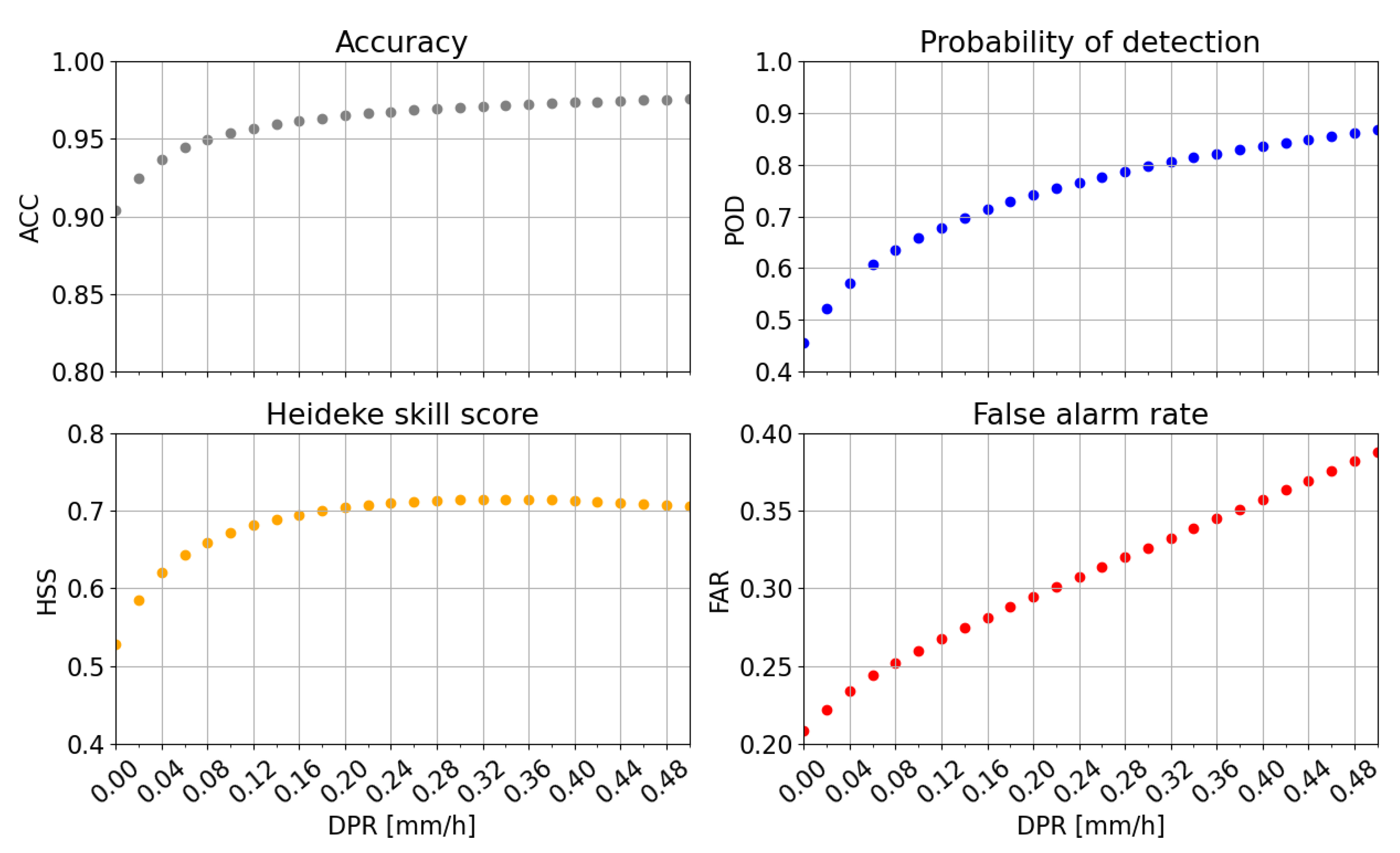
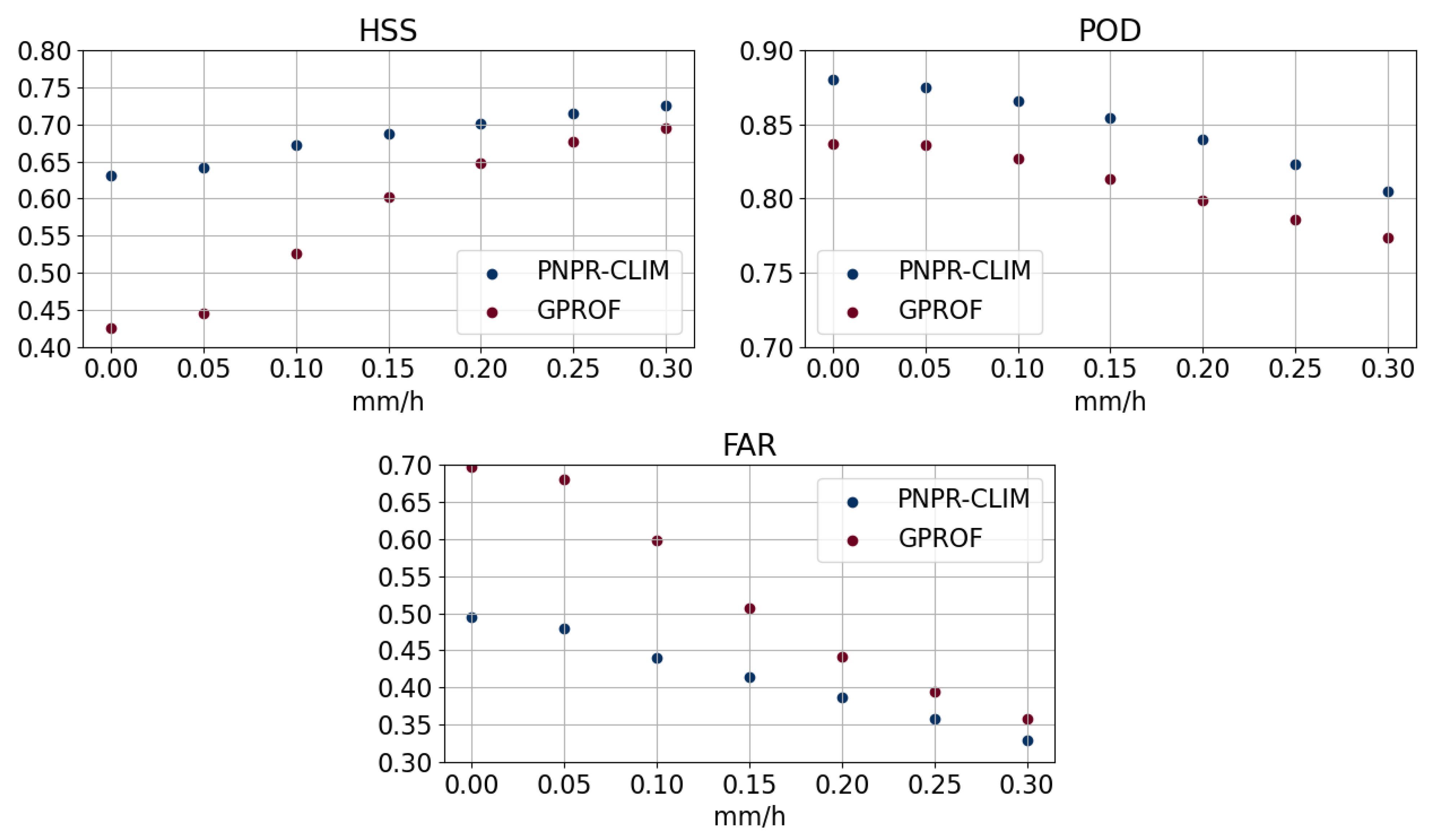
4.2.1. Precipitation Detection
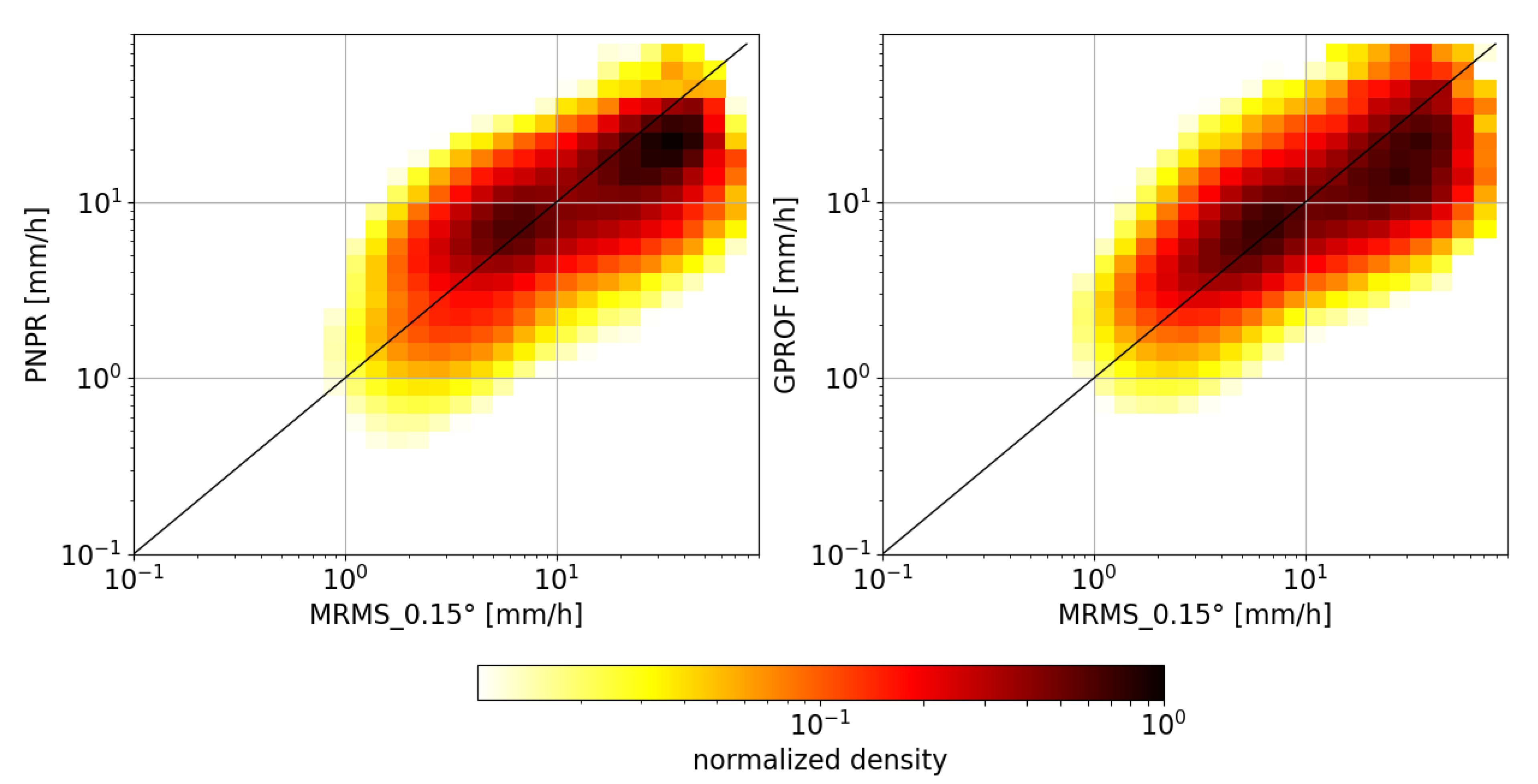
4.2.2. Precipitation Estimate
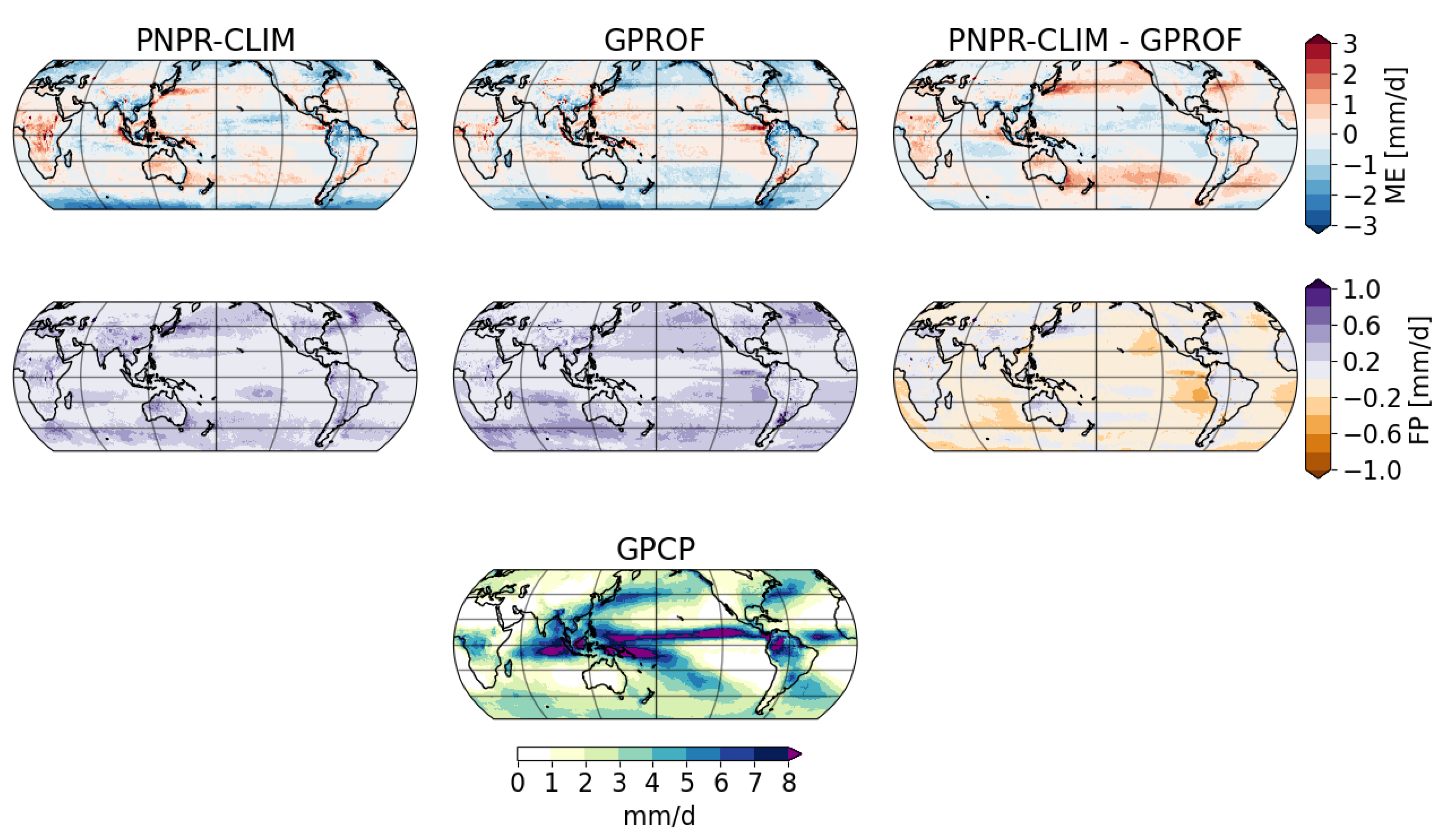
4.3. Global Comparison of PNPR-CLIM and GPROF with GPCP
4.3.1. Mean Errors
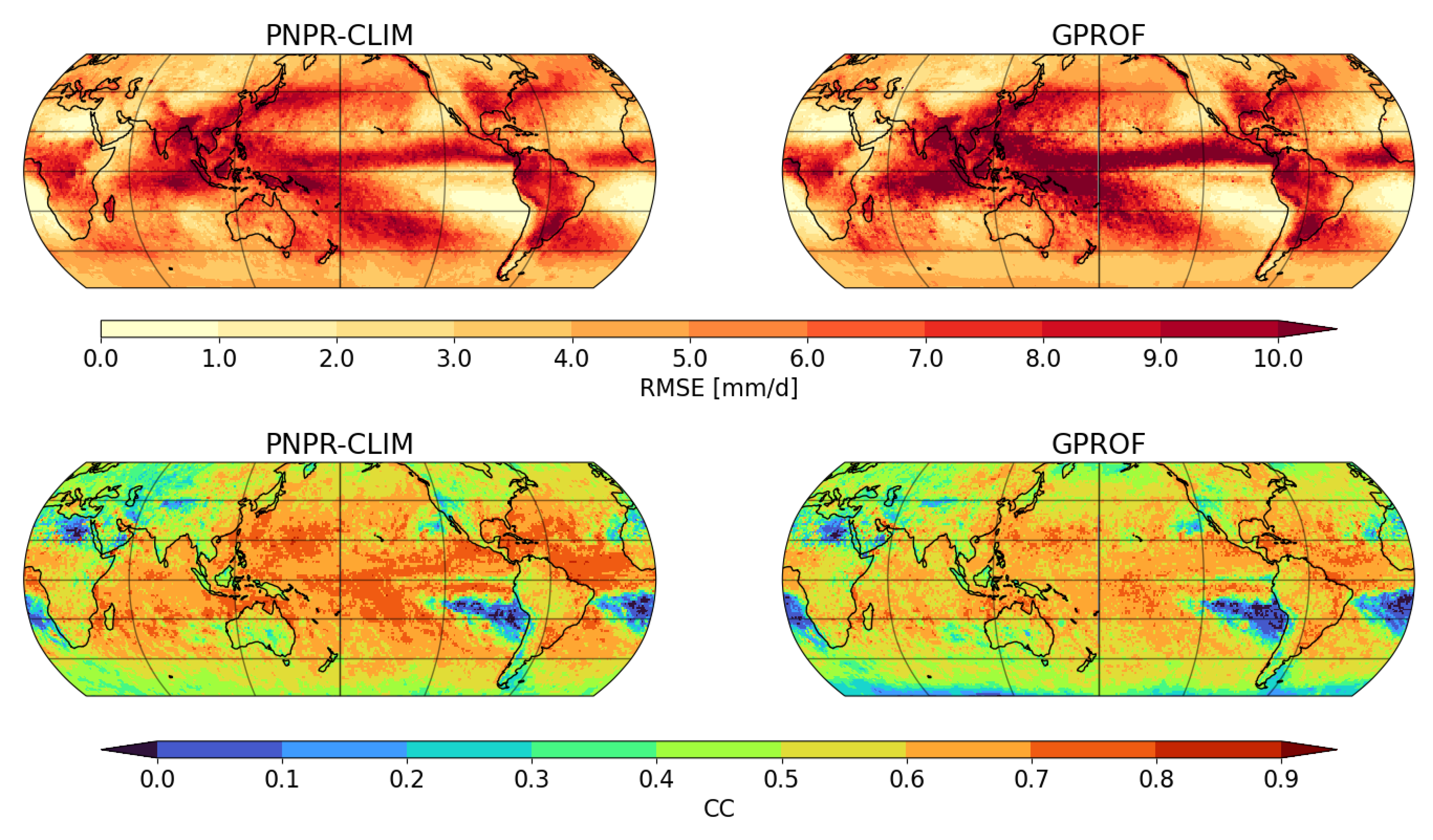
4.3.2. CC and RMSE
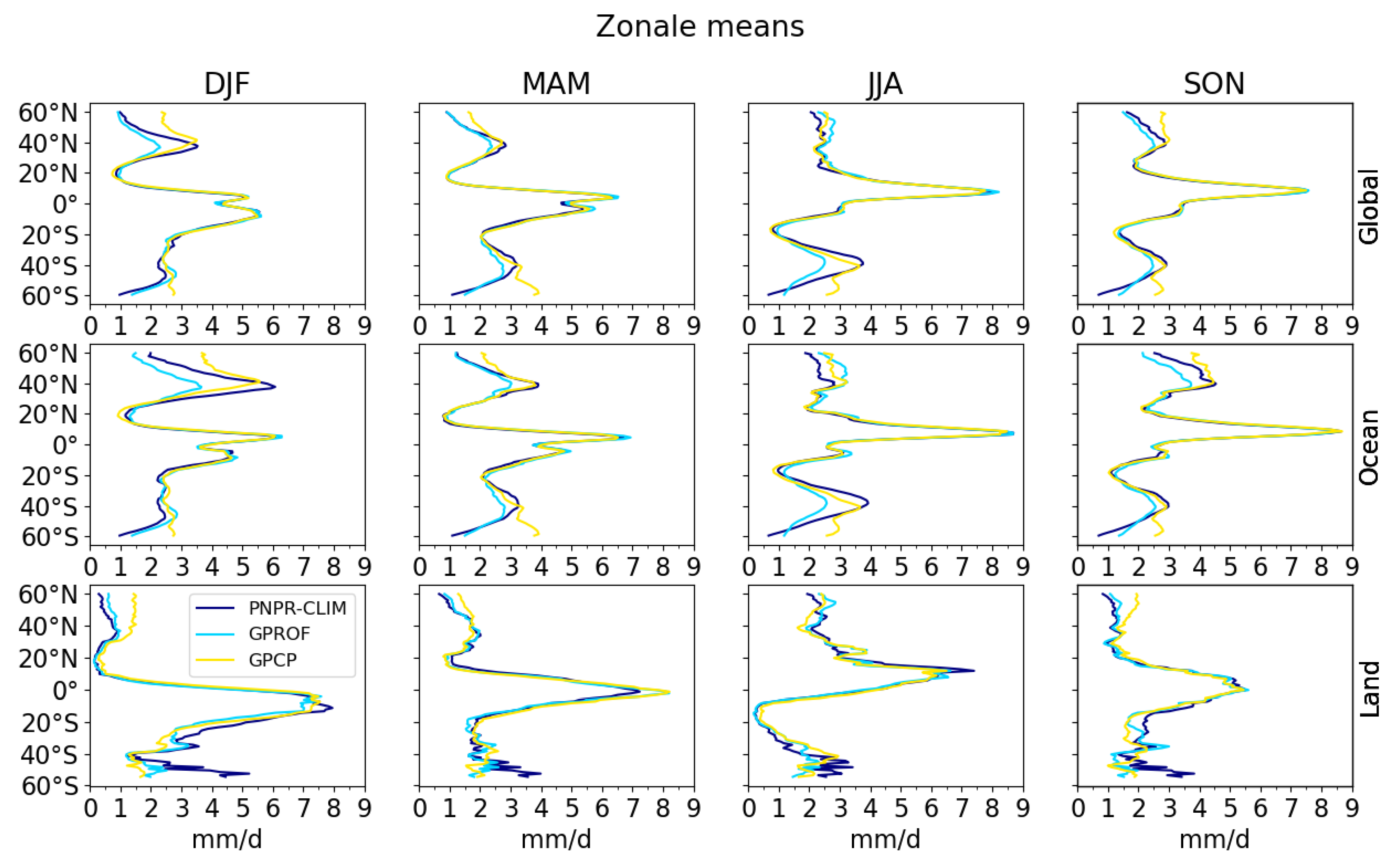
4.4. Zonal Means
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Lin, X.; Hou, A.Y. Evaluation of coincident passive microwave rainfall estimates using TRMM PR and ground measurements as references. J. Appl. Meteorol. Climatol. 2008, 47, 3170–3187. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.l.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Iturbide-Sanchez, F.; Boukabara, S.A.; Chen, R.; Garrett, K.; Grassotti, C.; Chen, W.; Weng, F. Assessment of a variational inversion system for rainfall rate over land and water surfaces. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3311–3333. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Kidd, C.; Matsui, T.; Chern, J.; Mohr, K.; Kummerow, C.; Randel, D. Global precipitation estimates from cross-track passive microwave observations using a physically based retrieval scheme. J. Hydrometeorol. 2016, 17, 383–400. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; Van Dijk, A.I.; McVicar, T.R.; Adler, R.F. MSWep v2 Global 3-hourly 0.1° precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Levizzani, V.; Cattani, E. Satellite Remote Sensing of Precipitation and the Terrestrial Water Cycle in a Changing Climate. Remote Sens. 2019, 11, 2301. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, B.; Ma, Z.; Chen, X.; Liu, D.; Qiu, J. Comprehensive comparisons of state-of-the-art gridded precipitation estimates for hydrological applications over southern China. Remote Sens. 2020, 12, 3997. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Kucera, P.A.; Lapeta, B. Leading Efforts to Improve Global Quantitative Precipitation Estimation. Bull. Am. Meteorol. Soc. 2014, 95, 26–29. [Google Scholar] [CrossRef]
- Wilheit, T. Algorithms for the retrieval of rainfall from passive microwave measurements. Remote Sens. Rev. 1994, 11, 163–194. [Google Scholar] [CrossRef]
- Weng, F.; Grody, N.C. Retrieval of ice cloud parameters using a microwave imaging radiometer. J. Atmos. Sci. 2000, 57, 1069–1081. [Google Scholar] [CrossRef]
- Bennartz, R.; Petty, G.W. The sensitivity of microwave remote sensing observations of precipitation to ice particle size distributions. J. Appl. Meteorol. 2001, 40, 345–364. [Google Scholar] [CrossRef]
- Bauer, P.; Moreau, E.; Di Michele, S. Hydrometeor retrieval accuracy using microwave window and sounding channel observations. J. Appl. Meteorol. 2005, 44, 1016–1032. [Google Scholar] [CrossRef]
- Kidd, C.; Matsui, T.; Ringerud, S. Precipitation Retrievals from Passive Microwave Cross-Track Sensors: The Precipitation Retrieval and Profiling Scheme. Remote Sens. 2021, 13, 947. [Google Scholar] [CrossRef]
- Wang, J.R.; Zhan, J.; Racette, P. Storm-Associated Microwave Radiometric Signatures in the Frequency Range of 90–220 GHz. J. Atmos. Ocean. Technol. 1997, 14, 13–31. [Google Scholar] [CrossRef]
- Staelin, D.H.; Chen, F.W. Precipitation observations near 54 and 183 GHz using the NOAA-15 satellite. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2322–2332. [Google Scholar] [CrossRef]
- Blackwell, W.; Chen, F. Neural Network Applications in High-Resolution Atmospheric Remote Sensing. Licoln Lab. J. 2005, 15, 299–322. [Google Scholar]
- Burns, B.A. Effects of precipitation and cloud ice on brightness temperatures in AMSU moisture channels. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1429–1437. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Weng, F.; Grody, N.C.; Zhao, L.; Meng, H.; Kongoli, C.; Pellegrino, P.; Qiu, S.; Dean, C. NOAA operational hydrological products derived from the advanced microwave sounding unit. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1036–1049. [Google Scholar] [CrossRef]
- Hong, G.; Heygster, G.; Miao, J.; Kunzi, K. Detection of tropical deep convective clouds from AMSU-B water vapor channels measurements. J. Geophys. Res. D Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Hong, G.; Heygster, G.; Notholt, J.; Buehler, S.A. Interannual to diurnal variations in tropical and subtropical deep convective clouds and convective overshooting from seven years of AMSU-B measurements. J. Clim. 2008, 21, 4168–4189. [Google Scholar] [CrossRef]
- Funatsu, B.M.; Claud, C.; Chaboureau, J.P. Potential of Advanced Microwave Sounding Unit to identify precipitating systems and associated upper-level features in the Mediterranean region: Case studies. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Funatsu, B.M.; Claud, C.; Chaboureau, J.P. Comparison between the large-scale environments of moderate and intense precipitating systems in the Mediterranean region. Mon. Weather Rev. 2009, 137, 3933–3959. [Google Scholar] [CrossRef]
- Laviola, S.; Levizzani, V. The 183-WSL fast rain rate retrieval algorithm. Part I: Retrieval design. Atmos. Res. 2011, 99, 443–461. [Google Scholar] [CrossRef]
- Ferraro, R. The Status of the NOAA/NESDIS Operational AMSU Precipitation Algorithm. In Proceedings of the 2nd Workshop of the International Precipitation Working Group, Monterey, CA, USA, 25–28 October 2004; p. 9. [Google Scholar]
- Qiu, S.; Pellegrino, P.; Ferraro, R.; Zhao, L. The improved AMSU rain-rate algorithm and its evaluation for a cool season event in the western United States. Weather Forecast. 2005, 20, 761–774. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Tzeng, Y.C.; Chen, K.S. A neural-network approach to radiometric sensing of land-surface parameters. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2718–2724. [Google Scholar] [CrossRef]
- Aires, F.; Prigent, C.; Rossow, W.B.; Rothstein, M. A new neural network approach including first guess for retrieval of atmospheric water vapor, cloud liquid water path, surface temperature, and emissivities over land from satellite microwave observations. J. Geophys. Res. Atmos. 2001, 106, 14887–17907. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Surussavadee, C.; Staelin, D. Global Millimeter-Wave Precipitation Retrievals Trained with a Cloud-Resolving Numerical Weather Prediction Model, Part I: Retrieval Design. IEEE Trans. Geosci. Remote Sens. 2008, 46, 99–108. [Google Scholar] [CrossRef]
- Mahesh, C.; Prakash, S.; Sathiyamoorthy, V.; Gairola, R.M. Artificial neural network based microwave precipitation estimation using scattering index and polarization corrected temperature. Atmos. Res. 2011, 102, 358–364. [Google Scholar] [CrossRef]
- Sanò, P.; Panegrossi, G.; Casella, D.; Di Paola, F.; Milani, L.; Mugnai, A.; Petracca, M.; Dietrich, S. The Passive microwave Neural network Precipitation Retrieval (PNPR) algorithm for AMSU/MHS observations: Description and application to European case studies. Atmos. Meas. Tech. 2015, 8, 837–857. [Google Scholar] [CrossRef]
- Sanò, P.; Panegrossi, G.; Casella, D.; Marra, A.C.; Di Paola, F.; Dietrich, S. The new Passive microwave Neural network Precipitation Retrieval (PNPR) algorithm for the cross-track scanning ATMS radiometer: Description and verification study over Europe and Africa using GPM and TRMM spaceborne radars. Atmos. Meas. Tech. 2016, 9, 5441–5460. [Google Scholar] [CrossRef]
- Sanò, P.; Panegrossi, G.; Casella, D.; Marra, A.C.; D’Adderio, L.P.; Rysman, J.F.; Dietrich, S. The passive microwave neural network precipitation retrieval (PNPR) algorithm for the CONICAL scanning Global Microwave Imager (GMI) radiometer. Remote Sens. 2018, 10, 1122. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Navarro, A.; Levizzani, V.; García-Ortega, E.; Huffman, G.J.; Kidd, C.; Kucera, P.A.; Kummerow, C.D.; Masunaga, H.; Petersen, W.A.; et al. Global precipitation measurements for validating climate models. Atmos. Res. 2017, 197, 1–20. [Google Scholar] [CrossRef]
- Marzano, F.S.; Mugnai, A.; Panegrossi, G.; Pierdicca, N.; Smith, E.A.; Turk, J. Bayesian estimation of precipitating cloud parameters from combined measurements of spaceborne microwave radiometer and radar. IEEE Trans. Geosci. Remote Sens. 1999, 37, 596–613. [Google Scholar] [CrossRef]
- Kummerow, C.; Poyner, P.; Berg, W.; Thomas-Stahle, J. The Effects of Rainfall Inhomogeneity on Climate Variability of Rainfall Estimated from Passive Microwave Sensors. J. Atmos. Ocean. Technol. 2004, 21, 624–638. [Google Scholar] [CrossRef][Green Version]
- Kummerow, C.D.; Randel, D.L.; Kulie, M.; Wang, N.Y.; Ferraro, R.; Munchak, S.J.; Petkovic, V. The Evolution of the Goddard Profiling Algorithm to a Fully Parametric Scheme. J. Atmos. Ocean. Technol. 2015, 32, 2265–2280. [Google Scholar] [CrossRef]
- Sanò, P.; Casella, D.; Mugnai, A.; Schiavon, G.; Smith, E.A.; Tripoli, G.J. Transitioning From CRD to CDRD in Bayesian Retrieval of Rainfall From Satellite Passive Microwave Measurements: Part 1. Algorithm Description and Testing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4119–4143. [Google Scholar] [CrossRef]
- Casella, D.; Panegrossi, G.; Sanò, P.; Dietrich, S.; Mugnai, A.; Smith, E.A.; Tripoli, G.J.; Formenton, M.; Di Paola, F.; Leung, W.H.; et al. Transitioning From CRD to CDRD in Bayesian Retrieval of Rainfall From Satellite Passive Microwave Measurements: Part 2. Overcoming Database Profile Selection Ambiguity by Consideration of Meteorological Control on Microphysics. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4650–4671. [Google Scholar] [CrossRef]
- Panegrossi, G.; Dietrich, S.; Marzano, F.S.; Mugnai, A.; Smith, E.A.; Xiang, X.; Tripoli, G.J.; Wang, P.K.; Poiares Baptista, J.P. Use of cloud model microphysics for passive microwave-based precipitation retrieval: Significance of consistency between model and measurement manifolds. J. Atmos. Sci. 1998, 55, 1644–1673. [Google Scholar] [CrossRef]
- Grecu, M.; Anagnostou, E.N. Overland precipitation estimation from TRMM passive microwave observations. J. Appl. Meteorol. 2001, 40, 1367–1380. [Google Scholar] [CrossRef]
- Casella, D.; Do Amaral, L.M.C.; Dietrich, S.; Marra, A.C.; Sano, P.; Panegrossi, G. The Cloud Dynamics and Radiation Database Algorithm for AMSR2: Exploitation of the GPM Observational Dataset for Operational Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3985–4001. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The global precipitation measurement (GPM) mission for science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Kidd, C.; Takayabu, Y.N.; Skofronick-Jackson, G.M.; Huffman, G.J.; Braun, S.A.; Kubota, T.; Turk, F.J. The Global Precipitation Measurement (GPM) Mission. In Satellite Precipitation Measurement: Volume 1; Springer International Publishing: Cham, Switzerland, 2020; Volume 67, pp. 3–23. [Google Scholar] [CrossRef]
- Iguchi, T. Dual-Frequency Precipitation Radar (DPR) on the Global Precipitation Measurement (GPM) Mission’s Core Observatory. In Satellite Precipitation Measurement: Volume 1; Springer International Publishing: Cham, Switzerland, 2020; Volume 1, pp. 183–192. [Google Scholar] [CrossRef]
- Speirs, P.; Gabella, M.; Berne, A. A comparison between the GPM dual-frequency precipitation radar and ground-based radar precipitation rate estimates in the Swiss Alps and Plateau. J. Hydrometeorol. 2017, 18, 1247–1269. [Google Scholar] [CrossRef]
- Biswas, S.K.; Chandrasekar, V. Cross-validation of observations between the GPM dual-frequency precipitation radar and ground based dual-polarization radars. Remote Sens. 2018, 10, 1773. [Google Scholar] [CrossRef]
- Petracca, M.; D’Adderio, L.P.; Porcù, F.; Vulpiani, G.; Sebastianelli, S.; Puca, S. Validation of GPM Dual-Frequency Precipitation Radar (DPR) rainfall products over Italy. J. Hydrometeorol. 2018, 19, 907–925. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Le, M. DPR Dual-Frequency Precipitation Classification. In Satellite Precipitation Measurement: Volume 1; Springer International Publishing: Cham, Switzerland, 2020; Volume 67, pp. 193–210. [Google Scholar] [CrossRef]
- Le, M.; Chandrasekar, V. Ground validation of surface snowfall algorithm in GPM dual-frequency precipitation radar. J. Atmos. Ocean. Technol. 2019, 36, 607–619. [Google Scholar] [CrossRef]
- Pejcic, V.; Garfias, P.S.; Mühlbauer, K.; Trömel, S.; Simmer, C. Comparison between precipitation estimates of ground-based weather radar composites and GPM’s DPR rainfall product over Germany. Meteorol. Z. 2020, 29, 451–466. [Google Scholar] [CrossRef]
- Brogniez, H.; English, S.; Mahfouf, J.F.; Behrendt, A.; Berg, W.; Boukabara, S.; Buehler, S.A.; Chambon, P.; Gambacorta, A.; Geer, A.; et al. A review of sources of systematic errors and uncertainties in observations and simulations at 183 GHz. Atmos. Meas. Tech. 2016, 9, 2207–2221. [Google Scholar] [CrossRef]
- Woolliams, E.; Mittaz, J.; Chris Merchant, C.; Dila, A. Harmonisation and Recalibration: A FIDUCEO perspective. GSICS Q. Summer Issue 2016, 10, 1–2. [Google Scholar] [CrossRef]
- Hans, I.; Burgdorf, M.; John, V.O.; Mittaz, J.; Buehler, S.A. Noise performance of microwave humidity sounders over their lifetime. Atmos. Meas. Tech. 2017, 10, 4927–4945. [Google Scholar] [CrossRef]
- Merchant, C.J.; Paul, F.; Popp, T.; Ablain, M.; Bontemps, S.; Defourny, P.; Hollmann, R.; Lavergne, T.; Laeng, A.; De Leeuw, G.; et al. Uncertainty information in climate data records from Earth observation. Earth Syst. Sci. Data 2017, 9, 511–527. [Google Scholar] [CrossRef]
- Burgdorf, M.; Hans, I.; Prange, M.; Lang, T.; Buehler, S.A. Inter-channel uniformity of a microwave sounder in space. Atmos. Meas. Tech. 2018, 11, 4005–4014. [Google Scholar] [CrossRef]
- Mugnai, A.; Smith, E.A.; Tripoli, G.J.; Bizzarri, B.; Casella, D.; Dietrich, S.; Di Paola, F.; Panegrossi, G.; Sanò, P. CDRD and PNPR satellite passive microwave precipitation retrieval algorithms: EuroTRMM/EURAINSAT origins and H-SAF operations. Nat. Hazards Earth Syst. Sci. 2013, 13, 887–912. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Rossow, W.B. Land surface microwave emissivities over the global for a decade. Bull. Am. Meteorol. Soc. 2006, 87, 1573–1584. [Google Scholar] [CrossRef]
- Ebtehaj, A.M.; Kummerow, C.D. Microwave retrievals of terrestrial precipitation over snow-covered surfaces: A lesson from the GPM satellite. Geophys. Res. Lett. 2017, 44, 6154–6162. [Google Scholar] [CrossRef]
- Rysman, J.F.; Panegrossi, G.; Sanò, P.; Marra, A.C.; Dietrich, S.; Milani, L.; Kulie, M.S. SLALOM: An all-surface snow water path retrieval algorithm for the GPM microwave imager. Remote Sens. 2018, 10, 1278. [Google Scholar] [CrossRef]
- Camplani, A.; Casella, D.; Sanò, P.; Panegrossi, G. The Passive microwave Empirical cold Surface Classification Algorithm (PESCA): Application to GMI and ATMS. J. Hyrometorol. 2021. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cocks, S.; Martinaitis, S.; et al. Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- Adler, R.; Wang, J.J.; Sapiano, M.; Huffman, G.; Bolvin, D.; Nelkin, E. Global Precipitation Climatology Project (GPCP) Climate Data Record (CDR), Version 1.3 (Daily); NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, J.; Simpson, M.; Arthur, A.; Grams, H.; Wang, Y.; Langston, C. Updates on the Radar Data Quality Control in the MRMS Quantitative Precipitation Estimation System. J. Atmos. Ocean. Technol. 2020, 37, 1521–1537. [Google Scholar] [CrossRef]
- Kummerow, C.; Giglio, L. A passive microwave technique for estimating rainfall and vertical structure information from space. Part I: Algorithm description. J. Appl. Meteorol. 1994, 33, 3–18. [Google Scholar] [CrossRef]
- Randel, D.L.; Kummerow, C.D.; Ringerud, S. The Goddard Profiling (GPROF) Precipitation Retrieval Algorithm. In Satellite Precipitation Measurement: Volume 1; Springer International Publishing: Cham, Switzerland, 2020; Volume 1, pp. 141–152. [Google Scholar] [CrossRef]
- Aires, F.; Prigent, C.; Bernardo, F.; Jiménez, C.; Saunders, R.; Brunel, P. A Tool to Estimate Land-Surface Emissivities at Microwave frequencies (TELSEM) for use in numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 137, 690–699. [Google Scholar] [CrossRef]
- Romanov, P.; Gutman, G.; Csiszar, I. Automated Monitoring of Snow Cover over North America with Multispectral Satellite Data. J. Appl. Meteorol. 2000, 39, 1866–1880. [Google Scholar] [CrossRef]
- Sims, E.M.; Liu, G. A Parameterization of the Probability of Snow–Rain Transition. J. Hydrometeorol. 2015, 16, 1466–1477. [Google Scholar] [CrossRef]
- Kidd, C.; Tan, J.; Kirstetter, P.E.; Petersen, W.A. Validation of the Version 05 Level 2 precipitation products from the GPM Core Observatory and constellation satellite sensors. Q. J. R. Meteorol. Soc. 2018, 144, 313–328. [Google Scholar] [CrossRef]
- Ciabatta, L.; Marra, A.C.; Panegrossi, G.; Casella, D.; Sanò, P.; Dietrich, S.; Massari, C.; Brocca, L. Daily precipitation estimation through different microwave sensors: Verification study over Italy. J. Hydrol. 2017, 545, 436–450. [Google Scholar] [CrossRef]
- Panegrossi, G.; Casella, D.; Dietrich, S.; Marra, A.C.; Sanò, P.; Mugnai, A.; Baldini, L.; Roberto, N.; Adirosi, E.; Cremonini, R.; et al. Use of the GPM Constellation for Monitoring Heavy Precipitation Events over the Mediterranean Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2733–2753. [Google Scholar] [CrossRef]
- Petković, V.; Kummerow, C.D. Performance of the GPM Passive Microwave Retrieval in the Balkan Flood Event of 2014. J. Hydrometeorol. 2015, 16, 2501–2518. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Elsevier Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2011. [Google Scholar]
- Grecu, M.; Olson, W.S.; Munchak, S.J.; Ringerud, S.; Liao, L.; Haddad, Z.; Kelley, B.L.; McLaughlin, S.F. The GPM Combined Algorithm. J. Atmos. Ocean. Technol. 2016, 33, 2225–2245. [Google Scholar] [CrossRef]
- You, Y.; Petkovic, V.; Tan, J.; Kroodsma, R.; Berg, W.; Kidd, C.; Peters-Lidard, C. Evaluation of V05 Precipitation Estimates from GPM Constellation Radiometers Using KuPR as the Reference. J. Hydrometeorol. 2020, 21, 705–728. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Anders, U.; Korn, O. Model selection in neural networks. Neural Netw. 1999, 12, 309–323. [Google Scholar] [CrossRef]
- Marzban, C. Basic Statistics and Basic AI: Neural Networks. In Artificial Intelligence Methods in the Environmental Sciences; Haupt, S.E., Pasini, A., Marzban, C., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 15–47. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kulie, M.; Milani, L.; Munchak, S.J.; Wood, N.B.; Levizzani, V. Satellite Estimation of Falling Snow: A Global Precipitation Measurement (GPM) Core Observatory Perspective. J. Appl. Meteorol. Climatol. 2019, 58, 1429–1448. [Google Scholar] [CrossRef] [PubMed]
- Behrangi, A.; Christensen, M.; Richardson, M.; Lebsock, M.; Stephens, G.; Huffman, G.J.; Bolvin, D.; Adler, R.F.; Gardner, A.; Lambrigtsen, B.; et al. Status of high-latitude precipitation estimates from observations and reanalyses. J. Geophys. Res. Atmos. 2016, 121, 4468–4486. [Google Scholar] [CrossRef]
- Panegrossi, G.; Casella, D.; Sanò, P.; Camplani, A.; Battaglia, A. Recent Advances and Challenges in Snowfall detection and Estimation. In Precipitation Science; Michaelides, S., Ed.; Elsevier: Radarweg, The Netherlands, 2021. [Google Scholar]
- Edel, L.; Rysman, J.F.; Claud, C.; Palerme, C.; Genthon, C. Potential of Passive Microwave around 183 GHz for Snowfall Detection in the Arctic. Remote Sens. 2019, 11, 2200. [Google Scholar] [CrossRef]
- Rysman, J.F.; Panegrossi, G.; Sanò, P.; Marra, A.C.; Dietrich, S.; Milani, L.; Kulie, M.S.; Casella, D.; Camplani, A.; Claud, C.; et al. Retrieving Surface Snowfall With the GPM Microwave Imager: A New Module for the SLALOM Algorithm. Geophys. Res. Lett. 2019, 46, 13593–13601. [Google Scholar] [CrossRef]
- Adhikari, A.; Ehsani, M.R.; Song, Y.; Behrangi, A. Comparative Assessment of Snowfall Retrieval from Microwave Humidity Sounders Using Machine Learning Methods. Earth Space Sci. 2020, 7. [Google Scholar] [CrossRef]
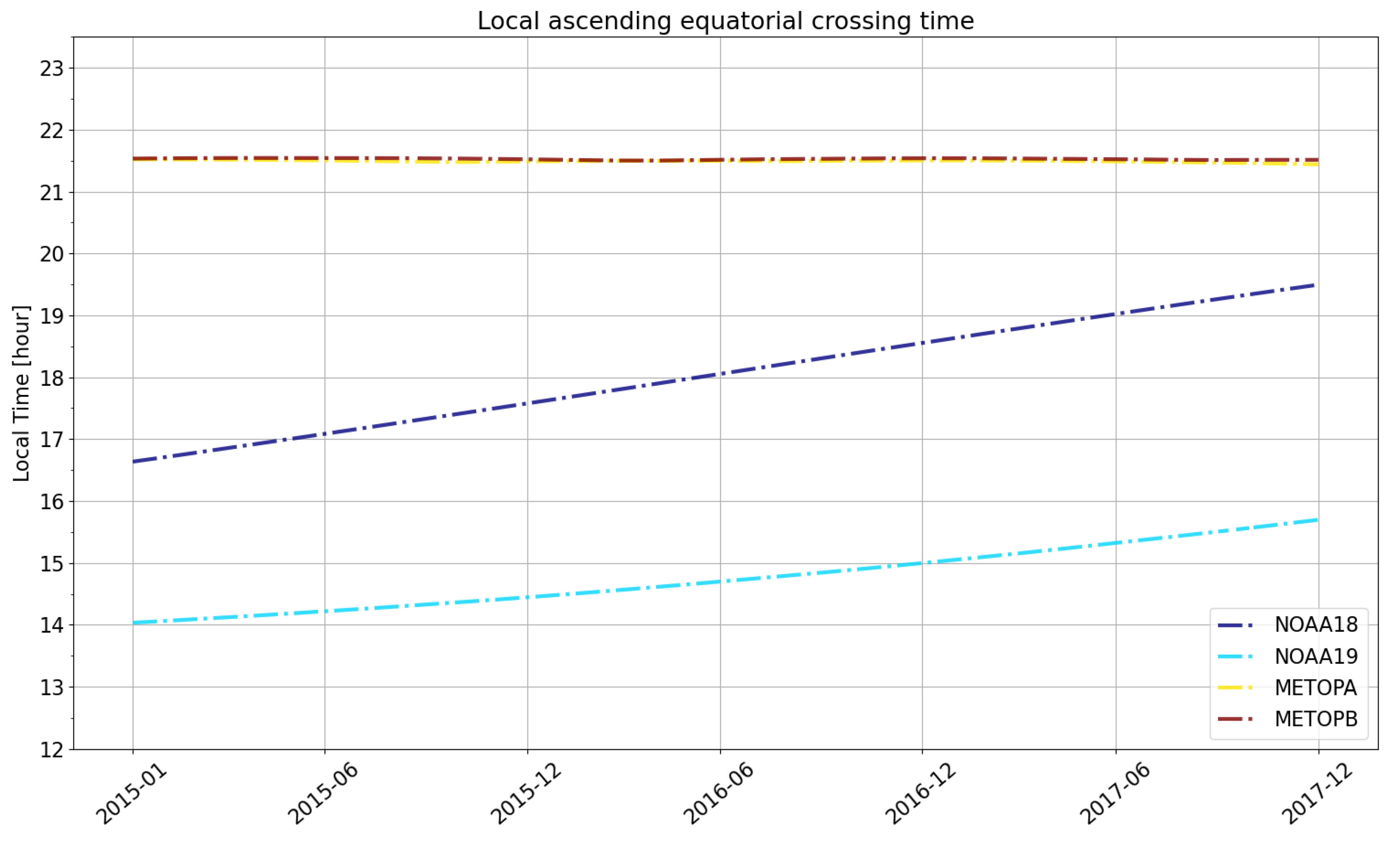

| Satellites | AMSU-B: NOAA-15, NOAA-16, NOAA-17 | |
|---|---|---|
| MHS: NOAA-18, NOAA-19, MetOp-A, MetOp-B, MetOp-C | ||
| MHS/AMSU-B Central Frequency (GHz) | MHS/AMSU-B Channel Bandwidth (MHz) | MHS/AMSU-B Channel Polarisation (Nadir) |
| 89.0 | 2800/1000 | V/V |
| 157.0/150.0 | 2800/1000 | V/V |
| 183.31 ± 1.0 | 1000/500 | H/V |
| 183.31 ± 3.0 | 2000/1000 | H/V |
| 190.311/183.31 ± 7.0 | 2000/2000 | V/V |
| Variable | Type | Source |
|---|---|---|
| Brightness Temperatures | Instantaneous | FIDUCEO |
| Sea-ice cover | Daily | ERA5 |
| Snow-cover | Daily | ERA5 |
| Freezing level | Monthly | ERA5 |
| Total precipitable water | Monthly | ERA5 |
| 2 m temperature | Monthly | ERA5 |
| Scan angle | Static | FIDUCEO |
| Surface type map | Static | ESA |
| Instrument | GPM DPR | |
| Bands | KaPR | KuPR |
| Launch time | 27 February 2014 | 27 February 2014 |
| Altitude (km) | 407 | 407 |
| Inclination angle (°) | 65 | 65 |
| Frequencies (GHz) | 35.547/35.553 | 13.597/13.603 |
| Horizontal res. at nadir (km) | 5.2 | 5.2 |
| Swath width (km) | 120 | 245 |
| Vertical resolution (m) | 250/500 | 250 |
| Minimum detectable Ze (dBZ) | 12 (KaHS)/18 (KaMS) | 18 |
| Measurement accuracy (dBZ) | < | < |
| Period | 1 January 2015/31 December 2016 |
| Geographical area | 65° S–65° N/180° W–180° E |
| Num. of pixels | 48 × |
| Num. of prec. pixels | 6.8 × |
| Reference product | DPR-GMI 2B-CMB v06A (swath NS) |
| AMSU-B/MHS BTs | FIDUCEO FCDR v4.1 |
| ME (mm/h) | RMSE (mm/h) | CC | |
|---|---|---|---|
| PNPR-CLIM vs. MRMS | −0.007 | 0.606 | 0.712 |
| GPROF vs. MRMS | 0.005 | 0.621 | 0.712 |
| PNPR-CLIM vs. GPROF | −0.012 | 0.393 | 0.853 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagaglini, L.; Sanò, P.; Casella, D.; Cattani, E.; Panegrossi, G. The Passive Microwave Neural Network Precipitation Retrieval Algorithm for Climate Applications (PNPR-CLIM): Design and Verification. Remote Sens. 2021, 13, 1701. https://doi.org/10.3390/rs13091701
Bagaglini L, Sanò P, Casella D, Cattani E, Panegrossi G. The Passive Microwave Neural Network Precipitation Retrieval Algorithm for Climate Applications (PNPR-CLIM): Design and Verification. Remote Sensing. 2021; 13(9):1701. https://doi.org/10.3390/rs13091701
Chicago/Turabian StyleBagaglini, Leonardo, Paolo Sanò, Daniele Casella, Elsa Cattani, and Giulia Panegrossi. 2021. "The Passive Microwave Neural Network Precipitation Retrieval Algorithm for Climate Applications (PNPR-CLIM): Design and Verification" Remote Sensing 13, no. 9: 1701. https://doi.org/10.3390/rs13091701
APA StyleBagaglini, L., Sanò, P., Casella, D., Cattani, E., & Panegrossi, G. (2021). The Passive Microwave Neural Network Precipitation Retrieval Algorithm for Climate Applications (PNPR-CLIM): Design and Verification. Remote Sensing, 13(9), 1701. https://doi.org/10.3390/rs13091701