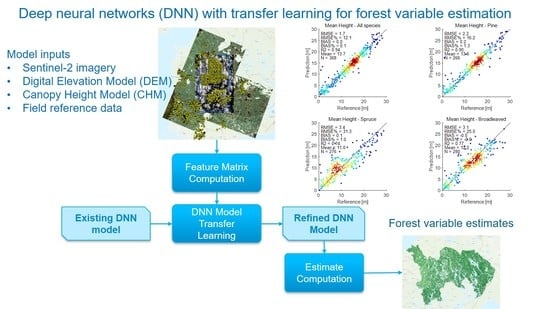
Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest
Abstract
1. Introduction
2. Materials
2.1. Study Site
2.2. Field Reference Data
2.3. Optical Satellite Imagery
2.4. Elevation Models
2.4.1. Digital Elevation Model
2.4.2. Canopy Height Model
2.5. Training, Validation, and Test Sets
2.5.1. Training Data Subsets
3. Methods
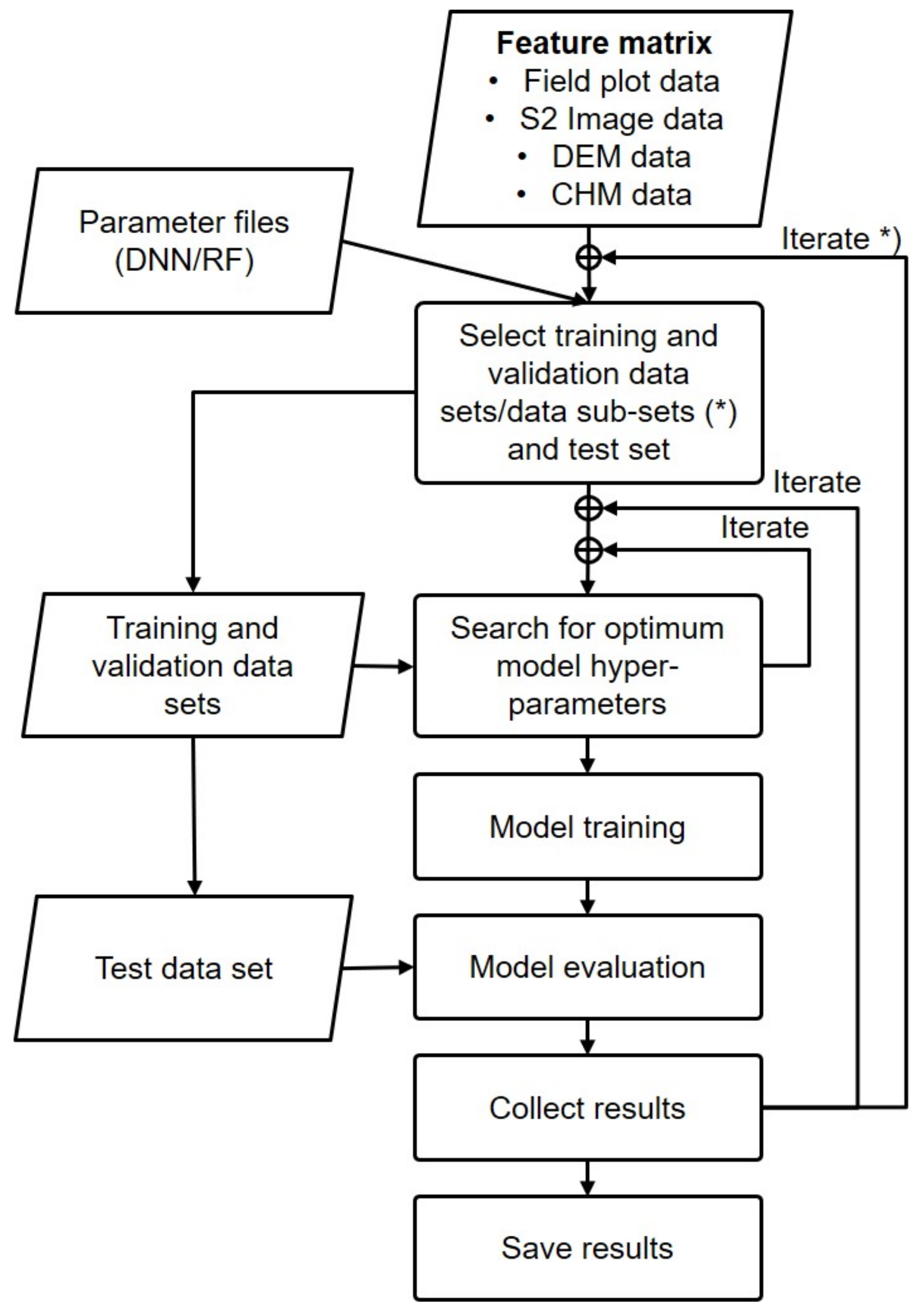
3.1. Study Concept
3.2. Deep Neural Network (DNN) Models
3.2.1. Transfer Learning
3.2.2. Hyper-Parameter Search
3.3. Test Setups
3.3.1. Different Input Data Sources
3.3.2. Size of Image Sampling Window
3.3.3. Minimal Amount of Reference Data
3.3.4. Number of DNN Hidden Layers
3.4. Random Forest (RF) Models
3.5. Model Performance Evaluation
4. Results
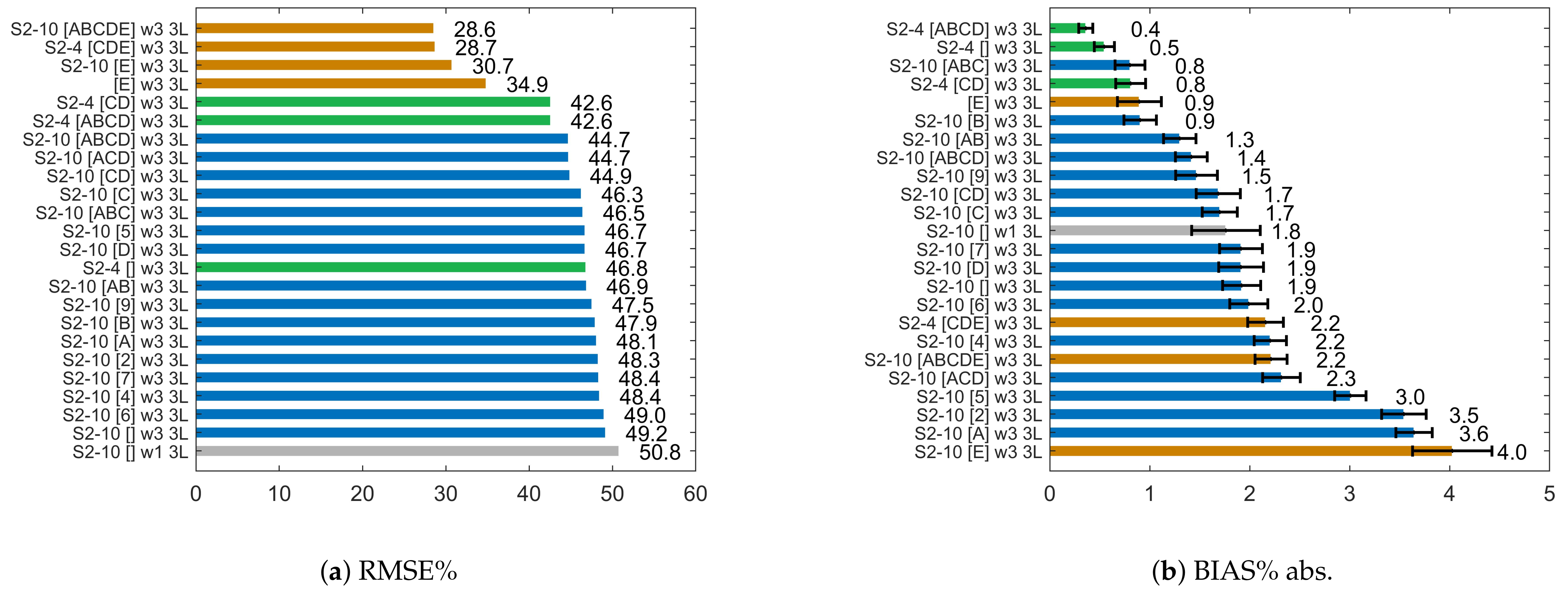
- S2-**: the used Sentinel-2 image channels: S2-4 = [B2, B3, B4, B8] (i.e., RGB and NIR) or S2-10 = [B2, B3, B4, B8, B5, B6, B7, B8A, B11, B12] (i.e., RGB, NIR, SWIR, and VRE bands);
- [****]: the auxiliary features or feature groups, labelled according to Table 3;
- w* = w1, w3 or w5: window size of the used Sentinel-2 image sampling scheme (1 × 1, 3 × 3 or 5 × 5 pixels, respectively);
- [*L]: the number of hidden layers in DNN (e.g., 3L = three hidden layers).
4.1. Effect of Different Input Features
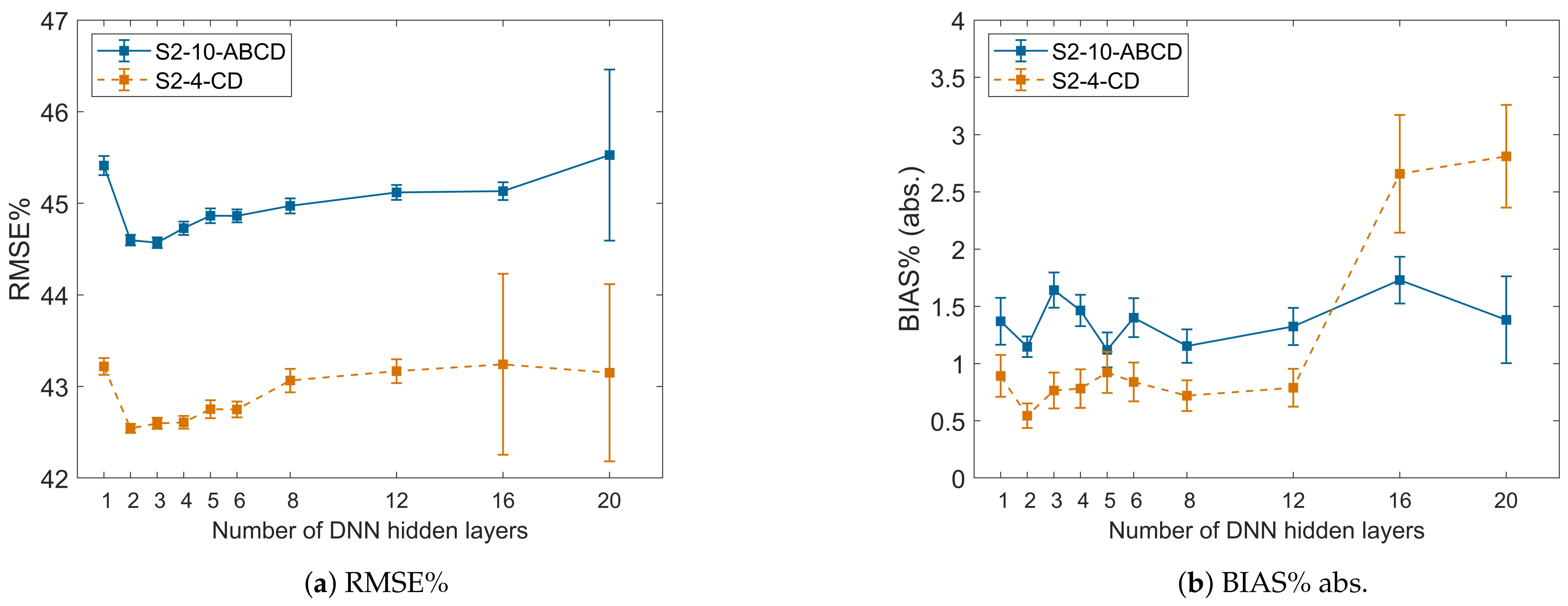
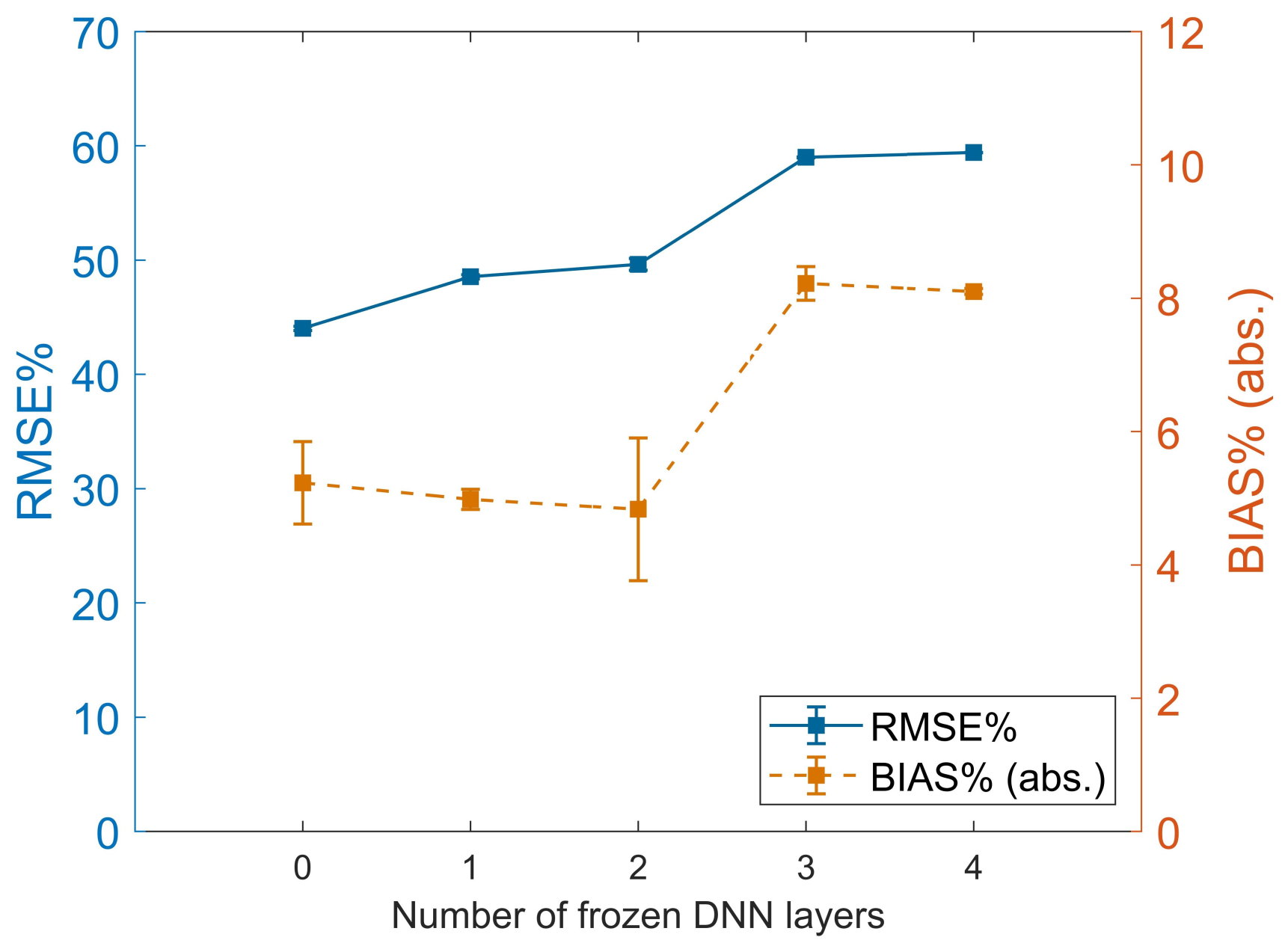
4.2. Effect of DNN Depth
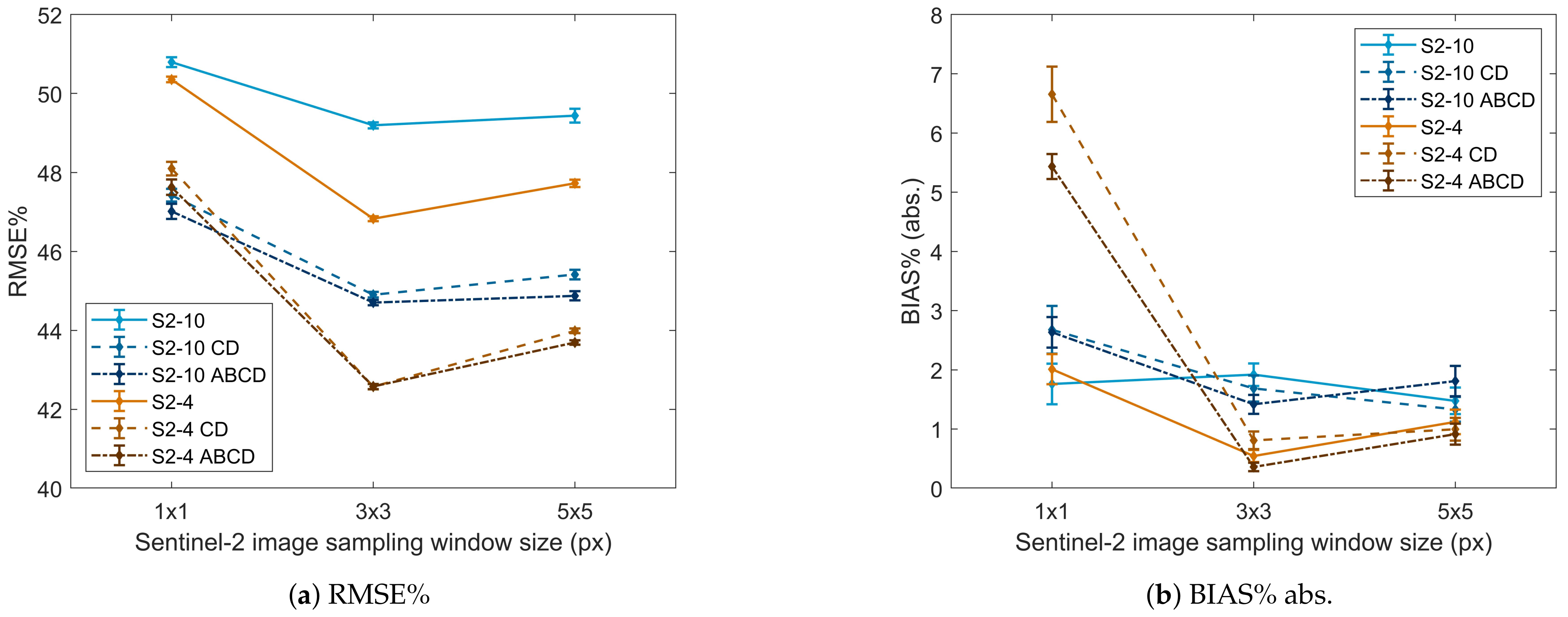
4.3. Effect of Image Sampling Window Size
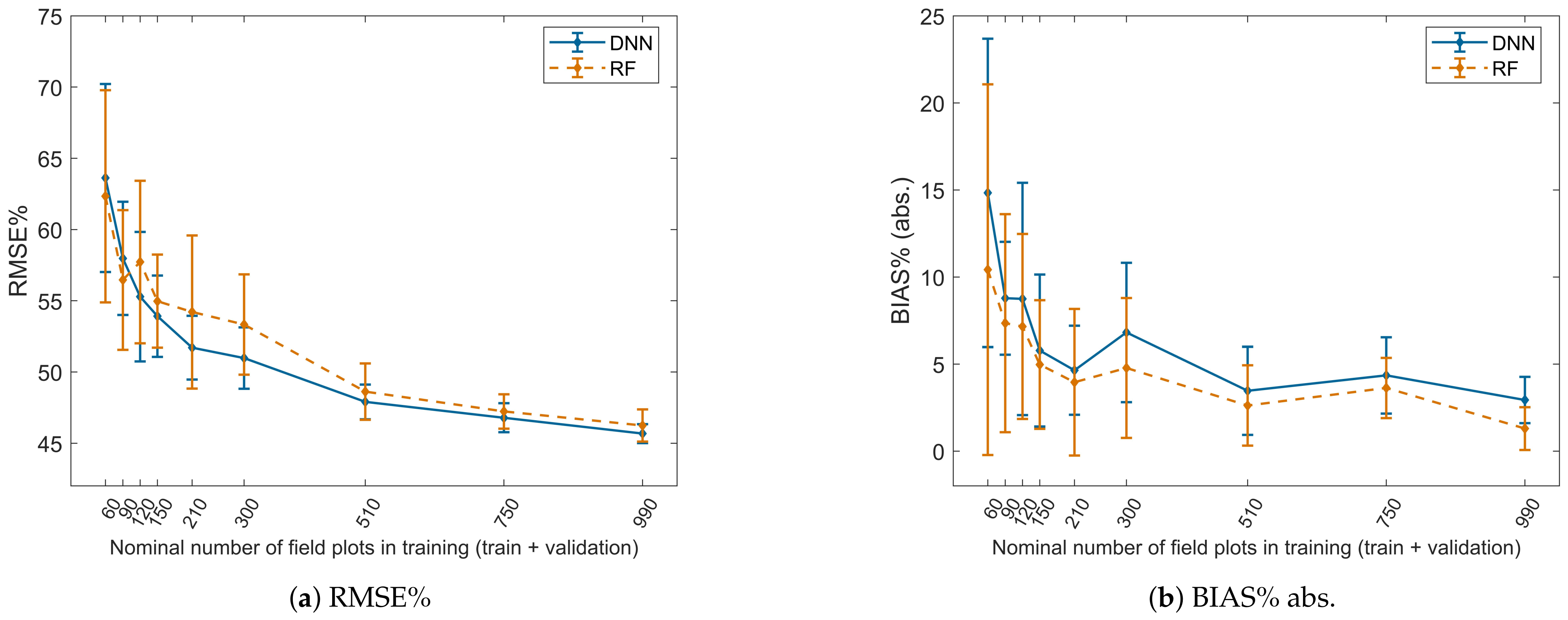
4.4. Effect of the Amount of Training Data
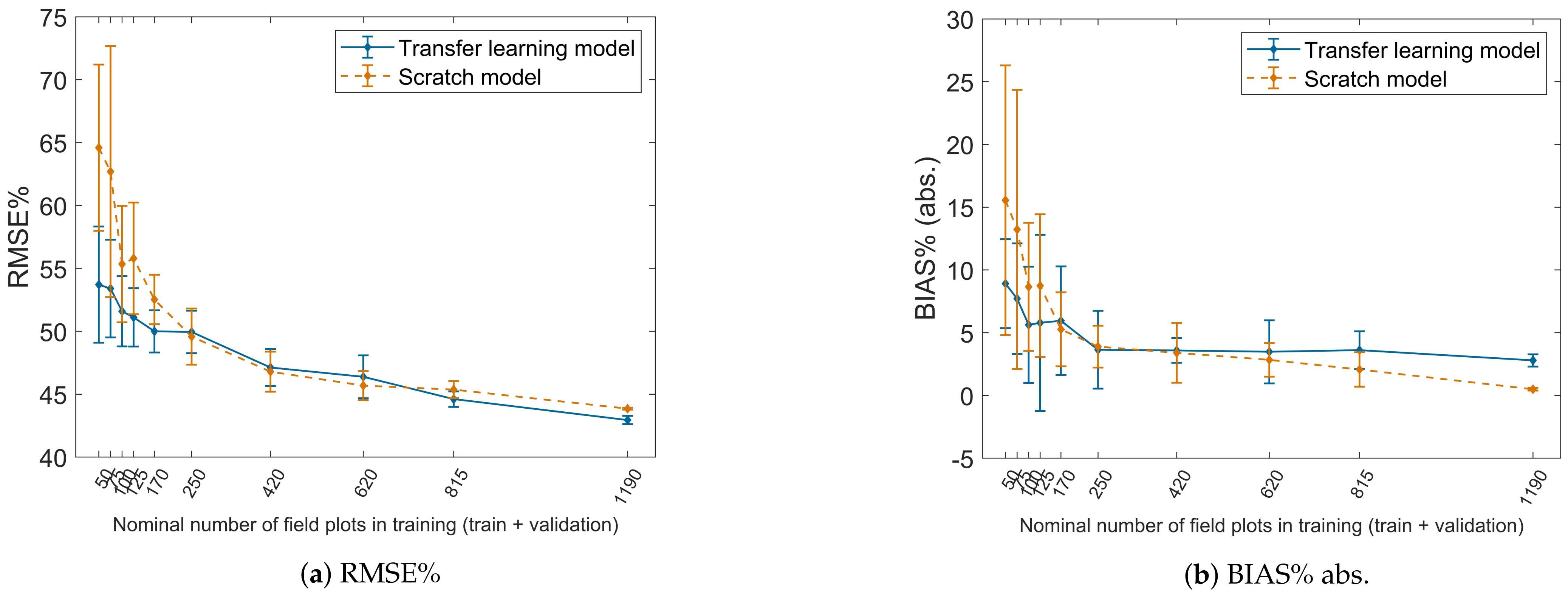
4.5. Transfer Learning Tests
4.6. The Performance for a Wider Set of Forest Variables
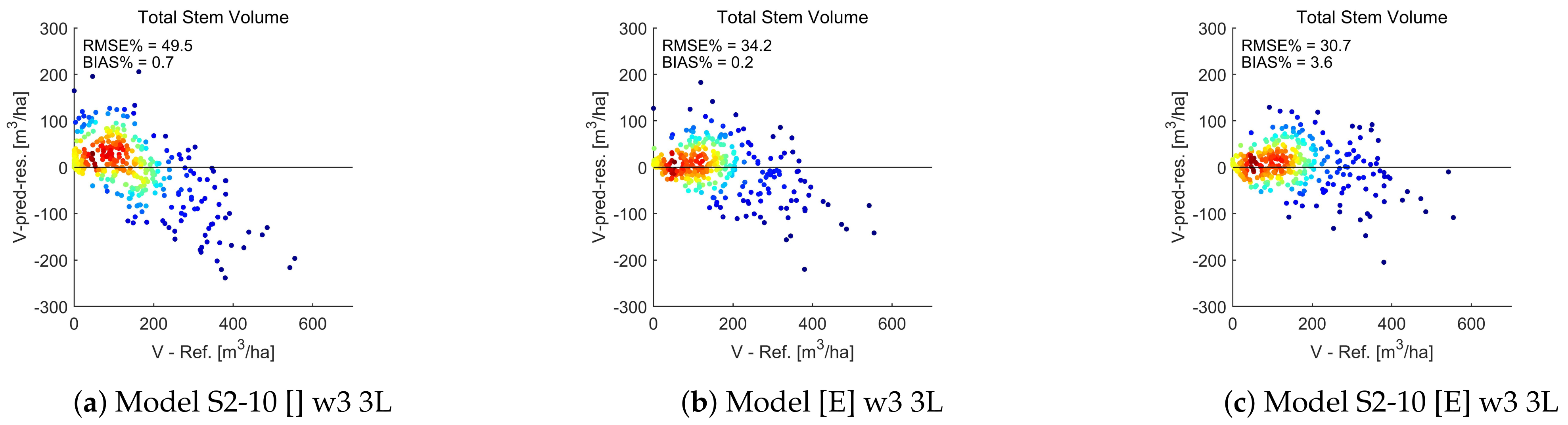
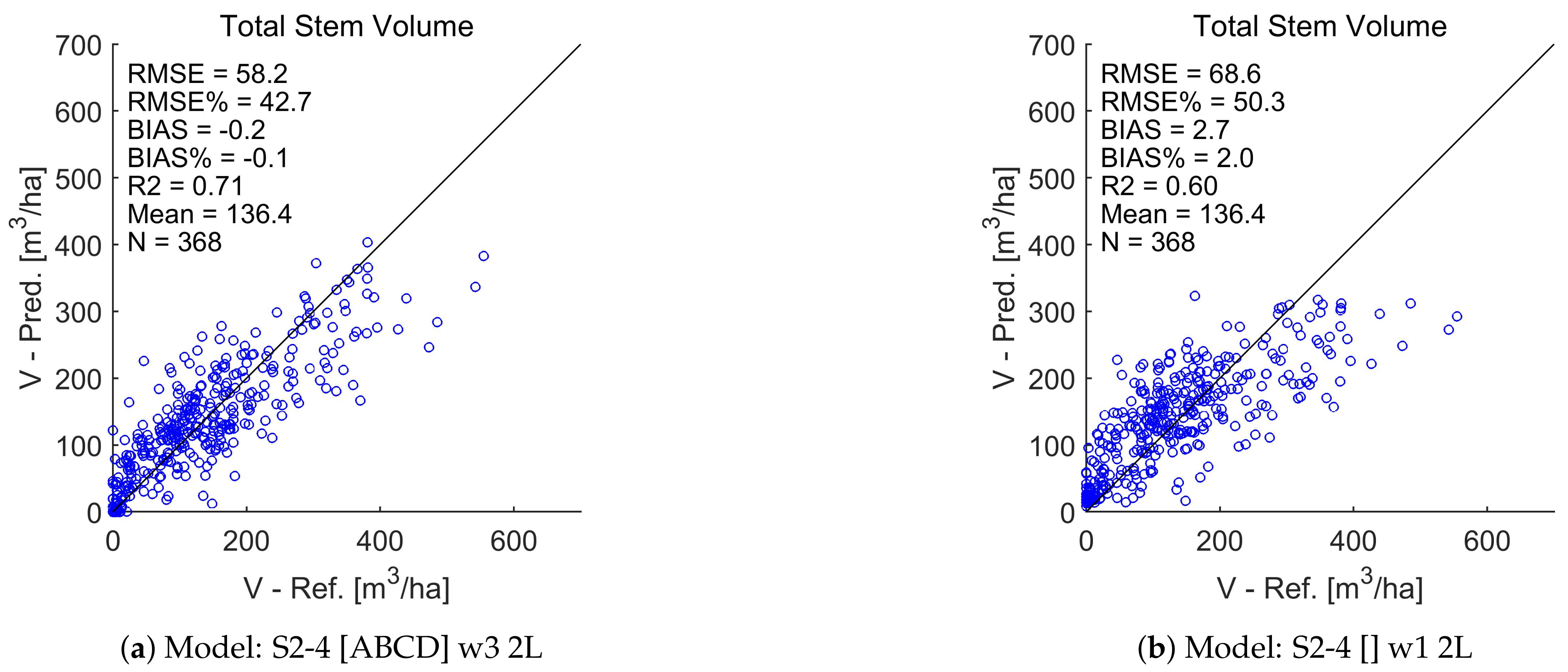
4.7. Total Stem Volume Estimates
5. Discussion
5.1. Sensitivity Analysis of Training Parameters
5.2. Comparison with Similar Studies
5.3. Comparison between DNNs and RF
5.4. Transfer Learning Performance and Applicability
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Aboveground Biomass |
| ALS | Airborne Laser Scanning |
| CHM | Canopy Height Model |
| CNN | Convolutional Neural Network |
| DBN | Deep Belief Network |
| DEM | Digital Elevation Model |
| DNN | Deep Neural Network |
| EO | Earth Observation |
| GSV | Growing Stock Volume |
| KNN | k-Nearest Neighbor |
| LiDAR | Light Detection And Ranging |
| NIR | Near Infra-Red |
| ReLU | Rectified Linear Unit |
| RF | Random Forest |
| RGB | Red Green Blue |
| RMSE | Root Mean-Squared Error |
| RNN | Recurrent Neural Network |
| S2 | Sentinel-2 |
| SELU | Scaled Exponential Linear Unit |
| Stdev | Standard Deviation |
| SVM | Support Vector Machines |
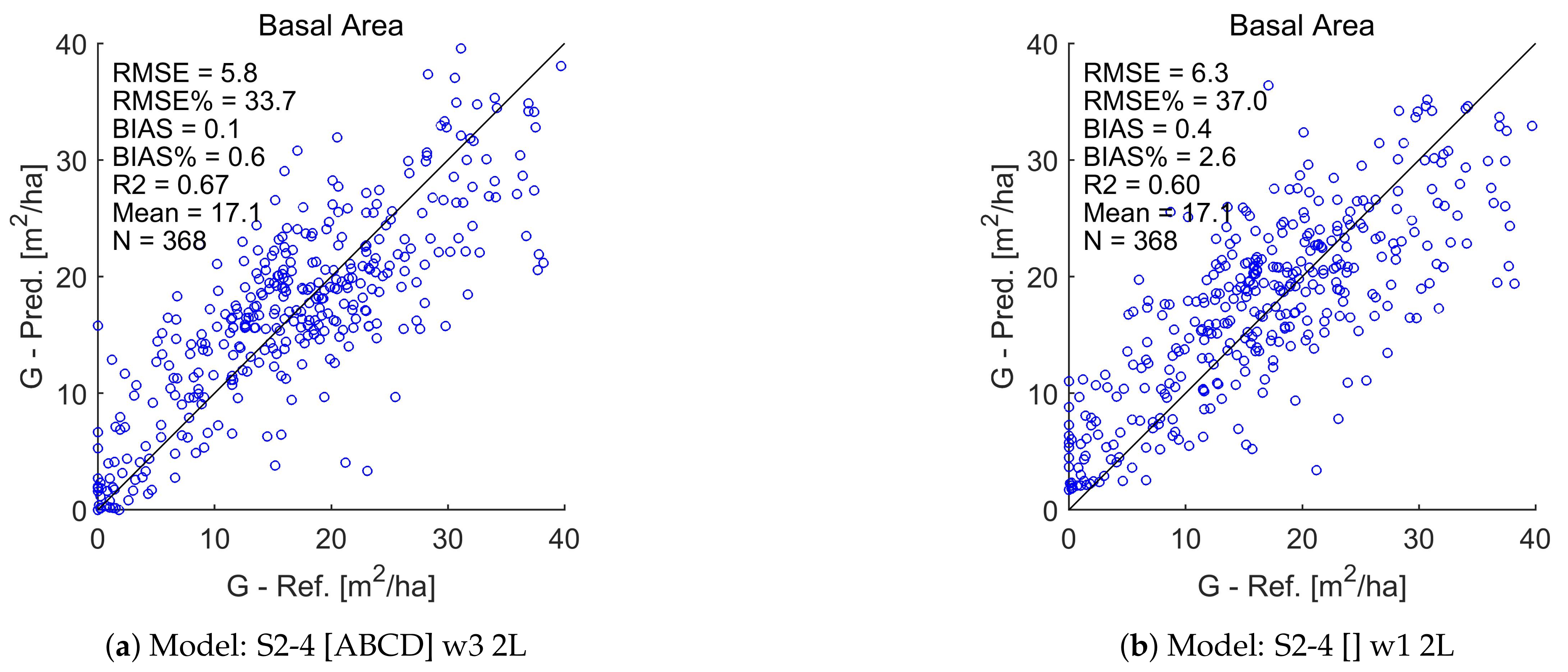
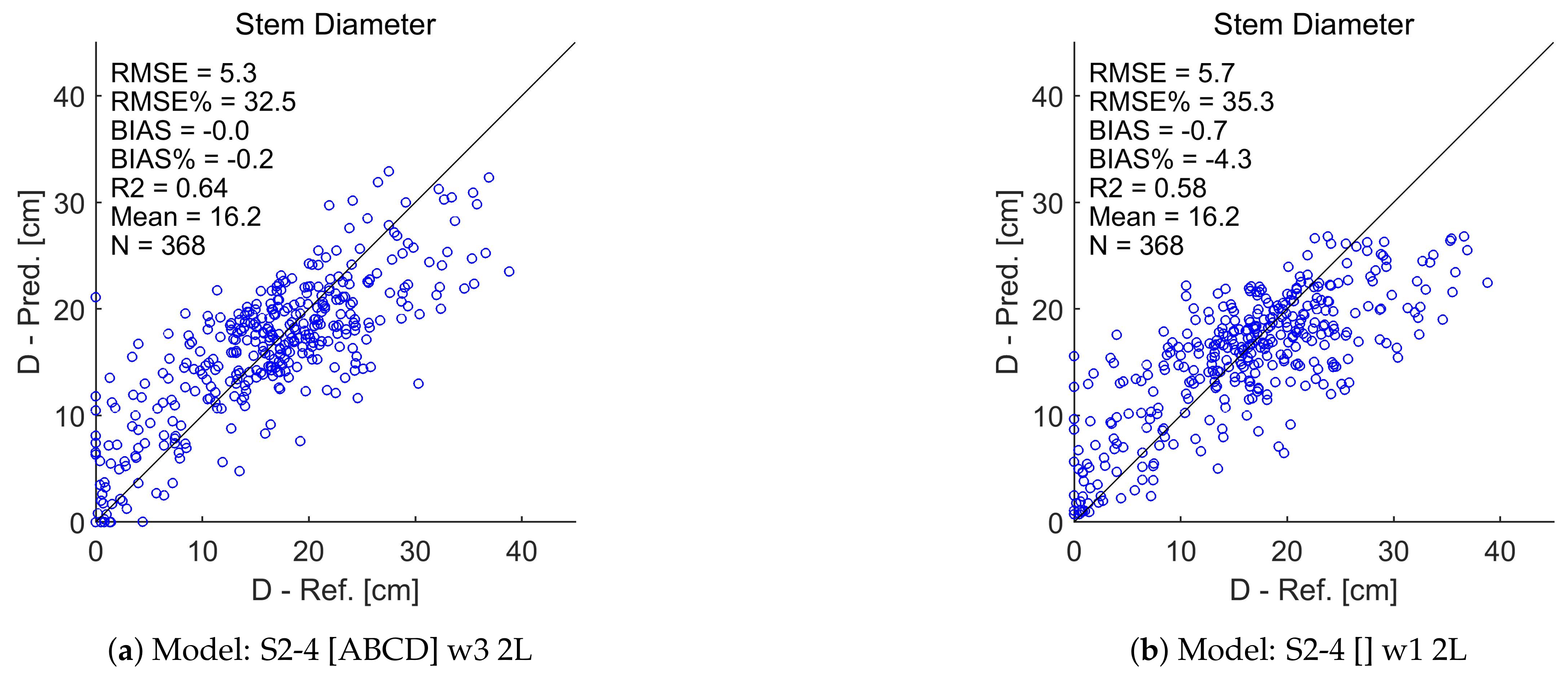
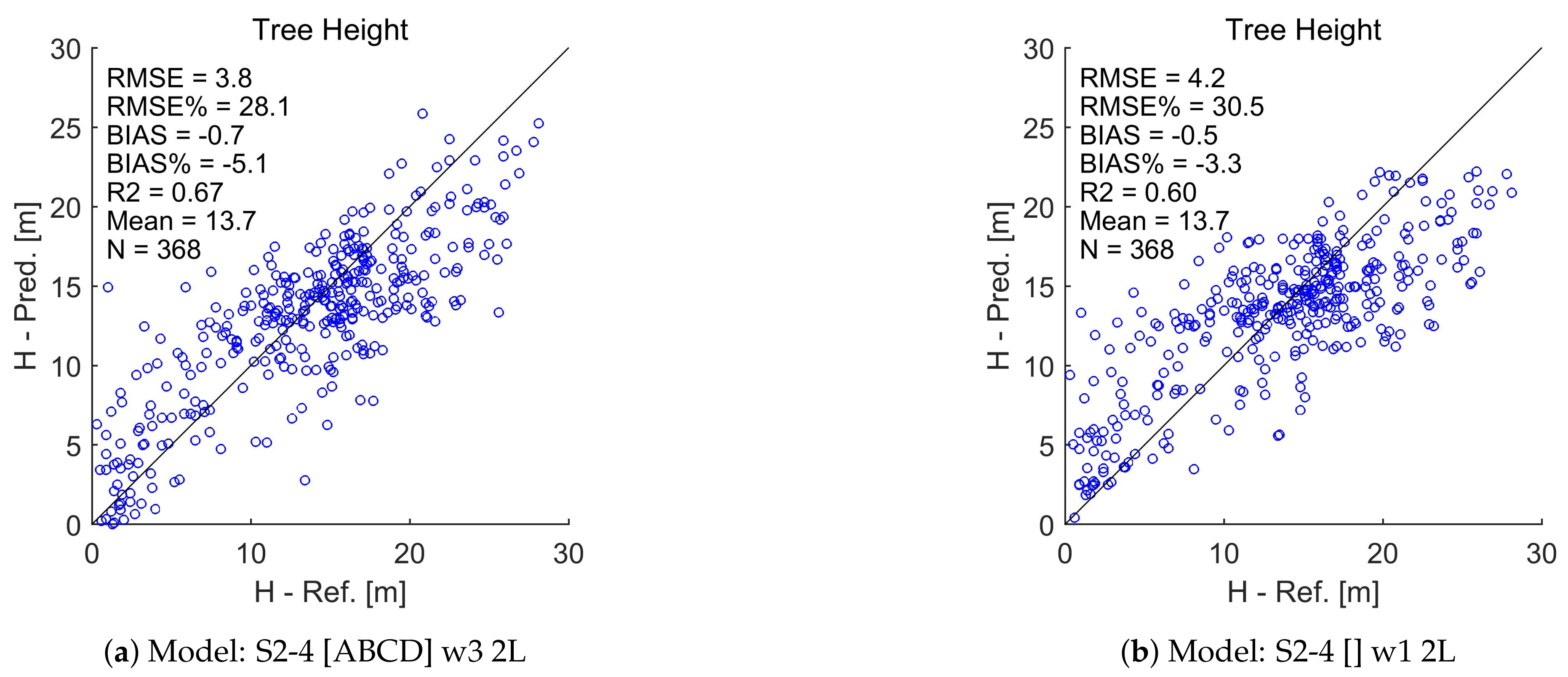
Appendix A. Test Set Scatterplots for Basal Area (G), Stem Diameter (D), and Tree Height (H)
References
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Tegel, K.; Baral, Y.; Junttila, V.; Kauranne, T.; Häme, T.; Praks, J. Tropical Forest Tree Height and Above Ground Biomass Mapping in Nepal Using Tandem-X and ALOS PALSAR Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5334–5336. [Google Scholar] [CrossRef]
- Keenan, R.; Reams, G.; Achard, F.; de Freitas, J.; Grainger, A.; Lindquist, E. Dynamics of global forest area: Results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 2015, 352, 9–20. [Google Scholar] [CrossRef]
- MäKelä, A.; Pulkkinen, M.; Kolari, P.; Lagergren, F.; Berbigier, P.; Lindroth, A.; Loustau, D.; Nikinmaa, E.; Vesala, T.; Hari, P. Developing an empirical model of stand GPP with the LUE approach: Analysis of eddy covariance data at five contrasting conifer sites in Europe. Glob. Chang. Biol. 2008, 14, 92–108. [Google Scholar] [CrossRef]
- Alberdi, I.; Bender, S.; Riedel, T.; Avitable, V.; Boriaud, O.; Bosela, M.; Camia, A.; Cañellas, I.; Castro Rego, F.; Fischer, C.; et al. Assessing forest availability for wood supply in Europe. For. Policy Econ. 2020, 111, 102032. [Google Scholar] [CrossRef]
- Haakana, H. Multi-Source Forest Inventory Data for Forest Production and Utilization Analyses at Different Levels; Dissertationes Forestales; Finnish Society of Forest Science: Helsinki, Finland; Faculty of Agriculture and Forestry of the University of Helsinki: Helsinki, Finland; School of Forest Sciences of the University of Eastern Finland: Joensuu, Finland, 2017. [Google Scholar] [CrossRef]
- Chang, T.; Rasmussen, B.P.; Dickson, B.G.; Zachmann, L.J. Chimera: A multi-task recurrent convolutional neural network for forest classification and structural estimation. Remote Sens. 2019, 11, 768. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Soille, P.; Burger, A.; De Marchi, D.; Kempeneers, P.; Rodriguez, D.; Syrris, V.; Vasilev, V. A versatile data-intensive computing platform for information retrieval from big geospatial data. Future Gener. Comput. Syst. 2018, 81, 30–40. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Gong, J. Deep neural network for remote-sensing image interpretation: Status and perspectives. Natl. Sci. Rev. 2019, 6, 1082–1086. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef]
- Tuia, D.; Verrelst, J.; Alonso, L.; Perez-Cruz, F.; Camps-Valls, G. Multioutput support vector regression for remote sensing biophysical parameter estimation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 804–808. [Google Scholar] [CrossRef]
- Wu, C.; Tao, H.; Zhai, M.; Lin, Y.; Wang, K.; Deng, J.; Shen, A.; Gan, M.; Li, J.; Yang, H. Using nonparametric modeling approaches and remote sensing imagery to estimate ecological welfare forest biomass. J. For. Res. 2018, 29, 151–161. [Google Scholar] [CrossRef]
- Zhu, X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Hu, Z.; Zhang, J.; Li, M.; Mo, L.; Molinier, M. Thin cloud removal in optical remote sensing images based on generative adversarial networks and physical model of cloud distortion. ISPRS J. Photogramm. Remote Sens. 2020, 166, 373–389. [Google Scholar] [CrossRef]
- Ball, J.; Anderson, D.; Chan, C. Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef]
- Mountrakis, G.; Li, J.; Lu, X.; Hellwich, O. Deep learning for remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2018, 145, 1–2. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian process for crop yield prediction based on remote sensing data. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4559–4565. [Google Scholar]
- Wolanin, A.; Mateo-García, G.; Camps-Valls, G.; Gómez-Chova, L.; Meroni, M.; Duveiller, G.; Liangzhi, Y.; Guanter, L. Estimating and understanding crop yields with explainable deep learning in the Indian Wheat Belt. Environ. Res. Lett. 2020, 15, 024019. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Lipping, T. Crop yield prediction with deep convolutional neural networks. Comput. Electron. Agric. 2019, 163, 104859. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, W.; Gan, H.; Peres, N.; Fraisse, C.; Zhang, Y.; He, Y. Strawberry yield prediction based on a deep neural network using high-resolution aerial orthoimages. Remote Sens. 2019, 11, 1584. [Google Scholar] [CrossRef]
- Song, X.; Zhang, G.; Liu, F.; Li, D.; Zhao, Y.; Yang, J. Modeling spatio-temporal distribution of soil moisture by deep learning-based cellular automata model. J. Arid Land 2016, 8, 734–748. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L.; Wang, L. Stacked Sparse Autoencoder Modeling Using the Synergy of Airborne LiDAR and Satellite Optical and SAR Data to Map Forest Above-Ground Biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep learning based retrieval of forest aboveground biomass from combined LiDAR and Landsat 8 data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef]
- Narine, L.; Popescu, S.; Malambo, L. Synergy of ICESat-2 and Landsat for mapping forest aboveground biomass with deep learning. Remote Sens. 2019, 11, 1503. [Google Scholar] [CrossRef]
- García-Gutiérrez, J.; González-Ferreiro, E.; Mateos-García, D.; Riquelme-Santos, J.C. A Preliminary Study of the Suitability of Deep Learning to Improve LiDAR-Derived Biomass Estimation. In Hybrid Artificial Intelligent Systems; Martínez-Álvarez, F., Troncoso, A., Quintián, H., Corchado, E., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 588–596. [Google Scholar]
- Liu, J.; Wang, X.; Wang, T. Classification of tree species and stock volume estimation in ground forest images using Deep Learning. Comput. Electron. Agric. 2019, 166, 105012. [Google Scholar] [CrossRef]
- Lang, N.; Schindler, K.; Wegner, J. Country-wide high-resolution vegetation height mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Halme, E.; Pellikka, P.; Mõttus, M. Utility of hyperspectral compared to multispectral remote sensing data in estimating forest biomass and structure variables in Finnish boreal forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101942. [Google Scholar] [CrossRef]
- Mutanen, T.; Sirro, L.; Rauste, Y. Tree height estimates in boreal forest using Gaussian process regression. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1757–1760. [Google Scholar] [CrossRef]
- Pan, S.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Bengio, Y. Deep Learning of Representations for Unsupervised and Transfer Learning. Proceedings of Machine Learning Research, ICML Workshop on Unsupervised and Transfer Learning, Edinburgh, Scotland, UK, 26 June–1 July 2012; Guyon, I., Dror, G., Lemaire, V., Taylor, G., Silver, D., Eds.; PMLR: Bellevue, DC, USA, 2012; Volume 27, pp. 17–36. [Google Scholar]
- Pratt, L.Y. Discriminability-Based Transfer between Neural Networks. Adv. Neural Inf. Process. Syst. 1993. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How Transferable Are Features in Deep Neural Networks? In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’14)—Volume 2; MIT Press: Cambridge, MA, USA, 2014; pp. 3320–3328. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep Transfer Learning for Crop Yield Prediction with Remote Sensing Data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies (COMPASS ’18), Menlo Park and San Jose, CA, USA, 20–22 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Wurm, M.; Stark, T.; Zhu, X.; Weigand, M.; Taubenböck, H. Semantic segmentation of slums in satellite images using transfer learning on fully convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2019, 150, 59–69. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Sendra, C. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar] [CrossRef]
- Rahman, H.; Dedieu, G. SMAC: A simplified method for the atmospheric correction of satellite measurements in the solar spectrum. Int. J. Remote Sens. 1994, 15, 123–143. [Google Scholar] [CrossRef]
- Tuominen, S.; Pitkänen, T.; Balazs, A.; Kangas, A. Improving Finnish Multi-Source National Forest Inventory by 3D Aerial Imaging. Silva Fennica 2017, 51, 7743. Available online: https://www.silvafennica.fi/article/7743/related/7743 (accessed on 17 June 2021).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 17 June 2021).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org (accessed on 17 June 2021).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:cs.LG/1412.6980. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:cs.NE/1207.0580. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Pedregosa, F. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. Understanding the exploding gradient problem. arXiv 2012, arXiv:1211.5063. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Wittke, S.; Yu, X.; Karjalainen, M.; Hyyppä, J.; Puttonen, E. Comparison of two-dimensional multitemporal Sentinel-2 data with three-dimensional remote sensing data sources for forest inventory parameter estimation over a boreal forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 167–178. [Google Scholar] [CrossRef]
- Persson, H.J.; Jonzén, J.; Nilsson, M. Combining TanDEM-X and Sentinel-2 for large-area species-wise prediction of forest biomass and volume. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102275. [Google Scholar] [CrossRef]
- Bohlin, J.; Bohlin, I.; Jonzén, J.; Nilsson, M. Mapping forest attributes using data from stereophotogrammetry of aerial images and field data from the national forest inventory. Silva Fenn. 2017, 51, 18. [Google Scholar] [CrossRef]
- Hawryło, P.; Wezyk, P. Predicting growing stock volume of Scots pine stands using Sentinel-2 satellite imagery and airborne image-derived point clouds. Forests 2018, 9, 274. [Google Scholar] [CrossRef]
- Schumacher, J.; Rattay, M.; Kirchhöfer, M.; Adler, P.; Kändler, G. Combination of multi-temporal Sentinel 2 images and aerial image based canopy height models for timber volume modelling. Forests 2019, 10, 746. [Google Scholar] [CrossRef]
- Hawryło, P.; Francini, S.; Chirici, G.; Giannetti, F.; Parkitna, K.; Krok, G.; Mitelsztedt, K.; Lisańczuk, M.; Stereńczak, K.; Ciesielski, M.; et al. The use of remotely sensed data and Polish NFI plots for prediction of growing stock volume using different predictive methods. Remote Sens. 2020, 12, 3331. [Google Scholar] [CrossRef]
- Ayrey, E.; Hayes, D.J.; Kilbride, J.B.; Fraver, S.; Kershaw, J.A.; Cook, B.D.; Weiskittel, A.R. Synthesizing Disparate LiDAR and Satellite Datasets through Deep Learning to Generate Wall-to-Wall Regional Forest Inventories. bioRxiv 2019. [Google Scholar] [CrossRef]

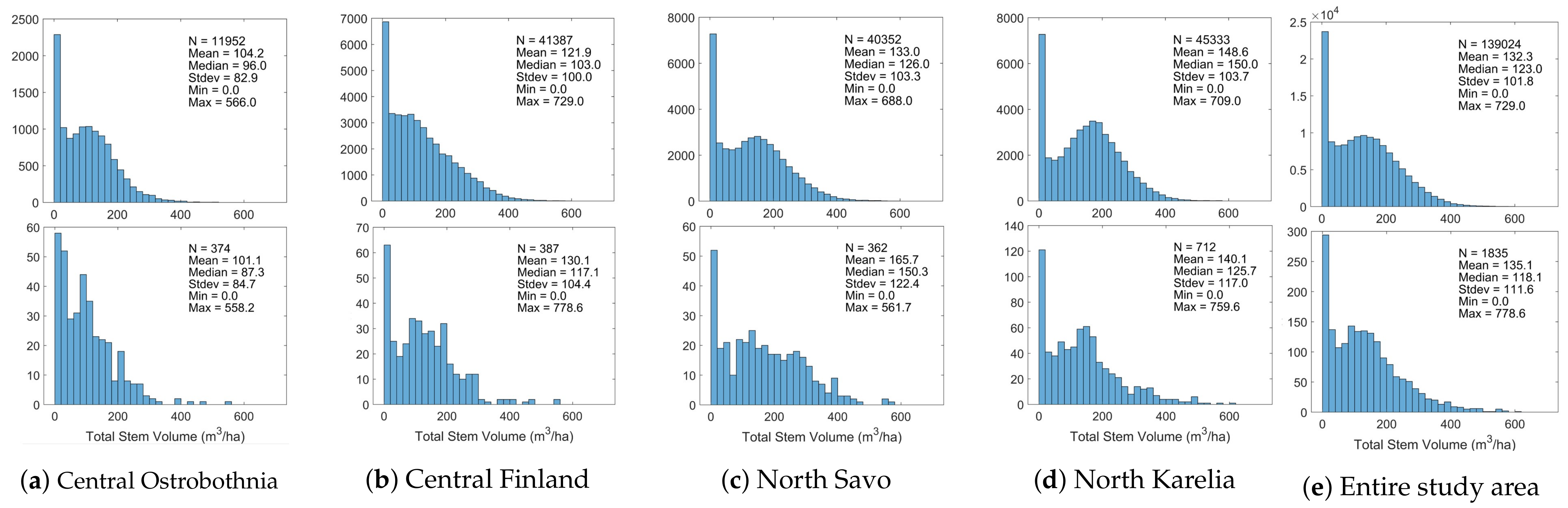
| Central Ostrobothnia | Central Finland | North Savo | North Karelia | |||||
|---|---|---|---|---|---|---|---|---|
| Forest Variable | Mean | Stdev | Mean | Stdev | Mean | Stdev | Mean | Stdev |
| Total Stem Volume (m/ha) | 100.8 | 84.6 | 130.3 | 104.4 | 165.7 | 122.4 | 140.1 | 117.0 |
| Stem Volume—pine (m/ha) | 69.4 | 67.0 | 69.1 | 86.4 | 64.1 | 91.4 | 48.4 | 75.5 |
| Stem Volume—spr (m/ha) | 14.1 | 43.6 | 36.7 | 68.1 | 64.3 | 113.2 | 59.9 | 93.0 |
| Stem Volume—bl (m/ha) | 17.5 | 33.7 | 24.3 | 41.3 | 37.2 | 61.1 | 31.8 | 45.9 |
| Basal Area—G (m/ha) | 14.0 | 8.7 | 16.6 | 10.2 | 19.4 | 11.1 | 17.4 | 10.8 |
| Basal Area—pine (m/ha) | 9.5 | 7.3 | 8.5 | 9.2 | 7.4 | 9.3 | 5.7 | 7.8 |
| Basal Area—spr (m/ha) | 1.9 | 4.8 | 4.8 | 7.7 | 7.3 | 11.3 | 7.4 | 9.3 |
| Basal Area—bl (m/ha) | 2.6 | 4.4 | 3.2 | 4.8 | 4.7 | 6.9 | 4.3 | 5.5 |
| Stem Diameter—D (cm) | 15.0 | 7.7 | 15.5 | 7.8 | 17.2 | 9.5 | 15.6 | 8.8 |
| Stem Diameter—pine (cm) | 15.0 | 8.8 | 13.1 | 10.4 | 11.5 | 11.9 | 10.7 | 11.2 |
| Stem Diameter—spr (cm) | 5.5 | 8.2 | 9.7 | 8.6 | 10.2 | 10.6 | 12.0 | 9.4 |
| Stem Diameter—bl (cm) | 7.4 | 7.2 | 8.9 | 8.1 | 9.7 | 9.1 | 9.9 | 8.2 |
| Tree Height—H (m) | 12.2 | 5.7 | 13.4 | 6.3 | 14.8 | 7.2 | 13.5 | 6.7 |
| Tree Height—pine (m) | 11.7 | 6.5 | 10.8 | 8.2 | 9.4 | 9.3 | 8.9 | 8.9 |
| Tree Height—spr (m) | 4.4 | 6.3 | 8.2 | 6.8 | 8.5 | 8.2 | 9.9 | 7.2 |
| Tree Height—bl (m) | 7.5 | 6.5 | 9.5 | 7.6 | 10.2 | 8.1 | 10.5 | 7.5 |
| Age—T (years) | 54.0 | 30.5 | 39.1 | 21.5 | 43.6 | 27.1 | 41.2 | 27.2 |
| Age—pine (years) | 53.4 | 34.1 | 32.9 | 27.0 | 30.9 | 33.1 | 28.8 | 32.3 |
| Age—spr (years) | 20.1 | 28.7 | 27.5 | 22.7 | 26.4 | 26.1 | 33.7 | 26.8 |
| Age—bl (years) | 27.2 | 24.9 | 22.6 | 19.3 | 25.3 | 23.0 | 25.7 | 21.8 |
| Stem Number—N (count) | 2196 | 3351 | 2287 | 3931 | 2625 | 4200 | 2685 | 4134 |
| Stem Number—pine (count) | 1049 | 1401 | 639 | 1043 | 630 | 1222 | 343 | 564 |
| Stem Number—spr (count) | 169 | 382 | 466 | 586 | 547 | 694 | 697 | 692 |
| Stem Number—bl (count) | 976 | 2683 | 1184 | 3594 | 1448 | 3568 | 1645 | 3852 |
| Number of field plots | 374 | 387 | 362 | 712 | ||||
| Band | Description | Spectral Range (nm) | Resolution (m) |
|---|---|---|---|
| 1 | Coastal aerosol | 433–453 | 60 |
| 2 | Blue | 458–523 | 10 |
| 3 | Green | 543–578 | 10 |
| 4 | Red | 650–680 | 10 |
| 5 | Vegetation Red Edge (RE1) | 698–713 | 20 |
| 6 | Vegetation Red Edge (RE2) | 733–748 | 20 |
| 7 | Vegetation Red Edge (RE3) | 773–793 | 20 |
| 8 | Near-Infrared (NIR) | 785–900 | 10 |
| 9 | Narrow NIR (nNir) | 855–875 | 20 |
| 10 | Water vapor | 935–955 | 60 |
| 11 | Shortwave infrared - Cirrus | 1360–1390 | 60 |
| 12 | Shortwave infrared (SWIR1) | 1565–1655 | 20 |
| 13 | Shortwave infrared (SWIR2) | 2100–2280 | 20 |
| Data Set#/Group | Input Data | Data Dimension |
|---|---|---|
| 1/I | S2 10 m and 20 m band data | 4, 10, 36, 90, 100, or 250 |
| 2/A | S2 acquisition date | 2 |
| 3/B | S2 target pixel location (Lat, Lon) | 2 |
| 4/C | S2 angles (azimuth and elevation) | 2 |
| 5/C | S2 sun angles (azimuth and elevation) | 2 |
| 6/A | S2 acq. time difference to field measurement (days) | 1 |
| 7/D | DEM data | 1 |
| 8/E | CHM data | 6 |
| 9/D | Terrain slope | 2, 18, or 50 |
| Training Set () | Validation Set () | Test Set () | ||||
|---|---|---|---|---|---|---|
| Forest Variable | Mean | Stdev | Mean | Stdev | Mean | Stdev |
| Stem Volume, V (m/ha) | 136.1 | 113.8 | 130.3 | 107.7 | 136.4 | 108.3 |
| Basal Area, G (m/ha) | 17.1 | 10.8 | 16.3 | 9.9 | 17.1 | 10.0 |
| Stem Diameter, D (cm) | 15.6 | 8.6 | 15.8 | 8.6 | 16.2 | 8.7 |
| Tree Height, H (m) | 13.4 | 6.6 | 13.6 | 6.6 | 13.7 | 6.5 |
| Age, T (years) | 43.3 | 27.6 | 44.0 | 27.6 | 45.5 | 26.3 |
| Stem Number, N (count) | 2532 | 3923 | 2487 | 4355 | 2361 | 3691 |
| Nbr | Factor | Default Value | Subsection |
|---|---|---|---|
| 1 | Different input data sources (features)—Table 3 | All except CHM data | Section 3.3.1 |
| 2 | Size of image sampling window | 3 × 3 pixels | Section 3.3.2 |
| 3 | Number of field plots | All (train + valid: 1467) | Section 3.3.3 |
| 4 | Number of DNN hidden layers | 3 | Section 3.3.4 |
| Number of | S2-4 [CD] | S2-10 [ABCD] | ||
|---|---|---|---|---|
| Hidden Layers | Nw | Nt/Nw | Nw | Nt/Nw |
| 1 | 3783 | 2.00 | 14521 | 0.52 |
| 2 | 5257 | 1.44 | 17352 | 0.44 |
| 3 | 5545 | 1.36 | 17640 | 0.43 |
| 4 | 5617 | 1.35 | 17712 | 0.43 |
| 5 | 6913 | 1.09 | 19480 | 0.39 |
| 6 | 6931 | 1.09 | 19498 | 0.39 |
| 8 | 7334 | 1.03 | 19901 | 0.38 |
| 12 | 7857 | 0.96 | 20424 | 0.37 |
| 16 | 10439 | 0.72 | 23006 | 0.33 |
| 20 | 12332 | 0.61 | 25843 | 0.29 |
| Factor Tested/Parameter Varied | Parameter Values | Section |
|---|---|---|
| Effect of different input features /DNN input feature combination | 24 different input combinations: (1) Ten S2 image bands, 1 × 1 sampling, 3 hidden layer DNN (S2-10 [] w1 3 L = baseline) (2) Ten S2 image bands + auxiliary features, 3 × 3 sampling, 3 hidden layer DNN (S2-10 [****] w3 3L) (3) Four S2 image bands + auxiliary features, 3 × 3 sampling, 3 hidden layer DNN (S2-4 [++++] w3 3L) (4) CHM features only (E) | Section 4.1 |
| Effect of DNN depth /Number of DNN hidden layers | Two input variable combinations: (1) S2-4-CD w3 xL (2) S2-10-ABCD w3 xL with ten different numbers of hidden layers: x = 1–6, 8, 12, 16 and 20 | Section 4.2 |
| Effect of image sampling window size /S2 image sampling window size | 1 × 1, 3 × 3 and 5 × 5 pixels windows | Section 4.3 |
| Effect of the amount of training data /Nominal number of field plots, training + validation sets combined | 60, 90, 120, 150, 210, 367 300, 510, 750, and 990 | Section 4.4 |
| Transfer learning tests | Section 4.5 |
| Proposed DNN Models | Simple Models | |||||
|---|---|---|---|---|---|---|
| S2-4 [ABCD] w3 2L | S2-4 [] w1 2L | |||||
| Forest Variable | RMSE% | BIAS% abs. | RMSE% | BIAS% abs. | ||
| Stem Volume (V) | 42.4 | 1.1 | 0.71 | 50.3 | 1.5 | 0.60 |
| Stem Volume/pine (V-pine) | 95.6 | 1.8 | 0.41 | 104.0 | 3.1 | 0.30 |
| Stem Volume/spruce (V-spr) | 138.3 | 14.3 | 0.47 | 153.1 | 16.6 | 0.35 |
| Stem Volume/broadleaved (V-bl) | 125.8 | 11.5 | 0.46 | 151.5 | 6.1 | 0.22 |
| Basal Area (G) | 33.0 | 0.4 | 0.68 | 36.9 | 1.5 | 0.60 |
| Basal Area/pine (G-pine) | 77.9 | 3.8 | 0.50 | 82.3 | 5.7 | 0.44 |
| Basal Area/spruce (G-spr) | 96.3 | 5.0 | 0.64 | 134.3 | 23.2 | 0.31 |
| Basal Area/broadleaved (G-bl) | 107.3 | 13.1 | 0.50 | 125.8 | 9.9 | 0.31 |
| Stem Diameter (D) | 33.1 | 4.8 | 0.62 | 35.4 | 4.2 | 0.57 |
| Stem Diameter/pine (D-pine) | 36.6 | 4.5 | 0.51 | 39.7 | 4.6 | 0.42 |
| Stem Diameter/spruce (D-spr) | 41.6 | 2.9 | 0.60 | 44.9 | 1.8 | 0.53 |
| Stem Diameter/broadleaved (D-bl) | 47.3 | 5.7 | 0.36 | 48.4 | 5.2 | 0.33 |
| Tree Height (H) | 28.2 | 2.9 | 0.65 | 30.7 | 2.9 | 0.59 |
| Tree Height/pine (H-pine) | 30.3 | 3 | 0.63 | 33.4 | 2.8 | 0.55 |
| Tree Height/spruce (H-spr) | 34.1 | 1.8 | 0.68 | 37.2 | 1.0 | 0.62 |
| Tree Height/broadleaved (H-bl) | 35.5 | 3.7 | 0.54 | 37.1 | 3.6 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astola, H.; Seitsonen, L.; Halme, E.; Molinier, M.; Lönnqvist, A. Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest. Remote Sens. 2021, 13, 2392. https://doi.org/10.3390/rs13122392
Astola H, Seitsonen L, Halme E, Molinier M, Lönnqvist A. Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest. Remote Sensing. 2021; 13(12):2392. https://doi.org/10.3390/rs13122392
Chicago/Turabian StyleAstola, Heikki, Lauri Seitsonen, Eelis Halme, Matthieu Molinier, and Anne Lönnqvist. 2021. "Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest" Remote Sensing 13, no. 12: 2392. https://doi.org/10.3390/rs13122392
APA StyleAstola, H., Seitsonen, L., Halme, E., Molinier, M., & Lönnqvist, A. (2021). Deep Neural Networks with Transfer Learning for Forest Variable Estimation Using Sentinel-2 Imagery in Boreal Forest. Remote Sensing, 13(12), 2392. https://doi.org/10.3390/rs13122392