Abstract
Water use efficiency (WUE) is a key index for understanding the ecosystem of carbon–water coupling. The undistinguishable carbon–water coupling mechanism and uncertainties of indirect methods by remote sensing products and process models render challenges for WUE remote sensing. In this paper, current progress in direct and indirect methods of WUE estimation by remote sensing is reviewed. Indirect methods based on gross primary production (GPP)/evapotranspiration (ET) from ground observation, processed models and remote sensing are the main ways to estimate WUE in which carbon and water cycles are independent processes. Various empirical models based on meteorological variables and remote sensed vegetation indices to estimate WUE proved the ability of remotely sensed data for WUE estimating. The analytical model provides a mechanistic opportunity for WUE estimation on an ecosystem scale, while the hypothesis has yet to be validated and applied for the shorter time scales. An optimized response of canopy conductance to atmospheric vapor pressure deficit (VPD) in an analytical model inverted from the conductance model has been also challenged. Partitioning transpiration (T) and evaporation (E) is a more complex phenomenon than that stated in the analytic model and needs a more precise remote sensing retrieval algorithm as well as ground validation, which is an opportunity for remote sensing to extrapolate WUE estimation from sites to a regional scale. Although studies on controlling the mechanism of environmental factors have provided an opportunity to improve WUE remote sensing, the mismatch in the spatial and temporal resolution of meteorological products and remote sensing data, as well as the uncertainty of meteorological reanalysis data, add further challenges. Therefore, improving the remote sensing-based methods of GPP and ET, developing high-quality meteorological forcing datasets and building mechanistic remote sensing models directly acting on carbon–water cycle coupling are possible ways to improve WUE remote sensing. Improvement in direct WUE remote sensing methods or remote sensing-driven ecosystem analysis methods can promote a better understanding of the global ecosystem carbon–water coupling mechanisms and vegetation functions–climate feedbacks to serve for the future global carbon neutrality.
1. Introduction
Water use efficiency (WUE) is a key metric of carbon–water coupling maintaining the trade-off between photosynthesis and water vapor loss on plant function, which is often defined as the ratio of gross primary production (GPP) and evapotranspiration (ET) on the ecosystem scale [1,2,3,4,5,6]. Previous studies have reported that the global forest WUE shows an upward trend with the rise in atmospheric carbon dioxide concentration as shown in Figure 1a,c [7,8]. However, based on satellite observations, the global average WUE has showed a significant downward trend before 2010, which is possibly due to the change in land use, and this phenomenon is improved during 2011–2014 as shown in Figure 1b [9]. As an independent ecological variable of the ecosystem responding to global changes, WUE is a key measurement to link the carbon and water cycle of ecosystems. Various researches have investigated the underlying mechanism of WUE at a single site by measuring flux with simple weather condition-driven models [10,11,12,13]. To reveal the effect of global change on the interaction of water–carbon cycles in ecosystems, several studies upscaled WUE from a single site to the regional/global scale through remote sensing techniques and ecological models [2,4,7,9,14,15,16,17]. The retrieval of spatial-temporal variability and control mechanism of WUE on regional scale ecosystems is helpful to evaluate and predict the impact of global changes on ecosystem water and carbon processes [18]. However, issues concerning the inconsistent response to environmental factors and indistinct carbon–water coupling mechanisms need to be resolved for effectively evaluating ecosystem functions with a higher requirement of long-lasting continuous and consistent spatial measurements to capture changes in water–carbon cycles.
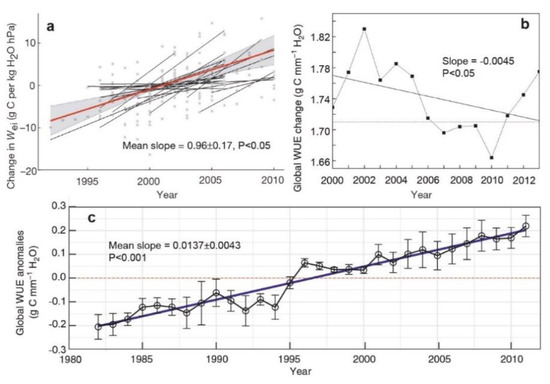
Figure 1.
Trends of global water use efficiency (WUE). (a) The annual change in WUE (, gC kg−1 H2O hPa. VPD is atmospheric vapor pressure deficit), calculated using daytime fluxes from summer months at 21 flux towers of temperate and boreal forest ecosystems (discussed in Section 2.2.1). The red line indicates mean trend over all sites and grey dots and black lines represent the trends of each site. Adapted with permission from ref. [7]. Copyright 2013 Nature Publishing Group, a division of Macmillan Publishers Limited (https://www.nature.com/. Accessed on 15 April 2021). (b) Change in global annual mean WUE, calculated using satellite remote sensing data (discussed in Section 2.2.3). The dashed line represents the mean value of WUE. Reprinted with permission from ref. [9]. Copyright 2014 The authors. (c) Global WUE anomalies, calculated using output of an analytical ecosystem WUE model (discussed in Section 2.3). The blue line represents the linear trend of WUE and the error bars are standard deviation (Source: Cheng et al., 2017 [8]). Adapted with permission from ref. [8]. Copyright 2017 The authors.
Indirect methods (i.e., based on remote sensing products and output of process models) [4,19], empirical models (i.e., based on meteorological variables, flux observations, and remotely sensed vegetation indices) [9,20], and analytical models [8] are applied to estimate the WUE and to analyze the response to environmental factors. Although an increasing trend exists in global forest WUE based on the result of site observation and process-based models, the global mean WUE from satellite observation was decreasing—before the year 2010—and then increased. However, satellite-observed WUE has uncertainties for validation at the site scale. Therefore, the applied remote sensing product(s) should be improved by precise remote sensing algorithms or to develop a more precise product(s). Here, we review the current progress in WUE remote sensing and guiding steps for the improvement in WUE estimation. Firstly, the measurement and process-based models of GPP and ET are reviewed, which are inputs of indirect methods of WUE estimation. Next, the response to environmental factors, especially optimal response to atmospheric vapor pressure deficit (VPD), are discussed by analyzing various empirical and analytical models. Moreover, the importance of vegetation dynamics including canopy structure and physiological parameters in WUE remote sensing is also reviewed. Finally, the main challenges of ecosystem WUE remote sensing are highlighted with possible recommendations to improve mechanistic-based WUE remote sensing for a better understanding of global ecosystem carbon–water coupling. This review also provides a direction for the next step of research work on ecosystem WUE remote sensing.
2. Background of WUE Estimation by Remote Sensing
2.1. Definition of Ecosystem WUE
The study on plant WUE began in the early 20th century and it has been going on for nearly a century. However, the research on plant WUE is still quite active, especially considering water physiology and ecology, which is mainly due to the importance of WUE in agriculture and forestry production. In this regard, different methods have been proposed to calculate WUE, relying on the purpose of investigation [21]. WUE has a variety of different definitions according to the prospects, categories, and priorities of different disciplines. For example, plant physiology focuses on the physiological efficiency of water; irrigation agronomy focuses on crop water productivity, total farmland WUE, field WUE, irrigation WUE, and precipitation utilization efficiency. In terms of ecology, a description of WUE-related ecological parameters is shown in Table 1.

Table 1.
Description of WUE-related ecological parameters.
At the single leaf or individual plant stage, there are two ways to express WUE: firstly, the ratio of net photosynthetic rate (Pn) to transpiration (T) to describe the instantaneous WUE of the plant leaf; secondly, the ratio of Pn to leaf stomatal conductance (gs), also known as intrinsic WUE (WUEi). When gs becomes the dominant limiting factor for plant–leaf gaseous exchange, WUEi is more suitable for describing the water use status of the plant photosynthesis process. If T and gs are significantly positively correlated, it leads to a significantly positive correlation between WUE and WUEi. The WUE and WUEi indicate that the plant (s) water use efficiency is significantly indifferent. For individual plants, WUE is equal to mass of dry matter per unit of T. For plant population, WUE is equal to mass of dry matter per unit of water consumption. At the ecosystem level, definitions of WUE are basically equivalent to that of plant population. Considering that measuring ET is relatively easier than T and that T is considered to be the main component of ET during the peak growing season, ET is approximately equal to T as the denominator of fraction on the ecosystem scale [17]. The classic definition of WUE is equal to GPP/ET or WUE is equal to NPP/ET (NPP, net primary production) as shown in Table 1.
The classical WUE is defined as GPP per unit of ET (gC kg−1 H2O), which is suitable for studying the carbon–water coupling characteristics of ecosystems and their responses to environmental changes on a monthly or a yearly scale, as shown in Figure 2 [6]. Recent studies have defined two new WUEs, i.e., Inherent WUE (IWUE), which is equal to (gC hPa kg−1 H2O) [6] and Underlying WUE (UWUE), which is equal to (gC hPa0.5 kg−1 H2O) [17,24,25]. These new definitions mainly consider the important influence of saturated VPD on the daily and hourly scale of carbon–water coupling. In fact, the two definitions of WUE, i.e., IWUE and UWUE, can be unified by a common formula such as the Optical WUE (OWUE), which is equal to (gC hPak* kg−1 H2O), and the only difference among them is the value of k. For specific ecosystems, the optimal value of k can be found by analyzing the ecosystem carbon–water coupling characteristics at different time scales [1,17,26]. Therefore, the selection of T or ET depends on the measurement at the ecosystem scale, while the choice of the WUE Equation, including VPD, is related to the influence of VPD on WUE trend, and changes in the physiological behavior of vegetation for future climate change.
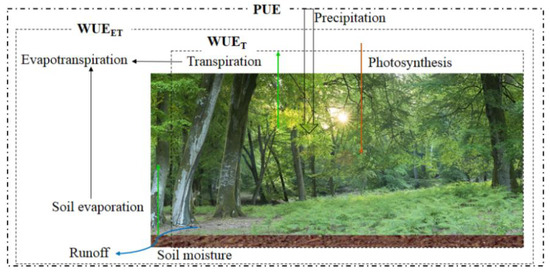
Figure 2.
Schematic diagram of the different processes involved in expressing the ecosystem WUE.
To assess data from the research and technology perspective, the calculation of water loss at ecosystems is always different, which has resulted in different understandings on the variability of WUE. In previous studies, the transpiration of vegetation is considered as the water loss from the ecosystem, which is consistent with the concept of Transpiration Use Efficiency (WUET) [19].
where, NEE is the net ecosystem carbon exchange, T is the transpiration. WUE based on this algorithm reflects the ability of the plant population to utilize water. With the progress in observation technology, an increasing number of studies have measured the total ET of the ecosystem (i.e., the sum of vegetation T and soil E) as the water loss of ecosystem [19]. Then, WUE is represented as:
At the regional scale, due to a lack of measured GPP and ET data, it is difficult to study the spatial pattern of WUE. The Precipitation Use Efficiency (PUE) is also used to analyze the spatial variability of water use along with the climate gradient of the ecosystem, for which more precise remotely sensed GPP and ET or the high resolution WUE remote sensing products are necessary to perform the spatial variability analysis of water loss of the ecosystem. WUE algorithms involve different ecological processes and their controlling mechanisms are also different. It can be seen from Figure 2 that the hydrological processes involved are gradually increasing from WUET to WUEET and PUE, and the spatial and that the temporal variability is more complicated. In addition, although there may be a relatively stable proportional relationship between GPP, NPP, and NEE on the long-time scale, photosynthetic and respiratory processes are controlled by different factors. A difference in numerator in the WUE definition may also lead to distinct variability and controlling mechanisms on a short time scale.
2.2. Indirect WUE Estimation by Measuring GPP and ET at the Ecosystem Level
2.2.1. Measurements Using Eddy Covariance Observations
The eddy covariance (EC) technique has enabled long-term and continuous measurements of water and CO2 flux in recent decades [23]. Based on the EC technique, the flux tower can obtain a continuous time series data of carbon and water flux at a site-specific terrestrial biosphere and the atmosphere, and then calculate the corresponding WUE. More than 900 flux observation sites have been registered for forests, grasslands, wetlands, farmlands and other ecosystems, which form a global flux research community (FLUXNET, http://fluxnet.ornl.gov/. Accessed on 15 January 2020). However, the flux tower observations based on an EC technique cannot compensate for the loss in spatial resolution. Measurements of net CO2 exchange and hydrothermal fluxes based on an EC technique can be transferred to the calculation of GPP and ET, while uncertainties including random and systematic errors still exist [27,28]. It is difficult to eliminate and avoid the systematic error in EC measurements due to several unclear error sources and a lack of background data [29]. Nevertheless, GPP is indirectly estimated by flux measurement, but through partitioning NEE into GPP and ecosystem respiration [30]. Limitation of continuous measurements in large areas also restrict studies on spatiotemporal variability of WUE at the regional scale.
In order to upscale the site-specific observations from local flux towers to the global level, Jung et al. [31,32] merged flux observations, satellite-based fraction of absorbed photosynthetic active radiation (FAPAR) and meteorological data using a model tree ensemble algorithm (MTE). The monthly global GPP and ET estimates, referred to as JUNG GPP and JUNG ET, were obtained by extrapolating flux observations from 178 sites are available at 0.5 spatial resolution for the period from 1982 to 2008. The GPP and ET estimation extrapolates the same flux-tower data, while ET is additionally corrected for energy balance closure by a constant Bowen ratio [32]. Although the MTE dataset started in 1982, the extrapolation of GPP estimation before 2000 was built on the response of GPP to the climate, which adds huge uncertainties in areas with no observation station(s) or years missing satellite-based FPAR data [33]. Large uncertainties of the MTE-GPP might also come from a lack of CO2 fertilization [33]. In addition, this product does not consider the source of uncertainties from input variables such as the uncertainty in EC observations and their partitioning, the uncertainty in satellite measurements of FPAR, and meteorological variables.
2.2.2. Advanced Indirect WUE Estimation via Process-Based Modeling
With the development of process-based models, a large number of process models have been to merge water and carbon cycle modules into one model through their coupling parts. Widely accepted process models included both water and carbon cycle modules which can simultaneously simulate GPP and ET to estimate WUE. However, the carbon and water cycles are two independent physical processes in the process models to estimate WUE. At a regional scale, remote sensing data is the main input of process models because of easy access to data. Land carbon models (Offline Models, TRENDY), including Community Land Model Carbon-Nitrogen version 4 (CLMCN4, [34,35,36,37]), Joint UK Land Environment Simulator (JULES, [38,39]) and ORganizing Carbon and Hydrology in Dynamic EcosystEms (ORCHIDEE, [40]), are popularly applied and belong to the land model component. Typical algorithms used in land carbon models for GPP and ET estimation have been built and developed in the past decades as listed in Table 2 and Table 3, which have more options for an indirect estimation of WUE.

Table 2.
Typical LUE models for estimating GPP.

Table 3.
Typical process-based models of ET estimation.
The light use efficiency (LUE) model was a widely used method of GPP estimation based on the fact that GPP is directly related to absorbed photosynthetically active radiation (APAR), in which LUE represents the efficiency of vegetation in converting solar energy to biomass through absorption and photosynthesis [41]. An LUE model has become one of the main tools for studying ecosystem GPP and its temporal and spatial variation characteristics using remote sensing information. The current background of most light use efficiency models goes back to a canopy-scale GPP modeling approach [41]. The basic assumption of this idea considers the vegetation canopy as a large leaf. The LUE has nothing to do with the direction and canopy structure of the canopy. The GPP has a simple linear relationship with photosynthetically active radiation (PAR) entering the canopy as follows:
where, εmax (gC MJ−1) represents the maximum LUE of the plant, f(·) is the environmental stress factor, and FPAR represents the proportion of PAR utilized by the canopy. Typical LUE models for estimating GPP are shown in Table 2.
Empirical models (i.e., based on remote sensing data) and process-based models (i.e., using remote sensing data as the main inputs) are the main methods for estimating ET. In this regard, empirical models are mainly comprised of regression models [48] and models based on machine learning methods [49,50,51]. Additionally, the process-based models are mainly transferred by the Penman–Monteith equation, such as the PM–MOD16 model [52], PM–Yuan model [53]), and Priestley–Taylor model (PT–JPL) [54]. The typical process-based models of ET estimation are shown in Table 3.
ET modeling involves complex physical processes controlled by several factors, leading to a more complicated estimation by remote sensing, especially for crop ecosystem. Dryland river basins frequently support both irrigated agriculture and riparian vegetation and remote sensing methods are needed to monitor water use by both crops and natural vegetation in irrigation districts [59]. Crop evapotranspiration (ETc) represents crop water requirements, which is affected by weather and actual crop conditions [60,61]. A useful method to estimate ETc or crop water requirements is to multiply reference evapotranspiration (ETr) by a crop coefficient (𝐾c). 𝐾c is typically taken from literature values and is affected by crop variety and growth stage. ETc is actually estimated from site measurements or satellite-based remote sensing methods. Using a satellite remote sensing-based vegetation index in combination with site measurements have shown a certain degree of accuracy for the estimation of ET with spatial and temporal distribution at different scales, i.e., regional or field scales [62]. Remote sensing methods for estimating ET losses by soil and vegetation over wide river stretches are required to allocate water needed for agricultural and environmental sectors [63].
Remotely sensed multispectral vegetation indices are a useful tool for quantifying the variability in crop water consumption during the growing season at regional and field scales [64]. Remote sensing can also estimate crop coefficients based on spectral reflectance of vegetation indices (VIs). Crop coefficients generated from VIs determine ETc better than a tabulated 𝐾c because VIs represent the actual crop growth conditions and can capture the spatial variability among different fields [65,66]. Moreover, net radiation is an important component of the energy balance, and its estimation accuracy has an impact on energy flux estimated from satellite data. In typical remote-sensing ET algorithms, the outgoing shortwave and longwave components of net radiation are obtained from remote sensing data, while the incoming shortwave and longwave components are typically estimated from weather data using empirical equations [67]. The surface energy balance approach, combined with empirical equations (e.g., based on MODIS VIs) for estimating shortwave and longwave radiation, is commonly used in remote sensing ET algorithms, with an error or an uncertainty of about 20% [64].
WUE is calculated as the quotient of GPP and ET as mentioned above by modeling carbon and water cycles, respectively. This method of WUE estimation is limited to the monitoring of seasonal variations in WUE, and to our understanding about the controlling factors and coupling water–carbon cycle feedback [68]. This seasonal response of WUE to climate change needs better observation-based validation to further improve predictions of ecosystem response to global change.
2.2.3. Advances in Indirect WUE Estimation by Remote Sensing
Remote sensing techniques, especially using MODIS data, has produced GPP and ET products with high spatial and temporal coverage [69,70,71], because both photosynthesis and ET are closely related to physiological characteristics and meteorological factors [72,73]. From there, ecosystem WUE across time and space can be calculated using MODIS-based GPP and ET products under the classical definition of WUE [74]. MODIS GPP and ET products are the most widely used and unique high resolution remote sensing data products for the indirect estimation of WUE. Although these products have been used to analyze the temporal and spatial patterns of global WUE for terrestrial ecosystems, the discrepancy with tower-based WUE at 8-day time scales still exist at specific sites [68,75].
Recently, various studies have shown a strong linear relationship between GPP and SIF using satellite and ground measurements for GPP estimation [76,77]. Global SIF products have also been retrieved with several time and space resolutions from spaceborne spectro-meters, such as the Orbiting Carbon Observatory2 (OCO-2), the TROPOspheric Monitoring Instrument (TROPOMI), the Global Ozone Monitoring Experiment 2 (GOME2), and the Greenhouse Gases Observing Satellite (GOSAT) [78,79,80]. A previous study has developed an algorithm of GPP estimation using SIF products, which have global coverage and can be used in all weathers [81]. Studies have also shown the empirical and mechanistic relationship between T and SIF to improve the T estimation [82,83,84]. Due to weak signal strength of SIF and a weak relationship between T and SIF, T produced by SIF needs further evaluation and research considerations [85]. However, these valuable products with GPP and ET algorithms provide new opportunities to estimate the terrestrial WUE at large scales. Further work is necessary to compare the WUE estimated from different remote sensing products.
2.3. Advances in Direct Estimation of Ecosystem WUE by Remote Sensing
Indirect estimation of WUE by ground observations, process models and MODIS products (GPP and ET) have reported large discrepancies in terms of both threshold and spatiotemporal patterns [86]. Direct estimation methods reflecting the response of environmental factors are necessary to calculate the ecosystem WUE accurately. Both biotic and abiotic factors control the variability of WUE, especially for the optical response to VPD and LAI, providing a basis for WUE remote sensing. Biotic factors include percent Nitrogen (N) in canopy, LAI and vegetation indices, while abiotic factors include carbon dioxide (CO2) concentration, VPD, temperature (Ta), precipitation (P), soil moisture (SM), phenology, land use change, and so on. Seasonal and annual variability of WUE is controlled and driven by CO2 concentration, LAI, and VPD, while it is very complex for shorter time scales. The annual increase in globally averaged atmospheric CO2 concentrations along with climate variabilities strongly affect WUE in growing season with the physiological effect of rising CO2 stomatal closure [4,7,87,88]. The response of WUE to VPD varies under different atmospheric and soil conditions, while it is considered to decrease with the increasing VPD [22]. However, the response might be not obvious when VPD is high [89] and may not exist at all during drought events [90]. In comparison to climatic variables, the structural parameters of vegetation and LAI mainly drive the seasonal variability of WUE having a positive relationship with GPP, ET, and WUE across plant functions [91]. Studies also showed that monthly WUE weakly responds to VPD, while it is positively sensitive to air temperature, and is negatively correlated with PAR at the interannual scale [91]. However, response to environmental factors is unclear and not uniform across different types of ecosystem, while this provides a basis to build mechanistic WUE estimating methods.
Few studies have reported a mechanistic estimation of WUE using remote sensing data. In this regard, previous studies have proved that MODIS-derived vegetation indices have a strong correlation with WUE at the ecosystem scale [75]. The existing empirical models are mainly based on a linear relationship of WUE with multiple factors such as MODIS-derived vegetation indices, meteorological data and flux observed data. Some existing empirical models are listed in Table 4.

Table 4.
Referenced empirical models of WUE estimation.
WUE differed significantly across biomasses as well as from the leaf level to the ecosystem scale [3]. Similarly, differences also exist at the spatial (i.e., from site to regional and even globally) and temporal (i.e., from half hourly/daily to 8 days/monthly) scales, and measurements are from flux observations to satellite measurements. Although some researches explored simple models of WUE based on meteorological variables from flux towers [10,11,12] and remote sensing products (MODIS NDVI, EVI, LAI et al.) [96,97], the universality and accuracy of them still need to be improved. Multiple collinearity of input variables (for example, collinearity between LST and EVI) for empirical models can also lead to an uncertainty of WUE estimation. Furthermore, empirical models are mainly based on simple regression methods lacking climatic and meteorological factor forcing.
The analytical model of WUE is derived from an optimal stomatal conductance model, which relies on the notion that WUE modeling can be directly scaled from the leaf level to the ecosystem scale and the assumption made is that during the growing season of vegetation [98,99].
The optimal stomatal conductance model developed by Medlyn et al. (2017) [100] is as follows:
where, GPP is equivalent to leaf net photosynthetic carbon uptake at the leaf level; Ca is atmospheric CO2 concentration (molCO2 mol−1 air); g1 is an empirical parameter fitted by the Ball stomatal conductance model (kPa0.5), which is the canopy conductance slope parameter at the ecosystem scale [101].
ET usually includes T (transpiration), E (evaporation), and Ei (evaporation from canopy interception). As defined in Section 2.1, WUE can be formulated as:
Based on an optimal stomatal conductance model, ecosystem WUE can be reformulated as:
where, Pa is the atmospheric pressure (kPa). The first term of the equation is ecosystem transpiration WUE (GPP/T). The second term is partitioning of T and E (T/ET) estimated by Beer’s Law. k is the radiation extinction coefficient. The expression of T/ET is a more complex phenomenon than that used in this model, and is a popular topic and a challenge to ecohydrology, especially by remote sensing techniques [8,102].
The developed analytical WUE model accounts for the main physiological parameter of vegetation (g1) and three key controlling factors (i.e., Ca, Pa and VPD), implying the importance of plant functional traits and the major drivers of change in ecosystem WUE at the annual time scale. Contributions of those controlling factors (Ca, VPD, LAI and ) to global WUE change are about 77 ± 20%, −27 ± 11%, 49 ± 16% and 0.2 ± 3%, respectively (Figure 3.), while the model explains the WUE for only 62% [8]. The advantage of this model is that it provides a meaningful conceptualization of WUE and the uncertainty in inputs can be quantified, while its limitation is that its application for shorter time scales needs to be tested and improved due to neglecting some important factors [8]. Additionally, it is also difficult to validate the assumption of through observations during the growing season. Measuring the third term, which is an evaporation from the canopy interception, is also a challenge with unavailable ground-based observations, and the main focus of remote sensing techniques is to solve it. Overall, all three terms in this model are needed to be validated independently, and so is the performance of the model.
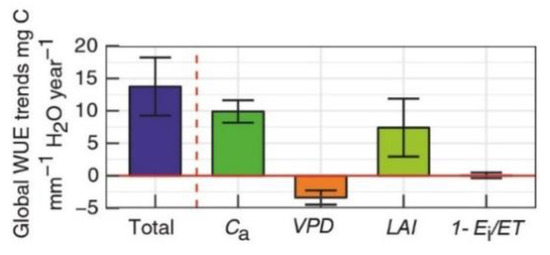
Figure 3.
Contributions of key controlling factors to global WUE change. The error bars are standard deviation (Source: Cheng et al., 2017 [8]). Reprinted with permission. Adapted with permission from ref. [8] Copyright 2017 The authors.
Ecosystem WUE modeled by the main controlling factors can directly capture the apparent variability, while the seasonal variability of g1, varying with the dynamics of biogeochemical cycles and vegetation growth, still need to be discussed. Moreover, the responses of WUE to VPD and vegetation indices have revealed the importance of variability in vegetation physiological parameters [8,75]. There is a good linear correlation between WUE and VIs, as shown in Figure 4a. It can also be observed that WUE exponentially respond to VPD (Figure 4b) at each growth stage of vegetation with a varying slope. Changes in slope across growth stages and for vegetation types should be considered based on the linear relationship between WUE and vegetation indices, or based on the embedded phenological information. The goodness of fit is mainly affected by the density of data because leaves grow and wither rapidly during the period of emergence and senescence, respectively, and fewer data are available. Experimentally, clarifying how slopes vary and how remote sensing parameters capture the rapid changes of vegetation during the spring and the fall is key to improve the direct estimation of WUE.
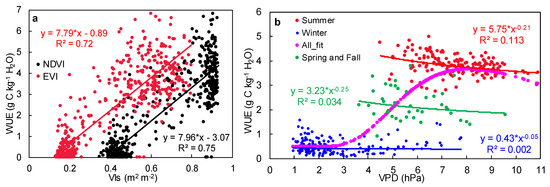
Figure 4.
Scatterplots between WUE and (a) VIs (WUE is indirectly estimated by flux observation. NDVI and EVI are calculated by MODIS reflectance products. GPP and ET data at 8-day time scale are averaged from daily observed data of FLUXNET (https://fluxnet.org/. Accessed on 15 January 2020)). Three temperate broadleaf forest sites, i.e., IT-Col, US-MMS and US-UMB are selected. The black and red lines represent the linear trend between WUE and EVI, and NDVI, respectively), and (b) VPD (The data are based on daily mean values of US-MMS site from 2000–2014. The pink curve indicates the resulted fitting equation, i.e., using daily data for the whole year. Winter and summer respectively represent the non-growth and growth periods, whereas spring and autumn respectively represent the emergence and senescence periods. The phenological information is determined by the rate of change in slope for the fitted curve’s double logistic function to the WUE time series).
2.4. Vegetation Growth Dominates the Seasonal Variability of the Ecosystem WUE
Vegetation is both the main body of carbon sequestration and the largest source of evapotranspiration in ecosystems and plays a key role in the seasonal variability of WUE [91]. As the main controlling factor of WUE, the CO2 has a direct effect on WUE, which decreases by about 20% due to the change in LAI for various types of vegetation [1]. In the analytical WUE model, the input structural and physiological parameters of vegetation are also important to evaluate the coupled water and carbon cycles and variations in WUE. At the same time, the LAI is a negative exponential response to WUE, and it explains about 43% of the variability in annual T/ET at the global ecosystem scale [103]. Vegetation indices (i.e., NDVI, EVI) show a strong correlation with WUE and can capture the seasonal variability of WUE at an 8-day scale across several ecosystems [96,97]. Correct measurement and modeling of WUE for various time scales, especially for shorter time scales at the ecosystem level, needs more understanding of ecosystem characteristics and its responses to environmental forcing [102]. Fortunately, a framework of this model provides an opportunity for coupling remote sensing algorithms. At the same time, a strong correlation between ecosystem WUE and vegetation indices also needs to couple environmental factors to improve WUE estimation in the peak growth period.
3. Challenges of Ecosystem WUE Remote Sensing
During the past few decades, remote sensing techniques have provided a large number of continuous data products for ecosystem research and those products have played a vital role in methodological innovation in ecosystem ecology [104]. However, remote sensing as a basic data source and improvements in accuracy—including temporal and spatial resolution—are still important issues for remote sensing algorithms and products. An analytical WUE model developed by Cheng et al. (2017) also requires long-term continuous and spatially consistent observations on vegetation structural and physiological parameters measured by remote sensing techniques [8]. Although existing empirical and mechanistic models have contributed a lot to the WUE remote sensing, reducing the uncertainty from both methods, input data is still a big challenge.
3.1. Uncertainties and Limitations of the Indirect Estimation of WUE by Remote-Sensed GPP and ET Products
The MODIS GPP and ET products can indirectly estimate ecosystem WUE at an 8-day time scale with the advantage of upscaling carbon and water cycles, but uncertainties remain due to defects in algorithms [97]. Model parameters are mainly from a simple look-up table and uncertainty in model inputs is the source of uncertainty for MODIS GPP and ET products [105,106]. A single set of parameters for MODIS-based GPP and ET algorithms cannot exhibit the spatial heterogeneity of physiological characteristics for each biome [75]. Moreover, soil types, atmospheric conditions and changes in vegetation also affect the variability of physiological parameters [107], which can lead to larger biases in GPP and ET [108]. A parameter optimization method is used to calibrate and reduce uncertainty for the carbon cycle models of MODIS to improve the performance [109]. Those uncertainties are indicated through comparative studies, which show a poor performance of ecosystem WUE estimated by MODIS products indirectly (Figure 5) [86,110]. Therefore, an evaluation and validation of MODIS-based WUE are needed to improve the algorithm and to have new reliable remote sensing products across space and time. More precise structural and physiological parameters of vegetation through remotely sensed data are also needed to improve WUE estimation.
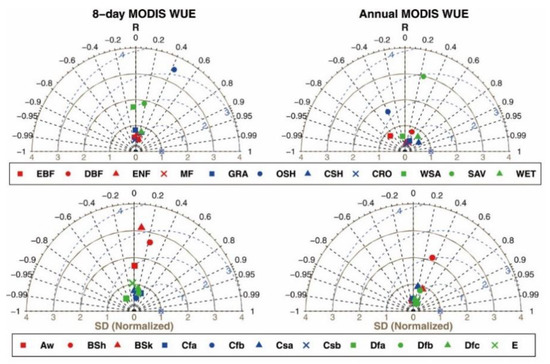
Figure 5.
Taylor diagrams of MODIS WUE compared to flux measurement for 11 plant functional types and climate zones at 8-day and annual time scales [86]. Reprinted with permission. Adapted with permission from ref. [86]. Copyright 2020 Elsevier.
3.2. Uncertainties in Remote Sensing-Based ET
ET is one of the most important components in the water cycle and is also more complex than other processes. The goal towards higher productivity and lower water loss (i.e., high WUE) has always been pursued by agricultural production and even ecosystem development—which meets the requirements of both vegetation and human beings—especially in order to adapt and respond to extreme weather conditions. However, larger uncertainties exist in remote sensing-based ET than that of production, as discussed in Section 2.2.2. Crop consumptive use (i.e., ETa) can be estimated as residual in the water balance equation. Water balance approaches provided accurate data for closed basins over long time spans (typically annual or longer) where changes in surface and groundwater storage are negligible compared to inflows and outflows. However, those conditions are not always met, and water balances are problematic over short time periods, even for individual fields. Crop coefficient methods tend to overestimate crop consumptive use because they are typically derived for optimal conditions, e.g., crops grown in lysimeter, whereas actual field crops have uneven stands, and are subjected to nutrient deficiency and periodic water stress between irrigation intervals. Moreover, neither of these approaches are easily adapted for vegetation, for which crop coefficients might be variable or unknown. Keeping these limitations in view, various researchers have developed numerous methods to estimate ETa through satellite remote sensing [111,112]. These methods fall into two broad categories: a surface energy balance (SEB) method, which uses satellite data from thermal infrared (TIR) bands to estimate sensible heat flux and then calculate latent heat flux (ETa) as residual in the SEB equation; and VI methods, which combine estimation of green foliage density with meteorological data to estimate evaporation from transpiring vegetation. VI-ETo methods [66] substitute a VI for Kc to calculate ETa based on locally measured ETo, while application in precision agriculture remains a challenge.
3.3. High-Quality Remote Sensed Vegetation Parameters for Direct Methods
An analytical WUE model is the unique method for mechanistically estimating WUE at present, while uncertainty still exits due to the neglected factors which may become important at shorter time scales. The first terms involved are the key meteorological controlling factors (Ca, Pa and VPD) and the physiological parameter g1, which can reflect bio-geographical variation in ecosystem WUE, while validation and improvement at a short time scale is a challenge by adding other important factors with unchanging ecological significance [8]. At the same time, another two main affecting factors, such as soil and drought conditions, are not coupled in the model [6,16]. At a regional or global scale, it is also a challenge to extrapolate input meteorological data with satellite data for matching it at a pixel scale. Although many re-analysis datasets of meteorological data have been produced, their spatial resolution is relatively low. The second term is T/ET, which is evaluated via Beer’s Law, which reflects the projective real foliage cover in the original equation. Partitioning T/ET is more complex than that of projective foliage cover and is also limited at the ecosystem scale from both ground-based observation and remote sensed measurement [103]. Remote sensing estimation and verification of soil evaporation and vegetation transpiration is a challenging issue. Due to the heterogeneity of land surfaces, the soil evaporation or vegetation transpiration observed at sites are still difficult to scale up to the satellite pixel scale, and it is impossible to verify the soil evaporation and vegetation transpiration based on low- and medium-resolution remote sensing data [113,114]. Besides, the third term in the analytical model, such as evaporation from canopy interception, is also a challenge due to a poor understanding on the underlying physical processes for both observation and remote sensing measurements [102,115]. Although Ei is considered to be an important component in remote sensing based on the ET algorithm, it is still difficult to independently validate this [116].
Overall, uncertainties in remote sensing products for estimating ecosystem WUE indirectly and for directing methods coupled with an underlying mechanism and remote-sensed vegetation dynamics remain issues to be solved. High temporal resolution remote sensing datasets and high spatial resolution meteorological products matching with remote sensing pixels are also challenges for remote sensing retrieval of ecosystem WUE at large scales. The development of remote sensing techniques associated with the understanding of carbon–water coupling are both opportunities and challenges for improving WUE remote sensing.
4. Possible Ways to Improve WUE Remote Sensing
4.1. Data Fusion Improves GPP and ET Products
Developing a higher spatial and temporal resolution of GPP and ET products is the indirect way to WUE remote sensing. Primarily, studies can be attempted to improve the performance of MODIS GPP and ET products at site and regional scales before developing new algorithms and products. Alternatively, using multi-source satellites, spectral data for the estimation of WUE via empirical models is also a choice at the site scale. A comparison of estimated WUE with vegetation indices from multi-platform (i.e., near ground, unmanned aerial vehicle (UAV), and satellites) or multi-sensors (i.e., multispectral, hyperspectral, and SIF) through an empirical relationship will be a valuable work for examining and improving the remote sensing retrieval of WUE. Research into WUE estimation using UAV remote sensing and Landsat measurements in recent years have rendered an option for comparative studies [117,118]. Moreover, EC tower-based WUE has also shown a stable linear relationship with MODIS land surface temperature (LST) products for specific ecosystem types, and can offer another way for WUE remote sensing [97]. Thermal remote sensing for LST detection has also been provided to use several products available from satellite platforms such as Landsat, Sentinel, and GOES [119,120,121]. Space-borne ECOSTRESS, mounted on the International Space Station produces thermally derived LST at very high temporal and spatial resolutions, which can be applied to capture diurnal variability of WUE [122]. UAV-borne thermal cameras can also portably measure the temperatures of different ecosystem components at the regional scale [123].
Through remote sensing techniques, a better detection of the characteristics of leaf internal biochemistry characteristics to interact with the canopy structure is also an important point for carbon uptake and for the water use of vegetation. For example, the canopy-reflected radiation measured by a satellite-borne sensor should be corrected based on a scattering spectrum of the leaf radiation measured on the ground. This bias is affected by the 3D canopy structure, which cannot be directly measured from space due to specular reflectance at the leaf surface, which is partly polarized and contains no information about its interior [124]. In addition, Hyperspectral Light Detection and Ranging (LiDAR) is an emerging approach to remote sensing techniques, acquiring both the spectral data and the structural parameters of vegetation and can scale the WUE remote sensing to three-dimensional ecological process research.
4.2. Intelligent Algorithms and Big Data Platforms Boost Remote Sensing Retrieval of WUE
Except for data fusion of multi-platform and or multi-sensor by remote sensing, integration of remote sensing and multi-process models is also an effective approach to achieve WUE remote sensing. Integration of those datasets and processes involve a large number of inputs, including remote sensing and climatic data, especially at large scales. Upscaling WUE modeling from a site to a regional level needs several climatic driving factors to be matched at the pixel level, which mainly depends on data reanalysis. A huge amount of data storage and computation on a personal computer is a big challenge. Therefore, a big data platform, for example Google Earth Engine, is a very useful tool to conduct the retrieval and analysis of GPP, ET, and WUE. The cloud-based platform provides free access to analysis through a command line operation, and continually updated satellite remote sensing data (e.g., MODIS, Landsat and Sentinel) and earth-observed climate driving data. Moreover, machine-learning algorithms can also be used for the retrieval of WUE regardless of the complexities underlying the mechanism in the coupling of the ecosystem carbon–water cycle, and simplifying complex physical models for onward simulation which were coupled in the retrieval process, such as radiative transfer models. Several machine learning algorithms, such as artificial neural networks [125], support vector machines [126], random forest [127], regression trees [128], and multivariate adaptive regression spline function [129], have been used for remote sensing retrievals of corresponding variables. Coupling the process model and machine learning methods may be a better way for remote sensing retrievals. Besides, artificial neural networks with meteorological data and remote sensing data as input and a random forest with meteorological data forcing as an input, have been proved to capture the seasonal and daily variabilities [96,130]. Direct estimation of ecosystem WUE by intelligent algorithms inputting meteorological forcing and remote sensing parameters will be also a choice before the underlying mechanism is clear.
4.3. Remote Sensing Methods Coupled with an Analytical Model
An analytical WUE model has provide a conceptualization of ecosystem WUE, under which data fusion from multiple platforms and sensors of structural and physiological parameters of vegetation as inputs can improve the WUE remote sensing. The evaporation from canopy interception and T/ET are two important terms in the analytical WUE model, and are also hot topics for research. Accurate remote sensing estimation for these two terms is not only an independent issue, but is also in favor of WUE estimating to upscale to large scales. With the integrated use of remote sensing data, the numerical simulation model, meteorological reanalysis data and ground observation data can also be used to produce high-level remote sensing products. Further analysis on the underlying mechanism of WUE at different time scales is necessary to build a more stable mechanistic model providing the basis of physical processes and biochemical mechanisms for a remote sensing inversion algorithm. On the contrary, the control of vegetation dynamics on the seasonal variability of WUE coupled with the stress of environmental factors (i.e., atmospheric conditions, soil moisture) is another approach to achieve WUE remote sensing inversion at large spatial scales and continuous time scales. Along with the development of high-precision remote sensing algorithms and products, if possible, developing new methods of remote sensing analysis for finely portraying the types, patterns, functions and processes of ecosystems to build the remote sensing-driven ecosystem assessment model is also a direction to follow and a challenge for the future.
5. Conclusions
New analytical approaches for WUE provide a theoretical framework to improve our understanding of ecosystem carbon–water cycle coupling, while assumptions need to be tested across different scales. Multiple approaches and new mechanistical models can then provide a more stable theoretical basis for WUE remote sensing to further improve satellite predictions. In addition, adding data fusion and comparison from multiple platforms and sensors, new remote sensing techniques are also necessary to correct the retrieval of canopy structural and physiological parameters related to the optical characteristics of leaf biochemical constituents. The remote sensing-driven ecosystem analysis methods will also be a direction to better understand the water and carbon cycles and its response to global change, land–atmosphere interaction and ecosystem services to achieve a methodological innovation. More importantly, WUE remote sensing provides a profound understanding of ecosystem carbon–water cycles, and will greatly promote an ecosystem management that contributes to carbon sequestration, emission reduction and the progress of global carbon neutrality.
Author Contributions
All authors contributed to writing the manuscript. W.C. contributed to the literature survey and the writing of the manuscript. S.U. and L.Y. contributed to a review of remote sensing-based ET, discussion of Section 3 and Section 4, and manuscript refinement. Y.L. contributed to designing this study and supervising. All authors have read and agreed to the published version of the manuscript.
Funding
This research and the APC were funded by the National Natural Science Foundation of China, grant number 31870531.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, S.; Yu, B.; Schwalm, C.R.; Ciais, P.; Zhang, Y.; Fisher, J.B.; Michalak, A.M.; Wang, W.; Poulter, B.; Huntzinger, D.N.; et al. Response of Water Use Efficiency to Global Environmental Change Based on Output from Terrestrial Biosphere Models. Glob. Biogeochem. Cycles 2017, 31, 1639–1655. [Google Scholar] [CrossRef]
- Sun, Y.; Piao, S.; Huang, M.; Ciais, P.; Zeng, Z.; Cheng, L.; Li, X.; Zhang, X.; Mao, J.; Peng, S.; et al. Global patterns and climate drivers of water-use efficiency in terrestrial ecosystems deduced from satellite-based datasets and carbon cycle models. Glob. Ecol. Biogeogr. 2016, 25, 311–323. [Google Scholar] [CrossRef]
- Guerrieri, R.; Lepine, L.; Asbjornsen, H.; Xiao, J.; Ollinger, S.V. Evapotranspiration and water use efficiency in relation to climate and canopy nitrogen in U.S. forests. J. Geophys. Res. Biogeosci. 2016, 121, 2610–2629. [Google Scholar] [CrossRef]
- Frank, D.C.; Poulter, B.; Saurer, M.; Esper, J.; Huntingford, C.; Helle, G.; Treydte, K.; Zimmermann, N.E.; Schleser, G.H.; Ahlström, A.; et al. Water-use efficiency and transpiration across European forests during the Anthropocene. Nat. Clim. Chang. 2015, 5, 579–583. [Google Scholar] [CrossRef]
- Maes, W.H.; Pagán, B.R.; Martens, B.; Gentine, P.; Guanter, L.; Steppe, K.; Verhoest, N.E.; Dorigo, W.; Li, X.; Xiao, J.; et al. Sun-induced fluorescence closely linked to ecosystem transpiration as evidenced by satellite data and radiative transfer models. Remote Sens. Environ. 2020, 249, 112030. [Google Scholar] [CrossRef]
- Beer, C.; Ciais, P.; Reichstein, M.; Baldocchi, D.; Law, B.; Papale, D.; Soussana, J.-F.; Ammann, C.; Buchmann, N.; Frank, D.; et al. Temporal and among-site variability of inherent water use efficiency at the ecosystem level. Glob. Biogeochem. Cycles 2009, 23, 2018. [Google Scholar] [CrossRef]
- Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nat. Cell Biol. 2013, 499, 324–327. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, L.; Wang, Y.; Canadell, J.G.; Chiew, F.H.S.; Beringer, J.; Li, L.; Miralles, D.G.; Piao, S.; Zhang, Y. Recent increases in terrestrial carbon uptake at little cost to the water cycle. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Desai, A.; Nagy, Z.; Luo, J.; Kolb, T.E.; Olioso, A.; Xu, X.; Yao, L.; Kutsch, W.; et al. How is water-use efficiency of terrestrial ecosystems distributed and changing on Earth? Sci. Rep. 2015, 4, 7483. [Google Scholar] [CrossRef]
- Sinclair, T.R.; Tanner, C.B.; Bennett, J.M. Water-Use Efficiency in Crop Production. Bioscience 1984, 34, 36–40. [Google Scholar] [CrossRef]
- Gutschick, V.P. Plant acclimation to elevated CO2—From simple regularities to biogeographic chaos. Ecol. Model. 2007, 200, 433–451. [Google Scholar] [CrossRef]
- Wang, J.; Miller, D.R.; Sammis, T.W.; Gutschick, V.P.; Simmons, L.J.; Andales, A.A. Energy balance measurements and a simple model for estimating pecan water use efficiency. Agric. Water Manag. 2007, 91, 92–101. [Google Scholar] [CrossRef]
- Lima, J.R.D.S.; Antonino, A.C.D.; De Souza, E.S.; Lira, C.A.B.D.O.; Silva, I.D.F.D. Seasonal and interannual variations of evapotranspiration, energy exchange, yield and water use efficiency of castor grown under rainfed conditions in northeastern Brazil. Ind. Crop. Prod. 2013, 50, 203–211. [Google Scholar] [CrossRef]
- Linderson, M.-L.; Mikkelsen, T.; Ibrom, A.; Lindroth, A.; Ro-Poulsen, H.; Pilegaard, K. Up-scaling of water use efficiency from leaf to canopy as based on leaf gas exchange relationships and the modeled in-canopy light distribution. Agric. For. Meteorol. 2012, 152, 201–211. [Google Scholar] [CrossRef]
- Xiao, J.; Sun, G.; Chen, J.; Chen, H.; Chen, S.; Dong, G.; Gao, S.; Guo, H.; Guo, J.; Han, S.; et al. Carbon fluxes, evapotranspiration, and water use efficiency of terrestrial ecosystems in China. Agric. For. Meteorol. 2013, 182–183, 76–90. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, J.; Ju, W.; Zhou, Y.; Wang, S.; Wu, X. Water use efficiency of China’s terrestrial ecosystems and responses to drought. Sci. Rep. 2015, 5, 13799. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. Daily underlying water use efficiency for AmeriFlux sites. J. Geophys. Res. Biogeosci. 2015, 120, 887–902. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef]
- Huang, M.; Piao, S.; Sun, Y.; Ciais, P.; Cheng, L.; Mao, J.; Poulter, B.; Shi, X.; Zeng, Z.; Wang, Y. Change in terrestrial ecosystem water-use efficiency over the last three decades. Glob. Chang. Biol. 2015, 21, 2366–2378. [Google Scholar] [CrossRef]
- Tang, X.; Ding, Z.; Li, H.; Li, X.; Luo, J.; Xie, J.; Chen, D. Characterizing ecosystem water-use efficiency of croplands with eddy covariance measurements and MODIS products. Ecol. Eng. 2015, 85, 212–217. [Google Scholar] [CrossRef]
- Kuglitsch, F.G.; Reichstein, M.; Beer, C.; Carrara, A.; Ceulemans, R.; Granier, A.; Janssens, I.A.; Koestner, B.; Lindroth, A.; Loustau, D.; et al. Characterisation of Ecosystem Water-Use Efficiency of European Forests from Eddy Covariance Measurements. Biogeosci. Discuss. 2008, 82, 204–212. [Google Scholar]
- Law, B.; Falge, E.; Gu, L.; Baldocchi, D.; Bakwin, P.; Berbigier, P.; Davis, K.; Dolman, A.; Falk, M.; Fuentes, J.; et al. Environmental controls over carbon dioxide and water vapor exchange of terrestrial vegetation. Agric. For. Meteorol. 2002, 113, 97–120. [Google Scholar] [CrossRef]
- Yu, G.; Song, X.; Wang, Q.; Liu, Y.; Guan, D.; Yan, J.; Sun, X.; Zhang, L.; Wen, X. Water-use efficiency of forest ecosystems in eastern China and its relations to climatic variables. New Phytol. 2008, 177, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. The effect of vapor pressure deficit on water use efficiency at the subdaily time scale. Geophys. Res. Lett. 2014, 41, 5005–5013. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Partitioning evapotranspiration based on the concept of underlying water use efficiency. Water Resour. Res. 2016, 52, 1160–1175. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, Y.; Huang, Y.; Wang, G. Water use efficiency and evapotranspiration partitioning for three typical ecosystems in the Heihe River Basin, northwestern China. Agric. For. Meteorol. 2018, 253–254, 261–273. [Google Scholar] [CrossRef]
- Scott, R.L.; Edwards, E.A.; Shuttleworth, W.; Huxman, T.E.; Watts, C.; Goodrich, D.C. Interannual and seasonal variation in fluxes of water and carbon dioxide from a riparian woodland ecosystem. Agric. For. Meteorol. 2004, 122, 65–84. [Google Scholar] [CrossRef]
- Dragoni, D.; Schmid, H.P.; Grimmond, C.S.B.; Loescher, H.W. Uncertainty of annual net ecosystem productivity estimated using eddy covariance flux measurements. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Post, H.; Hendricks-Franssen, H.-J.; Graf, A.; Schmidt, M.; Vereecken, H. Uncertainty analysis of eddy covariance CO2 flux measurements for different EC tower distances using an extended two-tower approach. Biogeosciences 2015, 12, 1205–1221. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Correction to “Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Space Phys. 2012, 117, 245–255. [Google Scholar] [CrossRef]
- Thornton, P.; Rosenbloom, N.A. Ecosystem model spin-up: Estimating steady state conditions in a coupled terrestrial carbon and nitrogen cycle model. Ecol. Model. 2005, 189, 25–48. [Google Scholar] [CrossRef]
- Thornton, P.E.; Lamarque, J.-F.; Rosenbloom, N.A.; Mahowald, N.M. Influence of carbon-nitrogen cycle coupling on land model response to CO2fertilization and climate variability. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Thornton, P.E.; Doney, S.; Lindsay, K.; Moore, J.K.; Mahowald, N.; Randerson, J.T.; Fung, I.; Lamarque, J.-F.; Feddema, J.J.; Lee, Y.-H. Carbon-nitrogen interactions regulate climate-carbon cycle feedbacks: Results from an atmosphere-ocean general circulation model. Biogeosciences 2009, 6, 2099–2120. [Google Scholar] [CrossRef]
- Randerson, J.T.; Hoffman, F.M.; Thornton, P.; Mahowald, N.M.; Lindsay, K.; Lee, Y.-H.; Nevison, C.D.; Doney, S.; Bonan, G.; Stöckli, R.; et al. Systematic assessment of terrestrial biogeochemistry in coupled climate-carbon models. Glob. Chang. Biol. 2009, 15, 2462–2484. [Google Scholar] [CrossRef]
- Best, M.J.; Pryor, M.; Clark, D.B.; Rooney, G.; Essery, R.L.H.; Menard, C.B.; Edwards, J.M.; Hendry, M.A.; Porson, A.; Gedney, N.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 1: Energy and water fluxes. Geosci. Model Dev. 2011, 4, 677–699. [Google Scholar] [CrossRef]
- Clark, D.B.; Mercado, L.M.; Sitch, S.; Jones, C.D.; Gedney, N.; Best, M.J.; Pryor, M.J.; Rooney, G.; Essery, R.L.H.; Blyth, E.M.; et al. The Joint UK Land Environment Simulator (JULES), model description–Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef]
- Krinner, G.; Viovy, N.; De Noblet-Ducoudré, N.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, 1–44. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Veroustraete, F.; Sabbe, H.; Eerens, H. Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data. Remote Sens. Environ. 2002, 83, 376–399. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E.; Wild, M.; Liang, S. Evidence for decadal variation in global terrestrial evapotranspiration between 1982 and 2002: 1. Model development. J. Geophys. Res. Atmos. 2010, 115, D20112. [Google Scholar] [CrossRef]
- Papale, D.; Valentini, R. Carbon Fluxes Assessment Using Artificial Neural Networks. Cell. Mol. Life Sci. 2003, 5, 763–781. [Google Scholar]
- Yang, K.; Shan, G.; Zhao, L. Application of Input Variables Selecting Method for Support Vector Machine Model. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation 2006, Dalian, China, 4 December 2006. [Google Scholar]
- Zhang, Q.; Cherkasova, L.; Smirni, E. A Regression-Based Analytic Model for Dynamic Resource Provisioning of Multi-Tier Applications. In Proceedings of the Fourth International Conference on Autonomic Computing (ICAC’07), Jacksonville, FL, USA, 11–15 June 2007; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2007; p. 27. [Google Scholar]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Monteith, J.L.; Waggoner, G.S.E. The Measurement and Control of Stomatal Resistance in the Field. J. Appl. Ecol. 1965, 2, 345. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On The Assessment of Surface Heat Flux and Evaporation Using Large-Seale Param-Eters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–223. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. An Improved Method for Estimating Global Evapotranspiration Based on Satellite Determination of Surface Net Radiation, Vegetation Index, Temperature, and Soil Moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Gontia, N.K.; Tiwari, K.N. Estimation of Crop Coefficient and Evapotranspiration of Wheat (Triticum aestivum) in an Irrigation Command Using Remote Sensing and GIS. Water Resour. Manag. 2009, 24, 1399–1414. [Google Scholar] [CrossRef]
- Adamala, S.; Rajwade, Y.A.; Reddy, Y.K. Estimation of wheat crop evapotranspiration using NDVI vegetation index. J. Appl. Nat. Sci. 2016, 8, 159–166. [Google Scholar] [CrossRef]
- Parmar, H.V.; Gontia, N.K. Remote Sensing Based Vegetation Indices and Crop Coefficient Relationship for Estimation of Crop Evapotranspiration in Ozat-Ii Canal Command. J. Agrometeorol. 2016, 18, 137–139. [Google Scholar]
- Kjaersgaard, J.; Allen, R.; Irmak, A. Improved methods for estimating monthly and growing season ET using METRIC applied to moderate resolution satellite imagery. Hydrol. Process. 2011, 25, 4028–4036. [Google Scholar] [CrossRef]
- Nagler, P.L.; Morino, K.; Murray, R.S.; Osterberg, J.; Glenn, E.P. An Empirical Algorithm for Estimating Agricultural and Riparian Evapotranspiration Using MODIS Enhanced Vegetation Index and Ground Measurements of ET. I. Description of Method. Remote Sens. 2009, 1, 1273–1297. [Google Scholar] [CrossRef]
- Hankerson, B.; Kjaersgaard, J.; Hay, C. Estimation of Evapotranspiration from Fields with and without Cover Crops Using Remote Sensing and in situ Methods. Remote Sens. 2012, 4, 3796–3812. [Google Scholar] [CrossRef]
- Lei, H.; Yang, D. Combining the Crop Coefficient of Winter Wheat and Summer Maize with a Remotely Sensed Vegetation Index for Estimating Evapotranspiration in the North China Plain. J. Hydrol. Eng. 2014, 19, 243–251. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Sun, Z.; Gebremichael, M.; Wang, Q.; Wang, J.; Sammis, T.W.; Nickless, A. Evaluation of Clear-Sky Incoming Radiation Estimating Equations Typically Used in Remote Sensing Evapotranspiration Algorithms. Remote Sens. 2013, 5, 4735–4752. [Google Scholar] [CrossRef]
- Huang, M.; Piao, S.; Zeng, Z.; Peng, S.; Ciais, P.; Cheng, L.; Mao, J.; Poulter, B.; Shi, X.; Yao, Y.; et al. Seasonal responses of terrestrial ecosystem water-use efficiency to climate change. Glob. Chang. Biol. 2015, 22, 2165–2177. [Google Scholar] [CrossRef] [PubMed]
- Sobrino, J.; Gómez, M.; Jiménez-Muñoz, J.; Olioso, A. Application of a simple algorithm to estimate daily evapotranspiration from NOAA–AVHRR images for the Iberian Peninsula. Remote Sens. Environ. 2007, 110, 139–148. [Google Scholar] [CrossRef]
- Donohue, R.; Hume, I.; Roderick, M.; McVicar, T.; Beringer, J.; Hutley, L.; Gallant, J.; Austin, J.; Van Gorsel, E.; Cleverly, J.; et al. Evaluation of the remote-sensing-based DIFFUSE model for estimating photosynthesis of vegetation. Remote Sens. Environ. 2014, 155, 349–365. [Google Scholar] [CrossRef]
- Yang, Y.; Long, D.; Shang, S. Remote estimation of terrestrial evapotranspiration without using meteorological data. Geophys. Res. Lett. 2013, 40, 3026–3030. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Zhang, L.; Li, H. Use of Remotely Sensed Actual Evapotranspiration to Improve Rainfall–Runoff Modeling in Southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
- Zscheischler, J.; Reichstein, M.; Von Buttlar, J.; Mu, M.; Randerson, J.T.; Mahecha, M.D. Carbon cycle extremes during the 21st century in CMIP5 models: Future evolution and attribution to climatic drivers. Geophys. Res. Lett. 2014, 41, 8853–8861. [Google Scholar] [CrossRef]
- Cho, E.; Choi, M. Regional scale spatio-temporal variability of soil moisture and its relationship with meteorological factors over the Korean peninsula. J. Hydrol. 2014, 516, 317–329. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Xu, X.; Luo, J.; Li, X.; Ding, Z.; Xie, J. Potential of MODIS data to track the variability in ecosystem water-use efficiency of temperate deciduous forests. Ecol. Eng. 2016, 91, 381–391. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.-E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.T.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef] [PubMed]
- Köehler, P.; Frankenberg, C.; Magney, T.S.; Guanter, L.; Joiner, J.; Landgraf, J. Global Retrievals of Solar-Induced Chlorophyll Fluorescence With TROPOMI: First Results and Intersensor Comparison to OCO-2. Geophys. Res. Lett. 2018, 45, 10–456. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Jung, M.; Joiner, J.; Guanter, L.; Köhler, P.; Magney, T. Overview of Solar-Induced chlorophyll Fluorescence (SIF) from the Orbiting Carbon Observatory-2: Retrieval, cross-mission comparison, and global monitoring for GPP. Remote Sens. Environ. 2018, 209, 808–823. [Google Scholar] [CrossRef]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: Methodology, simulations, and application to GOME-2. Atmos. Meas. Tech. 2013, 6, 2803–2823. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Zhang, Y.; Chen, J.M. Correcting Clear-Sky Bias in Gross Primary Production Modeling From Satellite Solar-Induced Chlorophyll Fluorescence Data. J. Geophys. Res. Biogeosci. 2020, 125. [Google Scholar] [CrossRef]
- Feng, H.; Xu, T.; Liu, L.; Zhou, S.; Zhao, J.; Liu, S.; Xu, Z.; Mao, K.; He, X.; Zhu, Z.; et al. Modeling Transpiration with Sun-Induced Chlorophyll Fluorescence Observations via Carbon-Water Coupling Methods. Remote Sens. 2021, 13, 804. [Google Scholar] [CrossRef]
- Shan, N.; Zhang, Y.; Chen, J.M.; Ju, W.; Migliavacca, M.; Peñuelas, J.; Yang, X.; Zhang, Z.; Nelson, J.A.; Goulas, Y. A model for estimating transpiration from remotely sensed solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2021, 252, 112134. [Google Scholar] [CrossRef]
- Shan, N.; Ju, W.; Migliavacca, M.; Martini, D.; Guanter, L.; Chen, J.; Goulas, Y.; Zhang, Y. Modeling canopy conductance and transpiration from solar-induced chlorophyll fluorescence. Agric. For. Meteorol. 2019, 268, 189–201. [Google Scholar] [CrossRef]
- Damm, A.; Haghighi, E.; Paul-Limoges, E.; van der Tol, C. On the seasonal relation of sun-induced chlorophyll fluorescence and transpiration in a temperate mixed forest. Agric. For. Meteorol. 2021, 304–305, 108386. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Zhang, S.; Wang, J.; Bai, Y.; Yao, F.; Guo, H. The potential of remote sensing-based models on global water-use efficiency estimation: An evaluation and intercomparison of an ecosystem model (BESS) and algorithm (MODIS) using site level and upscaled eddy covariance data. Agric. For. Meteorol. 2020, 287, 107959. [Google Scholar] [CrossRef]
- Peñuelas, J.; Terradas, J.; Lloret, F. Solving the conundrum of plant species coexistence: Water in space and time matters most. New Phytol. 2010, 189, 5–8. [Google Scholar] [CrossRef] [PubMed]
- Hommel, R.; Siegwolf, R.; Saurer, M.; Farquhar, G.D.; Kayler, Z.; Ferrio, J.P.; Gessler, A. Drought response of mesophyll conductance in forest understory species—Impacts on water-use efficiency and interactions with leaf water movement. Physiol. Plant. 2014, 152, 98–114. [Google Scholar] [CrossRef]
- Eamus, D.; Cleverly, J.; Boulain, N.; Grant, N.; Faux, R.; Villalobos-Vega, R. Carbon and water fluxes in an arid-zone Acacia savanna woodland: An analyses of seasonal patterns and responses to rainfall events. Agric. For. Meteorol. 2013, 182–183, 225–238. [Google Scholar] [CrossRef]
- Reichstein, M.D.; Baldocchi, S.; Running, J.; Tenhunen, R.; Valentini, S.; Rambal, J.; Ourcival, A.; Granier, O.; Bouriaud, C.B. Validation Effort of Modis Lai/Gpp/Npp Products at Fluxnet Sites. Nephrology 2002, 4, 243–245. [Google Scholar]
- Li, Y.; Shi, H.; Zhou, L.; Eamus, D.; Huete, A.; Li, L.; Cleverly, J.; Hu, Z.; Harahap, M.; Yu, Q.; et al. Disentangling Climate and LAI Effects on Seasonal Variability in Water Use Efficiency Across Terrestrial Ecosystems in China. J. Geophys. Res. Biogeosci. 2018, 123, 2429–2443. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, X.; Yu, G.; He, N.; Wang, Q.; Tian, J. Water use efficiency threshold for terrestrial ecosystem carbon sequestration in China under afforestation. Agric. For. Meteorol. 2014, 195–196, 32–37. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Liu, G.; Li, X.; Yao, L.; Xie, J.; Chang, S. Sensitivity of near real-time MODIS gross primary productivity in terrestrial forest based on eddy covariance measurements. Chin. Geogr. Sci. 2015, 25, 537–548. [Google Scholar] [CrossRef]
- Xie, J.; Chen, J.; Sun, G.; Zha, T.; Yang, B.; Chu, H.; Liu, J.; Wan, S.; Zhou, C.; Ma, H.; et al. Ten-year variability in ecosystem water use efficiency in an oak-dominated temperate forest under a warming climate. Agric. For. Meteorol. 2016, 218–219, 209–217. [Google Scholar] [CrossRef]
- Xu, X.; Xuguang, T. Remote Estimation of Ecosystem Water-Use Efficiency of Irrigated and Rainfed Maize Croplands with Modis Data Feb. Fresenius Environ. Bull. 2016, 25, 1383–1394. [Google Scholar]
- Wagle, P.; Gowda, P.H.; Xiao, X.; Kc, A. Parameterizing ecosystem light use efficiency and water use efficiency to estimate maize gross primary production and evapotranspiration using MODIS EVI. Agric. For. Meteorol. 2016, 222, 87–97. [Google Scholar] [CrossRef]
- Tang, X.; Ma, M.; Ding, Z.; Xu, X.; Yao, L.; Huang, X.; Gu, Q.; Song, L. Remotely Monitoring Ecosystem Water Use Efficiency of Grassland and Cropland in China’s Arid and Semi-Arid Regions with MODIS Data. Remote Sens. 2017, 9, 616. [Google Scholar] [CrossRef]
- Barton, C.V.; Duursma, R.A.; Medlyn, B.E.; Ellsworth, D.S.; Eamus, D.; Tissue, D.T.; Adams, M.; Conroy, J.; Crous, K.Y.; Liberloo, M.; et al. Effects of elevated atmospheric [CO2] on instantaneous transpiration efficiency at leaf and canopy scales in Eucalyptus saligna. Glob. Chang. Biol. 2011, 18, 585–595. [Google Scholar] [CrossRef]
- Wong, S.C.; Cowan, I.R.; Farquhar, G.D. Stomatal conductance correlates with photosynthetic capacity. Nat. Cell Biol. 1979, 282, 424–426. [Google Scholar] [CrossRef]
- Medlyn, B.E.; De Kauwe, M.; Lin, Y.; Knauer, J.; Duursma, R.A.; Williams, C.A.; Arneth, A.; Clement, R.; Isaac, P.; Limousin, J.; et al. How do leaf and ecosystem measures of water-use efficiency compare? New Phytol. 2017, 216, 758–770. [Google Scholar] [CrossRef]
- Ball, J.T.; Woodrow, I.E.; Berry, J. A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis under Different Environmental Conditions. Prog. Photosynth. Res. 1987, 221–224. [Google Scholar] [CrossRef]
- Stoy, P.C.; El-Madany, T.S.; Fisher, J.B.; Gentine, P.; Gerken, T.; Good, S.P.; Klosterhalfen, A.; Liu, S.; Miralles, D.G.; Perez-Priego, O.; et al. Reviews and syntheses: Turning the challenges of partitioning ecosystem evaporation and transpiration into opportunities. Biogeosciences 2019, 16, 3747–3775. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Barbosa, C.D.A.; Atkinson, P.M.; Dearing, J.A. Remote sensing of ecosystem services: A systematic review. Ecol. Indic. 2015, 52, 430–443. [Google Scholar] [CrossRef]
- Xiao, J.; Davis, K.J.; Urban, N.M.; Keller, K.; Saliendra, N.Z. Upscaling carbon fluxes from towers to the regional scale: Influence of parameter variability and land cover representation on regional flux estimates. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Quesada, C.A.; Lloyd, J.; Schwarz, M.; Patiño, S.; Baker, T.R.; Czimczik, C.; Fyllas, N.M.; Martinelli, L.; Nardoto, G.; Schmerler, J.; et al. Variations in chemical and physical properties of Amazon forest soils in relation to their genesis. Biogeosciences 2010, 7, 1515–1541. [Google Scholar] [CrossRef]
- Castanho, A.D.A.; Coe, M.T.; Costa, M.; Malhi, Y.; Galbraith, D.; Quesada, C.A. Improving simulated Amazon forest biomass and productivity by including spatial variation in biophysical parameters. Biogeosciences 2013, 10, 2255–2272. [Google Scholar] [CrossRef]
- Huang, X.; Xiao, J.; Wang, X.; Ma, M. Improving the global MODIS GPP model by optimizing parameters with FLUXNET data. Agric. For. Meteorol. 2021, 300, 108314. [Google Scholar] [CrossRef]
- Xue, B.-L.; Guo, Q.; Otto, A.; Xiao, J.; Tao, S.; Li, L. Global patterns, trends, and drivers of water use efficiency from 2000 to 2013. Ecosphere 2015, 6, 174. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating Remote Sensing and Ground Methods to Estimate Evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.; McCabe, M. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Condon, L.E. Connections between groundwater flow and transpiration partitioning. Science 2016, 353, 377–380. [Google Scholar] [CrossRef]
- Chen, H.; Huang, J.J.; McBean, E.; Singh, V.P. Evaluation of alternative two-source remote sensing models in partitioning of land evapotranspiration. J. Hydrol. 2021, 597, 126029. [Google Scholar] [CrossRef]
- van Dijk, A.I.; Gash, J.H.; van Gorsel, E.; Blanken, P.D.; Cescatti, A.; Emmel, C.; Gielen, B.; Harman, I.; Kiely, G.; Merbold, L.; et al. Rainfall interception and the coupled surface water and energy balance. Agric. For. Meteorol. 2015, 214–215, 402–415. [Google Scholar] [CrossRef]
- Wang, Y.; Li, R.; Min, Q.; Fu, Y.; Wang, Y.; Zhong, L.; Fu, Y. A three-source satellite algorithm for retrieving all-sky evapotranspiration rate using combined optical and microwave vegetation index at twenty AsiaFlux sites. Remote Sens. Environ. 2019, 235, 111463. [Google Scholar] [CrossRef]
- Peddinti, S.R.; Kambhammettu, B.V.N.P.; Rodda, S.R.; Thumaty, K.C.; Suradhaniwar, S. Dynamics of Ecosystem Water Use Efficiency in Citrus Orchards of Central India Using Eddy Covariance and Landsat Measurements. Ecosystem 2019, 23, 511–528. [Google Scholar] [CrossRef]
- Han, W.J.; Tang, L.; Zhang, Y.; Niu, T.W. Water Use Efficiency and Biomass Estimation Using Unmanned Aerial Vehicle (Uav) Remote Sensing. Trans. Chin. Soc. Agric. Mach. 2020, 52, 129–141. [Google Scholar]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; Fisher, J.B.; Baldocchi, D.D. ECOSTRESS estimates gross primary production with fine spatial resolution for different times of day from the International Space Station. Remote Sens. Environ. 2021, 258, 112360. [Google Scholar] [CrossRef]
- Pau, S.; Detto, M.; Kim, Y.; Still, C.J. Tropical forest temperature thresholds for gross primary productivity. Ecosphere 2018, 9, 02311. [Google Scholar] [CrossRef]
- Yang, B.; Knyazikhin, Y.; Lin, Y.; Yan, K.; Chen, C.; Park, T.; Choi, S.; Mõttus, M.; Rautiainen, M.; Myneni, R.B.; et al. Analyses of Impact of Needle Surface Properties on Estimation of Needle Absorption Spectrum: Case Study with Coniferous Needle and Shoot Samples. Remote Sens. 2016, 8, 563. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2007, 29, 617–663. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Donmez, C.; Berberoglu, S.; Erdogan, M.A.; Tanriover, A.A.; Cilek, A. Response of the regression tree model to high resolution remote sensing data for predicting percent tree cover in a Mediterranean ecosystem. Environ. Monit. Assess. 2015, 187, 4. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Ma, H.; Zhang, X.; Xiao, Z.; Zhao, X.; Jia, K.; Yao, Y.; Jia, A. GLASS Daytime All-Wave Net Radiation Product: Algorithm Development and Preliminary Validation. Remote Sens. 2016, 8, 222. [Google Scholar] [CrossRef]
- Nelson, J.A.; Carvalhais, N.; Cuntz, M.; Delpierre, N.; Knauer, J.; Ogée, J.; Migliavacca, M.; Reichstein, M.; Jung, M. Coupling Water and Carbon Fluxes to Constrain Estimates of Transpiration: The TEA Algorithm. J. Geophys. Res. Biogeosci. 2018, 123, 3617–3632. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).