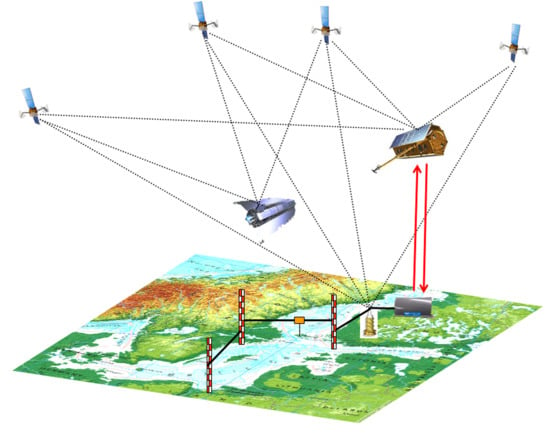
Geodetic SAR for Height System Unification and Sea Level Research—Observation Concept and Preliminary Results in the Baltic Sea
Abstract
1. Introduction
1.1. Height System Unification and Absolute Sea Level in a General Context
1.2. Scientific Challenges
- Connecting the tide gauge markers with the GNSS network geometrically in order to determine the relative vertical motion and to correct the tide gauge readings.
- Determine a GOCE based high resolution geoid height at tide gauge stations in order to deliver absolute heights of tide gauges with respect to a global equipotential surface as reference.
- Joint analysis of geometrical and physical reference frames to make them compatible and to determine corrections to be applied for combined analysis of geometric and physical heights.
1.3. Addressing the Scientific Challenges and Structure of the Paper
2. Test Case Baltic Sea
- Transponder Calibration: Two DLR owned transponders are installed at the DLR premises in Oberpfaffenhofen, Germany, as calibration stations. Both transponders are close to a permanent GNSS station and a standard trihedral CR with a dimension of 1.5 m. Additionally, SAR installations were surveyed by a local campaign with high precision GNSS receivers in order to enable an absolute comparison of positions. This calibration site specifically shall analyze the temporal stability of the ECR solutions and possible delay biases, which might be present in the ECR derived positions.
- Collocation Sites: These are locations where the ECR is directly tied to a tide gauge and a permanent GNSS station within some meters. These are the stations in Władysławowo, Łeba (both Poland) and Spikarna/Vinberget (Sweden). In addition, these sites can be used as second order calibration sites as they are directly tied to a permanent GNSS station as well.
- Tide Gauge Sites: The ECRs at the stations Emäsalo, Rauma, Loksa, and Forsmark are tied to local tide gauges. The resulting ECR positions are used to convert tide gauge heights to ellipsoidal heights and as such this experiment represents the standard case for the future assuming the performance of the absolute ECR positions is at centimeter level. The collocation sites can also be used for this experiment. One just needs to disregard the local tie to the GNSS station.
- Permanent GNSS Network Sites: The permanent GNSS stations Vergi, Loviisa, and Mårtsbo are equipped with an ECR, which is tied to the GNSS station but not linked with a tide gauge. These stations are intended to be used in order to perform an ellipsoidal height transfer from the GNSS station to the tide gauge station in a relative sense by doing differential ECR positioning (see Section 3). This short baseline experiment can be performed for linking Vergi to Loksa, Loviisa to Emäsalo, and Mårtsbo to Forsmark. In addition, the link between the collocation stations Władysławowo and Łeba can be used for this type of experiment.
- Long Baseline Experiment: Long baseline experiments crossing the Baltic Sea are planned by height transfer from Emäsalo to Loksa (North-South baseline) and for Spikarna/Vinberget and Forsmark/Kobben to Rauma (West-East baselines). These experiments shall link two tide gauges, which are connected via ECRs to permanent GNSS sites. The first experiment connects the tide gauges on both sides of the Gulf of Finland to a GNSS station, while the second is only tied on the Swedish side to the GNSS network.
- Tide Gauge Linking Experiment: Two nearby tide gauges are directly linked by means of ECR positions. For this experiment the Polish stations in Władysławowo and Łeba are used.
- Absolute versus Relative Coordinate Transfer: Coordinate transfer between two nearby SAR transponders is done either by absolute or by relative positioning technique (see Section 3). For this, a height transfer from ECR to ECR is done disregarding local ties to GNSS or tide gauge stations. The same baselines as identified for experiment 4 can be used for this analysis as well.
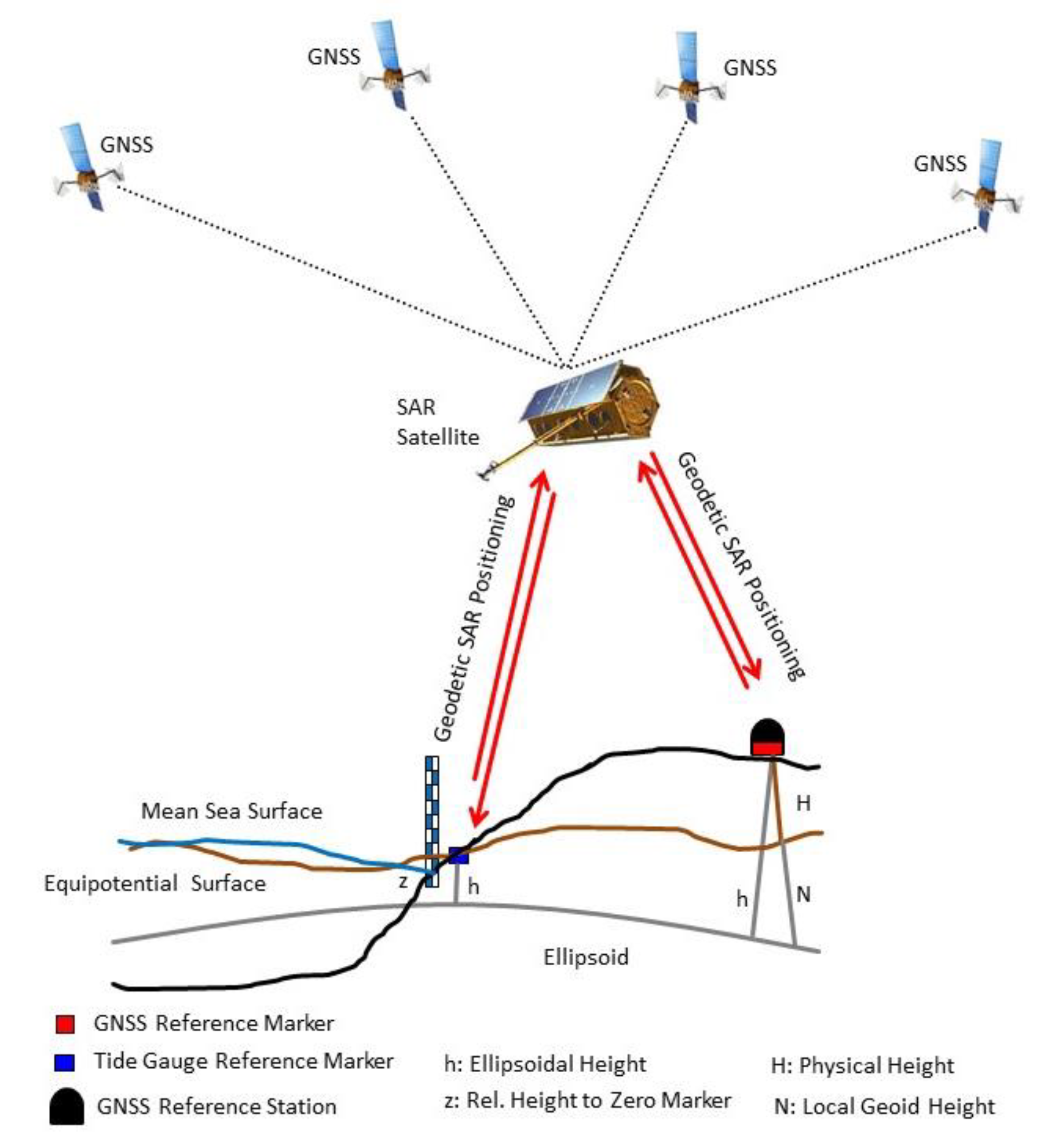
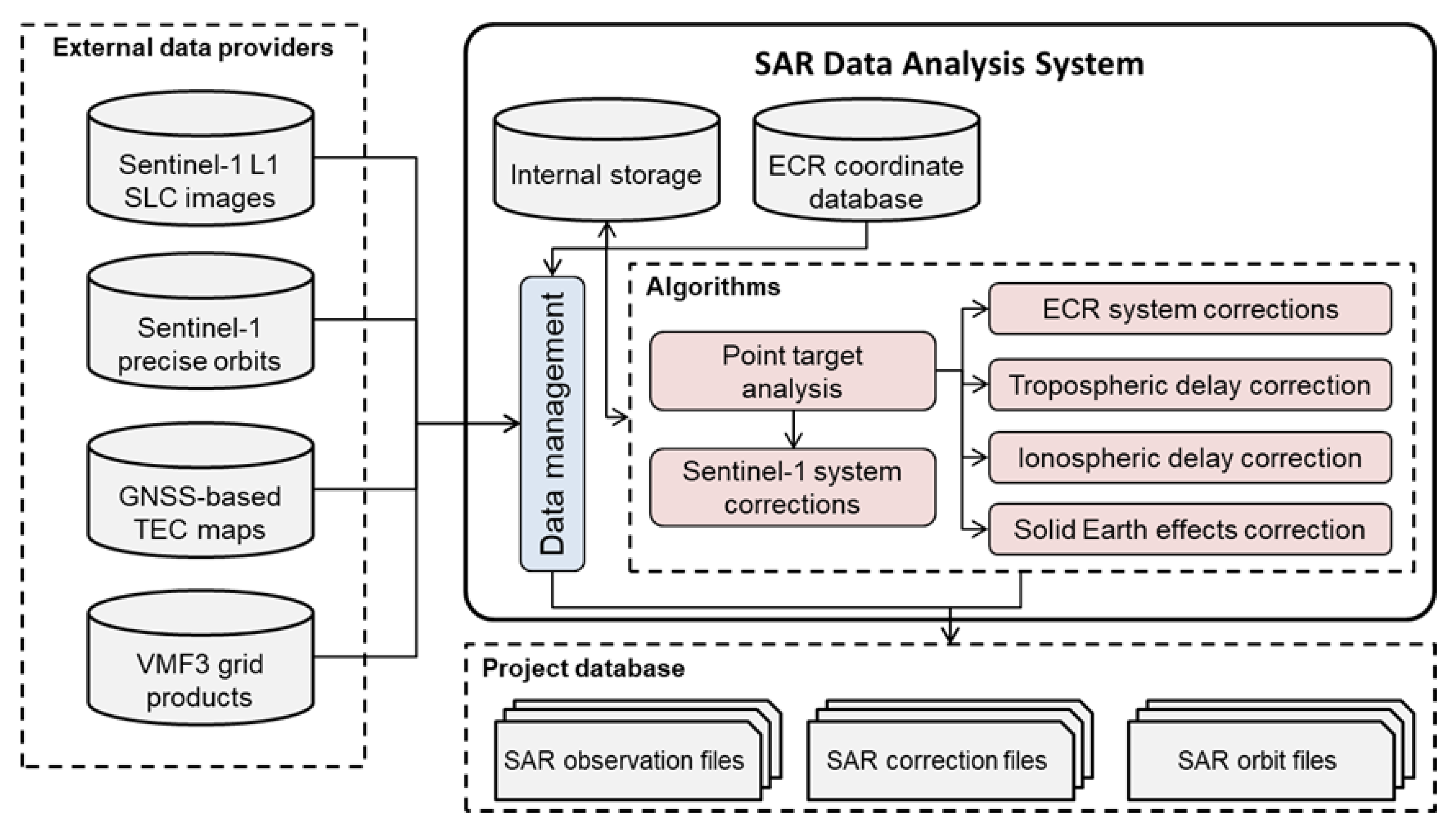
3. Geodetic SAR Data Analysis and Positioning Technique
3.1. SAR Data Analysis
3.1.1. SAR Image Point Target Analysis
3.1.2. Sentinel-1 Systematic Effects Correction
3.1.3. Tropospheric and Ionospheric Delay Corrections
3.1.4. Solid Earth Effects Correction
3.2. SAR Positioning
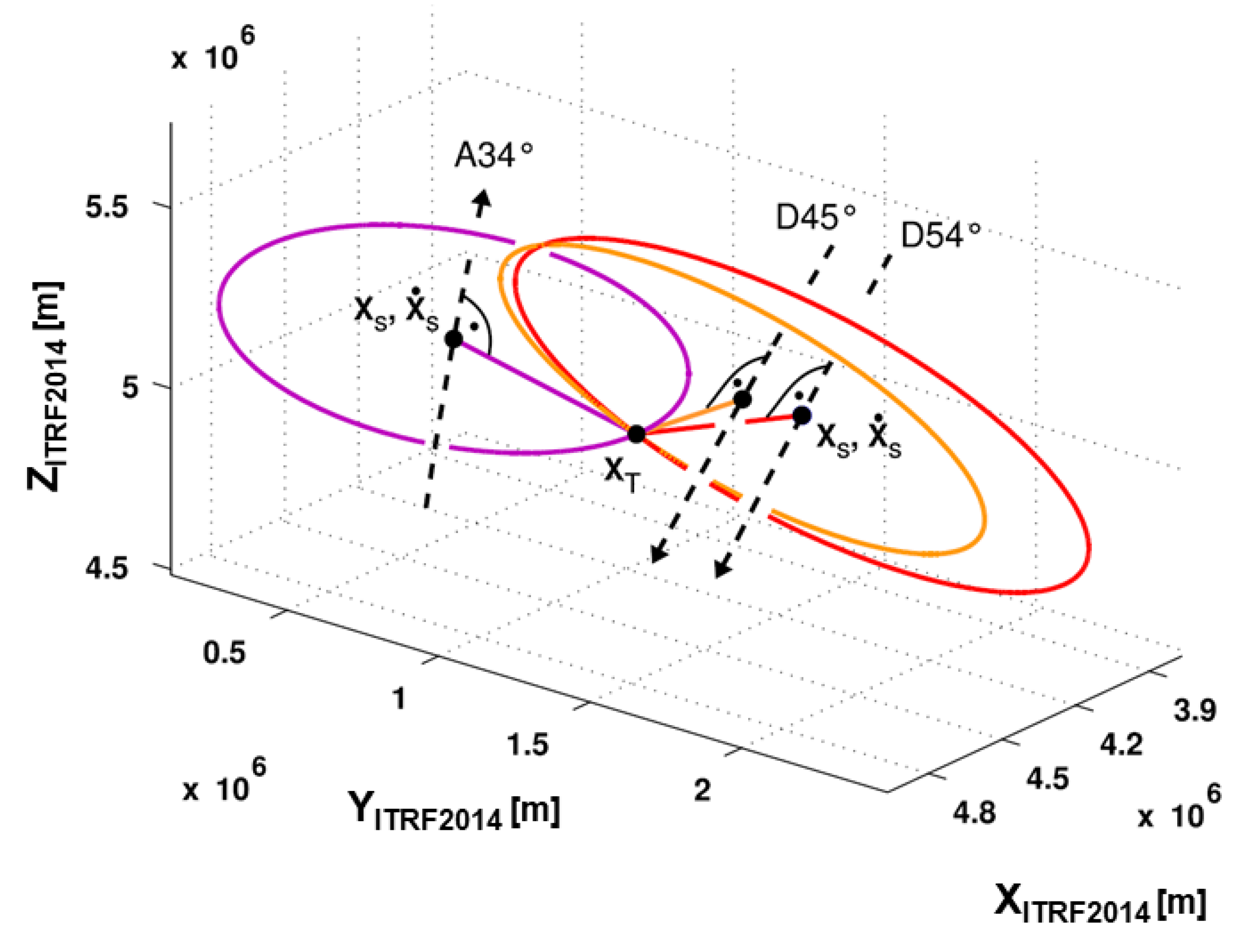
3.2.1. Absolute Positioning
- with:
- : position vector of radar target at epoch
- : position vector of sensor at epoch
- : velocity vector of sensor at epoch
- : speed of light
- : two-way signal travel time
3.2.2. Relative Positioning
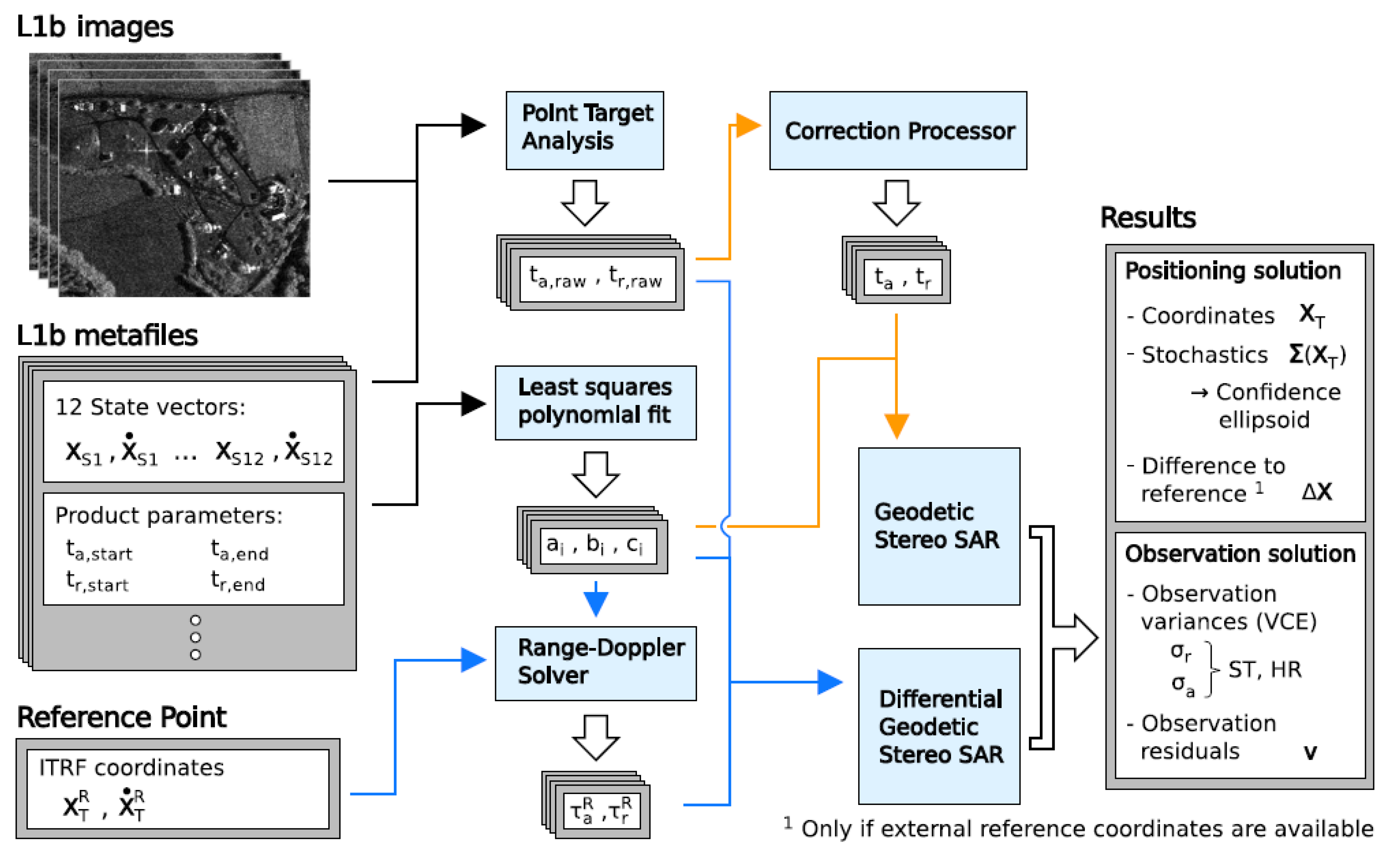
3.2.3. Data Processing Chain
- Azimuth and range are extracted at subpixel level from the Zero-Doppler SLC Sentinel-1 images using Point Target Analysis (PTA) (see Section 3.1).
- The raw timings are corrected for the geodynamic and atmospheric effects and SAR systematic effects.
- The polynomial orbit model’s coefficients are estimated by means of least squares fit.The Geodetic SAR algorithm as described in Section 3.2.1 is applied.
- Azimuth and range are extracted at subpixel level from the Zero-Doppler SLC Sentinel-1 images using Point Target Analysis (PTA) (see Section 3.1).
- The polynomial orbit model’s coefficients are estimated by means of least squares fit.
- The azimuth and range of the reference target are derived from the Range-Doppler equations.The Geodetic SAR algorithm as described in Section 3.2.2 is applied.
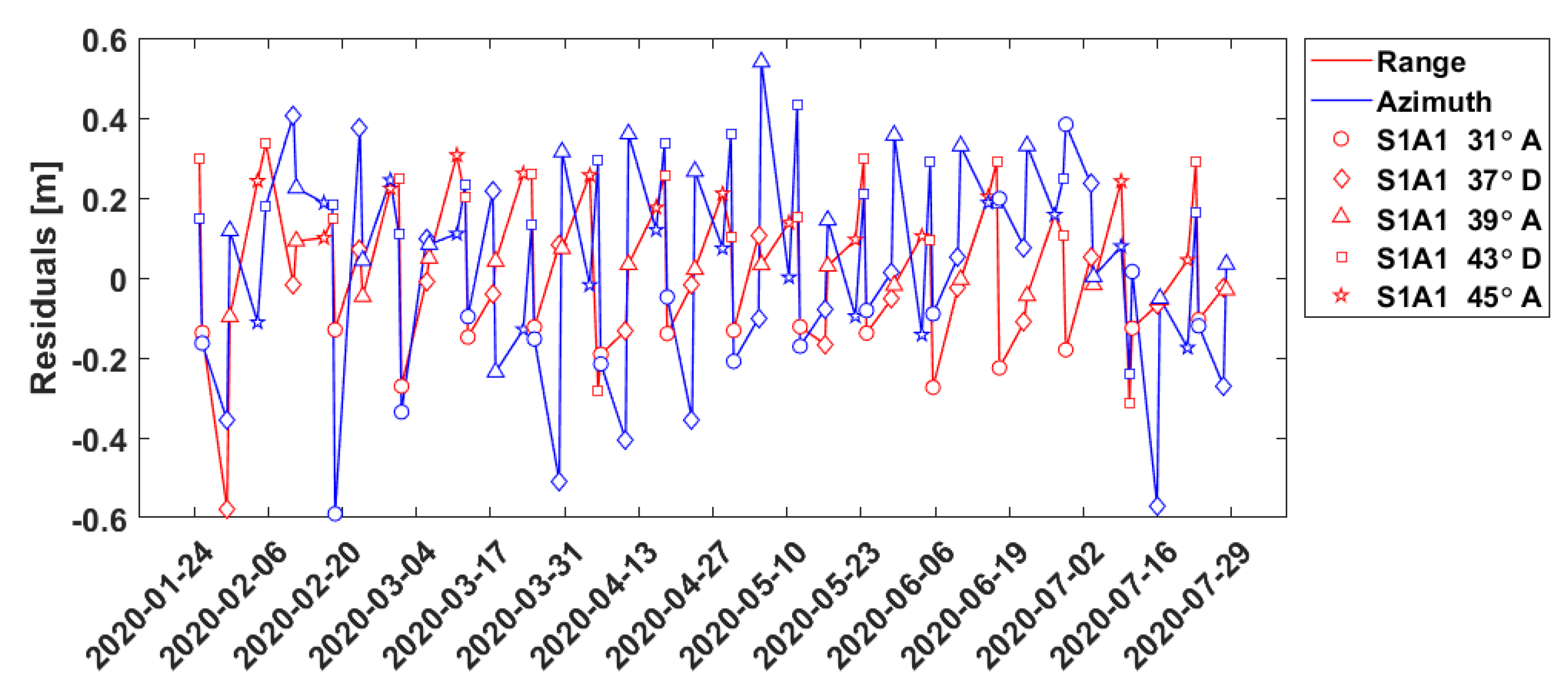
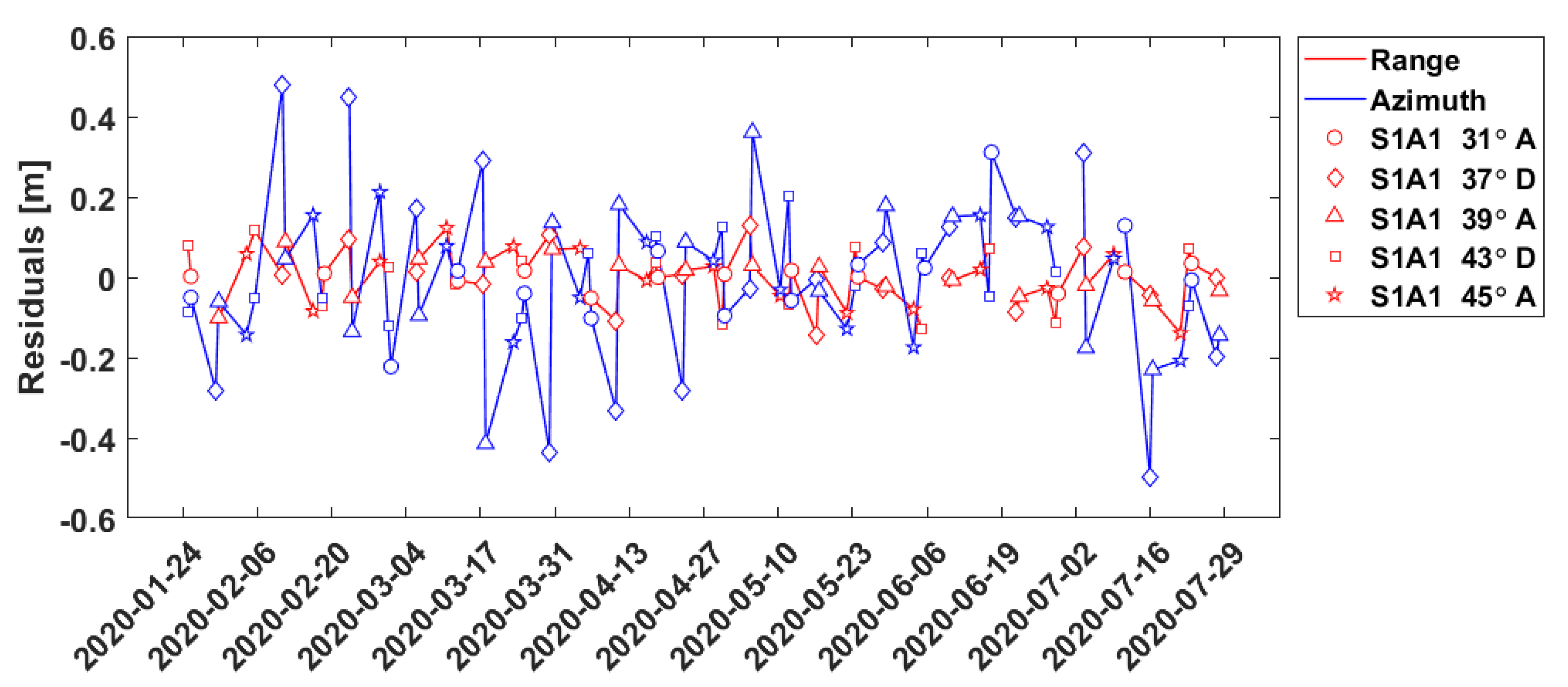
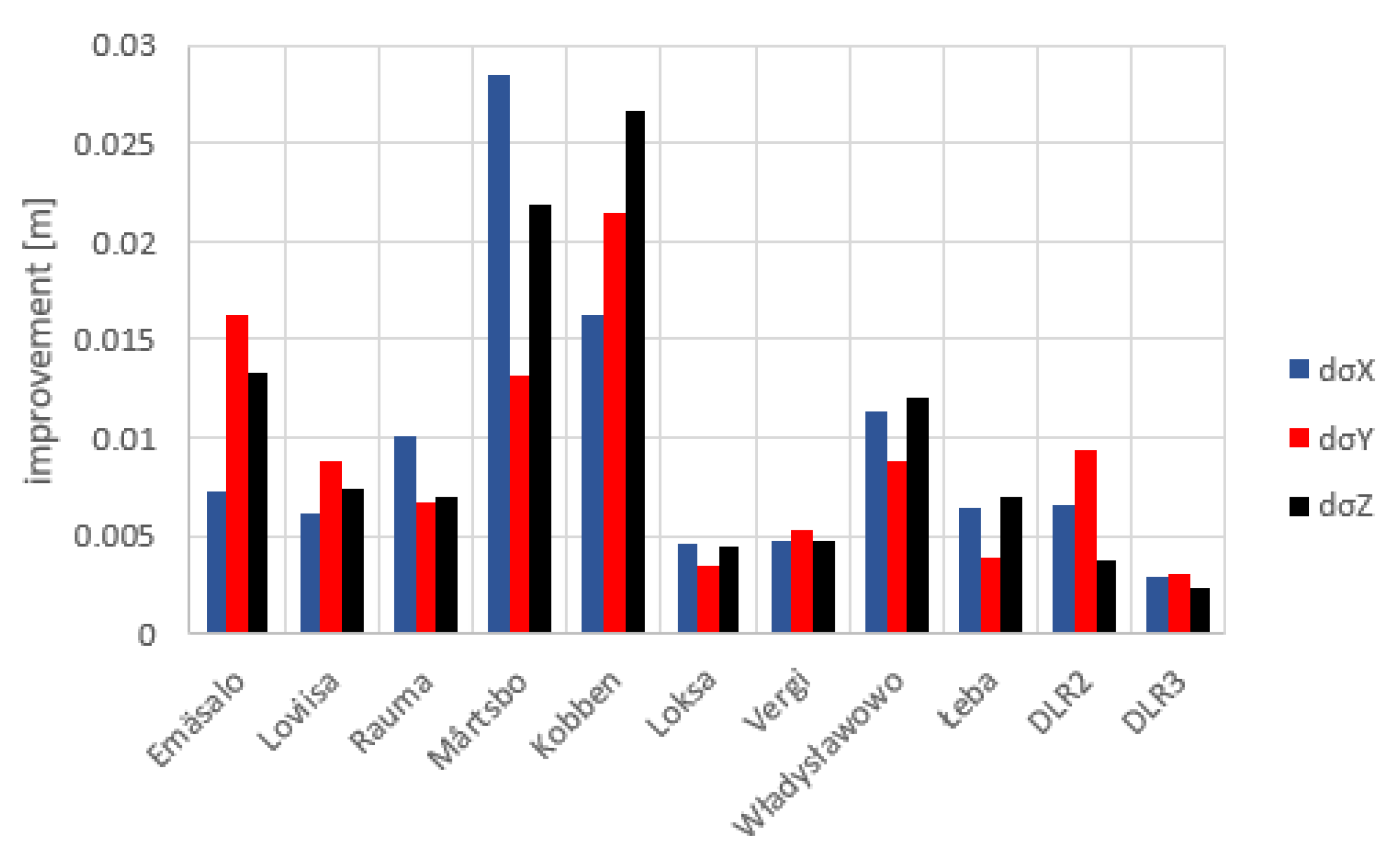
3.3. First Results and Discussion
- Outlier detection per incidence angle: Outlier detection is performed per incidence angle, using a 3σ-median condition. The median is computed using all available observations taken from the same incidence angle. The detection is performed separately for azimuth and range observations.
- Incidence-angle dependent biases: Two biases (range, azimuth) are computed for each incidence angle class. This means that for an ECR that receives signal from 5 different incidence angles, 10 biases will be estimated in total. The biases are computed using the mean of all observations that have not been marked as outliers.
4. Local Geoid Modeling
- Selection of local/regional gravity data from the Nordic Geodetic Commission (NKG) and Polish gravity databases and computation of surface gravity anomalies using the Geodetic Reference System 80 (GRS 80). The algorithms for the latter step are given in [49].
- To obtain a sufficient spectral overlap between the local/regional gravity and the satellite-only EGMs, gravity point data are selected from a rectangular gravity area overlapping the rectangular geoid area with at least 110 km in all directions (corresponding to 1-degree spherical distance in each direction). Two computation areas, one larger area over the Bay of Bothnia/Gulf of Finland (Sweden, Finland, and Estonia) and one smaller area surrounding the Polish tide gauges are foreseen. All methodological tests described below are made over the large main area.
- Computation of topographic RTM effects based on a Digital Elevation Model (DEM) using the algorithms in [43]. In this step, the NKG2015 DEM (called NKG_DEM2014) is used for Sweden, Finland, and Estonia, while for the other areas the SRTM3 [50] and GTOPO30 [51] DEMs are used (the latter for areas above 60° latitude). The RTM effect on the surface gravity anomaly is computed both for each gravity observation and for the gravity grid. The RTM effect on the height anomaly is computed for the geoid grid and for the tide gauge stations. As we are at or close to sea with limited topographic heights, the height anomaly is very close to the geoid height [52].
- Computation of the EGM effects for the gravity anomaly and height anomaly grids using the satellite-only EGMs. This is standard synthesis of solid spherical harmonics; see for instance [53]. An important parameter here is the maximum degree used for the synthesis. This parameter is chosen based on numerical tests with respect to the NKG2015 GNSS/leveling height anomalies in the large geoid area.
- Computation of reduced surface gravity anomalies by subtracting the EGM and RTM effects. Gross error detection is made using cross validation exactly as described in [54].
- For the LSMSA method: The surface gravity anomalies are gridded using Least Squares Collocation (LSC) with a 2nd order Gauss–Markov covariance function. After that, the RTM gravity anomaly grid is restored to get gridded surface gravity anomalies. All details can be found in [54].
- For the LSMSA method: the final geoid heights (height anomalies) are computed using the LSMSA method as implemented in [46], which is also summarized in [54]. The least squares modification of Stokes’ formula is chosen according to the formulation in [44]. The most crucial parameter choices here are to choose as realistic signal and noise degree variances as possible (for the EGM and for the local/regional gravity data). The chosen parameters are validated using GNSS/leveling data.
- For the 3D LSC method: the reduced height anomaly is computed using to the well-known standard formulas of three-dimensional LSC [40]. An empirical covariance function is estimated from the reduced gravity anomalies, to which a Tscherning-Rapp covariance function [41] is then fitted [42]. The standard uncertainties of the observations are taken from the NKG2015 version of the NKG gravity database. To speed up the grid computations, the large height anomaly grid is divided into small 1 x 1-degree grids with some small overlap, which are finally merged to obtain the final height anomaly grid. The point height anomalies in the tide gauges are computed without this approximation and compared to the grid values.
- For the 3D LSC method: the final geoid height (height anomaly) is computed by restoring the EGM and RTM effects, both pointwise in the tide gauges and grid wise.
- The standards to be applied for consistent combination with geometric heights are followed for both methods. The standards are the same as in the NKG2015 geoid model project implying zero permanent tide system and postglacial land uplift epoch 2000.0. Besides, the W0 value is chosen to the values obtained in the NKG2015 project (W0 = 62,636,858.18 m2/s2).
- The tested methods, EGMs, and parameter choices are evaluated in a relative sense using Finnish, Swedish, and Estonian GNSS/leveling height anomalies (inside the large geoid area over the northern/middle Baltic Sea including parts of Gulf of Finland). The GNSS/leveling should refer either to the national realizations of the European Vertical Reference System (EVRS) with postglacial land uplift epoch 2000.0 or to EVRF2007 (as for Poland). The GNSS observations in question must also be transformed from nontidal to zero permanent tide system.
- The NKG2016LU model will be used to convert the absolute geoid heights from epoch 2000.0 to the mean epoch for the SAR data analysis period.
- Then the NKG2016LU is compared with Grace Follow-on for the period covered with SAR observations. The study is limited to evaluating monthly mean values from one Science Data System center, namely GFZ (Helmholtz Centre Potsdam German Research Centre for Geosciences) [56].
5. Tide Gauge Data, Combination of Heights, and Reference System Issues
5.1. Tide Gauge Data Analysis
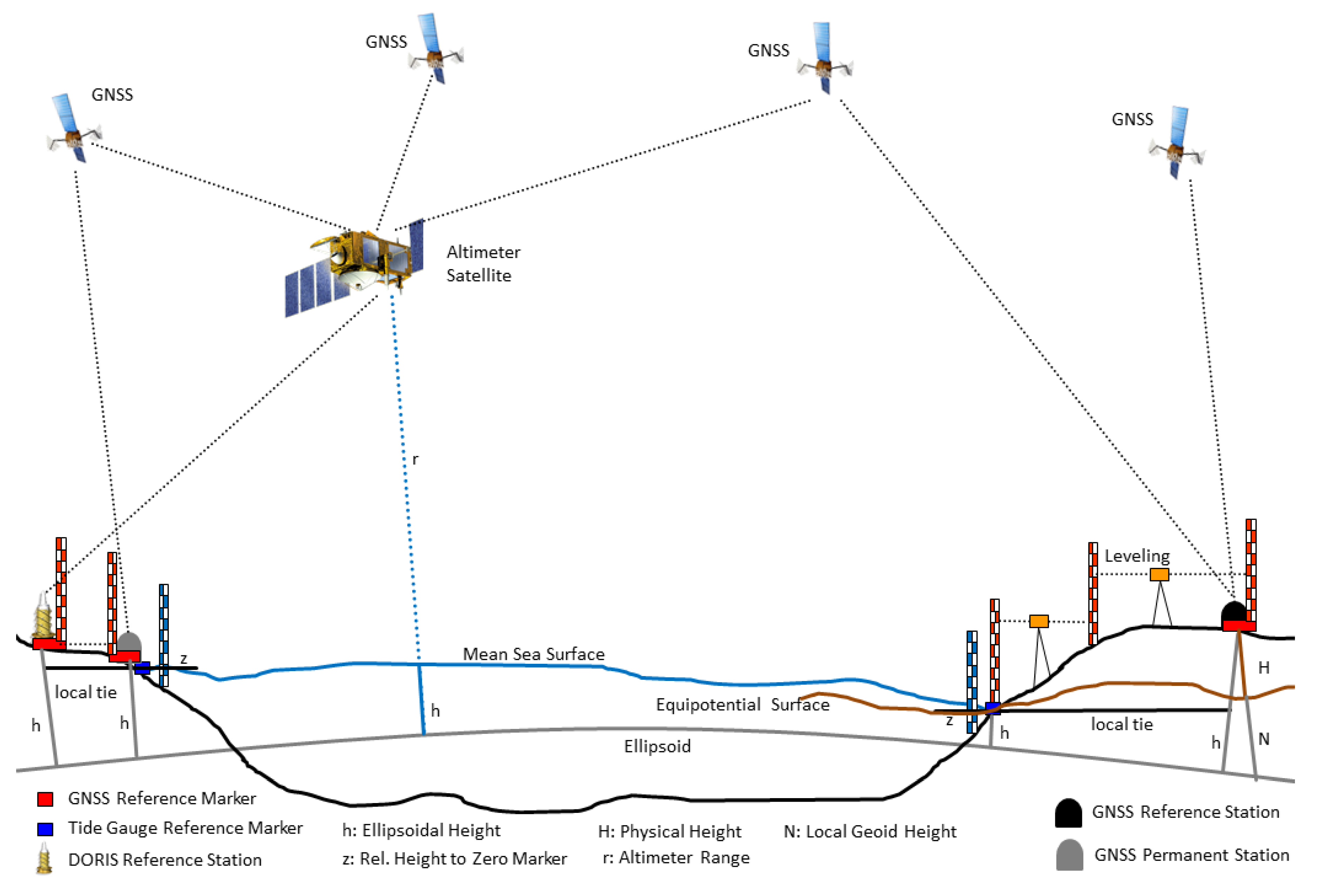
5.2. Computation of Absolute Sea Level Heights
- with:
- Height of tide gauge zero marker above reference ellipsoid at epoch t (ellipsoidal height) (from SAR or GNSS, Section 3)
- Height of reference equipotential surface above reference ellipsoid at tide gauge location at epoch t (geoid height/height anomaly, Section 4)
- Tide gauge sea level height above tide gauge zero marker at epoch t (relative sea level) (Section 5.1)
- Sea level height above reference equipotential surface at epoch t (absolute sea level height)
- with:
- Physical height of tide gauge zero marker above reference equipotential surface
5.3. Reference Frames and Joint Standards
- Nonlinear station motions: The ITRF realizations are primarily based on a linear model (station positions and constant velocities), and thus, nonlinear motions are visible in the station position residuals. The time series analysis of station positions reveals nonlinear motions of several millimeters or even more (up to a few centimeters) for some stations, which are caused by various effects such as neglected surface loading, e.g., [60]. These nonlinear station motions may cause errors in the order of a few millimeters when transforming the (regional) GNSS or SAR positioning solutions into the global reference frame. This is a dominating error source, which can affect the combinations and comparisons of different geometric and gravimetric quantities. Thus, this needs to be considered, e.g., by using the periodic signals of the ITRF2014 results (available on request from IGN [61], by using the DTRF2014 results, which consider for the first time nontidal loading corrections, [62], and by using geophysical models for the atmospheric, hydrological, and oceanic loading from the Global Geophysical Fluids Center (GGFC) or from other available sources.
- Extrapolation of ITRF results: The ITRF2014 and DTRF2014 contain data until the end of 2014. If GNSS (or SAR) solutions (processed for example in 2020) need to be transformed to the global reference frame, the station positions must be extrapolated over a time period of about ten years, since the reference epoch of ITRF2014 station positions is 2010.0. Assuming that station velocities may have an error of 2 mm/yr, the required extrapolation will cause a position error of about 2 cm. Since the nonlinear effects in station position time series (as discussed above) are visible mainly in the height components, this issue is critical.
- Realization of the ITRF origin, Center of Mass (CM) versus Center of Figure (CF): The ITRF origin is realized by SLR observations. Through the orbit dynamics, SLR determines the Center of Mass (CM). According to the IERS Conventions 2010 [36], the ITRF2014 (and DTRF2014) origin follows the mean Earth center of mass, averaged over the time span of SLR observations used and modeled as a secular (linear) function in time. The ITRF2014 provides an annual geocenter motion model derived from the same SLR data that defines the ITRF2014 long-term origin [61]. The DTRF2014 delivers the time series of the SLR translation parameters as an additional product [62], and the JTRF2014 realizes the origin at the quasi-instantaneous CM as sensed by SLR [63]. For further comparisons, also the multisatellite SLR solution computed at DGFI-TUM could be used within this project [60].
- The ETRS89 coincides with the ITRS at epoch 1989.0. This condition leads to consider that the 7 transformation parameters between ITRS and ETRS89 are all zeros at epoch 1989.0.
- The ETRS89 is fixed to the stable part of the Eurasian tectonic plate. This condition implies that the ETRS89 is comoving with the Eurasian tectonic plate, hence defining its time evolution. Therefore, the time derivatives of the seven parameters between ITRS and ETRS89 are zeros, except the three rotation rates. The three rotation rates are in fact the three components of the Eurasia angular velocity in the ITRFyy frames.
6. Summary, Conclusions, and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Church, J.A.; White, N.J. Sea-Level Rise from the Late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Meyssignac, B.; Cazenave, A. Sea level: A review of present-day and recent-past changes and variability. J. Geodyn. 2012, 58, 96–109. [Google Scholar] [CrossRef]
- Stammer, D.; Cazenave, A. Satellite Altimetry over Oceans and Land Surfaces; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-15177-9. [Google Scholar]
- Nerem, R.S.; Chambers, D.P.; Choe, C.; Mitchum, G.T. Estimating Mean Sea Level Change from the TOPEX - and Jason Altimeter Missions. Mar. Geod. 2010, 33, 435. [Google Scholar] [CrossRef]
- Woodworth, P.L.; Player, R. The Permanent Service for Mean Sea Level: An Update to the 21stCentury. J. Coast. Res. 2003, 19, 287–295. [Google Scholar]
- Wöppelmann, G.; Marcos, M.; Santamaría-Gómez, A.; Martín-Míguez, B.; Bouin, M.-N.; Gravelle, M. Evidence for a differential sea level rise between hemispheres over the twentieth century. Geophys. Res. Lett. 2014, 41, 1639–1643. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Martin Miguez, B.; Bouin, M.-N.; Altamimi, Z. Geocentric sea-level trend estimates from GPS analyses at relevant tide gauges world-wide. Glob. Planet. Chang. 2007, 57, 396–406. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Collilieux, X.; Guichard, M.; Míguez, B.M.; Tiphaneau, P.; Wöppelmann, G. Mitigating the effects of vertical land motion in tide gauge records using a state-of-the-art GPS velocity field. Glob. Planet. Chang. 2012, 98–99, 6–17. [Google Scholar] [CrossRef]
- Woodworth, P.L.; Hughes, C.W.; Bingham, R.J.; Gruber, T. Towards worldwide height system unification using ocean information. J. Geod. Sci. 2012, 2, 302–318. [Google Scholar] [CrossRef]
- Gruber, T.; Gerlach, C.; Haagmans, R. Intercontinental height datum connection with GOCE and GPS-levelling data. J. Geod. Sci. 2012, 2, 270–280. [Google Scholar] [CrossRef]
- Collilieux, X.; Wöppelmann, G. Global sea-level rise and its relation to the terrestrial reference frame. J. Geod. 2011, 85, 9–22. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Letetrel, C.; Santamaria, A.; Bouin, M.-N.; Collilieux, X.; Altamimi, Z.; Williams, S.D.P.; Miguez, B.M. Rates of sea-level change over the past century in a geocentric reference frame. Geophys. Res. Lett. 2009. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Coastal sea level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Schubert, T.; Mayer-Gürr, T.; Schuh, W.-D. The Earth’s Gravity Field as Seen by the GOCE Satellite—An Improved Sixth Release Derived with the Time-Wise Approach; GFZ Data Services, 2019; Available online: https://dataservices.gfz-potsdam.de/icgem/showshort.php?id=escidoc:4315891 (accessed on 13 November 2020).
- Förste, C.; Abrykosov, O.; Bruinsma, S.; Dahle, C.; König, R.; Lemoine, J.-M. ESA’s Release 6 GOCE Gravity Field Model by Means of the Direct Approach Based on Improved Filtering of the Reprocessed Gradients of the Entire Mission; GFZ Data Services, 2019; Available online: https://gfzpublic.gfz-potsdam.de/pubman/faces/ViewItemFullPage.jsp?itemId=item_4495891_2&view=EXPORT (accessed on 13 November 2020).
- Brooks, B.A.; Merrifield, M.A.; Foster, J.; Werner, C.L.; Gomez, F.; Bevis, M.; Gill, S. Space geodetic determination of spatial variability in relative sea level change, Los Angeles basin. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Eineder, M.; Minet, C.; Steigenberger, P.; Cong, X.; Fritz, T. Imaging Geodesy—Toward Centimeter-Level Ranging Accuracy with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2011, 49, 661–671. [Google Scholar] [CrossRef]
- Balss, U.; Gisinger, C.; Cong, X.Y.; Brcic, R.; Steigenberger, P.; Eineder, M.; Pail, R.; Hugentobler, U. High resolution geodetic earth observation with TerraSAR-X: Correction schemes and validation. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 4499–4502. [Google Scholar]
- Gisinger, C.; Balss, U.; Pail, R.; Zhu, X.X.; Montazeri, S.; Gernhardt, S.; Eineder, M. Precise Three-Dimensional Stereo Localization of Corner Reflectors and Persistent Scatterers With TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1782–1802. [Google Scholar] [CrossRef]
- Gisinger, C.; Schubert, A.; Breit, H.; Garthwaite, M.; Balss, U.; Willberg, M.; Small, D.; Eineder, M.; Miranda, N. In-Depth Verification of Sentinel-1 and TerraSAR-X Geolocation Accuracy Using the Australian Corner Reflector Array. IEEE Trans. Geosci. Remote Sens. 2020, 1–28. [Google Scholar] [CrossRef]
- Mahapatra, P.S.; Samiei-Esfahany, S.; van der Marel, H.; Hanssen, R.F. On the Use of Transponders as Coherent Radar Targets for SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1869–1878. [Google Scholar] [CrossRef]
- Gisinger, C.; Willberg, M.; Balss, U.; Klügel, T.; Mähler, S.; Pail, R.; Eineder, M. Differential geodetic stereo SAR with TerraSAR-X by exploiting small multi-directional radar reflectors. J. Geod. 2017, 91, 53–67. [Google Scholar] [CrossRef]
- Bloßfeld, M.; Müller, H.; Gerstl, M.; Štefka, V.; Bouman, J.; Göttl, F.; Horwath, M. Second-degree Stokes coefficients from multi-satellite SLR. J. Geod. 2015, 89, 857–871. [Google Scholar] [CrossRef]
- Poutanen, M.; Kakkuri, J. Final Results of the Baltic Sea Level 1997 GPS Campaign; Reports; Finnish Geodetic Institute: Helsinki, Finland, 1999; 182p. [Google Scholar]
- Kakkuri, J. Final Results of the Baltic Sea Level 1993 Campaign; Reports; Finnish Geodetic Institute: Helsinki, Finland, 1995. [Google Scholar]
- Sentinel High Level Operations Plan (HLOP)—Sentinel 1 SAR Document Library—User Guides—Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-1-sar/document-library/-/asset_publisher/1dO7RF5fJMbd/content/sentinel-high-level-operations-plan (accessed on 22 September 2020).
- di Meo, P.; Pausini, M.; Carnavale, G.; Trampuz, C.; Meta, A. ECR-C User Manual; Issue 1.6; MetaSensing BV: Noordwijk, The Netherlands, 2019. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House: London, UK, 2005; ISBN 978-1-58053-058-3. [Google Scholar]
- Piantanida, R.; Recchia, A.; Franceschi, N.; Valentino, A.; Miranda, N.; Schubert, A.; Small, D. Accurate Geometric Calibration of Sentinel-1 Data. In Proceedings of the EUSAR 2018—12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018; pp. 1–6. [Google Scholar]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. Refined discrete and empirical horizontal gradients in VLBI analysis. J. Geod. 2018, 92, 1387–1399. [Google Scholar] [CrossRef] [PubMed]
- Kouba, J. Implementation and testing of the gridded Vienna Mapping Function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Institut für Geodäsie und Photogrammetrie Eidg; Technische Hochschule Zürich: Zürich, Switzerland, 1999; ISBN 9783908440017. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Balss, U.; Cong, X.Y.; Brcic, R.; Rexer, M.; Minet, C.; Breit, H.; Eineder, M.; Fritz, T. High precision measurement on the absolute localization accuracy of TerraSAR-X. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1625–1628. [Google Scholar]
- Petit, G.; Luzum, B. IERS—IERS Conventions (2010); IERS Technical Note No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, German, 2010; ISBN 3-89888-989-6. [Google Scholar]
- Leberl, F.W. Radargrammetric Image Processing; Artech House: Norwood, MA, USA, 1990; ISBN 0-89006-273-0. [Google Scholar]
- Mikhail, E.M.; Ackermann, F.E. Observations and Least Squares; IEP: New York, NY, USA, 1976; ISBN 978-0-7002-2481-4. [Google Scholar]
- Xu, G. Sciences of Geodesy—II; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-27999-7. [Google Scholar]
- Moritz, H. Advanced Physical Geodesy; Wichmann; Abacus Press: Karlsruhe, Germany; Tunbridge, UK, 1980; ISBN 978-3-87907-106-7. [Google Scholar]
- Tscherning, C.; Rapp, R.H. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations, and Deflections of the Vertical Implied by Anomaly Degree Variance Models; Report No. 208; Department of Geodetic Science at the Ohio State University: Columbus, OH, USA, 1974. [Google Scholar]
- Tscherning, C.C. Geoid Determination by 3D Least-Squares Collocation. In Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Sansò, F., Sideris, M.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 311–336. ISBN 978-3-540-74700-0. [Google Scholar]
- Forsberg, R. A Study of Terrain Reduction, Density, Anomalies and Geophysical Inversion Methods in Gravity Field Modeling; Report No. 355; Department of Geodetic Science at the Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Sjöberg, L. Refined least squares modification of Stokes’ formula. Manuscr. Geod. 1991, 16, 367–375. [Google Scholar]
- Sjöberg, L.E.; Bagherbandi, M. Gravity Inversion and Integration—Theory and Applications in Geodesy and Geophysics; Sjöberg, L.E., Bagherbandi, M., Eds.; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-50298-4. [Google Scholar]
- Ågren, J.; Sjöberg, L.E.; Kiamehr, R. The new gravimetric quasigeoid model KTH08 over Sweden. J. Appl. Geod. 2009, 3, 143–153. [Google Scholar] [CrossRef]
- Ågren, J.; Strykowski, G.; Bilker-Koivula, M.; Omang, O.C.; Märdla, S.; Forsberg, R.; Ellmann, A.; Oja, T.; Liepinš, I.; Paršeliūnas, E.; et al. The NKG2015 Gravimetric Geoid Model for the Nordic-Baltic Region. In Proceedings of the 1st Joint Commission 2 and IGFS International Symposium on Gravity, Geoid and Height Systems, Thessaloniki, Greece, 19–23 September 2016. [Google Scholar] [CrossRef]
- Kvas, A.; Brockmann, J.M.; Krauss, S.; Schubert, T.; Gruber, T.; Meyer, U.; Mayer-Gürr, T.; Schuh, W.-D.; Jäggi, A.; Pail, R. GOCO06s—A satellite-only global gravity field model. Earth Syst. Sci. Data Discuss. 2020, 1–31. [Google Scholar] [CrossRef]
- Moritz, H. Geodetic Reference System 1980 by H. Moritz. J. Geod. 2000, 74, 128–162. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Earth Resources Observation and Science (EROS) Center, Global 30 Arc-Second Elevation (GTOPO30). 2017. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-global-30-arc-second-elevation-gtopo30?qt-science_center_objects=0#qt-science_center_objects (accessed on 13 November 2020).
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman & Co. Ltd.: New York, NY, USA, 1967; ISBN 0-7167-0233-9. [Google Scholar]
- Barthelmes, F. Definition of Functionals of the Geopotential and Their Calculation from Spherical Harmonic Models: Theory and Formulas Used by the Calculation Service of the International Centre for Global Earth Models (ICGEM); Scientific Technical Report STR 09/02; Potsdam, Germany, 2009; Available online: http://icgem.gfz-potsdam.de (accessed on 13 November 2020).
- Märdla, S.; Ågren, J.; Strykowski, G.; Oja, T.; Ellmann, A.; Forsberg, R.; Bilker-Koivula, M.; Omang, O.; Paršeliūnas, E.; Liepinš, I.; et al. From Discrete Gravity Survey Data to a High-resolution Gravity Field Representation in the Nordic-Baltic Region. Mar. Geod. 2017, 40, 416–453. [Google Scholar] [CrossRef]
- Vestøl, O.; Ågren, J.; Steffen, H.; Kierulf, H.; Tarasov, L. NKG2016LU: A new land uplift model for Fennoscandia and the Baltic Region. J. Geod. 2019, 93, 1759–1779. [Google Scholar] [CrossRef]
- Dahle, C.; Flechtner, F.; Murböck, M.; Michalak, G.; Neumayer, K.H.; Abrykosov, O.; Reinhold, A.; König, R. GRACE-FO Geopotential GSM Coefficients GFZ RL06. GFZ Data Services, 2019. Available online: https://gfzpublic.gfz-potsdam.de/pubman/faces/ViewItemFullPage.jsp?itemId=item_4330890_1 (accessed on 13 November 2020).
- Liibusk, A.; Ellmann, A.; Kõuts, T.; Jürgenson, H. Precise Hydrodynamic Leveling by Using Pressure Gauges. Mar. Geod. 2013, 36, 138–163. [Google Scholar] [CrossRef]
- Kollo, K.; Ellmann, A. Geodetic Reconciliation of Tide Gauge Network in Estonia. Geophysica 2019, 54, 27–38. [Google Scholar]
- Drewes, H.; Kuglitsch, F.G.; Adám, J.; Rózsa, S. The Geodesist’s Handbook 2016. J. Geod. 2016, 90, 907–1205. [Google Scholar] [CrossRef]
- Bloßfeld, M.; Seitz, M.; Angermann, D. Non-linear station motions in epoch and multi-year reference frames. J. Geod. 2014, 88, 45–63. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Seitz, M.; Bloßfeld, M.; Angermann, D.; Schmid, R.; Gerstl, M.; Seitz, F. The New DGFI-TUM Realization of the ITRS: DTRF2014 (Data); Deutsches Geodätisches Forschungsinstitut: Munich, Germany, 2016. [Google Scholar]
- Abbondanza, C.; Chin, T.M.; Gross, R.S.; Heflin, M.B.; Parker, J.W.; Soja, B.S.; van Dam, T.; Wu, X. JTRF2014, the JPL Kalman filter and smoother realization of the International Terrestrial Reference System. J. Geophys. Res. Solid Earth 2017, 122, 8474–8510. [Google Scholar] [CrossRef]

| Location | Local Tie | Operational Since | No. SAR Scenes (Status 7 August 2020) |
|---|---|---|---|
| Loksa, Estonia | Tide Gauge | 16 February 2020 | A: 66 D: 62 |
| Vergi, Estonia | GNSS | 6 March 2020 | A: 40 D: 39 |
| Emäsalo, Finland | Tide Gauge | 25 January 2020 | A: 48 D: 33 |
| Loviisa, Finland | GNSS | 6 February 2020 | A: 30 D: 31 |
| Rauma, Finland | Tide Gauge | 21 April 2020 | A: 28 D: 13 |
| Oberpfaffenhofen 112, Germany | GNSS | 10 January 2020 | A: 68 D: 35 |
| Oberpfaffenhofen 113, Germany | GNSS | 10 January 2020 | A: 68 D: 35 |
| Władysławowo, Poland | Tide Gauge, GNSS | 26 March 2020 | A: 29 D: 30 |
| Łeba, Poland | Tide Gauge, GNSS | 15 May 2020 | A: 20 D: 20 |
| Mårtsbo, Sweden | GNSS | 7 January 2020 | A: 47 D: 61 |
| Forsmark/Kobben, Sweden | Tide Gauge, GNSS | 1 June 2020 | A: 30 D: 20 |
| Spikarna/Vinberget, Sweden | Tide Gauge, GNSS | 1 October 2020 | - |
| Station | X [m] | Y [m] | Z [m] | σX [m] | σY [m] | σZ [m] |
|---|---|---|---|---|---|---|
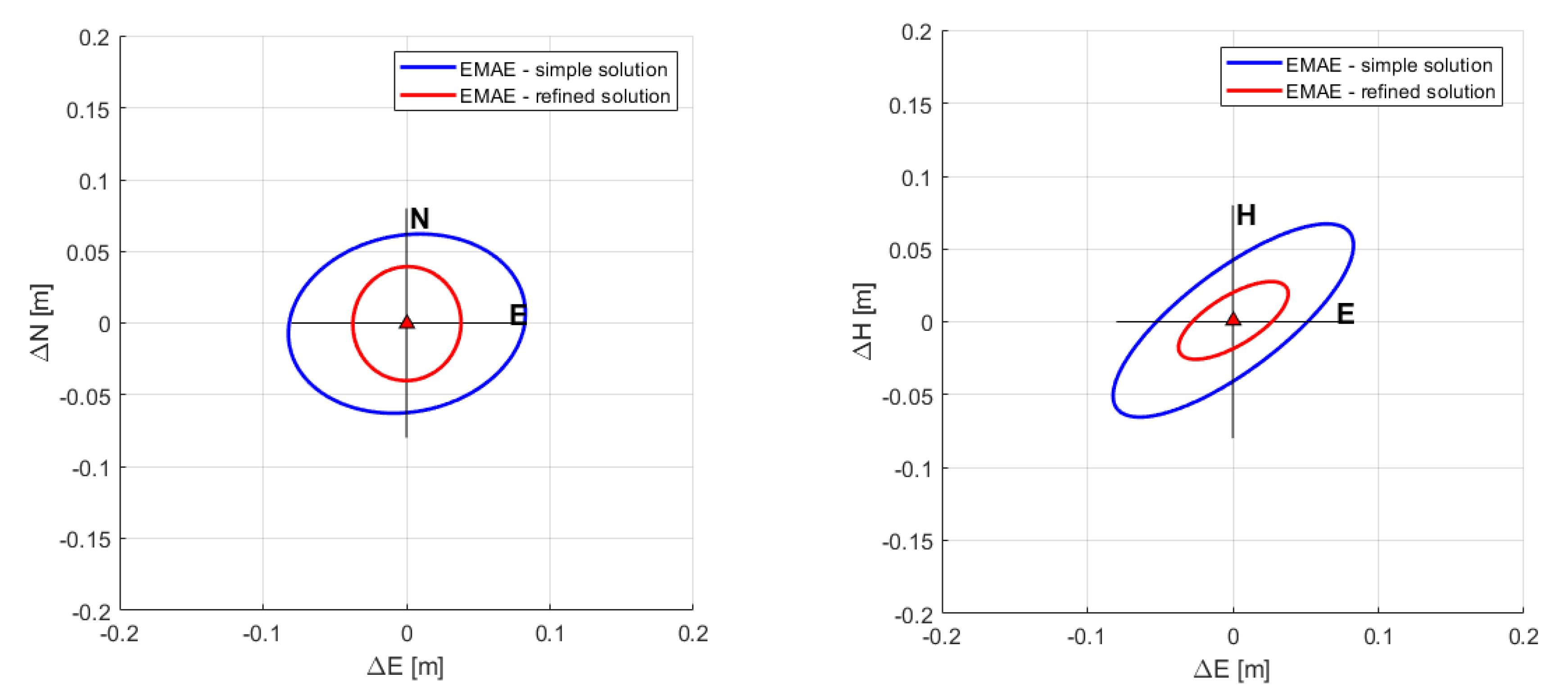
| Emäsalo | 2,864,911.2403 | 1,374,214.0007 | 5,511,816.3914 | 0.0182 | 0.0304 | 0.0252 |
| Station | X [m] | Y [m] | Z [m] | σX [m] | σY [m] | σZ [m] | # Images |
|---|---|---|---|---|---|---|---|
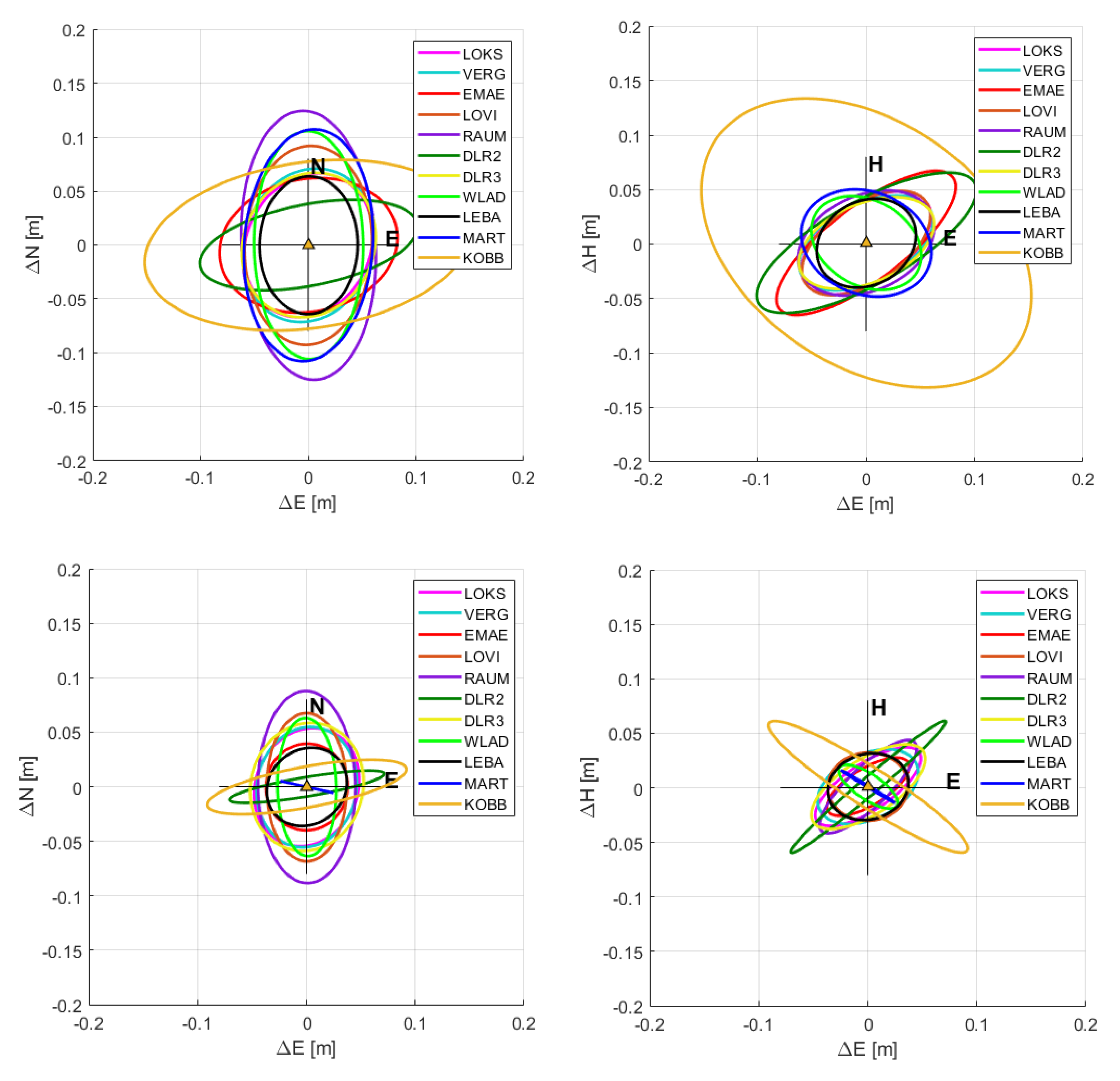
| Loksa | 2,916,917.0475 | 1,404,185.8224 | 5,477,092.8803 | 0.0150 | 0.0180 | 0.0167 | 122 |
| Vergi | 2,905,539.2084 | 1,423,459.6030 | 5,478,168.5668 | 0.0159 | 0.0167 | 0.0161 | 75 |
| Emäsalo | 2,864,911.2403 | 1,374,214.0007 | 5,511,816.3914 | 0.0110 | 0.0142 | 0.0119 | 77 |
| Loviisa | 2,828,355.1337 | 1,396,893.5857 | 5,524,905.6920 | 0.0186 | 0.0146 | 0.0174 | 72 |
| Rauma | 2,873,768.2500 | 1,127,721.6567 | 5,562,560.8600 | 0.0230 | 0.0190 | 0.0224 | 28 |
| DLR2 * | 4,186,628.1019 | 835,142.2965 | 4,723,655.3805 | 0.0064 | 0.0259 | 0.0182 | 21 |
| DLR3 * | 4,186,414.5203 | 834,943.1247 | 4,723,874.5032 | 0.0149 | 0.0194 | 0.0192 | 99 |
| Władysławowo | 3,496,341.5916 | 1,164,349.7496 | 5,188,401.5878 | 0.0166 | 0.0099 | 0.0162 | 55 |
| Łeba | 3,517,625.9637 | 1,111,457.7256 | 5,185,632.4938 | 0.0113 | 0.0126 | 0.0123 | 36 |
| Mårtsbo | 2,998,189.7529 | 931,452.1894 | 5,533,396.5062 | 0.0034 | 0.0080 | 0.0055 | 102 |
| Forsmark/Kobben | 2,998,999.6588 | 987,780.3943 | 5,523,190.5575 | 0.0248 | 0.0260 | 0.0163 | 43 |
| Convention | Semimajor Axis a [m] | Geocentric Grav. Constant GM [1012m3s−2] | Dynamic Form Factor
J2 [10−6] | Earth’s Rotation ω [rad sec−1] | Normal Potential U0 or W0 [m3s−2] |
|---|---|---|---|---|---|
| GRS80 | 6,378,137.0 | 398.600 5 | 1082.63 | 7.292 115 | 62,636,860.850 |
| EGM2008 | 6,378,136.3 | 398.600 4415 (1) | 1082.635 9 | 7.292 115 | 62,636,856.0 |
| IERS Conv. 2010 | 6,378,136.6 (2) | 398.600 4418 (3) | 1082.835 9 | 7.292 115 | 62,636,856.0 |
| IERS Conv. 2010 (update 2017) | 6,378,136.6 (2) | 398.600 4418 (3) | 1082.635 9 | 7.292 115 | 62,636,853.4 |
| IAG2015 | 62,636,853.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruber, T.; Ågren, J.; Angermann, D.; Ellmann, A.; Engfeldt, A.; Gisinger, C.; Jaworski, L.; Marila, S.; Nastula, J.; Nilfouroushan, F.; et al. Geodetic SAR for Height System Unification and Sea Level Research—Observation Concept and Preliminary Results in the Baltic Sea. Remote Sens. 2020, 12, 3747. https://doi.org/10.3390/rs12223747
Gruber T, Ågren J, Angermann D, Ellmann A, Engfeldt A, Gisinger C, Jaworski L, Marila S, Nastula J, Nilfouroushan F, et al. Geodetic SAR for Height System Unification and Sea Level Research—Observation Concept and Preliminary Results in the Baltic Sea. Remote Sensing. 2020; 12(22):3747. https://doi.org/10.3390/rs12223747
Chicago/Turabian StyleGruber, Thomas, Jonas Ågren, Detlef Angermann, Artu Ellmann, Andreas Engfeldt, Christoph Gisinger, Leszek Jaworski, Simo Marila, Jolanta Nastula, Faramarz Nilfouroushan, and et al. 2020. "Geodetic SAR for Height System Unification and Sea Level Research—Observation Concept and Preliminary Results in the Baltic Sea" Remote Sensing 12, no. 22: 3747. https://doi.org/10.3390/rs12223747
APA StyleGruber, T., Ågren, J., Angermann, D., Ellmann, A., Engfeldt, A., Gisinger, C., Jaworski, L., Marila, S., Nastula, J., Nilfouroushan, F., Oikonomidou, X., Poutanen, M., Saari, T., Schlaak, M., Światek, A., Varbla, S., & Zdunek, R. (2020). Geodetic SAR for Height System Unification and Sea Level Research—Observation Concept and Preliminary Results in the Baltic Sea. Remote Sensing, 12(22), 3747. https://doi.org/10.3390/rs12223747