Abstract
The elevation changes of ice sheets have been recognized as an essential climate variable. Long-term time series of these changes are an important parameter to understand climate change, and the longest time-series of ice sheet elevation changes can be derived from combining multiple Ku-band satellite altimetry missions. However, unresolved intermission biases obscure the record. Here, we revise the mathematical model commonly used in the literature to simultaneously correct for intermission bias and ascending–descending bias to ensure the self-consistency and cohesion of the elevation time series across missions. This updated approach is applied to combine Envisat and CryoSat-2 radar altimetry in the period of 2002–2019. We tested this approach by validating it against airborne and satellite laser altimetry. Combining the detailed temporal and spatial evolution of elevation changes with firn densification-modeled volume changes due to surface processes, we found that the Amundsen Sea sector accounts for most of the total volume loss of the Antarctic Ice Sheet (AIS), mainly from ice dynamics. However, surface processes dominate the volume changes in the key regions, such as the Totten Glacier sector, Dronning Maud Land, Princess Elizabeth Land, and the Bellingshausen Sea sector. Overall, accelerated volume loss in the West Antarctic continues to outpace the gains observed in the East Antarctic. The total volume change during 2002–2019 for the AIS was −68.7 ± 8.1 km3/y, with an acceleration of −5.5 ± 0.9 km3/y2.
1. Introduction
The elevation changes of ice sheets are the result of changes in ice sheet ice dynamics and weather-driven changes on the surface. The long-term evolution of ice sheet volume changes is an essential climate variable defined by the Global Climate Observing System (GCOS) to assess the impact of climate change and its contribution to sea level rise. Satellite altimetry can accurately measure the elevation of ice sheets and thereby provide valuable data for monitoring ice sheet changes at both local and continental scales. Since Zwally et al. (1983) [1] first used satellite altimetry measurements in ice sheet surveys, altimetry observations have been essential for studying ice sheet evolution [2,3,4,5,6,7,8]. However, limited by the effective lifetime of the satellite, a single mission cannot characterize the long-term evolution of the ice sheet [9,10]. Consequently, combining observations from multiple altimetric missions is needed to reconstruct the long-term evolution to improve our knowledge of the ice sheets’ responses to present climate change [10,11].
Accounting for the intermission bias caused by differences in the position of the centers of gravity of the two satellites and the phase of the antennae and bias caused by orbital errors, is primary important problem for cross-calibrating observations from multiple altimeter missions [12]. This intermission bias was regarded as a constant and was corrected by calculating the global average in the open sea through the intersection [13]. However, Zwally et al. (2005) [14] found that there was significant intersatellite elevation bias with a distinct spatial pattern over the ice sheets that did not occur over the oceans. This finding was also confirmed by maps of the along-track centered mean bias between the ERS-2 and Envisat altimeter height over the ice sheets and oceans given in Frappart et al. (2016) [15]. Therefore, Schröder et al. (2019) [10], Paolo et al. (2016) [11], Adusumilli et al. (2018) [16], and Sørensen et al. (2018) [17] accounted for the intermission bias at each grid cell using the observations over overlapping epochs.
Additionally, the correction of systematic elevation crossover bias due to the angle between the radar polarization and wind-induced features of the firn is also not trivial for processing radar altimetry data over ice sheets [18,19]. In cross-calibrating the observations from multiple radar altimeter missions, the bias can be divided into an intramission component and an intermission component [15]. The former is known as the ascending–descending bias (A–D bias), which refers to the time-independent part of the difference in the elevation measured on the ascending and descending tracks for the same altimetry mission. Previous studies have shown that the A–D bias is as large as a few meters with a distinct spatial pattern over ice sheets in the elevation measurements [18,19,20,21] and can lead to large errors in the estimation of elevation changes from altimetric observations [22]. Fortunately, Armitage et al. (2014) [18] found that systematic bias varies as a function of the angle between the radar polarization direction and the wind-induced firn azimuthal anisotropy direction. The A–D biases of CryoSat-2 [3,5] or Envisat [23] were successfully corrected by introducing a term of satellite flight direction into the least-squares model for elevation changes. Moreover, Helm et al. (2014) [2] and Schröder et al. (2019) [10] reduced the A–D bias by retracking the return signal waveform of the altimetry observations with a threshold retracker focused on the lower part of the leading edge and thus the surface scattering part. It is because Helm et al. (2014) [2] found the A–D bias is strongly dependent on the choice of the retracker. As for the latter, the intermission component, we call the intermission A–D bias in this study. Khvorostovsky (2012) [12] found that it significantly affected the intermission bias of elevation and backscatter coefficient.
In summary, in the previous studies, the intermission bias and the A–D bias were always corrected separately. In this study, we present an updated plane-fitting least-squares regression model for obtaining a long-term elevation time series of the Antarctic Ice Sheet (AIS) by combining radar altimetry missions. A larger amount of observations are used in the integrated adjustment model to correct the intermission bias and the A–D bias simultaneously. The updated approach is then utilized to develop a monthly elevation time series for a 5 km grid from June 2002 to April 2019 over the AIS and compare the results with those derived by airborne and ICESat laser altimetry observations. Finally, we study and discuss the spatial and temporal variations in the derived volume change of the AIS.
2. Data
2.1. Envisat and CryoSat-2 Altimetry Data
Envisat was launched in March 2002 and operated in a 35-day repeat orbit with a latitude limit of 81.5° S [24]. Here, we applied the recently reprocessed Geophysical Data Record Full Mission Reprocessing V3.0, which only provides the retracked elevations using the ICE-1 retracker from June 2002 to April 2012, to provide better consistency in the data records. The ICE-1 retracker uses standard Offset Centre Of Gravity (OCOG) retracking using a threshold of 0.25 for the OCOG amplitude [25]. Moreover, Davis (1997) [26], Nilsson et al. (2016) [27], and Schröder et al. (2017) [28] argued that such a threshold retracker is more precise in terms of ice sheet elevation measurements. The erroneous height records are culled using standard quality flags.
CryoSat-2 was launched in April 2010 using a 369-day full repeat orbit with a subcycle of 30 days and is still in operation. It operates at an altitude of 717 km with an inclination of 92° and provides coverage up to 88° S. CryoSat-2 measures the interior parts of the AIS in the Low-Resolution Mode (LRM), while using the novel Synthetic Aperture Radar Interferometric (SARIn) mode around the AIS margins. The LRM is equivalent to conventional Ku-band radar altimeters. SARIn is very suitable for measuring steep and complex topography across ice sheet margins because of the use of dual antennae operating in an interferometric mode [29]. The retracked LRM observations with the OCOG retracker from July 2010 to April 2019 were used in the following study to match the Envisat ICE-1 retracker elevations. As for the SARIn observations, the only retracked observations by the Wingham/Wallis model fit retracker provided by the product were used. The erroneous height records and SARIn records where the interferometric across-track location failed were removed.
Therefore, the period from July 2010 to April 2012 could be used to calibrate the intermission biases.
2.2. Laser Altimeter Elevation Datasets from the Operation IceBridge (OIB) Project and ICESat
In this study, based on previous studies, we presented an updated regression model to correct the intermission bias and the A–D bias simultaneously. To evaluate the performance of the model, we needed to validate its results. Here, we used laser altimeter elevation datasets obtained from NASA’s OIB project and ICESat mission.
The OIB project operated since 2009 to bridge the gap between the ICESat and ICESat-2 missions and maintain a continuous observational record over the Arctic and the Antarctic. The Airborne Topographic Mapper (ATM) is an important airborne laser altimeter payload for OIB projects that can provide surface elevation measurements with an accuracy of 10 cm or better [30]. In addition, some pre-IceBridge ATM elevation observations were also collected during 1993–2008.
From 2003 to 2009, ICESat was the first satellite laser altimeter mission, and, by operating in the near inferred spectrum, it provided precise observations of the surface elevation. Here, the latest release of ICESat data (GLA12, Version 34) was used to derive surface elevation change estimates in a 20 km grid via a repeat-track analysis [31]. Intercampaign bias correction and saturation correction were also applied. The final elevation change rate for each grid was generated from the median of surface height change rates to minimize the impact of the remaining outliers, thereby providing a good dataset for benchmarking our elevation change estimates from Envisat.
3. Algorithm for Elevation Time Series
3.1. The Updated Least-Squares Regression Model
Previous studies have demonstrated that elevation time series’ can be obtained by performing a least-squares regression on all elevation measurements within a grid cell, also known as “plane-fitting” [3,10,17,23]. Following these studies, the regression parameters can be expressed as
where is the elevation measured by the satellite altimetry missions at longitude (), latitude (), and time (); is the mean altitude of the bin with the center coordinates (, ) in which the least-squares regression is performed; is the reference epoch set to May 2010; ~ are the coefficients of a biquadratic surface model accounting for topography; is the elevation change rate constant; ~ describe the seasonal variations in elevation; is for the anomaly of backscattered power () to account for variations in the penetration depth of the radar signal; is for the intramission A–D bias, and is assigned a value of 1 for ascending tracks or 0 for descending tracks; is only used in CryoSat-2 data processing to account for the possible bias caused by the different retracking algorithms used for LRM and SARIn, and is 1 for LRM or 0 for SARIn; and denotes the residuals.
However, the regression model above is designed for CryoSat-2. It is not suitable for multimission processing, unless observations from multiple radar altimeter missions are also cross-calibrated. Cross-calibration is used to correct the bias between different satellite radar altimeter missions. As mentioned in Section 1, the bias between two radar altimeter missions, including the intermission bias and the intermission A–D bias, can be regarded as invariants in the local area [10,14,15,18] and can be modeled like A–D in Equation (1). Hence, the intermission extension of Equation (1) is given by
where and are for the intramission A–D bias of Envisat or CryoSat-2, and , , and are for the total static systematic biases of the intermission bias and the intermission A–D bias between Envisat and CryoSat-2. In this study, we referred to these total static systematic biases as the total intermission biases. The internal consistency between these biases (assuming they are constant over time) would give additional constraints, which were handled by the last three equations in Equation (2). Notably, here we discarded , as this bias could be modeled as a part of the intramission A–D bias.
3.2. Calculation of the Combined Elevation Time Series
We first performed the least-squares regression, as shown in Equation (2), at the intersections of the ascending and descending satellite ground tracks of Envisat to estimate all the parameters. For each of the intersections, an independent least-squares regression was estimated based on all Envisat and Cryosat-2 observations within 2.5 km of the center of an intersection. The first-round estimated parameters require that the number of observations of each satellite in an ascending or descending orbit shall not be less than 50. Then, an iterative procedure continues until parameters are estimated that pass the 3σ outlier rejection criteria, as in [6], or until the remaining observations in the bin cannot meet the thresholds. The thresholds require that the total observations be more than 100 and that the number of ascending or descending observations of each satellite be no less than 20. The estimations of the systematic biases , , , , , and over the AIS are determined at all intersections. To ensure a robust solution, we arbitrarily removed the intersections where one or more systematic biases exceeded 50 m. This editing step removed about 1.2% of the intersections over the AIS.
Then, we computed the least-squares regression shown in Equation (2) at a 2.5 km × 2.5 km grid to ensure the resolution of the results. For each of the grid nodes, all Envisat and Cryosat-2 observations within 2.5 km of the center of a grid node were used in the independent least-squares regression estimator. The same 3σ outlier rejection criteria and thresholds used in the least squares regression at the intersections above were also applied to ensure robust least square estimations. Due to a lack of observations, some of the 6 systematic bias parameters were not able to be estimated at some grid points. Here, interpolation of the corresponding parameters calculated at the intersections mentioned above were used. Then, the corrected elevation was calculated as
Here, the mean altitude of the bin is removed to facilitate the study of elevation changes; then, the elevation for a given month is derived from
where is the number of corrected elevations in month . With computed for all months in a given bin, a time series of elevation can be formed.
A floating median is a robust low-pass filter and was used in this study to identify and remove remaining outliers, similar to that in Schröder et al. (2019) [10]. Then, the monthly elevation estimations were smoothed using a spatiotemporal median filter to generate the final 5 km grid of the elevation time series. In the temporal domain, median filtering was performed on the monthly elevation estimations over 3 months (i.e., the given month, the previous month, and the next month) to eliminate high frequency errors. In the spatial domain, median filtering was operated over the monthly elevation estimations within a radius of 10 km from a grid node to minimize the impact of possible outliers. If the number of monthly elevation estimations within the 10 km radius was less than 9, the filtering radius would be expanded in steps of 10km until the radius was 30km, and the scaled median absolute deviation was used as the realistic error uncertainty of the elevation of the grid node as in Ewert et al. (2012) [32]. Then, the trend, acceleration, and other spatial-temporal characteristics of elevation and volume over the AIS can be derived from the elevation time series [4].
3.3. Calculation of Volume Changes for the AIS from the Combined Elevation Time Series
Long-term time series of volume changes are of great scientific value for the assessment of changes in the AIS and its response to climate change. After correcting for Glacial Isostatic Adjustment (GIA)-induced vertical crustal deformation and elastic solid earth rebound effects, the altimetric volume time series can be calculated from the elevation time series. In this study, the ICE-6G_C model [33] was used to correct for the uplift due to GIA. Elastic contributions were corrected by multiplying the elevation change by a scale factor α = 1.0205, which was inferred in Groh et al. (2012) [34]. For gridded values of a volume time series, the uncertainties were estimated using formal error propagation techniques. The GIA model does not have estimated uncertainties, so a standard deviation of 30% of the value for each grid point was used as a conservative estimate. For elastic deformation, the uncertainty of the scale factor α was considered negligible, similar to Schröder et al. (2019) [10]. Moreover, when summing up the volume time series for individual drainage basins and major sectors, the correlated uncertainties were accounted for according to the method in Schröder et al. (2019) [10], i.e., by applying a scaling factor derived from a 50 km autocorrelation radius to the squared uncertainties. To analyze and interpret volume changes of the AIS, we also calculated the surface volume changes due to surface processes (surface mass balance variations, liquid water processes, and firn compaction) using the Institute for Marine and Atmospheric Research Firn Densification Model (IMAU-FDM) [35].
4. Results
4.1. The Total Intermission Biases and the Intramission A–D Bias
A larger amount of observations from different missions are used simultaneously in the least-squares model to account for the total intermission biases and the intramission A–D bias is the highlight of our proposed algorithm. Figure 1 shows estimates of these biases derived at the intersections of the ascending and descending satellite ground tracks of Envisat. In this study, the mode mask boundary between CryoSat-2’s LRM and SARIn modes is used to simply divide flat areas and steep areas: CryoSat-2 uses the SARIn mode to measure the steep areas at the margins of the ice sheets, and the LRM mode over the flat interior of the ice sheets [2,29]. Corresponding statistics can be found in Table 1.
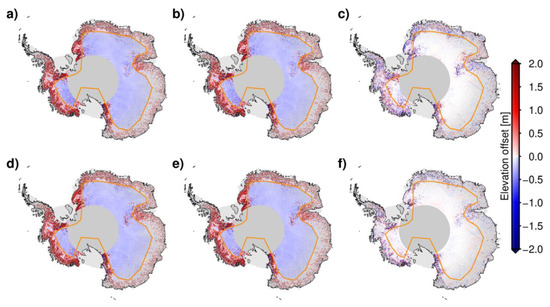
Figure 1.
Maps of the total intermission biases between CryoSat-2 ascending tracks and Envisat ascending tracks ((a), ), CryoSat-2 ascending tracks and Envisat descending tracks ((b), ), CryoSat-2 descending tracks and Envisat ascending tracks ((d), ), CryoSat-2 descending tracks and Envisat descending tracks ((e), ) and the intramission ascending–descending (A–D) bias of Envisat ((c), ) and CryoSat-2 ((f), ) at the intersections of Envisat’s ascending tracks and descending tracks. The mode mask boundary between CryoSat-2’s LRM and SARIn modes [29] is shown in orange.

Table 1.
Statistics of the total intermission biases and the intramission A–D bias of Envisat and CryoSat-2 at the intersections of Envisat’s ascending tracks and descending tracks over the CryoSat-2 LRM and SARIn mask areas. The number of intersections is 51,221 in the Low-Resolution Mode (LRM) mode area and 15,476 in the SARIn mode area. The median, mean, RMS, and the 10th and 90th percentile range (P90–P10) of the biases are given.
In terms of the intramission A–D bias, the spatial distributions of CryoSat-2 and Envisat exhibit similar patterns. Over the interior of the AIS, the bias is close to zero, while in the steeper SARIn area, the amplitude of bias exceeds 1 m (Figure 1c,f). The median, mean, RMS, and the 10th and 90th percentile range (P90-P10) over the SARIn mode area are 0.00 m, −0.14 m, 4.71 m, and 1.81 m for CryoSat-2 and 0.00 m, −1.38 m, 13.86 m, and 0.94 m for Envisat, while those over the LRM mode area are relatively close (Table 1). Whether using Cryosat-2 or Envisat, the mean and RMS of the intramission A–D bias over the SARIn area are much greater than those over the LRM area. This is mainly because the azimuthally anisotropic effects of polarization on altimetry measurements can be negligible over flat and homogeneous areas due to the similar dielectric conditions and low mispointing, but the opposite is true in steep and very active areas [27]. In general, the spatial distribution patterns and magnitude of the intramission A–D bias calculated in this study are consistent with those in Khvorostovsky (2012) [12], Davis (1997) [27], and McMillan et al. (2014) [5].
Given the total intermission biases between CryoSat-2 and Envisat, it can be seen from Figure 1 that all of them share the similar spatial distribution patterns. These biases are highly correlated to the topography slope of the ice sheets. In steep and complex areas, these biases can reach up to several meters, while in the flat interior of the AIS, these biases appear to be relatively uniform at a magnitude of about 0.2 m. According to Frappart et al. (2016) [15], the intermission bias in the flat interior of the AIS is mainly caused by orbital errors and differences in the position of the centers of gravity of the two satellites and the phase of the antennae, while the bias over the steep area originates from the geographical small-scale bias. Thus, the total intermission bias in the flat interior of the AIS shows a uniform distribution, but a higher amplitude of bias is found where the topography is steeper. Overall, the total intermission biases estimated in this study agree with those found in Frappart et al. (2016) [15]. This agreement gives us confidence in our updated least-squares model.
4.2. Comparison with OIB and ICESat
The results of our least-squares model are validated against the laser altimeter elevation datasets obtained from the OIB project and ICESat. Both datasets are taken from near-inferred laser altimeters, and their accuracy has been validated [36,37]. The results of our validation are shown in Figure 2.
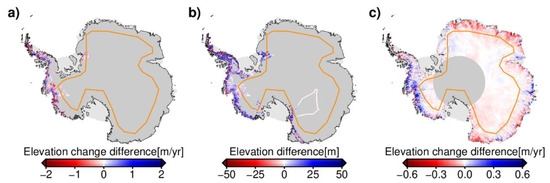
Figure 2.
Validation with laser altimeter elevation data obtained from the OIB and ICESat. Differences between the elevation changes derived from OIB observations and the combined elevation time series between 2002 and 2016 (a). Elevation differences between OIB observations and the combined elevation time series over the period of 2009–2018 (b). Difference between the average elevation change rates from the combined elevation time series and the average ICESat surface elevation change rates between 2003 and 2009 (c). The mode mask boundary between the CryoSat-2 LRM and SARIn modes is shown in orange.
Surface elevation changes can be obtained wherever there are coincident OIB ATM elevation measurements. To validate our results, we used the surface elevation changes from OIB ATM L4 [38]. These changes were computed from the OIB ATM elevation measurements observed during 2002–2016. The differences between elevation changes derived from OIB and the combined elevation time series () are shown in Figure 2a. To gain insight into the results of the intercomparison, we separated the evaluation results according to where or when the OIB ATM elevation measurements were observed to derived the OIB surface elevation changes for a grid cell, hereby referred to as the steeper SARIn area and the flat LRM area, and the periods before 2010, after 2010, and from 2002 to 2016. The OIB surface elevation change from 2002 to 2016 here refers to that is computed from a pair of coincident measurements, with one obtained before 2010 and the other after 2010. This allowed us to evaluate our time series in terms of their temporal and spatial distribution. The mean and RMS of these differences are given in Table 2. Meanwhile, statistics of the comparison between the OIB product and time series of Schröder et al.’s (2019) [10] elevation time series are also given in Table 2 to demonstrate the effects of different approaches to account for the intermission biases on the combined elevation time series. However, as shown in Figure 2a, the validation results are mainly concentrated along the outlet glaciers of the West Antarctic Ice Sheet (WAIS) and the Antarctic Peninsula Ice Sheet (APIS). Thus, intercomparison over the LRM area may be less persuasive. Over the SARIn area, the RMS of our results is nearly 30% smaller than that in Schröder et al. (2019) [10]. This suggests that our method is effective in correcting the systematic biases in the SARIn area. The decrease of the RMS by nearly 40% of the comparison of from 2002 to 2016 between ours results and that in Schröder et al. (2019) [10] further demonstrates the effectiveness of our method in intermission bias correction.

Table 2.
Statistics of the comparison between elevation changes derived from the combined elevation time series and those from Operation IceBridge (OIB) observations. The mean and RMS of the differences between elevation changes over the AIS and CryoSat-2 LRM and SARIn mask areas, as well as those acquired before 2010, after 2010, and from 2002 to 2016, are given. Note that the intercomparison results are mainly concentrated along the outlet glaciers of West Antarctica and the Antarctic Peninsula.
To make a consistent intercomparison, we used all surface elevations during 2009–2018 from OIB ATM L2 [39] within a 2.5-kilometer radius and a 4-day interval of our radar altimetry grid nodes. When comparing with the OIB surface elevations, the mean altitude of the bin (i.e., the in Equation (2)) is added back into the combined elevation time series. Figure 2b shows the map of the differences between the combined elevation time series and the OIB measurements. The differences are again the greatest in steep regions of the AIS, which is likely because that the radar altimeter has larger measurement errors in steeper areas due to the higher surface slope and roughness. Over the AIS, the median and RMS of the differences are 5.7 m and 28.7 m, respectively. They are better than the median of 25.4 m and RMS of 138.6 m of the differences between the interpolated grid cells of DEM in Slater et al. (2018) [40] and the OIB measurements, which are comparable with our combined time series in their processing strategy and resolution.
However, OIB ATM elevation observations are strongly concentrated along the outlet glaciers of West Antarctica and the Antarctic Peninsula. As a supplement, we also used ICESat data to validate our merged time series. For ICESat, the average elevation change rates for the period coinciding with ICESat over the AIS are first derived from our combined elevation time series by fitting a first-order polynomial and a sine with a 1-year period to account for the average elevation change rate and seasonal variations. Subsequently, the average elevation change rates from our combined results within a 10 km radius of an ICESat grid node are compared with the corresponding average ICESat rate. A map of the differences is shown in Figure 2c. Again, the largest differences are observed at steep areas. In the flat interior of the AIS, the differences are small. The higher surface slope and roughness are still the main sources of these differences. Changes in the penetration depth of the microwave signal into the snow due to changes in the snow surface characteristics is another important source of difference [41]. The median and RMS of the differences over the AIS are −1.1 cm/y and 10 cm/y, respectively, while the median and RMS are −1 cm/y and 11 cm/y for the differences between the average ICESat elevation change rates and those in Schröder et al. (2019) [10]. Thus, even if Schröder et al. (2019) [10] had used ICESat observations to construct their elevation time series, our results would still be comparable to theirs.
4.3. Elevation Time Series
As mentioned above, the average rates of elevation change over any subinterval can be obtained from the elevation time series using a fitting method with a first-order polynomial and a sine with a 1-year period. Unlike the information obtained directly from elevation observations, this method provides more accurate average rates for specific periods. The average elevation change rates over the periods of 2002–2010, 2010–2019, and 2002–2019 for our elevation time series are shown in Figure 3. Well-known long-term thinning and thickening spatial distribution patterns can be seen in these maps [2,4,5,10,31]. Overall, significant signs of thinning mainly occur across the Amundsen Sea sector, the Getz sector, and the Totten Glacier. A continuation of the signals of elevation uplift are observable in the Kamb Ice Stream and across Dronning Maud Land, while there are no significant changes in elevation across the interior of the East Antarctic Ice Sheet (EAIS). Whether over the Envisat period (2002–2010) with sparse observations or over the CryoSat-2 period (2010–2019) with dense observations, we obtained elevation change results that are in general agreement with other published results (Figure 3a,b). Comparing the results of the two periods, we find that thinning across the Amundsen Sea sector, the Getz sector, and Totten Glacier has significantly accelerated and expanded. Signs of thickening across Dronning Maud Land also show modest acceleration and expansion. In the coastal regions of Princess Elizabeth Land and the Bellingshausen Sea sector, elevation changes over the two periods show an opposite trend. Such significant interannual variations in elevation changes were previously reported in Schröder et al. (2019) [10].
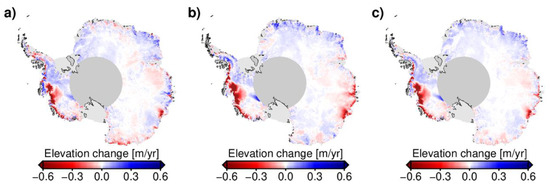
Figure 3.
Maps of the long-term elevation changes from the combined elevation time series over the periods of 2002–2010 (a), 2010–2019 (b) and 2002–2019 (c).
Moreover, to be comparable to Schröder et al. (2019) [10], we provide some points’ elevation time series in four representative regions in Figure 4. As shown in Figure 4a, Pine Island Glacier experienced a significant continuous thinning during 2002–2019. The rate of thinning decreases as its distance from the grounding line increases. The average rate of the elevation close to the grounding line (Point B) is −2.36 ± 0.02 m/y over 2002–2019, which far exceeds the thinning rate of −0.96 ± 0.01 m/y at Point C. The rate of thinning is not constant throughout the period but has slowed since 2010. This deceleration is most evident in the time series of Point B near grounding line but remains almost invisible in the time series of Point C far from grounding line. The spatial-temporal variations in the elevation change rates over Pine Island Glacier agree with those previously reported in Schröder et al. (2019) [10] and Flament and Remy [4].
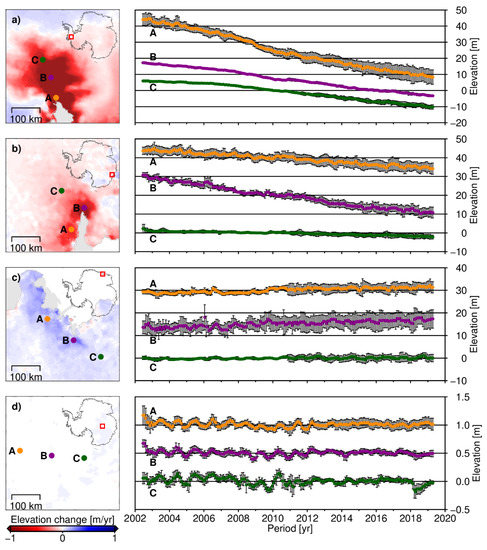
Figure 4.
Elevation time series for Pine Island Glacier (a), Totten Glacier (b), Dronning Maud Land (c), and Lake Vostok (d). The geographical locations of the selected points (A, B, and C) are marked in green, purple, and orange on the left maps of elevation changes over 2002–2017. The time series and their 1σ uncertainty ranges for each point are given in the right maps. The time series of the points A and B are shifted along the Elevation axis for better visibility.
In the EAIS, Totten Glacier has the most significant thinning. Examples of this glacier’s elevation time series are shown in Figure 4b. Similar to Pine Island Glacier, the largest thinning rates at Totten Glacier are observable near the grounding line. The mean thinning rate at Point B on the main tributary of Totten Glacier is −1.19 ± 0.01 m/y over 2002–2019. The thinning rate of Point A at the other tributary is −0.58 ± 0.01 m/y. Between the two tributaries, there is a ridge of thinning losing height much less rapidly than the surrounding fast-flowing areas. Flament and Remy [4] treat the ‘ridge’ as important evidence of the dynamic thinning of Totten Glacier. The time series of the examples indicates that there was no obvious acceleration or deceleration of the elevation change rates over 2002–2019. This confirms the previous results in Flament and Remy [4] and coincides with the flow velocity of Totten Glacier, which has remained constant since 2007 (as reported in Li et al. (2016) [42]).
Dronning Maud Land is located in the EAIS, which was chosen as an example of elevation uplift. In Figure 4c, we can observe a modest thickening over 2002–2019 in Dronning Maud Land. The largest thickening rate in the region is approximately 0.25 ± 0.01 m/y (Point B). The thickening rates at the other two points are 0.19 ± 0.01 m/y (Point A) and 0.05 ± 0.01 m/y (Point C). These thickening rates are in good agreement with the corresponding estimates in Schröder et al. (2019) [10]. Many previous studies have attributed the thickening of the ice sheet over the period in Dronning Maud Land to increased snowfall [5,10,15,43,44].
Lake Vostok is the largest of the subglacial lakes located far inland of the EAIS and is used to represent the slow-flowing interior. The corresponding elevation time series are shown in Figure 4d. The elevation change rates at the selected points of 3 ± 0.7 mm/y (Point A), 1.4 ± 0.5 mm/y (Point B), and 0.7 ± 0.5 mm/y (Point C) are in good agreement with the estimates of −3 ± 9 mm/y ~ 5 ± 9 mm/y from altimetry data in Schröder et al. (2019) [10] and −1 ± 5 mm/y from GNSS profiles in Schröder et al. (2017) [28].
4.4. Volume Time Series for the AIS
To quantitatively examine the changes in volume at a regional scale, the volume time series for six typical regions selected based on elevation change features are shown in Figure 5. It is very challenging to use radar altimetry data to estimate the surface elevation changes of ice sheets due to signal penetration into the snow. Fortunately, Legrésy and Rémy (1998) [45], Davis and Ferguson (2004) [46], and Slater et al. (2018) [40] have shown that the annual and subannual changes in the snowpack volume/surface scattering ratio can produce spurious changes in altimetric elevation. Therefore, in Figure 5, we also show the time series without seasonal oscillations. To clearly illustrate the relationship between surface volume changes and altimetric volume changes, time series with linear trends and seasonal oscillations removed are shown in Figure 6.
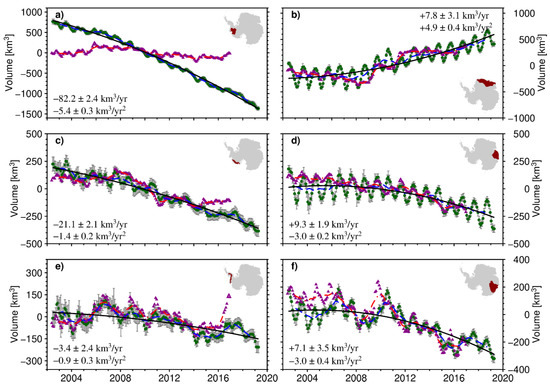
Figure 5.
Volume change of some subregions north of 81.5° S (Amundsen Sea sector (a), Dronning Maud Land (b), Getz sector (c), Princess Elizabeth Land (d), Bellingshausen Sea sector (e), and Totten Glacier sector (f)) from our combined altimetric time series (green dots) and the Institute for Marine and Atmospheric Research Firn Densification Model (IMAU-FDM) (purple triangles). The blue dashed curves and red dash-dotted curves are the time series after removing the seasonal oscillations using a 13-month moving average. Due to the defects of the moving average algorithm, the 6-month values at the beginning and end of the time series are not displayed. The solid black lines are the best-fit quadratic curves for the altimetric volume time series. Additionally, the altimetric volume time series’ linear and quadratic trend estimates are also included. The gray error bars show the 1σ uncertainty range of the altimetry data. The regions covered by each localization are shaded red in the inset. The boundaries refer to the Antarctic drainage systems in [47].
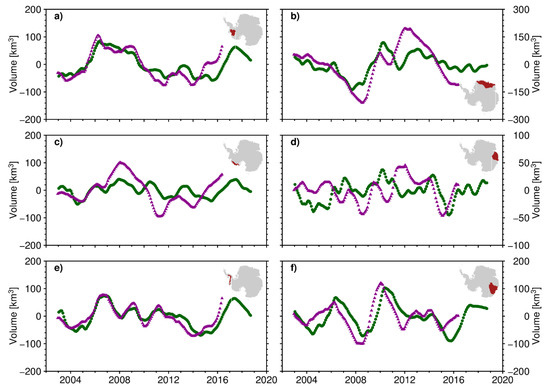
Figure 6.
Volume changes of some subregions north of 81.5° S (Amundsen Sea sector (a), Dronning Maud Land (b), Getz sector (c), Princess Elizabeth Land (d), Bellingshausen Sea sector (e), and Totten Glacier sector (f)) from our combined altimetric time series (green dots) and IMAU-FDM (purple triangles). After removing the long-term trends, seasonal oscillations were removed using a 13-month moving average. Due to the defects of the moving average algorithm, the 6-month values at the beginning and end of the time series are not displayed. The regions covered by each localization are shaded red in the inset. The boundaries refer to the Antarctic drainage systems in [47].
It can be clearly seen that there are strong interregional variations in the altimetric volume curves for smaller regions within Antarctica during 2002–2019. The Amundsen Sea sector (Figure 5a) displays a large coherent trend featuring a volume loss of −82.2 ± 2.4 km3/y with a significant acceleration of −5.4 ± 0.3 km3/y2. The time series reveals that this region experienced significant acceleration around 2006. Surface processes cannot cover the large coherent trends of accelerating volume loss. This means that sustained increases in ice discharge are the main reason for accelerated thinning, which agrees with many studies using observations from the Gravity Recovery and Climate Experiment (GRACE) [41,42,43,44]. There is a good consistency among the interannual changes in both volume time series (Figure 6a), with altimetric volume changes lagging behind those of the surface volume by several months.
The Getz sector and the Bellingshausen Sea sector are the other two regions of volume loss in the WAIS. The Getz sector has experienced a rapid volume loss of 21.1 ± 2.1 km3/y and acceleration of −1.4 ± 0.2 km3/y2 (Figure 5c). Figure 5e suggests that the Bellingshausen Sea sector has progressed to a less negative volume change at a rate of −3.4 ± 2.4 km3/y and an acceleration of −0.9 ± 0.3 km3/y2. The time series reveals that these two regions both experienced small losses in 2002–2006, followed by an increase in volume loss in 2007–2015 and regained volume in 2016. However, in contrast with the Bellingshausen Sea sector, discrepancies between altimetric and surface volume changes are very large in some subintervals in the Getz sector. This can be clearly seen from the time series of interannual changes (Figure 6c,e). Moreover, the interannual changes in altimetric volume in the Bellingshausen Sea sector are in good agreement with those of the surface volume change, except for a slight lag. This means that surface processes control the volume change in the Bellingshausen Sea sector, while ice discharge sometimes dominates the volume changes in the Getz sector.
In Dronning Maud Land, the volume change and acceleration for the entire period are 7.8 ± 3.1 km3/y and −4.9 ± 0.4 km3/y2, respectively. However, the relevant time series reveals that there is a significant change in its volume trend partway through the period of 2002–2019 (Figure 5b). Prior to the end of 2008, this area showed a slow increase in volume. Subsequently, the Dronning Maud Land experienced a continuous increase in volume gain. It can be seen from Figure 5b that surface processes dominate the volume change trends in Dronning Maud Land. The impact of two extreme accumulation events in 2009 and 2012 [48,49] can also be clearly seen in the volume time series, especially in Figure 6b. Several months after the surface volume changes, the altimetric volume responds.
In contrast with Dronning Maud Land, Princess Elizabeth Land, and the Totten Glacier sector show a gradual change from initial volume accumulation to volume loss (Figure 5d,f). The accelerations in volume change of these sectors are −3.0 ± 0.2 km3/y2 and −3.0 ± 0.4 km3/y2, respectively. The fluctuations of volume changes in 2008–2009 caused by surface process anomalies are most obvious in the Totten Glacier sector, as previously reported in Li et al. (2016) [42]. The trends of volume changes, especially accelerations, are dominated by surface processes in the two regions. The rapid volume loss of the Totten Glacier sector began in 2010. The difference is that the interannual oscillations of the Totten Glacier sector are consistent with its surface volume changes for the whole period, while those in Princess Elizabeth Land are not.
Figure 7 shows the derived volume time series for the entire AIS and the subregions of EAIS, WAIS, and APIS north of 81.5° S over 2002–2019. An overall volume loss of −68.7 ± 8.1 km3/y and an acceleration in loss of −5.5 ± 0.9 km3/y2 during 2002–2019 were detected. Overall, increasing volume loss is mainly a result of volume changes of the WAIS. The volume loss of the WAIS during 2002–2019 was −88.4 ± 3.9 km3/y with an acceleration of −8.1 ± 0.4 km3/y2. The APIS contributes to a small part of volume loss at a lower rate of −18.8 ± 2.2 km3/y, and its loss gradually slows, with an acceleration of +1.9 ± 0.2 km3/y2. The EAIS has experienced a steady volume gain at a rate of 38.5 ± 6.7 km3/y. The acceleration of the EAIS is 0.8 ± 0.8 km3/y2.
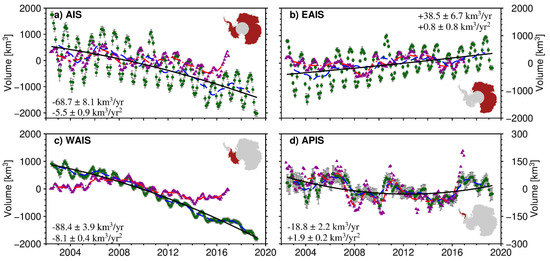
Figure 7.
Volume changes in the AIS north of 81.5° S (a) and the three subregions ((b): EAIS, (c): WAIS, and (d): APIS) from our combined altimetric time series (green dots) and IMAU-FDM (purple triangles). The blue dashed curves and red dash-dotted curves are the time series after removing seasonal oscillations using a 13-month moving average. Due to the defects of the moving average algorithm, the 6-month values at the beginning and end of the time series are not displayed. The solid black lines are the best-fit quadratic curves for the altimetric volume time series. Included are the altimetric volume time series linear and quadratic trend estimates. The gray error bars show the 1σ uncertainty range of the altimetry data. The regions covered by each localization are shaded red in the inset. The boundaries refer to the Antarctic drainage systems in [47].
Figure 8 shows the time series for the entire AIS and the subregions of EAIS, WAIS, and APIS with linear trends and seasonal oscillations removed. Figure 7 and Figure 8 show that surface volume changes can only explain a small proportion of the overall volume changes in the AIS. The biggest difference in long-term trends comes from the WAIS, although its interannual variations in surface and altimetric volume changes show good consistency. According to previous studies, the differences in long-term trends in the WAIS are possibly due to ice dynamics [4,5,44,50]. Similarly, because of dynamic thinning, surface processes cannot fully explain the altimetric volume changes in the APIS, especially during 2002–2006. Following the disintegration of the Larson B Ice Shelf in 2002, increased ice discharge occurred [51,52]. Although surface volume changes in some subregions are in good agreement with their altimetric volume changes, there are differences in both the long-term trends and the interannual variations between the two integrated volume time series for the EAIS. These differences can also be seen in Schröder et al. (2019) [10].
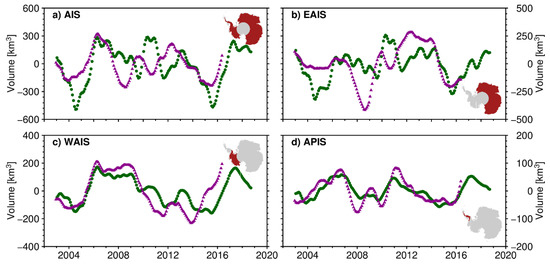
Figure 8.
Volume change of the AIS north of 81.5° S (a) and the three subregions ((b): EAIS, (c): WAIS, and (d): APIS) from our combined altimetric time series (green dots) and IMAU-FDM (purple triangles). After removing the long-term trends, seasonal oscillations were removed using a 13-month moving average. Due to the defects of the moving average algorithm, the 6-month values at the beginning and end of the time series are not displayed. The regions covered by each localization are shaded red in the inset. The boundaries refer to the Antarctic drainage systems in [47].
5. Discussion
Accurately correcting intermission biases is crucial for combining observations from different radar altimetry missions to study the long-term changes of ice sheets. Imperfect methods may lead to non-self-consistent combined results. This is why there are leap or step signals at the junctions between ERS-2 and Envisat and between Envisat and CryoSat-2 in the elevation time series shown in Figure 10 of Schröder et al. (2019) [10]. This can be attributed to the uncertainties in the intermission cross-calibration due to the short overlapping period. In this study, we constructed an updated plane-fitting least-squares regression model by introducing the comprehensive parameters of the intermission bias and the A–D bias and their internal consistency into the existing least-squares regression model. In contrast with previous methods, it allowed us to use a larger amount of observations in the same regression model for the integrated least-squares adjustment to improve the accuracy of cross-calibration of the data from different missions, and thereby to ensure a self-consistent and accurate elevation time series. We used Envisat and Cryosat-2 observations to test our model and successfully established a 5 km grid of monthly elevation time series over the AIS. The estimations of the total intermission biases and the intramission A–D bias are consistent with those in previous studies [5,15,18]. Moreover, the self-consistent elevation time series at the joint of the two satellites (Figure 4) show that our algorithm is effective in cross-calibration. The intercomparison between the surface elevation changes from OIB ATM L4 and from the combined elevation time series also demonstrate the effectiveness of our method in creating time series using data from different missions. In addition, comparisons with OIB-derived surface elevations and ICESat surface elevation changes also increased confidence in our merged time series. It should be noted that the difference in footprint size between Envisat data and CryoSat-2 SARIn-mode data may be a source of uncertainty in the estimates of intermission bias and in creating of the merged time series. Following the study by Adusumilli et al. (2018) [16], we believe that the point of closest approach (POCA) applied to generate Envisat and CryoSat-2 Level 2 products reduces the difference between topography sampled with the different satellite radar altimeter techniques. Certainly, it still needs further study to accurately calibrate the different techniques against each other in the future.
Our gridded monthly elevation time series allow for the analysis of temporal and spatial evolutions over 2002–2019. Well-known patterns of thinning and thickening were also confirmed in this study. Volume losses are mainly concentrated in the coastal sectors of the WAIS, especially in the Amundsen Sea sector, while the volume gains are mainly observable in the Dronning Maud Land of the EAIS [2,4,5,10,14]. A simple comparison of the elevation change rates of the two periods (2002–2010 vs. 2010–2019) reveals an expansion of thinning in the Pine Island Glacier and interannual fluctuations of elevation changes in Princess Elizabeth Land and the Bellingshausen Sea sector. Although these findings were previously reported [10,53,54], they indicate that our time series are reliable.
Due to signal penetration into the snow, the elevation changes derived from radar altimeters might not reflect the actual surface elevation changes [17,55]. However, including the backscatter coefficient in the least-squares regression model can only account for a part of the effect of surface penetration, as shown in Simonsen and Sorensen (2017) [3] and Sørensen et al. (2018) [17]. Indeed, there were spurious seasonal fluctuations caused by surface penetration in our combined results. However, this spurious signal also exists in Schröder et al. (2019) [10], even though the authors reprocessed their radar altimetry observations with a low threshold retracker able to produce spurious changes in elevation due to changes in surface penetration [27,28]. Therefore, radar altimetry data is generally considered to be very difficult to use for studying the changes caused by surface processes directly, especially for surface accumulation events. Nevertheless, the Greenland 2012 melt event provides us with an extreme example for which radar altimeters can detect the changes caused by surface processes. The formation of a refrozen melt layer can increase the reflective surface for radar altimeters instantaneously [55]. Comparably, other surface processes, such as firn compaction, can also form ice lenses to change the reflecting surface, allowing them to be observed by radar altimeters. That is to say, after a time-consuming process of firn compaction, accumulation events can be observed with time lags by radar altimeters. After removing seasonal variations to minimize the effects of surface penetration, more reliable estimates of the interannual and long-term variations caused by surface processes can be clearly seen from our combined altimetric time series, such as snowfall in Dronning Maud Land in 2009 and 2012 and snow accumulation in 2008–2009 in the Totten Glacier sector.
Therefore, together with surface volume changes, the integrated volume time series over larger regions enabled us to further improve our understanding of elevation change processes. The agreement between altimetric and surface volume changes in Dronning Maud Land indicates that surface processes dominate the variability of its volume changes. In other words, changes in ice dynamics do not significantly affect the time variability of its volume signal. This confirms that they are distal to areas with fast ice flow [56]. Modest thickening in Dronning Maud Land was associated with increases in snowfall due to its extreme accumulation events in 2019 and 2012 [54,57]. The long-term trend of altimetric volume changes of Princess Elizabeth Land are consistent with those of the surface volume. This result agrees with that in Schröder et al. (2019) [10], showing that thinning here is related to less snowfall. In the Totten Glacier sector and the Bellingshausen Sea sector, the altimetric and surface volume changes also agree well. The difference is that excessive ice discharge and grounding line retreats have made Totten Glacier and several Bellingshausen Sea glaciers thin [42,56]. However, the surface volume changes are so large that they still dominate the volume changes in these regions, such as the accelerated thinning of Totten Glacier over 2010–2015 [42].
As reported in previous studies [4,5,10,44,54], changes in the Amundsen Sea sector ice sheet are mainly driven by rapid ice discharge. Mouginot et al. (2014) [53] and Harig et al. (2015) [57] reported that flow acceleration and widening of Pine Island Glacier and Thwaites Glacier led to rapid acceleration loss in the Amundsen Sea sector. These factors agree with the pronounced differences that we observed between altimetric and surface volume changes here. In the Getz sector, we found that neither ice dynamics nor surface processes dominate volume changes over the entire period of 2002–2019. As reported in Shepherd et al. (2019) [54], the patterns of elevation changes in this sector reflect a complex mixture of surface processes and dynamic ice imbalances.
Overall, the accelerated ice volume loss in the coastal regions of WAIS continues to outpace the gains made in the EAIS. The volume loss of the AIS is mainly caused by ice discharge in the Amundsen Sea sector. Meanwhile, in Princess Elizabeth Land, the Totten Glacier sector of the EAIS, and the Bellingshausen Sea sector and Getz sector of the WAIS, surface processes also make a considerable contribution to volume loss. The contribution of surface processes in Princess Elizabeth Land and the Totten Glacier sector of the EAIS to the acceleration of volume loss over the AIS also cannot be ignored. Volume gains due to surface processes were mainly observed in the EAIS, especially in Dronning Maud Land.
6. Conclusions
In this study, we presented an updated plane-fitting least-squares regression model that combines different radar altimetry missions. Using this approach, we constructed a monthly elevation time series using 5 km grid cells over the AIS. Further analysis of the output estimates for the systematic biases and elevation time series shows that the intermission bias and the A–D bias were successfully corrected. Validation with airborne and ICESat laser altimetry observations indicates that our combined gridded monthly elevation time series are reliable.
Further analysis shows that our resulting elevation time series can provide detailed insight into temporal and spatial evolution of elevation for the AIS over 2002–2019. In addition to the well-known patterns of thinning and thickening, acceleration and increases in thinning in Pine Island Glacier and Thwaites Glacier, as well as interannual fluctuations in Princess Elizabeth Land and the Bellingshausen Sea sector, were shown very clearly. Overall, the volume loss in the WAIS continues to outpace the gains made in the EAIS. From 2002 to 2019, the total volume change estimates for the AIS were −68.7 ± 8.1 km3/y, with an acceleration of −5.5 ± 0.9 km3/y2. Most of the volume loss was from the Amundsen Sea sector and the Getz sector, and most of the acceleration was from the Amundsen Sea sector, Princess Elizabeth Land, and the Totten Glacier sector.
After removing the seasonal variations, we obtained the interannual and long-term variations caused by surface processes in our combined time series. With the help of additional surface volume changes derived from IMAU-FDM, we determined that ice discharge in the Amundsen Sea sector provides the largest accelerated volume loss of the AIS. However, surface processes still play an important role in the volume changes of the AIS. In addition to thickening in Dronning Maud Land, surface processes in regions such as the Totten Glacier sector, Princess Elizabeth Land, and the Bellingshausen Sea sector are the main sources of acceleration in volume loss for the AIS.
Author Contributions
B.Z., Q.Y., Z.W., and F.L. conceived the study, supervised the experiments, and improved the manuscript. J.L., J.A., T.L., and H.G. contributed to the analysis and discussion. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no.41941010), the National Key Research and Development Project of China (grant no. 2018YFC1406102), and the China Scholarship Council (grant no. 201906275017).
Acknowledgments
We would like to thank organizations that shared their datasets and software for use in this study. The Envisat and CryoSat-2 observations were obtained from the European Space Agency (ESA) Earth Online, and the airborne elevation data was provided by the National Snow and Ice Data Center (NSIDC). All geographical plots were produced using the Generic Mapping Tools (GMT). We also specifically thank Sebastian B. Simonsen, René Forsberg and Louise S. Sørensen for their comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zwally, H.J.; Bindschadler, R.A.; Brenner, A.C.; Martin, T.V.; Thomas, R.H. Surface elevation contours of greenland and antarctic ice sheets. J. Geophys Res. Ocean. 1983, 88, 1589–1596. [Google Scholar] [CrossRef]
- Helm, V.; Humbert, A.; Miller, H. Elevation and elevation change of Greenland and Antarctica derived from CryoSat-2. Cryosphere 2014, 8, 1539–1559. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Sorensen, L.S. Implications of changing scattering properties on Greenland ice sheet volume change from Cryosat-2 altimetry. Remote Sens. Environ. 2017, 190, 207–216. [Google Scholar] [CrossRef]
- Flament, T.; Remy, F. Dynamic thinning of Antarctic glaciers from along-track repeat radar altimetry. J. Glaciol. 2012, 58, 830–840. [Google Scholar] [CrossRef]
- McMillan, M.; Shepherd, A.; Sundal, A.; Briggs, K.; Muir, A.; Ridout, A.; Hogg, A.; Wingham, D. Increased ice losses from Antarctica detected by CryoSat-2. Geophys. Res. Lett. 2014, 41, 3899–3905. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Nielsen, K.; Lucas-Picher, P.; Spada, G.; Adalgeirsdottir, G.; Forsberg, R.; Hvidberg, C.S. Mass balance of the Greenland ice sheet (2003–2008) from ICESat data–The impact of interpolation, sampling and firn density. Cryosphere 2011, 5, 173–186. [Google Scholar] [CrossRef]
- Zwally, H.J.; Li, J.; Brenner, A.C.; Beckley, M.A.; Cornejo, H.G.; DiMarzio, J.P.; Giovinetto, M.B.; Neumann, T.A.; Robbins, J.; Saba, J.L.; et al. Greenland ice sheet mass balance: Distribution of increased mass loss with climate warming; 2003–07 versus 1992–2002. J. Glaciol. 2011, 57, 88–102. [Google Scholar] [CrossRef]
- Pritchard, H.D.; Arthern, R.J.; Vaughan, D.G.; Edwards, L.A. Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature 2009, 461, 971–975. [Google Scholar] [CrossRef]
- Wouters, B.; Bamber, J.L.; van den Broeke, M.R.; Lenaerts, J.T.M.; Sasgen, I. Limits in detecting acceleration of ice sheet mass loss due to climate variability. Nat. Geosci. 2013, 6, 613–616. [Google Scholar] [CrossRef]
- Schröder, L.; Horwath, M.; Dietrich, R.; Helm, V.; van den Broeke, M.R.; Ligtenberg, S.R.M. Four decades of Antarctic surface elevation changes from multi-mission satellite altimetry. Cryosphere 2019, 13, 427–449. [Google Scholar] [CrossRef]
- Paolo, F.S.; Fricker, H.A.; Padman, L. Constructing improved decadal records of Antarctic ice shelf height change from multiple satellite radar altimeters. Remote Sens. Environ. 2016, 177, 192–205. [Google Scholar] [CrossRef]
- Khvorostovsky, K.S. Merging and analysis of elevation time series over Greenland ice sheet from satellite radar altimetry. IEEE Trans. Geosci. Remote Sens. 2012, 50, 23–36. [Google Scholar] [CrossRef]
- Fricker, H.A.; Padman, L. Thirty years of elevation change on Antarctic Peninsula ice shelves from multimission satellite radar altimetry. J. Geophys. Res. Ocean. 2012, 117, C02026. [Google Scholar] [CrossRef]
- Zwally, H.J.; Giovinetto, M.B.; Li, J.; Cornejo, H.G.; Beckley, M.A.; Brenner, A.C.; Saba, J.L.; Yi, D.H. Mass changes of the Greenland and Antarctic ice sheets and shelves and contributions to sea-level rise: 1992–2002. J. Glaciol. 2005, 51, 509–527. [Google Scholar] [CrossRef]
- Frappart, F.; Legrésy, B.; Niño, F.; Blarel, F.; Fuller, N.; Fleury, S.; Birol, F.; Calmant, S. An ERS-2 altimetry reprocessing compatible with ENVISAT for long-term land and ice sheets studies. Remote Sens. Environ. 2016, 184, 558–581. [Google Scholar] [CrossRef]
- Adusumilli, S.; Fricker, H.A.; Siegfried, M.R.; Padman, L.; Paolo, F.S.; Ligtenberg, S.R.M. Variable basal melt rates of Antarctic Peninsula ice shelves, 1994–2016. Geophys. Res. Lett. 2018, 45, 4086–4095. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Forsberg, R.; Khvorostovsky, K.; Meister, R.; Engdahl, M.E. 25 years of elevation changes of the Greenland Ice Sheet from ERS, Envisat, and CryoSat-2 radar altimetry. Earth Planet. Sci. Lett. 2018, 495, 234–241. [Google Scholar] [CrossRef]
- Armitage, T.W.K.; Wingham, D.J.; Ridout, A.L. Meteorological origin of the static crossover pattern present in low-resolution-mode CryoSat-2 data over Central Antarctica. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1295–1299. [Google Scholar] [CrossRef]
- Remy, F.; Legresy, B.; Benveniste, J. On the azimuthally anisotropy effects of polarization for altimetric measurements. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3289–3296. [Google Scholar] [CrossRef]
- Arthern, R.J.; Wingham, D.J.; Ridout, A.L. Controls on ERS altimeter measurements over ice sheets: Footprint-scale topography, backscatter fluctuations, and the dependence of microwave penetration depth on satellite orientation. J. Geophys. Res. Atmos. 2001, 106, 33471–33484. [Google Scholar] [CrossRef]
- Legresy, B.; Remy, F.; Schaeffer, P. Different ERS altimeter measurements between ascending and descending tracks caused by wind induced features over ice sheets. Geophys. Res. Lett. 1999, 26, 2231–2234. [Google Scholar] [CrossRef]
- Yang, Q.M.; Yang, Y.D.; Wang, Z.M.; Zhang, B.J.; Jiang, H. Elevation change derived from SARAL/ALtiKa altimetric mission: Quality assessment and performance of the Ka-Band. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Yang, Y.D.; Li, F.; Hwang, C.; Ding, M.H.; Ran, J.J. Space-Time evolution of Greenland Ice Sheet elevation and mass from Envisat and GRACE data. J. Geophys. Res. Earth Surf. 2019, 124, 2079–2100. [Google Scholar] [CrossRef]
- Batoula, S.; Urien, S.; Picard, B.; Muir, A.; Roca, M.; Garcia, P. Envisat Altimetry Level 2 Product Handbook. CLS-ESLF-18-0003 2018, Issue 2.0. Available online: https://earth.esa.int/documents/700255/3528455/PH_light_3528452rev3528450_ESA.pdf/ (accessed on 22 July 2020).
- Wingham, D.; Rapley, C.; Griffiths, H. New techniques in satellite altimeter tracking systems. In Proceedings of the IGARSS Symposium, Zurich, Switzerland, 8–11 September 1986; Guyenne, T.D., Hunt, J.J., Eds.; European Space Agency Publications Division: Noordwijk, The Netherlands, 1986; Volume SP-254, pp. 1339–1344. [Google Scholar]
- Davis, C.H. A robust threshold retracking algorithm for measuring ice-sheet surface elevation change from satellite radar altimeters. IEEE Trans. Geosci. Remote Sens. 1997, 35, 974–979. [Google Scholar] [CrossRef]
- Nilsson, J.; Gardner, A.; Sørensen, L.S.; Forsberg, R. Improved retrieval of land ice topography from CryoSat-2 data and its impact for volume-change estimation of the Greenland Ice Sheet. Cryosphere 2016, 10, 2953–2969. [Google Scholar] [CrossRef]
- Schröder, L.; Richter, A.; Fedorov, D.V.; Eberlein, L.; Brovkov, E.V.; Popov, S.V.; Knöfel, C.; Horwath, M.; Dietrich, R.; Matveev, A.Y.; et al. Validation of satellite altimetry by kinematic GNSS in central East Antarctica. Cryosphere 2017, 11, 1111–1130. [Google Scholar] [CrossRef]
- Bouzinac, C. CryoSat Product Handbook. 2014. Available online: https://earth.esa.int/documents/10174/125272/CryoSat_Product_Handbook (accessed on 30 June 2020).
- Krabill, W.; Hanna, E.; Huybrechts, P.; Abdalati, W.; Cappelen, J.; Csatho, B.; Frederick, E.; Manizade, S.; Martin, C.; Sonntag, J.; et al. Greenland ice sheet: Increased coastal thinning. Geophys. Res. Lett. 2004, 31, L24402. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z.; Li, F.; An, J.; Yang, Y.; Liu, J. Estimation of present-day glacial isostatic adjustment, ice mass change and elastic vertical crustal deformation over the Antarctic ice sheet. J. Glaciol. 2017, 63, 703–715. [Google Scholar] [CrossRef]
- Ewert, H.; Groh, A.; Dietrich, R. Volume and mass changes of the Greenland ice sheet inferred from ICESat and GRACE. J. Geodyn. 2012, 59–60, 111–123. [Google Scholar] [CrossRef]
- Argus, D.F.; Peltier, W.R.; Drummond, R.; Moore, A.W. The Antarctica component of postglacial rebound model ICE-6G_C (VM5a) based on GPS positioning, exposure age dating of ice thicknesses, and relative sea level histories. Geophys. J. Int. 2014, 198, 537–563. [Google Scholar] [CrossRef]
- Groh, A.; Ewert, H.; Scheinert, M.; Fritsche, M.; Rülke, A.; Richter, A.; Rosenau, R.; Dietrich, R. An investigation of glacial isostatic adjustment over the Amundsen Sea sector, West Antarctica. Glob. Planet. Chang. 2012, 98–99, 45–53. [Google Scholar] [CrossRef]
- Ligtenberg, S.R.M.; Helsen, M.M.; van den Broeke, M.R. An improved semi-empirical model for the densification of Antarctic firn. Cryosphere 2011, 5, 809–819. [Google Scholar] [CrossRef]
- Martin, C.F.; Krabill, W.B.; Manizade, S.S.; Russell, R.L.; Sonntag, J.G.; Swift, R.N.; Yungel, J.K. Airborne Topographic Mapper Calibration Procedures and Accuracy Assessment. Nasa Technical Memorandum TM2012-21(February) 2012, 20120008479. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20120008479.pdf (accessed on 15 July 2020).
- Magruder, L.A.; Webb, C.E.; Urban, T.J.; Silverberg, E.C.; Schutz, B.E. ICESat altimetry data product verification at white sands space harbor. IEEE Trans. Geosci. Remote Sens. 2007, 45, 147–155. [Google Scholar] [CrossRef]
- Studinger, M. National Snow and Ice Data Center. IceBridge ATM L4 Surface Elevation Rate of Change; Version 1; updated 2018; USA NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014; Available online: https://nsidc.org/data/IDHDT4/versions/1 (accessed on 15 July 2020). [CrossRef]
- Studinger, M. IceBridge ATM L2 Icessn Elevation, Slope, and Roughness; Version 2; updated 2020; ASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014; Available online: https://nsidc.org/data/ILATM2/versions/2 (accessed on 15 July 2020). [CrossRef]
- Slater, T.; Shepherd, A.; McMillan, M.; Muir, A.; Gilbert, L.; Hogg, A.E.; Konrad, H.; Parrinello, T. A new digital elevation model of Antarctica derived from CryoSat-2 altimetry. Cryosphere 2018, 12, 1551–1562. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Meister, R.; Forsberg, R.; Levinsen, J.F.; Flament, T. Envisat-derived elevation changes of the Greenland ice sheet, and a comparison with ICESat results in the accumulation area. Remote Sens. Environ. 2015, 160, 56–62. [Google Scholar] [CrossRef]
- Li, X.; Rignot, E.; Mouginot, J.; Scheuchl, B. Ice flow dynamics and mass loss of Totten Glacier, East Antarctica, from 1989 to 2015. Geophys. Res. Lett. 2016, 43, 6366–6373. [Google Scholar] [CrossRef]
- Groh, A.; Ewert, H.; Rosenau, R.; Fagiolini, E.; Gruber, C.; Floricioiu, D.; Abdel Jaber, W.; Linow, S.; Flechtner, F.; Eineder, M.; et al. Mass, volume and velocity of the Antarctic ice sheet: Present-Day changes and error effects. Surv. Geophys. 2014, 35, 1481–1505. [Google Scholar] [CrossRef]
- Velicogna, I.; Sutterley, T.C.; van den Broeke, M.R. Regional acceleration in ice mass loss from Greenland and Antarctica using GRACE time-variable gravity data. Geophys. Res. Lett. 2014, 41, 8130–8137. [Google Scholar] [CrossRef]
- Legrésy, B.; Rémy, F. Using the temporal variability of satellite radar altimetric observations to map surface properties of the Antarctic ice sheet. J. Glaciol. 1998, 44, 197–206. [Google Scholar] [CrossRef]
- Davis, C.H.; Ferguson, A.C. Elevation change of the Antarctic ice sheet, 1995–2000, from ERS-2 satellite radar altimetry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2437–2445. [Google Scholar] [CrossRef]
- Zwally, H.J.; Giovinetto, M.B.; Beckley, M.A.; Saba, J.L. Antarctic and Greenland Drainage Systems. GSFC Cryospheric Sciences Laboratory. 2012. Available online: http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php (accessed on 15 July 2020).
- Boening, C.; Lebsock, M.; Landerer, F.; Stephens, G. Snowfall-driven mass change on the East Antarctic ice sheet. Geophys. Res. Lett. 2012, 39, L21501. [Google Scholar] [CrossRef]
- Lenaerts, J.T.M.; van Meijgaard, E.; van den Broeke, M.R.; Ligtenberg, S.R.M.; Horwath, M.; Isaksson, E. Recent snowfall anomalies in Dronning Maud Land, East Antarctica, in a historical and future climate perspective. Geophys. Res. Lett. 2013, 40, 2684–2688. [Google Scholar] [CrossRef]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar] [CrossRef]
- Shuman, C.A.; Berthier, E.; Scambos, T.A. 2001–2009 elevation and mass losses in the Larsen A and B embayments, Antarctic Peninsula. J. Glaciol. 2011, 57, 737–754. [Google Scholar] [CrossRef][Green Version]
- Berthier, E.; Scambos, T.A.; Shuman, C.A. Mass loss of Larsen B tributary glaciers (Antarctic Peninsula) unabated since 2002. Geophys. Res. Lett. 2012, 39, L13501. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E.; Scheuchl, B. Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013. Geophys. Res. Lett. 2014, 41, 1576–1584. [Google Scholar] [CrossRef]
- Shepherd, A.; Gilbert, L.; Muir, A.S.; Konrad, H.; McMillan, M.; Slater, T.; Briggs, K.H.; Sundal, A.V.; Hogg, A.E.; Engdahl, M.E. Trends in Antarctic ice sheet elevation and mass. Geophys. Res. Lett. 2019, 46, 8174–8183. [Google Scholar] [CrossRef]
- Nilsson, J.; Vallelonga, P.; Simonsen, S.B.; Sørensen, L.S.; Forsberg, R.; Dahl-Jensen, D.; Hirabayashi, M.; Goto-Azuma, K.; Hvidberg, C.S.; Kjær, H.A.; et al. Greenland 2012 melt event effects on CryoSat-2 radar altimetry. Geophys. Res. Lett. 2015, 42, 3919–3926. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Scambos, T.; Fahnstock, M.; Ligtenberg, S.; van den Broeke, M.; Nilsson, J. Increased West Antarctic and unchanged East Antarctic ice discharge over the last 7 years. Cryosphere 2018, 12, 521–547. [Google Scholar] [CrossRef]
- Harig, C.; Simons, F.J. Accelerated West Antarctic ice mass loss continues to outpace East Antarctic gains. Earth Planet. Sci. Lett. 2015, 415, 134–141. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).