On the Feasibility of Seafloor Topography Estimation from Airborne Gravity Gradients: Performance Analysis Using Real Data
Abstract
1. Introduction
2. Comparison between Airborne Gravimetry and Airborne Gravity Gradiometry
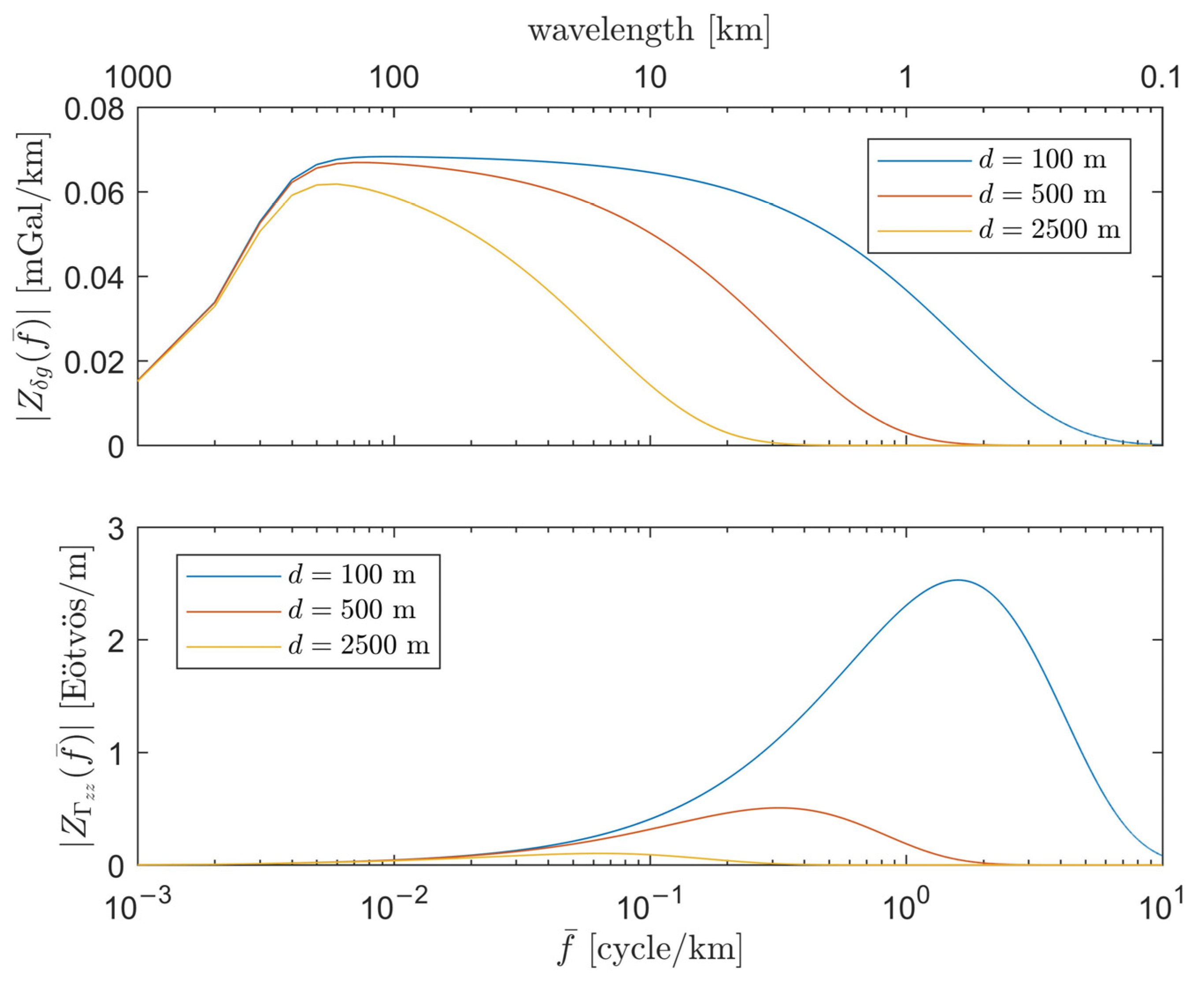
2.1. Resolution
2.2. Admittances
3. Numerical Experiments
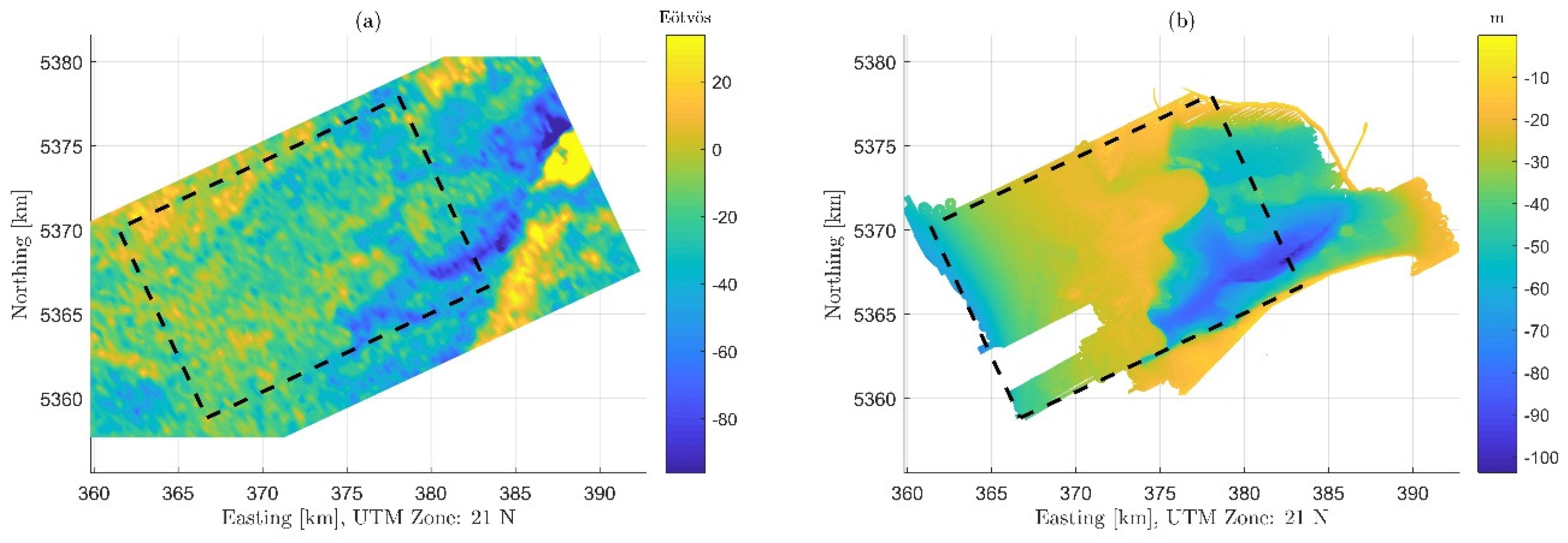
3.1. Airborne Gravity Gradients and Multibeam Bathymetry
3.2. Inversion Methods
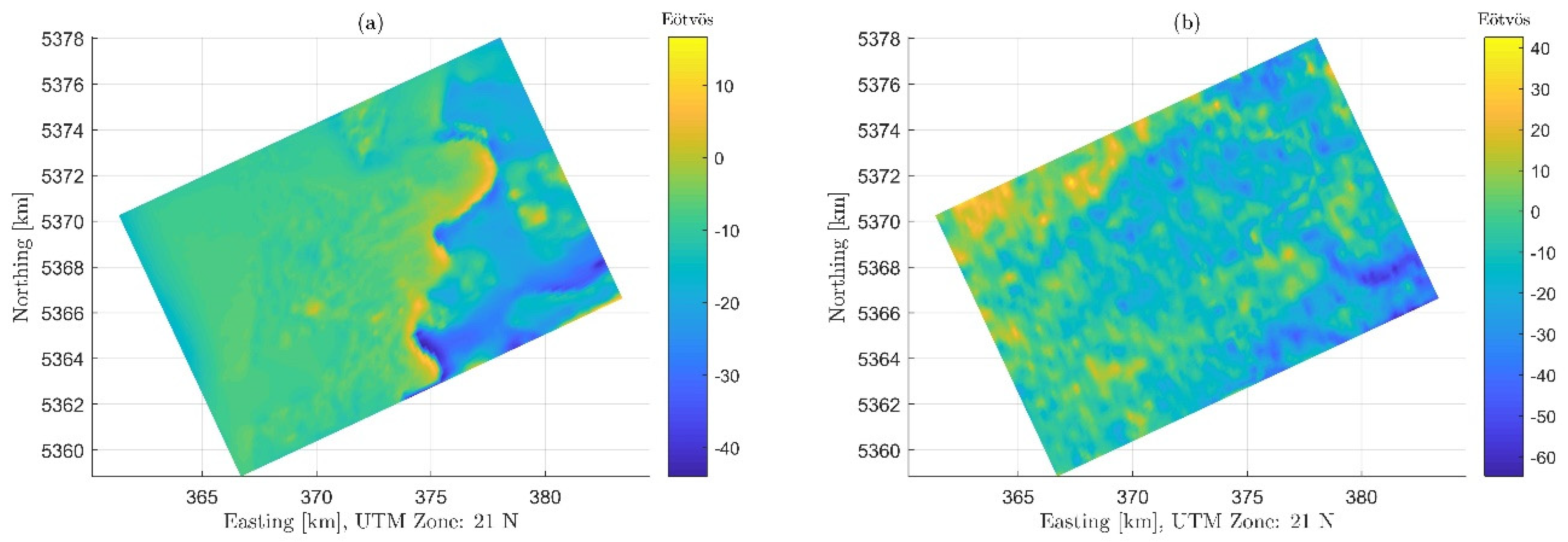
3.3. Analysis and Removal of the Non-Terrain Effects
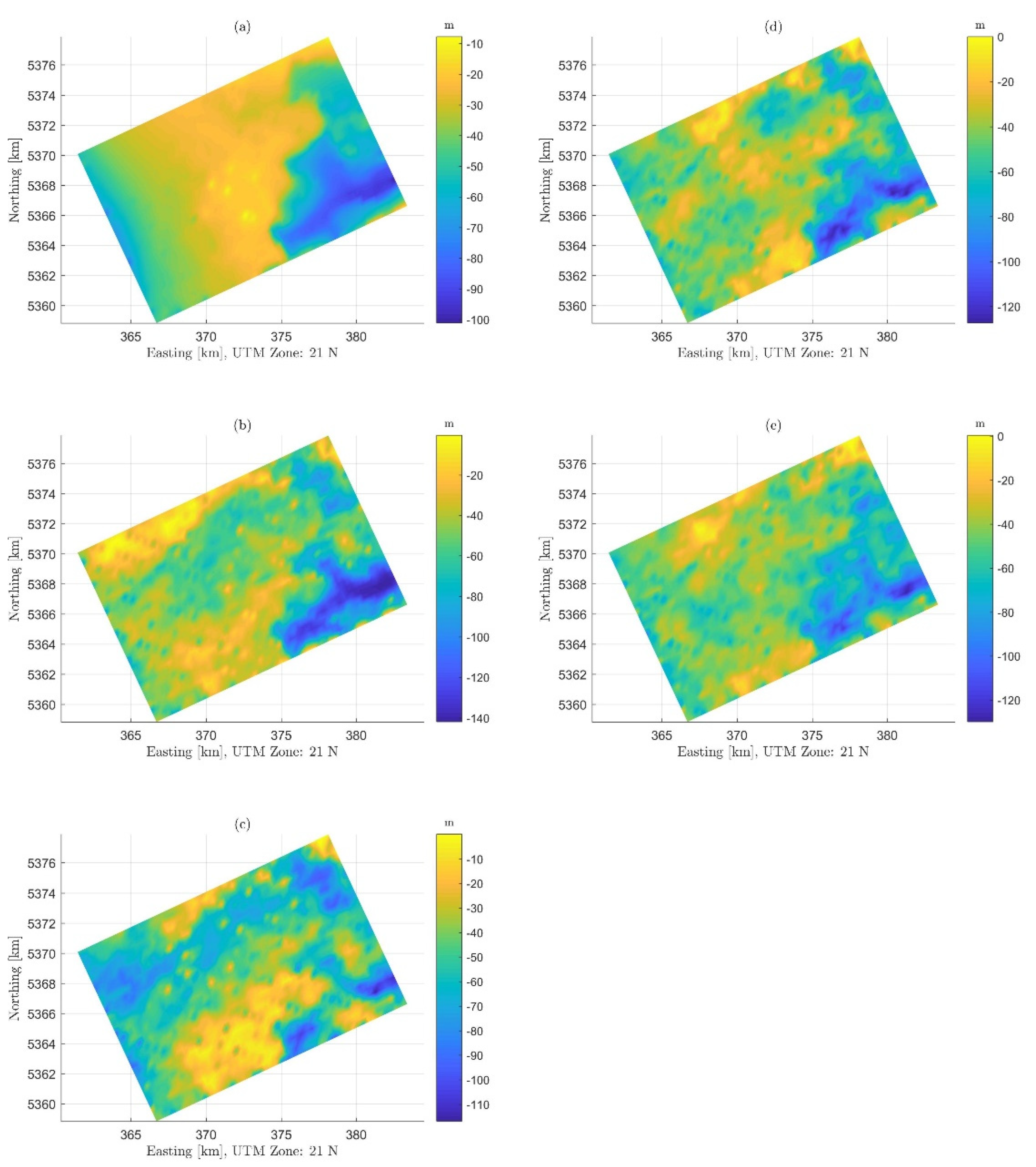
3.4. Results, Evaluation, and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jekeli, C. Vector gravimetry using GPS in free-fall and in an Earth-fixed frame. J. Geod. 1992, 66, 54–61. [Google Scholar] [CrossRef]
- Studinger, M.; Bell, R.E.; Tikku, A.A. Estimating the depth and shape of subglacial Lake Vostok’s water cavity from aerogravity data. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Greenbaum, J.S.; Blankenship, D.D.; Young, D.A.; Richter, T.G.; Roberts, J.L.; Aitken, A.R.A.; Legresy, B.; Schroeder, D.M.; Warner, R.C.; Van Ommen, T.D.; et al. Ocean access to a cavity beneath Totten Glacier in East Antarctica. Nat. Geosci. 2015, 8, 294–298. [Google Scholar] [CrossRef]
- Millan, R.; Rignot, E.; Bernier, V.; Morlighem, M.; Dutrieux, P. Bathymetry of the Amundsen Sea Embayment sector of West Antarctica from Operation IceBridge gravity and other data. Geophys. Res. Lett. 2017, 44, 1360–1368. [Google Scholar] [CrossRef]
- Muto, A.; Peters, L.E.; Gohl, K.; Sasgen, I.; Alley, R.B.; Anandakrishnan, S.; Riverman, K.L. Subglacial bathymetry and sediment distribution beneath Pine Island Glacier ice shelf modeled using aerogravity and in situ geophysical data: New results. Earth Planet. Sci. Lett. 2016, 433, 63–75. [Google Scholar] [CrossRef]
- Tinto, K.J.; Padman, L.; Siddoway, C.S.; Springer, S.R.; Fricker, H.A.; Das, I.; Caratori-Tontini, F.; Porter, D.F.; Frearson, N.P.; Howard, S.L.; et al. Ross Ice Shelf response to climate driven by the tectonic imprint on seafloor bathymetry. Nat. Geosci. 2019, 12, 441–449. [Google Scholar] [CrossRef]
- An, L.; Rignot, E.; Mouginot, J.; Millan, R. A Century of Stability of Avannarleq and Kujalleq Glaciers, West Greenland, Explained Using High-Resolution Airborne Gravity and Other Data. Geophys. Res. Lett. 2018, 45, 3156–3163. [Google Scholar] [CrossRef]
- Yang, J.; Luo, Z.; Tu, L. Ocean Access to Zachariæ Isstrøm Glacier, Northeast Greenland, Revealed by OMG Airborne Gravity. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020281. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Meng, S.; Lin, Y.; Xing, Z.; Zhang, C.; Yang, J.; Wan, X.; Qu, Z. Applying Iterative Method to Solving High-Order Terms of Seafloor Topography. Mar. Geod. 2019, 43, 63–85. [Google Scholar] [CrossRef]
- Gourlet, P.; Rignot, E.; Rivera, A.; Casassa, G. Ice thickness of the northern half of the Patagonia Icefields of South America from high-resolution airborne gravity surveys. Geophys. Res. Lett. 2016, 43, 241–249. [Google Scholar] [CrossRef]
- Dransfield, M. Airborne gravity gradiometry in the search for mineral deposits. In Proceedings of the Exploration 07, the Fifth Decennial International Conference on Mineral Exploration, Toronto, ON, Canada, 9–12 September 2017. [Google Scholar]
- Murphy, C.; Dickinson, J.; Salem, A. Depth estimating Full Tensor Gravity data with the Adaptive Tilt Angle method. ASEG Ext. Abstr. 2012, 2012, 1–3. [Google Scholar] [CrossRef]
- Studinger, M.; Koenig, L.; Martin, S.; Sonntag, J. Operation IceBridge: Using instrumented aircraft to bridge the observational gap between icesat and icesat-2. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Fenty, I.; Willis, J.; Khazendar, A.; Dinardo, S.; Forsberg, R.; Fukumori, I.; Holland, D.; Jakobsson, M.; Moller, D.; Morison, J.; et al. Oceans Melting Greenland: Early Results from NASA’s Ocean-Ice Mission in Greenland. Oceanography 2016, 29, 72–83. [Google Scholar] [CrossRef]
- Jekeli, C. Inertial Navigation Systems with Geodetic Applications; Walter de Gruyter GmbH: Berlin, Germany, 2001. [Google Scholar]
- Jekeli, C. On Precision Kinematic Accelerations for Airborne Gravimetry. J. Géod. Sci. 2011, 1, 367–378. [Google Scholar] [CrossRef]
- Parker, R.L. The Rapid Calculation of Potential Anomalies. Geophys. J. Int. 1973, 31, 447–455. [Google Scholar] [CrossRef]
- Watts, A.B. Isostasy and Flexure of the Lithosphere; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Banks, R.J.; Parker, R.L.; Huestis, S.P. Isostatic Compensation on a Continental Scale: Local Versus Regional Mechanisms. Geophys. J. Int. 1977, 51, 431–452. [Google Scholar] [CrossRef]
- Yang, J. Seafloor Topography Estimation from Gravity Gradients. Ph.D. Thesis, Division of Geodetic Science, School of Earth Sciences, The Ohio State University, Columbus, OH, USA, 2017. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=osu1512048462472145 (accessed on 5 May 2019).
- Jekeli, C. The downward continuation of aerial gravimetric data without density hypothesis. J. Geod. 1987, 61, 319–329. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry. J. Geophys. Res. Space Phys. 1994, 99, 21803–21824. [Google Scholar] [CrossRef]
- Kvas, A.; Mayer-Gürr, T.; Krauss, S.; Brockmann, J.M.; Schubert, T.; Schuh, W.-D.; Pail, R.; Gruber, T.; Jäggi, A.; Meyer, U. The Satellite-Only Gravity Field Model GOCO06s. GFZ Data Services; Helmholtz Centre Potsdam: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, Z.; Luo, Z. A New Hybrid Processing Strategy to Improve Temporal Gravity Field Solution. J. Geophys. Res. Solid Earth 2019, 124, 9415–9432. [Google Scholar] [CrossRef]
- Pawlowski, R.S. Preferential continuation for potential-field anomaly enhancement. Geophysics 1995, 60, 390–398. [Google Scholar] [CrossRef]
- Tinto, K.J.; Bell, R.E.; Cochran, J.R.; Münchow, A. Bathymetry in Petermann fjord from Operation IceBridge aerogravity. Earth Planet. Sci. Lett. 2015, 422, 58–66. [Google Scholar] [CrossRef][Green Version]
- Spector, A.; Grant, F.S. Statistical models for interpreting aeromagnetic data. Geophysics 1970, 35, 293–302. [Google Scholar] [CrossRef]
- Millan, R. Dynamics of Glaciers and Ice Sheets at the Ocean Margin from Airborne and Satellite Data. Ph.D. Thesis, Department of Earth System Science, University of California, Irvine, CA, USA, 2018. Available online: https://escholarship.org/uc/item/3bj084zr (accessed on 30 July 2019).
- Selman, D. Final Report of Processing and Acquisition of Air-FTG® Data and Magnetics in Bay St. George, Newfoundland/Labrador for Natural Resources Canada; Bell Geospace Inc.: Houston, TX, USA, 2013. [Google Scholar]
- Shaw, J.; Courtney, R.C. Multibeam bathymetry of glaciated terrain off southwest Newfoundland. Mar. Geol. 1997, 143, 125–135. [Google Scholar] [CrossRef]
- Ernstsen, V.B.; Noormets, R.; Hebbeln, D.; Bartholomä, A.; Flemming, B.W. Precision of high-resolution multibeam echo sounding coupled with high-accuracy positioning in a shallow water coastal environment. Geo Mar. Lett. 2006, 26, 141–149. [Google Scholar] [CrossRef]
- IHO. IHO Standards for Hydrographic Surveys (S-44), 5th ed.; International Hydrographic Bureau: Monaco, 2008. [Google Scholar]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Yang, J.; Jekeli, C.; Liu, L. Seafloor Topography Estimation from Gravity Gradients Using Simulated Annealing. J. Geophys. Res. Solid Earth 2018, 123, 6958–6975. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Jekeli, C. Extent and resolution requirements for the residual terrain effect in gravity gradiometry. Geophys. J. Int. 2013, 195, 211–221. [Google Scholar] [CrossRef]
- An, L.; Rignot, E.; Millan, R.; Tinto, K.J.; Willis, J. Bathymetry of Northwest Greenland Using “Ocean Melting Greenland” (OMG) High-Resolution Airborne Gravity and Other Data. Remote Sens. 2019, 11, 131. [Google Scholar] [CrossRef]
- Jordan, T.A.; Porter, D.; Tinto, K.; Millan, R.; Muto, A.; Hogan, K.; Larter, R.D.; Graham, A.G.C.; Paden, J.D. New gravity-derived bathymetry for the Thwaites, Crosson, and Dotson ice shelves revealing two ice shelf populations. Cryosphere 2020, 14, 2869–2882. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Wessel, P. Gridding with continuous curvature splines in tension. Geophysics 1990, 55, 293–305. [Google Scholar] [CrossRef]
- Howat, I.M.; Negrete, A.; Smith, B.E. The Greenland Ice Mapping Project (GIMP) land classification and surface elevation data sets. Cryosphere 2014, 8, 1509–1518. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| , density of sea water | 1030 kg/m3 |
| , density of the crust | 2670 kg/m3 |
| , density of the mantle | 3330 kg/m3 |
| , mean depth of sea water | 4500 m |
| , mean thickness of the crust | 6000 m |
| , Young’s modulus | kg·m−1·s−2 |
| , Poisson’s ratio | 0.27 |
| , effective elastic thickness | 45,000 m |
| No. | Mean | STD | RMS |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 16.77 | 14.25 | 22.01 |
| 2 | −0.11 | 14.52 | 14.52 |
| 3 | −1.09 | 11.36 | 11.41 |
| 4 | −0.23 | 10.39 | 10.39 |
| (a) 1 | (b) 2 | |||||
|---|---|---|---|---|---|---|
| No. | Mean | STD | RMS | Mean | STD | RMS |
| 0 | 1.56 | 2.64 | 3.06 | 0.11 | 0.29 | 0.31 |
| 1 | 14.39 | 19.27 | 24.05 | −0.08 | 6.23 | 6.23 |
| 2 | 9.39 | 22.43 | 24.32 | 0.75 | 5.75 | 5.80 |
| 3 | 9.00 | 14.82 | 17.34 | 1.12 | 4.20 | 4.35 |
| 4 | 11.60 | 14.05 | 18.22 | 0.87 | 4.29 | 4.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Luo, Z.; Tu, L.; Li, S.; Guo, J.; Fan, D. On the Feasibility of Seafloor Topography Estimation from Airborne Gravity Gradients: Performance Analysis Using Real Data. Remote Sens. 2020, 12, 4092. https://doi.org/10.3390/rs12244092
Yang J, Luo Z, Tu L, Li S, Guo J, Fan D. On the Feasibility of Seafloor Topography Estimation from Airborne Gravity Gradients: Performance Analysis Using Real Data. Remote Sensing. 2020; 12(24):4092. https://doi.org/10.3390/rs12244092
Chicago/Turabian StyleYang, Junjun, Zhicai Luo, Liangcheng Tu, Shanshan Li, Jingxue Guo, and Diao Fan. 2020. "On the Feasibility of Seafloor Topography Estimation from Airborne Gravity Gradients: Performance Analysis Using Real Data" Remote Sensing 12, no. 24: 4092. https://doi.org/10.3390/rs12244092
APA StyleYang, J., Luo, Z., Tu, L., Li, S., Guo, J., & Fan, D. (2020). On the Feasibility of Seafloor Topography Estimation from Airborne Gravity Gradients: Performance Analysis Using Real Data. Remote Sensing, 12(24), 4092. https://doi.org/10.3390/rs12244092