Temporal Gravity Signals in Reprocessed GOCE Gravitational Gradients
Abstract
1. Introduction
- (1)
- Which time-variable signals can be resolved by gravity field models solely based on GOCE SGG data? Are the improvements in the northern polar area due to the recent reprocessing good enough to detect ice mass variations in Greenland in GOCE SGG-only models?
- (2)
- What is the effect of incorporating GOCE SGG data in GRACE/GOCE SGG combination models with respect to time-variable signals?
- (3)
- How do the SH and mass concentration (mascon) gravity processing approaches compare in their ability to recover time-variable signals from GOCE SGG data?
2. Data and Methods
2.1. Data
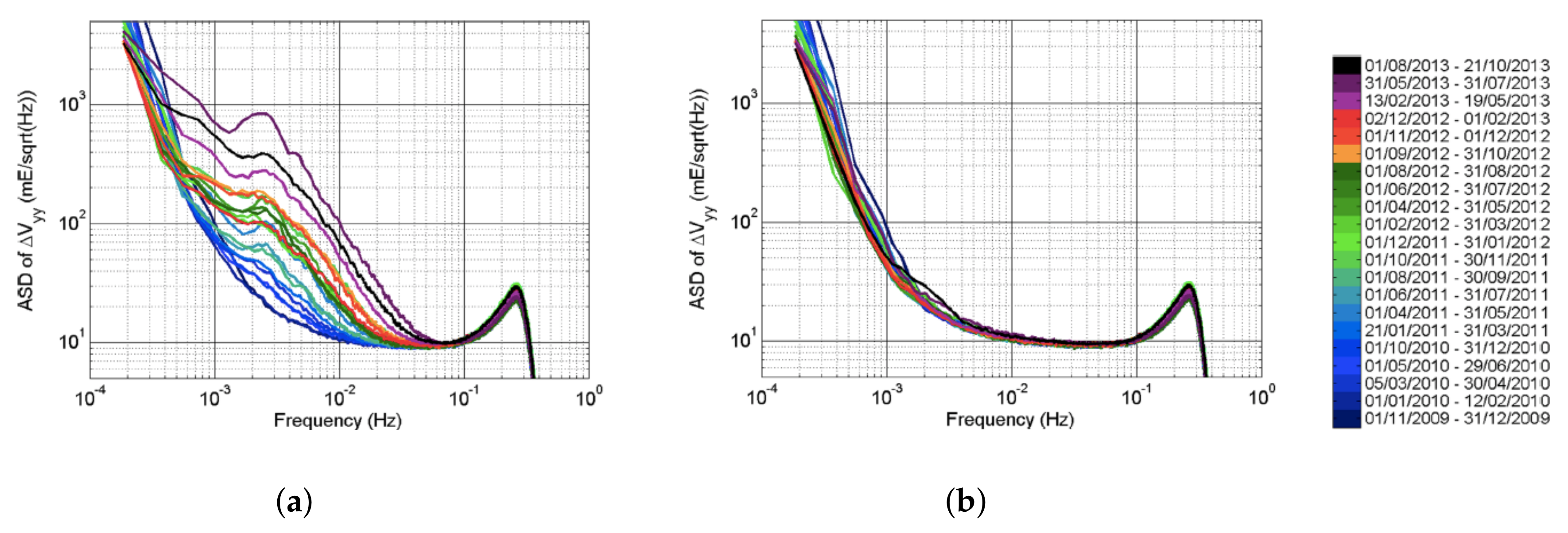
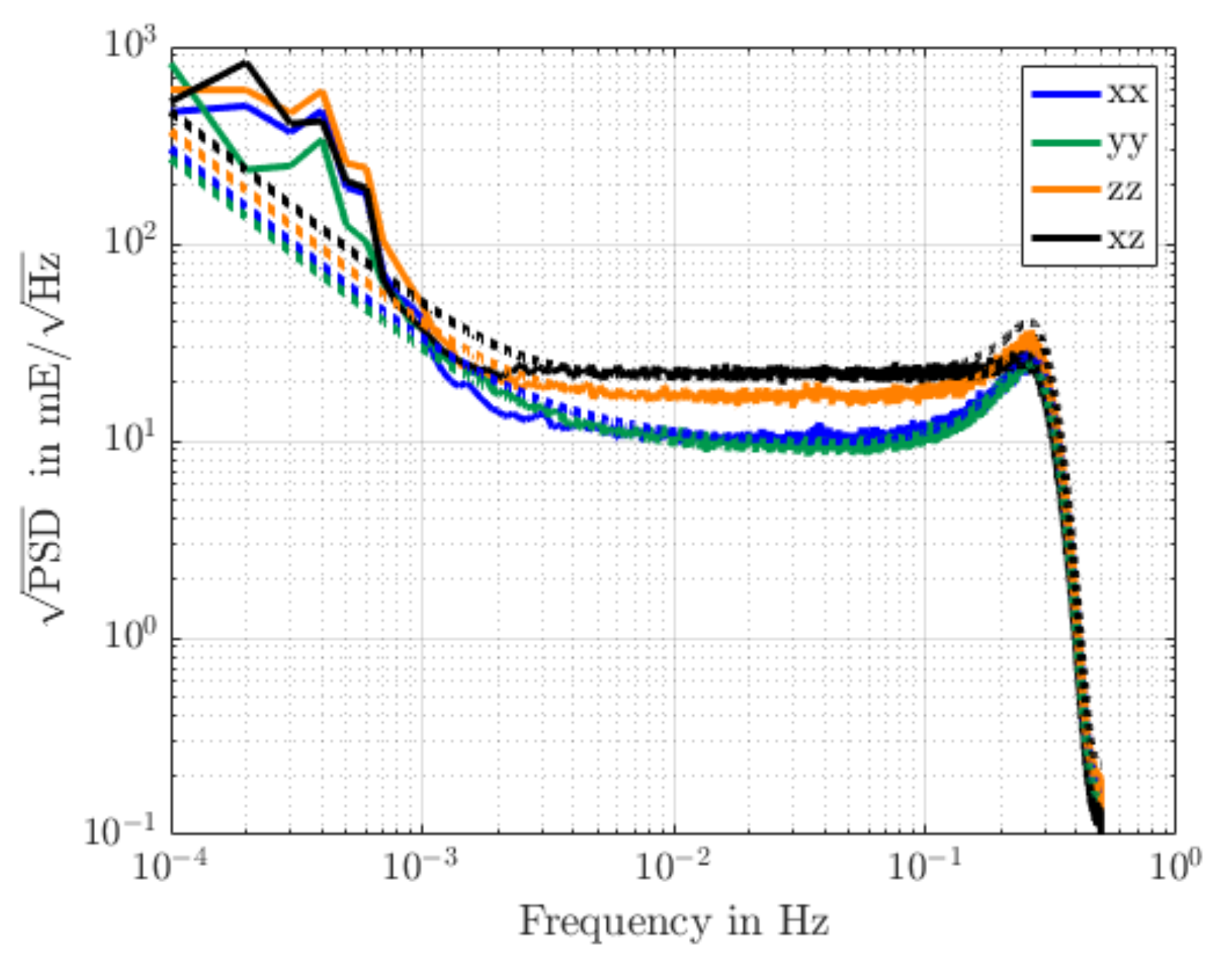
2.1.1. Real GOCE Satellite Gravitational Gradiometry Data
2.1.2. Synthetic GOCE Satellite Gravitational Gradiometry Data
2.2. Gravity Field Modeling
2.2.1. Preprocessing of the Level 1B Data
2.2.2. Spherical Harmonics Approach
2.2.3. Mascon Approach
Design Matrix Computation
2.2.4. GRACE/GOCE SGG Combination Models by the SH and Mascon Approaches
GRACE Design Matrix for Mascon Approach
2.2.5. Low-Pass Filter for Mascon Approach
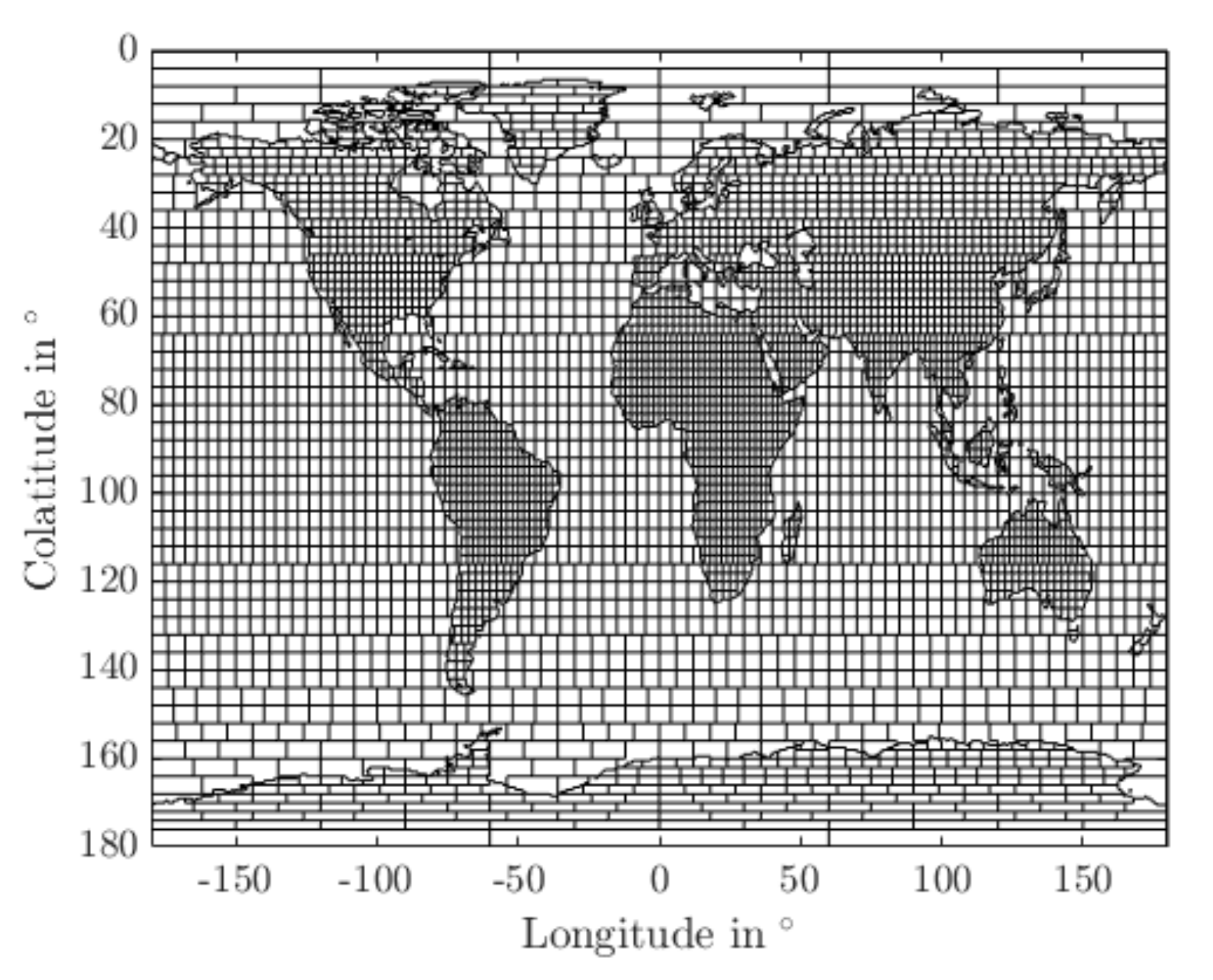
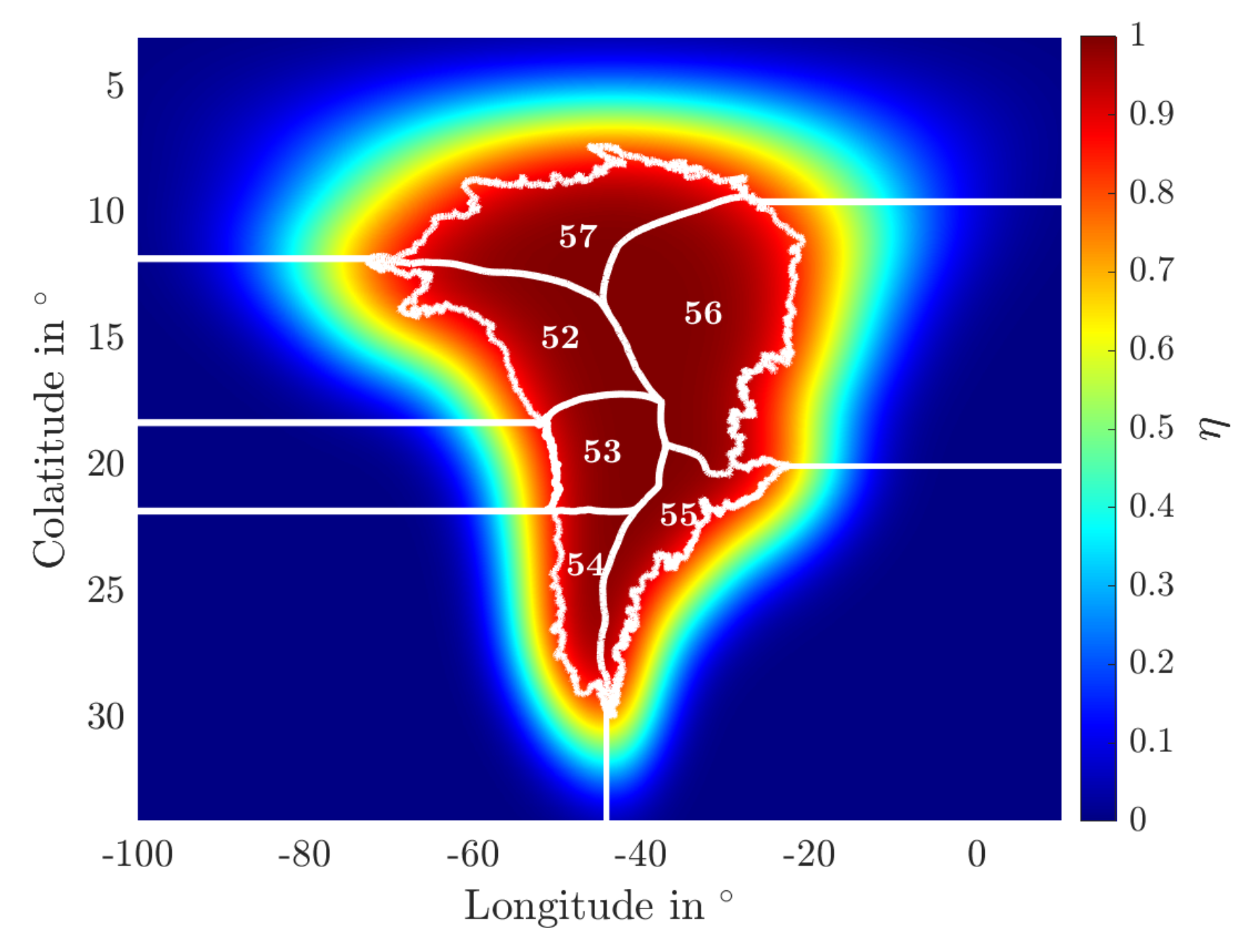
2.3. Computation of Regional Ice Mass Trends
2.3.1. Computation of Ice Mass Trends by the SH Approach
2.3.2. Computation of Ice Mass Trends by the Mascon Approach
3. Results
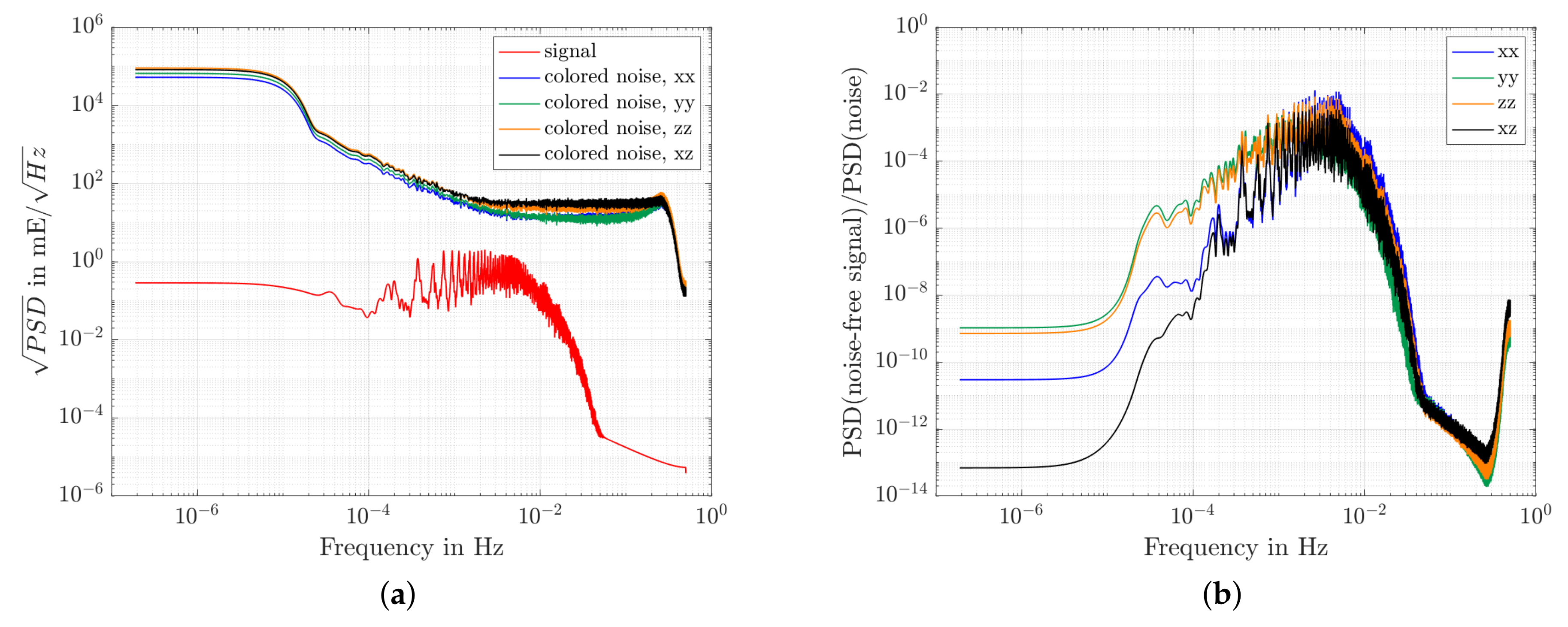
3.1. Time-Variable Gravity Signals in Synthetic GOCE SGG Data
3.1.1. SNR of Time-Variable Signals in Synthetic SGG Data
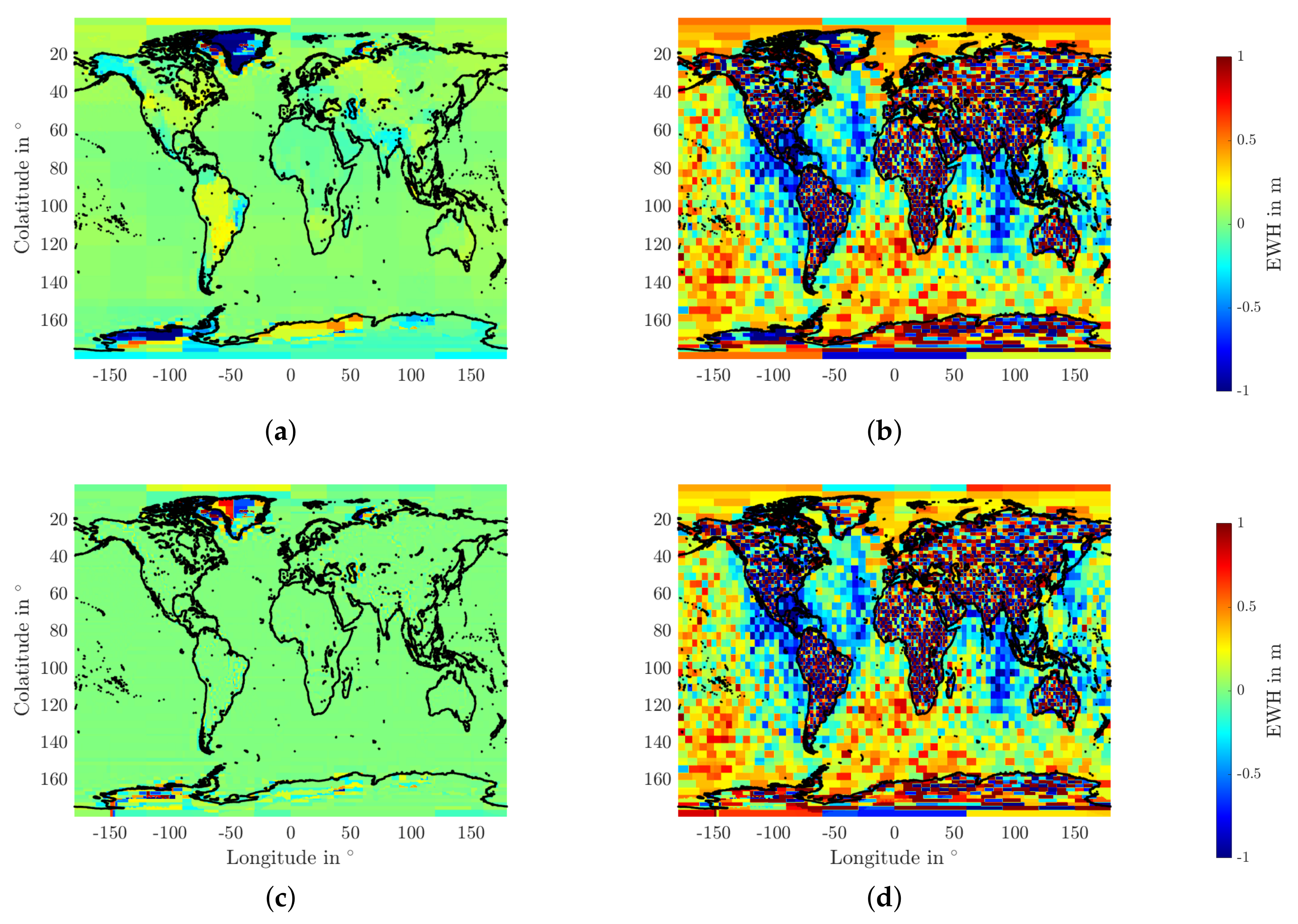
3.1.2. SH and Mascon Closed-Loop Results
- The ice mass trend signals in Greenland and West Antarctica accumulated over about 10 years were considered.
- Differences of a bi-monthly model to a low-noise reference model were analyzed.
- A mascon parametrization corresponding to Figure 6 and a SH parametrization of a maximum SH d/o 100 were used.
- GOCE-like colored noise corresponding to the PSDs of the designed filter models presented in Section 2.1.1 were included in the data.
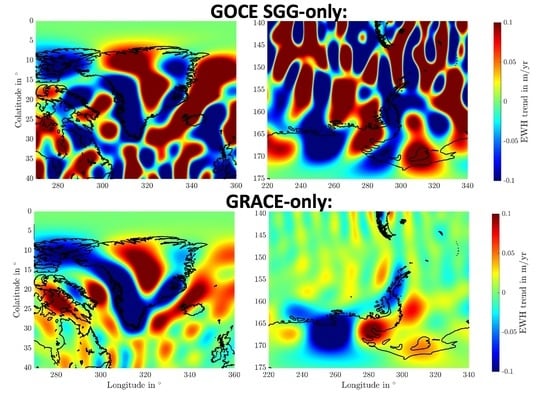
3.2. Time-Variable Signals in GOCE SGG-Only Models
3.2.1. Long-Term Signals
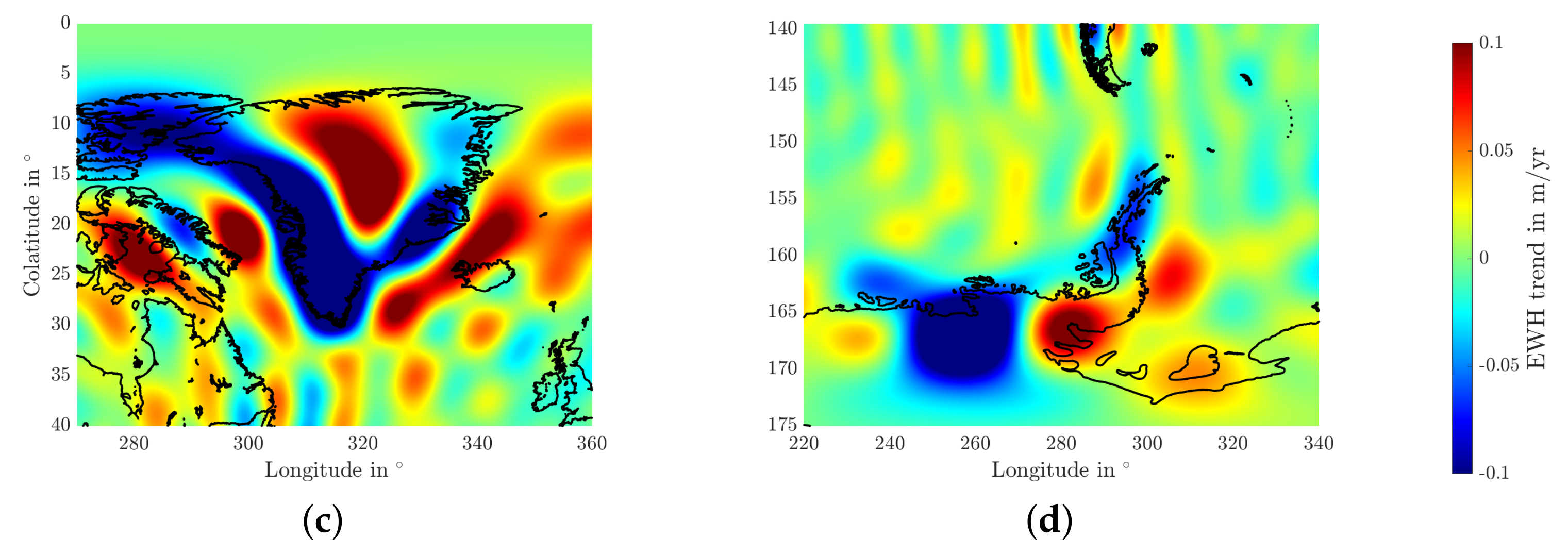
3.2.2. Ice Mass Trend Grids in Greenland and West Antarctica
3.2.3. Catchment Ice Mass Trends in Greenland
3.3. GRACE/GOCE SGG Combination Models
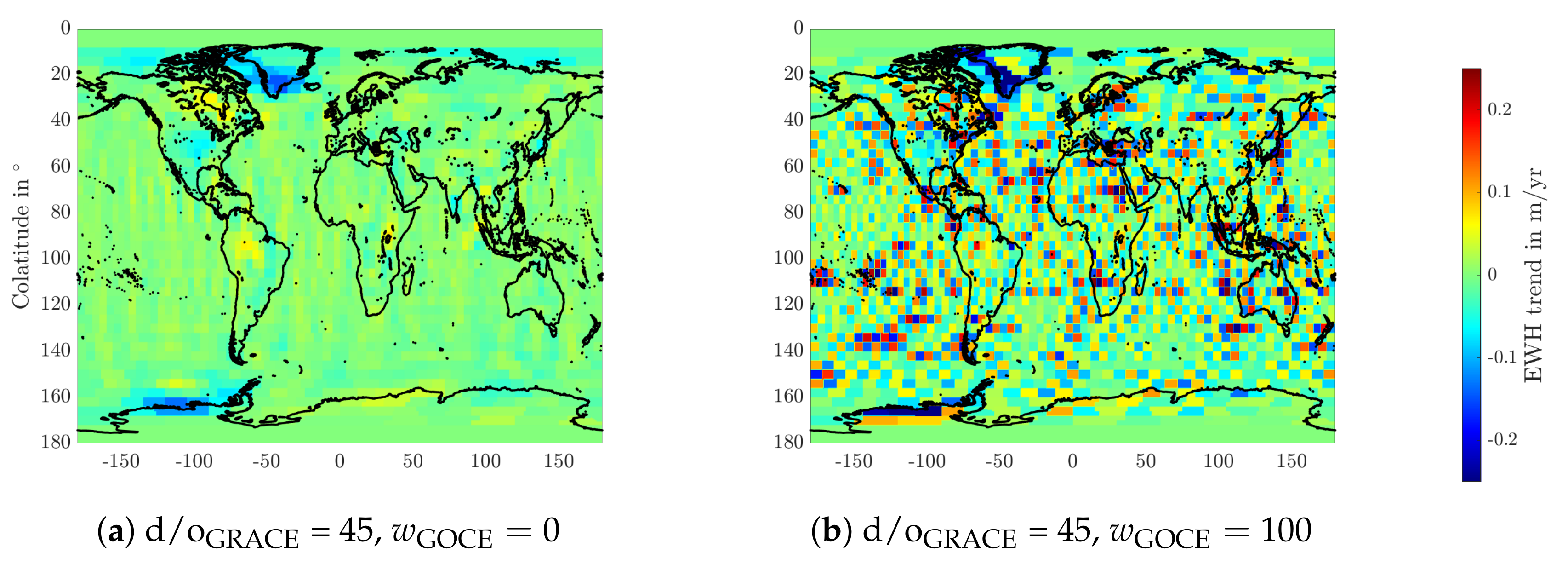
3.3.1. Mascon Combination Models
3.3.2. Impact of GOCE SGG Data in Monthly Combination Models
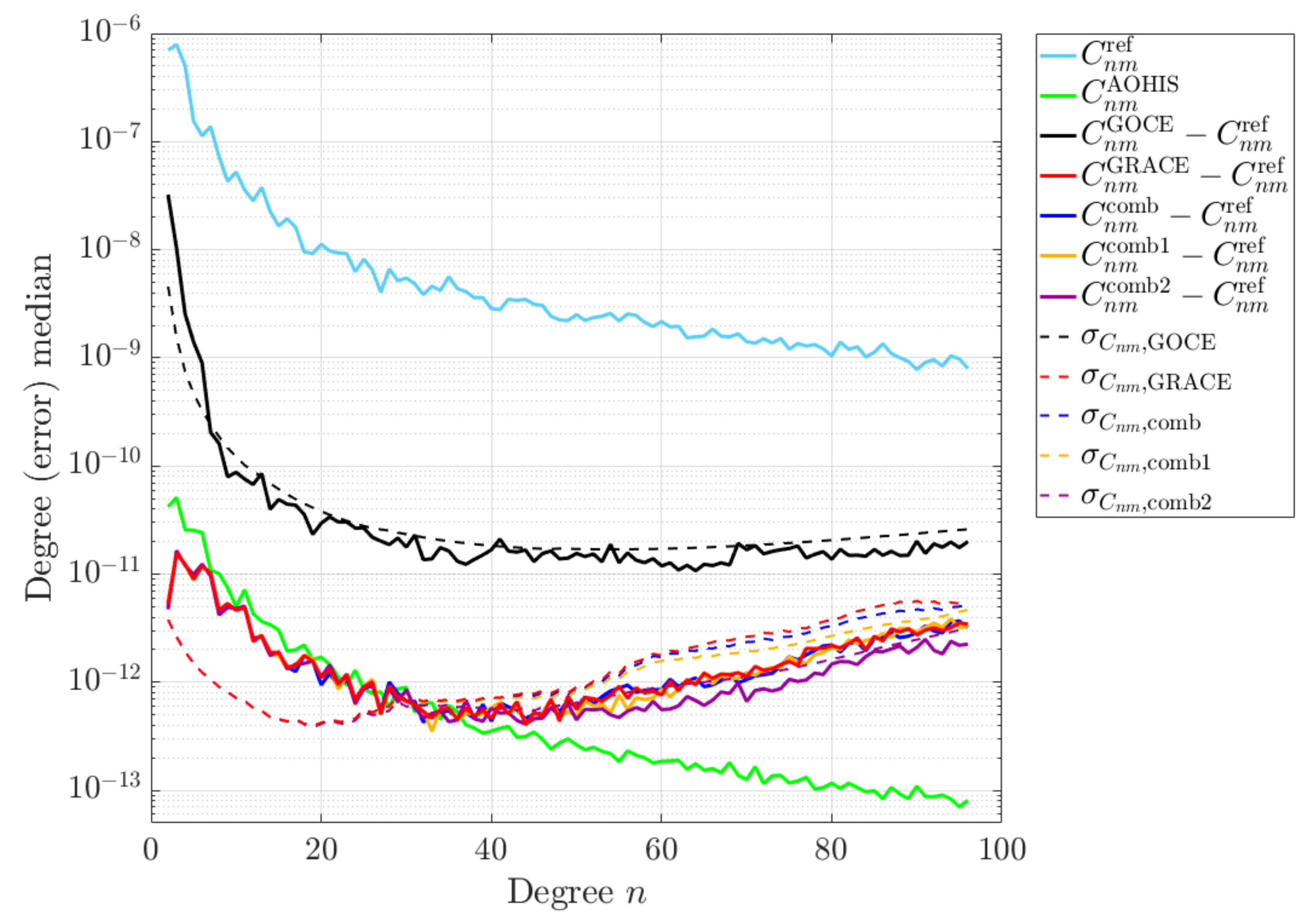
- “GRACE”: the ITSG-Grace2018 solution for September 2011,
- “GOCE”: the GOCE SGG-only solution for September 2011 based on the data period 1–30 September 2011,
- “comb.”: the combination of the associated GRACE and GOCE NEQ systems for September 2011,
- “comb. 1”: the combination of the GRACE NEQs for September 2011 and the GOCE NEQs for the data period 1 August 2013 to 1 October 2013, and
- “comb. 2”: the combination of the GRACE NEQs for September 2011 and the GOCE NEQs for the data period 28 October 2011 to 1 October 2013.
3.3.3. Greenland Ice Mass Trends from GRACE and Combination Models
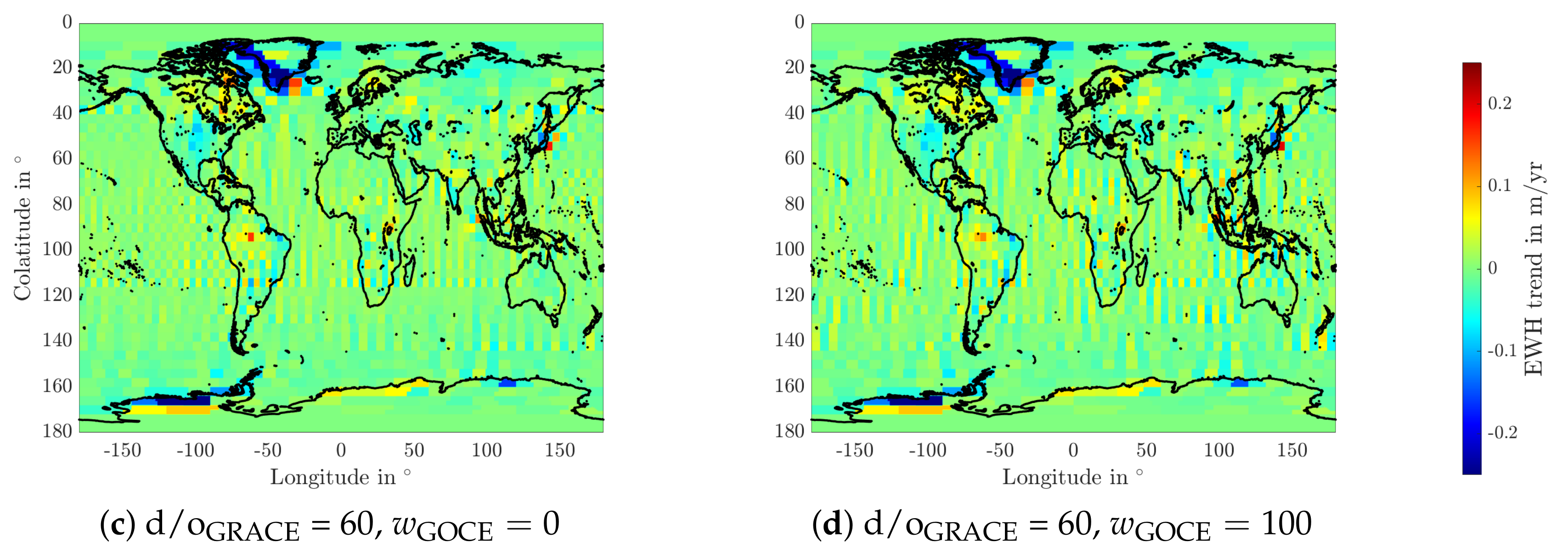
Effect of Varying Model Parameters in the SH and Mascon Approaches
Effect of Using a Mascon or SH Processing Approach
Effect of Using GRACE-only or Combination Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A/O | Atmosphere/Ocean |
| AOHIS | Atmosphere, Ocean, Hydrology, Ice, Solid Earth |
| ARMA | Autoregressive Moving-Average |
| ASD | Amplitude Spectral Density |
| d/o | SH degree and order |
| ESA | European Space Agency |
| EWH | Equivalent Water Height |
| GIA | Glacial Isostatic Adjustment |
| GOCE | Gravity field and steady-state Ocean Circulation Explorer |
| GRACE | Gravity Recovery And Climate Experiment |
| GRF | Gradiometer Reference Frame |
| IAPG | Institute of Astronomical and Physical Geodesy |
| mascon, MC | Mass Concentration |
| MBW | Measurement Bandwidth |
| moment magnitude | |
| NEQ | Normal Equation |
| PSD | Power Spectral Density |
| SGG | Satellite Gravitational Gradiometry |
| SH | Spherical Harmonic |
| SNR | Signal-to-Noise Ratio |
| SST-hl | high-low Satellite-to-Satellite Tracking |
| SST-ll | low-low Satellite-to-Satellite Tracking |
| TIM | Time-wise approach |
References
- Drinkwater, M.R.; Floberghagen, R.; Haagmans, R.; Muzi, D.; Popescu, A. GOCE: ESA’s First Earth Explorer Core Mission. In Space Sciences Series of ISSI; Springer: Dordrecht, The Netherlands, 2003; Volume 108, pp. 419–432. [Google Scholar] [CrossRef]
- Pail, R. Globale Schwerefeldmodellierung am Beispiel von GOCE. In Erdmessung und Satellitengeodäsie; Rummel, R., Freeden, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 5; pp. 217–257. [Google Scholar] [CrossRef]
- Drinkwater, M.R.; Haagmans, R.; Muzi, D.; Popescu, A.; Floberghagen, R.; Kern, M.; Fehringer, M. The GOCE gravity mission: ESA’s first core explorer. In Proceedings of the 3rd International GOCE User Workshop, Rome, Italy, 6–8 November 2007; pp. 1–8. [Google Scholar]
- Brockmann, J.M.; Schubert, T.; Schuh, W.D. An Improved Model of the Earth’s Gravity Field as Seen by the GOCE Satellite—The GO_CONS_EGM_TIM_RL06 Solution Computed with the Time-Wise Approach Based on Reprocessed Level 1B Products. J. Geod. 2020. in review. [Google Scholar]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Kusche, J. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 2007, 81, 733–749. [Google Scholar] [CrossRef]
- Van der Meijde, M.; Pail, R.; Bingham, R.; Floberghagen, R. GOCE data, models, and applications: A review. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 4–15. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Behzadpur, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Strasser, S.; Zehentner, N. ITSG-Grace2018—Monthly, Daily and Static Gravity Field Solutions from GRACE. 2018. Available online: https://dataservices.gfz-potsdam.de/icgem/showshort.php?id=escidoc:3600910 (accessed on 10 October 2019).
- Kvas, A.; Mayer-Gürr, T.; Krauss, S.; Brockmann, J.M.; Schubert, T.; Schuh, W.D.; Pail, R.; Gruber, T.; Jäggi, A.; Meyer, U. The Satellite-Only Gravity Field Model GOCO06s. 2019. Available online: https://dataservices.gfz-potsdam.de/icgem/showshort.php?id=escidoc:4081892 (accessed on 30 March 2020).
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2020, 94. [Google Scholar] [CrossRef]
- Fuchs, M.J.; Bouman, J.; Broerse, T.; Visser, P.; Vermeersen, B. Observing coseismic gravity change from the Japan Tohoku-Oki 2011 earthquake with GOCE gravity gradiometry. J. Geophys. Res. Solid Earth 2013, 118, 5712–5721. [Google Scholar] [CrossRef]
- Bouman, J.; Fuchs, M.; Ivins, E.; van der Wal, W.; Schrama, E.; Visser, P.; Horwath, M. Antarctic outlet glacier mass change resolved at basin scale from satellite gravity gradiometry. Geophys. Res. Lett. 2014, 41, 5919–5926. [Google Scholar] [CrossRef]
- Rexer, M.; Pail, R.; Fecher, T.; Meyer, U. Time Variable Gravity: Contributions of GOCE Satellite Data to Monthly and Bi-monthly GRACE Gravity Field Estimates. In Gravity, Geoid and Height Systems; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Farahani, H.H.; Ditmar, P.; Klees, R. Assessment of the added value of data from the GOCE satellite mission to time-varying gravity field modelling. J. Geod. 2013, 88, 157–178. [Google Scholar] [CrossRef]
- Peterseim, N.; Schlicht, A.; Stummer, C.; Yi, W. Impact of cross winds in polar regions on GOCE accelerometer and gradiometer data. In Proceedings of the 4th International GOCE User Workshop, Munich, Germany, 31 March–1 April 2011. [Google Scholar]
- Siemes, C.; Haagmans, R.; Kern, M.; Plank, G.; Floberghagen, R. Monitoring GOCE gradiometer calibration parameters using accelerometer and star sensor data: Methodology and first results. J. Geod. 2012, 86, 629–645. [Google Scholar] [CrossRef]
- Siemes, C. Improving GOCE cross-track gravity gradients. J. Geod. 2017, 92, 33–45. [Google Scholar] [CrossRef]
- Siemes, C.; Rexer, M.; Schlicht, A.; Haagmans, R. GOCE gradiometer data calibration. J. Geod. 2019. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Rieser, D.; Höck, E.; Brockmann, J.; Schuh, W.D.; Krasbutter, I.; Kusche, J.; Maier, A.; Krauss, S.; Hausleitner, W.; et al. The new combined satellite only model GOCO03s. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems (GGHS 2012), Venice, Italy, 9–12 October 2012. [Google Scholar]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Pail, R.; Bruinsma, S.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.D.; Höck, E.; Reguzzoni, M.; Brockmann, J.M.; Abrikosov, O.; et al. First GOCE gravity field models derived by three different approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
- Siemes, C. Digital Filtering Algorithms for Decorrelation within Large Least Squares Problems. Ph.D. Thesis, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, Germany, 2008. [Google Scholar]
- Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W.; Watkins, M.M. JPL GRACE and GRACE-FO Mascon Ocean, Ice, and Hydrology Equivalent Water Height Coastal Resolution Improvement (CRI) Filtered Release 06 Version 02, 2019. Available online: https://podaac.jpl.nasa.gov/dataset/TELLUS_GRAC-GRFO_MASCON_CRI_GRID_RL06_V2 (accessed on 7 April 2020).
- Pail, R.; Fecher, T.; Murböck, M.; Rexer, M.; Stetter, M.; Gruber, T.; Stummer, C. Impact of GOCE Level 1b data reprocessing on GOCE-only and combined gravity field models. Studia Geophys. Geod. 2012, 57, 155–173. [Google Scholar] [CrossRef]
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and Evaluation of a New GRACE-Only Gravity Field Time Series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef]
- Sneeuw, N.; van Gelderen, M. The polar gap. In Geodetic Boundary Value Problems in View of the One Centimeter Geoid; Springer: Berlin/Heidelberg, Germany, 1997; pp. 559–568. [Google Scholar] [CrossRef]
- Horwath, M.; Dietrich, R. Signal and error in mass change inferences from GRACE: The case of Antarctica. Geophys. J. Int. 2009, 177, 849–864. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; Springer: Vienna, Austria, 2006. [Google Scholar] [CrossRef]
- Rignot, E.; Mouginot, J. Ice flow in Greenland for the International Polar Year 2008–2009. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. Solid Earth 2002, 107, ETG 3–1–ETG 3–13. [Google Scholar] [CrossRef]
- Canuto, E.; Martella, P.; Sechi, G. Attitude and Drag Control: An Application to the GOCE Satellite. In Space Sciences Series of ISSI; Springer: Dordrecht, The Netherlands, 2003; pp. 357–366. [Google Scholar] [CrossRef]
- Simons, M.; Minson, S.E.; Sladen, A.; Ortega, F.; Jiang, J.; Owen, S.E.; Meng, L.; Ampuero, J.P.; Wei, S.; Chu, R.; et al. The 2011 Magnitude 9.0 Tohoku-Oki Earthquake: Mosaicking the Megathrust from Seconds to Centuries. Science 2011, 332, 1421–1425. [Google Scholar] [CrossRef] [PubMed]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Forootan, E.; Klemann, V.; Kusche, J.; Sasgen, I. The updated ESA Earth System Model for future gravity mission simulation studies. J. Geod. 2015, 89, 505–513. [Google Scholar] [CrossRef]
- Velicogna, I.; Mohajerani, Y.; Landerer, F.; Mouginot, J.; Noel, B.; Rignot, E.; Sutterley, T.; Broeke, M.; Wessem, M.; Wiese, D. Continuity of Ice Sheet Mass Loss in Greenland and Antarctica From the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Nahavandchi, H.; Joodaki, G.; Schwarz, V. GRACE-derived ice-mass loss spread over Greenland. J. Geod. Sci. 2015, 5. [Google Scholar] [CrossRef]








| Case | I | II | III | IV |
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | |
| 60 | 60 | 96 | 96 | |
| coefficients of the polar gap wedge included | yes | no | yes | no |
| Catchment Nr. | 52 | 53 | 54 | 55 | 56 | 57 | |
|---|---|---|---|---|---|---|---|
| MC, | GRACE | ||||||
| comb. | |||||||
| 23.9 | 1.5 | 3.4 | −0.7 | −7.1 | −420.9 | ||
| MC, | GRACE | ||||||
| comb. | |||||||
| 17.8 | 1.5 | 2.8 | −0.7 | −10.9 | −642.9 | ||
| MC, | GRACE | ||||||
| comb. | |||||||
| 9.5 | 1.7 | 1.9 | −0.6 | −18.8 | −38.9 | ||
| SH, case I | GRACE | ||||||
| comb. | |||||||
| 0.5 | 0.5 | 0.3 | 0.4 | 1.4 | 1.1 | ||
| SH, case II | GRACE | ||||||
| comb. | |||||||
| −0.05 | 0.1 | 0.06 | 0.01 | −0.5 | −0.3 | ||
| SH, case III | GRACE | ||||||
| comb. | |||||||
| −0.4 | −0.6 | 0.9 | 1.4 | 6.6 | −2.2 | ||
| SH, case IV | GRACE | ||||||
| comb. | |||||||
| −0.3 | −1.5 | −0.6 | 1.2 | 8.3 | −7.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heller, B.; Siegismund, F.; Pail, R.; Gruber, T.; Haagmans, R. Temporal Gravity Signals in Reprocessed GOCE Gravitational Gradients. Remote Sens. 2020, 12, 3483. https://doi.org/10.3390/rs12213483
Heller B, Siegismund F, Pail R, Gruber T, Haagmans R. Temporal Gravity Signals in Reprocessed GOCE Gravitational Gradients. Remote Sensing. 2020; 12(21):3483. https://doi.org/10.3390/rs12213483
Chicago/Turabian StyleHeller, Betty, Frank Siegismund, Roland Pail, Thomas Gruber, and Roger Haagmans. 2020. "Temporal Gravity Signals in Reprocessed GOCE Gravitational Gradients" Remote Sensing 12, no. 21: 3483. https://doi.org/10.3390/rs12213483
APA StyleHeller, B., Siegismund, F., Pail, R., Gruber, T., & Haagmans, R. (2020). Temporal Gravity Signals in Reprocessed GOCE Gravitational Gradients. Remote Sensing, 12(21), 3483. https://doi.org/10.3390/rs12213483