Abstract
Differences in topographic structure, vegetation structure, and surface wetness exist between peatland classes, making active remote sensing techniques such as SAR and LiDAR promising for peatland mapping. As the timing of green-up, senescence, and hydrologic conditions vary differently in peatland classes, and in comparison with upland classes, full growing-season time series SAR imagery was expected to produce higher accuracy classification results than using only a few select SAR images. Both interferometric coherence, amplitude and difference in amplitude time series datasets were assessed, as it was hypothesized that these may be able to capture subtle changes in phenology and hydrology, which in turn differentiate classes throughout a growing season. Groups of variables were compared for their effectiveness in Random Forest classification for both Sentinel-1 and Radarsat-2. The Shapley value was used to determine the contribution of each group of variables in thirty scenarios, and Mean Decrease in Accuracy was compared to evaluate its ability to rank variables by relative importance. Despite being dual-pol, the results of classifications using Sentinel-1 coherence (12-day repeat) were significantly better than using fully polarimetric RADARSAT-2 coherence (24-day repeat), likely owing to the difference in baseline and specific acquisition dates of the data in this study. Overall, full growing season Sentinel-1 coherence time series produced higher accuracy results than fully polarimetric quad pol RADARSAT-2 coherence amplitude, difference in amplitude and polarimetric decomposition time series. Using a full growing season of time-series imagery in classification resulted in higher accuracy than using a few dates over a growing season. Using mean decrease in accuracy to rank and reduce variables resulted in a weaker classification than if the entire time series is used.
1. Introduction
Like all wetlands, peatlands have great economic, societal, and environmental value, including forming a habitat for various unique species and species at risk [1], playing a role in the hydrologic cycle [2] and in sequestering carbon [3]. Despite these benefits, globally, they are subject to degradation through burning, conversion to farmland, and organic soil extraction for economic purposes [4]. While in general peatlands are the most widespread type of wetland internationally, there are several sub-classes of peatlands, which are formed based on specific characteristics of local hydrology, geology, and water chemistry (e.g., bog, poor fen, rich fen [5]). There are often many similar physical characteristics between different peatland classes (e.g., open bog and poor fen are both dominated by Sphagnum mosses), and conversely, there are often many highly variable features within a single class of peatland (e.g., rich fens vary widely in their vegetation composition, owing to local water chemistry). However, differences between and within the classes of peatland relate to differences in ecosystem services [5], thus mapping the extent of different peatland classes is widely studied [6,7].
Owing to their waterlogged surfaces and often dense vegetation, field data collection in peatlands can be physically demanding, time-consuming, and expensive. For these reasons, remote sensing is an attractive option for mapping peatlands. Similarities in multi-spectral imagery between peatland classes and upland classes (e.g., treed bog versus upland forest), and between peatland classes themselves (e.g., open bog and open poor fen), has resulted in poor accuracy when using a variety of different classifiers. Therefore, there are two main challenges in peatland mapping: (1) to differentiate treed bog from upland forest, as their canopies can appear similar in multi-spectral imagery [8]; and (2) to differentiate poor fen from bog, as these are both sphagnum-dominated ecosystems and can also appear similar spectrally [9]. However, differences in topographic structure, vegetation structure, or surface wetness exist between these classes, making active remote sensing techniques such as Synthetic Aperture Radar (SAR) and Light Detection and Ranging (LiDAR) promising for peatland mapping [10,11,12]. While LiDAR is able to capture these important characteristics at high spatial resolutions, it is expensive to acquire, and thus not widely collected and not often collected repeatedly over time.
1.1. SAR for Time Series Mapping
As SAR should be sensitive to variations in vegetation structure and wetness, several studies have assessed a variety of different SAR parameters, including polarimetric decompositions [10,13,14,15,16]. In some studies, SAR has been shown to be useful for differentiating fen from bog based on differences in wetness and prevalence of grasses [13]. As well, differences in wetness and vegetation canopy between treed bog and upland forest should also be distinguishable with SAR. However, it has been found that SAR data alone do not produce high accuracy classification results in many peatland mapping scenarios. The addition of a digital elevation model (DEM) or Landsat imagery has been found to improve results, with a combination of sensors together providing superior results to either one alone [10,12].
Most classifications of peatlands have been completed using a single image or a few intermittent images, often using different SAR beam-modes to capture different physical conditions that can be characterized at different incident angles [16], or using a few dates throughout the growing season to capture extremes in vegetation and wetness in spring and fall [12]. However, different peatland classes exhibit variability in temporal signatures in vegetation green-up and senescence, surface wetness, and water table depths. By only collecting imagery on a few extreme dates, the variability in timing of green-up/senescence and flashiness of hydrologic conditions may not be captured. Recently, Li et al. [17] demonstrated that full growing season time series Sentinel-1 amplitude data enabled the differentiation of treed and non-treed wetland, and results were improved in comparison with using single images or using time-series with missing observations. However, this study did not differentiate treed peatlands from other types of treed wetlands. Similarly, Karlson et al. [18] used Sentinel-1 intensity and found high classification accuracy using intensity time series alone but noted significant improvement in accuracy when a high-resolution DEM and derivatives were also included.
1.2. Interferometric Coherence Used in Classification
SAR sensors record both the amplitude and phase of backscattered signals. The phase is affected by differences in the satellite orbits in the two passes, topography, ground deformation or displacement, atmospheric propagation delays, and systematic and environmental noise [19]. SAR interferometry is the collection and processing of two SAR images of the same location captured from two spatially separate positions producing an interferometric pair. The two images can be captured through a single pass (two receiving antennas on the same platform), or from repeat passes where one or more sensors acquires images at two different times, with two parallel or nearly parallel flight-paths over the same area. The interferometric baseline is the relative difference in position between the sensors when they capture the two images. For images to be used as an interferometric pair, they must be the same mode (e.g., both must have the same polarization and incident angle).
Several authors have recently incorporated time-series coherence into classification, observing increased accuracy over using intensity alone for mapping a variety of environments or conditions including urban areas [20], flooding [21], and general land-use mapping [22,23]. Notably, Sica et al. [23] fit an exponential model to their time series data to compute two coherence parameters; that is, the estimated target decorrelation constant, which measures how fast the exponential model decreases, and the long term coherence, which takes into account situations where a target might not decorrelate over a long period of time (e.g., hard surfaces). Using these parameters alongside the incident angle resulted in an overall accuracy around 78%, but a higher accuracy was obtained using intensity and incident angle alone (88%) or all parameters combined (91%).
InSAR has also been used for monitoring water levels in herbaceous wetlands [24,25], where high coherence is attributed to double-bounce scattering. In these cases, water acts as the surface plane and emergent, herbaceous vegetation (e.g., grasses, cattails) acts as a vertical structure enabling a secondary reflection or “double-bounce” backscatter. While small pools do exist in some peatlands, peatlands are not generally dominated by standing water. Further, when they exist, emergent vegetation is rare and is often not herbaceous, but rather comprised of woody, vascular plants. Brisco et al. [26] found high coherence in both marsh and swamp classes, which both exhibit standing water and some exhibit woody vegetation. They observed that, in these types of environments, if an interaction between the canopy and water exists, it can become depolarized and still maintain coherence. They attribute this to the fact that the underlying water layer provides a stable, uniform dielectric plane that results in coherent backscatter. Although their study was carried out in swamps and marshes, there may be a similar mechanism that results in high coherence in peatlands. In the case of peatlands where no standing water exists, the water table beneath the surface of the peat may act as the stable dielectric plane, and the dry sphagnum moss layer above the water table acts as depolarizing vegetation. Brisco et al. [26] also created a visualization scheme that highlights diversity in wetland type and structure, where the standard deviation in coherence and intensity were mapped to red and blue colour channels, respectively, and the mean coherence was mapped to the green channel. They did not test these statistics of their coherence time series in classification. Additionally, InSAR has been used in peatlands in a few instances to monitor surface degradation and displacement [27].
1.3. Variable Selection in Classification
Variable selection is often necessary or desired in remote sensing image classification analyses. When introducing variables or environments into an analysis, understanding the degree to which variables contribute to a particular criteria of interest (e.g., overall or class-specific accuracies) can provide insight into the nature of the study area or problem. Further, using this information to reduce the number of variables, when necessary, is important as it can lead to reduced processing times, reduced data redundancy, and sometimes higher accuracy. In these cases, determining a subset of variables that contribute most to a classification is an important task. The random forest classification algorithm has been used by many authors to assess the importance of variables and reduce the number of variables in classification, and in the interpretation of which topographic and physiographic features are most important in separating different classes [28]. However, several authors have indicated issues with using mean decrease in accuracy (MDA) for variable selection when highly correlated variables are included in the classification, or when too few trees are used in the classification [29].
Conversely, the Shapley value [30,31] produces unbiased estimates of variable contribution (i.e., importance) regardless of correlated variables and the classification parameters (so long as the classification parameters produce unbiased accuracy metrics and stable accuracy values). The Shapley value method, as introduced by Nandlall and Millard [32] and used here, treats each user-defined group of variables (where a group could contain one or more variables) as players in a collaborative game, where the goal of the game is to maximize the accuracy of the classifier. To compute the Shapley value, each classification was run multiple times (i.e., one model run for the full set of players (i.e., groups) as well as each of the possible subsets, excluding the empty set). In each run, a different combination of players is used; based on the change in accuracy during each run, the contribution of each player can be calculated. In this application, the Shapley value of each player represents the contribution made by that player to the overall accuracy of the classifier (and thus has the same units as accuracy, e.g., percentage). For more information on the how the Shapley value can be used in classification scenarios, the reader is directed to [32].
1.4. Objectives
Different peatland classes exhibit variability in temporal signatures in vegetation green-up and senescence, surface wetness, and water table depths. By only collecting imagery on a few extreme dates, the variability in timing of green-up/senescence and flashiness of hydrologic conditions may not be captured. Therefore, we hypothesized that full growing-season time series SAR imagery may produce higher accuracy results than using a few images. Additionally, we expected that variables that capture differences in time (i.e., coherence, difference in amplitude) may provide different information to a classifier than a time series of amplitude images that capture conditions on a given date. Thus, the main objectives of this study are (1a) to compare a Radarsat-2 (RS2) time series to Sentinel-1 (S1) time series to determine if the shorter temporal baseline of Sentinel-1 leads to improved classification results and (1b) to assess the impact of datasets that were acquired in different seasons (shorter lengths of time) to determine if imagery from one particular season contributed more to the classification than another, (2a) determine if coherence, amplitude, or difference in amplitude between image pairs produced better classification results for both S1 and RS2; and (2b) for coherence, amplitude, and difference of amplitude groups of variables, assess different polarization combinations (quad pol combinations for RS2, dual pol combinations for S1) and different RS2 Fine Quad incident angles.
2. Study Area
This study was conducted at Alfred Bog, a mined, temperate peatland in Eastern Ontario, Canada (Figure 1). This peatland has been the subject of several other studies and several remote sensing methods have been used to create peatland ecosystem maps of this site (e.g., [11,12]). A full description of the site and ecosystem characteristics can be found in Millard et al. [11]. The peatland consists of three peatland classes: open fen, open shrub bog, and treed bog (Figure 1). In some locations, the peatland naturally grades into upland forest, but in others, it abruptly ends at a current peat mining site or agricultural field. This peatland was monitored intensively during the growing seasons of 2013 and 2014 [33] in all peatland classes. Since 2015, it has only been monitored using a single meteorological station (met station) located in the shrub bog. Figure 2 displays the water table, rain, and soil moisture data collected at a shrub bog site throughout the year. At the met station during 2017, water tables vary from 24 cm to 36 cm below the surface (Figure 2); however, the fen area of the peatland is generally much wetter than the shrub bog with water tables close to or at the surface in many areas. The fen water table is much more responsive to rain events than the bog (flashy). Spring and fall are generally wetter than summer, with a slight draw down in water table and reduction in wetness through August and September.
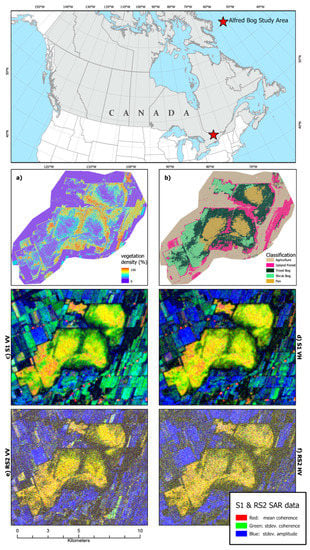
Figure 1.
Map showing general location of Alfred bog within Canada (top) and insets; (a) vegetation density map derived from LiDAR; (b) classification derived from Landsat and LiDAR previous used by Millard and Richardson, 2018; and (c), (d), (e), (f) Red-Green-Blue (RGB) colour composite of coherence using Sentinel-1 and RADARSAT-2 generated from VV and VH polarization. S1, Sentinel-1; RS2, Radarsat-2.
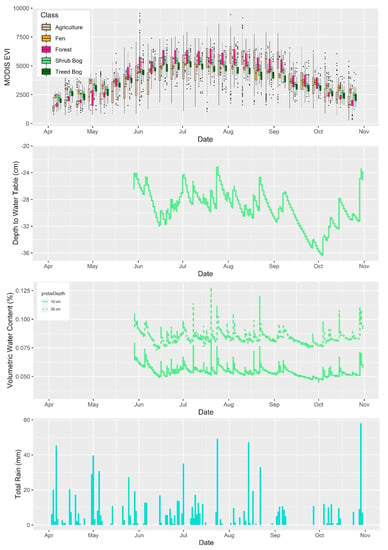
Figure 2.
Enhanced vegetation index (EVI) from MODIS Aqua and Terra, depth to water table from the surface of the peatland, soil moisture at two depths, and rain—all measured over the 2017 growing season. Water table and soil moisture are measured at a meteorological station located in the shrub bog area of Alfred Bog. These measurements were commenced in late May 2017. Rain was measured at Environment and Climate Change Canada’s weather station in St. Albert, Ontario, approximately 40 km south east of Alfred Bog.
Peatland vegetation is relatively sparse, especially in shrub bog and fen areas (Figure 1a and Figure 2, top panel). The fen exhibits string-flark patterning in some areas, with strings (ridges) being higher in elevation, drier, and covered in either shrubs or short trees. Flarks (hollows/depressions) are usually saturated at the surface or may exhibit standing water, depending on the recent rain conditions. Figure 2 (top panel) displays boxplots of the enhanced vegetation index (EVI) produced from MODIS composites throughout the 2017 growing season. In all classes in the study area, vegetation is at its maximum in late June through early August. The shrub bog and fen classes exhibit lower EVI than treed bog, forest, and agriculture throughout the growing season until mid-September, when fen EVI is within the same range or higher as forest and agriculture, but with reduced variability. During this period, treed bog EVI is reduced. Coherence and amplitude for both S1 and RS2 are displayed in Figure 3, which visually indicates no separability between classes using S1 or RS2 amplitude on any given date. In S1 coherence, a distinct separability is visible between peatland and non-peatland classes on most dates throughout the growing season, with the exception of mid-June, which coincides with low water table conditions and the beginning of vegetation green-up. However, on many dates, there is no distinction in the boxplots between the peatland classes. S1-coherence values are greater than 0.5 on many dates. RS2 coherence is significantly reduced in all classes, but some areas of the fen class increased to a coherence level greater than 0.4 in September.
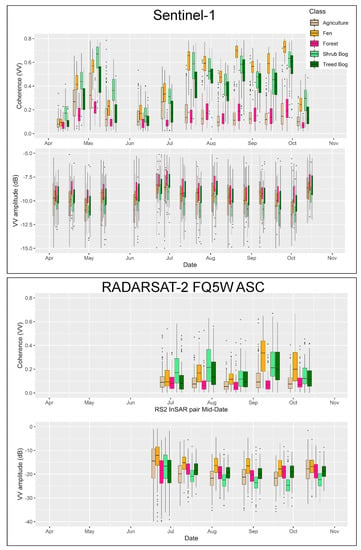
Figure 3.
Example of coherence and amplitude of RADARSAT-2 FQ5 Ascending (ASC) mode and Sentinel-1 VV imagery during the growing season of 2017 by class. Date for each image acquisition is at the mid-point of the group of boxplots (e.g., for RS2 FQ5ASC mode imagery, the first image is acquired on 20 June 2017).
3. Data and Methods
3.1. Choice of SAR Sensors
There are several SAR sensors currently in operation, and many different options available between and within a single sensor. Generally, when choosing an SAR sensor to map peatlands, the wavelength (e.g., C-band, L-band, and X-band are common), polarization options (fully polarimetric sensors offer more information than dual or single-pol sensors), and spatial resolution are important. While L-band has been shown to provide unique information about peatland surfaces and is relatively insensitive to variability in vegetation [25], there are no publicly available L-band sensors in operation. Historic ALOS-1 imagery is available, but, as an archive, does not capture current conditions in peatlands. The European Space Agency’s (ESA) S1 constellation (two C-band, dual-pol VV and VH sensors with a 6- or 12-day repeat orbit) are open access and data are available for download shortly after acquisition. S1 has several modes, with the most commonly-collected over the Canadian landmass being the interferometric wide mode (IW), which repeatedly collects data using the same orbit geometry enabling interferometric products to be produced every 6 to 12 days.
Canada currently operates RADARSAT-2 (RS2; a single C-band, quad-pol sensor with a 24-day repeat orbit) and the Radarsat Constellation Mission (RCM; three C-band, compact-pol sensors with up to a 4-day repeat orbit). RS2 is operated as a commercial sensor, but the owners of the sensor (Maxar) have an agreement with the Government of Canada to provide access to a quota of RS2 scenes to government departments. However, owing to the wide variety of modes available from RS2, users request imagery for a specific location, date, and mode, but must go through a “deconfliction” process whereby any conflicts between user requests are manually dealt with by the Canadian Space Agency before the image acquisition. This sometimes results in changes in the requested beam-mode and/or incident angle, so that sharing can occur between two users in a general area, or cancelation of the order owing a higher priority order (e.g., emergency) or a commercial order. Conversely, RCM will be operated with a “standard coverage”, where the specific beam-mode, repeat frequency, and resolution of the coverage vary by region within Canada. These modes are chosen in consultation with government departments based on their operational needs. Therefore, the repeatable coverage of S1 and RCM enables the collection of consistent and comparable data over time, which enables time series and interferometric analyses for peatlands across Canada, and internationally.
3.2. Training Data
Single pixel training data were collected throughout the study area using a combination of field visits and visual image interpretation (for details, see [11]). In the past, this training dataset at this site has been shown to produce high accuracy classification results with both LiDAR and Landsat data as input [11,12,32,33]. The training data were collected ensuring an equal number of points per class, based on the previous classification completed by Millard and Richardson [33]. A total of 250 points were randomly distributed throughout each of the five classes (1250 points in total). The class label for each point was verified visually with high resolution optical imagery.
3.3. Sentinel-1 Processing
S1 processing was completed using ESA’s Geohazards Thematic Exploitation Platform (GEP). GEP is an ESA originated R&D activity on the earth observation (EO) ground segment to demonstrate the benefits of new technologies for large scale processing of EO data. The platform was designed to support the geohazards community’s objectives. The platform allows both on demand processing for specific user needs and systematic processing to address common information needs of the geohazards community, as well as massive processing on multi-tenant computing resources in the Cloud. To exploit the geo-information generated using the platform, the GEP leverages open APIs for the integration of interactive processing and post-processing services. Today, the GEP allows the exploitation of 70+ terabytes of ERS and ENVISAT archive data and the Copernicus Sentinel-1, Sentinel-2, and Sentinel-3 available online. It offers about 40 EO processing services ranging from different categories such as conventional InSAR/optical services for earthquake response, to land subsidence and volcanoes monitoring, and advanced terrain motion services for SAR time series analysis. The code for the COIN processor in the GEP is available on github [34] and is based on the SNAP toolbox [35].
In this study, the COIN (“Coherence and Intensity Change”) application was used to produce a coherence image and a primary (reference) amplitude image for each Sentinel-1A TOPSAR interferometric wide mode image pair that was acquired over the study area from 1 April to 1 November 2017. This date range ensured that no snow still existed on the peatland at the time of acquisition and resulted in 15 pairs (16 images; Table 1). A pair consisted of a set of images from the same orbit acquired 12 days apart. The primary image was always selected as the image that occurred earliest in time. COIN pairs were calculated for both VV and VH polarizations [34]. S1 precise orbits were selected for processing and the Shuttle Radar Topography Mission (SRTM) 3 Arc-Second (90 m) DEM was used [34]. A coherence window of 10 × 40 pixels in azimuth and range was used, as well as a multilook of 2 and 8 in range and azimuth. Coherence products were output at 15 m spatial resolution.

Table 1.
List of Sentinel-1 (S1) and Radarsat-2 (RS2) images acquired in 2017 used to create interferometric pairs. All RS2 images were acquired 24 days apart. All S1 images were acquired 12 days apart, except for 12 May–5 June, where an image was missing from the archive/was not acquired, and 23 June, where an S1-B image was available enabling 6-day separation of images. ASC = Ascending orbit, DESC = Descending orbit
The COIN application produces several products, but only the coherence (abbreviated as “S1-coh”) and the primary amplitude image (abbreviated as “S1-amp”) were downloaded. Following Brisco et al. (2017) [26], for each polarization in the S1 time series, we also produced nine metrics to be used in classification and visualization (standard deviation of coherence and amplitude, and mean coherence). For each polarization, the difference in amplitude (abbreviated as “S1-diff”) was also calculated between image pairs (based on the 12-day orbit). The “diff” variables were included as it was expected that they may capture the unique ecohydrological changes, similar to coherence.
3.4. RADARSAT-2 Processing
All available Fine Quad Wide images of beam-mode FQW1ASC, FQW5ASC and FQ5WDESC were selected over the study area in 24-day intervals from 1 April to 1 November 2017 using MacDonald Detwiller and Associates’ Acquisition Planning Tool. These beam-modes were selected as they had been previously collected at this site for other studies. However, owing to conflicts with higher priority users, a time series of images for the full growing season could not be acquired for any specific beam mode. In this study, six FQ1DESC images were acquired between 20 June and 18 October 2017, in addition to six FQ1DESC images acquired on the same dates as the FQ1ASC images; five FQ1ASC images were acquired between 21 July and 25 October 2017 (17 images; Table 1). Each of these images was acquired in single-look complex (SLC) format and scaled using Land-LUT [36].
These RS2 images were processed using PCI Geomatica v2018 software to produce amplitude images (abbreviated as “RS2-amp”) and difference in amplitude (abbreviated as “RS2-diff”). The raw imagery was converted to sigma-nought backscatter in the following polarizations: HH, HV (considered synonymous with VH), and VV. Several polarimetric decomposition parameters were also computed (abbreviated as “RS2-decomp”) using the PCI Geomatica Polarimetric Workstation extension: Freeman Durden [37], Cloude-Pottier [38], and Touzi [13]. These were chosen based on previous work using decompositions in classification and modelling in peatlands (for information on the processing of and use of these decompositions in peatland ecosystem mapping, see [10,33]). Finally, coherence (abbreviated as “RS2-coh”) was calculated in PCI Geomatica using the Interferometry extension, resulting in 16 pairs. Each image pair was coregistered with sub-pixel accuracy. Using PCI’s automatic coregistration and resampling algorithm (INSCOREG), control points are acquired automatically, outliers are removed, and pixels are resampled to match the reference file. A total of 500 Ground Control Points (GCPs) were used and a minimum acceptance score of 0.75 was used in coregistration. Next, a filtered interferogram was created for each image pair, using a 9 × 9-pixel window, for each polarization (HH, HV, VV). Finally, the amplitude and coherence data were converted to real numbers at a 15 m spatial resolution. Similar to S1, RS2 difference in amplitude images (“RS2-diff”) were computed by subtracting the amplitude of the secondary image from that of the primary image in each pair.
3.5. Random Forest Classification Scenarios and the Shapley Value
All images were clipped to the study area, and then stacked into one multi-channel file. Including all dates for amplitude, amplitude difference and decompositions, all date pairs for coherence, and difference images for both sensors resulted in a stack of more than 600 channels.
To investigate which variables and combinations of variables produce the highest classification accuracy, and which variables and combinations contribute the most to these classifications, we created thirty (30) scenarios that allowed for the assessment of different sensors, polarizations, types of variables (amp, coh, decomp, diff), beam-modes, and seasonality (Table 2). For each scenario, variables were arranged into variable-groupings (abbreviated as “groups”) based on assessment criteria. Some scenarios included two groups (e.g., comparing all RS2 variables compared with all S1 variables), whereas others included up to four different groups. Classifications were generated by the RandomForest algorithm [39] in the randomForest package [40] of R [41], using 1000 trees (ntree), and the square root of the number of variables was tested at each split (mtry). The parameter mtry controls the diversity of the grown trees in the random forest model. The value of mtry, equal to the square root of the number of predictor variables, provides optimum diversity for the RF models [42] so that useful information in predictor variables can potentially contribute to the majority vote. The number of trees directly affects the stability of the accuracies. To achieve stable accuracy values, the guidelines suggested by Behnamian et al. [43] have been followed in this study. These parameters, ntree and mtry, have been shown to produce optimal random forest performance and consistent results at this site and others in the past [11,43].

Table 2.
Results of scenarios that compare different sensors, data types, seasons, and so on, listed by objective addressed and sensors used in assessment. Bold font in Shapley value column indicates the most important group of variables in that comparison. Italicized font in overall accuracy column indicates the classification scenario with the highest overall accuracy.
3.6. Assessing Variable Importance and the Contribution of Groups of Variables
We produced estimates of variable contribution using the Shapley value. To compute the Shapley value, for each scenario, classifications were run several times, based on the number of variable groups in the scenario. Accuracy metrics (out of bag) were averaged based on all model runs in each scenario. We also assessed variable importance using MDA, but only ran this analysis one time with all variables for each scenario using 10,000 trees. This large number of trees was used because producing stable variable importance values requires assessment of the number of trees and, in the past, a minimum of 10,000 trees was required at this site using similar input data and classes [43]. However, we note that we have included many highly correlated variables in classification, which has been shown to introduce bias in MDA rankings [29] and, therefore, the interpretation of this analysis should be considered carefully. To determine if the number of variables could be reduced based on the MDA variable importance ranking, we then used the 10 and 20 most important variables in classification alone in order.
4. Results
4.1. Assessment of Overall, User’s, and Producer’s Accuracy
Accuracy assessments for all 30 scenarios are displayed in Figure 4 and scenarios are described in Table 2. Using only growing season time series SAR imagery for classification, including short baseline (12-day) dual-pol SAR data, resulted in the highest classification accuracy. The highest overall classification accuracy was produced using all RS2 and S1 channels (all coherence, amplitude, and difference channels—Figure 4 and Figure 5). However, both the RS2/S1-coherence and S1-coh classifications produced results within 1% of the “best” results. All classifications that included S1-coh produced high accuracy results. The lowest classification accuracy was found using S1-diff, with less than 50% accuracy overall in several classes. With longer baselines (24 days), coherence alone did not produce high accuracy results, but when used in addition to amplitude, difference, or decomposition variables, this led to increases in classification accuracy. However, these were never as accurate as using short-baseline (S1) coherence information. For example, RS2-coh alone resulted in low accuracy (<60%), but the classification improved to 68% when amplitude and difference variables were included.
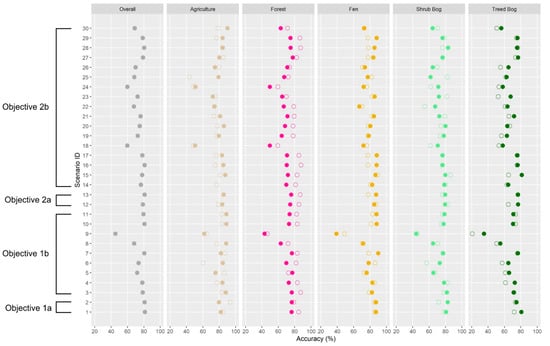
Figure 4.
Overall, user’s, and producer’s accuracy per class for the 30 scenarios. Scenario information (including which variables are included in each) is listed in Table 2; hollow and solid circles represent producer’s and user’s accuracies, respectively. The objectives that each of the classifications address are indicated on the left.
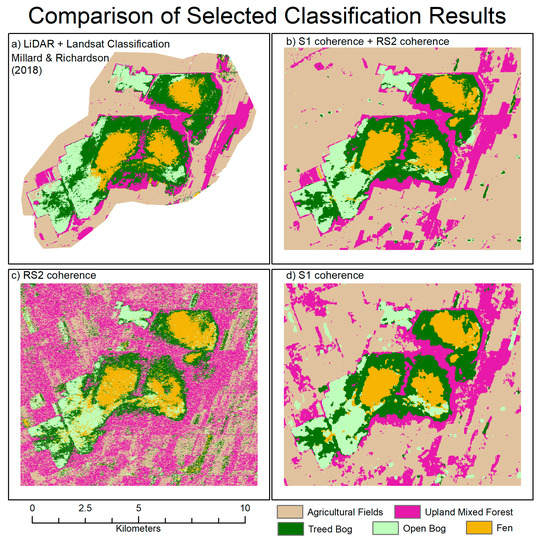
Figure 5.
Comparison of coherence-based classifications. (a) Previous classification created using a combination of Landsat-8 and LiDAR data used in Millard and Richardson, 2018. (b) S1-coh + RS2-coh = 81.2% accuracy, (c) RS2-coh = 59.7% accuracy, (d) S1-coh = 80.9% accuracy.
High user’s (UA) and producer’s accuracies (PA) were found in peatland classes in several classification scenarios: (1) in all scenarios where both RS2 and S1 were combined; (2) in all classifications where S1-coh was included; and (3) in classifications where RS2-coh was combined with amplitude, difference in amplitude, or decompositions, except when using only HV polarization (Figure 4). RS2 generally produced lower user’s and producer’s accuracy in the shrub bog and treed bog than when using S1 datasets. The S1-amp and S1-diff classification also produced low user’s and producer’s accuracy in all classes except agriculture. S1-coh alone produced the highest user’s and producer’s accuracies in the wetland classes.
There was no consistency in which sensor, or by including any type of variable, produced the highest UA or PA in the peatland classes; however, almost all classifications that produced the highest UA or PA included a coherence variable. Two exceptions are PA for shrub bog and fen, where accuracy was highest using RS2-amp, RS2-diff, S1-amp, and S1-diff together (86.4% and 89.1% PA, respectively).
The highest UA in the agriculture class was obtained using S1-amp and S1-diff together (90.1% UA), but the highest PA in agriculture was obtained using S1coh only. UA forest was low in many classification scenarios. UA was less than 75% in most scenarios except those including S1-coh and RS2-diff, or where RS2-decomp and RS2-amp were combined with S1-amp and S1-diff, or where all RS2 parameters were included (8 of 30 scenarios). PA for forest was acceptably high in many scenarios, with the best results being obtained using RS2-coh and S1-coh together.
Statistical metrics of S1 and RS2 coherence, as described in Brisco et al. [26], were produced for visualization (Figure 1); we also used these 12 variables alone in classification. The RGB visualization method introduced by Brisco et al. [26] indicates that peatlands have distinct temporal coherence patterns as compared with other surrounding classes and within the peatland. The combination of mean, standard deviation, and maximum for the full growing season S1-coh and S1-amp produced an overall accuracy of 78.6%, which is similar to the S1-coh classifications where each individual pair was used. User’s and producer’s accuracies were also similar to the S1-coh classifications. This indicates that producing statistical metrics of coherence and amplitude may be a potential solution to reducing the number of channels used in image classification.
4.2. Comparing Variable Importance (MDA), Contributions, and Interactions (Shapley Value)
When mean decrease in accuracy (MDA) was used to assess individual variable importance, the most important variables were mainly made up of a mix of S1-amp and S1-coh. The top 10 most important variables included VH amplitude from May, June, and August; VV amplitude from June; and both VH and VV coherence from August and September (Figure 6). For rankings of the 10–20 most important variables, both VV and VH coherence dominated the list. Between rankings 20–30 of the most important variables, several RS2 variables are included, such as Freeman Durden power due to rough surface (October); HH; pedestal height (June); and the first, second, and third Eigenvalue. Figure 6 displays the top 30 ranked variables, their importance, and the type of variable (S1-coh, RS2-amp, and so on). Most of these RS2 variables were produced using FQ1 imagery, except pedestal height, which was produced using the FQ5 image. We ran three additional RF classifications with the top 10, 20, and 30 variables only, and found that using only the 10 most important variables resulted in a lower classification accuracy (74.7% overall, but unacceptably low user’s and producer’s accuracy (<65%) in the peatland classes). Including the top 20 and 30 variables resulted in overall accuracies of 78.6% and 79.2% respectively, and user’s and producer’s accuracies were between 68% and 70% for wetland classes. This indicates that, although the top 10 variables were made up of S1-coh and S1-amp, which, as a complete time series produced high results, classification accuracy was reduced when only a selection of the time series was used.
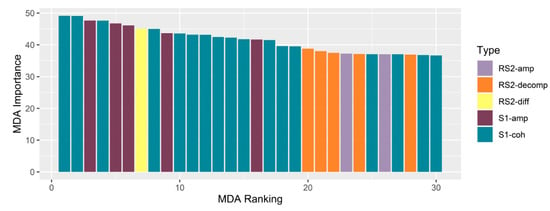
Figure 6.
Variable importance and type for top 30 variables, based on mean decrease in accuracy (MDA) ranking using all RS2 and S1 channels.
When RS2 and S1 were used in classification together, S1 always resulted in a higher Shapley value, with one exception, indicating that it was generally contributing more to overall classification accuracy than RS2. The only exception to this was when quad-pol RS2 amplitude and S1 dual-pol amplitude were used in combination; however, this classification resulted in poor UA and PA in the treed bog class, and poor UA in forests. S1 produced the greatest difference in contribution when coherence was used, indicating that of all the variables types tested, short-baseline dual-pol coherence contributed the most to the classification. As noted earlier, this set of variables alone produced high accuracy, and accuracy was only increased slightly when RS2 variables and other S1 variables were included; therefore, we do not note any interactions between coherence and other variables that lead to an increase in classification accuracy. Conversely, there were no scenarios where RS2-coh (long-baseline) group of variables provided the highest overall accuracy. When S1-coh is not included in classifications, RS2 quad-pol amp values are usually more important than S1-amp or S1-diff. One exception occurred in comparing the contributions of RS2-decomp and RS2-amp against S1-amp and S1-diff.
In assessing different types of RS2 variables, RS2-amp always contributed more to the classification than coherence when both quad and dual-pol scenarios were considered. The opposite was found for S1, where coherence provided much more to classifications than amplitude or difference variables, even in single polarization scenarios (either VV or VH). This indicates that RS2 data were highly important to the above-mentioned scenarios when quad-pol amplitude was considered without coherence.
In assessing the contribution of variable seasonality, a fair comparison cannot be made between RS2 and S1 as the RS2 data did not include any spring images. However, when all RS2 variables were considered alone and when amplitude alone was considered, the summer images contributed marginally more to the classification than fall images. When considering decompositions and difference variables, fall images contributed considerably more than summer images. In assessing S1 variable seasonality, in all cases, spring contributed somewhat less to the classification than fall and summer, which resulted in very similar contributions for both amp and diff scenarios. When all S1 variables were considered together, however, summer images contributed slightly more than fall images (Shapley value of 0.28 vs. 0.25).
Several scenarios assessing the contribution of polarization were made. In comparing polarizations within a single RS2 data type, there was no consensus among the scenarios indicating any single polarization that consistently contributed more. For coherence, HH and VV resulted in the same Shapley value (0.21), where HV contributed less (0.18). HH resulted in a considerably higher Shapley value when only assessing the difference variables (0.31 vs. 0.21 and 0.18), but when comparing intensity, HV contributed more. However, all RS2 scenarios where polarizations were compared were completed using a single RS2 data type, and the classification results were poor in all cases. For S1, VV produced somewhat higher contributions than VH. VH produced higher contributions than VV for both S1 diff and amp, but similar to RS2, S1 scenarios where a single variable type was used, the classification results were poor, with the exception of when coherence was used alone.
Overall, the results indicate that growing season short-baseline time-series coherence can produce high accuracy classifications, including using coherence data alone for classification, and contributes the most to all classifications where these variables were included.
5. Discussion
5.1. Issues with Collecting Time Series Data
In this study, short-baseline dual-pol (S1, 12-day) coherence collected over one growing season (15 pairs) produced highly accurate classification results and accuracy only increased slightly when time-series amplitude images were added. The resulting classifications were able to differentiate important wetland classes with higher accuracy than has been achieved using single-image, fully polarimetric decomposition parameters, and at similar levels of accuracy as those obtained in the past using LiDAR or Landsat imagery. In the past, a combination of Landsat and RS2 had been the preferred sensor for mapping peatland classes at this site. However, although Landsat is freely available, the spatial resolution is somewhat coarse and, therefore, Sentinel-2 and Sentinel-1 coherence fusion should be explored. In the past, SAR amplitude and polarimetric decomposition parameters have not been widely successful for differentiating peatland classes and multi-source imagery was required. When this is the case, decisions often need to be made to up-scale or down-scale image parameters so all can be stacked into one raster file for classification. For example, when working with S1 and Landsat data, scaling S1 up to 30 m spatial resolution will result in generalization of spatial detail, whereas oversampling Landsat imagery to match 15 m S1 would result in resampled pixels (providing no additional information), more data storage requirements, and longer processing times.
Seventeen longer-baseline quad-pol (Radarsat-2, 24 day) coherence time series datasets were also collected over one growing season, but these data were collected using three different beam modes and two different incident angles. The results did not indicate that RS2 coherence could be used for mapping peatland classes as low accuracy was achieved (<60%). As amplitude, polarimetric decompositions alone produced significantly higher accuracy than coherence alone and RS2 coherence always resulted in a lower contribution than these other variables, the effort to include coherence pairs from RS2 imagery does not seem necessary in this classification scenario. This is likely owing to the configuration of the coherence pairs in this specific time series. Long baselines result in degraded coherence over time, and, because peatlands are somewhat vegetated, small changes in vegetation between acquisitions, or changes in wetness or wind during the acquisition [24], will result in decorrelation and, therefore, less meaningful information provided to the classifier. Moreover, because we were unable to capture an entire growing season with a single beam-mode/incident angle, it is possible that some of the important temporal changes in the different peatland classes are not captured in the time series (i.e., missing April–June images). This may also be compounded by the fact that we have acquired FQ1DESC and FQ5ASC images on the same dates (morning and evening), so although we have the same total number of images as we have in the S1 time series, the RS2 data time series captures much less temporal variability than S1. The dense time series that S1 standard coverage provides has been proven to be more valuable for monitoring peatland ecosystems than collecting fully-polarimetric data with a less-dense time series.
Algorithms in ESA’s Geohazard Thematic Exploitation Platform enabled quick and easy processing of S1 coherence and amplitude images. As the GEP is a cloud-based processing service, only the results are downloaded and can be visually assessed online for errors before downloading. This resulted in significantly less data than if it had been locally processed using SNAP or other InSAR processing software. However, options for processing via the exposed on-demand processing services are somewhat limited in comparison with using a full InSAR processing software. For example, only two DEMs are available for terrain correction (GETASSE30 and SRTM 3 arc-second). However, a variety of different processor options are available including COIN (used here) and the SNAP interferometric processor, which can produce displacement measurements as well. Moreover, additional capabilities would be available leveraging the GEP development and integration environment (based on Jupyter Notebooks), which allows accessing full functionality of InSAR and optical processing software (such as SNAP and the Orfeo toolboxes).
5.2. Comparison of Variable Importance (MDA) and Contribution (Shapley)
While MDA simply provides an estimate of how much a single variable is important to the classification (based on the averaged decrease in accuracy when that variable is removed from a classification), the Shapley value provides a measure of percentage-wise contribution made by a group of variables (or a variable, though computationally expensive) for classification in a specific scenario.
In this study, ranking variables solely using MDA did not provide a robust method of variable selection, as variable importance rankings not only do not allow an assessment of the interaction between variables to be assessed, but also are biased in the presence of correlated predictor variables [39,42]. When the temporal signatures of different classes vary, the interaction between different variables will provide more meaningful information than a single variable alone, noting that multi-temporal predictor variables over an area of interest could be inevitably correlated. As RF is based on classification and regression trees, variable interaction is modeled within the tree [44], but MDA does not necessarily reflect the power of these interactions when correlated variables are included. The Shapley value enables the exploration of additional information about interactions between groups of variables by showing what each contributes individually, although it is up to the user to define the groups. While estimating a Shapley value for each variable is technically possible, in practice, the number of groups is limited by the fact that the number of unique combinations of “groups” scales exponentially, requiring a large number of classifications to be run [30]. For example, if we wanted to test which S1 coherence interferometric pair contributed most to the classification, as we have 15 unique S1 coherence pairs, this would result in 15 “groups” for comparison by the Shapley value algorithm. Therefore, there would be 32,767 unique combinations of “groups” (215-1), thus RF classification would need to be run 32,767 times to produce the Shapley value. Depending on the dataset being used and RF parameters, this could take a considerable amount of time and computing power (Figure 7). It is notable that this is one of the reasons only 1000 trees are grown in the RF models in this study; however, the stability of the accuracy values is controlled as described in [39]. On the other hand, for five groups, there are only 31 unique combinations, which is significantly more feasible. Figure 7 indicates the runtime and output file size in MiB using the cooptrees package [45] in R to compute the Shapley value based on 1–11 players.
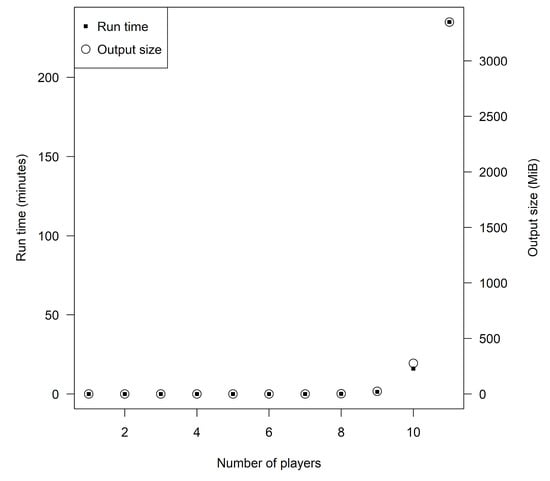
Figure 7.
Indicating run-time and output file size for 1–11 player scenarios for computing the Shapley value using the cooptrees package in R using dual-28 core Intel Xeon Gold processors. Note: the time and memory allocation listed above does not include the allotments for running the random forest (RF) classification models, only for calculating the Shapley value.
The Shapley value is, therefore, useful when deciding between different sensors, or different data types, or in cases where the variables are already reduced to a small number and the user is interested in assessing the contribution of each individual variable. In this study, the Shapley value indicated that S1 coherence contributed most to almost all of the classifications in which it was included. Thus, in an operational context, we would prioritize processing S1 coherence data, rather than processing RS2 polarimetric decomposition parameters. Importantly, this guidance was not easily interpretable from the accuracy assessments, confusion matrix, or MDA variable importance values.
6. Conclusions
In this study, we determined that growing season time series Sentinel-1 short-baseline (12-day) coherence data could produce classifications of acceptable overall accuracy, as well as acceptable user’s and producer’s accuracy in peatland classes. The results of the S1 coherence classifications were significantly better than using RS2 coherence, likely owing to the difference in baseline and specific acquisition dates of the data in this study. However, when amplitude or polarimetric decomposition parameters were also included, RS2 produced acceptable levels of accuracy as well. Despite being dual-pol, the use of S1 led to higher accuracies than both quad-pol Radarsat-2 data. This is attributed to the shorter temporal baseline (12 days vs. 24 days) and, although both sensors collected a similar number of images over the growing season, a full growing season time-series was able to be collected with S1, but the RS2 dataset excluded spring images, and duplicate dates were acquired at different incident angles, resulting in a coarser time-series. With repeatable coverage available in Sentinel, it was possible to obtain images in the same geometry throughout the growing season without issues of conflict, thereby providing an estimate of change every 12 days. S1 coherence (12-day repeat) contributed most to almost all of the classifications in which it was included, where RS2 coherence (24-day repeat) was not found to contribute highly in the classification of peatland ecosystems. Therefore, in an operational peatland mapping situation, it is recommended to prioritize processing S1 coherence data, rather than processing RS2 polarimetric decomposition parameters.
This study also demonstrated the use of Shapley values in comparing different sensors, types of variables, or seasonal data. Mean decrease in accuracy, as calculated through the random forest classifier, is biased when correlated variables are included, making it difficult to determine the true and proportional importance of a single variable with respect to other variables. Importantly, MDA does not consider interactions between variables. In using time-series data in classification, the variability between and within different ecosystems throughout the time-series has been shown to produce higher accuracy results than using a few dates over a growing season, thus using MDA to rank and reduce low ranking variables can result in a weaker classification than if the entire time series is used. Importantly, the use of the Shapley value enables the identification of the importance of using the entire time series, whereas this benefit was not easily interpretable from the accuracy assessments, confusion matrix, or MDA variable importance values.
The use of short-baseline time-series coherence in classification will be extended to mapping other peatlands and wetland ecosystems. Future work will also assess the temporal patterns in coherence in relation to temporal patterns in vegetation and hydrologic change across a single growing season, and between growing seasons at several temperate and subarctic peatland sites.
Author Contributions
Conceptualization, K.M.; methodology, K.M.; software, P.K. and F.P.; validation, K.M., A.B., S.B. and S.N.; formal analysis K.M. and P.K.; writing—original draft preparation, K.M. and F.P; writing—review and editing, K.M., P.K., S.N., S.B., A.B. and F.P.; visualization K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Murray Richardson and Marisa Ramey for assisting with original training data collection; Gabriel Gosselin (PCI Geomatics) is thanked for his expertise with PCI Geomatica’s InSAR tools; Karim Mattar (DRDC) is thanked for providing InSAR support and knowledge.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Warner, B.; Asada, T. Biological diversity of peatlands in Canada. Aquat. Sci. 2006, 68, 240–253. [Google Scholar] [CrossRef]
- Bullock, A.; Acreman, M. The role of wetlands in the hydrological cycle. Hydrol. Earth Syst. Sci. 2003, 7, 358–389. [Google Scholar] [CrossRef]
- Gorham, E. Northern Peatlands: Role in the Carbon Cycle and Probably Responses to Climatic Warming. Ecol. Appl. 1991, 1, 182–185. [Google Scholar] [CrossRef] [PubMed]
- Poulin, M.; Rochefort, L.; Pellerin, S.; Thibault, J. Threats and protection for peatlands in Eastern Canada. La Conserv. Des Tourbières 2004, 79, 331–344. [Google Scholar] [CrossRef]
- Wieder, R.; Vitt, D. (Eds.) Boreal Peatland Ecosystems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rebelo, L.; Finlayson, C.; Nagabhatla, N. Remote sensing and GIS for wetland inventory, mapping and change analysis. J. Environ. Manag. 2009, 90, 2144–2153. [Google Scholar] [CrossRef] [PubMed]
- Chasmer, L.; Mahoney, C.; Millard, K.; Nelson, K.; Peters, D.; Merchant, M.; Hopkinson, C.; Brisco, B.; Niemann, O.; Montgomery, J.; et al. Remote Sensing of Boreal Wetlands 2: Methods for Evaluating Boreal Wetland Ecosystem State and Drivers of Change. Remote Sens. 2020, 12, 1321. [Google Scholar] [CrossRef]
- Brown, E.; Aitkenhead, M.; Wright, R.; Aalders, I. Mapping and classification of peatland on the Isle of Lewis using Landsat ETM+. Scott. Geogr. J. 2007, 123, 173–192. [Google Scholar] [CrossRef]
- Krankina, O.; Pflugmacher, D.; Friedl, M.; Cohen, W.; Nelson, P.; Baccini, A. Meeting the challenge of mapping peatlands with remotely sensed data. Biogesciences 2008, 5, 1809–1820. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. Fusion of LiDAR elevation and canopy derivatives with polarimetric SAR decomposition for wetland classification using Random Forest. Can. J. Remote Sens. 2013, 39, 290–307. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. On the importance of training data sample selection in Random Forest classification: A case study in peatland mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef]
- White, L.; Millard, K.; Banks, S.; Richardson, M.; Pasher, J.; Duffe, J. Moving to the RADARSAT Constellation Mission: Comparing synthesized Compact polarimetry and dual polarimetry data with fully polarimetric RADARSAT-2 data for image classification of wetlands. Remote Sens. 2017, 9, 573. [Google Scholar] [CrossRef]
- Touzi, R.; Deschamps, A.; Rother, G. Wetland characterization using polarimetric RADARSAT-2 capability. Can. J. Remote Sens. 2007, 33 (Suppl. 1), S56–S67. [Google Scholar] [CrossRef]
- Touzi, R.; Deschamps, A.; Rother, G. Phase of Target Scattering for Wetland Characterization Using Polarimetric C-Band SAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3241–3261. [Google Scholar] [CrossRef]
- Touzi, R.; Gosselin, G. Polarimetric Radarsat-2 wetland classification using Touzi Decomposition: Case of the Lac Saint-Pierre Ramsar wetland. Can. J. Remote Sens. 2014, 39, 491–506. [Google Scholar] [CrossRef]
- Merchant, M.; Adams, J.; Berg, A.; Baltzer, J.; Quinton, W.; Chasmer, L. Contributions of C-band SAR data and polarimetric decompositions to subartcic boreal peatland mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 1467–1482. [Google Scholar] [CrossRef]
- Li, Z.; Chen, H.; White, J.; Wulder, M.; Hermosilla, T. Discriminating treed and non-treed wetlands in boreal ecosystems using time series Sentinel-1 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 102007. [Google Scholar] [CrossRef]
- Karlson, M.; Galfalk, M.; Crill, P.; Cousquet, P.; Saunois, M.; Bastviken, D. Delineating northern peatlands using Sentinel-1 time series and terrain indices from local and regional digital elevation models. Remote Sens. Environ. 2019, 231, 111252. [Google Scholar] [CrossRef]
- Henderson, F.; Lewis, A. Radar Fundamentals: Technical Perspective. In Principals and Applications of Imaging Radar—Manual of Remote Sensing, 2nd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Corbane, C.; Pesaresi, M.; Kemper, T.; Sabo, F.; Ferri, S.; Syrris, V. Enhanced automatic detection of human settlements using Sentinel-1 interferometric coherence. Int. J. Remote Sens. 2017, 39, 842–853. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M.; Schlaffer, S.; Natsuaki, R. Urban Flood Mapping Using SAR Intensity and Interferometric Coherence via Bayesian Network Fusion. Remote Sens. 2019, 11, 2231. [Google Scholar] [CrossRef]
- Jin, H.; Mountrakis, G.; Stehman, S. Assessing integration of intensity, polarimetric scattering, interferometric coherence and spatial texture metrics in PALSAR derived landcover classification. ISPRS J. Photogramm. Remote Sens. 2014, 98, 70–84. [Google Scholar] [CrossRef]
- Sica, F.; Pulella, A.; Nannini, M.; Pinheiro, M.; Rizzioli, P. Repeat-pass SAR interferometry for land cover classification: A methodology using Sentinel-1 Short-Time-Series. Remote Sens. Environ. 2019, 232, 111277. [Google Scholar] [CrossRef]
- Hong, S.; Wdowinski, S.; Kim, S.; Won, J.-S. Multi-temporal monitoring of wetland water levels in the Florida Everglades using interferometric Synthetic Aperture Radar (InSAR). Remote Sens. Environ. 2010, 114, 2436–2447. [Google Scholar] [CrossRef]
- Wdowinski, S.; Kim, S.; Amelung, F.; Dixon, T.; Miralles-Wilhelm, F.; Sonenshein, R. Space-based detection of wetlands’ surface water level changes from L-band SAR interferometry. Remote Sens. Environ. 2008, 112, 681–696. [Google Scholar] [CrossRef]
- Brisco, B.; Ahern, F.; Murnaghan, K.; White, L.; Canisus, F.; Lancaster, P. Seasonal Change in Wetland Coherence as an Aid to Wetland Monitoring. Remote Sens. 2019, 9, 158. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Z.; Waldron, S.; Tanaka, A. InSAR Time Series Analysis of L-band data for understanding tropical peatland degradation and restoration. Remote Sens. 2019, 11, 2592. [Google Scholar] [CrossRef]
- Duro, D.; Franklin, S.; Dube, M. Multi-scale object based image analysis and feature selection of multi-sensor earth observation imagery using random forests. Int. J. Remote Sens. 2012, 33, 4502–4526. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance in random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Shapley, L. A value for n-person Games. Ann. Math. Stud. 1953, 28, 307–317. [Google Scholar]
- Roth, A. The Shapley Value: Essays in Honor of Lloyd S. Shapley; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nandlall, S.; Millard, K. Quantifying the Relative Importance of Groups of Variables in Remote Sensing Classifiers using Shapley Value and Game Theory. IEEE Geosci. Remote Sens. Lett. 2020, 17, 42–46. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. Quantifying the Relative Contributions of Vegetation and Soil Moisture Conditions to Polarimetric C-Band SAR Response in a Temperate Peatland. Remote Sens. Environ. 2018, 206, 123–138. [Google Scholar] [CrossRef]
- Terradue Geohazards TEP Github Repository. Available online: https://github.com/geohazards-tep/dcs-rss-snap-s1-coin (accessed on 25 July 2020).
- Sentinel Application Platform (SNAP). Available online: https://step.esa.int/main/toolboxes/snap/ (accessed on 25 July 2020).
- Radarsat-2 Application Look-up Tables (LUTs). Available online: https://mdacorporation.com/docs/default-source/technical-documents/geospatial-services/radarsat-2-application-look-up-tables.pdf (accessed on 25 July 2020).
- Freeman, A.; Durden, S. A Three Component Scattering Model for Polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 6878. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org/ (accessed on 29 June 2020).
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Behnamian, A.; Millard, K.; Banks, S.; White, L.; Richardson, M.; Pasher, J. A Systematic Approach for Variable Selection with Random Forests: Achieving Stable Variable Importance Values. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1988–1992. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Fontenla, M. Cooptrees: Cooperative Aspects of Optimal Trees in Weighted Graphs, R Package version 1.0; 2014. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).