Advanced Control Strategies for Cleaner Energy Conversion in Biomass Gasification

Abstract

The escalating climate crisis necessitates urgent and decisive action to mitigate greenhouse gas emissions. Gasification stands out as a highly adaptable process for energy conversion, capable of handling a wide range of feedstocks, from coal to biomass. The process plays a significant role in improving sustainability by converting these feedstocks into synthesic gas (syngas), which can be used as a cleaner energy source or as a building block for producing various chemicals. The utilization of syngas obtained through gasification not only reduces the reliance on fossil fuels but also helps in reducing greenhouse gases (GHGs), thereby contributing to a more sustainable energy landscape. To maintain optimal operational conditions and ensure the quality and safety of the product, an effective control system is crucial in the gasification process. This paper presents a comparative analysis of three control strategies applied to a numerical model of rice husk gasification: classical control, fuzzy logic control, and dynamic matrix control. The analysis is based on a comprehensive model that includes the equations necessary to capture the dynamic behavior of the gasification process across its various stages. The goal is to identify the most effective control strategy, and the performance of each control strategy is evaluated based on the integral of the absolute value of the error (IAE). The results indicatethat fuzzy logic control consistently outperforms classical control techniques, demonstrating superior disturbance rejection, enhanced stability, and overall improved control accuracy. These findings highlight the importance of selecting an appropriate advanced control strategy to optimize sustainable gasification processes.

1. Introduction

The use of biomass in gasification processes significantly contributes to environmental sustainability by reducing carbon emissions compared to conventional fuels [1,2,3]. Lowering carbon emissions in the industrial sector is a critical step toward achieving a successful energy transition [4]. A primary goal in gasifier reactors is to optimize the concentrations of the various chemical species produced by fine-tuning the hydrodynamic behavior of the particles involved [5].Achieving this requires a robust control strategy capable of managing potential disturbances in input variables, as highlighted by Wu et al. [6] and Huang et al. [7]. These strategies enable the precise regulation of key operational parameters, such as temperature, ensuring stable and efficient reactor performance. In the context of resource efficiency and environmental impact, the use of gasification to produce synthesis gas (syngas) is particularly significant; by optimizing the gasification process, it is possible to maximize the yield of syngas while minimizing waste and emissions, making it a more sustainable option for energy production and chemical manufacturing [8,9]. The efficient control of this process is essential not only to improve performance but also to ensure that resources are utilized effectively, reducing the overall environmental footprint [10]. Various studies have explored advanced control methods, each offering distinct advantages and challenges [11]. These methods include the following. (i) Adaptive Control (AC): AC enhances system performance by adjusting parameters in real time to account for changes or disturbances. It is particularly effective for systems with highly nonlinear and dynamic behaviors, potentially improving energy efficiency. However, AC can be complex to tune and optimize compared to non-adaptive methods [12]. (ii) Model-Free Extremum Seeking Control: This method offers reduced computational requirements and design efforts, making it simpler to implement. However, it may suffer from lower accuracy and tuning difficulties and may not be suitable for systems with complex and nonlinear dynamics. (iii) Model Predictive Control (MPC): MPC is adept at handling varying operating conditions by predicting future behavior and optimizing control inputs accordingly. Despite its flexibility, MPC involves solving an optimization problem at each time step, which can be computationally intensive. It also requires the careful tuning of parameters such as the prediction horizon, control horizon, and weighting factors [13]. (iv) Sliding Mode Control (SMC): SMC is known for its robustness, fast response time, high accuracy, and low sensitivity. It is relatively simple to implement and can lead to energy savings. However, SMC can require high control effort, which might result in increased energy consumption and wear on system components [14]. Proportional Integral Derivative (PID) controllers are a prominent choice for process control and are widely utilized in production systems [15]. Despite their prevalence, recent studies on the modeling of the gasification thermochemical process have opened up new avenues for exploring alternative control strategies [16,17,18,19,20]. Moreover, research efforts have increasingly focused on addressing the complex and highly nonlinear nature of gasification processes [21,22,23,24,25], leading to the development of dynamic models that more accurately represent gasification behavior in fluidized bed reactors. While traditional PID control and its variants have been widely applied to gasification systems [26,27,28,29,30], advanced control strategies have emerged to better manage the nonlinearities inherent in these processes [31,32,33,34,35,36,37]. These advanced techniques are designed to enhance both the precision and stability of control systems in such complex environments. Given the pervasive use of PID controllers across various applications, it becomes essential to evaluate their performance in comparison to newer control strategies.

This study evaluates the performance of three control strategies—classical control (PID), fuzzy logic control (FLC), and dynamic matrix control (DMC)—in the rice husk gasification process, using the integral of absolute error (IAE) as the main performance metric. The paper is structured as follows: Section 2.1 discusses the selection of biomass feedstock, Section 2.2 develops the dynamic model of the gasification process, and Section 2.3 outlines the configuration of the three control strategies—PID, FLC, and DMC. Section 3 presents a comparison of the control strategies, assessing their performance against disturbances in the process using the IAE metric, and Section 4 summarizes the key conclusions.

2. Materials and Methods

2.1. Biomass Feedstock

The biomass selected for the numerical modeling of the gasification process is rice husk, due to its high volatile matter content. As a byproduct of the rice milling industry, rice husk is abundantly available in various regions worldwide, making its utilization a valuable contribution to sustainable energy practices [38].

2.1.1. Ultimate Analysis

Ultimate analysis is a technique that provides information on the content of each of the chemical elements that constitute biomass fuel. Thus, Table 1 presents the elemental composition of rice husk sourced from Colombia [39], which was utilized in the numerical model developed in this study.

Table 1. Ultimate analysis of rice husk (dry basis) [39].

Parameter	Value (% wt)
Carbon	39.1
Hydrogen	5.2
Nitrogen	0.25
Oxygen	37.2
Sulphur	0.43
Moisture	8.9

2.1.2. Proximate Analysis of Rice Husk

Proximate analysis provides the mass content of fixed carbon, ash, and volatile matter in a solid fuel after thermal decomposition. For the rice husk used in this study [39], the composition is detailed in Table 2.

Table 2. Proximate analysis of rice husk [39].

Parameter	Value (% wt)
Fixed carbon	16.67
Ash	17.89
Volatile matter	65.47

2.2. Dynamic Model of the Gasification Process

The dynamic modeling of the fluidized bed gasification process follows a two-stage approach, encompassing the combustion and subsequent reduction of biomass, as detailed in Section 2.2.2 and Section 2.2.6, respectively. This model enables the determination of species composition within various reactor zones and the temperature distribution within the bed. Additionally, hydrodynamic parameters are incorporated into the energy and molar balances performed.

2.2.1. Process Description

In a fluidized bed gasifier, biomass undergoes thermochemical transformations facilitated by a structured setup. The gasifier includes a distributor plate for air injection and a biomass distribution system featuring an endless screw with a cooling jacket. The screw, which is supplied by a feedstock tank, moves the biomass into the reactor. Air, compressed and preheated to 1023 K, is introduced through the reactor’s bottom. Sand, chosen for its effective heat transfer properties, forms the bed material, ensuring uniform fluidization between the sand particles and biomass. This fluidization creates bubbles due to pressure differences within the emulsion. During the gasification process, the circulating air interacts with the biomass, initiating convection that removes moisture from the material in the drying stage. The biomass, with its high calorific value, undergoes thermal decomposition at temperatures above 600 K.

This study does not focus on the initial stages of drying and pyrolysis due to their complexity and the intricate transfer phenomena occurring in the dense bed phase. Instead, it centers on the subsequent stages of the gasification process. In the subsequent gasification stages, the char produced from pyrolysis and other volatile components undergo partial oxidation in the presence of oxygen. This partial oxidation generates the energy required for the endothermic reactions within the gasifier. During this stage, turbulence in the bed is intensified by rising bubbles, reaching the highest temperatures of the process. Some biomass char does not react and is instead reduced through multiple heterogeneous reactions. By the end of the process, synthesis gas is produced—a mixture of chemical species at approximately 1100 K. This gas includes unreacted carbon and rises with the air due to density differences. One of the crucial components of the synthesis gas is hydrogen, which serves as a fundamental fuel base in the gasification process.

2.2.2. Combustion Stage

During the combustion stage, thermal oxidation occurs as the gasifying agent diffuses into the porous carbonaceous matrix. Temperatures approaching 1100 K are achieved, allowing chemical reactions to take place across the entire surface of the char particle. This process begins following the release of volatiles from the fuel and is influenced by factors such as heating rate and particle size. The char combustion mechanism is inherently complex, involving both mass and heat transfer phenomena. Consequently, the governing equations for this stage are developed, incorporating molar balances for the components entering and leaving the control volume, along with a comprehensive energy balance.

2.2.3. Energy Balance in Combustion

Exothermic combustion reactions constitute the primary energy source driving the reduction and pyrolysis processes within the dense zone of the fluidized bed reactor. Consequently, an energy balance of the combustion stage is essential for quantifying the net change in total energy within the control volume, resulting from the interaction of air and pyrolysis gas flows. Additionally, the heat released during the oxidation reactions, representing the chemical energy of the process, must be accounted for in the energy balance presented in Equation (1).

$$\begin{array}{cc}\hfill C_p\left(t\right)f_p\left(t\right)c_{pp}{T}_p\left(t\right)& + C_A{f}_A\left(t\right)c_{pA}{T}_A\left(t\right)-{\left[q_R\left(t\right)\right]}_c-C_c\left(t\right)f_b\left(t\right)c_{pc}{T}_c\left(t\right)\hfill \\ \hfill & =c_{\nu c}{H}_r{A}_t{\displaystyle \frac{d}{dt}}\left[C_c\left(t\right)T_c\left(t\right)\right]\hfill \end{array}$$

(1)

Here, ${\left[q_R\left(t\right)\right]}_c$ is derived from the energy associated with chemical reactions, as expressed in Equation (2).

$$\begin{array}{cc}\hfill {\left[q_R\left(t\right)\right]}_c& =A_s{[\Delta H_r]}_{cp-C}{\left[r_C\left(t\right)\right]}_{cp-C}+A_R{H}_{fb}{[\Delta H_r]}_{O-MC}{\left[r_{CO}\left(t\right)\right]}_{O-MC}\hfill \\ \hfill & + A_R{H}_{fb}\left(t\right){[\Delta H_r]}_{O-H}{\left[r_{O_2}\left(t\right)\right]}_{O-H}\hfill \end{array}$$

(2)

2.2.4. Reaction Rates in Combustion

Rate expressions, as outlined in [17], describe the changes in concentration of reactants and products during combustion reactions. These kinetic models facilitate the quantification of formation and depletion rates of components involved in exothermic reactions with oxygen. Equation (3) presents the reaction rate of carbon (partial combustion of char), Equation (4) details the reaction rate of carbon monoxide (partial oxidation of carbon monoxide), Equation (5) illustrates the reaction rate of hydrogen (partial oxidation of hydrogen), and Equation (6) specifies the total concentration of combustion product species.

$${\left[r_C\left(t\right)\right]}_{cp-C}=A_1{T}_c\left(t\right)e^{-{\displaystyle \frac{E_{a1}}{R{T}_c\left(t\right)}}}{\left[C_{O_2}\left(t\right)\right]}_c$$

(3)

$${\left[r_{CO}\left(t\right)\right]}_{O-MC}=A_2{e}^{-{\displaystyle \frac{E_{a2}}{R{T}_c\left(t\right)}}}{\left[C_{CO}\left(t\right)\right]}_c{\left[C_{O_2}^{0.25}\left(t\right)\right]}_c{\left[C_{H_{2}O}^{0.5}\left(t\right)\right]}_c$$

(4)

$${\left[R_{H_2}\left(t\right)\right]}_{O-H}=A_3{e}^{-{\displaystyle \frac{E_{a3}}{R{T}_c\left(t\right)}}}{\left[C_{H_2}\left(t\right)\right]}_c{\left[C_{O_2}\left(t\right)\right]}_c$$

(5)

$$\begin{array}{cc}\hfill C_c\left(t\right)& ={\left[C_{H_2}\left(t\right)\right]}_c+{\left[C_{O_2}\left(t\right)\right]}_c+{\left[C_{CO}\left(t\right)\right]}_c+{\left[C_{H_{2}O}\left(t\right)\right]}_c+{\left[C_C\left(t\right)\right]}_c+{\left[C_{C{H}_4}\right]}_c\hfill \\ \hfill & + {\left[C_{C{O}_2}\left(t\right)\right]}_c+C_{N_2}\hfill \end{array}$$

(6)

2.2.5. Molar Balances in Combustion

Molar balances describe the changes in the concentration of each species involved in combustion chemical reactions. Equation (7) illustrates the case for C, Equation (8) for $H_2$, Equation (9) for $CO$, Equation (10) for $C{O}_2$, Equation (11) for $O_2$, and Equation (12) for $H_{2}O$.

$$\begin{array}{cc}\hfill {\left[C_C\left(t\right)\right]}_{pir}{f}_{pir}\left(t\right)-{\left[C_C\left(t\right)\right]}_c{f}_b\left(t\right)-A_s{\left[r_C\left(t\right)\right]}_{cp-C}& =H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_C\left(t\right)\right]}_c\right]\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\left[C_{H_2}\left(t\right)\right]}_{pir}{f}_{pir}\left(t\right)-{\left[C_{H_2}\left(t\right)\right]}_c{f}_b\left(t\right)-A_t{H}_{fb}{\left[r_{H_2}\left(t\right)\right]}_{O-H}& =H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{H_2}\left(t\right)\right]}_c\right]\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\left[C_{CO}\left(t\right)\right]}_{pir}{f}_{pir}\left(t\right)& +\left[A_s{\left[r_C\left(t\right)\right]}_{cp-C}-A_t{H}_{fb}{\left[r_{CO}\left(t\right)\right]}_{O-MC}\right]-{\left[C_{CO}\left(t\right)\right]}_c{f}_b\left(t\right)\hfill \\ \hfill & =H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{CO}\left(t\right)\right]}_c\right]\hfill \end{array}$$

(9)

$${\left[C_{C{O}_2}\left(t\right)\right]}_{pir}{f}_{pir}\left(t\right)+\left[A_t{H}_{fb}{\left[r_{CO}\left(t\right)\right]}_{O-MC}\right]-{\left[C_{C{O}_2}\left(t\right)\right]}_c{f}_b\left(t\right)=H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{C{O}_2}\left(t\right)\right]}_c\right]$$

(10)

$$\begin{array}{cc}\hfill {\left[C_{O_2}\right]}_A{f}_A\left(t\right)& - {\displaystyle \frac{1}{2}}\times \left[A_s{\left[r_C\left(t\right)\right]}_{cp-C}+A_t{H}_{fb}{\left[r_{CO}\left(t\right)\right]}_{O-MC}+A_t{H}_{fb}{\left[r_{H_2}\left(t\right)\right]}_{O-H}\right]\hfill \\ \hfill & - {\left[C_{O_2}\left(t\right)\right]}_c{f}_b\left(t\right)=H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{O_2}\left(t\right)\right]}_c\right]\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill A_t{H}_{fb}{\left[r_{H_2}\left(t\right)\right]}_{O-H}-{\left[C_{H_{2}O}\left(t\right)\right]}_c{f}_b\left(t\right)& =H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{H_{2}O}\left(t\right)\right]}_c\right]\hfill \end{array}$$

(12)

2.2.6. Reduction Stage

During this stage, a series of endothermic reactions take place and consume a large part of the heat generated during the process. In the reduction, the carbonaceous residue of the biomass is transformed into a gaseous mixture known as syngas. However, some of these reactions are heterogeneous, since they take place uniformly over the entire surface of the solid, and at the same speed. In fact, there is a diffusion of the gaseous molecules over the pores of the particle until they reach its active center.

2.2.7. Energy Balance in Reduction

The heat generated during combustion reactions is transferred through mass flow to the reduction stage, where chemical species interact, resulting in the formation of gasification products, as shown in Equation (13). The energy associated with the reduction reactions is described in Equation (14).

$$\begin{array}{cc}\hfill C_c\left(t\right)f_b\left(t\right)c_{pc}{T}_c\left(t\right)& - {\left[q_R\left(t\right)\right]}_{red}-C_{red}\left(t\right)f_b\left(t\right)c_{pred}{T}_{red}\left(t\right)\hfill \\ \hfill & =c_{\nu red}{H}_r{A}_t{\displaystyle \frac{d}{dt}}\left[C_{red}\left(t\right)T_{red}\left(t\right)\right]\hfill \end{array}$$

(13)

$${\left[q_R\left(t\right)\right]}_{red}=A_s{[\Delta H_r]}_B{\left[r_C\left(t\right)\right]}_B+A_s{[\Delta H_r]}_{sg}{\left[r_C\left(t\right)\right]}_{sg}+A_s{[\Delta H_r]}_M{\left[r_C\left(t\right)\right]}_M$$

(14)

2.2.8. Reaction Rates in Reduction

During this stage, the primary chemical reactions of the process occur, converting the solid residue from pyrolysis into gas. Below are the expressions that describe the kinetic behavior of the heterogeneous reactions taking place in the dense zone of the reactor [40]. Equation (15) presents the reaction rate of carbon (Boudouard reaction), Equation (16) details the reaction rate of carbon (steam gasification), Equation (17) describes the reaction rate of carbon (methanation reaction), and Equation (18) specifies the total concentration of reduction products.

$${\left[r_C\left(t\right)\right]}_B=A_4{T}_{red}\left(t\right)e^{-{\displaystyle \frac{E_{a4}}{R{T}_{red}\left(t\right)}}}{\left[C_{C{O}_2}\left(t\right)\right]}_{red}$$

(15)

$${\left[r_C\left(t\right)\right]}_{sg}=A_5{T}_{red}\left(t\right)e^{-{\displaystyle \frac{E_{a5}}{R{T}_{red}\left(t\right)}}}{\left[C_{H_{2}O}\left(t\right)\right]}_{red}$$

(16)

$${\left[r_C\left(t\right)\right]}_M=A_6{T}_{red}\left(t\right)e^{-{\displaystyle \frac{E_{a6}}{R{T}_{red}\left(t\right)}}}{\left[C_{H_2}\left(t\right)\right]}_{red}$$

(17)

$$\begin{array}{cc}\hfill C_{red}\left(t\right)& ={\left[C_{C{H}_4}\left(t\right)\right]}_{red}+{\left[C_{H_{2}O}\left(t\right)\right]}_{red}+{\left[C_{CO}\left(t\right)\right]}_{red}+{\left[C_{C{O}_2}\left(t\right)\right]}_{red}\hfill \\ \hfill & + {\left[C_C\left(t\right)\right]}_{red}+{\left[C_{O_2}\left(t\right)\right]}_{red}+C_{N_2}+ {\left[C_{H_2}\left(t\right)\right]}_{red}\hfill \end{array}$$

(18)

2.2.9. Molar Balances in Reduction

The molar balances of the chemical species interacting in the reduction stage are presented as follows: Equation (19) illustrates the case for C, Equation (20) for $H_2$, Equation (21) for $CO$, Equation (22) for $C{O}_2$, Equation (23) for $C{H}_4$, and Equation (24) for $H_{2}O$.

$$\begin{array}{cc}\hfill {\left[C_C\left(t\right)\right]}_c{f}_b\left(t\right)& - {\left[C_C\left(t\right)\right]}_{red}{f}_b\left(t\right)-A_s\left[{\left[r_C\left(t\right)\right]}_B+{\left[r_C\left(t\right)\right]}_{sg}+{\left[r_C\left(t\right)\right]}_M\right]\hfill \\ \hfill & =H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_C\left(t\right)\right]}_{red}\right]\hfill \end{array}$$

(19)

$${\left[C_{H_2}\left(t\right)\right]}_c{f}_b\left(t\right)-{\left[C_{H_2}\left(t\right)\right]}_{red}{f}_b\left(t\right)+2A_s{\left[r_C\left(t\right)\right]}_M=H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{H_2}\left(t\right)\right]}_{red}\right]$$

(20)

$$\begin{array}{cc}\hfill {\left[C_{CO}\left(t\right)\right]}_c{f}_b\left(t\right)& - {\left[C_{CO}\left(t\right)\right]}_{red}{f}_b\left(t\right)+\left[2A_s{\left[r_C\left(t\right)\right]}_B+A_s{\left[r_C\left(t\right)\right]}_{sg}\right]\hfill \\ \hfill & =H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{CO}\left(t\right)\right]}_{red}\right]\hfill \end{array}$$

(21)

$${\left[C_{C{O}_2}\left(t\right)\right]}_c{f}_b\left(t\right)-{\left[C_{C{O}_2}\left(t\right)\right]}_{red}{f}_b\left(t\right)-A_s{\left[r_C\left(t\right)\right]}_B=H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{C{O}_2}\left(t\right)\right]}_{red}\right]$$

(22)

$${\left[C_{C{H}_4}\left(t\right)\right]}_c{f}_b\left(t\right)-{\left[C_{C{H}_4}\left(t\right)\right]}_{red}{f}_b\left(t\right)-A_s{\left[r_C\left(t\right)\right]}_M=H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{C{H}_4}\left(t\right)\right]}_{red}\right]$$

(23)

$${\left[C_{H_{2}O}\left(t\right)\right]}_c{f}_b\left(t\right)-{\left[C_{H_{2}O}\left(t\right)\right]}_{red}{f}_b\left(t\right)-A_s{\left[r_C\left(t\right)\right]}_{sg}=H_r{A}_t{\displaystyle \frac{d}{dt}}\left[{\left[C_{H_{2}O}\left(t\right)\right]}_{red}\right]$$

(24)

The system of Equations (1) to (24) is sufficient to describe the phenomenology associated with the analyzed process.

2.2.10. Process Steady State

In the sustainable gasification process of rice husk for the generation of syngas such as $H_2$, $C{O}_2$, and $C{H}_4$, hydrogen is identified as one of the primary metrics in this study due to its high energy content and increasing importance as a clean energy source. Monitoring the behavior of hydrogen as a control strategy allows for the evaluation of the gasification process’s efficiency, as it indicates how effectively carbon and hydrogen bonds in the rice husk are being broken during gasification to produce synthesic gases [41]. Related studies on the optimization of rice husk gasification have shown that increasing and optimizing the temperature can boost the hydrogen content in syngas from 1.18% to 57.73% [42]. These findings align with the results obtained from the numerical model in this study, which show a hydrogen content of ∼54%. Throughout the gasification process, various disturbances can impact the concentration of hydrogen in the output. To effectively manage these disturbances, it is crucial to understand how the system responds to irregularities in the input variables. Identifying the primary disturbances affecting the process allows for better control and adjustment. Figure 1 and Figure 2 illustrate the effects of a 10% variation in the gasification stage parameters on the controlled variable, specifically hydrogen concentration, as predicted by our numerical model. This behavior is conventionally termed open-loop behavior, indicating that there is no intervention from a control system. These illustrations provide insights into how such adjustments can significantly affect hydrogen levels, highlighting the sensitivity of our system to parameter changes. These figures provide insights into the system’s behavior in response to different disturbances, highlighting the need for robust control strategies to maintain optimal hydrogen production.

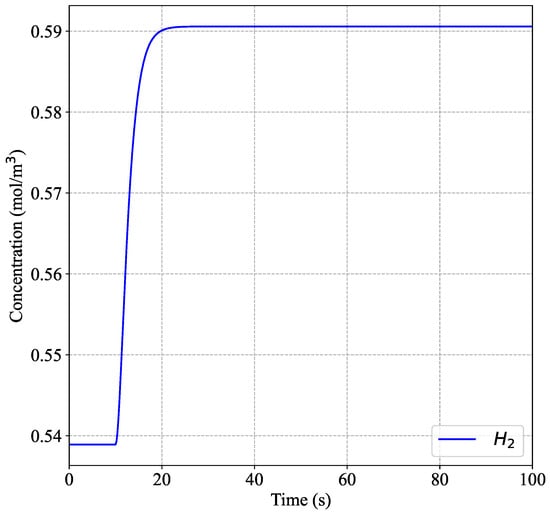
Figure 1. Predicted hydrogen concentration response to a 10% increase in inlet airflow from the numerical model.

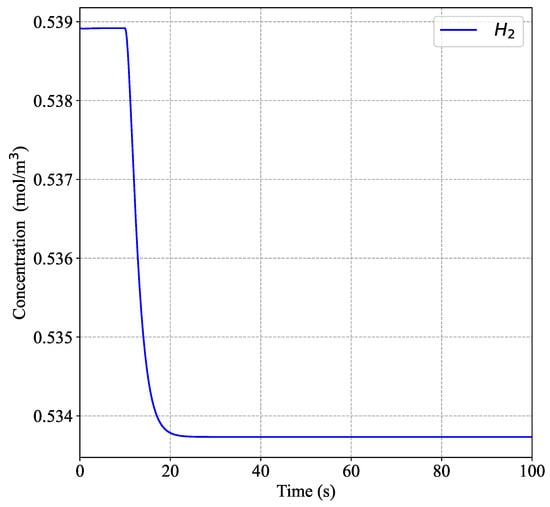
Figure 2. Predicted hydrogen concentration response to a -10% decrease in oxygen concentration from the numerical model.

Table 3 outlines the operating conditions necessary to achieve complete fluidization within the gasification process. These conditions represent the minimum requirements needed to ensure the effective development and operation of the entire process [43]. For modeling purposes, the Reynolds number represents the minimum fluid velocity at which particles begin to separate and remain suspended individually.

Table 3. Hydrodynamic parameters of the bed for the steady state.

Parameter	Value	Units
System pressure	103,666.65	Pa
Bed porosity at minimum fluidization rate	0.68
Pressure-drop in bed	2341.65	Pa
Minimum fluidization height	0.29	m
Final fluidization height	0.37	m
Reynolds number	0.27
Archimedes number	76.07
Dynamic viscosity	4.20 × 10−5	N s/m2
Fluidization Velocity	0.90	m/s

2.2.11. Process Identification

In this step, the process behavior is characterized by manually adjusting the controller signal in an open-loop configuration. The magnitude of this adjustment should be sufficient to induce a noticeable variation in the process output, but not so extreme as to cause instability in the system response.

This procedure involves varying the controller output signal by $\Delta m$ = 10% (equivalent to a 10% decrease in $CO$ concentration) and recording the resulting change in the controlled variable, which in this study is the hydrogen concentration. Figure 3 displays the process response curve, showing how the hydrogen concentration drops until it reaches stability according to the reduction in $CO$ concentration. The sensor data captures these changes, providing insight into the process’s dynamic behavior and response to the controller adjustment.

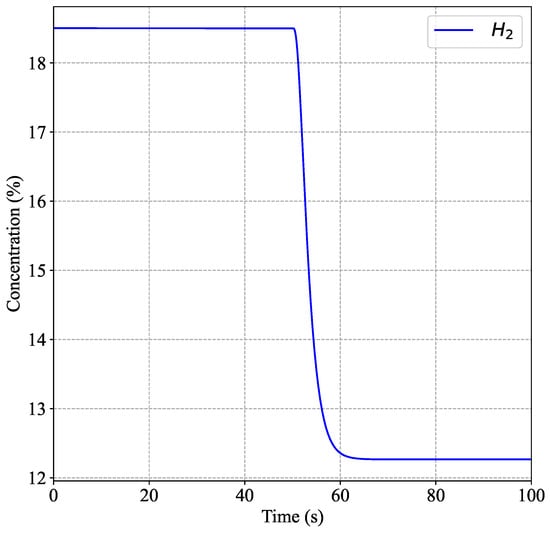
Figure 3. Predicted hydrogen concentration response to a 10% decrease in $CO$ concentration.

The fluidized bed gasification process fits a first-order model plus deadtime using the Fit 3 method, proposed by Smith [44]. The values for the gain ($K_p$), dead time ($t_0$), and process time constant ($\tau$) are −0.62, 2.29, and 2.52, respectively.

2.3. Control Strategies

2.3.1. Classic Feedback Control (PID)

The control strategy aims to maintain the hydrogen concentration at its setpoint by regulating the airflow entering the gasifier. To achieve this, the process is modeled as a First-Order Plus Dead Time (FOPDT) system. Once the model is established, the controller must be tuned to account for the system’s dynamic responses. This tuning process involves adjusting the controller settings to ensure optimal performance and stability in response to changes and disturbances in the system.

In this study, controller tuning is conducted to address disturbances in the process input using the equations proposed by Murrill and Smith [45]. This approach focuses on minimizing the IAE. The controller gain for this process is negative, indicating that increases in inlet airflow result in lower hydrogen concentration values. The tuned parameters are $K_C=-2.51$, ${\tau }_I=2.67$, and ${\tau }_D=1.09$. Additionally, the reference value for the outlet hydrogen concentration is set at 0.54 mol/m³ under steady-state conditions.

2.3.2. Fuzzy Logic Control (FLC)

For fluidized bed gasification, implementing a rule-based fuzzy logic control loop offers a robust approach to guide control decisions effectively. This method provides significant advantages over classical control techniques, particularly in its ability to manage high non-linearities, resulting in a more responsive system. As detailed in Table 4, a set of fundamental fuzzy inference rules governs the gasification process. The linguistic variables utilized—Negative Big (NB), Negative Small (NS), Zero (Z), Positive Small (PS), and Positive Big (PB)—represent values ranging from −1.0 to 1.0, with corresponding numerical assignments of NB = −0.8, NS = −0.4, Z = 0.0, PS = 0.4, and PB = 0.8. These rules are informed by system-specific data and designed to optimize the control strategy for effective results. The tuning of the fuzzy controller is achieved through the equations proposed in [46], incorporating a suppression factor of five. While the implemented fuzzy logic controller exhibits an oscillating response in a steady state— a characteristic behavior of such controllers—this initial instability typically diminishes over time as the system adjusts, leading to reduced overshoot after the initial operational phase.

Table 4. Fuzzy inference rules for the gasification process.

	e (error)
	Δm	NB	NS	Z	PS	PB
	NB	NB	NB	NM	NS	Z
$\Delta e$	NS	NB	NM	NS	Z	PS
	Z	NM	NS	Z	PS	PM
	PS	NS	Z	PS	PM	PB
	PB	Z	PS	PM	PB	PB

2.3.3. Dynamic Matrix Control (DMC)

This strategy employs a predictive algorithm model grounded in the principle of superposition. In the context of gasification within a fluidized bed, dynamic matrix control becomes effective once the system’s response to variations in the controller output signal is understood. By measuring how changes in operating parameters affect hydrogen concentration, it is possible to determine the optimal controller signal needed to maintain process stability.

To implement the DMC strategy in the gasification process, the first thing is to find the characteristic curve of the sensor’s response against a change in controller output. Then, the sampling time is determined, which in this case has a value of 0.2 s after the start of the change. Later, the control horizon is established with a value of five, which refers to the magnitude of the output vector to be predicted. Next, the DMC algorithm is applied using the least squares method, and the suppression factor ($\lambda$) is obtained using Equation (25) proposed by [47].

$${\lambda }_i^2={\displaystyle \frac{M}{500}}\sum _{j=1}^R\left[{\gamma }_j^2{K}_{ij}^2\left(P-k_{ij}-{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\tau }_{ij}}{T}}+2-{\displaystyle \frac{M-1}{2}}\right)\right]$$

(25)

here, M represents the model horizon, R denotes the measured output, and ${\gamma }_j$ signifies the weights assigned to the controlled variables. The prediction horizon is indicated by P, while T refers to the sample time. Additionally, $K_{ij}$, ${\tau }_{ij}$, and $k_{ij}$ represent the model parameters. When the DMC is adapted to the process in a steady state, it becomes evident that the response curve of the process is smooth and exhibits minimal oscillation, which is ideal for maintaining stability. Furthermore, this predictive strategy is advantageous as it does not necessitate rewriting code and remains non-aggressive even when the control horizon is extended.

3. Results

The evaluation of control strategies is made through changes in input variables, to measure the degree of efficiency of each control strategy. As it is a simple control loop, the response capacity of the strategies is studied when controlling the hydrogen concentration in the synthesis gas. In this case, the performance indicator used is IAE.

3.1. Comparison and Evaluation of the Control Strategies

In this study, the input parameters related to pyrolysis temperature and oxygen concentration are varied, as these are the two most critical conditions influencing the reference value of the controlled variable.

3.1.1. Disturbances Associated with Pyrolysis Temperature

As an initial part of the analysis, the pyrolysis temperature is increased by 200 K beyond its typical operating range. This temperature adjustment is based on scenarios where such levels, approaching the combustion temperature, might be encountered. As a result of this disturbance, the hydrogen concentration decreases due to the impact on the equilibrium constant of the reaction. The IAE values for this disturbance, as detailed in Table 5, reflect the performance of various implemented controllers under these conditions.

Table 5. IAE values for a change in the pyrolysis temperature of +200 K.

	PID (+200 K)	DMC (+200 K)	FLC (+200 K)
IAE	3.89	1.26	1.24

The analysis reveals that the FLC (IAE = 1.24) demonstrates superior performance in response to disturbances compared to the other control strategies. Notably, DMC also performs well (IAE = 1.26), though it exhibits higher setpoint deviations than the fuzzy logic controller. In contrast, the PID controller shows less effectiveness, with an IAE value of 3.89. These IAE values clearly indicate that the FLC approach is more adept at maintaining stability and minimizing deviation from the setpoint during disturbances. Additionally, Figure 4 displays the response curves of each controller to the disturbance, highlighting the overshoot associated with each control strategy. This allows for a detailed comparison of how each method handles the disturbance.

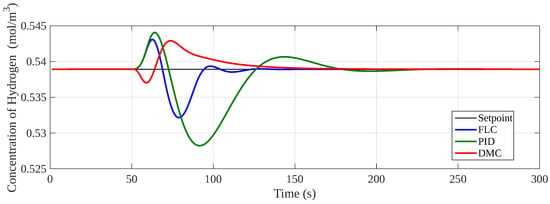
Figure 4. Behavior of the control strategies against a change in the pyrolysis temperature of +200 K.

In the second analysis, the inlet temperature of the volatile products involved in the combustion process is adjusted to 673 K. Under these new disturbance conditions, the IAE values, presented in Table 6, are calculated to assess the performance of the controllers.

Table 6. IAE values for a change in the pyrolysis temperature of −200 K.

	PID (−200 K)	DMC (−200 K)	FLC (−200 K)
IAE	3.42	1.15	0.98

The analysis indicates that FLC is the most effective in maintaining hydrogen concentration with minimal deviation, achieving an IAE of 0.98. In contrast, the PID controller exhibits difficulties in adapting to the dynamic nature of the fluidized bed gasification process, as evidenced by its higher IAE of 3.42. DMC performs reasonably well, with an IAE of 1.15. Notably, the IAE values for this temperature adjustment test are lower than those recorded during the temperature increase scenario, suggesting that the controllers exhibit improved performance when the pyrolysis temperature decreases. The behavior of the various control strategies under these conditions is illustrated in Figure 5.

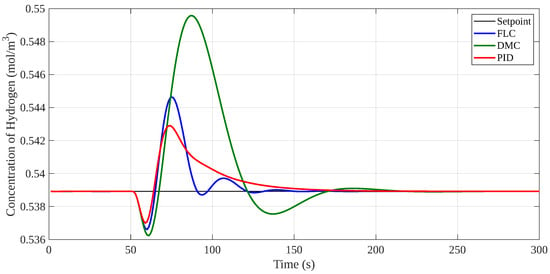
Figure 5. Behavior of the control strategies against a change in the pyrolysis temperature of −200 K.

A decrease in the volatilization temperature leads to an increase in the hydrogen concentration at the outlet. This disturbance is favorable but represents a discontinuity in the process since this variable directly affects all stages of gasification. Therefore, the DMC and FLC controllers present better responses in terms of stability to bring the variable to the setpoint.

3.1.2. Disturbances Associated with the Gasifying Agent

The air introduced into the reactor not only serves to fluidize the bed but also ensures proper combustion. However, disturbances related to the gasifying agent, such as variations in oxygen concentration, can significantly affect hydrogen concentration. This model examines the impact of oxygen concentration on the controlled variable and its broader effects on the combustion process.

This analysis was conducted by increasing the oxygen concentration by 2.5 mol/m³, a change that significantly impacts the concentration levels in the synthesis gas. Following this disturbance, the IAE values for the various implemented control strategies were calculated. These values are detailed in Table 7.

Table 7. IAE values for a change in oxygen concentration +2.5 mol/m³.

	PID (+2.5 mol/m3)	DMC (+2.5 mol/m3)	FLC (+2.5 mol/m3)
IAE	1.49	0.51	0.48

The increase in oxygen concentration results in a heightened burning rate of the char, primarily due to the altered air–fuel ratio within the gasifier. This increase introduces irregularities in the combustion process, as illustrated in Figure 6. The analysis of the IAE values reveals that all control strategies are affected by these changes: the FLC achieves an IAE of 0.48, while DMC records an IAE of 0.51, both indicating effective performance. However, the PID controller shows a higher IAE of 1.49, suggesting that it struggles more significantly to adapt to the excess oxidant conditions. This comparison highlights the superior responsiveness of the FLC and DMC in managing the irregularities associated with increased oxygen concentration in the gasification process.

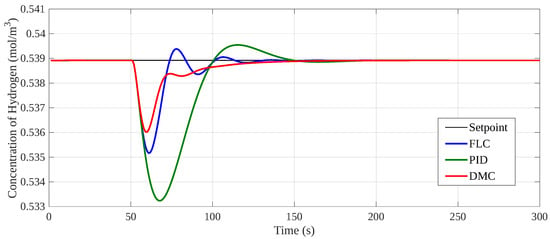
Figure 6. Behavior of the control strategies against a change in oxygen concentration +2.5 mol/m³.

In Figure 6, the controllers stabilize within the same time interval, demonstrating a notable reduction in oscillations around the control point. The Fuzzy Logic Control (FLC) strategy, in particular, shows a strong response to this disturbance. Conversely, if the oxygen concentration in the gasification air decreases, there is a substantial increase in the controlled variable. The IAE values for each control strategy under this condition are presented in Table 8.

Table 8. IAE values for a change in oxygen concentration −2.5 mol/m³.

	PID (−2.5 mol/m3)	DMC (−2.5 mol/m3)	FLC (−2.5 mol/m3)
IAE	1.63	0.52	0.50

The behavior of the controllers in response to this disturbance is depicted in Figure 7. The IAE values for this scenario are marginally higher than those observed in the previous test, indicating a slightly more challenging disturbance. Despite this, DMC outperforms the other strategies, as reflected in its low IAE value of 0.52, demonstrating its ability to efficiently stabilize the process. FLC also performs effectively, achieving a comparable IAE of 0.50. In contrast, the PID controller shows a significantly higher IAE of 1.63, indicating that it is less adept at managing the disturbance. Overall, the DMC and FLC controllers exhibit superior control, maintaining process stability with minimal deviations.

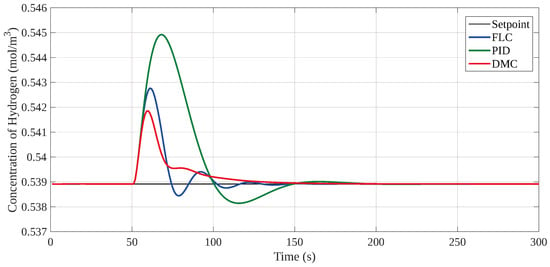
Figure 7. Behavior of the control strategies against a change in oxygen concentration −2.5 mol/m³.

4. Conclusions

In this study, a numerical model was used to compare and evaluate the performance of some control strategies; the following conclusion can be drawn from the study:

• The control by fuzzy logic was much more efficient against disturbances, keeping the controlled variable inside the operating range. This can be noticed by the low IAE values obtained using the FLC in comparison with the results using both PID and DMC.
• The FLC showed very good stability characteristics: it featured small oscillations around the set point. This stability is a result of the intrinsic ability of the FLC to cope with the nonlinearities and uncertainties of the gasification process.
• A key finding from this study is the significant advantage of FLC in promoting sustainability through more efficient resource utilization in biomass gasification.
• FLC is the most efficient of the controlled variables in the presence of temperature disturbances. As a matter of fact, in all the cases analyzed here, the FLC was shown to be much better than DMC and PID control according to IAE, thus proving its higher capacity for adapting to temperature-related disturbances. This efficiency not only ensures optimal operation but also maximizes the yield of valuable synthesis gas while minimizing waste and energy consumption.
• The PID performance was poor compared to other implemented strategies. This clearly shows the limited performance expected from the classical control in the presence of complex dynamics and nonlinearities existing in the processes of biomass gasification.
• The advantages of FLC in biomass gasification are evident, particularly in its ability to handle process non-linearities and enhance efficiency. However, the practical implementation of such control strategies in industrial applications may present challenges, such as tuning complexity and integration with existing systems. Further research is recommended to address these limitations and optimize their industrial viability.