Evaluation of Social Stability Risk of Adjusting Goods Vehicle Calculation Method Based on Optimal Combination Weighting—Cloud Model

Abstract

In order to solve the social stability risk problem of the adjusting goods vehicle calculation method (AGVCM) in the cancellation of toll stations at expressway provincial boundaries, a social stability risk evaluation model was proposed. Firstly, based on the possible time stages of the AGVCM, we built the social stability risk evaluation index system of the AGVCM including 4 levels, 3 grades, and 60 indicators. Secondly, we used the semantic information of cloud model to transform qualitative description and quantitative evaluation, calculated the risk level for social stability risk evaluation of AGVCM according to an integrated cloud algorithm, and proposed an optimal combination weighting—cloud model for the social stability risk evaluation of AGVCM. Finally, the feasibility of the evaluation model is verified by a case study in Yunnan province in China. The results showed that the cloud model’s numerical characteristic of social stability risk evaluation of AGVCM in Yunnan based on the optimal combination weighting—cloud model is (0.28, 0.073, 0.0008), implying the risk level is “small” and the conclusion is basically consistent with current standards. The model contains rich process information, which is helpful to better effectively eliminate the subjectivity and arbitrariness in the evaluation process of identifying the key factors affecting the project risk level.

1. Introduction

On 16 May 2019, the General Office of the State Council of the People’s Republic of China issued an implementation plan for deepening reforms of the toll road system to cancel the provincial toll station of expressways in China. It puts forward the requirements for adjusting the charging mode of freight car tolls and revising the standards of the classification of vehicle types for toll roads and unified tolling in China according to vehicle (axle) types. On 31 May 2019, the Ministry of Transport of the People’s Republic of China issued a classification of toll road vehicles standard. According to the document, the provinces have been carrying out the cancellation of adjusting goods vehicle calculation method (AGVCM) at toll stations on the interprovincial expressways among provinces [1]. According to the statistics of China Statistical Yearbook 2019 regarding expressway vehicle ownership, until the end of 2018, the number of China’s cargo vehicle ownership was 135.82 million, tonnage was 128.7297 million tons, and employees exceeded 21 million people. Therefore, AGVCM involves a wide range of complex procedures and many uncertainties, which may easily affect the relevant interest groups and lead to social stability problems if not handled properly. Therefore, it is of great significance to scientifically analyze the risk factors that may be caused by AGVCM and evaluate the risk level of each relevant group in order to promote the implementation of AGVCM in an efficient, orderly and stable manner.

Since the adoption of the National Environmental Policy Act in 1969 [2], many foreign scholars have conducted research on the definition of risk [3,4,5], research frameworks [6], and evaluation methods [7,8,9], and the issue of social stability risk in the transport sector has also gradually gained attention. Ghosh used principal component analysis to analyze the key risk factors for the Thailand Metro project [10]. Wei Chen studied the social stability risk assessment of rail transit construction projects from the subjective and objective perspectives [11]. Zou Yuhui and Liu Xiaohui studied the risk identification and risk estimation of social stability risk analysis, taking Taiyuan Rail Transit Line 2. and Zhengzhou Rail Transit Line 1 as examples, respectively [12,13]. Du Zhe studied the identification and evaluation methods of risk factors involved in the social stability risk assessment of rail transit [14]. Taking the characteristics of highway projects as a starting point, Hu Liang constructed a social stability risk evaluation index system and conducted a risk evaluation study using AHP [15]. Dong Zhi studied the social stability risk of highway projects based on the entropy weight extension matter–element model on the basis of constructing a social stability risk assessment index system combined with the characteristics of highway projects at various stages of construction [16]. Liu Shuai used the AHP method to evaluate the social stability risk of taxi reservation in the Wulingyuan district of Zhangjiajie [17]. Li Jun used the single-factor risk assessment method to study the impact of airport construction on social stability risk [18]. Li Fei studied the social stability risks of the project, taking into account the characteristics of an integrated passenger hub station [19]. Because the social stability risk assessment of major administrative decision-making has long been operated in a non-rule-of-law manner, Lin studied the social stability evaluation system for major administrative decisions [20]. Hong studied the social stability risk factors of large industrial construction projects under the concept of interactive fairness about land acquisition and demolition [21]. Wang, Jiang and Liu studied the problems and countermeasures of social stability risk assessment in China [22,23,24]. According to the characteristics of floods, Xu studied the topology map for the evolution of flood social stability risk based on the investigation conducted on the flood that occurred in Hunan Province in August 2013 [25]. In addition, some scholars had studied the social stability risk assessment of large industrial construction projects, housing demolition, river comprehensive improvement projects, rural land integrated consolidation, land-integrated renovation projects and so on [26,27,28,29]. In summary, social stability risk assessment in the field of transportation has achieved some results, but few studies focus on the social stability risk assessment of AGVCM. The social stability risk assessment of AGVCM involves a number of relevant groups, and the evaluation index systems of highway construction projects, rail transit and integrated hub stations have large differences. Most of the existing studies use qualitative or quantitative methods, such as the expert decision-making and hierarchical analysis methods, ignoring the fuzzy randomness of the human factor involved in the adjusting goods vehicle calculation method, which leads to a discrepancy between the assessment results and the objective results.

On the basis of analyzing the social stability risk factors of the adjusting goods vehicle calculation method, this study establishes an AGVCM social stability risk evaluation index system, proposing AGVCM social stability risk optimal combination weighting—cloud model evaluation modeling, and then regards the social stability risk evaluation project of adjusting goods vehicle in Yunnan Province as an example to carry out empirical analysis, in order to provide a theoretical basis for the social stability risk evaluation of adjusting goods vehicles.

2. AGVCM Social Stability Risk Evaluation Index System

2.1. AGVCM Social Stability Risk Factor Identification

The social stability risk factors of AGVCM refer to the collection of potential social instability factors caused by the correlation and coupling between interest-related groups and various uncertain factors in the process of project promotion. These risk factors are associated with a wide range of subjects, and most of them are related to the interests of the people. Incomplete identification, improper preventive measures or unscientific treatment can easily lead to social contradictions and social instability. AGVCM social stability risk factor identification is the basis for constructing a risk assessment index system and carrying out the assessment. According to the project stage (decision-making, preparation, implementation, operation), this study identifies the project from four aspects: legitimacy, rationality, feasibility and controllability.

(1)

Project legitimacy: This refers to whether the implementation of the project meets the requirements of laws and regulations in the decision-making and preparation stage of the AGVCM project. It mainly includes four factors, namely whether the implementation of the adjusting goods vehicle calculation method is consistent with the relevant existing laws, regulations, norms and national policies, whether it is consistent with the national economic and social development plans and industrial policies of the national regions, whether the approval is carried out in accordance with the responsibilities and authority of the departments, and whether the decision-making process and procedures are in line with regulation.

(2)

Project rationality: This refers to whether the implementation of the AGVCM project meets the requirements of scientific development law in the implementation and operation stage. It mainly includes four factors: the impact of project implementation on economic development, the impact on industry development, the impact on employment, and the impact on regional basic living prices.

(3)

Project Feasibility: This refers to the implementation and operation stage of the AGVCM project, and whether the implementation of the project is supported by sound schemes and measures. It mainly includes five factors, namely, energy consumption, air pollutant emission, noise and vibration, regional traffic and mass travel.

(4)

Project Controllability: This refers to the ability to control mass incidents and social negative public opinion after the implementation of the AGVCM project. It mainly includes four factors, namely the influence of the legitimate rights and interests of stakeholders, stakeholders’ attitudes, public opinion risk and risk prevention.

2.2. AGVCM Social Stability Risk Evaluation Index System

This study combines the entire process risk identification of an AGVCM project and develops the AGVCM social stability risk evaluation index system according to the interaction of risk factors. The indexing system is divided into four layers, and the goal layer is the social stability risk of AGVCM. The first grade indexes layer contains four indicators, namely, project legitimacy, project rationality, project feasibility and project controllability. The second-grade index layer contains 17 indicators, including regulatory policy coherence, national economy and industrial policy coherence, and approval process. The third-grade index layer contains 39 indicators, which are the subdivided indicators of the second-grade index layer, as shown in Table 1.

Table 1. AGVCM social stability risk evaluation index system.

Goal Layer	First Grade Indexes	Second Grade Indexes	Third Grade Indexes
AGVCM Social Stability Risk A	Project legitimacy B1	Legislative and policy consistency C1	Consistency with current laws, regulations and norms D1
			Consistency with national policies D2
		National economic and industrial policy consistency C2	Consistency with national and regional economic and social development planning D3
			Consistency with national and regional industrial policies D4
		Approval process C3	The approval department has approval authority D5
			Examination and approval department within the scope of authority D6
		Decision-making process C4	Decision-making process compliance D7
			Decision-making process compliance D8
	Project Rationality B2	Economic development impact C5	Promote regional economic development D9
			Social transport efficiency D10
		Industry development impact C6	Industrial structure and layout D11
			Integrated transport system development D12
		Employment impact C7	Toll collector employment D13
			Employment of others D14
		Regional basic living price impact C8	Logistics freight D15
			Price impact D16
	Project Feasibility B3	Energy consumption impact C9	Sustainable development D17
			Energy consumption impact D18
		Emission effects of air pollutants C10	Vehicle emissions D19
			Environmental pollution D20
		Noise and vibration impact C11	Noise impact D21
			Vibration impact D22
		Regional traffic impact C12	Road network access efficiency D23
			Traffic safety D24
			Traffic flow and regional road network matching degree D25
		Mass travel impact C13	Travel mode D26
			Travel time D27
			Travel distance D28
			Service level D29
	Project Controllability B4	Impact on the legal rights of stakeholders C14	Impact on the legitimate rights and interests of toll road investors D30
			Impact on the legal rights and interests of toll road operators D31
			Impact on the legal rights of toll road users (goods vehicle companies and drivers) D32
		Stakeholder attitude C15	Attitudes of toll road investors D33
			Attitudes of toll road operators D34
			Attitudes of toll road users (goods vehicle companies and drivers) D35
		Public opinion risk C16	Media opinion guide D36
			Publicity explained D37
		Risk prevention C17	Preventive and defensive measures D38
			Effective measures D39

3. AGVCM Social Stability Risk Optimal Combination Weighting—Cloud Model Evaluation Modeling

The AGVCM social stability risk evaluation is mainly to quantify the impact or loss of project implementation on social stability before the occurrence of risk events. On the basis of risk investigation, this study intends to determine the weight of each index by using the combination weighting method combined with the opinions of planning, design, construction, environmental assessment, government and other participants (hereinafter referred to as “participants”) to reduce the randomness of evaluation. At the same time, in order to solve the uncertainty conversion between qualitative and quantitative indicators in the evaluation index system, the cloud model is used to judge the social stability risk level of AGVCM.

3.1. AGVCM Social Stability Risk Evaluation Index Optimal Combination Weighting Calculation

After the AGVCM social stability risk evaluation index system has been established, the indicators are assigned different weight values. When assigning weights to individual indicators, the participants combine the weight set level to divide each indicator for scoring. As the results are subjective, this paper uses the combined weighting method to calculate the weights.

3.1.1. Subjective Weight Set

In this study, AHP [30,31] is used to calculate the subjective weight of the AGVCM social stability risk evaluation index. The calculation steps are as follows:

• Index normalization processing

Let A = (a_ij)_n×n be the pairwise judgment matrix of the lower index to the upper index, then we have

$${\overline{a}}_{ij}=\frac{a_{ij}}{{\displaystyle \sum _{i=1}^n{a}_{ij}}}$$

(1)

In the formula, a_ij represents the comparison result of the importance of i index and j index, ${\overline{a}}_{ij}$ is the normalized value of a_ij.

2.

Subjective weight calculation

Let W_s be a subjective weight set, then:

W_s = {w_s1, w_s2,…, w_sn}

(2)

In the formula $w_{si}=\frac{{\displaystyle \sum _{j=1}^n{\overline{a}}_{ij}}}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\overline{a}}_{ij}}}}$.

3.

Consistency test calculation

Let CR be the consistency ratio, then

$$CR=\frac{{\lambda }_{\max }-n}{(n-1)RI}$$

(3)

In the formula, ${\lambda }_{\max }$ is the maximum number of characteristic tests. ${\lambda }_{\max }=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{(A{W}_s)}_i}{w_{si}}}$, RI is a random consistency index value. When CR < 0.1, the consistency of the judgment matrix is within an acceptable range, that is, the comparison results are correct, otherwise the judgment matrix needs to be corrected.

3.1.2. Objective Weight Set

This study uses the EWM to calculate the objective weight of the AGVCM social stability risk index, which is calculated as follows:

• Index standardization

Set x_ik as the evaluation score of the k-participant for the i-level index, the standardized process of the index score is:

$$a_{ik}=\frac{x_{ik}-x_{\min }}{x_{\max }-x_{\min }}$$

(4)

In the formula, x_ik as the evaluation score of the k-participant for the i-level index, i = 1, 2,..., P, P is the number of the third-level indicators of the evaluation index system. k = 1, 2,..., K, K is the number of evaluators. x_max, x_min are the maximum and minimum values of the importance evaluation of the same indicator by the participants.

2.

Index entropy calculation

Combining Equation (4), the entropy value of the AGVCM social stability risk index is:

$$G_i=-\frac{1}{\ln (K)}{\displaystyle \sum _{k=1}^K\frac{1+a_{ik}}{{\displaystyle \sum _{k=1}^K(1+a_{ik})}}\ln (\frac{1+a_{ik}}{{\displaystyle \sum _{k=1}^K(1+a_{ik})}})}$$

(5)

3.

Index entropy weight calculation

Let W₀ be the set of objective weights, then the AGVCM social stability risk index entropy weight W₀ is

W₀ = {w₀₁, w₀₂,…, w_0n}

(6)

In the formula $w_{0i}=\frac{1-G_i}{P-{\displaystyle \sum _{i=1}^P{G}_i}}$, and ${\displaystyle \sum _{i=1}^P{w}_{0i}}=1$.

3.1.3. Optimal Combination Weighting Set

In order to fully express the subjectivity and objectivity of the evaluators in the weight set, this paper uses the combination weighting method to calculate the index weight. Let w_i be the value of the combined assignment weight for the i index, then

w_i = aw_si + bw_0i

(7)

In the formula, a and b are the optimization factors for the subjective and objective weights, respectively.

Assuming that the minimum deviation between the combined weighting weight and each subjective weight and objective weight is set as the objective, the following planning model is established:

$$Z=\min ({\displaystyle \sum _{i=1}^P[{(w_i-w_{si})}^2+{(w_i-w_{0i})}^2]})$$

(8)

$$s.t.\left\{\begin{array}{l}a+b=1\\ a>0\\ b>0\end{array}\right.$$

(9)

Combining Equation (8), the model can be deformed to:

$$Z=\min ({\displaystyle \sum _{i=1}^P[{(w_{si}-w_{0i})}^2+{(2a^2-2a+1)}^2]})$$

(10)

$$s.t. 0<a<1$$

(11)

From Equations (10) and (11), it is easy to conclude that the optimal solution of the planning model is:

$$\left\{\begin{array}{l}a=0.5\\ b=0.5\end{array}\right.$$

(12)

Based on the above analysis, W is set as the optimal combination weighting weight set, and then:

W = 0.5W_s + 0.5W₀

(13)

3.2. AGVCM Social Stability Risk Evaluation Index Cloud

The numerical characteristics of the cloud are characterized by three values of expectation, entropy and super-entropy, reflecting the quantitative nature of the qualitative description. This study omits the computational rules of the cloud model and the cloud parameter calculation process and focuses on the associated evaluation cloud generation [32]. Combined with the actual situation of AGVCM project, this paper divides the evaluation results of social stability risk indicators into five language values [32], and sets the evaluation cloud as V, where V = {significant, large, general, small, tiny}.

The corresponding cloud parameters are calculated by the reverse cloud generator method and described by the normal cloud. The corresponding cloud number characteristics are significant (1, 0.061, 0.003), large (0.76, 0.061, 0.004), general (0.51, 0.061, 0.004), small (0.29, 0.061, 0.004) and tiny (0.001, 0.061, 0.002). AGVCM social stability risk evaluation index cloud is shown in Figure 1:

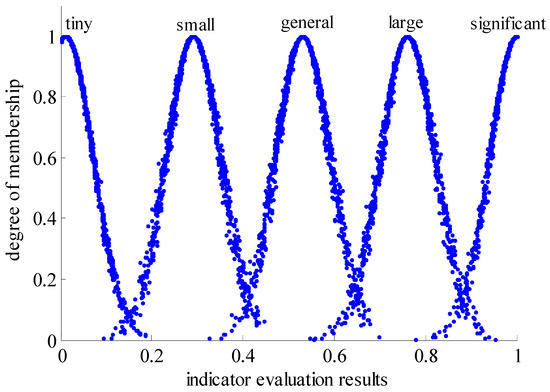
Figure 1. AGVCM social stability risk evaluation index cloud.

3.3. AGVCM Social Stability Risk Evaluation Comprehensive Cloud

Combined with the 2.2 index cloud language value level, the participants are invited to grade the index system. On the basis of obtaining the evaluation results, the cloud digital characteristics of each index T = U (E_x, E_n, H_e) are calculated by using the comprehensive cloud algorithm for the same type of cloud, and then

$$\left\{\begin{array}{l}{E}_{xj}=\frac{E_{xj1}{E}_{nj1}+E_{xj2}{E}_{nj2}+\cdots +E_{xji}{E}_{nji}}{E_{nj1}+E_{nj2}+\cdots +E_{nji}}\\ E_{nj}=E_{nj1}+E_{nj2}+\cdots +E_{nji}\\ H_{ej}=\frac{H_{ej1}{E}_{nj1}+H_{ej2}{E}_{nj2}+\cdots +H_{eji}{E}_{nji}}{E_{nj1}+E_{nj2}+\cdots +E_{nji}}\end{array}\right.$$

(14)

In the formula, i is the number of commentator, (E_xji, E_nji, H_eji) is the cloud characteristic value of the jth indicator in a layer after qualitative judgment by the ith commentator, (E_xi, E_ni, H_ei) is the cloud characteristic value of the jth indicator in a layer. Combined with Equation (13) and Equation (14), we can obtain the cloud digital characteristics of the upper layer index. The formula is as follows:

$$\left\{\begin{array}{l}{E}_x=\frac{E_{x1}{E}_{n1}+E_{x2}{E}_{n2}+\cdots +E_{xj}{E}_{nj}}{E_{n1}+E_{n2}+\cdots +E_{nj}}\\ E_n=\sqrt{w_1^2{E}_{n1}^2+w_2^2{E}_{n2}^2+\cdots +w_j^2{E}_{nj}^2}\\ H_e=\sqrt{w_1^2{H}_{e1}^2+w_2^2{H}_{e2}^2+\cdots +w_j^2{H}_{ej}^2}\end{array}\right.$$

(15)

In the formula, (Ex, En, H_e) is the cloud characteristic value of the upper indicator in that layer. Thus, the digital features of AGVCM social stability risk evaluation comprehensive cloud modeling can be calculated.

4. Example Application Analysis

This study takes Yunnan’s AGVCM social stability risk evaluation project as an example, and invites commentators to evaluate the social stability risk of adjusting goods vehicle according to the evaluation index system and evaluation criteria established in this study.

4.1. Determining the Assignment of Optimal Combination Weighting

According to the 2.1.1 and 2.1.2 model, this paper uses the analytic hierarchy process and entropy weight method to calculate the subjective weight and objective weight, combined with Formula (13), using the optimal combination weighting method to calculate the combination weighting, as shown in Table 2.

Table 2. Social stability risk evaluation index weight of AGVCM.

Index Code	AHP Weighting	EWM Weighting	Combination Weighting	Index Code	AHP Weighting	EWM Weighting	Combination Weighting
B1	0.4203	0.4603	0.4403	B2	0.2685	0.2816	0.2751
B3	0.1213	0.0716	0.0965	B4	0.1899	0.1865	0.1882
C1	0.4092	0.3934	0.4013	C10	0.1377	0.1278	0.1327
C2	0.2896	0.2428	0.2662	C11	0.0692	0.0780	0.0736
C3	0.0966	0.1365	0.1165	C12	0.2514	0.2275	0.2395
C4	0.2046	0.2272	0.2159	C13	0.4328	0.4823	0.4576
C5	0.4782	0.5053	0.4917	C14	0.2470	0.2892	0.2681
C6	0.1441	0.1423	0.1432	C15	0.4276	0.3821	0.4048
C7	0.1017	0.0940	0.0978	C16	0.1627	0.1448	0.1538
C8	0.2760	0.2584	0.2672	C17	0.1627	0.1839	0.1733
C9	0.1088	0.0844	0.0966	D1	0.3331	0.3097	0.3214
D2	0.6669	0.6903	0.6786	D21	0.7976	0.9412	0.8694
D3	0.6664	0.6268	0.6466	D22	0.2024	0.0588	0.1306
D4	0.3336	0.3732	0.3534	D23	0.0623	0.0215	0.0419
D5	0.3333	0.2470	0.2902	D24	0.7443	0.9068	0.8255
D6	0.6667	0.7530	0.7098	D25	0.1934	0.0717	0.1326
D7	0.3337	0.4056	0.3697	D26	0.5342	0.6502	0.5922
D8	0.6663	0.5944	0.6303	D27	0.2034	0.1608	0.1821
D9	0.8333	0.8526	0.8430	D28	0.1711	0.1572	0.1642
D10	0.1667	0.1474	0.1570	D29	0.0913	0.0318	0.0615
D11	0.8005	0.8730	0.8368	D30	0.0938	0.0168	0.0553
D12	0.1995	0.1270	0.1632	D31	0.2793	0.1791	0.2292
D13	0.8321	0.9505	0.8913	D32	0.6269	0.8041	0.7155
D14	0.1679	0.0495	0.1087	D33	0.1170	0.1158	0.1164
D15	0.1997	0.1889	0.1943	D34	0.2685	0.2909	0.2797
D16	0.8003	0.8111	0.8057	D35	0.6145	0.5933	0.6039
D17	0.5000	0.4712	0.4856	D36	0.7994	0.9006	0.8500
D18	0.5000	0.5288	0.5144	D37	0.2006	0.0994	0.1500
D19	0.5000	0.4552	0.4776	D38	0.1656	0.0633	0.1145
D20	0.5000	0.5448	0.5224	D39	0.8344	0.9367	0.8855

4.2. AGVCM Social Stability Risk Evaluation Comprehensive

In this study, five experts were invited to score the indicators of the evaluation index system, and the evaluation results are shown in Table 3.

Table 3. Social stability risk evaluation index weight of AGVCM.

Index Code	Expert 1	Expert 2	Expert 3	Expert 4	Expert 5
D1	small	small	small	tiny	small
D2	tiny	tiny	small	tiny	small
D3	small	tiny	small	small	tiny
D4	small	small	small	small	tiny
D5	small	tiny	tiny	tiny	small
D6	small	tiny	small	small	small
D7	small	small	tiny	tiny	tiny
D8	tiny	small	small	small	tiny
D9	tiny	tiny	small	small	small
D10	small	general	general	small	small
D11	small	small	small	tiny	tiny
D12	small	small	tiny	tiny	small
D13	large	general	general	large	general
D14	tiny	tiny	small	tiny	small
D15	general	small	small	small	small
D16	general	general	general	small	general
D17	small	tiny	tiny	tiny	small
D18	small	tiny	small	small	tiny
D19	tiny	tiny	tiny	tiny	small
D20	small	small	tiny	tiny	small
D21	tiny	tiny	tiny	tiny	small
D22	small	tiny	small	small	tiny
D23	tiny	small	small	small	tiny
D24	small	small	small	small	small
D25	small	small	tiny	tiny	tiny
D26	tiny	small	tiny	tiny	small
D27	small	small	tiny	small	small
D28	small	small	small	small	small
D29	small	small	tiny	small	tiny
D30	general	small	small	general	small
D31	small	small	small	general	small
D32	general	general	general	large	large
D33	small	small	small	small	small
D34	general	small	general	general	general
D35	general	large	large	large	general
D36	large	general	large	large	large
D37	general	large	general	general	general
D38	large	general	general	large	large
D39	general	general	general	large	general

According to the comprehensive cloud algorithm in Equation (14), the qualitative description of index in Table 3 is transformed into the quantitative evaluation of cloud of digital characteristics, and the cloud model’s digital characteristics corresponding to the three-level index are obtained. Therefore, according to the Equation (15), the cloud model’s digital characteristics corresponding to the secondary index can be obtained. In this way, the numerical characteristics of the cloud model for each level of indicators in the AGVCM social stability risk evaluation index system can be obtained, as shown in Table 4, the evaluation cloud of first grade indexes as shown in Figure 2.

Table 4. Cloud model numerical characteristic of index system.

Index Code	Evaluation Cloud (Ex,En,He)	Grade	Index Code	Evaluation Cloud (Ex,En,He)	Grade	Index Code	Evaluation Cloud (Ex,En,He)	Grade
B1	(0.17, 0.123, 0.0012)	small	C17	(0.57, 0.272, 0.0036)	general	D20	(0.17, 0.305, 0.0032)	small
B2	(0.30, 0.152, 0.0017)	small	D1	(0.23, 0.305, 0.0036)	small	D21	(0.06, 0.305, 0.0024)	tiny
B3	(0.18, 0.116, 0.0012)	small	D2	(0.12, 0.305, 0.0028)	tiny	D22	(0.17, 0.305, 0.0032)	small
B4	(0.58, 0.121, 0.0016)	general	D3	(0.17, 0.305, 0.0032)	small	D23	(0.17, 0.305, 0.0032)	small
C1	(0.15, 0.229, 0.0022)	small	D4	(0.23, 0.305, 0.0036)	small	D24	(0.29, 0.305, 0.0040)	small
C2	(0.19, 0.225, 0.0024)	small	D5	(0.12, 0.305, 0.0028)	tiny	D25	(0.12, 0.305, 0.0028)	tiny
C3	(0.20, 0.234, 0.0027)	small	D6	(0.23, 0.305, 0.0036)	small	D26	(0.12, 0.305, 0.0028)	tiny
C4	(0.15, 0.223, 0.0023)	small	D7	(0.12, 0.305, 0.0028)	tiny	D27	(0.23, 0.305, 0.0036)	small
C5	(0.21, 0.262, 0.0028)	small	D8	(0.17, 0.305, 0.0032)	small	D28	(0.29, 0.305, 0.0040)	small
C6	(0.17, 0.260, 0.0027)	small	D9	(0.17, 0.305, 0.0032)	small	D29	(0.17, 0.305, 0.0032)	small
C7	(0.56, 0.274, 0.0036)	general	D10	(0.38, 0.305, 0.0040)	small	D30	(0.38, 0.305, 0.0040)	small
C8	(0.44, 0.253, 0.0033)	general	D11	(0.17, 0.305, 0.0032)	small	D31	(0.33, 0.305, 0.0040)	small
C9	(0.15, 0.216, 0.0021)	small	D12	(0.17, 0.305, 0.0032)	small	D32	(0.61, 0.305, 0.0040)	general
C10	(0.12, 0.216, 0.0020)	tiny	D13	(0.61, 0.305, 0.0040)	general	D33	(0.29, 0.305, 0.0040)	small
C11	(0.07, 0.268, 0.0021)	tiny	D14	(0.12, 0.305, 0.0028)	tiny	D34	(0.47, 0.305, 0.0040)	general
C12	(0.26, 0.255, 0.0033)	small	D15	(0.33, 0.305, 0.0040)	small	D35	(0.66, 0.305, 0.0040)	large
C13	(0.17, 0.196, 0.0019)	small	D16	(0.47, 0.305, 0.0040)	general	D36	(0.71, 0.305, 0.0040)	large
C14	(0.53, 0.230, 0.0030)	general	D17	(0.12, 0.305, 0.0028)	tiny	D37	(0.56, 0.305, 0.0040)	general
C15	(0.56, 0.206, 0.0027)	general	D18	(0.17, 0.305, 0.0032)	small	D38	(0.66, 0.305, 0.0040)	large
C16	(0.69, 0.263, 0.0035)	large	D19	(0.06, 0.305, 0.0024)	tiny	D39	(0.56, 0.305, 0.0040)	general

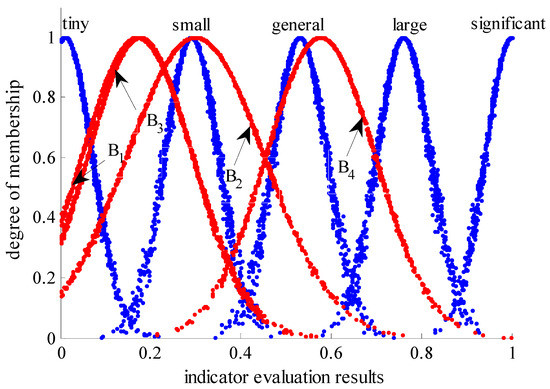
Figure 2. Evaluation cloud of first grade indexes. B1–B4 in Table 1.

According to Table 4 and Equation (15), the numerical characteristics of the evaluation cloud model for the target layer of AGVCM social stability risk evaluation can be obtained as (0.28, 0.073, 0.0008), and the evaluation result cloud diagram is shown in Figure 3.

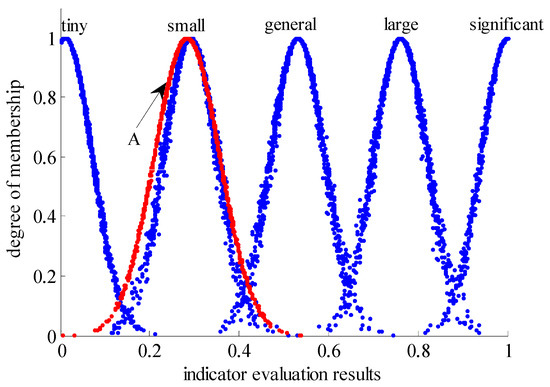
Figure 3. Evaluation cloud of first grade indexes. A in Table 1.

As can be seen from Figure 3, the evaluation results are located between “tiny” and “small”, and tend to “small” cloud range, belonging to “small”. Therefore, this project’s risk level is “small”.

4.3. Comparison Results

In order to verify the reliability of the evaluation of the AGVCM social stability risk optimal combination weighting—cloud model, this paper relies on the interim measures for social stability risk assessment of major fixed asset investment projects (hereinafter referred to as the Measures) of the National Development and Reform Commission to evaluate the social stability risk evaluation index system and weights of the AGVCM, and the comparison results are shown in Table 5.

Table 5. Cloud model numerical characteristic of index system.

Index Code	Optimal Combination weighting—cloud model		Measures
	Evaluation Cloud (Ex,En,He)	Grade	Risk Degree	Weighting	Risk Index	Grade
B1	(0.17, 0.123, 0.0012)	small	0.09	0.4236	0.04	tiny
B2	(0.30, 0.152, 0.0017)	small	0.16	0.2683	0.04	small
B3	(0.18, 0.116, 0.0012)	small	0.12	0.1238	0.01	tiny
B4	(0.58, 0.121, 0.0016)	general	0.36	0.1843	0.07	small
A	(0.28, 0.073, 0.0008)	small	0.16			small

Table 5 shows: (1) The risk assessment results of the optimal combination weighting—cloud model are basically consistent with the evaluation results of t Measures, which proves the validity and reliability of the model. (2) The assessment risk level of some aspects is higher than the assessment in Measures, indicating that the model is helpful in better identifying the key factors affecting the project risk level, t, so as to formulate targeted prevention and mitigation of Measures.

5. Conclusions

(1)

The AGVCM social stability risk evaluation index system, which consists of 4 levels, 3 grades and 60 indexes, was systematically constructed by identifying risks in 4 aspects: legality, reasonableness, feasibility and controllability, according to the time stage of risk occurrence.

(2)

The proposed AGVCM social stability risk optimal combination weighting—cloud model establishes an optimal combination weighting model with the objective of minimizing the deviation of the combination weighting from the weighting of the hierarchical analysis method and the entropy weighting method, respectively, and uses the optimal combination weighting to comprehensively characteries the subjective and objective attitudes of the participants. The model also uses the semantic information of the cloud model to qualitatively describe and quantitatively evaluate the indexes, and accurately calculates the risk level of AGVCM evaluation based on the integrated cloud algorithm, effectively eliminating subjectivity and arbitrariness in the evaluation process.

(3)

Taking the AGVCM project in Yunnan Province as an example, the AGVCM social stability risk evaluation was calculated to be “less” based on the combination weights of the indexes and the numerical characteristics of the cloud model. Comparing the evaluation results with those of Measures, the simulation results show that the findings of the optimal combination weighting—cloud model basically match those of Measures, verifying the validity and reliability of the model and algorithm. The evaluation results of the optimal combination weighting—cloud model contain rich process information, which is helpful for the evaluation results of the model and better identification of the key factors affecting the risk level of the project. It shows that the evaluation is more intuitive, scientific and effective than the evaluation results of Measures.

(4)

The evaluation method proposed in this study has certain reference value for AGVCM social stability risk identification and evaluation, and can be applied to the social stability risk evaluation of similar major projects, but the evaluation index system will be different due to the influence of factors such as geography, policy and implementation conditions, etc. Later, we will focus on the classification and accuracy of the evaluation model based on the factors we have found.