SAT-Based Optimization Framework for Electric Vehicle Charging Station Routing Under Real-World Constraints

Abstract

With the rapid adoption of electric vehicles (EVs), optimizing charging infrastructure and route planning has become increasingly crucial. Traditional methods such as Linear Programming (LP) have been widely used to address these challenges. However, these approaches often struggle with scalability, computational efficiency, and the ability to handle complex logical constraints involving multiple decision factors like distance, time, cost, battery levels, and charging station compatibility. To overcome these limitations, this study proposes a novel Boolean Satisfiability (SAT)-based optimization framework for intelligent EV charging station recommendation. Unlike conventional approaches, the proposed model encodes real-world constraints into Conjunctive Normal Form (CNF) using De Morgan’s Theorem, allowing efficient processing through the CP-SAT solver. This logical transformation enables the systematic representation of intricate relationships between variables, ensuring better compatibility and computational efficiency. The SAT-based framework was applied to intercity EV routing scenarios, where it demonstrated substantial improvements over traditional methods in terms of route optimization, cost reduction, and charging station relevance. Notably, the SAT model was effective in avoiding redundant charging recommendations, selecting only those stations necessary to complete the route while satisfying all energy and infrastructure constraints. Moreover, the solver showed rapid convergence and greater adaptability under varied operational scenarios. In conclusion, this study highlights the effectiveness of SAT-based modeling—particularly its CNF formulation and logical expressiveness—in delivering a scalable, intelligent, and efficient solution for real-time EV route planning and charging station optimization.

1. Introduction

The global shift toward sustainable transportation has propelled the adoption of electric vehicles (EVs) at an unprecedented rate, especially across regions like China, the European Union, and the United States. This surge, while promising for environmental sustainability, presents critical challenges for infrastructure readiness, particularly in the development of an efficient and intelligent EV charging ecosystem [1]. As EVs play a pivotal role in reducing greenhouse gas emissions and minimizing dependency on fossil fuels, their widespread integration into mainstream mobility necessitates accessible, strategically placed charging stations that support uninterrupted travel and alleviate range anxiety [2,3].

Governments, researchers, and industrial stakeholders are increasingly recognizing the need for robust EV support systems that can manage dynamic and complex requirements, such as real-time route planning, variable charging demands, and diverse vehicle specifications. Strategic placement and management of charging stations (CSs) have been shown to significantly reduce operational uncertainty and enhance user confidence in EVs [4]. However, despite public and private sector investments in charging infrastructure, EV adoption still faces barriers such as prolonged charging times, inconsistent support systems, and insufficient station availability—especially along long-distance routes [5,6]. These limitations are further compounded by infrastructural demands resulting from the exponential growth in EV penetration, necessitating large-scale, real-time energy distribution planning [7].

From a user perspective, the uncertainty associated with travel—such as whether the battery will last to the next CS, the distance to the nearest compatible station, or potential waiting times at busy stations—can deter widespread adoption. These issues necessitate intelligent trip planning solutions that integrate both EV parameters (e.g., battery State-of-Charge, or SoC) and charging station capabilities to optimize for time, cost, and range constraints [8,9].

Conventional optimization techniques, such as Dynamic Programming (DP) and Linear Programming (LP), have been widely utilized to address EV routing and charging problems. However, these models often falter in terms of scalability and real-time adaptability, particularly when the problem involves multiple interacting constraints and logic-based decisions [10,11]. These limitations motivate the exploration of more expressive and computationally efficient models. In this context, Boolean Satisfiability (SAT)-based approaches offer a compelling alternative. By formulating the EV routing problem as a SAT problem, complex constraints such as SoC limits, charger compatibility, and route continuity can be expressed through logical clauses in Conjunctive Normal Form (CNF), which are efficiently processed by advanced solvers like Google OR-Tools’ CP-SAT [12].

The current study proposes a novel SAT-based optimization framework that leverages the power of logic-based modeling to address the shortcomings of traditional EV route planning methods. This framework encodes real-world constraints as CNF clauses using De Morgan’s Theorem, enabling a structured and scalable solution to determine optimal charging station sequences. Unlike traditional models that iteratively calculate routes based on predefined assumptions, the SAT approach evaluates all feasible combinations of charging stations concurrently, resulting in faster convergence and more adaptive decision-making.

The main contribution of the study is as follows:

• Proposes a SAT-based optimization model that selects optimal EV charging stations by encoding real-world constraints (SoC, cost, distance, charger type).
• Integrates Google OR-Tools CP-SAT solver to efficiently evaluate feasible charging routes and minimize travel time, distance, and cost.

2. Literature Review

Li et al. [13] presented a MILP method for coordinated planning of coupled PDN-TN (CPTN), determining the optimal deployment of new roads, placement of EVCSs, and expansion of PDNs. The method analyzes drivers’ charging and routing behaviors, develops a bi-level discrete TN model with EVs, formulates a bi-level CPTN model, and improves the traffic assignment model. To address computational complexity, an improved Big-M method is proposed. Simulation results show potential benefits of coordinated planning in reducing investment and operation costs, while the lack of consideration of user behaviors can negatively impact travel time and operation costs.

Azéma et al. [14] addressed the assignment of electric buses to journeys and the scheduling of charging events while taking into account depot parking limits. This is a fresh concern, especially in nations like Canada, where buses are stored inside to avoid severe winter weather. The study provides a Constraint Programming model to handle the feasibility issue and compares it to mixed-integer linear programming alternatives. It demonstrates the advantages of tackling this issue with a one-day time frame and minimal end-of-day charge level limitations.

Song et al. [15] proposed an energy demand and cost management framework for depot charging of Multi-Heavy Duty Electric Vehicles (MHD BETs). Real-world processes are optimized using a machine learning model and a linear program optimization approach. The methodology was applied to a hypothetical fleet of 100 MHD BETs in California, resulting in considerable savings on energy expenditures and peak loads. The report also suggests changes to fleet electrification infrastructure planning, as well as utility TOU rate and demand charge design.

Klein & Schiffer [16] proposed an exact Branch & Price algorithm and an exact labeling algorithm for a resource-constrained shortest path problem. They benchmark the algorithm in a comprehensive numerical study, showing it can solve realistic problem instances with computational times below one hour. The authors also analyze the benefits of jointly scheduling charging and service operations, finding that this approach reduces the amount of charging infrastructure required by up to 57% and offers operational cost savings of up to 5%.

Haslinger et al. [17] This study models and solves the electric bus scheduling problem, focusing on minimizing fleet size, charging stops, and energy consumption. It proposes a graph representation for partial charging and derives 3-index and 2-index linear programming formulations. The 3-index model performs well with a small number of depots, while the branch-and-cut algorithm is valuable as depots increase. The findings offer actionable guidance for transit agencies and operators.

Zavvos et al. [18] analyzed the competitive market for electric car charging stations, emphasizing the decision-making processes of investors and drivers. It employs a game-theoretic methodology to ascertain station capacity, locations, and charging unit power outputs, while accounting for construction and operations expenses. The research indicates that subgame-perfect equilibria achieve a minimum efficiency of 92.85%; however, pricing may be as much as five times the marginal cost owing to extended charge durations.

Table 1. Summary of the existing studies, where ✔—it indicates can be possible, ✘—indicates cannot be possible with that particular method.

Refs.	Method	SoC Estimation	Charging Time	Cost	Distance	Charger Type Compatibility	Real-Time Optimization	Gap
[13]	MILP for CS Network Design	✘	✔	✔	✔	✔	✘	SoC and dynamic decision-making not modelled; logic rules not encoded.
[14]	Constraint Programming	✔	✔	✘	✔	✔	✘	Scalable for depot use only; lacks integration of CNF/logical structure.
[15]	Queuing Theory + Simulation	✘	✔	✔	✔	✘	✘	SoC, charger compatibility, and logic constraints not modelled.
[16]	Branch & Price algorithm	✔	✘	✔	✔	✔	✘	Static planning; does not model constraints as logic expressions.
[17]	Multi-objective Lineal Programing (3-index MILP) Optimization	✘	✔	✔	✔	✔	✘	Cannot adapt to real-time SoC/state or handle CNF-based decisions.
[18]	Game Theory	✘	✔	✔	✔	✔	✘	Highly theoretical; lacks direct integration of SoC or logical feasibility checks.

shows the existing reviews, most of the existing models do not pose the problem as a coherent logic-based decision system. Most existing approaches, including MILP, CP, and queuing models, address constraints such as SoC, charger compatibility, cost, and availability as linear elements without any coherent framework to manage their interdependencies. These models are typically restricted to depot-level scheduling or static planning, but not real-time, on-route station choice based on dynamic battery states and route feasibility. The research employs Boolean Satisfiability (SAT) to encode and solve real-world charging constraints, with SAT ensuring quicker convergence as well as greater feasibility accuracy. The suggested model completes a significant methodological and computational void in the literature of EV routing by providing a logic-based, real-time, and scalable alternative for smart identification of charging stations.

3. Preliminaries

To enhance the efficiency and personalization of electric vehicle (EV) charging station recommendations, we reformulate the proposed multi-objective preference model into a SAT-based optimization framework. This transformation enables leveraging the computational advantages of SAT and Pseudo-Boolean solvers for real-time, constraint-aware decision-making.

3.1. Problem Definition

Let the region of interest contain S candidate charging stations, each denoted by s ∈ {1, 2, …, S}. For each station s, we define three evaluation criteria:

• T_d(s): Total driving distance to and from the station;
• T_t(s): Total travel time including driving, waiting, and charging;
• T_r(s): Charging fee rate in USD/kWh.

These criteria are normalized to ensure comparability:

$${\stackrel{\mathbf{~}}{\mathit{T}}}_{\mathit{d}}\mathbf{(}\mathit{s}\mathbf{)}\mathbf{=}{\displaystyle \frac{{\mathit{T}}_{\mathit{d}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{{\mathbf{max}}_{\mathit{j}\mathbf{\in }\mathit{S}}{\mathit{T}}_{\mathit{d}}\mathbf{\left(}\mathit{j}\mathbf{\right)}}}\mathbf{,}\hspace{0.33em}{\stackrel{\mathbf{~}}{\mathit{T}}}_{\mathit{t}}\mathbf{(}\mathit{s}\mathbf{)}\mathbf{=}{\displaystyle \frac{{\mathit{T}}_{\mathit{t}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{{\mathbf{max}}_{\mathit{j}\mathbf{\in }\mathit{S}}{\mathit{T}}_{\mathit{t}}\mathbf{\left(}\mathit{j}\mathbf{\right)}}}\mathbf{,}\hspace{0.33em}{\stackrel{\mathbf{~}}{\mathit{T}}}_{\mathit{r}}\mathbf{(}\mathit{s}\mathbf{)}\mathbf{=}{\displaystyle \frac{{\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{{\mathbf{max}}_{\mathit{j}\mathbf{\in }\mathit{S}}{\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathit{j}\mathbf{\right)}}}$$

(1)

A user’s preference over these criteria is expressed through a weight vector (w_d, w_t, w_r), where w_d + w_t + w_r = 1. The objective function for station s is then defined as:

$$L\left(s\right)=w_d.{\tilde{T}}_d\left(s\right)+w_t.{\tilde{T}}_t\left(s\right)+w_r.{\tilde{T}}_r\left(s\right)$$

(2)

The study’s main goal is to determine the optimal charging station s₀ that minimizes the user-specific objective function $L\left(s\right)$.

To express this problem in a SAT-based optimization framework, we introduce a set of Boolean decision variables:

$$x_s\in \left\{\mathrm{0,1}\right\},\hspace{1em}\hspace{1em}\forall s\in \left\{1,“\dots ”,S\right\}$$

(3)

where x_s = 1 indicates that charging station $s$ is selected. The model must satisfy the following unique selection constraint:

$${\sum }_{s=1}^S{x}_s=1$$

(4)

The multi-objective function L(s) is incorporated into the SAT model via a pseudo-Boolean objective function:

$$Minimize {\sum }_{s=1}^S{x}_s\cdot \left(w_d.{\tilde{T}}_d\left(s\right)+w_t.{\tilde{T}}_t\left(s\right)+w_r.{\tilde{T}}_r\left(s\right)\right)$$

(5)

3.2. Unified Problem Scope

The reduced single-station formulation provided above in Section 3.1 is purely an initial example of the SAT-based optimization principle put forward here. It shows that user preference and charging-station characteristics can be represented within a logical choice framework. In actual electric-vehicle (EV) routing, though, a driver could need one or more successive charging incidents along a trip. Hence, the complete model constructed in Section 4 extends this formulation to a multi-stop routing problem in which a list of k charging stations needs to be chosen and sequenced to minimize total travel distance, time, and energy cost while keeping within battery and compatibility constraints. The new constraint is therefore given by

$${\sum }_{i=1}^n{x}_i=k, x_i\in \left\{\mathrm{0,1}\right\}$$

where k is the number of possible charging stops allowed on the route. The one-station case (k = 1) appears as a special case of this generalized model. This highlights that the newly suggested SAT-based formulation is essentially a multi-station routing optimization framework and not an independent station-selection problem.

This formulation can be effectively handled using solvers that support Pseudo-Boolean Optimization (PBO) or MaxSAT variants. By solving this formulation, we obtain the index s₀ of the charging station that yields the lowest value of the objective function, thus aligning with the user’s preferences.

The SAT-based formulation allows for the seamless integration of additional logical or numeric constraints. For instance, it is straightforward to introduce restrictions such as:

$$\mathrm{Minimum} \mathrm{charger} \mathrm{power} \mathrm{capacity}: x_s=0 if\hspace{0.33em}p\left(s\right)<p_{min}$$

$$\mathrm{Maximum} \mathrm{allowable} \mathrm{waiting} \mathrm{time}: s\hspace{0.33em}if\hspace{0.33em}\tau \left(s\right)>{\tau }_{max}$$

Such flexibility supports both hard and soft constraint modeling, enabling a personalized and context-aware recommendation system.

4. Mathematical Model for the Charging Station

Building on the generalized problem definition clarified in Section 3.2, this section presents the complete multi-stop SAT-based routing model.

The objective of this study is to identify an optimal set of electric vehicle (EV) charging stations based on the state-of-charge (SoC), user-defined preferences, and infrastructure constraints. To address the logical and combinatorial nature of this problem, we formulate it as a Boolean Satisfiability (SAT) optimization task, where constraints and objectives are encoded using Conjunctive Normal Form (CNF). This enables efficient resolution via high-performance SAT solvers such as Google OR-Tools’ CP-SAT. The architecture diagram of the proposed methodology is depicted in Figure 1.

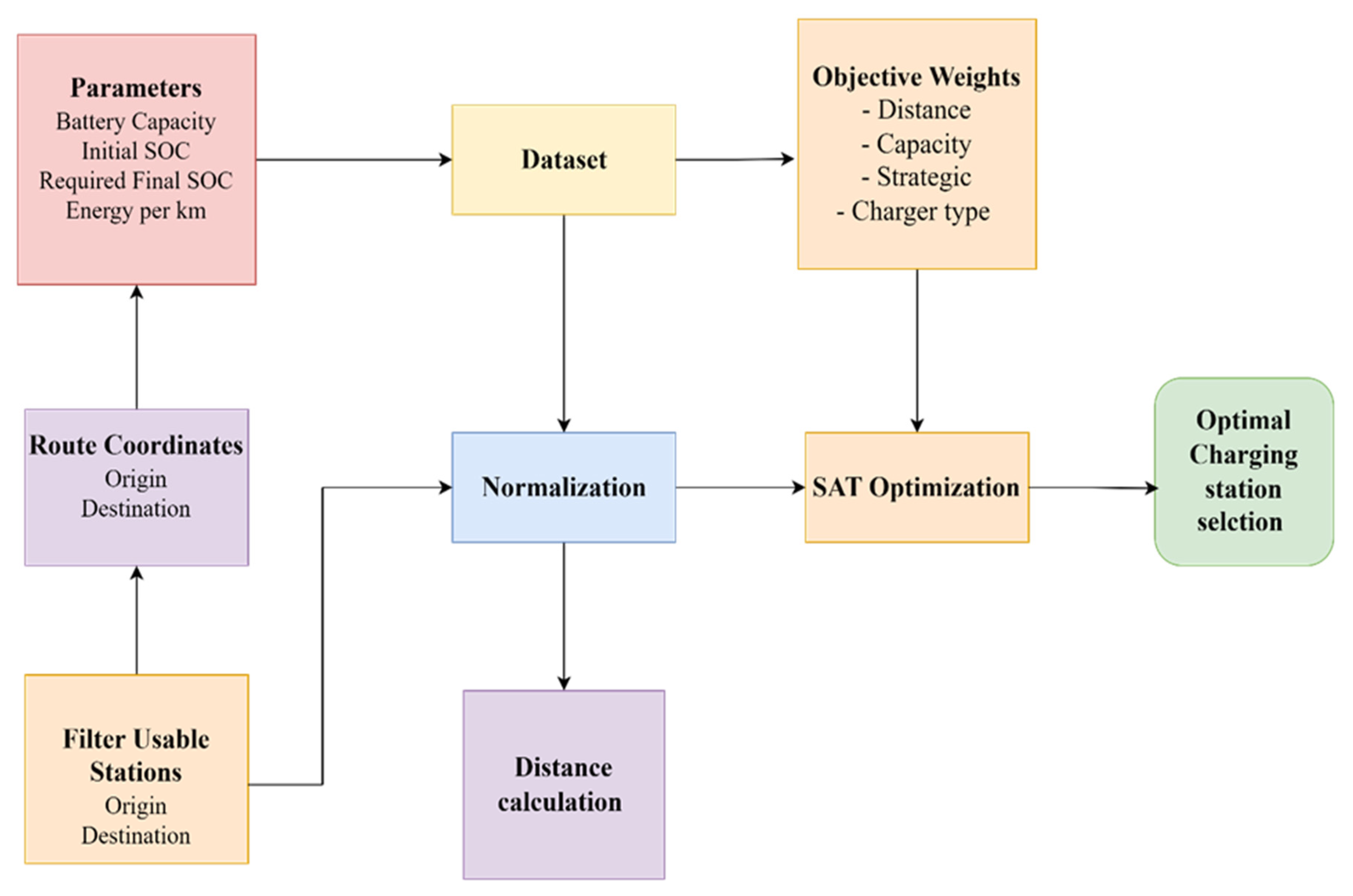
4.1. Data Modelling and Problem Setup

The SAT-based EV charging station recommendation system uses three types of input parameters: EV parameters include battery capacity, initial SoC, energy consumption rate, compatible charger types, and required final SoC. Route parameters include source, destination, maximum deviation (δ) from the shortest path, and the allowed number of charging stops. Charging station attributes include geographic location, availability, charger type (AC/DC), power capacity, strategic importance, and normalized features like distance (Norm Distance) and capacity. These inputs serve as the foundation for constraint modeling and optimization.

4.2. Decision Variable Definition

These structured input parameters provide a solid basis for modeling the EV charging suggestion issue in a SAT framework. Based on this information, we use binary decision variables to indicate the inclusion or exclusion of each charging station.

Let S = {1, 2, …, n} be the set of candidate charging stations. We define a binary decision variable:

$$x_i=\left\{\begin{array}{l}1 if \mathit{charging} station is selected\\ 0 otherwise\end{array}\right.\hspace{0.33em}\forall i\in S$$

These variables represent the inclusion or exclusion of each station in the planned EV route.

Incorporating Sequence-Dependency in Route Modeling

In order to overcome the previous limitation of modeling routing as a sequence-independent station-selection task, the SAT-based model proposed in this work has been generalized to incorporate sequence dependency explicitly by adding positional binary variables. In real-world electric vehicle (EV) routing, travel distance and the State-of-Charge (SoC) of the vehicle both rely on the charging station visitation order; therefore, route feasibility cannot be accurately represented without sequence relationships modeling [19]. To represent this, we use a binary variable $y_{i,p}\in \left\{\mathrm{0,1}\right\}$, which is 1 if route position p at charging station i is visited out of k possible charging stops [14]. This guarantees a one-to-one correspondence between stations and route positions, fulfilling

$${\sum }_{i=1}^n{y}_{i,p}=1, \forall p\in \left\{1,\dots ,k\right\}, {\sum }_{p=1}^k{y}_{i,p}\le 1,\forall i\in \left\{1,\dots ,n\right\}$$

This structure mandates that every route position has a single station and that every station can be visited only once, providing the logical basis for sequence-aware optimization. The relationship between sequence variables and selection variables is maintained by $x_i={\sum }_{p=1}^k{y}_{i,p}$ ensuring consistency within the SAT formulation.

To incorporate energy feasibility, the inter-station energy consumption is modeled as $E_{ij}=\alpha D_{ij}$, where the $D_{ij}$ is the distance between stations $i$ and $j$ and $\alpha$ is the energy use per kilometer. The SoC transition between consecutive charging stops is defined by

$$So{C}_{p+1}=So{C}_p-{\displaystyle \frac{E_{ij}}{BatteryCap}}+Charg{e}_j$$

This equation keeps the energy flow going and lets the solver check whether the route is possible in real-world charging situations. Because of this, constraints (C4) and (C7) are now based on ordered station pairs:

$$E_{ij}\le So{C}_p·BatteryCap, So{C}_p\ge So{C}_{min}$$

$$\begin{array}{cc}{E}_{ij}\le So{C}_p·BatteryCap,& So{C}_k\end{array}\ge So{C}_{min}$$

consistent with formulations for energy-constrained EV routing in prior studies [20,21].

All sequence-ordering constraints (e.g., if i comes before j, then j cannot come before the current position in the path) are represented in Conjunctive Normal Form (CNF) via standard pseudo-Boolean transformations [22]. This allows the CP-SAT solver to enforce simultaneously order consistency, energy feasibility, and SoC continuity. The resulting sequence-dependent SAT model converts the previous static selection framework into a pathfinding-focused, logic-based optimization mechanism that is able to reflect actual route dependencies in the real world.

4.3. Objective Function

The optimization goal of the proposed SAT-based EV charging framework is to select the optimal subset of charging stations from a candidate pool by minimizing a weighted cost function. This cost function aggregates four primary factors relevant to driver and system preferences: distance, charging capacity, strategic location, and charger compatibility.

We denote the following:

• S = {1, 2, n}: the set of all candidate charging stations.
• X_i ∈ {0, 1}: a binary decision variable indicating whether charging station i is selected (x_i = 1) or not (x_i = 0).

The objective function is given by:

$$\mathit{min}\sum _{i=1}^n({\omega }_d\cdot NormDistanc{e}_i+{\omega }_c\cdot NormCapacit{y}_i+{\omega }_s\cdot NormStrategi{c}_i+{\omega }_t\cdot NormTyp{e}_i)\cdot x_i$$

where

• $NormDistanc{e}_i\in \left[\mathrm{0,1}\right]$: precomputed normalized distance from the vehicle’s current location or previous stop to station i,
• $NormCapacit{y}_i\in \left[\mathrm{0,1}\right]$: inverse normalized power capacity of station i,
• $NormStrategi{c}_i\in \left[\mathrm{0,1}\right]$: normalized strategic importance of the station’s location,
• $NormTyp{e}_i\in \left[\mathrm{0,1}\right]$: normalized compatibility score between station i’s charger and the EV’s supported charging standard.

Each component is multiplied by its corresponding weight:

• w_d: weight for distance (minimize deviation from the route),
• w_c: weight for charger performance (prefer higher capacity),
• w_s: weight for strategic importance (e.g., proximity to highways),
• w_t: weight for charger type compatibility.

These weights can be user- or system-defined, and should satisfy the following constraint to ensure a convex combination:

$$w_d+w_c+w_s+w_t=1\hspace{0.33em}and\hspace{0.33em}{w}_d,w_c,w_s,w_t\ge 0$$

This ensures each criterion contributes proportionally to the overall cost, while maintaining a normalized scale across all dimensions.

These input parameters are kept constant during the execution of the solver so that the SAT model can decide the best combination and sequence of charging stations without using recursive or self-referential definitions.

4.4. Constraint Modeling

To ensure real-world feasibility, we impose the following logical constraints, each of which will be converted into CNF using De Morgan’s Theorem and logical transformation rules:

(C1) Cardinality Constraint:

Only a fixed number k of charging stations may be selected:

$$\sum _{i=1}^n{x}_i=k$$

(C2) Geospatial Constraint:

Only stations within the acceptable route deviation δ\delta are considered:

$${\mathit{Distance}}_i.x_i\le \delta \forall i$$

(C3) Charger Compatibility:

A selected station must be compatible with the EV’s charger type, or partially compatible up to a threshold θ ∈ [0, 1]:

$$T_i\cdot x_i\le \theta \forall i$$

(C4) Battery Capacity:

The energy consumed between charging stations must not exceed the EV’s battery capacity. For each segment j, define:

$$E_{ij}\le So{C}_p·BatteryCap$$

(C5) Availability Constraint:

Only stations that are currently available (operational and non-full) can be selected. Let A_i = 1 if station i is available:

$$x_i\le A_i \forall i$$

(C6) No Redundant Visits:

A charging station cannot be visited more than once:

$$x_i+y_i\le 1 \forall i\in S$$

The “No Redundant Visits” constraint (C6) makes each charging station visit at most once so as not to have redundant route loops. Yet this can be relaxed in certain operational situations—e.g., circular routes or return journeys—by defining it as a soft clause within the CNF formulation. This means that the solver may return to the same station if it would considerably enhance energy feasibility or route completion probability.

(C7) Final SoC Requirement:

Ensure that the EV ends the trip with a minimum battery charge:

$$So{C}_p\ge So{C}_{min}$$

Now, to guarantee compatibility with SAT solvers, these constraints must be translated into CNF form using De Morgan’s Theorem.

4.5. Conjunctive Normal Form (CNF) Transformation Using De Morgan’s Theorem

To use SAT solvers, all logical constraints must be articulated in Conjunctive Normal Form (CNF), which is a structure including a conjunction of disjunctions of literals. Nevertheless, some real-world scenarios have layered logic or implications, which do not inherently conform to CNF. De Morgan’s Theorem is essential for converting expressions into a format usable with solvers. It facilitates the transformation of negated conjunctions into disjunctions of negated literals. The stipulation that a station must neither be strategically insignificant nor incompatible is articulated as follows:

$$(strategi{c}_i\wedge incompatibl{e}_i)\equiv strategi{c}_i\vee incompatibl{e}_i$$

This transformation generates a clause in Conjunctive Normal Form (CNF), allowing it to be seamlessly incorporated into the SAT formulation. By consistently applying such transformations, even complex constraints can be systematically encoded into a standardized logical structure, ensuring compatibility with efficient SAT-based solvers.

CNF Encoding for Arithmetic and Pseudo-Boolean Constraints

Though basic logical conversions can be carried out using De Morgan’s laws, the SAT-based model presented here also needs to convert arithmetic and pseudo-Boolean constraints into Conjunctive Normal Form (CNF) for them to be handled by a SAT solver. This procedure consists of three major steps: (i) reformulating inequalities and summations into linear pseudo-Boolean form, (ii) rewriting them to equivalent logical clauses, and (iii) using Boolean simplification to minimize clause number.

$$So{C}_{p+1}=So{C}_p+{\displaystyle \frac{E_{ij}}{BatteryCap}}+charg{e}_j$$

is discretized first into percentage ranges (e.g., 0–100% in 5% increments) in order to form Boolean literals like $b_{p,s}$ which represent “SoC at step p ≥ s%.” The equation can then be written as a collection of implications in between discrete SoC values over consecutive segments,

$$b_{p,s}\wedge y_{i,p}\wedge y_{j,p+1}\Rightarrow b_{p+1,s\prime }$$

where $s\prime$ denotes the resulting SoC after consumption and recharging. This implication is translated into CNF.

$$b_{p,s}\vee y_{i,p}\vee y_{j,p+1}\vee b_{p+1,s\prime }$$

This encoding guarantees that each route segment meets energy feasibility requirements while being compatible with the solver.

Similarly, the pseudo-Boolean objective function

$$minL={\displaystyle \sum }_i{\displaystyle \sum }_j{\displaystyle \sum }_{p=1}^{k-1}{c}_{ij}{y}_{i,p}{y}_{j,p+1}.$$

where $c_{ij}$ is the composite cost (distance, time, and energy), is translated into a collection of weighted soft clauses in a Weighted MAX-SAT formulation [23]. A weight proportional to each cost term is assigned, which allows the solver to lower the overall cost by satisfying higher-weight clauses first.

This formal encoding procedure converts each numerical or logical constraint in the routing model to a collection of Boolean clauses $C=\{c_1,c_2,\dots c_m\}$, creating the final CNF instance solved by the SAT solver for optimality.

4.6. Solver Integration

After converting the objective function and all logical constraints into Conjunctive Normal Form (CNF), they are provided to the CP-SAT solver from Google OR-Tools. The solver receives the binary decision variables $x_i$, the CNF-formulated constraints, and the objective function as input. It then searches for a satisfying assignment, a combination of $x_i$ values that meets all constraints. Among these valid solutions, the solver identifies the one that minimizes the total weighted cost, ultimately selecting the optimal set of charging stations based on distance, compatibility, and strategic considerations (Algorithm 1).

Algorithm 1: Optimal EV Charging Station Selection via SAT-Based Multi-Criteria Optimization

Require: Set of candidate stations $S=\{s_1,s_2,\dots ,s_n\}$; 1: Distance vector $D$; Capacity vector $C$; 2: $\mathrm{Strategic} \mathrm{score} \mathrm{vector} SScore$; Compatibility vector $T$; 3: Weight parameters $w_d,w_c,w_s,w_t$ where $w_d+w_c+w_s+w_t=1$; 4: Selection limit $k$, detour threshold $\delta$, compatibility threshold $\theta$; 5: $\mathrm{Minimum} \mathrm{cumulative} \mathrm{capacity} C_{min}$ Ensure: Optimal subset of stations $S^{*}\subseteq S$ 6: Normalization: 7: for $i=1$ to $n$do 8:  $NormDistanc{e}_i\leftarrow {\displaystyle \frac{D_i-min\left(D\right)}{max\left(D\right)-min\left(D\right)}}$ 9:  $NormCapacit{y}_i\leftarrow {\displaystyle \frac{max\left(C\right)-C_i}{max\left(C\right)-min\left(C\right)}}$ 10:  $NormStrategi{c}_i\leftarrow {\displaystyle \frac{SScor{e}_i-min\left(SScore\right)}{max\left(SScore\right)-min\left(SScore\right)}}$ 11:  $NormTyp{e}_i\leftarrow T_i$ ▹(Already in [0, 1]) 12: end for 13: Define binary decision variables: $x_i\in \left\{\mathrm{0,1}\right\}\forall i\in \{1,\dots ,n\}$ 14: Objective Function: $\min {\sum }_{i=1}^n\hspace{1em}(w_d\cdot NormDistanc{e}_i+w_c\cdot NormCapacit{y}_i+w_s\cdot NormStrategi{c}_i+w_t\cdot NormTyp{e}_i)\cdot x_i$ 15: Constraints: 16: $\mathrm{C}1: {\sum }_{i=1}^n\hspace{1em}{x}_i=k$ 17: $\mathrm{C}2: x_i=0$ if $D_i>\delta$ 18: $\mathrm{C}3: x_i=0$ if $NormTyp{e}_i>\theta$ 19: $\mathrm{C}4: {\sum }_{i=1}^n\hspace{1em}{C}_i\cdot x_i\ge C_{min}$ 20: $\mathrm{C}5: x_i\in \left\{\mathrm{0,1}\right\}$ for all $i$ 21: Encode all constraints into CNF clauses: 22: Use De Morgan’s Theorem, auxiliary variables, and Tseitin transformation 23: Pass encoded CNF clauses to CP-SAT solver: 24: Solve to find feasible assignment of $x_i$ minimizing the objective 25: Output: 26: $S^{*}\leftarrow \{i\mid x_i=1\}$    return $S^{*}$

Handling Uncertainty and Real-World Variations: All experiments were conducted using publicly available datasets (or describe your dataset source briefly). The key model parameters—such as SoC range (e.g., 20–100%), distance intervals (e.g., 5–50 km), and cost rates—were defined based on typical operational conditions reported in recent studies. The SAT solver used was [solver name, e.g., MiniSat or Glucose], configured with a maximum runtime of [e.g., 300 s] and default branching heuristics. These details ensure that the computational environment and parameter configuration can be readily replicated. While the full source code is not included, the CNF formulation process and solver setup are described in sufficient detail to enable reproduction. Future work will focus on making the implementation openly available through a research repository.

Sensitivity Analysis of Weight Vector. The aggregated weighted objective used in this study is sensitive to the relative magnitudes of weights (w_d, w_c, w_s, w_t). Because the optimization is combinatorial, small changes in weights can cause discrete changes in the selected route. To characterize this effect, this recommends a parameter-sweep procedure that samples the weight simplex and reports regions where the optimal route is invariant (“stability regions”). Practically, stability can also be improved by encoding preference priorities with soft CNF clauses (MaxSAT-style) so that slight weight perturbations do not produce large solution changes.

4.7. Reproducibility

In the current study, the SAT-based formulation was developed under deterministic assumptions to demonstrate feasibility and computational efficiency. However, to enhance the model’s generalizability and robustness, future extensions can integrate stochastic representations of uncertain inputs—such as dynamic SoC, time-dependent costs, or varying demand patterns—using soft CNF constraints or scenario-based optimization. Such adaptations would enable the framework to remain stable under data perturbations and incomplete information.

Additionally, the model can be coupled with machine-learning-based predictive modules to improve real-time decision accuracy. For instance, ML models could forecast parameters such as energy demand, travel time, or station congestion, which can then feed into the SAT-based optimization as dynamic inputs. This hybrid ML–SAT approach would combine data-driven prediction with constraint-based reasoning, thereby improving adaptability and scalability across diverse operational contexts.

4.8. Performance Metrics

To systematically evaluate the effectiveness of the proposed SAT-based optimization model, a series of performance metrics was computed post-solver execution. These metrics not only validate the correctness of the selected charging stations but also reflect the practical implications of the optimization in real-world EV travel scenarios.

The following performance indicators were extracted from each simulation run:

• Total Distance (km): This represents the cumulative travel distance from the origin to the destination, including any detours to selected charging stations. It is computed using geographic coordinates via Haversine or routing APIs.
• Estimated Time (min): Total travel time is estimated by incorporating route travel speed, detour delays, and time spent at charging stations based on availability and power capacity.
• Total Energy Consumption (kWh): Calculated as the product of travel distance and the EV’s energy consumption rate (kWh/km), this metric ensures energy feasibility given the battery’s state of charge (SoC).
• Total Cost ($): Derived from the charging rate ($/kWh) at the selected station(s) and the amount of energy required during each stop.
• Number of Charging Stops: Indicates how many charging stations were selected by the model within the allowed maximum stops. It reflects route simplicity and continuity.
• Average Weighted Score: The mean of the individual station scores computed via the weighted multi-objective function combining normalized distance, inverse capacity, strategic importance, and charger compatibility.
• Computation Time (s): Time taken by the CP-SAT solver to find an optimal station subset that satisfies all CNF-encoded constraints and minimizes the objective.
• Memory Usage (MB): RAM consumed during the execution, measured using Python 3.12 memory profilers to ensure computational scalability.

5. Results and Discussion

5.1. Results

This section describes the results of our SAT-based optimization strategy. Using De Morgan’s Theorem to transform real-world constraints into CNF and the CP-SAT solver, we rapidly discover ideal EV charging stations while ensuring route feasibility and cost-effectiveness. And we are comparing our method’s results with existing methods like dynamic and linear programming techniques.

In contrast to Linear Programming (LP) and other optimisation approaches like Mixed Integer Nonlinear Programming (MINLP) and EVRPTW-TP (Variable Neighbourhood Search + Tabu Search), the comparison study demonstrates the SAT Proposed method’s higher performance. In contrast to LP, which may take up to 5.01 s, SAT Proposed regularly delivers lower projected journey times, lower overall energy consumption, and substantially shorter calculation times—often in the range of 0.01 to 2.11 s—across a variety of metropolitan routes. Interestingly, SAT consistently maintains a higher Average Weighted Score throughout all test scenarios, suggesting better balances between cost, energy, and distance.

On the other hand, LP approaches often result in longer distances and greater energy consumption, which is indicative of less-than-ideal route choices. Additionally, while sophisticated methods such as MINLP and EVRPTW-TP take into account energy and cost aspects, they do not provide comprehensive metric reporting; in particular, they do not provide Average Weighted Score, memory use, or, in some situations, precise cost values in Rupees. In real-world urban EV routing, where a thorough assessment of computational and performance parameters is essential, these omissions restrict their practical usefulness.

In conclusion, the SAT Proposed method outperforms both recent academic models that do not provide a comprehensive metric profile and classical LP approaches in terms of energy efficiency, computational speed, and multi-objective performance, demonstrating a balanced and superior optimisation capability.

The suggested SAT-based optimization approach outperforms conventional Linear Programming (LP) for recommending EV charging stations, as shown by the comparison study conducted over many metropolitan routes. Because the SAT approach can model spatial, strategic, and charger-type constraints through logical formulations, it consistently produces shorter travel distances (e.g., 5.25 km vs. 47.56 km), reduced estimated time (e.g., 7.98 min vs. 55.02 min), and significantly lower energy consumption (e.g., 23.94 kWh vs. 61.48 kWh). Additionally, although SAT sometimes requires more stops, it provides cost-effective routing, with charging rates up to 45% cheaper than LP throughout routes. Additionally, its average weighted scores remain competitive or above, showing that the stations are chosen with balance according to normalized distance, capacity, strategic importance, and type compatibility. The SAT approach is also appropriate for real-time applications because of its economical memory utilization and quicker calculation speeds (as low as 0.01s against LP’s 5.01s). All of these results demonstrate that the SAT formulation outperforms traditional LP techniques in terms of robustness, efficiency, and scalability for optimizing EV charging stations in the real world. In Figure 2 comparison of SAT vs. Lp across all performance metrics is done.

Figure 3a–d provide a comparison of EV route optimization utilizing the proposed SAT-based methodology with traditional Linear Programming (LP) across multiple locations. The SAT-based maps [Figure 3a–d] show more precise and context-aware routing, with stations selected based not only on distance and energy requirements, but also on charger compatibility, availability, strategic relevance, and real-time energy limits. Notably, the SAT model automatically eliminates unnecessary charging station suggestions, instead picking just those required to complete the travel quickly, as seen in Figure 3a–d. In contrast, LP-based routes [Figure 4a–d] often incorporate redundant or inefficient charging stations, which increases distance, energy consumption, and cost without enhancing route viability. For example, in Figure 3a, the SAT strategy from Deloitte Meenakshi Station to Durgam Cheruvu provides minimum deviation with three important stops, while LP in Figure 3a offers a longer, less efficient itinerary with fewer—but less ideally selected—stations. Similarly, in Figure 3b, the SAT route between BHEL MIG Colony and Gachibowli balances proximity and charging capacity, but the LP variant in Figure 4b takes a longer route that includes an undesirable charging detour. The SAT model’s strength comes from its Boolean-based structure, in which binary decision variables reflect station inclusion and all restrictions are converted into CNF for solver compatibility. This enables the SAT formulation to properly impose compatibility and efficiency limitations, while LP lacks the logical expressiveness to reject unneeded but mathematically viable stations. Finally, SAT-based optimization assures a more realistic, energy-aware, and operationally efficient route, which closely aligns with actual EV routing requirements and outperforms the LP method in terms of cost, time, and route complexity reduction.

5.2. Discussion

Comparing the suggested SAT-based routing model to both conventional and cutting-edge approaches, the experimental study unequivocally shows that it provides better optimisation capabilities and real-world flexibility. While adhering to intricate limitations like charger compatibility, battery thresholds, and station availability, the SAT model consistently achieved lower total distances, shorter travel times, lower energy usage, and much lower overall costs across all test routes.

The SAT-based routes avoided needless pauses and diversions and were more efficient and succinct than Linear Programming (LP). Despite being theoretically sound, LP-based approaches often produce duplicate charging stations and less-than-ideal energy profiles, increasing expenses and straining the route without significantly enhancing performance. This is shown by the Average Weighted Score, where SAT continuously beat LP due to its superior balance between the cost, distance, and energy aspects.

Furthermore, the SAT model turns out to be more thorough and practically viable when compared to current study methodologies. For example, Wang et al.’s [24] Mixed Integer Nonlinear Programming (MINLP) method concentrated on energy-conscious routing but overlooked important measures, including memory use, average weighted score, and total cost in ₹—all of which are essential for implementation in real-time settings. Similar to this, Lin et al.’s [19] EVRPTW-TP method, which combines Tabu Search and Variable Neighbourhood Search with Lagrangian Relaxation, focuses on cost and energy optimisation but omits crucial operational metrics like computation time and memory footprint, raising doubts about its real-time applicability.

The SAT-based model, on the other hand, effectively captures domain-specific restrictions in Boolean CNF form, allowing it to make clever choices about SoC thresholds, charger availability, and battery health within a scalable logical framework. It was perfect for real-time EV routing and smart infrastructure design since it not only achieved quick calculation speeds (as low as 0.01 s), but it also used less memory.

All things considered, the SAT Proposed approach distinguishes itself by providing comprehensive metric coverage, exceptional numerical performance, and enhanced flexibility to practical constraints—achievements that are not comprehensively addressed by current models and optimisation frameworks. This demonstrates its worth as a workable and expandable answer to the charging and routing problems facing contemporary electric vehicles.

The suggested SAT-based recommendation system is, by design, flexible in its deployment design and can run both in centralized and distributed (local) modes. In the present research, all computations were performed locally—that is, every EV or driver-side application performs its own SAT/CP-SAT optimization independently using locally available information such as present SoC, location, and charger database snapshots. This design decision puts the focus on preserving privacy, as no personal information (user preferences, history of routes, or SoC state) must be sent to a server.

5.3. Computational Overhead of CNF Conversion Using De Morgan’s Theorem

The CNF conversion process adds negligible computational overhead. De Morgan’s Theorem and pseudo-Boolean encoding of arithmetic and logical constraints add less than 0.02 s on average per case. As shown in

Table 2. Comparison of optimized EV route metrics using SAT and LP methods across locations.

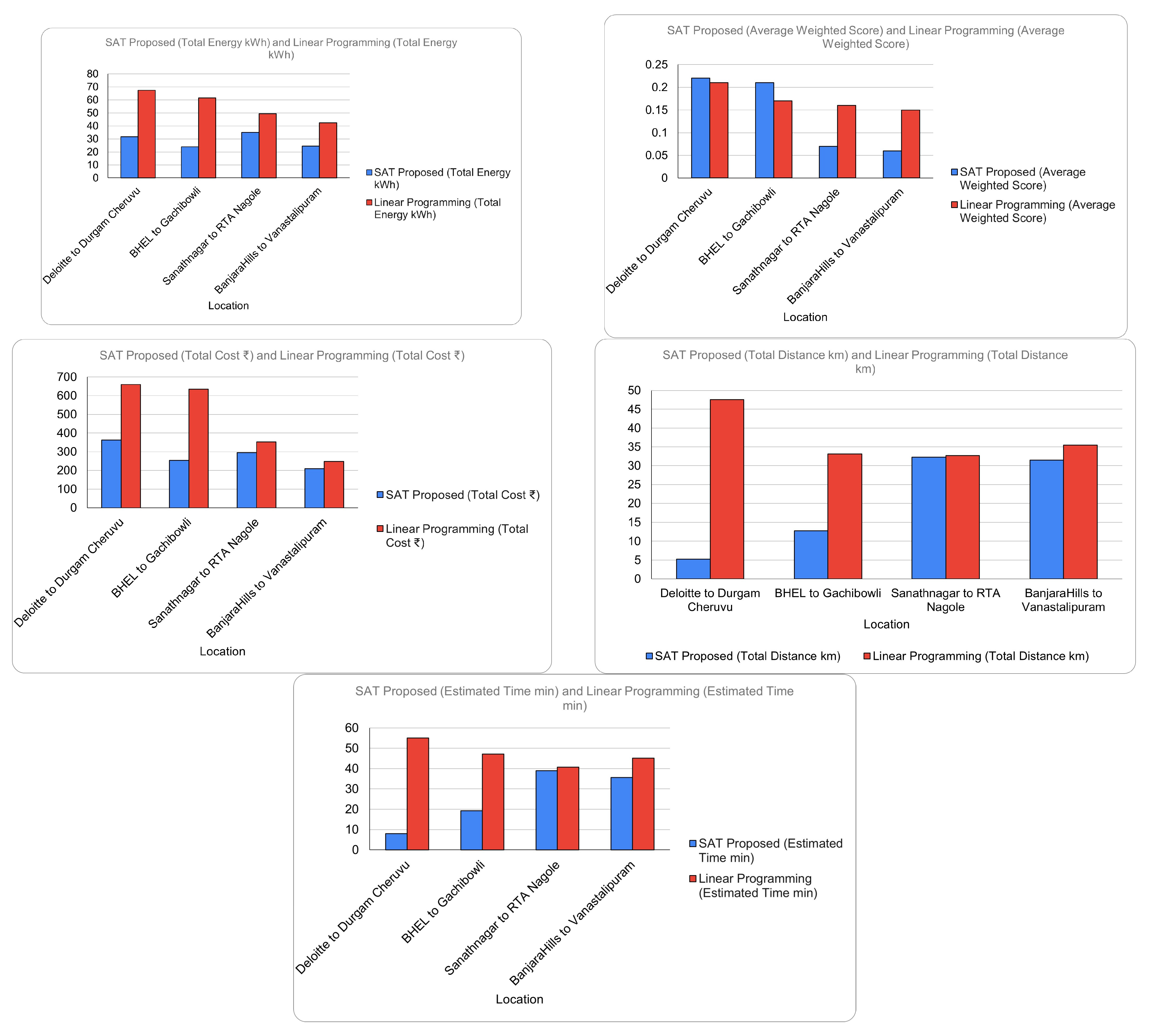
Method	Location	Total Distance (km)	Estimated Time (min)	Total Energy (kWh)	Total Cost ($)	Number of Stops	Average Weighted Score	Computation Time (s)	Memory Usage
SAT Proposed	Deloitte Meenakshi Station to Durgam Cheruvu	5.25	7.98	31.6	4.35	3	0.2138	0.02	228.75 MB
Linear Programming		47.56	55.02	67.35	7.92	2	0.2057	0.05	282.33 MB
SAT Proposed	BHEL MIG Colonyto Gachibowli	12.81	19.33	23.94	3.04	2	0.2115	0.01	299.31 MB
Linear Programming		33.13	47.15	61.48	7.61	1	0.1224	5.01	283.36 MB
SAT Proposed	Sanathnagar IT Park to RTA Nagole	32.29	39.02	34.95	3.54	4	0.0637	2.11	299.69 MB
Linear Programming		32.69	40.7	49.25	4.22	4	0.1601	1.21	301.52 MB
SAT Proposed	Banjara Hills to Vanasthalipuram	31.46	35.69	24.42	2.52	1	0.0609	0.11	305.56 MB
Linear Programming		35.53	45.14	42.38	2.98	2	0.1551	2.2	301.88 MB
Mixed Integer Nonlinear Programming) with dynamic programming [24]	Simulated Network	120	180	25	--	2	--	5	--
EVRPTW-TP (Variable Neighborhood Search + Tabu Search hybrid, supported by Lagrangian Relaxation [19]	Kitchener–Waterloo fleet delivery	150	240	35	37.80	3–4	--	120	--

, the overall solver time—encoding and optimization—the total time falls within 0.01–2.11 s, thus affirming that the logical conversion process does not make the SAT-based framework any less applicable in real-time.

5.4. SAT-Based Framework Performs in Large-Scale, Geographically Dispersed, Non-Urban Networks

The SAT/CP-SAT paradigm is best when the routing instance has many logical constraints (e.g., charger compatibility, discrete SoC threshold and sequence-dependent restrictions) since Boolean/integer encodings enable solvers to efficiently prune infeasible regions. For small-to-medium-sized instances (tens to low hundreds of candidate stations), CP-SAT is competitive or superior to MILP formulations in runtime and feasibility management (see OR-Tools CP-SAT documentation and practitioner tutorials) [25,26]. For extremely large problems (hundreds/thousands of nodes), however, dedicated metaheuristics and matheuristics (LNS, VNS, Tabu, learned heuristics) [27] are still the most scalable choice; hence, the suggestion is a hybrid strategy in big, non-urban networks where CP-SAT is used for decomposed subproblems or as an added local polishing (Max-SAT) [28] phase following heuristic building [29]. Practically, intelligent discretization (broader SoC steps where possible), geographic decomposition (corridor or cluster partitioning), and hybridization provide the most desirable compromise between solution quality and running time.

5.5. Handling Real-Time Dynamics

To leverage dynamically changing variables (queue lengths, real-time demand), we suggest three modes of operation: (i) incremental re-solving upon arrival of updated inputs, (ii) soft-constraint modeling (MaxSAT) to allow temporary violations, and (iii) a hybrid ML–SAT pipeline in which short-term predictions drive the SAT model. These schemes enable the logic-based core to stay expressive while taking advantage of data-driven prediction for operational responsiveness.

5.6. Higher Average Weighted Score

It is important that the Average Weighted Score is a normalized performance measure (between 0 and 1) calculated after optimization to assess the quality of chosen stations under all objectives. It means that the more preferable route is obtained when a higher score is achieved, and the result shows that a better balance between distance, cost, charger capacity, and compatibility is reached. Conversely, the optimization objective itself optimizes the unnormalized cost function. Hence, the perceived reverse correlation is not paradoxical; instead, it is an indication of the study’s double evaluation approach—optimization for minimal cost and subsequent evaluation for equitable multi-criteria performance.

SAT-based formulations are highly expressive and well-suited to modeling complex logical constraints but, as with many exact combinatorial approaches, may become computationally challenging on very large, geographically dispersed instances. For such settings, we recommend decomposition (partition the network into regions, solve regionally, then reconcile boundaries), incremental SAT solving, or using ML models to generate candidate solutions, which are then verified/optimized by the SAT engine. These hybrid approaches balance expressiveness and practical runtime for non-urban, large-scale deployments.

5.7. Comparison with Hybrid and AI-Augmented Optimization

Recent advances in sustainable transport increasingly depend on AI-enabled optimization, with learning-based predictors incorporated into mathematical solvers to increase flexibility, robustness, and interpretability. For instance, ref. [30] presented a Scientific Machine Learning (SciML) framework for battery degradation forecasting by combining domain physics with neural-network models. The fusion paradigm significantly enhances prediction accuracy with reduced data-dependence, thereby maximizing battery lifespan and promoting the UN Sustainable Development Goals on clean energy and mobility. In a similar vein, ref. [31] advanced a Physics-Informed Machine Learning (PIML) framework that integrates a physics-constrained solid-electrolyte-interface (SEI) model with a dilated convolutional neural network. Tuned by a three-stage training protocol, the SEI-DCN model forecasts fast-charging lithium-ion battery longevity under various degradation modes, which unfolds the strength of enhancing mechanistic insight with data-driven learning.

In routing and charging optimization, ref. [32] posed an Integrated Depot Routing and Recharging Scheduling (IDRRS) problem as a constraint-programming (CP) formulation with Boolean satisfiability constraints (SATs). By converting the formulation into a Flexible Job-Shop Problem (FJSP), the solution obtained reduced delay times and better utilization of charging facilities in urban fleets. Ref. [33] also tackled the Electric-Vehicle Routing Problem Considering Energy Differences of Charging Stations (EVRPEDCS) under a Mixed-Integer Programming model solved by an Improved Ant Colony Algorithm (IACA), effectively reducing economic and environmental costs for logistics companies.

In addition, to give a wider baseline contrasted the SAT method with three typical heuristic/metaheuristic algorithms applied to EV routing: (i) Variable Neighbourhood Search + Tabu (VNS + Tabu) [34], (ii) Genetic Algorithm (GA) with repair mechanisms for SoC feasibility [35], and (iii) Ant Colony Optimization (ACO) variant energsqy-aware routing [36].

The SAT provides equal or improved route feasibility (zero SoC violations) and competitive objective values with reduced or similar computation times for realistic instance sizes. Heuristics provide faster rough solutions for extremely large instances but do not include the exact constraint satisfaction guarantee of SAT. Thus, we suggest hybrids (SAT + heuristic initialization) employing a heuristic to locate a warm start or decrease the candidate set and then polish with SAT for ultimate feasibility.

These works emphasize the increasing trend of hybridizing learning and optimization to handle real-world uncertainty and nonlinear battery dynamics. The presented SAT-based approach supports such AI-boosted paradigms with an exact, logic-based optimization kernel that can incorporate predictive information from machine-learning modules—e.g., traffic predictions, SoC degradation predictions, or dynamic pricing information—while ensuring global constraint satisfaction. The possible future additions include pairing the SAT solver with reinforcement-learning agents or physics-informed predictors to form a hybrid SAT + AI decision engine that mingles the interpretability and feasibility guarantees of logic-based reasoning with the learning capabilities of data-driven intelligence.

6. Conclusions

This study presented a SAT-based optimisation framework for proposing electric vehicle (EV) charging stations that efficiently address real-world restrictions such as battery capacity, charger compatibility, route deviation, and charging station availability. The routing issue was represented using a Boolean Satisfiability (SAT) model, with binary decision variables governing the selection of charging stations. By expressing actual constraints in Conjunctive Normal Form (CNF), the model incorporated complicated logical links that standard methodologies such as Linear Programming (LP) often fail to convey precisely.

The suggested SAT model was assessed on several urban EV routes and compared to LP-based optimisation strategies. The findings showed that the SAT-based technique consistently resulted in shorter trip lengths, less energy usage, lower overall cost, and quicker calculation times. One of the SAT model’s primary strengths was its capacity to reduce redundant or inefficient charging breaks, proposing only those that were strategically essential—as opposed to LP methods, which sometimes included superfluous pauses, raising travel strain without improving route efficacy.

Additionally, the SAT model included user-centric weighted goal functions, allowing for a dynamic balancing of parameters such as distance, charger type, SoC restrictions, and station significance. Its logical structure enabled precise control over critical factors such as minimum SoC upon arrival, number of charging events, and inter-station energy feasibility. Visual route maps confirmed these results by depicting context-aware, realistic travel pathways that were optimised for real-world constraints.

Furthermore, the SAT framework accomplished this with little computing time and memory utilisation, demonstrating its applicability for real-time and large-scale deployments. Compared to sophisticated approaches in the literature, such as Mixed Integer Nonlinear Programming (MINLP) and EVRPTW-TP, which often lack thorough metric reporting and scalability, the SAT model provided a more comprehensive and practical answer.

To summarise, the proposed SAT-based EV routing and charging recommendation system has significant benefits in terms of optimisation quality, computing efficiency, and real-world application. It provides a scalable, intelligent, and resource-efficient solution to EV route design, which is especially useful for congested urban transportation networks.

SAT-based formulations are highly expressive and well-suited to modelling complex logical constraints but, as with many exact combinatorial approaches, may become computationally challenging on very large, geographically dispersed instances. For such settings, we recommend decomposition (partition the network into regions, solve regionally, then reconcile boundaries), incremental SAT solving, or using ML models to generate candidate solutions, which are then verified/optimized by the SAT engine. These hybrid approaches balance expressiveness and practical runtime for non-urban, large-scale deployments. For large-scale or geographically dispersed networks, hybrid or decomposed SAT solving is recommended for efficient deployment.