Abstract
The flexible job shop scheduling problem is a well-known combinatorial optimization problem. This paper proposes an improved shuffled frog-leaping algorithm to solve the flexible job shop scheduling problem. The algorithm possesses an adjustment sequence to design the strategy of local searching and an extremal optimization in information exchange. The computational result shows that the proposed algorithm has a powerful search capability in solving the flexible job shop scheduling problem compared with other heuristic algorithms, such as the genetic algorithm, tabu search and ant colony optimization. Moreover, the results also show that the improved strategies could improve the performance of the algorithm effectively.
1. Introduction
The scheduling of operations has a vital role in the planning and managing of manufacturing processes. The job-shop scheduling problem (JSP) is one of the most popular scheduling models in practice. In the JSP, a set of jobs should be processed with a set of machines, and each job consists of a sequence of consecutive operations. Moreover, a machine can only process one operation at one time, and the operation cannot be interrupted. Additionally, JSP is aimed at minimizing the number of operations for these jobs under the above constraints.
The flexible job-shop scheduling problem (FJSP) is an extension of the conventional JSP, in which operations are allowed to be processed on any one of the existed machines. FJSP is more complicated than JSP, because FJSP not only needs to identify the arrangement of all processes of all machines, but also needs to determine the sequence of processes on each machine. FJSP breaks through the uniqueness restriction of resources. Each process can be completed by many different machines, so that the job shop scheduling problem is closer to the real production process.
JSP has been proven to be an NP-hard problem [1], and even for a simple instance with only ten operations and ten available machines for selection, it is still hard to search for a convincing result. As an extension of JSP, FJSP is more complicated to solve. A lot of the literature believes that adopting a heuristic method is a reasonable approach for solving this kind of complex problem [2–9]. Thus, there are many researchers who have used heuristic methods to solve FJSP. Brandimarte [10] attempted to use a hierarchical approach to solve the flexible job shop scheduling problem, and a tabu search is adopted to enhance the effectiveness of the approach. Fattahi et al. [11] proposed a mathematical model for the flexible job shop scheduling problem, and two heuristic approaches (tabu search and simulated annealing heuristics) are also introduced to solve the real size problems. Gao et al. [12] developed a hybrid genetic algorithm to solve the flexible job shop scheduling problem. In the algorithm, the two vectors are used to represent the solution, the individuals of GA are improved by a variable neighborhood descent and the advanced genetic operators are presented by a special chromosome structurer. Yao et al. [2] presented an improved ant colony optimization to solve FJSP, and an adaptive parameter, crossover operation and pheromone updating strategy are used to improve the performance of the algorithm.
The shuffled frog-leaping algorithm (SFLA) was developed by Eusuff and Lansey [13]. It is a meta-heuristic optimization method, which combines the advantages of the genetic-based memetic algorithm (MA) and the social behavior-based PSO algorithm [14]. A meme is a kind of information body, which can be distributed, reproduced and exchanged by infecting the thoughts of human beings or animals. The most salient characteristic of the meme algorithm is that memes can share and exchange experience, knowledge and information along with relying on a local search method in the process of evolution. Therefore, with the meme algorithm allows an individual of the traditional genetic algorithm model to become more intelligent. The group of SFLA consists of the frog group in which the individual frogs can communicate with each other. Each frog can be seen as a meme carrier. Along with the communication among frogs, the meme evolution can be performed during the searching process of the algorithm. Due to its efficiency and practical value, SFLA has attracted more attention and has been successfully used in a number of classical combinatorial optimization problems [15–19].
In 1999, a new general-purpose local search optimization approach, extremal optimization (EO), was proposed by Boettcher and Percus [20]. The strategy was evolved by the fundamentals of statistical physics and self-organized criticality [21]. The weakest species and its nearest neighbors in the population are always forced to mutate in the evolution process of this method. Thus, EO can effectively eliminate the worst components in the sub-optimal solutions and has been widely used to solve some optimization problems [22,23].
In general, the local exploration strategy that updates the worst solution in each memeplex is important for the performance of the algorithm; because the local exploration reveals that the leaping position of the worst frog is substantially influenced by the local/global best position and limited to the range between the current position and the best position. Thus, the local search strategy based on the adjustment order is adapted to enlarge the local search space. Moreover, EO is introduced to improve the local search ability of SFLA.
The remainder of the paper is organized as follows. A mathematical model for FJSP is presented in Section 2. The shuffled frog-leaping algorithm is introduced in Section 3. In Section 4, we present an improved shuffled frog-leaping algorithm with an extremal optimization and an adjustment strategy. Some computational results are discussed in Section 5, and the conclusions are provided in Section 6.
2. Problem Description
FJSP is a kind of resource allocation problem, i.e., given M machines and the N work pieces, FJSP aims to minimize the operating time by optimizing the arrangement of the operations of all jobs t. A set of machines M = {M1,M2,…,Mm} and a set of independent jobs J = {J1,J2,…,Jn} are given. Additionally, each job Ji consists of a sequence of operations Oij, where Oij represents the j-th operation of the job i. All of the operations of each job should be performed one after another in a given order. Each operation Oij can be processed on any machine among a subset Mi,j ⊆ M of compatible machines. Based on the different conditions of resource restriction, the flexible job shop scheduling problem can be divided into a total flexible job-shop scheduling (T-FJSP) problem and a partial flexible job-shop scheduling (P-FJSP) problem. In T-FJSP, every process of each operation can choose any one machine to be processed; in P-FJSP, some processes of some work pieces can be processed on any one of the machines, and some certain processes can only choose parts of machines.
All jobs and machines are available at Time 0, and a machine can only execute one operation at a given time. The processing time of each operation is dependent of the machine, and pmi represents the processing time of operation Oij on machine i. If the operation Oij cannot be processed on machine k, the processing time pmk is assumed as ∞. Each operation must be completed without interruption during its process. The objective of FJSP is to assign each operation to one machine that is capable of performing it and to determine the starting time for each operation in order to minimize the makespan. In order to describe the FJSP well, Figure 1 is an example of FJSP with three jobs and five machines. In Figure 1, (0, 0, 0) means spending zero seconds on the first machine, zero seconds on the second one and zero seconds on the third one.
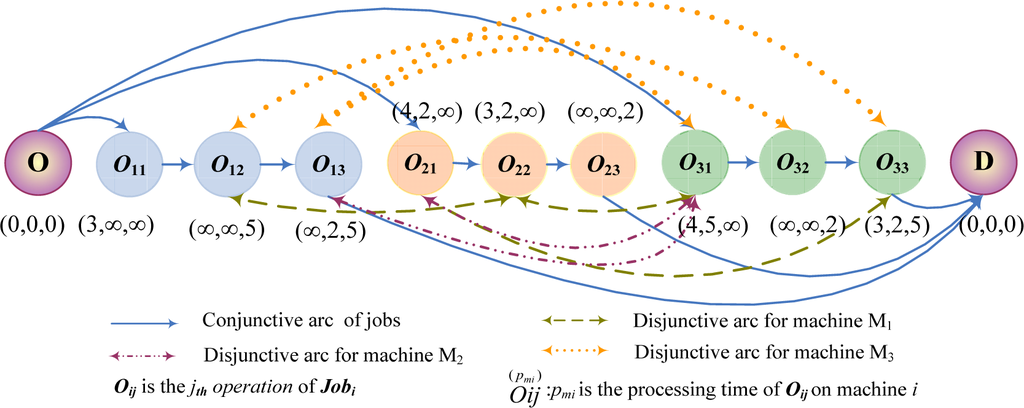
Figure 1.
An example of the flexible job scheduling problem (FJSP).
Therefore, the flexible job-shop scheduling problem model can be described as follows:
Subject to
where
n is the total number of jobs; m is the total number of machines; hj is the total number of operations of job j(j ∈ n); Ojh is the h-th operation of job j (h = 1,2,…,hj); pijh is the processing time of the h-th operation of job j on the machine (I ∈ m); sjh is the start processing time of the h-th operation of job j; cjh is the completion time of the h-th operation of job j; L is a given big integer; Cmax is the maximum completion time.
Formulas (a) and (b) are the operation constraints of each job. Formula (c) is the time constraint of each job. Formulas (d) and (e) assume that only one machine can process one operation at a time. Formula (f) is the constraint of the machine, which assumes that the same operation can only be processed by one machine. Formulas (g) and (h) show that the circulating operation can be permitted on each machine. Formula (i) shows that each parameter must be positive number.
3. Shuffled Frog-Leaping Algorithm
In the shuffled frog-leaping algorithm, the population consists of frogs of a similar structure. Each frog represents a solution. The entire population is divided into many subgroups. Different subgroups can be regarded as different frog memes. Each subgroup performs a local search. They can communicate with each other and improve their memes among local individuals. After a pre-defined number of memetic evolution steps, information is passed between memeplexes in a shuffling process. Shuffling ensures that the cultural evolution towards any particular interest is free from bias. The local search and the shuffling processes alternate until satisfying the stopping criteria.
For a problem of D dimension, a frog is thought of as Fi = {fi1, fi2,…,fiD}. The algorithm first randomly generates S frogs as the initial population and notes them in descending order according to the fitness of each frog. Then, the entire population is divided into m subgroups, and each subgroup contains n frogs. From the initial population, the first frog is selected in the first sub-group, and the second frog is selected in the second group, until the first m frog is selected in the m-th subgroup. Then, the (m + 1)-th frog is selected in the first subgroup. Repeat the process, until all frogs are distributed. In each subgroup, the frog with the best fitness and the one with the worst fitness are denoted as Fb and Fw, respectively; while in the total population, the frog with the best fitness is denoted as Fg. The main work of SFLA is to update the position of the worst-performing frog through an iterative operation in each sub-memeplex. Its position is improved by learning from the best frog of the sub-memeplex or its own population and position. In each sub-memeplex, the new position of the worst frog is updated according to the following equation.
Formula (4) is used to calculate the updating step di. Rand () is the random number between zero and one; Formula (5) updates the position of Fw. dmax is the maximum step. If a better solution is attained, then the better one will replace the worst individual. Otherwise, Fg will be used instead of Fb. Then, recalculate Formula (4). If you still cannot get a better solution, a new explanation generated randomly will replace the worst individual. Repeat until a predetermined number of iterations. Additionally, complete the round of the local search of various subgroups. Then, all subgroups of the frogs are re-ranked in mixed order and divided into sub-groups for the next round of local search.
The general structure of SFLA can be described as follows:
- Step 1. Initialization. According to the characteristics and scale of the problem, a reasonable m and n is determined at first.
- Step 2. Produce a virtual population with F individuals (F = m * n). For the D dimension optimization problem, the individuals of the population are D dimension variables and represent the frogs’ current position. The fitness function is used to determine if the performance of the first individual’s position is good.
- Step 3. Divide the total population and the number of individuals in descending order.
- Step 4. Divide the population into population m: Y1, Y2, …, Ym. Each sub-population contains n frogs. For example: if m = 3, then the first frog is put into the first population, the second frog is put into the second population, the third frog is put into the third population, the fourth frog is put into the first population, and so on.
- Step 5. In each sub-population, with its evolution, the positions of individuals have been improved. The following steps are the process of the sub-population meme evolution.
- Step 5.0. Set im = 0. im represents the number of the sub-populations, which is from zero to m. Set it equal to zero. im represents the number of evolutions, which is from zero to N (the maximum evolution iteration in each sub-population).
In each sub-population, compute Fb, Fw and Fg, respectively [24].
- Step 5.1. im = im + 1.
- Step 5.2. in = in + 1.
- Step 5.3. Try to adjust the position of the worst frog. The moving distance of the worst frog should be: di = Rand () * (Fb −Fw). After moving, the new position of the worst frog is: Fw = Fw (the current position) + di.
- Step 5.4. If Step 5.3 could produce a better solution, use the frog in the new position instead of the worst one; or use Fg instead of Fb.
- Step 5.5. If better frogs cannot be generated after trying the above method, immediately generate the next individual to replace the worst frog Fw.
- Step 5.6. If in < N, then perform Step 5.2.
- Step 5.7. If im < m, then perform Step 5.1.
- Step 6. Implementation of mixed operations.
After carrying out a certain number of meme evolutions, merge each sub-population Y1, Y2, …, Ym to X, namely X = {Yk, k = 1, 2,… M}. Descend X again, and update the best frog Fg in the populations.
- Step 7. Check the termination conditions. If the iterative termination conditions are met, then stop. Otherwise, do Step 4 again.
Usually, the frog reaching the defined maximum evolution number or representing the global optimal solution does not changes anymore, and the shuffled frog-leaping algorithm stops.
4. Improved SFLA for FJSP
4.1 Generation of Solutions
Because the flexible job shop scheduling problem is a discrete combinatorial optimization problem, the shuffled frog-leaping algorithm requires discretization to adapt to the optimization of this problem. The form of the code is the key of the algorithm and with an appropriate FJSP could be solved effectively. This paper adopts a segmented integer coding method. The coding method is operated easily, which is adapted to T-FJSP and P-FJSP. In the method, the solution of the code consists of two parts, namely machine selection and operation selection.
Figure 2 is an example of the coding scheme of Figure 1. In the encoding form, the machine section length and the operation section length are both equal to the sum of all operations. In the machine section, each position is ranked according to the process order of jobs and operations. From Figure 2, it can be found that the operation O11 can be processed on five machines {M1, M2, M3, M4, M5}, so five is placed in the first square. The operation O12 can be processed on two machines {M2, M4}, and in the same way, the machine section is coded. In the operation section, the code is noted by the time sequence of all of the operations of all jobs. For example, O21 is the first operation; thus, the first square is placed at two, which is the job number. As shown in Figure 2, the code of the operation section is 2321321, which represents the operation sequence: O21-O31-O22-O11-O31-O23-O12.

Figure 2.
An example of the coding scheme.
4.2 Local Search
A local search strategy was designed to search the local optimum in different directions and to make the local optimal individual in the ethnic groups gradually tend toward the optimal individual. However, the frog population is divided into a plurality of groups, and each group is locally searched; SFLA can easily fall into a premature or local-best solution. In order to avoid frog individuals getting trapped in a local optimum prematurely and to accelerate the convergence rate, a specific principle is used to select a certain number of individual to construct the sub-population.
The local search formula is changed to the following:
S means the adjustment vector, and Smax means the maximum step size allowed to change by frog individual. Set Fw = {1, 3, 5, 2, 4}, Fb = {2, 1, 5, 3, 4}; the maximum step size allowed to change Smax = 3, rand = 0.5. Therefore, Fg(1) = 1 + min{int[0.5 × (2 − 1)],3} = 1; Fg(2) = 3 + min{int[0.5 × (1 − 3)],3} = 2, and so on. Finally, the new solution Fg can be attained as {1, 2, 5, 4, 3}.
4.3 Improvement Strategies
Although in the literature [25], the shuffled frog-leaping algorithm with local search can guarantee the feasibility of the updated solution, the step size is still selected randomly. Therefore, on the basis of the literature [25], this paper designed the local search strategy by introducing the adjustment factor and adjustment order.
Adjustment order is an attempt to adjust one feasible solution to another one [26]. In local search, the method in which the worst solution in a sub-group is optimized by the adjustment order is more reasonable than the simple step size selection. Therefore, this paper introduced this idea into updating the worst solution in the sub-group during the local search.
4.3.1 Adjustment Factor
The steps for the adjustment factor are as follows: If the solution set is U = (Ui) and the operation set is (1, 2,…, d), the adjustment is defined as TO(i1,i2)(i = 1,2,…,d). Thus, the operation of Ui1 will be put before Ui2. U′ = U + TO(i1,i2) is the new solution of U based on the adjustment factor. For example, if U = (1 3 5 2 4), the adjustment factor is TO (4,2), then U′ = U + TO (2,4) = (1 2 3 5 4).
4.3.2 Adjustment Sequence
The adjustment sequence is one or more adjustment factors are ranked in sequence, which is noted as ST. ST = (TO1, TO2,…, TON) · TO1,TO2,…,TON are the adjustment factors. UA and UB are two different solutions. The adjustment sequence ST(UB Θ UA) means adjusting UA to UB, namely, UB=UA + ST (UB Θ UA)=UA + (TO1 TO2,…, TON) = [(UA + TO1)+ TO1]+…+ TON. For example, let UA = (1 3 5 2 4), UA = (3 1 4 2 5). We need make an adjustment sequence ST (UB Θ UA), and make sure
. Therefore, for the first adjustment sequence
, we can get
, and the second adjustment sequence is
, and so on. Then, we can get ST(UB Θ UA) = (TO1(2,1), TO2(5,3), TO3(5,4)).
4.3.3 Extremal Optimization
Extremal optimization (EO) is an optimization that evolves a single individual (i.e., chromosome) S = (x1, x2, …, xd). Each component xi in the current individual S is considered to be a species and is assigned a fitness value ki. There is only a mutation operator in EO, and it is applied to the component with the worst species successively. The individual can update its components and evolve toward the optimal solution. The process requires a suitable representation that allows the solution components to be assigned a quality measure (i.e., fitness). This approach differs from holistic ones, such as evolutionary algorithms, which assign equal fitness to all components of a solution based on their collective evaluation against an objective function. The EO algorithm is as follows [27].
- Step 1. Randomly generate an individual S = (x1, x2, x3, x4). Set the optimal solution Sbest = S.
- Step 2. For the current S:
- Evaluate the fitness λi for each component xi, i = 1, 2,…,d. And d is the vector number of the solution space;
- Find j satisfying λj ≤ λi for all i, xj being the worst species;
- Choose S′ ∈ N(S), such that xj must change its state by mutation operator; N(S) is the neighborhood of S;
- Accept S = S′ unconditionally;
- If the current cost function value is less than the minimum cost function value, i.e., C(S) < C(Sbest), then set Sbest = S.
- Step 3. Repeat Step 2 as long as desired;
- Step 4. Return Sbest and C(Sbest).
4.4 The Update the Strategy of the Frog Individual
The differences among frog individuals are their adjustment sequences. The number of adjustment sequences is not negative. Therefore, the update strategy of the frog individual is:
In which the length of (ST(UB Θ UW)) means the number of all adjustment factors in adjustment sequence ST(UB Θ UW), l means the number of adjustment factor in ST(UB Θ UW) chosen to update UW and s means update the adjustment sequence for UW. Figure 3 is used to explain an example of the update strategy of the frog individual from UB to Uq. From Figure 3, it can be attained that the length of ST(UB Θ UW) = 5, l = 3, s = (TO1, TO2, TO3.
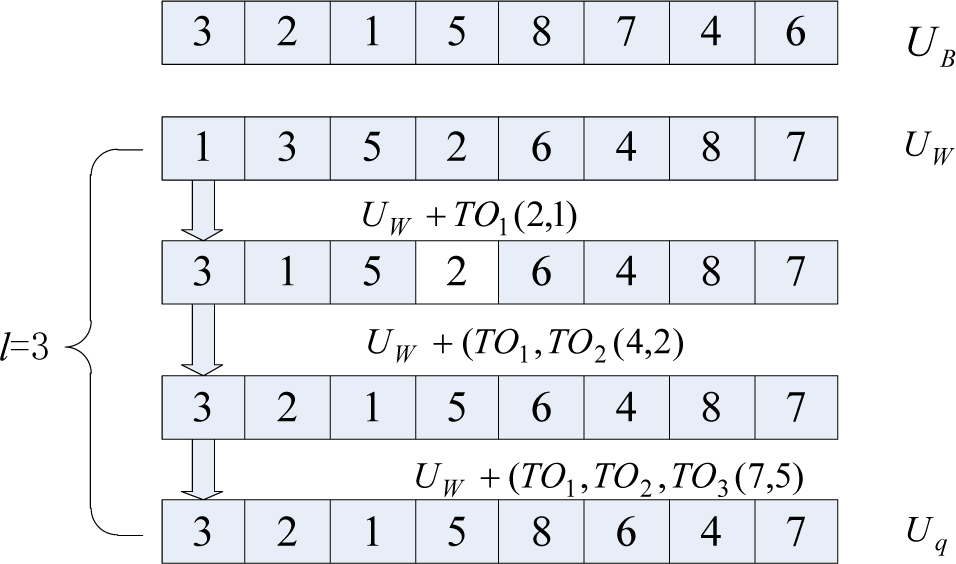
Figure 3.
The update strategy of the frog individual.
5. Numerical Experiments and Discussion
This section describes the computational experiments used to test the performance of the proposed algorithm. There are 10 FJSP benchmark problems [27], which have been widely used as benchmark problems to examine the feasibility of the algorithms [2,28,29]. The number of jobs ranges from 10 to 20; the number of machines ranges from four to 15; the number of operations for each job ranges from five to 15; and the number of operations for all jobs ranges from 55 to 240. Lower best-known solutions (LB) and upper best-known solutions (UB) represent the lower and upper values from the best-known solutions. In this paper, the improved SFLA (ISFLA) parameters used for the instances are P = 1000, Q = 1000, N = 5000, ρ = 0.8 and Pc = 0.4 In order to conduct the experiment, we implement the algorithm in C++ language and run it on a PC with 2.0 GHz, 512 MB of RAM memory and a Pentium processor running at 1,000 MHz. The results of the ISFLA on the instances are shown in Table 1, which are compared with the genetic algorithm (GA) [28], tabu search (TS) [29], artificial immune algorithm (AIA) [20] and ant colony optimization (ACO) [2]. The numbers in bold are the best among the five approaches. We used 10 standard cases (MK01-MK02) proposed in [27] to test our model.

Table 1.
Performance comparison between improved shuffled frog-leaping algorithm (ISFLA) and other algorithms. The numbers in bold are the best among the five approaches. TS, tabu search; AIA, artificial immune algorithm.
From Table 1, it can be found that the ISFLA used in this paper is able to find most of the best-known solutions, especially for problems of higher flexibility. Besides, the method can provide competitive solutions for most problems. We also find that our ISFLA has better performance than or similar performance as the ACO, TS and the AIA. The results indicate that our algorithm is a potential algorithm for FJSP when compared with other heuristic algorithms (GA, TS and AIA).
To evaluate the three improved strategies, four shuffled frog-leaping algorithms with different strategies are constructed. This first is a standard SFLA with the adjustment factor (denoted by SFLA + AF); the second one is a standard SFLA with the adjustment order (AO) (denoted by SFLA + AO); the third one is a standard SFLA with the extremal optimization (denoted by SFLA + EO); and the fourth one is a standard SFLA with the three improved strategies (denoted by ISFLA). The comparison results about the optimal value, average value and relative error and average computing time between the four different SFLAs are shown in Table 2.

Table 2.
Computational results of the MK09 problem of several methods. AF, adjustment factor; AO, adjustment order; EO, extremal optimization.
For the MK09 problem, the errors are within 10% compared to the approximate optimal solution. The simulation results show that when the improved leapfrog algorithm does not fall into the local convergence, the combination of three improved strategies can improve the searching performance of SFLA and accelerate the convergence speed of the algorithm. From the results in Tables 1 and 2, it can be found that the improved algorithm in this paper is a powerful method for solving FJSP with reasonable precision and computing speed.
6. Conclusions
This paper presents an improved SFLA with some strategies for FJSP. The objective of the research is to minimize the makespan in FJSP. The shuffled frog-leaping algorithm with local search can guarantee the feasibility of the updated solution; however, the step size is still selected randomly. To attain a reasonable step size, the adjustment factor and adjustment order are adopted. Moreover, an extremal optimization is used to exchange the information among individuals. The effectiveness of the improved shuffled frog leaping algorithm is evaluated using a set of well-known instances. The results indicate that the results gained by ISFLA are often the same or slightly better than those gained by the other algorithms for the FJSP. Furthermore, the results also show that the improved strategies effectively improve the performance of the algorithm.
References
- Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of f1owshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar]
- Yao, B.Z.; Hu, P.; Lu, X.H.; Gao, J.J.; Zhang, M.H. Transit network design based on travel time reliability. Transp. Res. Part C 2014a, 43, 233–248. [Google Scholar]
- Yao, B.Z.; Yao, J.B.; Zhang, M.H.; Yu, L. Improved support vector machine regression in multi-step-ahead prediction for rock displacement surrounding a tunnel. Scientia Iranica. 2014b, 21, 1309–1316. [Google Scholar]
- Yao, B.Z.; Hu, P.; Zhang, M.H.; Jin, M.Q. A Support Vector Machine with the Tabu Search Algorithm For Freeway Incident Detection. Int. J. Appl. Math. Comput. Sci. 2014c, 24, 397–404. [Google Scholar]
- Yu, B.; Yang, Z.Z.; Yao, B.Z. An Improved Ant Colony Optimization for Vehicle Routing Problem. Eur. J. Oper. Res. 2009, 196, 171–176. [Google Scholar]
- Yu, B.; Yang, Z.Z. An ant colony optimization model: The period vehicle routing problem with time windows. Transp. Res. Part E 2011, 47, 166–181. [Google Scholar]
- Yu, B.; Yang, Z.Z.; Li, S. Real-Time Partway Deadheading Strategy Based on Transit Service Reliability Assessment. Transp. Res. Part A 2012a, 46, 1265–1279. [Google Scholar]
- Yu, B.; Yang, Z.Z.; Jin, P.H.; Wu, S.H.; Yao, B.Z. Transit route network design-maximizing direct and transfer demand density. Transp. Res. Part C 2012b, 22, 58–75. [Google Scholar]
- Yao, B.Z.; Yang, C.Y.; Yao, J.B.; Hu, J.J.; Sun, J. An Improved Ant Colony Optimization for Flexible Job Shop Scheduling Problems. Adv. Sci. Lett. 2011, 4, 2127–2131. [Google Scholar]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in a simple model of evolution. Phys. Rev. Lett. 1993, 71, 4083–4086. [Google Scholar]
- Fattahi, P.; Mehrabad, M.S.; Jolai, F. Mathematical Modeling and Heuristic Approaches to Flexible Job Shop Scheduling Problems. J. Intell. Manuf. 2007, 18, 331–342. [Google Scholar]
- Gao, L.; Sun, Y.; Gen, M. A Hybrid Genetic and Variable Neighborhood Descent Algorithm for Flexible Job Shop Scheduling Problems. Comput. Oper. Res. 2008, 35, 2892–2907. [Google Scholar]
- Eusuff, M.; Lansey, K. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. J. Water Resour. Plan. Manag. 2003, 129, 10–25. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization, Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia; 1995; pp. 1942–1948.
- Alireza, R.V.; Mostafa, D.; Hamed, R.; Ehsan, S. A novel hybrid multi-objective shuffled frog-leaping algorithm for a bi-criteria permutation flow shop scheduling problem. Int. J. Adv. Manuf. Technol. 2009, 41, 1227–1239. [Google Scholar]
- Bhaduri, A. Color image segmentation using clonal selection-based shuffled frog leaping algorithm, Proceedings of the ARTCom 2009—International Conference on Advances in Recent Technologies in Communication and Computing, Kottayam, India, 27–28 October 2009; pp. 517–520.
- Babak, A.; Mohammad, F.; Ali, M. Application of shuffled frog-leaping algorithm on clustering. Int. J. Adv. Manuf. Technol. 2009, 45, 199–209. [Google Scholar]
- Li, X.; Luo, J.P.; Chen, M.R.; Wang, N. An improved shuffled frog-leaping algorithm with extremal optimization for continuous optimization. Inf. Sci. 2012, 192, 143–151. [Google Scholar]
- Luo, J.P.; Li, X.; Chen, M.R. Improved Shuffled Frog Leaping Algorithm for Solving CVRP. J. Electr. Inf. Technol. 2011, 33, 429–434. [Google Scholar]
- Boettcher, S.; Percus, A.G. Extremal Optimization: Methods derived from Co-Evolution, Proceedings of the Genetic and Evolutionary Computation Conference, New York, NY, USA, 13 April 1999; pp. 101–106.
- Bagheri, A.; Zandieh, M.; Mahdavi, I.; Yazdani, M. An Artificial Immune Algorithm for The Flexible Job-Shop Scheduling Problem. Future Gener. Comput. Syst. 2010, 26, 533–541. [Google Scholar]
- Boettcher, S. Extremal Optimization for the Sherrington-Kirkpatrick Spin Glass. Eur. Phys. J. B 2005, 46, 501–505. [Google Scholar]
- Chen, M.R.; Lu, Y.Z. A novel elitist multiobjective optimization algorithm: Multiobjective extremal optimization. Eur. J. Oper. Res. 2008, 188, 637–651. [Google Scholar]
- Alireza, R.V.A.; Ali, H.M. A hybrid multi-object shuffled frog leaping algorithm for a mixed-model assembly line sequencing problem. Comput. Ind. Eng. 2007, 53, 642–666. [Google Scholar]
- Luo, X.H.; Yang, Y.; Li, X. Solving TSP with shuffled frog-leaping algorithm, Proceedings of the Eighth International Conference on Intelligent Systems Design and Applications, Kaohsiung, Taiwan, 26–28 November 2008; pp. 228–232.
- Wang, C.R.; Zhang, J.W.; Yang, J.; Hu, C. A modified particle swarm optimization algorithm and its application for solving traveling salesman problem, Proceedings of the ICNN&B ′05. International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; pp. 689–694.
- Brandimarte, P. Routing and Scheduling in a Flexible Job Shop by Taboo Search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar]
- Pezzella, F.; Morganti, G.; Ciaschetti, G. A Genetic Algorithm for the Flexible Job-Shop Scheduling Problem. Comput. Oper. Res. 2008, 35, 3202–3212. [Google Scholar]
- Mastrolilli, M.; Gambardella, L.M. Effective Neighbourhood Functions for the Flexible Job Shop Problem. J. Sched. 2000, 3, 3–20. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).