Abstract
We give a -approximation algorithm for finding stable matchings that runs in time. The previous most well-known algorithm, by McDermid, has the same approximation ratio but runs in time, where n denotes the number of people and m is the total length of the preference lists in a given instance. In addition, the algorithm and the analysis are much simpler. We also give the extension of the algorithm for computing stablemany-to-many matchings.
1. Introduction
In the paper, we consider a variant of the problem called Stable Matchings, known also in the literature as the Stable Marriage problem. The problem is defined as follows. We are given two sets W and U of women and men. Each woman w of W has a preference list of a subset of men, and similarly, each man m of U has a preference list of a subset of women. The preference lists are linearly ordered lists of ties, which are subsets of men (or respectively, women), who are equally good for a given woman (respectively, man). Ties are disjoint and can contain also one person, appropriately a man or a woman. Thus if m and are on list of woman w, then either (1) w prefers m to , or in other words, m is better for w than ; or (2) m and are in a tie on and then we say that w is indifferent between m and or that m and are equally good for her; or (3) w prefers to m. Man m and woman w are said to be mutually acceptable to each other if they belong to each other’s preference lists. The most preferred person(s) is (are) at the top of the preference lists. A matching is a set of pairs such that and m and w are mutually acceptable, and each man/woman belongs to at most one pair. If belongs to a certain matching M, then we write , which means that in M woman w is a partner of m, and analogously that . If man m (or woman w) is not contained in any pair of a matching M, then we say that m (or w) is unmatched or free in M. A matching M is called stable if it does not admit a blocking pair. A pair is blocking for M if (1) m and w are mutually acceptable; (2) m is unmatched or prefers w to ; and (3) w is unmatched or prefers m to . Each instance of the problem can be represented by a bipartite graph with vertices of U representing men, vertices of W representing women and edges E connecting all mutually acceptable pairs of men and women. The problem we are interested in is that of finding a stable matching that has the largest cardinality. The version in which there are no ties in the preference lists of men and women has been long known and an algorithm by Gale and Shapley [] solves it exactly in time, where m denotes the number of edges in the underlying graph. In the version without ties a stable matching always exists, and every stable matching has the same cardinality. If we allow ties, as in the problem we consider in this paper, then a stable matching also always exists and can be found via the Gale-Shapley algorithm by breaking ties arbitrarily. However, the sizes of stable matchings can vary considerably, and the problem of finding a stable matching of maximum cardinality is -hard, which was shown by Manlove et al. in []. Therefore it is desirable to devise an approximation algorithm for the problem.
Previous and related results Previous approximation algorithms were presented in [,,,,]. Currently the best approximation algorithm is by McDermid [] and achieves the approximation guarantee . Its running time is , where n denotes the number of vertices and m the number of edges. Inapproximabilty results were shown in [,,]. For a variant of the Stable Matchings problem, in which ties are allowed on one side only, an approximation algorithm achieving the ratio has been given in []. A slightly different linear time -approximation algorithm based on an earlier version of this paper was given by Király in []. The conference version of this paper appeared also in the proceedings of WAOA’11 (Workshop on Approximation and Online Algorithms) [].
Our results While constructing approximation algorithms, the goal is not only to achieve a good approximation guarantee but also good running time. We give a 3/2-approximation algorithm that runs in time and additionally is significantly simpler than that of McDermid. In devising the algorithm we were led by the observation that it suffices to find a stable matching that will not create a dangerous path, which is defined later. We also give the extension of the algorithm for computing stable many-to-many matchings, which runs in time, where c denotes the minimum of the maximal capacities in each side of the bipartition. In particular, it means that we give an -time algorithm for the Hospitals-Residents problem, improving on an time algorithm given by McDermid, where d denotes the maximal capacity of a hospital. McDermid’s algorithm follows from the reduction of the Hospitals-Residents problem to the Stable Matchings problem by "cloning" hospitals. The approach by cloning does not work if the vertices on both sides of the bipartition are allowed to have capacities larger than 1. Since these problems have many practical applications (see [,,], for example), we believe our algorithms will be of help.
2. Algorithm
For a given instance of the problem let denote an optimal (i.e., largest) stable matching and let be any two matchings. We say that e is an M-edge if . A path P or a cycle C is called alternating (w.r.t. M) if its edges alternate between M-edges and edges of E∖M. It is well known from matching theory (see [] for example) that disintegrates into a set of alternating paths and alternating cycles. (For two sets , the set denotes ∖Y) ∪ (Y∖.) Let S denote a set of maximal alternating paths and cycles of . Consider any alternating cycle C of S or any alternating path P of even length of S. Then both C and P contain the same number of M-edges and -edges. Consider an alternating path P of length of S. Then either or . Therefore, if M is stable and S does not contain a path of length 3 with the middle edge being an M-edge, then and M is a -approximation of . To achieve a -approximation, we will eliminate such potential paths of length 3 of .
Accordingly, we define a dangerous path w.r.t. a matching M to be an alternating path such that w and m are unmatched in M (which means that is in M and do not belong to M) and is not a blocking pair for the matching . We need to concern ourselves only with dangerous paths w.r.t. a matching M that can be extended to a stable matching, i.e., M is such that there exists a stable matching with . Therefore, if is a dangerous path w.r.t. M, then w and do not form a blocking pair for M, which means that is at least as good for as w, and similarly, and m do not form a blocking pair for M, hence is at least as good for as m. Since is not a blocking pair for the matching , either is indifferent between w and and then we say that P is a masculine dangerous path, or is indifferent between m and and then we say that P is a feminine dangerous path. A path P can of course be both a masculine and a feminine dangerous path.
We also introduce the following terminology.
- If man m is matched to woman w and there is at least one free woman such that w and are equally good for m, then we say that is a satellite of m and m is satellitic.
- If woman w is matched to a satellitic man m, then we say that w is co-satellitic.
- If is such that w is free and there is at least one free woman such that w and are equally good for m, then e is called special, and consequently, is also called special.
- If man m has at least one free woman incident with him, then he is said to be subsatellitic.
- Woman w matched to a subsatellitic man m and not co-satellitic is said to be co-subsatellitic w.r.t. if m and are equally good for her.
Figure 1 illustrates the notions introduced above.
Let us notice that if a free man m has a co-satellitic woman w on his list, then it is possible that he belongs to a masculine dangerous path, and analogously, if a free man m has a woman w on his list who is co-subsatellitic with respect to him, then it is possible that he belongs to a feminine dangerous path.
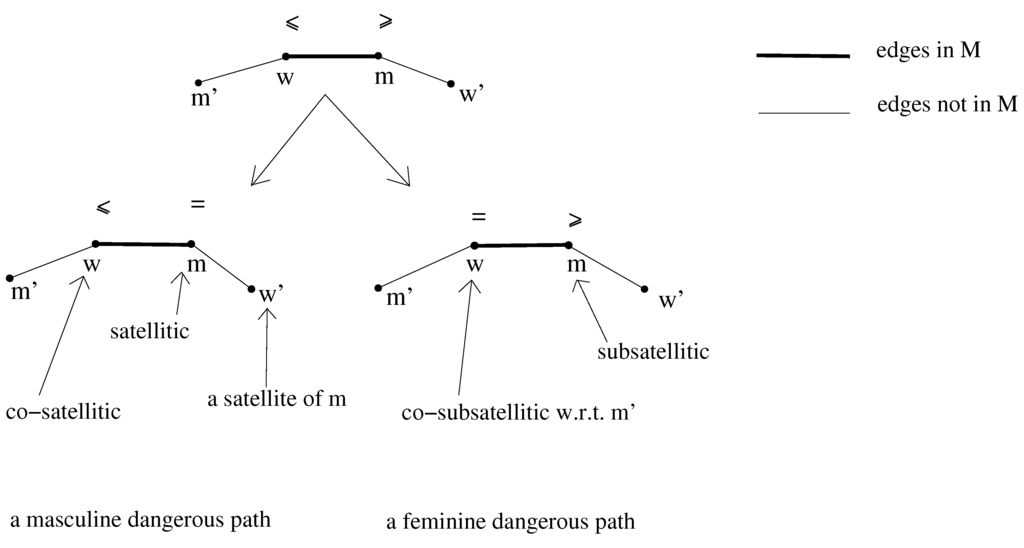
Figure 1.
The description of a dangerous path and its two types: a feminine dangerous path and a masculine dangerous path.
2.1. Description of Algorithm GS Modified
Algorithm GS Modified given further on is to some extent modeled on the Gale-Shapley algorithm in which men propose to women on their lists and women dispose. In the course of running the algorithm, preference lists will diminish and some additional lists will be built. If at some point a free man m has a nonempty list , it means that he has not yet proposed to all women on his list and potentially belongs to a blocking pair or a masculine dangerous path. If a free man m has a nonempty list , it means that he potentially belongs to a feminine dangerous path.
Whenever it is man m’s turn to propose and , he would like to get matched to the best possible woman on his list without creating a blocking pair (as in GS algorithm) but also ensure that he does not belong to any masculine dangerous path. To this end, m proposes to the woman w to whom he has not yet proposed and who is as high on as possible. If w is free or matched to someone worse for her than m, she accepts m and rejects her current partner if she had one. If w is co-satellitic, which means that she is matched to some man such that there is a free woman who is equally good for as w, then it means that m currently belongs to a masculine dangerous path . In this case w does not care whether m is better for her than and accepts him while rejecting , and immediately afterwards proposes to , who accepts him. This operation can be very well viewed as though proposed to without having proposed to w first, and some time later m proposed to w. (Here edge was special at the moment proposed to w for the first time and that’s why if gets rejected by , he will propose to w again, because in this case w was not removed from . Let us notice that if were allowed to remove w from his list at the moment he proposed to w for the first time and the edge was special, then after being rejected by later on, he would not propose to w for the second time, and as a result a blocking pair involving and w might arise.) To avoid multiple operations of this kind concerning one woman, we will assume that given a tie, a man proposes to unmatched women before proposing to matched ones. This ensures that in the above scenario, m cannot become satellitic after being matched with w. If a woman w to whom m proposes is matched to man equally good for her as m, and w is co-subsatellitic w.r.t. m, meaning that has some free women on his list, then at the current moment m belongs to a feminine dangerous path. What happens now is that w rejects m but m adds w to his list . (Woman w does not accept m because m may be subsatellitic as well.) In every other case w rejects m.
If man m has proposed to all women on his list and remained free, but his list is nonempty, he will propose to women on starting from the top. If he proposes to w, and w is matched to some man who is equally good for her as m, and additionally, is subsatellitic, then w accepts m and rejects . Otherwise w rejects him. Let us notice that it cannot happen that w prefers m to , because man m had proposed to all women on his list before proceeding to list . Therefore he must have been rejected by w at some point, which means that w must be now matched to someone at least as good for her as m. (This will also be formally proved in the next section.)
Algorithm GS Modified
Each man m’s preference list is organized in such a way that if contains a tie t, then free women in t come before matched women in t. At the beginning all women are free and ties on men’s lists are broken arbitrarily, and in the course of running the algorithm, whenever woman w becomes matched for the first time, say to man m, we move her to the end of every tie she belongs to.
while there exists a free man m with a nonempty list or a nonempty list
if , then
woman at the top of m’ s list
if is not special, then remove w from
if w is free, then
else if w is co-satellitic, then
let be a satellite of
if is not special, then remove from
∖
else if w prefers m to , then ∖
else if w is co-subsatellitic w.r.t. m, then add w to the end of list
else
woman at the top of m’ s list
remove w from
if w is co-subsatellitic w.r.t. m, then ∖
First we show how Algorithm GS Modified runs on the following example. Suppose the preference lists of men and women are as follows. The brackets indicate ties.
Suppose that man starts. He proposes to woman and gets accepted ( is a special edge and is a satellite of ). Now suppose that it is ’s turn to propose. (It might also be or .) He proposes to woman and gets accepted, because is co-satellitic. Man gets matched with woman . Next proposes to woman and gets accepted. Now proposes to (as was a special edge) and gets accepted. Then proposes to and gets accepted. Next proposes to and gets rejected, but is co-subsatellitic w.r.t. , and adds to his list . Afterwards proposes to again, this time from , and gets accepted. Finally proposes to andgets accepted.
3. Correctness of Algorithm GS Modified
In this section we prove the correctness of Algorithm GS Modified.
If and m proposes to w, then we will sometimes say that m proposes from (to w). If and m proposes to w, then we will sometimes say that m proposes from (to w).
Lemma 1.
- If woman w becomes matched, she will stay matched.
- Woman w can become co-satellitic only the first time someone, say m, proposes to her and only if at the time of the proposal edge is special. If a co-satellitic woman w receives a proposal, she always accepts it and is no longer co-satellitic.
- If woman w is matched to man m and is not co-satellitic, she can accept man only if is at least as good for her as m. Moreover, if is better for her than m, she always accepts him. If is equally good for her as m, then she accepts him only if she is co-subsatellitic w.r.t. and proposes from .
- If woman w matched to man m is not co-satellitic and changes m for , who is equally good for her as m, then m is subsatellitic and is not.
Proof. Statements 1 and 3 follow directly from the description of Algorithm GS Modified.
Let us prove statement 2. If w is matched and m proposes to her, then there is no free woman incident with m who is equally good for m as w (because then m would propose to before proposing to w). As a result, if w becomes matched to m, she will not become co-satellitic and she will cease to be co-satellitic if she was before.
It remains to prove statement 4. If w changes m for who is equally good for her as m (and w is not co-satellitic), then by statement 3, proposes from and m is subsatellitic. Man proposing from does not have any free women incident with him. □
Lemma 2. Let M denote a matching computed by Algorithm GS Modified. Then the underlying graph does not contain blocking pairs and dangerous paths w.r.t. M.
Proof. Suppose that is a blocking pair. Man m is either free or is worse for him than w. It means that at some point m proposed to w from when edge was not special. (Clearly, at some point m proposed to w from . Assume that at that point edge was special. Then w was free and accepted m. However, m got rejected later and therefore proposed to w from again, when edge was no longer special.) If w rejected him then, then by claim 2 of Lemma 1, w was not co-satellitic and, by claim 3 of Lemma 1, was matched to someone at least as good for her as m and thus would have stayed matched to someone as good for her as m. If w accepted m, then after getting matched to m she was not co-satellitic, and by claim 3 of Lemma 1, would have stayed matched to someone at least as good for her as m. Either way we get a contradiction.
Suppose now that the graph contains a masculine dangerous path such that . Thus m is satellitic and w is co-satellitic. Since she is co-satellitic, it means that the only proposal she ever got was from m, but must have proposed to her too, a contradiction.
Finally, suppose that the graph contains a feminine dangerous path such that . Thus m is subsatellitic and w is co-subsatellitic w.r.t. , also is not subsatellitic. At some point, proposed to w from when was not special. If he got accepted at that moment, then later on he could not become rejected, because by claim 3 of Lemma 1, after accepting woman w was not co-satellitic, and by claim 4 of Lemma 1, could not accept a subsatellitic man equally good for her as her current partner. Therefore he was rejected then, and w was already matched with m (by claims 3 and 4 of Lemma 1). Hence w was co-subsatellitic w.r.t. (because m was subsatellitic), and added w to the end of list . Thus later proposed to w from . According to the algorithm, w would have accepted him and could not later on become matched to someone subsatellitic and equally good for her as . A contradiction. □
Theorem 1. Algorithm GS Modified computes a stable matching M which is a - approximation of the optimal solution. Algorithm GS Modified runs in time.
Proof. By Lemma 2, matching M computed by Algorithm GS Modified is stable and does not contain dangerous paths. Therefore M is a -approximation of the optimal solution.
The running time of the algorithm is proportional to the sum of the lengths of lists and . By the length of list or we mean the number of people on it and not the number of ties. Each edge of is scanned at most twice–twice only if the first time it was scanned, it was special, and each edge of is scanned at most once. Checking whether a given woman w is co-satellitic or co-subsatellitic can be done in constant time as follows. Suppose that w is matched to man m. We look at the tie at the top of list . If this tie contains woman w and some free woman , then w is co-satellitic, otherwise she is not. (Recall that the free women proceed matched ones in a tie.) To facilitate checking whether a given man is subsatellitic, each man has the counter of free women incident with him, and whenever a woman becomes matched and moves herself to the end of the ties, men decrease their respective counters. The number of movements in the ties is upperbounded by the sum of the lengths of lists as once a woman becomes matched, she stays so. □
Let us finally make the following remark.
If we break ties and run the classic Gale-Shapley algorithm, then the cardinality of the computed matching depends on the order in which we break ties. Algorithm GS Modified outputs a matching that would have been output by the GS algorithm if ties were broken as follows. Men’s lists would be identical to those at the beginning of Algorithm GS Modified but for one thing: if at some point during running Algorithm GS Modified, man m proposes to a co-satellitic woman w, and as a result m gets matched to w, and w’s partner gets matched to his satellite , then a tie on would be broken in such a way that comes before w. Every tie t on a woman w’s list would be first broken into in such a way that denotes the first man of t to whom w got matched without becoming co-satellitic, and assuming that it happened at some step S, denotes the first man of t who proposed to w after step S, denotes the second man of t, who proposed to w after step S and so on. Next we would make the following alterations on women’s lists: if at some point, man m proposes from to a co-subsatellitic woman w matched to , then a tie on would be broken in such a way that m comes before .
4. Extension to Bipartite Stable b-Matchings
Suppose we have a simple bipartite graph , where and are disjoint sets, and a function b: . Then a subset is called a b-matching if for each it is , where denotes the degree of vertex v in the graph . We refer to the vertices of U and W as U-agents and W-agents, respectively. Each U-agent u of U has a preference list of a subset of W-agents, and analogously, each W-agent w has a preference list of a subset of U-agents. The preference lists are linearly ordered lists of ties. The majority of the terminology for stable matchings goes through for stable b-matchings. Instead of saying that some agent or vertex is free, we will use the term unsaturated: agent v is unsaturated in a b-matching M if and if , then we will say that v is saturated. For any agent v we will denote the set : by . A pair is blocking for a b-matching M if (1) u and w are mutually acceptable; (2) u is unsaturated or prefers w to one of the W-agents of ; and (3) w is unsaturated or prefers u to one of the U-agents of . A b-matching M is said to be stable if it does not admit a blocking pair. As previously, we are interested in finding a stable b-matching of largest size. Let us also note that if for each u in U we have , then the problem is known under the name Hospitals-Residents problem or one-to-many stable matching problem.
Alternating paths and cycles are defined for b-matchings in an analogous way as for matchings, but we do not require paths and cycles to be simple, i.e., an alternating path P w.r.t. a b-matching M is defined as any sequence of edges such that the edges alternate between M-edges and edges of E∖M, and an alternating cycle C w.r.t. M is defined as an alternating path (w.r.t. M) that ends and begins with the same vertex, i.e., the sequence of edges has the form . As before, for any two b-matchings M and , the symmetric difference can be partitioned into maximal alternating paths and cycles (i.e., no two alternating paths from the partition can be combined to form one alternating path). A given stable b-matching M might not be a 3/2-approximation of , where denotes a stable b-matching of maximum size, only if the underlying graph contains a dangerous path defined as follows. If M is a stable b-matching, then a path is called dangerous with respect to M if u and are U-agents, w and are W-agents, is in M, are not in M, w and u are unsaturated in M, and are saturated in M, and is not a blocking pair for the b-matching . Since is not blocking for M, w is not better for than any of the W-agents currently belonging to , and analogously, u is not better for than any of the U-agents currently belonging to . Thus if P is dangerous, then either w and are equally good for and then P is called a masculine dangerous path, or u and are equally good for and then P is called a feminine dangerous path.
An approximation algorithm for finding stable b-matchings is constructed analogously to the algorithm for finding stable matchings. U-agents play the role of men and W-agents play the role of women. For convenience, we shall refer to a U-agent as "he" and to a W-agent as "she". We adapt the terminology from the one-to-one setting to the current one as follows.
- If a U-agent u is in , and there is at least one unsaturated W-agent different from w such that w and are equally good for u, then we say that is a satellite of u w.r.t. w and u is satellitic w.r.t. w.
- W-agent w belonging to such that u is satellitic w.r.t. w is said to be co-satellitic.
- If is such that w is unsaturated and there is at least one unsaturated W-agent such that w and are equally good for u, then e is called special, and consequently, is also called special.
- If a U-agent u has at least one unsaturated W-agent incident with him, then he iscalled subsatellitic.
- A saturated and not co-satellitic W-agent such that u is subsatellitic is said to be co-subsatellitic w.r.t. if and u and are equally good for her.
- By a worst U-agent belonging to we will mean any U-agent such that there is no other U-agent who is worse for w than u.
Algorithm ASBM (short for Approximate Stable b-Matching)
Each U-agent u’s preference list is organized in such a way that if contains a tie t, then unsaturated W-agents in t come before saturated W-agents in t. At the beginning, all W-agents are unsaturated and ties on U-agents’s lists are broken arbitrarily, and in the course of running the algorithm, whenever W-agent w becomes saturated for the first time, we move her to the end of every tie she belongs to.
while there exists an unsaturated U-agent u with a nonempty list or a nonempty list
if , then
W-agent at the top of u’ s list
if is not special, then remove w from
if w is unsaturated, then
else if w is co-satellitic, then
let be a satellite of a U-agent w.r.t. w
if is not special, then remove from
∖
else if w prefers u to a worst U-agent in , then
let denote any worst U-agent belonging to
∖
if w is co-subsatellitic w.r.t. , then add w to the end of list
else if w is co-subsatellitic w.r.t. u, then add w to the end of list .
else
W-agent at the top of u’ s list
remove w from
if w is co-subsatellitic w.r.t. u, then
let denote a subsatellitic U-agent in equally good for w as u
∖
if w is co-subsatellitic w.r.t. , then add w to the end of
5. Correctness of Algorithm ASBM
The correctness of Algorithm ASBM is proved in a very similar way as the correctness of Algorithm GS Modified.
Lemma 3.
- If a W-agent becomes saturated, she will stay saturated.
- A co-satellitic W-agent w accepts every proposal. Once a saturated W-agent is not co-satellitic, she cannot become co-satellitic later.
- A W-agent can reject u only if w is saturated and a) u is satellitic w.r.t. w (w is co-satellitic), or b) w is not co-satellitic, u is one of the worst U-agents belonging to , and w receives a proposal from who is better for w than u, or c) w is not co-satellitic and u is one of the worst U-agents belonging to , u is subsatellitic, and w is co-subsatellitic w.r.t. who proposes from
- A saturated W-agent w who is not co-satellitic can accept a U-agent only if is at least as good for w as a worst U-agent ; moreover if is equally good for w as u, then w accepts only if w is co-subsatellitic w.r.t. and proposes from .
The proof of Lemma 3 is very similar to that of Lemma 1 and follows directly from the description of Algorithm ASBM.
Theorem 2. Let M denote a b-matching computed by Algorithm ASBM. Then M is a -approximation of an optimal stable b-matching.
Proof. We will show that the underlying graph does not contain blocking pairs and dangerous paths with respect to M. The non-existence of a dangerous path for the stable matching found guarantees the approximation ratio .
Suppose that is a blocking pair. Agent u is either unsaturated or there exists worse for u than w. It means that at some point u proposed to w from when edge was not special. If u’s proposal to w was rejected, then at that point w was saturated and not co-satellitic, and the worst was at least as good as u for w (by Lemma 3), and thus (also by claim 4 of Lemma 3) w could not later become matched to some who is worse for w than u. Therefore u got accepted then and later got rejected. Since at the moment of that proposal edge was not special, u was not satellitic w.r.t. w (and clearly could not become satellitic later.) By claim 3 of Lemma 3, W-agent w was not co-satellitic at the moment of rejecting u, and the worst U-agent belonging to was u. Therefore by claim 4 of Lemma 3, w could not later become matched to some who is worse for her than u. A contradiction.
Suppose now that the graph contains a masculine dangerous path such that . Thus u is satellitic w.r.t. w and w is co-satellitic. It means that at some point proposed to w from when edge was not special. Then w was either co-satellitic, because she is co-satellitic now, or unsaturated. Therefore got accepted. Later on he was clearly rejected. However, by claim 3 ofLemma 3 and the description of the algorithm ABSM, this is impossible, because a co-satellitic w rejects only U-agents who are satellitic w.r.t. w.
Finally, suppose that the graph contains a feminine dangerous path such that . Thus w is co-subsatellitic w.r.t. , and u is subsatellitic. At some point proposed to w from when edge was not special. If he got rejected, then w was not co-satellitic, and a worst U-agent was equally good for her as and hence as u. By the description of the algorithm, at that point w was co-subsatellitic w.r.t. , and added w to the end of list . If he was accepted (i.e., when he was proposing from and edge was not special), then later he was rejected, and by the description of the algorithm, he also must have added w to the end of list . When proposed to w from , w was still co-subsatellitic w.r.t. (because w is co-subsatellitic w.r.t. now), hence was accepted (because proposing from is not subsatellitic) and could not have got rejected later if there were still subsatellitic U-agents matched with w who were equally good as for w. A contradiction. □
6. Data Structures and Running Time
Each agent a (either a U-agent or a W-agent) has a preference list , which is a list of lists, i.e., we have a list for each tie. For each list we have access to both its first and last element.
Each agent has a pointer to their position in every tie they belong to (here a 1-element list is also considered a tie). Whenever W-agent w gets saturated for the first time, w goes over her whole list and moves herself to the end of every tie she belongs to, as explained in the description of Algorithm ASBM. This operation takes time.
Every W-agent w stores information about U-agents currently belonging to in a priority queue. U-agents belonging to who are equally good for w are kept in one list, thus the priority queue contains lists. Each such list is associated with a priority value, which is the position the U-agents on that list have on the initial list , i.e., the U-agents that are at the top tie of list have priorityequal to 1. We implement a priority queue as a balanced tree with an additional pointer to the maximum element. We will use the following operations:
- finding the maximum element (takes time)
- deleting a given element (takes time, where n denotes the number of elements in apriority queue)
- inserting a given element (takes time)
- finding an element having a certain priority value (takes time).
After deleting or inserting an element we update the pointer to the maximum element, which takes time.
Each U-agent u keeps track of W-agents currently belonging to in a list.
Each U-agent u has the counter of the number of unsaturated W-agents incident with him, and whenever a saturated W-agent moves herself to the end of the ties, U-agents also decrease respective counters. Therefore checking if u is subsatellitic takes constant time.
Each W-agent w has a separate list of satellitic U-agents w.r.t. w belonging to . Every time w gets matched to some new U-agent u who is satellitic with respect to w, she adds u to . When we want to check if w is co-satellitic, we go over and for each check if u is still satellitic w.r.t. w. Checking if a U-agent u is satellitic w.r.t. w can be done as follows. W-agent w has a pointer to her position in a tie t on . We also have access to the first element of t. If the first element of t is unsaturated, then it means that u is satellitic w.r.t. w. This way we can also find a satellite of a satellitic U-agent in . If u is not satellitic w.r.t. w, we remove u from , otherwise we do an appropriate exchange. Once u is removed from , he will not be added to again. It is so since once u has no unsaturated W-agents equally good for him as w on his list, it will stay so. Hence the overall time Algorithm ASBM spends on is .
Each list describing a tie within the priority queue of U-agents belonging to is organized in such a way that subsatellitic U-agents proceed U-agents that are not subsatellitic. Whenever a U-agent u ceases to be subsatellitic, we move him to the end of every list in every priority queue he is in. Moving u to the end of every such list takes time. Every u ceases to be subsatellitic at most once in the course of running the algorithm. Therefore the total time spent on moving U-agents who ceased to be subsatellitic to the ends of priority queues does not exceed . This way, to see if w is co-subsatellitic w.r.t. u, we look at the list in the priority queue containing U-agents in that are equally good for w as u and see if the first U-agent on this list is subsatellitic.
Each U-agent u makes a proposal to every W-agent on at most twice and to every W-agent on at most once. The second statement follows from the observation that whenever an agent u proposes from , he does not have any unsaturated W-agents on . After each such proposal, Algorithm ASBM performs at most two insertions and at most one deletion on a suitable priority queue. Each insertion and each deletion into a priority queue containing U-agents belonging to takes at most time.
Summing all the arguments together, we get that the running time of Algorithm ASBM is , where m denotes the number of edges in G. If , then we can swap the roles of U-agents and W-agents. Therefore we can state the following.
Theorem 3. The running time of Algorithm ASBM is , where and m denotes the number of the edges.
Acknowledgments
I would like to thank anonymous referees for many helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdulkadiroglu, A.; Pathak, P.A.; Roth, A.E. Strategy-proofness vs. Efficiency in matching with indifferences: Redesigning the NYC high school match. Am. Econ. Rev. 2009, 99, 1954–1978. [Google Scholar] [CrossRef]
- Erdil, A.; Haluk, E. What’s the Matter with Tie-Breaking? Improving Efficiency in School Choice. Am. Econ. Rev. 2008, 98, 669–689. [Google Scholar]
- Gale, D.; Shapley, L.S. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Halldórsson, M.M.; Irving, R.W.; Iwama, K.; Manlove, D.; Miyazaki, S.; Morita, Y.; Scott, S. Approximability results for stable marriage problems with ties. Theor. Comp. Sci. 2003, 306, 431–447. [Google Scholar] [CrossRef]
- Halldórsson, M.M.; Iwama, K.; Miyazaki, S.; Yanagisawa, H. Improved approximation results for the stable marriage problem. ACM Trans. Algorithms 2007, 3, 30. [Google Scholar] [CrossRef]
- Irving, R.W.; Manlove, D. Finding large stable matchings. ACM J. Exp. Algorithmics 2009, 14. article 2. [Google Scholar] [CrossRef]
- Iwama, K.; Miyazaki, S.; Okamoto, K. A ()-approximation algorithm for the stable marriage problem. IEICE Trans. 2006, 89-D, 2380–2387. [Google Scholar]
- Iwama, K.; Miyazaki, S.; Yamauchi, N. A ()-approximation algorithm for the stable marriage problem. Algorithmica 2008, 51, 342–356. [Google Scholar] [CrossRef]
- Iwama, K.; Miyazaki, S.; Yamauchi, N. A 1:875-approximation algorithm for the stable marriage problem. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA, New Orleans, January 7–9, 2007; Bansal, N., Pruhs, K., Stein, C., Eds.; pp. 288–297.
- Iwama, K.; Miyazaki, S.; Yanagisawa, H. A 25/17-Approximation algorithm for the stable marriage problem with one-sided ties. Lect. Notes Comp. Sci. 2010, 6347, 135–146. [Google Scholar]
- Király, Z. Better and simpler approximation algorithms for the stable marriage problem. Algorithmica 2011, 60, 3–20. [Google Scholar] [CrossRef]
- Király, Z. Approximation of Maximum Stable Marriage; Technical Report TR-2011-0; The Egerváry Research Group: Budapest, Hungary, 2011. [Google Scholar]
- Lovász, L.; Plummer, M.D. Matching Theory. In Annals of Discrete Mathematics 29, North-Holland, Amsterdam, 1986.
- Manlove, D.; Irving, R.W.; Iwama, K.; Miyazaki, S.; Morita, Y. Hard variants of stable marriage. Theor. Comput. Sci. 2002, 276, 261–279. [Google Scholar] [CrossRef]
- McDermid, E. A 3/2-approximation algorithm for general stable marriage. In Proceedings of the Automata, Languages and Programming, 36th International Colloquium, ICALP, Rhodes, Greece, 2009; Albers, S., Marchetti-Spaccamela, A., Matias, Y., Nikoletseas, S.E., Thomas, W., Eds.; pp. 689–700.
- Paluch, K.E. Faster and simpler approximation of stable matchings. In Proceedings of the WAOA ’11: 9th Workshop on Approximation and Online Algorithms, Saarbruecken, Germany, 2011; Solis-Oba, R., Persiano, G., Eds.; pp. 176–187.
- Yanagisawa, H. Approximation Algorithms for Stable Marriage Problems. Ph.D. Thesis, Kyoto University, Kyoto, Janpan, 2007. [Google Scholar]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).