2D/3D Pattern Formation Comparison Using Spectral Methods to Solve Nonlinear Partial Differential Equations of Condensed and Soft Matter

Abstract

It is well known that nonlinear partial differential equations (NLPDEs) can only be solved numerically and that fourth-order NLPDEs in their derivatives require unconventional methods. This paper explains spectral numerical methods for obtaining a numerical solution by Fast Fourier Transform (FFT), implemented under Python in tis version 3.1 and their libraries (NumPy, Tkinter). Examples of NLPDEs typical of Condensed Matter Physics to be solved numerically are the conserved Cahn–Hilliard, Swift–Hohenberg and conserved Swift–Hohenberg equations. The last two equations are solved by the first- and second-order exponential integrator method, while the first of these equations is solved by the conventional FFT method. The Cahn–Hilliard equation, a phase-field model with an extended Ginzburg–Landau-like functional, is solved in two-dimensional (2D) to reproduce the evolution of the microstructure of an amorphous alloy Ce₇₅Al_{25 − x}Gax, which is compared with the experimental micrography of the literature. Finally, three-dimensional (3D) simulations were performed using numerical solutions by FFT. The second-order exponential integrator method algorithm for the Swift–Hohenberg equation implementation is successfully obtained under Python by FFT to simulate different 3D patterns that cannot be obtained with the conventional FFT method. All these 2D/3D simulations have applications in Materials Science and Engineering.

1. Introduction

It is of paramount importance to find the numerical solutions of different nonlinear partial differential equations (NLPDEs). These are ubiquitous in various areas of science, such as nonlinear physics, nonlinear chemistry, mathematical biology and computational science, and engineering in materials. The numerical solution of an NLPDE is an essential ingredient of two-dimensional (2D) and three-dimensional (3D) computational simulation. There are several methods for finding a numerical approximation of these equations. Pseudo-spectral methods are based on replacing NLPDEs with an equation of ordinary difference [1,2,3,4]. These types of procedures are challenging to implement in a high-level programming language. Nevertheless, the spectral methods of implementation are easy under Python and their libraries [5,6,7,8,9] to develop numerical 2D and 3D solutions, because it reduces the calculation time of the numerical solution compared to Euler’s and finite difference methods, which are based on derivative approximation [10,11]. In this sense, new libraries under Python have been developed to facilitate 3D computational simulation such as Mayavi [12], PyVista [13], or FiPy, which uses the finite volume method to reduce the NLPDE to a form tractable to linear solvers [14], or libraries such as FEniCS [15,16] that use more general theoretical schemes such as the Finite Element Method for the same purpose.

There is also extensive use of FFT both directly and indirectly as a component in other algorithms for microstructure simulation of various materials [10,17]. Specifically, the microstructure evolution was simulated due to the substitution of Ga in the amorphous alloy Ce₇₅Al_{25 − x}Ga_x in 2D [4] and 3D systems using the phase-field method based on the Cahn–Hilliard equation by the conventional FFT method. This algorithm is described in detail, and was used as the basis for the development and implementation under Python, and the conserved and not conserved Swift–Hohenberg equations by the first- and second-order exponential integrative method were also used, respectively.

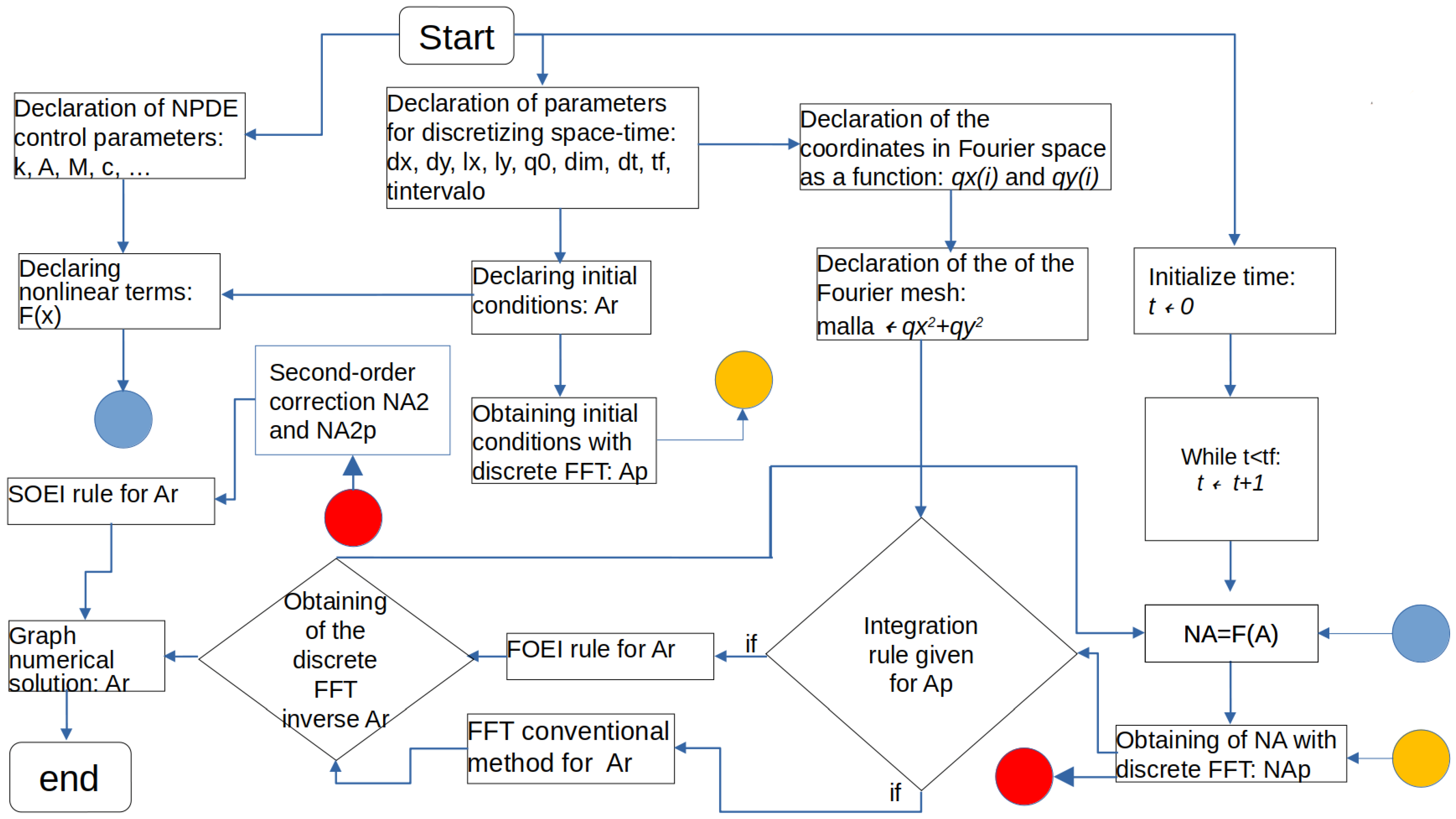
2. Materials Mathematical Models and Their Integration Rules

Cahn–Hilliard equation: As an example, a phase-field model based on the Cahn–Hilliard equation is used to understand the evolution of the microstructure due to the substitution of Ga in the amorphous alloy Ce₇₅Al_{25 − x}Ga_x [4,17]. The spatial–temporal evolution is expressed for the Cahn–Hilliard equation (CHE):

$${\displaystyle \frac{\partial c}{\partial t}}={𝛻}^{2}M\left({\displaystyle \frac{\delta F}{\delta c}}\right),$$

(1)

Another requirement for any problem to be modeled by any phase-field model is that a free energy function must be defined (for isothermal cases and non-isothermal cases, functional free entropy) depending on the order parameter [4]. The general expression of the free energy functional is shown in Equation (2) [4,10]:

$$F[c]={\int }_V\left[f\left(c\right)+{\displaystyle \frac{1}{2}}k{\left(𝛻c\right)}^2+{\displaystyle \frac{\alpha }{2}}{\left({𝛻}^{2}c\right)}^2\right]dr$$

(2)

The first term on the left side of the equation is a free energy density of the global phase as a function of concentration, the second term denotes the energy of the interface due to the gradient present in the concentration, and the last term represents a lowest-order correction to free energy due to compositional gradients [18,19]. Note that in this section, α = 0 for simplicity and as a first approximation and κ is the energy coefficient of the gradient. The chemical energy f(c) is described for example, as a single, double-well potential:

$$f\left(c\right)=A{c}^2{\left(1-c\right)}^2-{\displaystyle \frac{\alpha }{2}}{c}^2$$

(3)

where A is a positive constant, which controls the magnitude of the energy barrier between two phases of equilibrium. It is well known that the numerical iteration equation from the conventional FFT method for Equation (1) is as [10,20]:

$${\left\{c\right\}}_q^{n+1}={\displaystyle \frac{{\left\{c\right\}}_q^n-∆t{k}^{2}M{\left\{\frac{\delta f}{\delta c}\right\}}_q^n}{1+∆t{q}^{4}Mk}},$$

(4)

where q is a mode in Fourier space. The parameters used were obtained from the literature [4], and others were modified. In Appendix A,

Table A1. Control parameter values of Figure 2 and Figure 3 in code source for the CHE.

Parameter	Figure 2a	Figure 2c	Figure 3a	Figure 3b	Figure 3c
L × L	1282	1283	643	1283	1282
C0	0.5	0.5	0.75	0.75	0.75
K	0.01	0.001	0.001	0.001	0.001
M	1.0	1.0	1.0	1.0	1.0
A	1.0	1.0	1.0	1.0	1.0
T	1.0	0.1	1.0	3.0	1.0
dx	0.5	0.5	0.5	0.5	0.5
Dt	0.001	0.001	0.0001	0.001	0.001
Iterations	1000	100	10,000	3000	1000

, each of them is shown. Section 4.1 presents the source code that solves the Cahn–Hilliard phase-field equation with the FFT method following the algorithm in ref. [4] to understand the nature of the evolution of the microstructure due to the substitution of Ga in the amorphous alloy Ce₇₅Al_{25 − x}Ga_x. The 2D simulation is used with the Python 3.9.1 program (and libraries: NumPy, math, Tkinter) [5,6,7,8,9].

Swift–Hohenberg equation: The first-order exponential integrative method [21,22] is based on the exact integration of the linear part of the initial value problem because the linear part is integrated exactly. This can help mitigate the rigidity of a differential equation. Exponential integrators can be constructed to be explicit or implicit for numerical ordinary differential equations or serve as time integrators for numerical partial differential equations. An advantage of this method is the ability to solve Swift–Hohenberg type equations [18,23]:

$${\displaystyle \frac{\partial \psi }{\partial t}}={\gamma }^2\psi +g{\psi }^2-{\psi }^3-\lambda {\left(1+{𝛻}^2\right)}^2\psi +\eta (r,t)$$

(5)

This cannot be solved using the method described in Section 4.1 and has recently been used to obtain porous polymeric materials, such as in Ref. [20]. If Equation (5) is to be used following the 3D printing technique, it would not be possible to obtain porous polymeric materials.

The Swift–Hohenberg equation has now been solved by exponential integrator methods [21,22], such as the second-order implicit pseudo-spectral method developed in reference [2,18,24,25]. The iteration numerical discretization equation is as follows:

$$\tilde{\psi }\left(t+∆t\right)=exp\left(b∆t\right)\tilde{\psi }\left(t\right)+{\tilde{N}}_0\left[{\displaystyle \frac{exp\left(b∆t\right)-1}{b}}\right]+{\tilde{N}}_1\left[{\displaystyle \frac{exp\left(b∆t\right)-\left(1+b∆t\right)}{b^2∆t}}\right]$$

(6)

where $b(\gamma ,q)=({\gamma }^2-\lambda ){\left(1-q^2\right)}^{2}dt$, and ${\tilde{N}}_0$ and ${\tilde{N}}_1$ are the nonlinear terms such that

$$\begin{array}{l}\widetilde{N_0}=\left[g\widetilde{{\varphi }^2}\left(q,t_0\right)-\widetilde{{\varphi }^3}\left(q,t_0\right)\right],\\ {\tilde{N}}_1=\left\{\left(g{\widetilde{{\varphi }^2}}_{temp}-{\widetilde{{\varphi }^3}}_{temp}\right)\left(q,t_0+∆t\right)-\left[g\widetilde{{\varphi }^2}-\widetilde{{\varphi }^3}\right]\left(q,t_0\right)\right\}\end{array}$$

(7)

where again q represents a mode in Fourier space. In Python simulation, this method has been widely used to simulate grain boundaries of crystal lattices [24,25], ferrofluids [18], and deblock copolymer grain boundary dynamics [3], but they are complicated methods to implement in 2D and 3D in programming languages of high level such as Fortran to obtain a numerical solution of the Swift–Hohenberg equation (SHE).

Conserved Swift–Hohenberg equation: The conserved Swift–Hohenberg equation is perhaps the simplest example of a 3D pattern-forming system used in crystal phase-field models [26] (see Equation (8) with g = 0). Moreover, when using the Swift–Hohenberg equation with a conserved order parameter, one can achieve the simplest microscopic description of the thermodynamic transition from a fluid state to a crystalline state [26,27]. Dissipative dynamics models are commonly associated with a proposed functional that has a conserved [26] or non-conserved order parameter [28]. The nonlinear partial differential model of a Swift–Hohenberg with a conserved order parameter is such as [26,29]:

$${\displaystyle \frac{\partial \psi }{\partial t}}=M_{\psi }{𝛻}^2\left\{-\varepsilon \psi -g{\psi }^2+{\psi }^3-\lambda {\left(1+{𝛻}^2\right)}^2\psi \right\}$$

(8)

The method used to obtain the numerical solution was the FFT based on the implicit pseudo-spectral way [2]. The iteration numerical discretization equation is similar to Equation (6), but with the modification $b(\varepsilon ,q)=q^2(\varepsilon -\lambda ){\left(1-q^2\right)}^{2}dt$,

$$\begin{array}{l}\widetilde{N_0}=q^2\left[g\widetilde{{\varphi }^2}\left(q,t_0\right)-\widetilde{{\varphi }^3}\left(q,t_0\right)\right],\\ {\tilde{N}}_1=q^2\left\{\left[g{\widetilde{{\varphi }^2}}_{temp}-{\widetilde{{\varphi }^2}}_{temp}\right]\left(q,t_0+∆t\right)-\left[g\widetilde{{\varphi }^2}-\widetilde{{\varphi }^3}\right]\left(q,t_0\right)\right\}\end{array}$$

(9)

The reader can see a detailed description of Equations (6) and (9) in Refs. [2,20].

On the other hand, in a recent study [30], a model like Equation (8) can be seen, but with g = 0 and with term $\gamma {\left|\nabla \mathsf{\psi }\right|}^2$ being added to this equation. So, the conserved Swift–Hohenberg equation is transformed into a non-potential equation, and due to that, there is no functional associated with Equation (8). Therefore, the non-potential conserved Swift–Hohenberg equation is written as

$${\displaystyle \frac{\partial \psi }{\partial t}}=M_{\psi }{𝛻}^2\left\{-\varepsilon \psi +{\psi }^3-\lambda {\left(1+{𝛻}^2\right)}^2\psi \right\}+\gamma {\left|\nabla \mathsf{\psi }\right|}^2$$

(10)

where $\gamma$ is a parameter control such as can be selected conveniently to demonstrate the equivalence between Equations (9) and (10) in Fourier space as follows. Equation (10) in this space takes the form:

$${\displaystyle \frac{d\tilde{\psi }}{dt}}=-q^2{M}_{\psi }\left[-\epsilon \tilde{\psi }+\widetilde{{\psi }^3}-\lambda {\left(1-q^2\right)}^2\right]+\gamma {\displaystyle \frac{q^2}{2}}\widetilde{{\psi }^2},$$

(11)

where the non-potential term in the Fourier space is such that

$${\left|𝛻\psi \right|}^2=𝛻\psi ·𝛻\psi ={\displaystyle \frac{{𝛻}^2{\psi }^2}{2}}-\psi {\nabla }^2\psi ⟹\stackrel{~}{{\left|𝛻\psi \right|}^2=-{\displaystyle \frac{q^2}{2}}}\widetilde{{\psi }^2}-\sqrt{2\pi }\tilde{\psi }\ast \widetilde{{\nabla }^2\psi }={\displaystyle \frac{q^2}{2}}\widetilde{{\psi }^2}$$

While Equation (8) in Fourier space is

$${\displaystyle \frac{d\tilde{\psi }}{dt}}=-q^2{M}_{\psi }\left[-\epsilon \tilde{\psi }+\widetilde{{\psi }^3}-\lambda {\left(1-q^2\right)}^2\right]+g{q}^2{M}_{\psi }\widetilde{{\psi }^2}$$

(12)

So, equating (11) and (12) and simplifying similar terms, we obtain that

$$\gamma {\displaystyle \frac{q^2}{2}}\widetilde{{\psi }^2}=g{q}^2{M}_{\psi }\widetilde{{\psi }^2}$$

Hence, $\gamma =2g{M}_{\psi }$. It is the equivalent control parameter in Fourier space. Thus, the 2D/3D numerical solutions obtained for the conserved Swift–Hohenberg equation are similar to its associated equation in the non-potential form according to the scaling determined by the value of the $\gamma =2g{M}_{\psi }$ parameter.

3. Materials and Methods

The Equations (4), (6), (7), and (9) were solved with the algorithm present in Figure 1, whose pseudo-code is shown in Algorithm 1. In this case, the programming language used takes on importance because it is an intermediate language, which allows for better use of the RAM memory of the computer equipment used to implement a specific numerical method. Furthermore, it is well known that the numerical methods implemented in our research are more efficient than finite difference methods. This implies that the combination of the algorithm and intermediate programming language has a computational efficiency greater than or equal to that of high-level programming languages.

Algorithm 1 was implemented under Python by means of the implicit pseudo-spectral method described in Ref. [2], which is extended easily to 3D space. A spatial domain is discretized by a mesh of N_x × N_y × N_z nodes for any of these equations and is an approach that applies the discrete Fourier transform to obtain the solution of the corresponding scalar field. This method provides optimal accuracy in the rate of convergence for smooth solutions. The nonlinear terms calculus is integrated using an exponential propagation procedure described in detail in Refs. [3,18,31] with the nonlinear terms being handled explicitly in Equation (6) by means of a fully implicit procedure, while the conventional spectral method used to solve Equation (4) is implemented in analogous form to the way followed in Equation (6), but without employing an exponential propagator. For a better approximation, nonlinear terms can be treated as a linear system of differential equations modified by a nonlinear forcing term. These terms are integrated by a predictor–corrector method to second-order. It can be shown that the overall technique is second-order accurate in a time step bigger than with the finite difference methods [27]. The implicit pseudo-spectral method is extended to array algorithms as follows. It is well known that the Fourier transform changes to a gridded cubic space (GCS) with a mesh of N_x × N_y × N_z nodes in a Fourier transformed (FTS) with (q_x)_i × (q_y)_j × (q_z)_k node numbers such that

$$-\left({\displaystyle \frac{N_x}{2}}-1\right)\le i\le N_x/2,-\left({\displaystyle \frac{N_y}{2}}-1\right)\le i\le N_y/2\mathrm{and}-\left({\displaystyle \frac{N_z}{2}}-1\right)\le i\le N_z/2.$$

The equations that define the coordinates of each point on the GCS mesh are

$$x_i={\displaystyle \frac{\left(i-1\right)L_x}{N_x}},i=1,\dots ,N_x,y_j={\displaystyle \frac{\left(j-1\right)L_y}{N_y}},j=1,\dots ,Ny,z_k={\displaystyle \frac{\left(k-1\right)L_z}{N_z}},k=1,\dots ,N_z$$

where $L_x,L_y,$ and $L_z$ are the dimensions of the spatial region in the x, y, and z directions. Furthermore, the points on the FTS mesh are such that ${\left(q_x\right)}_i={\displaystyle \frac{2\pi i}{L_x}},{\left(q_y\right)}_j={\displaystyle \frac{2\pi j}{L_y}},{\left(q_z\right)}_k=2\pi k/L_z$. To solve the SHE [Equation (6)] a random initial conditions array from GCS was developed and then the numerical method was applied under the array of FTS of ${\left(q_x\right)}_i\times {\left(q_y\right)}_j\times {\left(q_z\right)}_k$ nodes. The “NumPy” library [9] for Python distribution allows us to evaluate simultaneously the implicit pseudo-spectral algorithm method in the FTS matrix utilizing an initial conditions matrix seed, in which the discrete Fourier transform is applied. The NumPy library contains the FFT.py module that is a simple interface to the FFTPACK, FORTRAN library, which is a powerful standard library for conducting Fast Fourier Transforms of real and complex data sets. This implies a higher computational efficiency, for example to calculate the nonlinear terms in Fourier space at all the time steps: the GCS array is taken to calculate the nonlinear terms given in Equation (5), for which 7 arithmetic operations need to be performed. The GCS array has a dimension of 128 × 128 and 16,384 nodes (in the 2D case) or a dimension of 128 × 128 × 128 and 2,097,152 nodes (in the 3D case), where the number of nodes is multiplied by 7 in each case. That is, for the 2D case, it is required to perform 16,384 × 7 = 114,688 operations, while for the 3D case, 2,097,152 × 7 = 14,680,064 operations. All these operations are performed using the GCS array given by the variable Ar and the function F(Ar), which are then transformed into an equal number of additional operations using the FTS array (see Figure 1: boxes connected by blue and yellow circles and lines 6, 7, 12, and 13). In total, 114,688 × 2 = 229,376 (in the 2D case or 29,360,128 operations for the 3D case) are the number of operations needed to simultaneously calculate the nonlinear terms in Fourier space for all time steps. The reader can calculate the number of operations to be performed in the case of meshes with dimensions of 256 × 256 nodes. In high-level programming languages, this computation process is serial and there is no simultaneous computation process. This is the main difference between Python with its libraries (NumPy [9], Tkinter [8], and Mayavi [12]) and conventional languages such as Fortran, C, Mathlab, and Mathematica, to name a few. Thus, the proposed algorithm is characterized by being modular, where each module establishes an array containing the information necessary to complete thousands of simultaneous operations (see lines 1 to 8 of the Algorithm and their scheme version of Figure 1). Furthermore, the efficiency of the calculation of operations is repeated for every time step and extends to the iterations necessary to complete any of the three numerical methods developed in this research work (see lines 10 to 19 of the Algorithm 1 and Figure 1): conventional FFT method, first-order exponential approximation (FOEI), and second-order exponential integration (SOEI), which are derived from the exponential time differentiation scheme with second-order Runge–Kutta approximation ETD2RK (see Section 4.4 and Appendix A,

Table A5. Comparison of computational time efficiency of the three different FFT methods where dx = 0.5, and with a mesh of 128 × 128 nodes.

Algorithm Type	Time (u. a.)	Time Step	Computational Time (s)	Iteration Number	${\mathit{q}}_0$	Morphology
Conventional FFT	14,000	0.01	2345.825	1400,000	5 dx	Lamellar Phase
Exponential of 1rt. order	370	0.001	728.485	360,000
Exponential of 2° order	90,000	0.1	1804.712	900,000
Conventional FFT	2000	0.01	333.719	200,000	1.0	Lamellar Phase
Exponential of 1rt. order	100	0.001	196.663	100,000
Exponential of 2° order	2000	0.1	43.287	20,000
Conventional FFT	150,000	0.01	265.035	15,000	5 dx	Labyrinths
Exponential of 1rt. order	----	0.001	----	----
Exponential of 2° order	90,000	0.1	188.352	9000
Conventional FFT	26,000	0.01	467.210	260,000	5 dx	Labyrinths
Exponential of 1rt. order	----	0.001	----	----
Exponential of 2° order	8000	0.1	164.248	80,000
Conventional FFT	1600	0.01	281.799	160,000	1.0	Dots and stripes
Exponential of 1rt. order	----	0.001	----	----
Exponential of 2° order	3000	0.1	60.485	30,000
Conventional FFT	10,000	0.01	190.490	100,000	5 dx	Dots and stripes
Exponential of 1rt. order	----	0.001	----	----
Exponential of 2° order	3000	0.1	63.377	30,000

). In the subsequent results sections, each of these methods and their implementation under Python and its libraries (NumPy [9], Tkinter [8], and Mayavi [12]) are described in detail. In the case of the numerical implementation of Equation (6), it is similar to the one described to solve Equations (8)–(12).

Algorithm 1: Pseudo-code of spectral methods to solve nonlinear partial differential equation.

1: Declaration of NPDE control parameters: k, A, M, c0, γ, g, λ, ε

2: Declaration of parameters for discretizing space-time: dx, dy, lx, ly, q0, dim = (lx,ly), dt, tf, tintervalo

3: Declaration of the coordinate in Fourier space as a function: qx(i)

4: Declaration of the coordinate in Fourier space as a function: qy(i)

5: Declaration of the Fourier mesh as an array of dimension dim: malla

6: Declaring nonlinear terms as a function: F(X)

7: Declaring initial conditions as an array: Ar

8: Obtaining initial conditions with discrete FFT as an array: Ap

9: Initialize time counter: t ← 0

10: While t < tf:

11:      t ← t + 1

12:      Nonlinear function call: NA = F(Ar)

13:      Obtaining of NA with discrete FFT: NAp

14:      Integration rule given for Equations (4), (6) and (7) or (6)–(9): Ap

15:      Obtaining of the discrete FFT inverse: Ar

16:      Nonlinear function call second: NA2 = F(Ar)

17:      Obtaining of NA with discrete FFT for the second time: NA2p

18:      Second-order correction of the integration rule: Ap

19:      Obtaining of the discrete FFT inverse for the second time: Ar

20:      if t % tintervalo ← 0:

21:          Graph numerical solution: Ar

22:      Updates the counter by an order of magnitude: tintervalo

23: end while

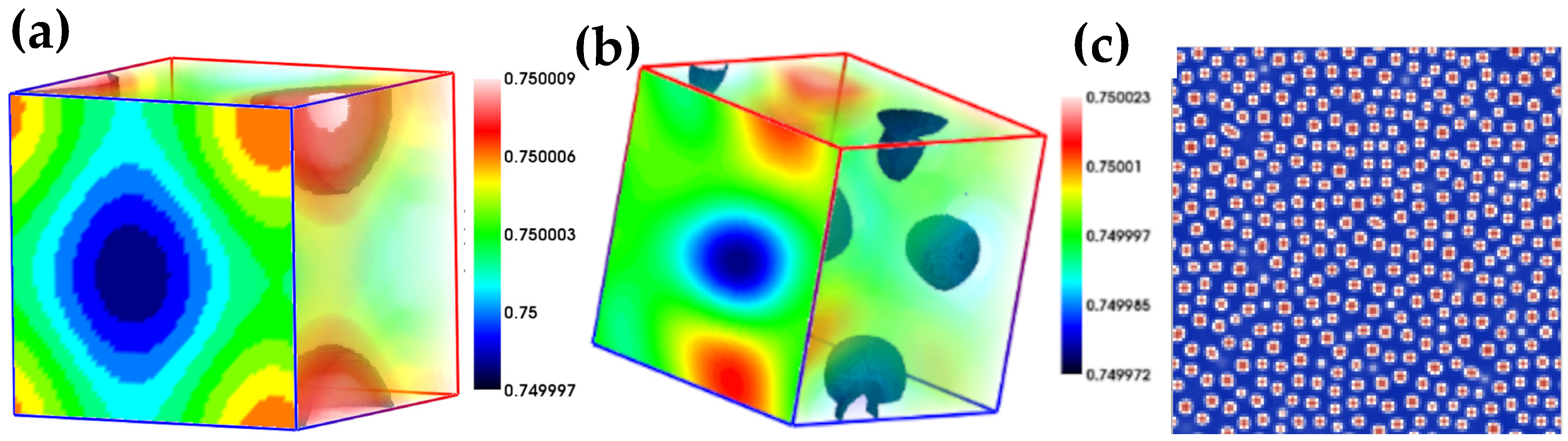
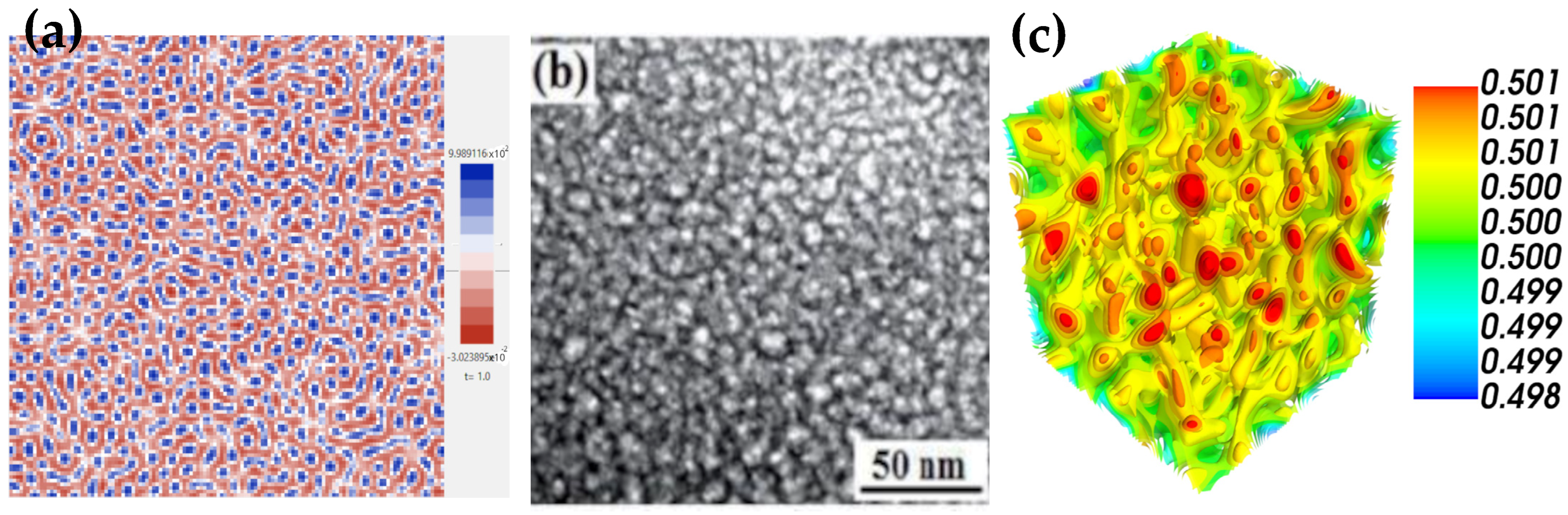
4. Results of the 2D and 3D Simulations

4.1. Python Implementation of the Cahn–Hilliard Equation: Source Code

In the following lines 1 to 59, the source code in Python programming language to solve the Cahn–Hilliard equation [see Equation (1)] employing its iteration equation, Equation (4), is presented.

Table 1. Interpretation of each of the code lines.

Number Line	Interpretation
1–4	Libraries used.
5–9	Simulation-specific material parameters.
7	Gradient energy coefficient.
10	Print the value of the control parameters on the screen.
8	Energy barrier value.
11–13	Time integration parameters.
14–15	Parameters of the simulation cell for the mesh. Distance between nodes in “x” and “y” directions.
16	Fourier mode of mesh.
18	Number of grid points in the x-direction.
19	Number of grid points in the y-direction.
20	Mesh size or total number of simulation grid points.
21	Iteration interval for plotting a 2D (or 3D) pattern.
23–31	Discretization of the Fourier space from −2π to 2π and from 0 to 2π.
33	Definition of the discretized Fourier Space.
34	Array forming the normalized Fourier space.
35	Print the dimension of the Fourier space array.
37–39	Fretché’s functional derivative statement.
41–43	Statement of random initial conditions from 3D space to the Fourier space.
44	Print FFT array dimension of initial condition.
45–47	Graphical part call with PyLab to display the numerical solution.
48–54	FFT algorithm.
47	Initialize variable t.
49	Cycle over time.
50	Counter.
51	Call the function of the nonlinear terms.
52	Transformation of nonlinear terms to Fourier space.
53	Modified Euler’s rule in Fourier space, Equation (4).
54	Inverse transforms the solution to real space.
55–57	Lines of code to display the solution at iteration t or at dimensionless time t dt.
58–59	Counter update for real-time display for a variable interval.

interprets the lines of the FFT algorithm and its source code.

1	from math import *
2	from numpy import *
3	from numpy.fft import *
4
5	k = 1.0
6	M = 1.0 #movilidad
7	A = 1.0 #barrera de energía
8	c0 = 0.5
9	print (“M=“, M, “c0=“, c0)
10	t0 = 0
11	tf = 150,000
12	dt = 0.01 (0.001 for 3D pattern)
13	dx = 0.5
14	dy = dx
15	q0 = 1.0 * dx
16	q02 = q0 * q0
17	lx = 128
18	ly = lx
19	dim = (lx, ly)
20	tintervalo = 100
21
22	def qx(i):
23	if (i < lx/2):
24	qxi = 2.0 * pi * float(i − 1)/(float(lx) * dx)
25	else:
26	qxi = −2.0 * pi * float(lx – i + 1)/(float(lx) * dx)
27	return qxi
28	def qy(j):
29	qyi = ((2.0 * pi) * float(j − 1))/(float(ly) * dy)
30	return qyi
31
32	malla = array([[qx(i) * qx(i) + qy(j) * qy(j) for j in range(1, int((ly + 2)/2 + 1))] for i in range(1, int(lx + 1))])
33	p2 = malla/q02
34	print (‘q02’, malla.shape)
35
36	def F(x):
37	s = 2 * A * x * (1 − x)*(1 − 2 * x)
38	return s
39
40	noise_str = 0.5 * 10**(−3)
41	A = uniform((c0 − noise_str), (c0 + noise_str), dim)
42	Ap = rfft2(A, dim, (−2, −1))
43	print (Ap.shape)
44	import numpy as np
45	import matplotlib.pyplot as plt
46	t = t0
47	while t < tf:
48	t = t + 1
49	NA = F(A)
50	Nap = rfft2(NA, dim, (−2, −1))
51	Ap = (Ap − dt * (p2 * M) * (NAp))/(1 + dt * (p2 * p2) * (M * k))
52	A = irfft2(Ap, dim, (−2, −1))
53	if t % tintervalo == 0:
54	plt.imshow(A, cmap =‘bwr’)
55	plt.imshow(A, cmap = ‘bwr’)
56	plt.title(“Cahn–Hilliard equation”)
57	plt.show()
58	if t == tintervalo * 10:
59	tintervalo = 10 * tintervalo

The source code includes functions for differential operations with boundary conditions, statistics, and other complementary functions to simplify the programming solutions of spatiotemporal PDENL. One feature is that the functions excluded in all operations to modify rows and columns on the edge of the matrix remain as periodic boundary conditions with line 43: Ap = rfft2(A, dim, (−2, −1)) and A = irfft2(Ap, dim, (−2, −1)) and their inverse. We can calculate the two-dimensional FFT of the random initial condition array in the Fourier space. A: the input array. Dim: the sequence of integers that form the FFT. Axes: the sequence of integers, axes on which to calculate the FFT.

The 2D simulation was performed for a square simulation cell with lx = 128, ly = 128 nodes with mesh cell size: dx = dy = 0.5. All parameters used in these simulations were with a mobility of M = 1.0, an energy barrier of A = 1.0, an energy coefficient of the gradient of k = 0.01, and α = 0, to reproduce phase separation patterns with initial average concentrations (0.5 and 0.75) during the time steps of 1000, without considering the fluid flow. The red and blue regions show the phases rich in Al and rich in Ga, respectively. The patterns generated are shown in Figure 2a,c.

The numerical microstructure simulated in this work with an initial composition of c_0 = 0.5 was compared with the experimental microstructure of the alloy Ce₇₅Al₂₁Ga₄ by micrograph of Ref. [4]. Both microstructures have approximately the same characteristics as the spinodal decomposition phases [see Figure 2a,b]. Comparing the experimental image, it can be noticed that the microstructures match, even more closely resembling the one we achieved than the 2D pattern of the literature simulation [17].

The 3D simulation was performed in a cell of mesh with 128 × 128 × 128 nodes with an initial concentration of 0.5, and for the concentration of 0.75, with a three-dimensional cell of mesh with 64 × 64 × 64 nodes and 128 × 128 × 128 nodes. In Figure 3, it is observed that when the initial concentration of the Ga phase is at 0.75, the microstructure is like droplets. In this case, lines 23–33 must be replaced by the next lines that extend the mesh to 3D:

• 23 def qx(i):
• 24  if (i < lx/2):
• 25       qxi = 2.0 * pi * float(i − 1)/(float(lx) * dx)
• 26        else:
• 27       qxi = −2.0 * pi * float(lx – i + 1)/(float(lx) * dx)
• 28        return qxi
• 29 def qy(j):
• 30        if (j < ly/2):
• 31      qyi = 2.0 * pi * float(j − 1)/(float(ly) * dy)
• 32        else:
• 33      qyi = −2.0*pi*float(ly − j + 1)/(float(ly) * dy)
• 34        return qyi
• 35 def qz(k):
• 36     qzi = ((2.0 * pi) * float(k − 1))/(float(lz) * dz)
• 37     return qzi
• 38 malla = array([[[qx(i) * qx(i) + qy(j) * qy(j) + qz(k) * qz(k) for k in range(1, int((lz + 2)/2 + 1))] for j in range(1, int(ly + 1))] for i in range(1, int(lx + 1))])

Also, lines 57 and 58 should be replaced in code of pages 6 to 8 by

• 57      print(A [64, 64, 64], “t=”, t * dt, “n=”, t)
• 58      G.display(A [32, :, :])
• 59      G.time(t * dt)
• 60      archive = open(“test3DFFT”+str(t)+“.pkl”,“wb”)
• 61      pickle.dump (A, archive)
• 62      archive.close()
• 63 if t == tintervalo * 10
• 64      tintervalo = 10 * tintervalo

Figure 3. (a) Three-dimensional structure using 64 × 64 × 64 nodes, dt = 0.0001, c = 0.75 to 10,000 iterations; (b) 3D structure using 128 × 128 × 128 nodes, dt = 0.001, c = 0.75 and 3000 iterations; (c) evolution of the microstructure based on an average initial concentration of 0.75, using 128 × 128 nodes, and dt = 0.001 with a total of 3000 iterations (see Table A1). The droplet-like morphologies observed at high Ga concentrations are consistent with previous reports in Ref. [17].

Figure 3. (a) Three-dimensional structure using 64 × 64 × 64 nodes, dt = 0.0001, c = 0.75 to 10,000 iterations; (b) 3D structure using 128 × 128 × 128 nodes, dt = 0.001, c = 0.75 and 3000 iterations; (c) evolution of the microstructure based on an average initial concentration of 0.75, using 128 × 128 nodes, and dt = 0.001 with a total of 3000 iterations (see Table A1). The droplet-like morphologies observed at high Ga concentrations are consistent with previous reports in Ref. [17].

Lines 57 to 59 plot the slices of the array solution “A”, while lines 60 to 61 are saved to a data file in pkl format, which can be plotted with library Mayavi. Finally, do not forget to add the pickle library using the command: import pickle.

4.2. Implementation Under Python for Numerically Solving the Swift–Hohenberg Equation

The implementation in Python of a simulation algorithm for the Swift–Hohenberg equation (SHE) using the first-order exponential method takes, as its basis, the algorithm described in Section 4.1. The origin of this numerical method is the exponential time differencing (ETD) scheme, which involves exact integration of the governing equations followed by an approximation of an integral involving the nonlinear terms [21,31]. In our case, the simplest method used to solve the SHE numerically is named ETD1, modifying the energy gradient coefficient parameters of lines 6, 7, and 8 of the code by λ, γ, and g. However, lines 41 and 42 were removed and substituted by initial condition A = uniform (−sqrt (gamma**2), sqrt (gamma**2, dim). Line 38 of the code is modified by the nonlinear terms of the Equations (6) and (7) as follows: s = g * x**2 − x**3, while for line 53, it is replaced by the following line:

Ap = exp(−(gama**2 − lamda * (1 − p2)**2) * dt) * Ap + (1 − exp(−(gama**2 lamda * (1p2)**2) * dt))  * Nap/(gama**2 − lamda * (1 − p2)**2),

which refers to the iteration rule of the first-order exponential method. In addition, the following lines corresponding to additive noise are added to the time counterpart (between lines 50 and 51): ruido = eta*uniform(−1.0, 1.0, dim) and their inverse transform: ruidop = rfft2(ruido, dim, (−2, −1)). Two-dimensional patterns were performed for a square simulation cell with mesh of lx = 128 and ly = 128 nodes and mesh step size of dx = dy = 0.05. All parameters used in these simulations were with a time interval dt = 0.01, a maximum grid separation size limited by q0 = 2π/λ0, and where the control parameters κ, λ, γ, and g are given in

Table A2. Control parameter values of Figure 4 for the implementation under Python of the SHE.

Parameter	Figure 4d	Figure 4e	Figure 4f	Figure 4g	Figure 4h	Figure 4i
L × L	1282	1282	1282	1283	1283	1283
T	5.0	20	0.001	5.0	20	0.001
$\epsilon$	0.0	0.0	1.0	0.0	0.0	1.0
$\gamma$	0.5	0.5	0.13	0.5	0.5	0.13
G	−3	−3	−1	−3	−3	−1
Dt	0.01	0.01	0.01	0.01	0.01	0.01
Iterations	500	2000	100,000	5500	2000	100,000

of Appendix A. For the 3D simulations, the same parameters were used. In Figure 4, the patterns obtained are shown. The extension to the 3D case is conducted in a similar way to the Cahn–Hilliard equation in Section 4.1, using 23 to 38 and 57 to 64.

Typically, the Swift–Hohenberg equation is used in 2D pattern formation simulations of deblock copolymers phase transitions [23,28], grain boundaries of crystal lattice [3,24,25], chaotic domain flows [2], and ferrofluid phases and alloy microstructures [20]. However, here, 2D patterns are presented of the Swift–Hohenberg equation applied to some biological systems as follows. In the pattern obtained with the parameters ε = 0, γ = 0.5, g = −3 at 5000 iterations, as shown in Figure 4d, we observed a couple of random dots that resemble the complex patterns found on the skin of the Potamotrygon motoro manta ray shown in Figure 4a.

In Figure 4e pattern with the same parameters as above, but at 20,000 iterations, a gut-like morphology is obtained in blue color in a homogeneous red phase. We can attribute it to the similarity it has with the bacterium Bacillus subtilis with a Gram-positive morphology with oval or cylindrical ellipsoidal spores shown in Figure 4b. Concerning the pattern with parameters = 1.0, γ = 0.13, and g = −1; (see Figure 4f), a series of ordered points is obtained, simulating an ordering of the atoms as in a crystal or with the morphology of a honeycomb as shown in Figure 4c.

4.3. Python Implementation for Numerically Solving the Cahn–Hilliard–Swift–Hohenberg Equation

The simplicity and ease of the implementation under Python of the previously explained mathematical models allow a special contribution to the creation of new mathematical models such as the Cahn–Hilliard–Swift–Hohenberg equation. This type of equation can be understood as a lowest-order correction of the free energy due to the composition of gradients in the Cahn–Hilliard equation. The derivation of the Cahn–Hilliard equation with the spatial terms of the Swift–Hohenberg equation from Equations (1) to (3) is presented in Appendix C. Similarly, based on the code described in Section 4.1 (FFT conventional method), line 53 is replaced by the following line:

Ap = (Ap − dt * (p2 * M) * (NAp))/(1 + dt * (p2 * (1 − p2)**2) * (M * k)).

Thus, obtaining the numerical algorithm that solves a Cahn–Hilliard–Swift–Hohenberg type given by the Equations (1)–(4) with α = k/2, the 2D simulations were performed for a square cell with a mesh of 256 × 256 nodes and with mesh step dx = dy = 0.5. All parameters used in these simulations were with a mobility M = 1.0, an energy barrier of A = 1.0, and an energy coefficient of k = 0.01. Figure 4 shows the temporal evolution of the 2D patterns due to the phase separation with different initial average concentrations (0.45, 0.65, and 0.75). We note that this numerical algorithm improves the solution and reproduces exactly the patterns with the numerical method used in Section 4.1. These patterns have similarities with different microstructures of some alloys. Figure 4a,d shows similarity with the experimental microstructure of Ce₇₅Al₂₁Ga₄ alloy [17] [see Figure 5g], Figure 5c,f with the microstructure of a Ti-6Al.4V alloy [32] [see Figure 5h], and Figure 5b,e with the microstructure of an A356 aluminum alloy [33] with a globular morphology [see Figure 5i].

A significant change was performed at line 42 of the algorithm, and modifying the initial concentration to 0.3 yields an interesting pattern at 800,000 iterations, as shown in Figure 4. We note that it shows a globular morphology similar to that of Ref. [33]. Therefore, an initial structure similar to that of a drop is successfully shown, and as the volume fraction of the Ga-rich phase increases, it forms an interconnected structure in the initial stage. As the microstructure increases, it changes, managing to observe that when an average concentration of 0.5 is used, it resembles the experimental microstructure of the literature with the 2D patterns obtained from the numerical solutions of conventional FFT methods [1].

4.4. Implementation of the Algorithm ETD2RK for Numerically Solving the Conserved SHE

Finally, to implement the second-order exponential integrator algorithm to solve the conserved SHE, a modification is made to the algorithm described in Section 4.1. Again, the origin of this numerical method is the exponential time differencing (ETD) scheme, which is analogous to the improved Euler method but with a Runge–Kutta-type approximation [21,31]. This method is commonly known as ETD2RK [31]. The code is modified to implement Equations (8) and (9) in a similar way to the previous code in Section 4.2. This section will be presented below the routine for the 3D case of the conserved SHE. The reader can implement this routine for the 2D case, deleting a dimension here. If the reader wishes to see a detailed description of this method, they can review Refs. [2,18,26,34] and even for an extended system of two EDPNLs, Refs. [22,35].

In what follows, the numerical results obtained by the three different algorithms are compared. We compared the FFT conventional algorithm for solving the Cahn–Hilliard equation and the algorithm of the first- and second-order exponential method for solving the conserved SHE given by Equation (8). It is observed that the only one that generates 2D patterns with parameters ε = −0.2, −1, −2; λ = 1 and g = 0, −2 is the second-order exponential integrator algorithm (SOEI) [see Figure 6a–c].

It is observed that when ε takes values are greater than −1, the mazes begin to form increasingly complex patterns. These 2D patterns reproduce those presented in Refs. [11,18,23,24,27,28] while the other two algorithms are not able to reproduce the numerical solutions presented in the literature. Figure 6d–f shows the patterns obtained with the algorithm to solve the Cahn–Hilliard equation, and Figure 6g–i shows the patterns produced by the first-order exponential integrator (FOEI) method. This is because these numerical methods do not allow the finding of numerical solutions by initially generating a 2D pattern with stripes, labyrinths, and hexagonal-point morphologies, i.e., it is not possible to visualize a 2D pattern.

On the other hand, Figure 6j–l shows 3D patterns of different phases obtained with the numerical algorithm to solve the conserved SHE. The extension of source code to the 3D case is carried out in a way like the routines presented in Section 4.1, lines 23 to 38, but it is necessary to substitute lines 53 to 60 by the following:

Source code extension routines for the 3D case:

• 53 b = −q2 * (gamma-lambda(1 − q2)**2) * dt
• 54 Ap = exp(b * dt) − p2 * NAp * (exp(b * dt) − 1)/b
• 55 A = ifft(Ap, dim, (−3, −2, −1))
• 56 NA2 = F(A)
• 57 NAp2 = rfft(NA2, dim, (−3, −2, −1))
• 58 Ap = Ap − p2 * (NAp2 − NAp) * (exp(b * dt) − (1 + b * dt))/(b * dt**2)
• 59 A = ifft(Ap, dim, (−3, −2, −1))
• 60    if t % tintervalo == 0:
• 61        print(A [64, 64, 64], “t=”,t * dt, “n=”, t)
• 62        archive = open(“test3DFFT”+str(t)+ “.pkl”, ”wb”)
• 63        pickle.dump(A, archive)
• 64        archive.close()
• 65    if t == tintervalo * 10:
• 66      tintervalo = 10 * tintervalo

The first one shows a hexagonal–tubular morphology as in Refs. [22,36,37], and in the upper part, the pattern is observed in a droplet-like shape in a hexagonal phase, while in Figure 5k, it is observed in a morphology with an asymmetric gyroid phase as in Refs. [36,38], and finally Figure 6l shows a spheres morphology or nodular phase similar to that reported in Refs. [22,27,39].

A final numerical experiment was performed to compare computational performance times between the conventional FFT algorithm for solving the Cahn–Hilliard equation and the second-order exponential algorithm. The results are shown in Table A5 of Appendix A, from which it is inferred that the SOEI algorithm has a lower computational calculation time than the other algorithm. Another important result is the size of the domains that form the morphology of the pattern. Figure 6g–i shows the patterns with morphologies of guts, labyrinths and points obtained by solving the conserved SHE equation using the conventional FFT algorithm (see Table A5). In this algorithm, it is used with a different Fourier mode than the one used in the patterns of Figure 6a–c.

5. Discussion

In recent years, the development of different programming languages of type open sources to solve nonlinear PDE [1,2,21,31] has had an exponential boom. For example, the enormous work based on Matlap software (in its version R2024a), although it requires a license to be used, is currently found in countless universities to develop programming codes that solve phase-field models [10]. Furthermore, the development of the intermediate language Python [8] has positioned itself internationally as a flexible language, easy to understand and for programming by scientists and technologists. Python is an open-source language that has the property of developing in an easy and fast way, scientific computing libraries such as NumPy [6,7,9], and 3D visualization software such as Mayavi in its version 2.0 [12] or PyVista in its version 2.7 [13] with the importance of promoting scientific research. This is the case of the libraries FiPy [14], FEniCS [15], and DOLFIN [16] that solve the functionals associated with mathematical models of the PFC type [26] by changing the geometry of the solution domain in a very simple and pleasant way (FiPy). In all these ways to solve nonlinear PDE, the code and the algorithm interpenetrate almost to the point of becoming one, due to their interrelation and simplicity. This implies the implementation in Python and its libraries (NumPy, Sipy, Tkinter, etc.) of algorithms such as the Discrete Fast Fourier Transform, which are difficult to implement in older programming languages (such as FORTRAN or C), and is a numerical tool that has been widely used to obtain numerical approximations to problems in Condensed Matter Physics and Materials Science and Engineering.

Examples of this are the study of 2D crystal lattices [24], the behavior of ternary mixtures [27], the pigmentation of vertebrate animals [35], the study of polymeric phase transitions [22], the morphology of microstructures of two-component alloys [18,32,33], and superconductivity [30] (the 2D pattern of Figure 5a–c are very similar to Abrikosov vortices of superconductive phases obtained of non-potential conserved SHE). Even the implementation of spectral algorithms to solve nonlinear PDE has generated a new type of technology to obtain polymeric materials with controlled porosity, using 3D printing technology by Foundry Filament Modeling [20,34].

6. Conclusions

The phase-field model manages to describe the microstructure with compositional domains to observe the spinodal decomposition of the alloy. The microstructure was obtained after solving the Cahn–Hilliard phase separation equation using phase-field modeling. It has been found that both the drop-shaped structure and the interconnected structure appearing in the phase-field modeling resemble the one reported in the literature and the experimental one.

An algorithm was created that manages to simulate the spatial–temporal dynamics of a Cahn–Hillard-Swift–Hohenberg type equation, similarly reproducing the patterns generated with the Cahn–Hilliard solving algorithm, and even improving the solution of the patterns. Moreover, this model has not been published in the literature cited in this paper.

The implementation of the Swift–Hohenberg equation algorithm by the first-order exponential integrator method and the Cahn–Hilliard equation algorithm diverges with control parameter values that the second-order exponential integrator method (SOEI) has for solving the conserved Swift–Hohenberg equation if it succeeds in forming patterns. Even more, the SOEI method has been successful in solving EDPN when the conventional FFT method has failed. For example, in Refs. [1,10,20], the conventional FFT method has been implemented for solving equations of the Cahn–Hilliard type, but our results show that this method cannot obtain a numerical solution to the Swift–Hohenberg equation.

Finally, three different algorithms were successfully implemented for the 3D case employing the Fast Fourier Transform under the Python programming language and its NumPy, Tkinter, and Mayavi libraries. The conventional FFT method has been solved in 2D and 3D equations of the Cahn–Hilliard type, inclusive with a functional Swift–Hohenberg type. At the same time, the exponential integrator method of first- and second-order has been solved successfully in 2D and 3D equations of the non-potential, non-conserved, and conserved Swift–Hohenberg type.