Machine Learning Systems Tuned by Bayesian Optimization to Forecast Electricity Demand and Production

Abstract

Given the critical importance of accurate energy demand and production forecasting in managing power grids and integrating renewable energy sources, this study explores the application of advanced machine learning techniques to forecast electricity load and wind generation data in Austria, Germany, and the Netherlands at different sampling frequencies: 15 min and 60 min. Specifically, we assess the performance of the convolutional neural networks (CNNs), temporal CNN (TCNN), Long Short-Term Memory (LSTM), bidirectional LSTM (BiLSTM), Gated Recurrent Unit (GRU), bidirectional GRU (BiGRU), and the deep neural network (DNN). In addition, the standard machine learning models, namely the k-nearest neighbors (kNN) algorithm and decision trees (DTs), are adopted as baseline predictive models. Bayesian optimization is applied for hyperparameter tuning across multiple models. In total, 54 experimental tasks were performed. For the electricity load at 15 min intervals, the DT shows exceptional performance, while for the electricity load at 60 min intervals, DNN performs the best, in general. For wind generation at 15 min intervals, DT is the best performer, while for wind generation at 60 min intervals, both DT and TCNN provide good results, in general. The insights derived from this study not only advance the field of energy forecasting but also offer practical implications for energy policymakers and stakeholders in optimizing grid performance and renewable energy integration.

1. Introduction

Electricity load and wind generation forecasting tasks are critical elements of modern energy systems. For instance, optimal capacity and production management are crucial issues in planning power systems, which require strategic decisions across the generation, storage, and transmission plants. In this regard, electricity load and wind generation are crucial components for the long-term power system expansion, planning, and optimization. Indeed, electricity load and wind generation serve as the foundation of energy system management, ensuring that the balance between supply and demand is precisely maintained [1]. In this regard, the ability to predict electricity load and wind generation with high precision allows for a more efficient and reliable grid operation, reducing the risk of blackouts and ensuring that energy is available when and where it is needed most [2]. The motivation to build forecasting models is driven by the need to support the growing reliance on renewable energy. Since the world moves towards a more sustainable energy future, the role of accurate forecasting becomes increasingly important. Indeed, it enables energy systems to integrate renewable sources more effectively, reducing reliance on fossil fuels and lowering carbon emissions [3]. However, the integration of renewable energy sources, such as wind power, into the energy mix introduces new challenges and complexities in forecasting. For instance, renewable sources like wind are inherently more influenced by environmental conditions, which can fluctuate widely and unpredictably [4]. Therefore, the challenge lies not only in managing the unpredictability but also in effectively using time series data to create accurate models that could explain the temporal variability [5]. Hence, by improving the accuracy of electricity load and wind generation forecasts, stakeholders can make more informed decisions, paving the way for a more resilient, efficient, and sustainable energy future.

To enhance prediction accuracy, scholars have proposed various approaches to forecast electricity load and wind generation. In the context of electricity load forecasting, for instance, Kaytez [6] presented a comprehensive study focusing on forecasting Turkey’s net electricity consumption using a hybrid model. This model integrates the Autoregressive Integrated Moving Average (ARIMA) method with the Least Squares Support Vector Machine (LS-SVM) to enhance forecasting accuracy. The main findings demonstrate the hybrid model’s superior performance over traditional models like multiple linear regression and single ARIMA models, as well as the official forecasts. Gao et al. [7] presented a hybrid machine learning model for forecasting residential electricity consumption in China, combining an Extreme Learning Machine (ELM) optimized by the Jaya algorithm with online search data as predictors. The model’s effectiveness was validated through comparative analysis with traditional models and standalone ELM, showing superior performance in accuracy metrics. Albuquerque et al. [8] conducted a comprehensive analysis to forecast the Brazilian power electricity consumption using machine learning models, specifically Random Forest and Lasso Lars, and compared their performance to benchmark specifications such as ARIMA and a random walk process. The study revealed that machine learning methods significantly outperform traditional models in accuracy for short to medium-term forecasting. Saranj and Zolfaghari [9] adopted a hybrid model that combines Adaptive Wavelet Transform (AWT) with Long Short-Term Memory (LSTM) networks and ARIMA with exogenous inputs and generalized autoregressive conditional heteroskedasticity (GARCH) models. This approach was designed to enhance prediction accuracy by addressing the multi-frequency characteristics of electricity consumption data. The study tested the model using data from the UK market, considering various exogenous variables such as climate conditions and calendar dates. The hybrid model demonstrated superior performance over traditional forecasting models and alternative filtering methods, indicating its effectiveness in improving the predictive power for short-term electricity consumption forecasting.

In the context of wind generation forecasting, Huang et al. [10] explored an advanced wind speed forecasting model using a genetic algorithm to optimize the Long Short-Term Memory network and further enhanced it through ensemble learning with a Differential Evolution-based No Negative Constraint Theory. The model demonstrated superior forecasting performance compared to traditional and single model approaches when applied to two wind farms in Inner Mongolia, China, and Sotavento, Galicia, Spain. Yaghoubirad et al. [11] evaluated LSTM, Gated Recurrent Unit (GRU), CNNs (convolutional neural networks), and CNN-LSTM models for multistep ahead wind speed and power generation forecasting in Zabol City, Iran, over 6 months, 1 year, and 5 years. The simulation results showed that the GRU is the most accurate, particularly when utilizing multivariate data. Li et al. [12] introduced a combined forecasting system for optimal wind speed prediction based on data denoising, fuzzification, and multi-objective optimization. The findings demonstrated that the proposed integrated forecasting system enhanced both the prediction capacity and accuracy of wind speed forecasts.

The main purpose of our study is to conduct a comprehensive comparative analysis of various deep learning systems for forecasting electricity load and wind generation in three European countries. This research seeks to shed light on the relative strengths and weaknesses of a broad array of predictive deep learning systems when applied to the specific challenges and data characteristics found in these regions.

In this regard, the main contributions of our work are threefold. First, we implement and compare various deep learning models, including Convolutional Neural Networks (CNNs), the Temporal Convolutional Neural Network (TCNN), Long Short-Term Memory (LSTM), Bidirectional Long Short-Term Memory (BiLSTM), Gated Recurrent Unit (GRU), Bidirectional Gated Recurrent Unit (BiGRU), and Deep Neural Network (DNN). In addition, the standard machine learning models, namely the K-nearest neighbors (KNN) algorithm and decision trees (DTs), are adopted as baseline models. Hence, these predictive models represent a blend of classical machine learning algorithms and more recent deep learning approaches. Second, implementing and training the models involves delicately tuning hyperparameters. In this regard, Bayesian optimization is applied to all predictive models to achieve the best accuracy. Third, all predictive systems are compared across different time intervals. Indeed, a key aspect of this research is the comparison of model performance across different forecasting horizons, specifically 15 min and 60 min intervals. This analysis is critical because the optimal model for short-term forecasting may not necessarily perform best over longer intervals, due to the different dynamics and uncertainties involved.

The outcomes of this research hold significant implications for the energy sector, particularly in terms of enhancing the reliability, efficiency, and sustainability of energy systems in Europe and beyond. Furthermore, the findings contribute to the extension of the current knowledge in predictive modeling and time series analysis. Indeed, by conducting comparative analysis, the research also shows how the predictability of electricity load and wind generation changes over different time scales and how each model adapts to these changes. Therefore, the experimental results would guide utilities, grid operators, and policymakers in selecting and deploying forecasting models that best meet their needs in their specific context.

The remaining framework of this study is organized as follows. The next section presents deep learning models. To illustrate the forecasting performance of all predictive systems, Section 3 presents the simulation results. Finally, Section 4 touches upon the specific discussion of the results and concludes the paper.

2. Materials and Methods

The general framework of our study is shown in Figure 1. As shown, time series data is fed to deep learning (DL) systems and standard machine learning (ML) models to predict the output, for instance, step-ahead electricity load and wind generation. The values of the parameters of each predictive system are optimized by using the Bayesian optimization technique. Finally, model assessment is performed in the last stage. Specifically, its forecasting performance is evaluated based on a set of performance measures. The predictive models are described in the following subsections.

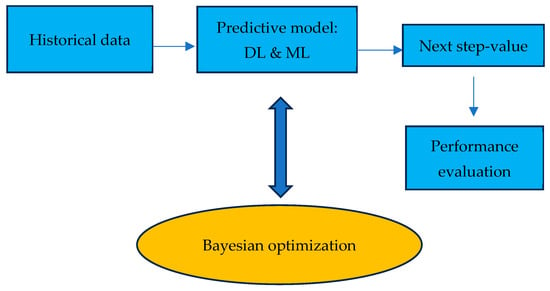
Figure 1. Flowchart of the experiments.

2.1. CNN

The Convolutional Neural Network [13] is known for its ability to perform automatic feature extraction. CNNs utilize layers of convolutional filters that are applied over the input data, enabling the model to learn increasingly complex features at each layer. This eliminates the need for manual feature selection, reducing the risk of human bias and error. In time series analysis, CNNs can identify and learn important features from raw data sequences without pre-defined assumptions. Once a feature is learned, a CNN can recognize it in any part of the data sequence.

To implement the CNN model, the model begins with a Conv1D layer since we have sequential data with one spatial dimension. The layer uses a specified number of filters and a kernel size to scan through the input data. The relu activation function is employed to introduce non-linearity, enabling the model to learn more complex patterns. Mathematically, this convolution operation computes the inner product between a subsequence of the input data X (with length k, the kernel size) and the filter w:

$$C_i={\sum }_{i=1}^k{w}_i·X_i$$

(1)

Following the convolutional layer, a maxpooling1D layer reduces the dimensionality of the data, which helps in reducing computation as well as controlling overfitting by abstracting the features extracted by the convolutional layers. Then, a flatten layer is used to transform the pooled feature map into a single linear vector, and a dropout layer is used to prevent overfitting. The architecture concludes with a dense layer that uses a linear activation function. Finally, the model is compiled with the adam optimizer with a learning rate of 0.001, and the loss function is set to mean squared error. We set up the parameter search space for optimization targeting the CNN model’s filter, kernel size, pool size, and dropout rate. Filter determines the number of filters in the convolutional layers, ranging from 16 to 256. Kernel size defines the size of the window to be used in each convolutional filter, set between 2 and 8. Pool size dictates the size of the pooling window, ranging from 2 to 4. Dropout rate controls the proportion of neurons to drop out during training, set between 0.0 and 0.5.

2.2. TCNN

The Temporal Convolutional Neural Network (TCNN) [14] is a variant of the traditional convolutional neural network specifically designed to handle sequence prediction problems more effectively, particularly in time series forecasting. TCNNs use causal convolutions, which ensure that the output at a given time is only determined by past inputs. This is a significant advantage for making predictions in real-time scenarios, where future data cannot be assumed to be available. The model includes several Conv1D layers with a causal padding option, ensuring that the convolution output for a specific timestamp can only depend on current and past data. Mathematically, for a given input sequence X, a dilated causal convolution at time step t with a kernel size k, dilation rate d, and filter weights w is defined as:

$$y\left(t\right)={\sum }_{i=0}^{k-1}{w}_i·x_{t-d·i}$$

(2)

In our model, the dilation rate starts at 1 and increases with each subsequent layer. For instance, when d = 1 for the first layer, it becomes 2 for the second layer, 3 for the third layer, and so on, expanding the receptive field exponentially. Each convolutional layer is followed by an activation layer set to relu to capture non-linearity in the model. This is coupled with a dropout layer to prevent overfitting by randomly omitting a proportion of the feature detectors during training. Afterwards, this is followed by a flatten layer, and a dense layer with a linear activation function. Finally, the model is compiled using the adam optimizer, with a learning rate of 0.001 and mean squared error as the loss function. The parameter space for TCNN tuning includes the settings of the number of convolutional layers, filter, kernel size, dilation rate, and dropout rate. Specifically, the number of convolutional layers varies from 2 to 4, filters are adjusted between 16 and 256, kernel size extends from 2 to 8, dilation rate is set from 1 to 2, and dropout rate spans from 0.0 to 0.5.

2.3. LSTM

The Long Short-Term Memory [15] network is a type of recurrent neural network (RNN) specifically designed to address the shortcomings of traditional RNNs, particularly in handling long-term dependencies. Traditional RNNs often struggle with the vanishing gradient problem, where information from earlier input data is lost as it propagates through the network. LSTMs address this issue with their unique architecture of gates that regulate the flow of information. LSTMs contain memory cells that can maintain information in memory for long periods of time. Each LSTM cell has three gates: the forget gate, the input gate, and the output gate, which are all used to manage the flow of information. For each time step t, the memory cell stat $C_t$ is updated based on the current input $X_t$ and the previous hidden state $H_{t-1}$, which are described as follows:

(a)

Forget Gate: Decides which part of the previous cell state to retain or forget.

$$f_t=ReLU\left(X_t{U}_f+H_{t-1}{W}_f\right)$$

(3)

(b)

Input Gate: Decides how much new information should be added to the cell state.

$$i_t=ReLU\left(X_t{U}_i+H_{t-1}{W}_i\right)$$

(4)

(c)

New Candidate Memory: Generates the candidate new information for the memory cell.

$$N_t=\mathit{tanh}\left(X_t{U}_c+H_{t-1}{W}_c\right)$$

(5)

(d)

Cell State Update: The cell state is updated based on the forget and input gate outputs.

$$C_t=f_t·C_{t-1}+i_t·N_t$$

(6)

(e)

Output Gate: Controls the information flow from the cell to the next hidden state.

$$O_t=ReLU\left(X_t{U}_o+H_{t-1}{W}_o\right)$$

(7)

(f)

Hidden State Update: The hidden state is passed to the next LSTM layer or the output layer.

$$H_t=O_t·\tanh \left(C_t\right)$$

(8)

The architecture of LSTM begins with the first LSTM layer. This first LSTM layer processes input sequences and ensures that the output includes sequences necessary for chaining multiple LSTM layers. Following the first LSTM layer, a dropout layer is introduced to prevent overfitting. Then a subsequent LSTM layer receives sequences from the previous layer, further refining the model’s ability to learn from the data. The output from this layer does not return sequences, preparing for a final dense output layer. A dense layer with a linear activation function produces the final output of the model. Finally, the model is compiled using the adam optimizer, with a learning rate of 0.001 and the mean squared error as the loss function. In the parameter search space, the number of neurons for the first and second LSTM layers is individually defined, allowing the model to capture complexities in the data at different levels of abstraction. Specifically, the number of neurons for the first LSTM ranges from 16 to 128, while the second spans from 8 to 64. Additionally, the dropout rate is adjustable within a range from 0.0 to 0.5.

2.4. BiLSTM

The Bidirectional Long Short-Term Memory (BiLSTM) network is an enhancement of the LSTM model that involves training two LSTMs on the input sequence: one with the input in natural order and the other in reverse order. This approach allows the model to gather information from both past and future states simultaneously. The outputs of the forward and backward layers at each time step t are concatenated to form a single output vector. Mathematically, the hidden state at time step t in the BiLSMT is

$$H_t^{BiLSTM}=\left[H_t^{forward},H_t^{backward}\right]$$

(9)

By processing data from both directions, BiLSTMs capture a richer understanding of the context and thus capture dependencies and features that may be missed by single-direction LSTMs. Like LSTM, BiLSTM requires longer training times and greater demands on computational resources. The first BiLSTM layer is a bidirectional wrapper applied to an LSTM layer with a hyper-tunable number of neurons in each direction. This configuration allows the layer to process the input sequence both forwards and backwards. The second BiLSTM layer similarly utilizes the bidirectional wrapper on an LSTM layer with another hyper-tunable number of neurons. Dropout layers are interspersed between BiLSTM layers to prevent overfitting. The final layer is a dense layer with a linear activation function. Lastly, the model is compiled with the adam optimizer with a learning rate of 0.001, and the loss function is the mean squared error. The parameter search space designated for the BiLSTM model is like that of the LSTM as well. Specifically, the number of units in the first BiLSTM layer is set between 16 and 128, while the second can range from 8 to 64. Additionally, the dropout rate is configurable from 0.0 to 0.5.

2.5. GRU

The Gated Recurrent Unit [16] is a type of RNN, like the LSTM network, but designed to be simpler and more efficient in certain scenarios. GRUs have only two gates: update and reset. The following formulas describe the key operations within each GRU:

(a)

Update Gate: The update gate controls how much of the previous hidden state should be carried forward to the current time step.

$$z_t=ReLU\left(X_t{U}_z+H_{t-1}{W}_z\right)$$

(10)

(b)

Reset Gate: The reset gate decides how much of the previous hidden state should be forgotten when computing the candidate hidden state. And it controls the contribution of the previous hidden state to the candidate hidden state computation.

$$r_t=ReLU\left(X_t{U}_r+H_{t-1}{W}_r\right)$$

(11)

(c)

Candidate Hidden State: The candidate hidden state is computed based on the reset gate’s influence on the previous hidden state. The reset gate allows the model to determine how much of the previous hidden state to use in computing the new candidate hidden state.

$${\tilde{h}}_t=\mathit{tanh}\left(X_t{U}_h+\left(r_t·H_{t-1}\right)W_h\right)$$

(12)

(d)

Hidden State Update: The final hidden state is updated by combining the previous hidden state and the candidate hidden state using the update gate. This formula balances the influence of past and new information, controlled by the update gate.

$$h_t=\left(1-z_t\right)·H_{t-1}+z_t·{\tilde{h}}_t$$

(13)

GRUs require fewer parameters than LSTMs because they lack an output gate, making them faster to train while still capturing dependencies in sequence data effectively. This reduction in complexity often leads to faster training times without a significant decrease in performance, especially in tasks where long-term dependencies are less critical. The first GRU layer processes the input sequence and provides a temporal dimension output that is necessary for chaining to the next recurrent layer. The second GRU layer further refines the ability of the model to learn from the temporal data, processing the sequence output from the previous GRU layer. Interspersed between the GRU layers, dropout layers help mitigate the risk of overfitting. A dense layer with a single neuron concludes the model. Finally, the model is compiled with the adam optimizer, with a learning rate of 0.001 and mean squared error as the loss function. The hyperparameter search space defined for the GRU model is identical to that of the LSTM. Notably, the number of neurons in the initial GRU layer varies between 16 and 128, and for the subsequent layer, it ranges from 8 to 64. The dropout rate is adjustable, with values spanning from 0.0 to 0.5.

2.6. BiGRU

The Bidirectional Gated Recurrent Unit (BiGRU) model extends the traditional GRU architecture. BiGRUs process sequences both forwards and backwards, enabling the model to access past and future context. At each time step t, the hidden states from both directions are concatenated:

$$H_t^{BiGRU}=\left[H_t^{forward},H_t^{backward}\right]$$

(14)

Compared to BiLSTMs, BiGRUs typically have fewer parameters due to the simpler gating mechanisms of GRUs. Despite being more efficient than BiLSTMs, BiGRUs still require more computational resources than their unidirectional counterparts due to processing sequences twice. The model architecture begins with a Bidirectional wrapper applied to a GRU layer. After each BiGRU layer, dropout layers help reduce overfitting. The second BiGRU layer adds further depth to the model’s ability to process information bidirectionally. A dense layer with linear activation serves as the output layer. The model is compiled using the adam optimizer with a learning rate of 0.001, and the loss function is the mean squared error. The parameter search space for the BiGRU model is consistent with that of other RNN models previously discussed. Specifically, it allows for the number of neurons in the first BiGRU layer to range from 16 to 128 and in the second BiGRU layer from 8 to 64. Additionally, the dropout rate is adjustable from 0.0 to 0.5.

2.7. DNN

The Deep Neural Network (DNN) is a standard, straightforward multilayer perceptron (MLP) consisting of fully connected layers. Each layer performs a linear transformation of the input, followed by a non-linear activation function. Mathematically, the operation in a dense layer is described as:

$$y_i=f\left({\sum }_{j=1}^n{w}_{ij}{x}_j+b_i\right)$$

(15)

where $y_i$ is the output of the i-th neuron, $w_{ij}$ is the weight associated with the connection between the j-th input and the i-th neuron, $x_j$ is the j-th input to the neuron, $b_i$ is the bias term, and $f\left(·\right)$ is the activation function. In our implementation, each hidden layer uses the relu activation function, which allows the model to capture more complex patterns in the data by only passing positive values through the layers.

$$ReLU\left(x\right)=\max \left(0,x\right)$$

(16)

This type of neural network is fundamental in deep learning, offering a baseline architecture from which more complex models evolve. With multiple hidden layers, DNNs can learn complex patterns and relationships in the data. And DNNs are inherently scalable, capable of handling large datasets and expanding in complexity as needed by adding more layers or neurons. Unlike RNNs or CNNs, DNNs treat input features as independent and identically distributed. They fail to recognize the context or sequence in the input data, which is often crucial for more complex tasks. The structure of the DNN is defined to be flexible, allowing adjustments in the number of layers and units to suit different complexity requirements and dataset characteristics. The model starts with a dense layer, processing the input data, with the activation function of relu. Subsequently, a loop constructs additional layers as part of the optimization process to determine the optimal number of layers for the model. Each subsequent layer uses the same number of units and activation function, stacking up the network’s capability to learn more complex patterns. The model ends with a final dense layer with one neuron and a linear activation function. Finally, the model is compiled with the adam optimizer, with a learning rate of 0.001 and the loss function of mean squared error. The parameter search space for a DNN model is relatively simple, primarily involving the adjustment of the model’s depth, which is set to vary between 1 and 3 layers. The parameter units determine the number of neurons per layer, with a range extending from 8 to 256.

2.8. kNN Algorithm

The k-nearest neighbors [17] algorithm is a simple, versatile, and widely used machine learning method based on feature similarity. Unlike many other machine learning algorithms that require a training phase to learn a model, kNN makes predictions using the entire dataset as the model. Nonetheless, one of the major drawbacks of kNN is its computational inefficiency, especially with large datasets. Every prediction requires a distance calculation to all training points, which can be computationally expensive and slow.

In kNN regression, the model finds k-nearest neighbors to a given input point using a distance metric and then makes a prediction by averaging the target values of these neighbors. Mathematically, the predicted value for an input is

$$\widehat{y}\left(x\right)={\displaystyle \frac{1}{k}}{\sum }_{i=1}^k{y}_i$$

(17)

We set the range for k from 3 to 10. This parameter determines the number of nearest neighbors to be considered when making predictions. Then, we configure the weights parameter, which presents two categorical options: uniform and distance. Under the uniform setting, each neighbor contributes equally to the final prediction. Conversely, the distance option assigns greater importance to nearer neighbors. The third parameter p is the power parameter for the Minkowski metric. When p = 1, the distance metric used is Manhattan distance:

$$d\left(x,x^{\prime }\right)={\sum }_{i=1}^n\left|x_i-x_i^{\prime }\right|$$

(18)

When p = 2, it is the Euclidean distance given by

$$d\left(x,x^{\prime }\right)=\sqrt{{\sum }_{i=1}^n{\left(x_i-x_i^{\prime }\right)}^2 }$$

(19)

The parameter space for the kNN model has been established, and we will leave it to the optimization process to decide the optimal parameters.

2.9. Decision Tree

The decision tree (DT) [18] is a non-parametric supervised learning method used for both classification and regression tasks. Decision trees can manage complex, non-linear relationships. A decision tree builds a tree-like structure by splitting the data at each node based on the feature that increases the homogeneity of the target variable within each region. In regression trees, the goal is to minimize the variance of the target variable within each region after splitting the data. Mathematically, for a given split at node t, the split criterion is based on reducing the mean squared error (MSE). The MSE at a node is calculated as

$${MSE}_t={\displaystyle \frac{1}{N_t}}{\sum }_{i=1}^{N_t}{\left(y_i-{\overline{y}}_t\right)}^2$$

(20)

The decision tree evaluates every possible split and selects the one that maximizes the reduction in MSE, which is also referred to as variance reduction:

$$\Delta MSE={MSE}_{parent}-\left({\displaystyle \frac{N_{left}}{N_{parent}}}{MSE}_{left}+{\displaystyle \frac{N_{right}}{N_{parent}}}{MSE}_{right}\right)$$

(21)

The tree continues to split until one of the stopping criteria is met: the maximum number of levels in the tree, the minimum samples of a node to perform a split, or the minimum number of samples a leaf node must have. Once the tree has reached a leaf node, it predicts the output by averaging the target values of the samples in that node:

$$\widehat{y}\left(x\right)={\displaystyle \frac{1}{N_{leaf}}}{\sum }_{i=1}^{N_{leaf}}{y}_i$$

(22)

In contrast to various neural network models, decision trees have inherent limitations in extrapolating beyond the scope of the training data. This characteristic presents a significant challenge in time-series forecasting, where it is frequently necessary to predict future values that extend past the range observed within the training dataset. We define the parameter search space to facilitate the exploration and optimization of model parameters. We set the maximum depth parameter range between 3 and 20. A deeper tree can capture more intricate patterns within the dataset. However, it also runs the risk of learning noise rather than the underlying data trends. Conversely, setting a shallower tree enhances the model’s generalizability but may not capture enough complexity from the data. We set the range for “minimum samples split between 2 and 20”. This parameter specifies the minimum number of samples required to split an internal node within the decision tree. Higher values restrict the tree’s complexity, while lower values facilitate a more liberal growth of the tree. The last parameter is as follows: “minimum samples leaf is set within a range from 1 to 10”. This parameter determines the minimum number of samples required in a leaf node. A lower threshold in this range may capture highly specific patterns, and, conversely, a higher value promotes better generalization.

2.10. Bayesian Optimization

Bayesian optimization [19] is specifically designed to identify an optimal set of parameters that achieves minimal values for the loss function. This technique utilizes a probabilistic model to predict the performance of the models given different hyperparameter settings and iteratively updates the model based on the outcomes of the evaluations. This method is effective compared to random or grid search approaches, particularly under conditions where model performance evaluations are computationally demanding or when navigating a vast hyperparameter space. The optimization process can be described in the following steps:

a.

Gaussian Process Surrogate Model: In Bayesian Optimization, a Gaussian Process (GP) is commonly used as a surrogate model for the objective function $f\left(x\right)$. Given the current evaluations of the function at different hyperparameter values, the GP predicts the function value at any new point $x$ by providing a mean prediction $\mu \left(x\right)$ and uncertainty $\sigma \left(x\right)$. The GP regression model can be expressed as

$$f\left(x\right)\sim GP\left(\mu \left(x\right),k\left(x,x^{\prime }\right)\right)$$

(23)

where $k\left(x,x’\right)$ is the kernel function representing the correlation between different points in the search space.

b.

Acquisition Function: The acquisition function $\alpha \left(x\right)$ selects the next set of hyperparameters to evaluate by balancing high uncertainty and low mean prediction. Common acquisition functions used include

⚬

Expected Improvement (EI):

$${\alpha }_{EI}\left(x\right)=E\left[\max \left(0,f\left(x\right)-f\left(x^{+}\right)\right)\right]$$

(24)

where $f\left(x^{+}\right)$ is the best observed objective function value.

⚬

Upper Confidence Bound (UCB):

$${\alpha }_{UCB}\left(x\right)=\mu \left(x\right)+\kappa \sigma \left(x\right)$$

(25)

where $\mu \left(x\right)$ is the predicted mean, $\sigma \left(x\right)$ is the uncertainty, and $\kappa$ is a parameter that controls the balance between exploration and exploitation.

c.

Objective Function Evaluation: Once the next set of hyperparameters is selected using the acquisition function, the model is trained using those hyperparameters, and the validation performance is evaluated.

d.

Optimization Process: The process continues for a specified number of iterations, refining the hyperparameters to optimize the objective function. Mathematically, at each iteration, Bayesian Optimization selects hyperparameters by optimizing the function:

$$x_{next}=\arg \mathrm{m}\mathrm{a}\mathrm{x}\alpha \left(\left.x\right|\mu \left(x\right),\sigma \left(x\right)\right)$$

(26)

where $\alpha \left(x\right)$ is the acquisition function, $\mu \left(x\right)$ is the predicted mean function from the GP, and $\sigma \left(x\right)$ is the predicted uncertainty. At the end of this phase, we will have robust models that can effectively predict outcomes based on the trends and patterns identified in the training data.

2.11. Performance Measures

Now that we have the best models using the optimal parameters, the next step is to evaluate these models. This evaluation is crucial for determining which model yields the most accurate forecasts for each specific dataset. During the data preparation phase, the dataset was carefully partitioned, reserving 20% as a test set. This subset, which the models have never seen before, can reflect the models’ ability to predict the new, unseen data. For a comprehensive evaluation, four key metrics have been selected: root mean squared error (RMSE), mean absolute error (MAE), mean absolute deviation (MAD), and mean absolute scaled error (MASE).

The RMSE is a widely used measure of the differences between values predicted by a model and the values actually observed. It squares the errors before averaging them, which penalizes larger errors.

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(27)

The MAE measures the average magnitude of the errors in a set of predictions, without considering their direction. It is the average over the test sample of the absolute differences between prediction and actual observation, where all individual differences have equal weight.

$$MAE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(28)

Similarly to MAE, the MAD measures the average absolute deviation of data points relative to a dataset’s mean. It is a measure of dispersion.

$$MAD={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|y_i-{\mu }_y\right|$$

(29)

Finally, the MASE measures the accuracy of forecasts relative to a naïve benchmark prediction, typically the value from the previous period. It is especially useful because it is scale-independent and can handle data with zeros. An MASE less than one indicates that the model performs better than a naïve baseline model. It is particularly suitable for time-series data because it normalizes the error based on the historical data variability.

$$MASE={\displaystyle \frac{\frac{1}{n}{\sum }_{i=1}^n\left|y_i-{\widehat{y}}_i\right|}{\frac{1}{n-1}{\sum }_{i=2}^n\left|y_i-y_{i-1}\right|}}$$

(30)

We will compare the performance of each model within individual markets to identify which model predicts the most accurately in a specific market context. Subsequently, this analysis will be extended to compare the best-performing models from each market against each other across different markets. We can thus identify the most effective model for a particular market and assess the generalizability and robustness of the model across different market environments. Moreover, we will have valuable insights into the relative strengths and weaknesses of the models, which will help make informed decisions about model selection and deployment in different market situations.

3. Results

The original dataset is sourced from the Open Power System Data platform [20], which provides preprocessed and continuous data from the European Network of Transmission System Operators for Electricity (ENTSO-E) Transparency platform. It contains a time series of electricity loads and wind power generation in megawatts. The data is aggregated based on country, control area, or bidding zone, covering the European Union and some neighboring countries. All variables are available in hourly resolution, and some are available in higher resolution, including half-hourly and quarter-hourly formats, spanning from 2015 to mid-2020. The datasets are first divided into two domains—electricity load and wind generation. And for each domain, the datasets are separated by different countries—Austria (AT), Germany (DE), and the Netherlands (NT). Finally, the datasets are further differentiated by 15 min and 60 min intervals. Given the limitations of our research infrastructure, handling such large datasets could be overly demanding. To mitigate this, we strategically select only the most recent 10,000 observations from each dataset to use in our model training and testing processes. This selection reduces computational load and storage requirements, thereby alleviating the strain on our research facility.

For the electricity load, Table 1 presents the evaluation results of electrical loads for 15 min intervals for Austria. The decision tree (DT) model shows the lowest RMSE, MAE, and MASE values at 63.07, 46.77, and 0.71, respectively. The DT also demonstrates considerable efficiency in terms of optimization time, requiring only 1.17 min. While this duration is slightly longer than that for the kNN, it is substantially quicker compared to the neural network models. The DNN also shows commendable performance among deep learning models with a low optimization time of 3.92 min. Yet overall, the DT proves to be the most effective model for this dataset. For illustration purposes, Figure 2 displays the true versus predicted values by each model when applied to forecast Austria’s electrical loads at 15 min intervals. Table 2 presents the evaluation results of electrical loads for 15 min intervals for Germany. The results also identify the decision tree as the most proficient model in terms of RMSE, MAE, MASE, and optimization time. The GRU ranks second with an RMSE of 710.93 and an MAE of 526.08. However, its optimization time takes about 36 min, which is much higher than the 0.25 min of the tree. Thus, the DT is identified as the best model for this dataset. Figure 2 displays the true versus predicted values by each model. Table 3 presents the evaluation results of electrical loads for 15 min intervals for the Netherlands. Once again, DT shows exceptional performance with the lowest RMSE, MAE, and MASE values. Moreover, it takes only 0.36 min to optimize. However, the MASE values for other models in this market exceed 1. Their performance does not surpass that of a simple naïve benchmark.

Table 1. Evaluation Results for Austria’s Electricity Load (15 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	164.22	128.31	1008.30	1.93	5.07
TCNN	101.02	78.38	988.29	1.18	271.32
LSTM	202.28	170.68	995.37	2.57	41.08
BiLSTM	129.36	99.06	1014.16	1.49	83.43
GRU	90.06	72.37	998.05	1.09	40.46
BiGRU	122.81	98.70	992.23	1.49	76.80
DNN	74.22	57.15	1002.09	0.86	3.92
kNN	123.96	97.71	1005.88	1.47	0.33
DT	63.07	46.77	1005.82	0.71	1.17

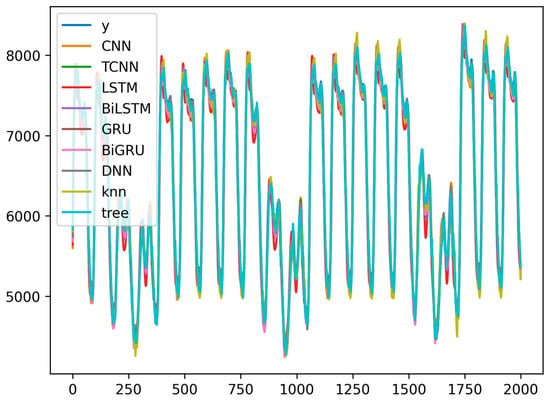
Figure 2. Plots of predicted values for Austria’s electricity load at 15 min intervals versus the true value y. The observation number is shown on the x-axis, and the predicted value is shown on the y-axis. The unit of the variable y is in megawatts.

Table 2. Evaluation Results for Germany’s Electricity Load (15 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	1531.60	1201.88	7952.66	2.26	5.23
TCNN	1301.13	995.12	8124.17	1.87	201.07
LSTM	1458.86	1108.28	8274.61	2.09	43.08
BiLSTM	1151.74	859.83	7948.68	1.62	82.22
GRU	710.93	526.08	8057.85	0.99	35.77
BiGRU	1169.70	970.33	8224.91	1.83	81.47
DNN	964.24	795.62	7974.43	1.50	3.69
kNN	1078.55	765.21	7974.71	1.44	0.34
DT	476.06	351.20	8113.38	0.66	0.25

Table 3. Evaluation Results for the Netherlands’ Electricity Load (15 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	579.66	454.99	1279.64	3.47	6.24
TCNN	531.33	458.01	1353.38	3.50	199.55
LSTM	603.68	491.99	1343.66	3.76	48.10
BiLSTM	288.31	220.70	1337.44	1.69	96.50
GRU	387.51	302.98	1288.35	2.31	54.89
BiGRU	392.22	324.74	1309.96	2.48	92.64
DNN	320.27	265.89	1335.56	2.03	4.04
kNN	528.58	393.56	1221.29	3.01	0.57
DT	166.91	107.21	1302.92	0.82	0.36

Table 4 presents the results of 60 min intervals of electrical loads for Austria. For 60 min interval in the same market, although DT still performs strongly, DNN takes the first place with better RMSE, MAE, and MASE. In terms of time used, the DT is still in first place, and DNN, although longer than the decision tree, is acceptable compared to the other neural network models. Table 5 presents the results of 60 min intervals of electrical loads for Germany. DNN exhibits outstanding performance with the lowest RMSE, MAE, and MASE. And all models demonstrate improved performance to varying degrees, on the 60 min dataset compared to 15 min intervals. Table 6 presents the results of 60 min intervals of electrical loads for the Netherlands. DNN retains its preeminent position. And the DT performs robustly. Notably, TCNN stands out as a significant spot, securing second place in terms of error metrics. However, the optimization time for the TCNN is a considerable drawback. TCNN takes approximately 209 min to optimize for this dataset alone.

Table 4. Evaluation Results for Austria’s Electricity Load (60 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	320.62	250.44	937.87	1.07	8.40
TCNN	461.24	437.99	1064.05	1.86	290.55
LSTM	602.14	513.50	760.96	2.19	60.64
BiLSTM	319.49	257.52	895.50	1.10	120.59
GRU	254.98	189.56	941.03	0.81	50.20
BiGRU	215.09	175.17	972.80	0.75	108.37
DNN	119.98	90.09	1004.36	0.38	4.60
kNN	160.70	124.65	1002.79	0.53	0.41
DT	136.50	99.64	999.60	0.42	0.35

Table 5. Evaluation Results for Germany’s Electricity Load (60 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	1903.04	1254.28	7585.96	0.69	5.21
TCNN	1083.49	784.54	7699.85	0.43	205.13
LSTM	2806.71	2061.80	7153.53	1.13	42.81
BiLSTM	1890.08	1429.04	7639.69	0.78	81.20
GRU	1506.70	1161.04	7580.95	0.64	35.93
BiGRU	1436.11	1090.38	7771.06	0.60	68.11
DNN	809.76	609.66	7905.96	0.33	3.29
kNN	983.67	749.60	7915.07	0.41	0.36
DT	960.88	721.90	7928.43	0.40	0.21

Table 6. Evaluation Results for the Netherlands’ Electricity Load (60 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	531.04	380.77	1103.86	1.05	6.51
TCNN	358.62	256.75	1168.39	0.71	209.14
LSTM	1161.89	930.44	693.73	2.58	53.13
BiLSTM	824.52	683.11	1015.22	1.89	112.32
GRU	657.00	553.35	1177.89	1.53	54.52
BiGRU	441.83	338.57	1206.93	0.94	95.14
DNN	335.28	246.16	1197.70	0.68	5.15
kNN	665.96	482.78	1194.83	1.34	0.52
DT	375.28	269.35	1219.41	0.75	0.41

For wind generation, Table 7 presents the evaluation results of 15 min intervals for Austria. Returning to the 15 min intervals, the DT once again reclaims its position as the top-performing model. It is worth noting that the metrics of TCNN are slightly lower than those of DT. However, the time used for TCNN is still a significant drawback, approximately 1000 times that of DT. For illustration purposes, Figure 3 displays the true versus predicted values by each model for wind generation in Austria. Table 8 presents the evaluation results of 15 min intervals for Germany. As shown in the time series plots presented in preliminary analyses, the wind market exhibits significant randomness, which impacts the performance of forecasting models. Only DT stands out with an MASE value less than 1. Although the metrics are not initially promising, the models generally conform to the actual trend. Table 9 presents the evaluation results of 15 min intervals for the Netherlands. In this dataset, none of the models can make satisfactory predictions. Among the models, the DT, typically the better model, exhibits only modest results.

Table 7. Evaluation Results for Austria’s Wind Generation (15 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	86.71	55.61	543.39	1.83	6.34
TCNN	49.05	31.03	543.45	1.02	275.37
LSTM	137.67	96.55	530.15	3.17	43.83
BiLSTM	96.90	72.30	538.13	2.38	84.39
GRU	76.27	51.79	537.82	1.70	35.70
BiGRU	72.11	51.04	558.54	1.68	76.18
DNN	131.41	94.59	522.23	3.11	3.47
kNN	134.96	87.94	532.94	2.89	0.36
DT	47.61	30.28	548.70	1.00	0.21

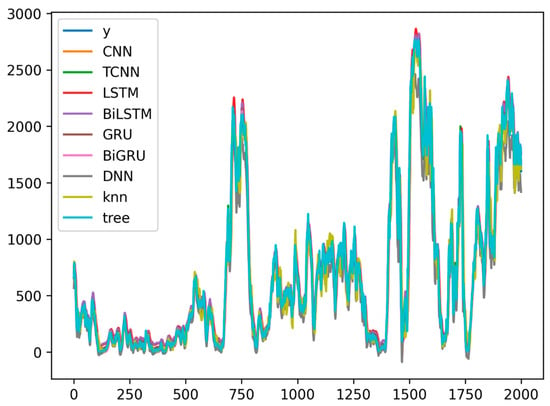
Figure 3. Plots of predicted values for Austria’s wind generation at 15 min intervals versus the true value y. The observation number is shown on the x-axis, and the predicted value is shown on the y-axis. The unit of the variable y is in megawatts.

Table 8. Evaluation Results for Germany’s Wind Generation (15 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	1089.05	799.40	5043.56	3.75	4.21
TCNN	582.33	414.58	5352.63	1.94	196.70
LSTM	997.84	704.16	5075.81	3.30	41.34
BiLSTM	869.45	666.12	5286.35	3.12	79.75
GRU	687.55	474.10	5100.22	2.22	35.19
BiGRU	686.10	536.30	5208.85	2.51	77.77
DNN	450.76	321.39	5200.90	1.51	3.17
kNN	889.23	638.81	5103.64	2.99	0.37
DT	253.29	178.07	5223.61	0.83	0.22

Table 9. Evaluation Results for the Netherlands’ Wind Generation (15 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	81.34	58.35	355.78	2.64	4.26
TCNN	45.00	32.83	343.11	1.49	199.61
LSTM	69.86	49.43	342.20	2.24	38.54
BiLSTM	64.25	46.10	342.83	2.09	73.46
GRU	51.78	37.13	359.19	1.68	31.66
BiGRU	53.72	37.32	357.55	1.69	69.67
DNN	45.17	31.63	343.48	1.43	4.82
kNN	74.19	51.00	347.47	2.31	0.36
DT	37.06	24.90	357.32	1.13	0.28

The next three tables show the wind market at 60 min intervals. Table 10 presents the results of Austria. Among the models, TCNN, DT, and BiGRU are relatively superior. However, while these models outperform their counterparts, they all have an MASE greater than 1. Table 11 presents the results of 60 min intervals for Germany. As with the corresponding 15 min market, DT becomes the only model with an MASE value of less than 1. DNN has an MASE slightly above 1, which narrowly misses the benchmark. Lastly, Table 12 presents the results of 60 min intervals for the Netherlands. The DT again performs best, with an RMSE of 78.82. However, its MASE is slightly above the benchmark at 1.01. TCNN closely follows, with an RMSE of 83.59 and an MASE of 1.09.

Table 10. Evaluation Results for Austria’s Wind Generation (60 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	204.43	139.14	445.32	1.46	4.90
TCNN	153.52	99.65	447.48	1.05	289.37
LSTM	236.93	182.37	420.69	1.92	38.86
BiLSTM	234.10	178.87	478.34	1.88	90.91
GRU	169.11	112.71	470.58	1.19	48.15
BiGRU	156.80	98.55	472.54	1.04	94.36
DNN	166.92	110.01	459.52	1.16	3.22
kNN	254.46	176.06	426.64	1.85	0.38
DT	155.56	100.03	470.63	1.05	0.25

Table 11. Evaluation Results for Germany’s Wind Generation (60 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	1885.93	1401.90	5281.51	1.98	7.02
TCNN	2399.06	1945.11	5223.12	2.74	202.02
LSTM	2416.48	1885.91	4572.87	2.66	51.41
BiLSTM	2344.06	1949.61	4925.83	2.75	83.73
GRU	1350.46	1018.58	5252.57	1.44	34.19
BiGRU	1358.89	1002.56	5191.29	1.41	77.57
DNN	1008.61	758.25	5248.66	1.07	3.67
kNN	2228.24	1623.88	4911.05	2.29	0.35
DT	765.73	554.87	5332.17	0.78	0.26

Table 12. Evaluation Results for the Netherlands’ Wind Generation (60 min Intervals).

Model	RMSE	MAE	MAD	MASE	Optimization Time Used (min)
CNN	124.25	90.14	365.67	1.64	5.22
TCNN	83.59	60.10	397.16	1.09	148.45
LSTM	145.28	112.25	353.87	2.04	37.73
BiLSTM	104.73	76.66	367.15	1.40	88.66
GRU	90.09	65.88	378.76	1.20	38.16
BiGRU	87.53	62.84	378.54	1.14	75.44
DNN	92.51	66.62	378.68	1.21	3.68
kNN	147.00	112.01	357.58	2.04	0.34
DT	78.82	55.65	377.81	1.01	0.27

4. Discussion and Conclusions

Energy markets are receiving growing attention in academia. For instance, recent research works covered various problems, including crude oil price prediction [21,22], fossil energy market forecasting including crude oil, natural gas, propane, kerosene, gasoline, heating oil, and coal [23,24], electricity consumption prediction in various countries [25,26,27,28], complexity analysis in crude oil, gasoline, and heating oil under the COVID-19 pandemic [29], and the impact of the pandemic outbreak on WTI market efficiency [30]. In addition, machine learning is receiving growing attention in supply chain analytics [31,32,33,34,35,36]. The main purpose of the study is to forecast electricity load and wind generation in Europe. We contributed to the literature in the following aspects: (a) we considered the task of data forecasting applied to two major energy problems: electricity load and wind generation; (b) we implemented and compared different optimized deep learning models; (c) we used Bayesian optimization to fine tune the deep learning models; (d) we compared deep learning models against standard machine learning models; (e) we utilized of quarterly hour and hourly frequency sampling for electricity load and wind generation data modeling and forecasting; and (f) we compared models across different energy markets and expanded the applicability of models, addressing the gap in understanding model performance in diverse contexts.

The experimental results show that among the various models tested, the decision tree consistently outperforms others in forecasting accuracy for almost every dataset. DNN is the most effective for predicting electricity loads at the 60 min interval. The results of DNN imply the potential of advanced machine learning techniques in enhancing traditional energy forecasting methods.

In terms of experimental results, the performance of the neural network models is somewhat below expectations, with only DNN demonstrating notable proficiency within the 60 min interval for electricity load datasets. The optimization is limited to thirty iterations in the research, which may not be sufficient for all neural network models to find the optimal parameter combinations. Apart from that, external factors inherent to the data itself, such as the unpredictable peak in electricity loads and the inherently volatile nature of wind, pose significant challenges to model accuracy. All these factors introduce complexities that exacerbate the difficulty of achieving high performance.

For wind generation, there are significant challenges due to the inherent irregularity and unpredictability of wind patterns. As a result, almost every model evaluated in this study underperforms relative to expectations. The stochastic nature of wind makes it complex for models, and this difficulty is reflected in the consistently moderate performance. Hence, there is a need for research and development in this field to enhance the predictive capabilities of models dealing with such volatile energy sources.

The study offers actionable insights for energy policymakers and professionals on selecting and implementing forecasting models that can handle the complexities of modern energy systems. These findings not only pave the way for more reliable energy forecasting models but also contribute to the broader discourse on integrating machine learning into energy management systems, thereby supporting more sustainable and efficient energy use globally. The research highlights the potential for these technologies to transform energy operations, emphasizing the critical role of accurate forecasting in the transition to more adaptive and resilient energy systems.