A Multi-Strategy Improved Honey Badger Algorithm for Engineering Design Problems
Abstract
1. Introduction
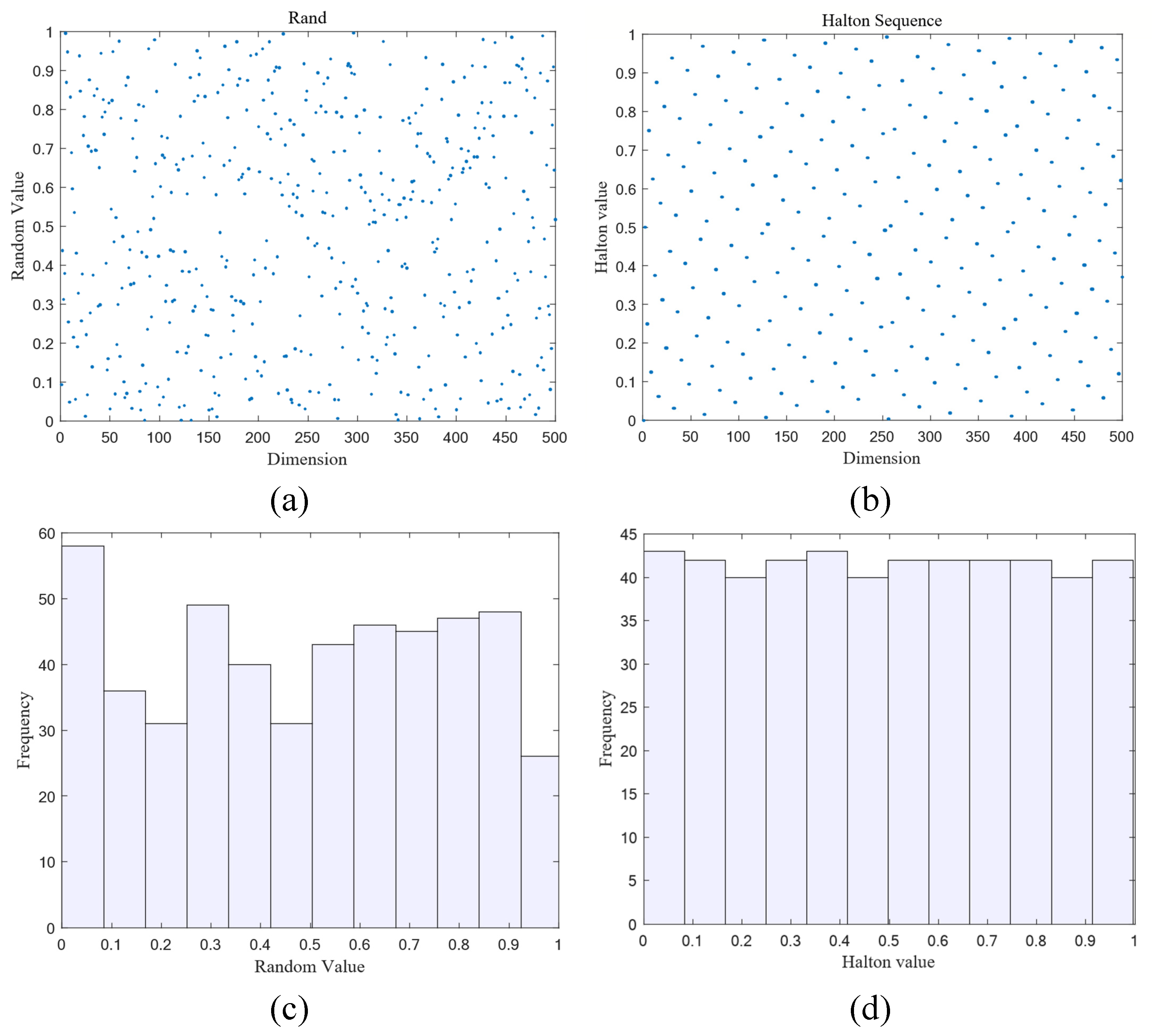
- The introduction of Halton sequence to initialize the population improves the initial diversity of the population and helps to avoid early convergence of the algorithm to local optimal solutions;
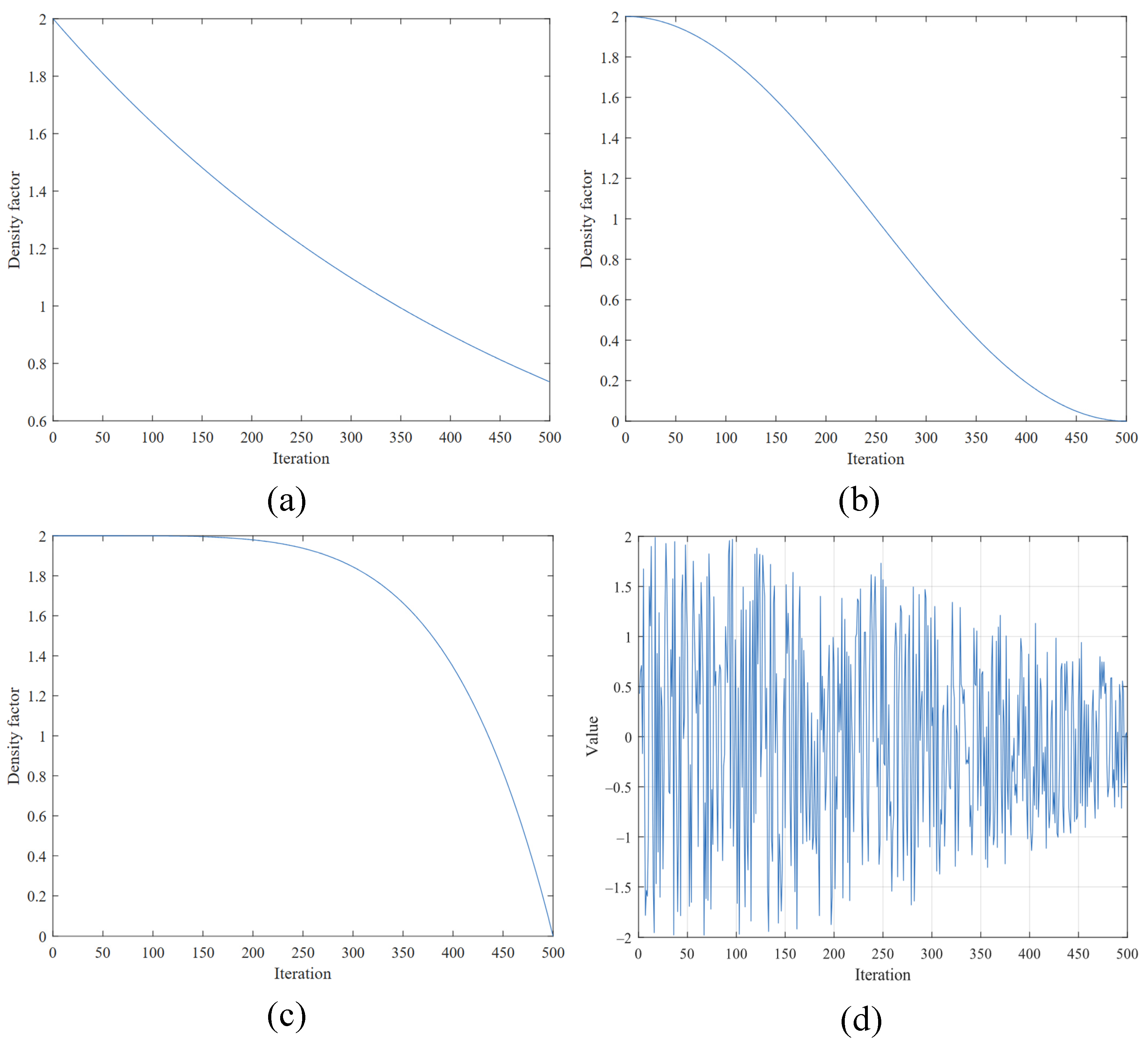
- The combination of the dynamic density factor of the water waves allows the algorithm to explore a wider search range and improves the adaptability and solving ability for complex functions;
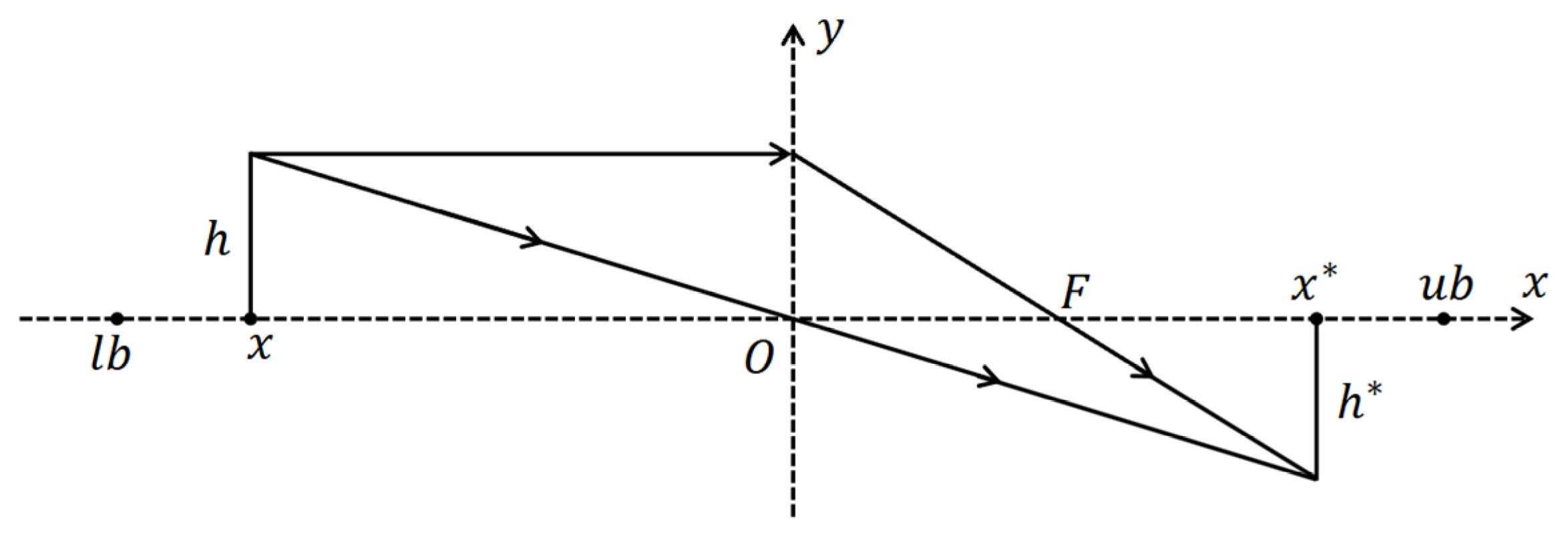
- The learning strategy based on the lens imaging principle improves the ability of the algorithm to escape from local optimal solutions and enhances the global search capability;
- The proposed algorithm is tested for performance on 23 benchmark test functions and applied to four engineering design problems, where the algorithm shows great advantages.
2. Algorithm Design
2.1. Honey Badger Algorithm
2.2. Proposed Algorithm
2.2.1. Halton Sequence Initializes the Population
2.2.2. Water Wave Dynamic Density Factor
2.2.3. Lens Opposition-Based Learning
| Algorithm 1. Pseudo code of MIHBA |
| , , , . |
| Initialize the population positions using the Halton mapping as shown in Equations (7)–(9). |
| . |
| . |
| do |
| Update the decreasing factor using Equation (12). |
| to do |
| using Equation (2). |
| then |
| using Equation (4). |
| Else |
| Update the position using Equation (6). |
| end if |
| Update the global best position using the lens opposition-based learning as described in Equation (16). |
| then |
| . |
| end if |
| then |
| . |
| end if |
| end for |
| end while Stop criteria satisfied. |
2.3. Subsection
2.3.1. Time Complexity
2.3.2. Space Complexity
3. Experiments
3.1. Experimental Setup and Evaluation Criteria
3.2. Test Functions
3.3. The Sensitivity Analysis About P, t
3.4. Results of Comparative Experiments
3.5. Results of Ablation Experiments
3.6. Friedman Test
3.7. Wilcoxon Signed-Rank Test
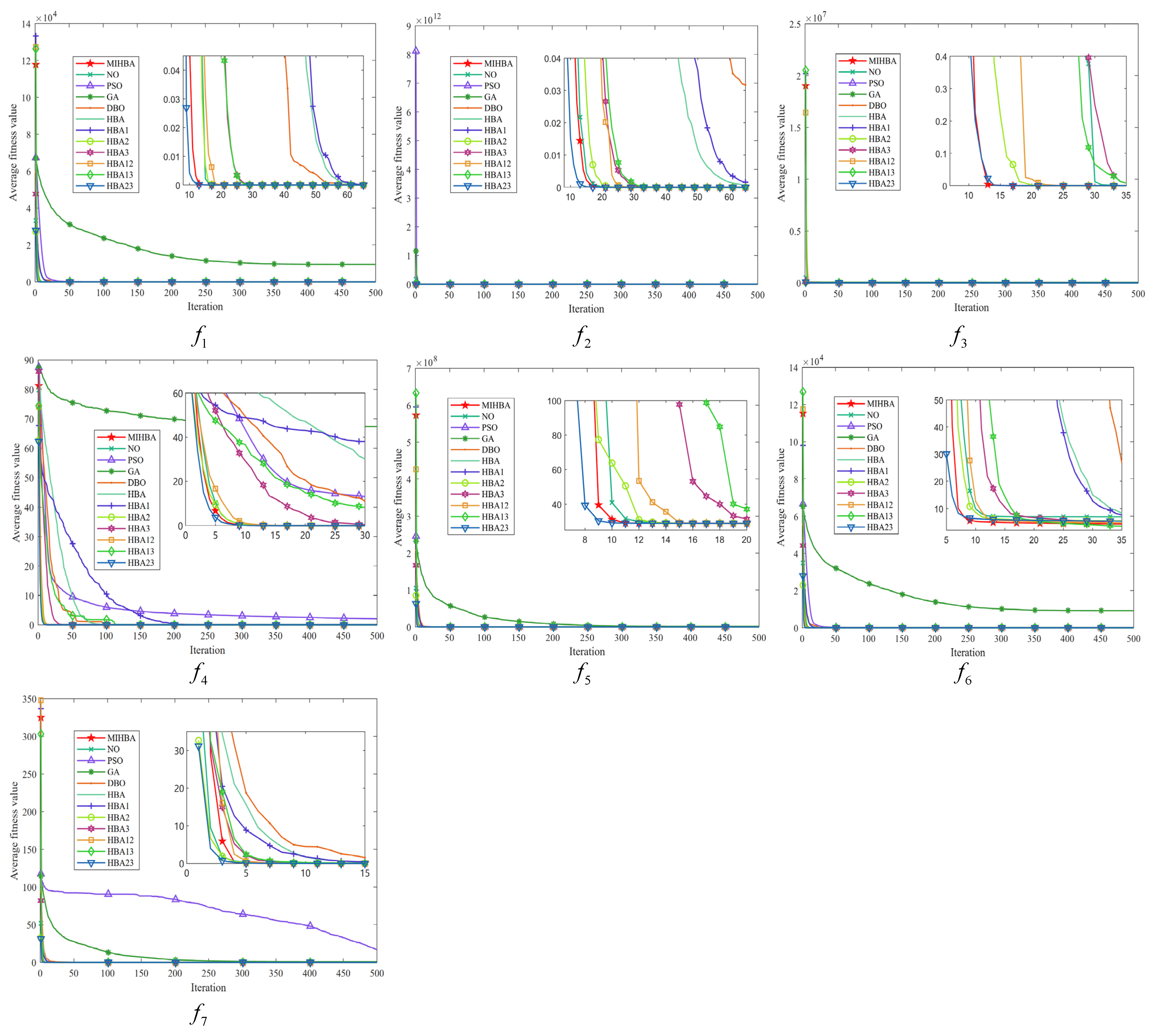
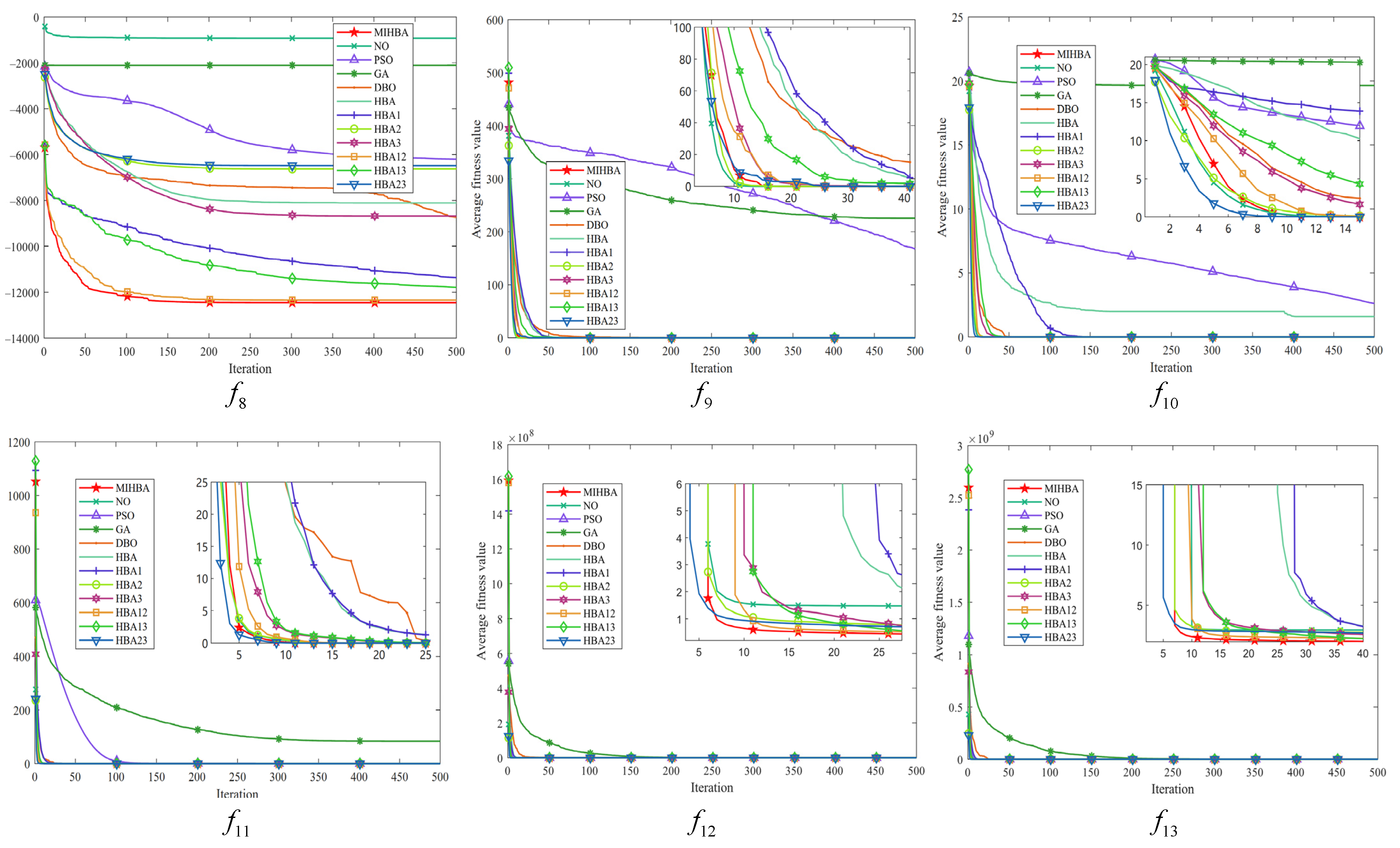
3.8. Convergence Analysis
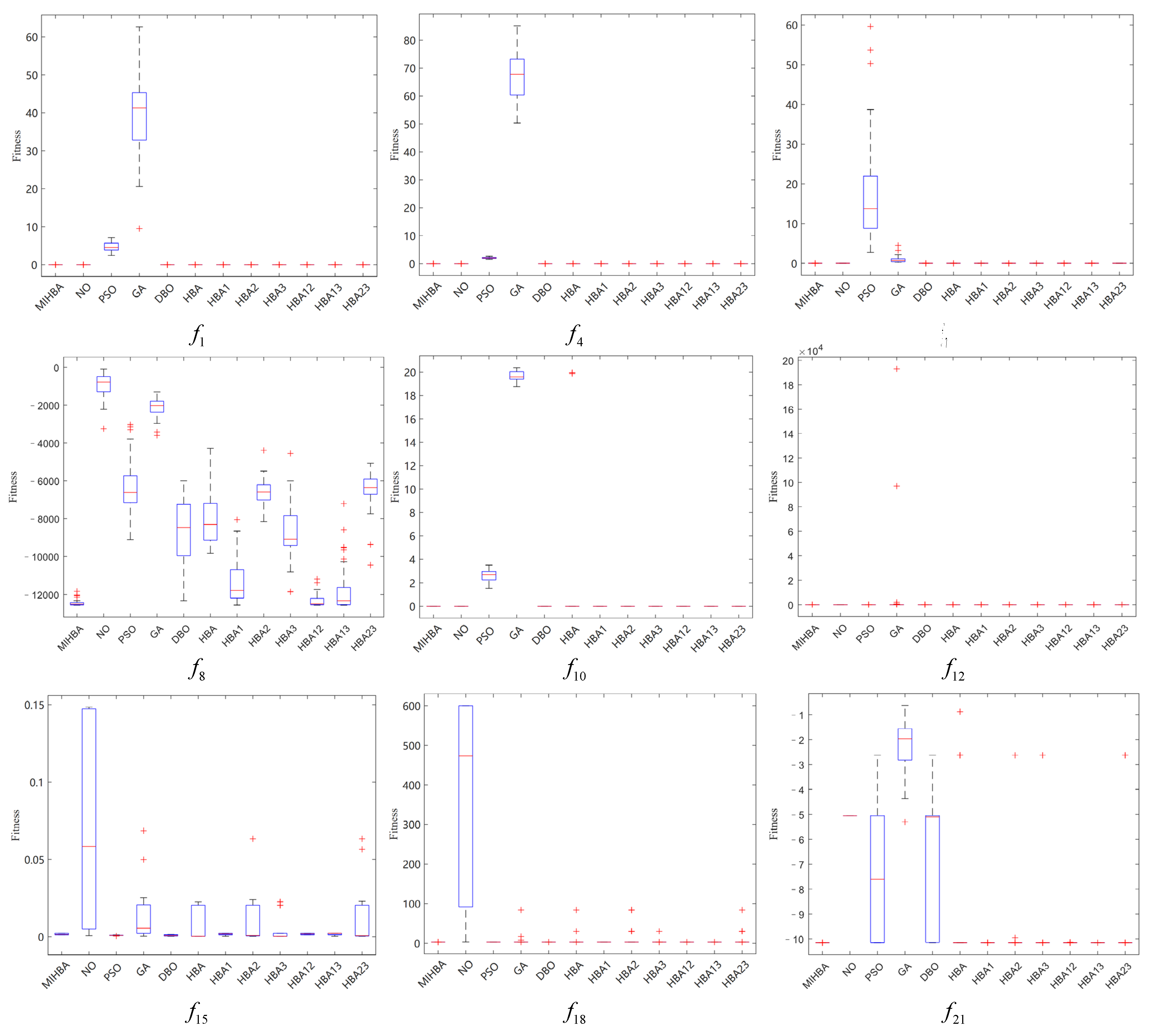
3.9. Stability Analysis
4. Application
4.1. Gear Train Design Problems
4.2. Pressure Vessel Design Problems
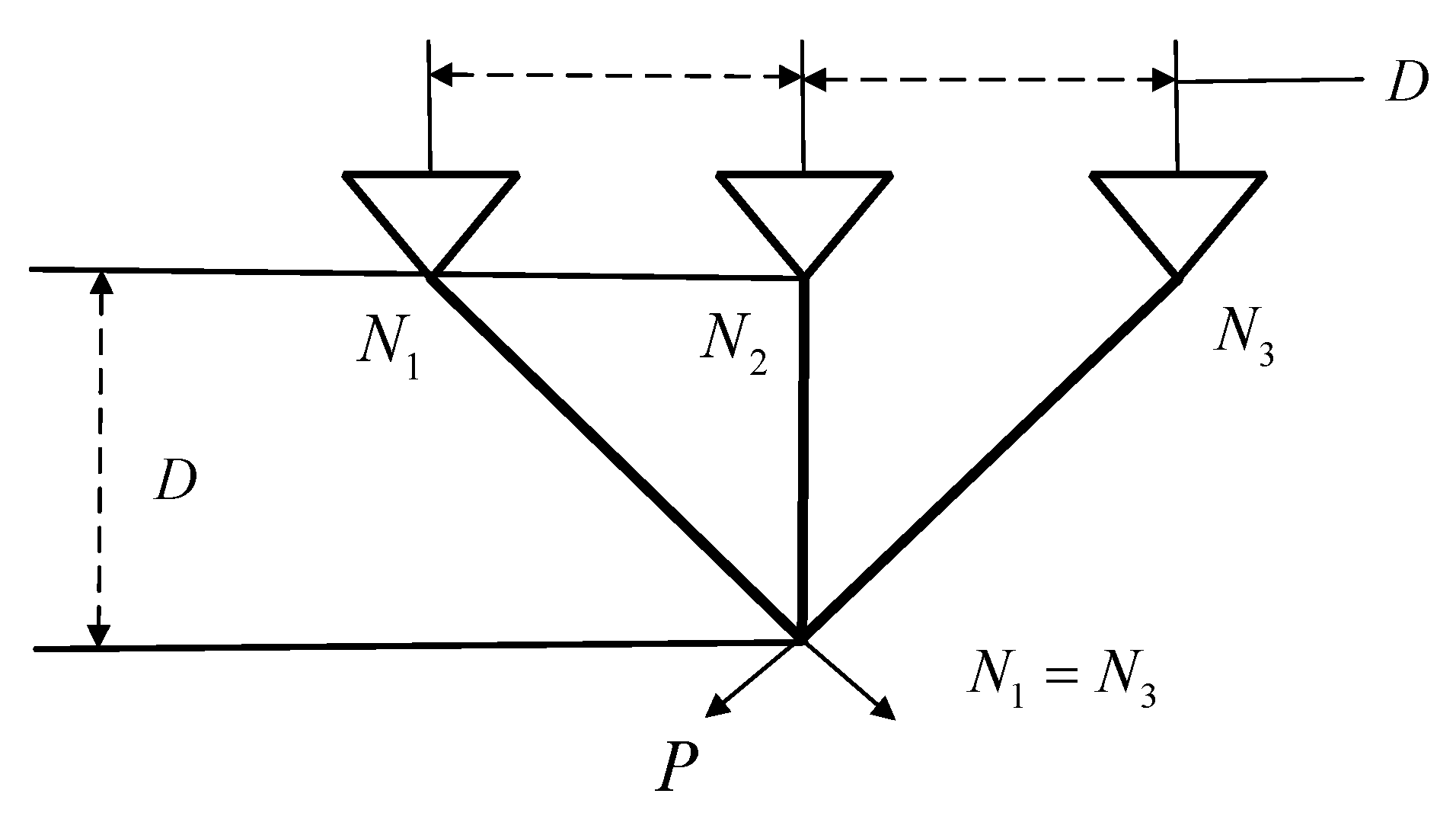
4.3. Three-Rod Truss Design Problems
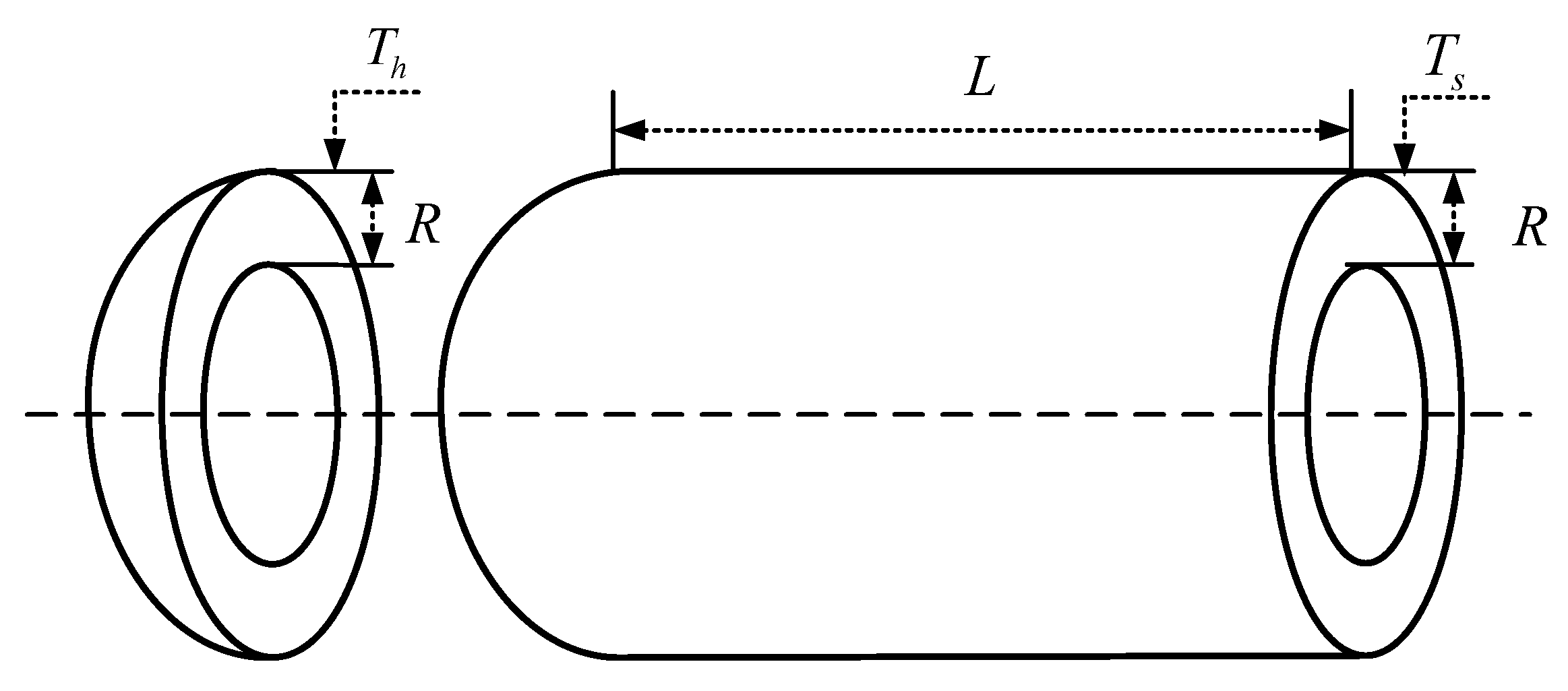
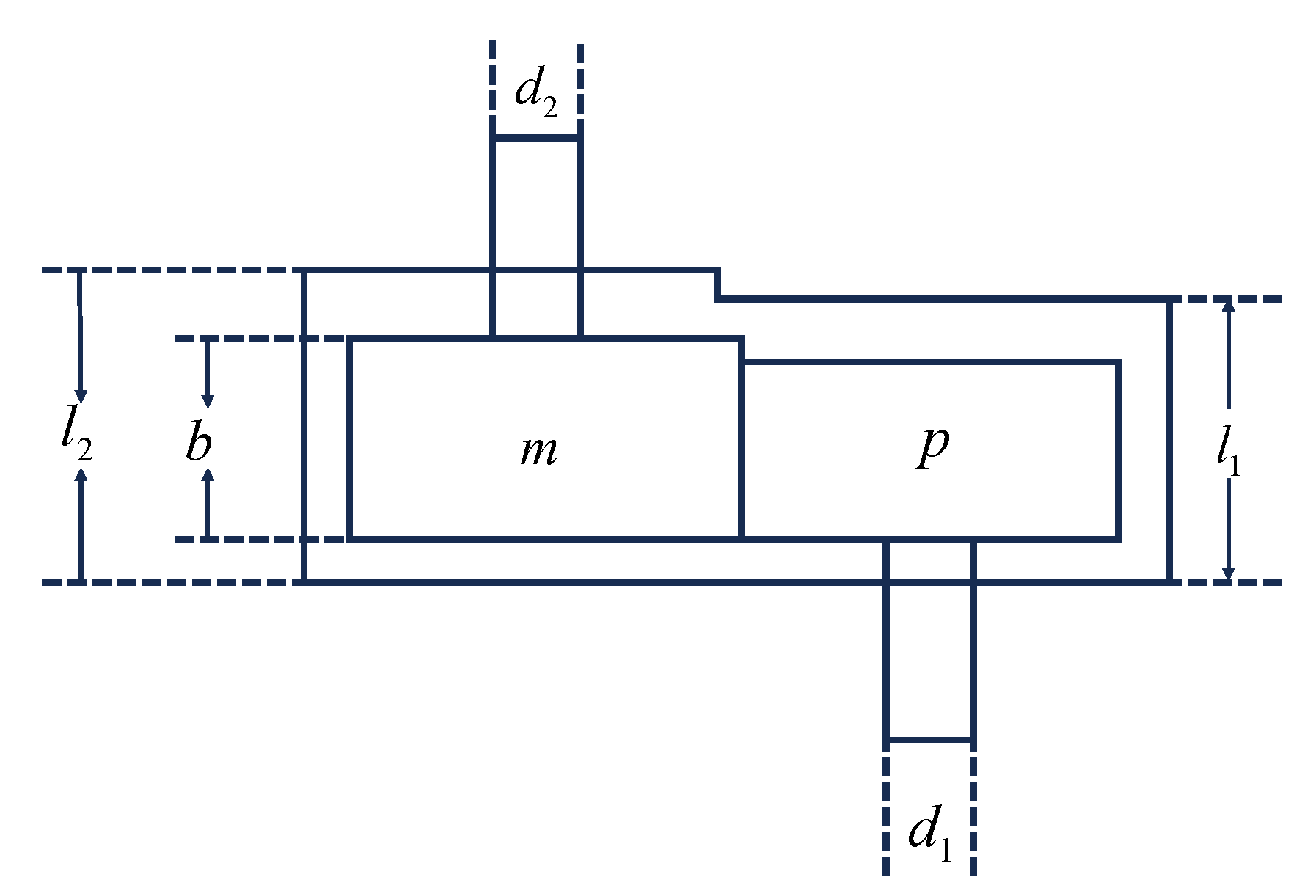
4.4. Reducer Design Problems
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.; Cao, H.; Shi, J.; Pei, S.; Zhang, B.; She, K. A comprehensive multi-parameter optimization method of squeeze film damper-rotor system using hunter-prey optimization algorithm. Tribol. Int. 2024, 194, 109538. [Google Scholar] [CrossRef]
- Jing, R.; Song, B.; Gao, R.; Yang, C.; Hao, X. A variable gradient descent shape optimization method for guide tee resistance reduction. J. Build. Eng. 2024, 95, 110161. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, X. A transient formulation of entropy and heat transfer coefficients of Newton’s cooling law with the unifying entropy potential difference in compressible flows. Int. J. Therm. Sci. 2024, 205, 109253. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.; Chen, Y.; Chen, H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, M.; Montazeri, Z.; Trojovská, E. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Amiri, M.; Hashjin, N.; Montazeri, M. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Fan, Z.; Xiao, Z.; Li, X.; Huang, Z.; Zhang, C. MSBWO: A Multi-Strategies Improved Beluga Whale Optimization Algorithm for Feature Selection. Biomimetics 2024, 9, 572. [Google Scholar] [CrossRef] [PubMed]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Baghalzadeh Shishehgarkhaneh, M. Energy valley optimizer: A novel metaheuristic algorithm for global and engineering optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef]
- Zolfi, K. Gold rush optimizer: A new population-based metaheuristic algorithm. Oper. Res. Decis. 2023, 33, 113–150. Available online: https://api.semanticscholar.org/CorpusID:258203735 (accessed on 16 April 2023).
- Wang, P.; Xin, G. Quantum theory of intelligent optimization algorithms. Acta Autom. Sin. 2023, 49, 2396–2408. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra Optimization Algorithm: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2022, 262, 110248. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.; Sumari, P.; Geem, Z.; Gandomi, A. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Dehkordi, A.; Sadiq, A.; Mirjalili, S.; Ghafoor, K. Nonlinear-based Chaotic Harris Hawks Optimizer: Algorithm and Internet of Vehicles application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Jena, B.; Naik, M.K.; Wunnava, A.; Panda, R. A Differential Squirrel Search Algorithm. Adv. Intell. Comput. Commun. 2021, 202, 143–152. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Liu, Z.; Nishi, T. Multipopulation Ensemble Particle Swarm Optimizer for Engineering Design Problems. Math. Probl. Eng. 2020, 2020, 1450985. [Google Scholar] [CrossRef]
- Hashim, F.; Houssein, E.; Hussain, K.; Mabrouk, M.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Bansal, A.; Sangtani, V.; Bhukya, M. Optimal configuration and sensitivity analysis of hybrid nanogrid for futuristic residential application using honey badger algorithm. Energy Convers. Manag. 2024, 315, 118784. [Google Scholar] [CrossRef]
- Jose, R.; Paulraj, E.; Rajesh, P. Enhancing Steady-State power flow optimization in smart grids with a hybrid converter using GBDT-HBA technique. Expert Syst. Appl. 2024, 258, 125047. [Google Scholar] [CrossRef]
- Wilson, A.; Kiran, W.; Radhamani, A.; Bharathi, A. Optimizing energy-efficient cluster head selection in wireless sensor networks using a binarized spiking neural network and honey badger algorithm. Knowl.-Based Syst. 2024, 299, 112039. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, K.; Chen, X.; Cui, L.; Zhang, J.; Cang, Y. Cgh-gto method for model parameter identification based on improved grey wolf optimizer, honey badger algorithm, and gorilla troops optimizer. Energy 2024, 296, 131163. [Google Scholar] [CrossRef]
- Ren, X.; Li, L.; Ji, B.; Liu, J. Design and analysis of solar hybrid combined cooling, heating and power system: A bi-level optimization model. Energy 2024, 292, 130362. [Google Scholar] [CrossRef]
- Wang, B.; Kang, H.; Sun, G.; Li, J. Efficient traffic-based IoT device identification using a feature selection approach with Lévy flight-based sine chaotic sub-swarm binary honey badger algorithm. Appl. Soft Comput. 2024, 155, 111455. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Li, Y.; Zhang, S.; Wang, Y.; Wang, X. Improved honey badger algorithm based on elementary function density factors and mathematical spirals in polar coor-dinate systema. Artif. Intell. Rev. 2024, 57, 55. [Google Scholar] [CrossRef]
- Huang, P.; Zhou, Y.; Deng, W.; Zhao, H.; Luo, Q.; Wei, Y. Orthogonal opposition-based learning honey badger algorithm with differential evolution for global optimization and engineering design problems. Alex. Eng. J. 2024, 91, 348–367. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, T.; Li, C. Migration time prediction and assessment of toxic fumes under forced ventilation in underground mines. Undergr. Space 2024, 18, 273–294. [Google Scholar] [CrossRef]
- Zhong, H.; Cong, M.; Wang, M.; Du, Y.; Liu, D. HB-RRT: A path planning algorithm for mobile robots using Halton sequence-based rapidly-exploring random tree. Eng. Appl. Artif. Intell. 2024, 133, 108362. [Google Scholar] [CrossRef]
- Duan, Y.; Yu, X. A collaboration-based hybrid GWO-SCA optimizer for engineering optimization problems. Eng. Appl. Artif. Intell. 2023, 2013, 119017. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Q.; Song, H.; Han, T.; Li, T. CMGWO: Grey wolf optimizer for fusion cell-like P systems. Heliyon 2024, 10, e34496. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y. Water wave optimization: A new nature-inspired metaheuristic. Comput. Oper. Res. 2015, 55, 1–11. [Google Scholar] [CrossRef]
- Yu, F.; Guan, J.; Wu, H.; Chen, Y.; Xia, X. Lens imaging opposition-based learning for differential evolution with cauchy perturbation. Appl. Soft Comput. 2024, 152, 111211. [Google Scholar] [CrossRef]
- Choi, T.; Pachauri, N. Adaptive search space for stochastic opposition-based learning in differential evolution. Knowl.-Based Syst. 2024, 300, 112172. [Google Scholar] [CrossRef]
- Bernardo, M.; Daniel, Z.; Erik, C.; Fernando, F.; Alma, R. A better balance in me-taheuristic algorithms: Does it exist? Swarm. Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Abdi, G.; Sheikhani, A.; Kordrostami, S.; Zarei, B.; Rad, M. Identifying communities in complex networks using learning-based genetic algorithm. Ain Shams Eng. J. 2024, in press. [Google Scholar] [CrossRef]
- Lyu, Y.; Jin, X.; Xue, Q.; Jia, Z.; Du, Z. An optimal configuration strategy of multi-chiller system based on overlap analysis and improved GA. Build. Environ. 2024, 266, 112117. [Google Scholar] [CrossRef]
- Abualigah, L.; Al-qaness, M.; Abd, E. The non-monopolize search (NO): A novel single-based local search optimization algorithm. Neural Comput. Appl. 2024, 36, 5305–5332. [Google Scholar] [CrossRef]
- Zhu, D.; Shen, J.; Zhang, Y.; Li, W.; Zhu, X.; Zhou, C.; Cheng, S.; Yao, Y. Multi-strategy particle swarm optimization with adaptive forgetting for base station layout. Swarm Evol. Comput. 2024, 91, 101737. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, N.; Chen, H.; Weng, S. Bayesian damage identification of an unsymmetrical frame structure with an improved PSO algorithm. Structures 2023, 57, 105119. [Google Scholar] [CrossRef]
- Lu, Q.; Chen, Y.; Zhang, X. Grinding process optimization considering carbon emissions, cost and time based on an improved dung beetle algorithm. Comput. Ind. Eng. 2024, 197, 110600. [Google Scholar] [CrossRef]
- Röhmel, J. The permutation distribution of the Friedman test. Comput. Stat. Data Anal. 1997, 26, 83–99. [Google Scholar] [CrossRef]
- Dewan, I.; Rao, B. Wilcoxon-signed rank test for associated sequences. Stat. Probab. Lett. 2005, 71, 131–142. [Google Scholar] [CrossRef]
- Zhuo, Y.; Zhang, T.; Du, F.; Liu, R. A parallel particle swarm optimization algorithm based on GPU/CUDA. Appl. Soft Comput. 2023, 144, 110499. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, K.; Chen, X.; Chen, Z.; Gao, F. Multi-objective optimization design method for the dimensions and control parameters of curling hexapod robot based on application performance. Mech. Mach. Theory 2024, 204, 105831. [Google Scholar] [CrossRef]



| Function | Dimension | Domain | Theoretical Optimum |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−500, 500] | −12,569.4 | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−50, 50] | 0 | |
| 30 | [−50, 50] | 0 | |
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.00003075 | |
| 2 | [−5, 5] | −1.0316285 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [0, 1] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10 | |
| 4 | [0, 10] | −10 | |
| 4 | [0, 10] | −10 |
| Function | Criterion | P/t | P/t | P/t |
|---|---|---|---|---|
| 15/1000 | 30/500 | 60/250 | ||
| f | Mean | 0.0000 × 100 | 0.0000 × 100 | 1.2449 × 10−213 |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 1.5 | 1.5 | 3 | |
| Mean | 0.0000 × 100 | 2.1815 × 10−211 | 4.4099 × 10−110 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 1.6352 × 10−109 | |
| Rank | 1 | 2 | 3 | |
| Mean | 0.0000 × 100 | 0.0000 × 100 | 3.0434 × 10−201 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 1.5 | 1.5 | 3 | |
| Mean | 0.0000 × 100 | 8.8038 × 10−202 | 7.7190 × 10−105 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 3.6422 × 10−104 | |
| Rank | 1 | 2 | 3 | |
| Mean | 2.8811 × 101 | 2.8576 × 101 | 2.8695 × 101 | |
| SD | 1.5692 × 10−1 | 3.2195 × 10−1 | 2.8470 × 10−1 | |
| Rank | 2 | 1 | 3 | |
| Mean | 3.2683 × 100 | 3.1940 × 100 | 2.7047 × 100 | |
| SD | 1.3931 × 100 | 1.0974 × 100 | 1.0262 × 100 | |
| Rank | 3 | 2 | 1 | |
| Mean | 3.8137 × 10−4 | 2.5721 × 10−4 | 2.5611 × 10−4 | |
| SD | 3.2160 × 10−4 | 2.6331 × 10−4 | 2.2611 × 10−4 | |
| Rank | 3 | 2 | 1 | |
| Mean | −1.2293 × 104 | −1.2455 × 104 | −1.2441 × 104 | |
| SD | 2.9838 × 102 | 1.6206 × 102 | 1.9268 × 102 | |
| Rank | 3 | 1 | 2 | |
| Mean | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 2 | 2 | 2 | |
| Mean | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 2 | 2 | 2 | |
| Mean | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 2 | 2 | 2 | |
| Mean | 2.5736 × 10−1 | 2.4112 × 10−1 | 1.7331 × 10−1 | |
| SD | 2.7247 × 10−1 | 1.6118 × 10−1 | 1.7408 × 10−1 | |
| Rank | 3 | 2 | 1 | |
| Mean | 1.9765 × 100 | 1.7823 × 100 | 1.5983 × 100 | |
| SD | 7.7008 × 10−1 | 6.7126 × 10−1 | 6.5243 × 10−1 | |
| Rank | 3 | 2 | 1 | |
| Mean | 2.9411 × 100 | 3.4290 × 100 | 2.3035 × 100 | |
| SD | 8.9217 × 10−1 | 1.9069 × 100 | 1.6986 × 100 | |
| Rank | 1 | 3 | 2 | |
| Mean | 2.1147 × 10−3 | 1.6665 × 10−3 | 1.3744 × 10−3 | |
| SD | 1.0278 × 10−3 | 4.3485 × 10−4 | 3.4597 × 10−4 | |
| Rank | 3 | 2 | 1 | |
| Mean | −1.0130 × 100 | −8.8472 × 10−1 | −9.6634 × 10−1 | |
| SD | 1.1539 × 10−1 | 3.1674 × 10−1 | 2.2367 × 10−1 | |
| Rank | 1 | 3 | 2 | |
| Mean | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | |
| SD | 1.1839 × 10−14 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 3 | 1.5 | 1.5 | |
| Mean | 4.1660 × 100 | 3.0000 × 100 | 3.0000 × 100 | |
| SD | 5.3452 × 100 | 7.4694 × 10−15 | 3.8756 × 10−15 | |
| Rank | 3 | 1.5 | 1.5 | |
| Mean | −3.6990 × 100 | −3.8626 × 100 | −3.8628 × 100 | |
| SD | 2.9147 × 10−1 | 1.1146 × 10−3 | 1.4827 × 10−13 | |
| Rank | 3 | 2 | 1 | |
| Mean | −3.2541 × 100 | −3.2004 × 100 | −3.1947 × 100 | |
| SD | 6.5043 × 10−2 | 1.4440 × 10−2 | 2.8326 × 10−2 | |
| Rank | 1 | 2 | 3 | |
| Mean | −1.0150 × 101 | −1.0153 × 101 | −1.0153 × 101 | |
| SD | 1.4456 × 10−2 | 3.1420 × 10−8 | 2.7968 × 10−7 | |
| Rank | 3 | 1 | 2 | |
| Mean | −1.0403 × 101 | −1.0403 × 101 | −1.0403 × 101 | |
| SD | 3.0841 × 10−4 | 8.5220 × 10−8 | 4.2074 × 10−9 | |
| Rank | 3 | 2 | 1 | |
| Mean | −1.0367 × 101 | −8.9298 × 100 | −3.3961 × 100 | |
| SD | 1.1467 × 100 | 3.2466 × 100 | 2.6635 × 100 | |
| Rank | 1 | 2 | 3 | |
| Rank-Count | 50 | 43 | 45 | |
| Ave-Rank | 2.174 | 1.869 | 1.957 | |
| Overall-Rank | 3 | 1 | 2 | |
| Algorithm | Parameters | Value |
|---|---|---|
| NO | 1 | |
| PSO | 2 | |
| 2 | ||
| 0.9 | ||
| 0.6 | ||
| GA | 0.9 | |
| 0.2 | ||
| DBO | 0.2 | |
| HBA Series | 6 | |
| 2 | ||
| [−1, 1] |
| Function | Criterion | NO | PSO | GA | DBO | HBA | MIHBA |
|---|---|---|---|---|---|---|---|
| Mean | 7.3003 × 10−185 | 2.4640 × 100 | 9.4741 × 103 | 2.2951 × 10−114 | 4.7283 × 10−135 | 0.0000 × 100 | |
| SD | 0.0000 × 100 | 1.1232 × 100 | 5.8262 × 103 | 1.1000 × 10−113 | 3.1823 × 10−134 | 0.0000 × 100 | |
| Rank | 2 | 5 | 6 | 4 | 3 | 1 | |
| Mean | 1.2667 × 10−95 | 4.6171 × 100 | 4.0060 × 101 | 4.7724 × 10−57 | 1.8214 × 10−72 | 2.1815 × 10−211 | |
| SD | 5.0335 × 10−95 | 1.1213 × 100 | 9.8511 × 100 | 3.3579 × 10−56 | 4.3810 × 10−72 | 0.0000 × 100 | |
| Rank | 2 | 5 | 6 | 4 | 3 | 1 | |
| Mean | 2.2392 × 10−158 | 1.8283 × 102 | 4.0361 × 104 | 1.5087 × 10−43 | 3.3967 × 10−96 | 0.0000 × 100 | |
| SD | 1.5833 × 10−157 | 5.4112 × 101 | 1.3818 × 104 | 1.0668 × 10−42 | 1.8422 × 10−95 | 0.0000 × 100 | |
| Rank | 2 | 5 | 6 | 4 | 3 | 1 | |
| Mean | 2.8770 × 10−92 | 2.0464 × 100 | 6.7351 × 101 | 4.6272 × 10−54 | 3.5493 × 10−57 | 8.8038 × 10−202 | |
| SD | 1.8518 × 10−91 | 2.3739 × 10−1 | 8.4169 × 100 | 2.7100 × 10−53 | 1.8516 × 10−56 | 0.0000 × 100 | |
| Rank | 2 | 5 | 6 | 4 | 3 | 1 | |
| Mean | 8.2510 × 10−30 | 1.1298 × 103 | 1.5814 × 106 | 2.5750 × 101 | 2.4107 × 101 | 2.8576 × 101 | |
| SD | 1.0323 × 10−29 | 7.1313 × 102 | 2.0583 × 106 | 1.9964 × 10−1 | 9.4081 × 10−1 | 3.2195 × 10−1 | |
| Rank | 1 | 5 | 6 | 3 | 2 | 4 | |
| Mean | 6.8816 × 100 | 2.4789 × 100 | 9.2284 × 103 | 1.5846 × 10−2 | 3.0077 × 10−2 | 3.1940 × 100 | |
| SD | 8.2198 × 10−1 | 1.2106 × 100 | 5.0355 × 103 | 5.9135 × 10−2 | 8.1659 × 10−2 | 1.0974 × 100 | |
| Rank | 5 | 3 | 6 | 1 | 2 | 4 | |
| Mean | 3.9573 × 10−3 | 1.7060 × 101 | 9.0373 × 10−1 | 1.2122 × 10−3 | 4.5094 × 10−4 | 2.5721 × 10−4 | |
| SD | 3.4920 × 10−3 | 1.2841 × 101 | 7.8983 × 10−1 | 1.0887 × 10−3 | 4.3386 × 10−4 | 2.6331 × 10−4 | |
| Rank | 4 | 6 | 5 | 3 | 2 | 1 | |
| Mean | −9.2645 × 102 | −6.2006 × 103 | −2.1082 × 103 | −8.7402 × 103 | −8.1146 × 103 | −1.2455 × 104 | |
| SD | 6.0439 × 102 | 1.3820 × 103 | 4.7463 × 102 | 1.7062 × 103 | 1.3014 × 103 | 1.6206 × 102 | |
| Rank | 6 | 4 | 5 | 2 | 3 | 1 | |
| Mean | 0.0000 × 100 | 1.6733 × 102 | 2.2556 × 102 | 3.7809 × 10−1 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 0.0000 × 100 | 3.2186 × 101 | 3.5442 × 101 | 1.5686 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 2 | 5 | 6 | 4 | 2 | 2 | |
| Mean | 8.8818 × 10−16 | 2.6233 × 100 | 1.9645 × 101 | 8.8818 × 10−16 | 1.5945 × 100 | 8.8818 × 10−16 | |
| SD | 0.0000 × 100 | 4.8205 × 10−1 | 4.3168 × 10−1 | 0.0000 × 100 | 5.4623 × 100 | 0.0000 × 100 | |
| Rank | 2 | 4 | 6 | 2 | 5 | 2 | |
| Mean | 0.0000 × 100 | 1.2469 × 10−1 | 8.3818 × 101 | 1.5363 × 10−3 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 0.0000 × 100 | 5.2338 × 10−2 | 5.7330 × 101 | 1.0863 × 10−2 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 2 | 5 | 6 | 4 | 2 | 2 | |
| Mean | 1.4334 × 100 | 5.6601 × 10−2 | 5.9015 × 103 | 7.4402 × 10−4 | 3.1293 × 10−3 | 2.4112 × 10−1 | |
| SD | 2.8723 × 10−1 | 5.7002 × 10−2 | 3.0280 × 104 | 2.5328 × 10−3 | 1.4709 × 10−2 | 1.6118 × 10−1 | |
| Rank | 5 | 3 | 6 | 1 | 2 | 4 | |
| Mean | 1.8699 × 10−32 | 5.5405 × 10−1 | 5.2614 × 105 | 6.1309 × 10−1 | 4.1696 × 10−1 | 1.7823 × 100 | |
| SD | 9.4408 × 10−33 | 2.2252 × 10−1 | 1.2456 × 106 | 5.0675 × 10−1 | 3.4127 × 10−1 | 6.7126 × 10−1 | |
| Rank | 1 | 3 | 6 | 4 | 2 | 5 | |
| Mean | 1.2277 × 101 | 3.1880 × 100 | 9.9800 × 10−1 | 1.3150 × 100 | 1.5304 × 100 | 3.4290 × 100 | |
| SD | 1.3645 × 100 | 2.3948 × 100 | 4.8340 × 10−10 | 8.8063 × 10−1 | 1.5614 × 100 | 1.9069 × 100 | |
| Rank | 6 | 5 | 1 | 2 | 3 | 4 | |
| Mean | 7.1715 × 10−2 | 8.8753 × 10−4 | 1.0915 × 10−2 | 8.0347 × 10−4 | 5.9713 × 10−3 | 1.6665 × 10−3 | |
| SD | 6.3231 × 10−2 | 1.3918 × 10−4 | 1.3053 × 10−2 | 3.9753 × 10−4 | 9.2543 × 10−3 | 4.3485 × 10−4 | |
| Rank | 6 | 1 | 5 | 2 | 4 | 3 | |
| Mean | −3.4420 × 10−1 | −1.0316 × 100 | −9.5284 × 10−1 | −1.0316 × 100 | −1.0316 × 100 | −8.8472 × 10−1 | |
| SD | 3.7077 × 10−1 | 4.3145 × 10−16 | 9.9834 × 10−2 | 1.6764 × 10−7 | 3.4164 × 10−16 | 3.1674 × 10−1 | |
| Rank | 6 | 1 | 4 | 3 | 2 | 5 | |
| Mean | 5.9065 × 100 | 3.9789 × 10−1 | 7.1239 × 101 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | |
| SD | 8.1139 × 100 | 0.0000 × 100 | 7.6469 × 100 | 2.5202 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 5 | 2.5 | 6 | 2.5 | 2.5 | 2.5 | |
| Mean | 3.7968 × 102 | 3.0000 × 100 | 4.9999 × 100 | 3.0000 × 100 | 5.1600 × 100 | 3.0000 × 100 | |
| SD | 2.4405 × 102 | 6.6417 × 10−15 | 1.1593 × 101 | 2.6119 × 10−15 | 1.2001 × 101 | 7.4694 × 10−15 | |
| Rank | 6 | 1.5 | 4 | 1.5 | 5 | 1.5 | |
| Mean | −1.4201 × 100 | −3.8628 × 100 | −3.3076 × 100 | −3.8611 × 100 | −3.8615 × 100 | −3.8626 × 100 | |
| SD | 1.0736 × 100 | 9.5794 × 10−16 | 3.6983 × 10−1 | 3.2588 × 10−3 | 2.9188 × 10−3 | 1.1146 × 10−3 | |
| Rank | 6 | 1 | 5 | 4 | 3 | 2 | |
| Mean | −1.1995 × 100 | −3.2625 × 100 | −1.4049 × 100 | −3.2381 × 100 | −3.2469 × 100 | −3.2004 × 100 | |
| SD | 7.2506 × 10−1 | 6.0050 × 10−2 | 4.8656 × 10−1 | 1.0375 × 10−1 | 7.0311 × 10−2 | 1.4440 × 10−2 | |
| Rank | 6 | 1 | 5 | 4 | 3 | 2 | |
| Mean | −5.0552 × 100 | −7.1528 × 100 | −2.1951 × 100 | −6.6436 × 100 | −8.7291 × 100 | −1.0153 × 101 | |
| SD | 0.0000 × 100 | 3.1403 × 100 | 9.6407 × 10−1 | 2.5711 × 100 | 3.0861 × 100 | 3.1420 × 10−8 | |
| Rank | 3 | 5 | 6 | 4 | 2 | 1 | |
| Mean | −5.0877 × 100 | −9.3099 × 100 | −2.0067 × 100 | −8.0030 × 100 | −9.0115 × 100 | −1.0403 × 101 | |
| SD | 0.0000 × 100 | 2.4042 × 100 | 8.4662 × 10−1 | 2.9063 × 100 | 3.0265 × 100 | 8.5220 × 10−8 | |
| Rank | 5 | 2 | 6 | 4 | 3 | 1 | |
| Mean | −5.1285 × 100 | −9.4642 × 100 | −1.7977 × 100 | −8.9748 × 100 | −8.4113 × 100 | −8.9298 × 100 | |
| SD | 8.9720 × 10−16 | 2.3292 × 100 | 6.5073 × 10−1 | 2.5559 × 100 | 3.3086 × 100 | 3.2466 × 100 | |
| Rank | 4 | 1 | 6 | 2 | 5 | 3 | |
| Rank-Count | 89 | 79 | 124 | 69 | 66.5 | 54 | |
| Ave-Rank | 3.8696 | 3.4348 | 5.3913 | 3.0000 | 2.8913 | 2.3478 | |
| Overall-Rank | 5 | 4 | 6 | 3 | 2 | 1 |
| Algorithm | Halton | Water Wave Dynamic Density Factor | Lens Opposition-Based Learning |
|---|---|---|---|
| HBA | |||
| HBA1 | ✓ | ||
| HBA2 | ✓ | ||
| HBA3 | ✓ | ||
| HBA12 | ✓ | ✓ | |
| HBA13 | ✓ | ✓ | |
| HBA23 | ✓ | ✓ | |
| MIHBA | ✓ | ✓ | ✓ |
| Function | Criterion | HBA | HBA1 | HBA2 | HBA3 | HBA12 | HBA13 | HBA23 | MIHBA |
|---|---|---|---|---|---|---|---|---|---|
| Mean | 4.7283 × 10−135 | 1.7723 × 10−134 | 3.7719 × 10−240 | 9.5105 × 10−256 | 3.8876 × 10−238 | 2.0207 × 10−258 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 3.1823 × 10−134 | 1.0698 × 10−133 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 7 | 8 | 5 | 4 | 6 | 3 | 1.5 | 1.5 | |
| Mean | 1.8214 × 10−72 | 1.5383 × 10−71 | 1.9881 × 10−124 | 4.6686 × 10−135 | 6.6283 × 10−124 | 3.8114 × 10−133 | 7.4191 × 10−210 | 2.1815 × 10−211 | |
| SD | 4.3810 × 10−72 | 4.4108 × 10−71 | 1.3312 × 10−123 | 3.0048 × 10−134 | 4.4163 × 10−123 | 2.6888 × 10−132 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 7 | 8 | 5 | 3 | 6 | 4 | 2 | 1 | |
| Mean | 3.3967 × 10−96 | 1.8412 × 10−97 | 2.2601 × 10−226 | 2.2645 × 10−215 | 2.0049 × 10−220 | 2.0154 × 10−221 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 1.8422 × 10−95 | 1.0975 × 10−96 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 8 | 7 | 3 | 6 | 5 | 4 | 1.5 | 1.5 | |
| Mean | 3.5493 × 10−57 | 6.7229 × 10−44 | 1.4246 × 10−118 | 2.2832 × 10−119 | 2.9398 × 10−119 | 1.2983 × 10−110 | 3.6497 × 10−198 | 8.8038 × 10−202 | |
| SD | 1.8516 × 10−56 | 2.4640 × 10−43 | 8.8713 × 10−118 | 1.1773 × 10−118 | 1.2212 × 10−118 | 6.8046 × 10−110 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 7 | 8 | 5 | 3 | 4 | 6 | 2 | 1 | |
| Mean | 2.4107 × 101 | 2.3986 × 101 | 2.8699 × 101 | 2.3815 × 101 | 2.8608 × 101 | 2.3783 × 101 | 2.8675 × 101 | 2.8576 × 101 | |
| SD | 9.4081 × 10−1 | 8.5190 × 10−1 | 2.8744 × 10−1 | 5.6154 × 10−1 | 3.0152 × 10−1 | 8.0837 × 10−1 | 3.2828 × 10−1 | 3.2195 × 10−1 | |
| Rank | 4 | 3 | 7 | 1 | 6 | 2 | 8 | 5 | |
| Mean | 3.0077 × 10−2 | 1.5175 × 10−2 | 4.4300 × 100 | 2.0162 × 10−2 | 3.6728 × 100 | 1.1255 × 10−2 | 4.3189 × 100 | 3.1940 × 100 | |
| SD | 8.1659 × 10−2 | 5.9595 × 10−2 | 7.8025 × 10−1 | 6.8143 × 10−2 | 1.0744 × 100 | 4.9958 × 10−2 | 7.4332 × 10−1 | 1.0974 × 100 | |
| Rank | 4 | 2 | 8 | 3 | 6 | 1 | 7 | 5 | |
| Mean | 4.5094 × 10−4 | 4.1968 × 10−4 | 2.8189 × 10−4 | 3.5129 × 10−4 | 3.8020 × 10−4 | 3.7453 × 10−4 | 3.7404 × 10−4 | 2.5721 × 10−4 | |
| SD | 4.3386 × 10−4 | 3.7204 × 10−4 | 3.7439 × 10−4 | 3.0190 × 10−4 | 3.6380 × 10−4 | 2.5372 × 10−4 | 3.6974 × 10−4 | 2.6331 × 10−4 | |
| Rank | 8 | 7 | 4 | 3 | 6 | 2 | 5 | 1 | |
| Mean | −8.1146 × 103 | −1.1362 × 104 | −6.6279 × 103 | −8.6794 × 103 | −1.2342 × 104 | −1.1789 × 104 | −6.4823 × 103 | −1.2455 × 104 | |
| SD | 1.3014 × 103 | 1.1693 × 103 | 7.0940 × 102 | 1.3760 × 103 | 3.0113 × 102 | 1.1924 × 103 | 9.4440 × 102 | 1.6206 × 102 | |
| Rank | 6 | 4 | 7 | 5 | 2 | 3 | 8 | 1 | |
| f9 | Mean | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | |
| Mean | 1.5945 × 100 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| SD | 5.4623 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 8 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| Mean | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | |
| Mean | 3.1293 × 10−3 | 3.9397 × 10−4 | 4.5782 × 10−1 | 8.4754 × 10−6 | 3.1053 × 10−1 | 6.5165 × 10−4 | 4.4263 × 10−1 | 2.4112 × 10−1 | |
| SD | 1.4709 × 10−2 | 1.5503 × 10−3 | 1.9787 × 10−1 | 1.3619 × 10−5 | 2.4469 × 10−1 | 1.9603 × 10−3 | 1.6113 × 10−1 | 1.6118 × 10−1 | |
| Rank | 4 | 2 | 8 | 1 | 6 | 3 | 7 | 5 | |
| Mean | 4.1696 × 10−1 | 4.2182 × 10−1 | 2.4608 × 100 | 1.0587 × 100 | 2.0050 × 100 | 4.8950 × 10−1 | 2.4024 × 100 | 1.7823 × 100 | |
| SD | 3.4127 × 10−1 | 3.6345 × 10−1 | 3.3591 × 10−1 | 4.9331 × 10−1 | 5.4848 × 10−1 | 4.6493 × 10−1 | 2.9277 × 10−1 | 6.7126 × 10−1 | |
| Rank | 1 | 2 | 8 | 4 | 6 | 3 | 7 | 5 | |
| Mean | 1.5304 × 100 | 1.7284 × 100 | 4.8083 × 100 | 1.5299 × 100 | 3.4278 × 100 | 1.6693 × 100 | 3.2449 × 100 | 3.4290 × 100 | |
| SD | 1.5614 × 100 | 1.6678 × 100 | 3.5082 × 100 | 1.6356 × 100 | 2.0498 × 100 | 1.6030 × 100 | 2.6254 × 100 | 1.9069 × 100 | |
| Rank | 1 | 4 | 8 | 2 | 6 | 3 | 7 | 5 | |
| Mean | 5.9713 × 10−3 | 1.7166 × 10−3 | 7.9111 × 10−3 | 5.5807 × 10−3 | 1.7706 × 10−3 | 1.8942 × 10−3 | 7.9738 × 10−3 | 1.6665 × 10−3 | |
| SD | 9.2543 × 10−3 | 5.7402 × 10−4 | 1.1928 × 10−2 | 8.8396 × 10−3 | 4.4023 × 10−4 | 5.2223 × 10−4 | 1.3768 × 10−2 | 4.3485 × 10−4 | |
| Rank | 6 | 3 | 7 | 5 | 2 | 4 | 8 | 1 | |
| Mean | −1.0316 × 100 | −1.0316 × 100 | −1.0153 × 100 | −1.0316 × 100 | −8.5207 × 10−1 | −1.0316 × 100 | −9.8266 × 10−1 | −8.8472 × 10−1 | |
| SD | 3.4164 × 10−16 | 3.3269 × 10−16 | 1.1542 × 10−1 | 3.0917 × 10−16 | 3.4153 × 10−1 | 3.1879 × 10−16 | 1.9580 × 10−1 | 3.1674 × 10−1 | |
| Rank | 4 | 1 | 5 | 2 | 8 | 3 | 6 | 7 | |
| Mean | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | 3.9789 × 10−1 | |
| SD | 0.0000 × 100 | 0.0000 × 100 | 8.2352 × 10−16 | 0.0000 × 100 | 3.5198 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| Rank | 3.5 | 3.5 | 8 | 3.5 | 7 | 3.5 | 3.5 | 3.5 | |
| f18 | Mean | 5.1600 × 100 | 3.0000 × 100 | 1.2180 × 101 | 3.5400 × 100 | 3.0000 × 100 | 3.0000 × 100 | 7.8600 × 100 | 3.0000 × 100 |
| SD | 1.2001 × 101 | 1.7843 × 10−15 | 2.0850 × 101 | 3.8184 × 100 | 1.0560 × 10−14 | 1.9106 × 10−15 | 1.4109 × 101 | 7.4694 × 10−15 | |
| Rank | 6 | 1 | 8 | 5 | 4 | 2 | 7 | 3 | |
| Mean | −3.8615 × 100 | −3.8615 × 100 | −3.8317 × 100 | −3.8468 × 100 | −3.8628 × 100 | −3.8625 × 100 | −3.8162 × 100 | −3.8626 × 100 | |
| SD | 2.9188 × 10−3 | 2.9188 × 10−3 | 1.5299 × 10−1 | 1.0927 × 10−1 | 2.8931 × 10−11 | 1.5601 × 10−3 | 1.8540 × 10−1 | 1.1146 × 10−3 | |
| Rank | 4 | 5 | 7 | 6 | 1 | 3 | 8 | 2 | |
| Mean | −3.2469 × 100 | −3.1984 × 100 | −3.2729 × 100 | −3.2742 × 100 | −3.2028 × 100 | −3.2026 × 100 | −3.2552 × 100 | −3.2004 × 100 | |
| SD | 7.0311 × 10−2 | 1.6450 × 10−2 | 6.9087 × 10−2 | 5.9130 × 10−2 | 3.8330 × 10−4 | 1.5673 × 10−3 | 7.1978 × 10−2 | 1.4440 × 10−2 | |
| Rank | 8 | 7 | 2 | 1 | 3 | 4 | 6 | 5 | |
| Mean | −8.7291 × 100 | −1.0153 × 101 | −9.9987 × 100 | −9.8523 × 100 | −1.0153 × 101 | −1.0153 × 101 | −9.5514 × 100 | −1.0153 × 101 | |
| SD | 3.0861 × 100 | 2.7213 × 10−15 | 1.0637 × 100 | 1.4891 × 100 | 3.1098 × 10−3 | 3.1183 × 10−15 | 2.0616 × 100 | 3.1420 × 10−8 | |
| Rank | 8 | 2 | 5 | 6 | 4 | 2 | 7 | 2 | |
| Mean | −9.0115 × 100 | −1.0403 × 101 | −7.8663 × 100 | −9.5057 × 100 | −1.0403 × 101 | −1.0269 × 101 | −8.3035 × 100 | −1.0403 × 101 | |
| SD | 3.0265 × 100 | 1.3899 × 10−15 | 3.5968 × 100 | 2.4577 × 100 | 2.9170 × 10−6 | 9.4450 × 10−1 | 3.4108 × 100 | 8.5220 × 10−8 | |
| Rank | 6 | 1 | 8 | 5 | 3 | 4 | 7 | 2 | |
| Mean | −8.4113 × 100 | −5.6190 × 100 | −7.5025 × 100 | −8.5479 × 100 | −3.4246 × 100 | −5.9353 × 100 | −8.2796 × 100 | −8.9298 × 100 | |
| SD | 3.3086 × 100 | 3.9071 × 100 | 3.7837 × 100 | 3.4047 × 100 | 2.6604 × 100 | 3.9568 × 100 | 3.5025 × 100 | 3.2466 × 100 | |
| Rank | 3 | 7 | 5 | 2 | 8 | 6 | 4 | 1 | |
| Rank-Count | 122.5 | 98.5 | 136 | 83.5 | 112 | 78.5 | 125.5 | 71.5 | |
| Ave-Rank | 5.3261 | 4.2826 | 5.9130 | 3.6304 | 4.8696 | 3.4130 | 5.4565 | 3.1087 | |
| Overall-Rank | 6 | 4 | 8 | 3 | 5 | 2 | 7 | 1 | |
| Function | NO | PSO | GA | DBO | HBA | HBA1 |
|---|---|---|---|---|---|---|
| 7 | 11 | 12 | 10 | 8 | 9 | |
| 7 | 11 | 12 | 10 | 8 | 9 | |
| f3 | 7 | 11 | 12 | 10 | 9 | 8 |
| 7 | 11 | 12 | 9 | 8 | 10 | |
| 10 | 12 | 11 | 9 | 8 | 7 | |
| 12 | 10 | 11 | 5 | 7 | 4 | |
| 5 | 11 | 12 | 10 | 5 | 5 | |
| 5 | 11 | 12 | 5 | 10 | 5 | |
| 5 | 11 | 12 | 10 | 5 | 5 | |
| 12 | 2 | 11 | 1 | 8 | 4 | |
| 11 | 5.5 | 12 | 5.5 | 5.5 | 5.5 | |
| 12 | 3.5 | 8 | 3.5 | 9 | 3.5 | |
| 12 | 1.5 | 11 | 7 | 5 | 6 | |
| 11 | 9 | 12 | 10 | 8 | 2.5 | |
| 11 | 6 | 12 | 9 | 7 | 2 | |
| Rank-Count | 134 | 126.5 | 172 | 114 | 110.5 | 85.5 |
| Ave-Rank | 8.9333 | 8.4333 | 11.4667 | 7.6000 | 7.3667 | 5.7000 |
| Overall–Rank | 11 | 10 | 12 | 9 | 8 | 5.5 |
| Function | HBA2 | HBA3 | HBA12 | HBA13 | HBA23 | MIHBA |
| 5 | 4 | 6 | 3 | 1.5 | 1.5 | |
| 5 | 3 | 6 | 4 | 2 | 1 | |
| f3 | 3 | 6 | 5 | 4 | 1.5 | 1.5 |
| 5 | 3 | 4 | 6 | 2 | 1 | |
| 2 | 3 | 6 | 5 | 4 | 1 | |
| 8 | 6 | 2 | 3 | 9 | 1 | |
| 5 | 5 | 5 | 5 | 5 | 5 | |
| 5 | 5 | 5 | 5 | 5 | 5 | |
| 5 | 5 | 5 | 5 | 5 | 5 | |
| f15 | 9 | 7 | 5 | 6 | 10 | 3 |
| 5.5 | 5.5 | 5.5 | 5.5 | 5.5 | 5.5 | |
| 11 | 7 | 3.5 | 3.5 | 10 | 3.5 | |
| 9 | 8 | 1.5 | 4 | 10 | 3 | |
| f21 | 5 | 6 | 2.5 | 2.5 | 7 | 2.5 |
| 10 | 5 | 2 | 4 | 8 | 2 | |
| Rank-Count | 92.5 | 78.5 | 64 | 65.5 | 85.5 | 41.5 |
| Ave-Rank | 6.1667 | 5.2333 | 4.2667 | 4.3667 | 5.7000 | 2.7667 |
| Overall-Rank | 7 | 4 | 2 | 3 | 5.5 | 1 |
| Functions | NO vs. MIHBA | PSO vs. MIHBA | GA vs. MIHBA | DBO vs. MIHBA | HBA vs. MIHBA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | |
| 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | |
| f3 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 |
| 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | |
| 4.8145 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | |
| 1.5267 × 10−17 | 1 | 9.4778 × 10−4 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | |
| 1.5537 × 10−12 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 8.4857 × 10−14 | 1 | 1.3969 × 10−3 | 1 | |
| 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 1.3657 × 10−17 | 1 | 7.0661 × 10−18 | 1 | |
| NaN | 0 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 8.2226 × 10−2 | 0 | NaN | 0 | |
| NaN | 0 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | NaN | 0 | 4.3349 × 10−2 | 1 | |
| NaN | 0 | 3.3111 × 10−20 | 1 | 3.3111 × 10−20 | 1 | 3.2709 × 10−1 | 0 | NaN | 0 | |
| 7.8197 × 10−18 | 1 | 3.0946 × 10−13 | 1 | 7.0661 × 10−18 | 1 | 7.0661 × 10−18 | 1 | 1.1417 × 10−17 | 1 | |
| f13 | 5.8250 × 10−18 | 1 | 5.2389 × 10−15 | 1 | 7.0661 × 10−18 | 1 | 1.7158 × 10−12 | 1 | 2.8599 × 10−15 | 1 |
| f14 | 1.0931 × 10−17 | 1 | 1.7752 × 10−2 | 1 | 5.4090 × 10−12 | 1 | 9.2297 × 10−14 | 1 | 2.4401 × 10−12 | 1 |
| 1.8228 × 10−12 | 1 | 7.0121 × 10−18 | 1 | 1.1158 × 10−8 | 1 | 8.3451 × 10−12 | 1 | 3.8154 × 10−3 | 1 | |
| 2.8961 × 10−13 | 1 | 2.5068 × 10−1 | 0 | 2.1714 × 10−8 | 1 | 2.6399 × 10−4 | 1 | 6.6781 × 10−6 | 1 | |
| 3.3072 × 10−20 | 1 | NaN | 0 | 3.3111 × 10−20 | 1 | 3.2709 × 10−1 | 0 | NaN | 0 | |
| 4.5418 × 10−18 | 1 | 8.0551 × 10−4 | 1 | 6.8062 × 10−18 | 1 | 1.8974 × 10−5 | 1 | 7.7869 × 10−4 | 1 | |
| 7.2628 × 10−18 | 1 | 2.2866 × 10−7 | 1 | 6.8385 × 10−18 | 1 | 2.0178 × 10−5 | 1 | 3.7619 × 10−8 | 1 | |
| 7.0661 × 10−18 | 1 | 1.8392 × 10−17 | 1 | 7.0661 × 10−18 | 1 | 2.2274 × 10−2 | 1 | 1.1090 × 10−7 | 1 | |
| 3.3111 × 10−20 | 1 | 1.7289 × 10−3 | 1 | 7.0661 × 10−18 | 1 | 4.3822 × 10−9 | 1 | 2.7414 × 10−8 | 1 | |
| 3.3111 × 10−20 | 1 | 4.1793 × 10−1 | 0 | 7.0661 × 10−18 | 1 | 2.5307 × 10−1 | 0 | 2.5381 × 10−8 | 1 | |
| 3.3222 × 10−8 | 1 | 9.8724 × 10−2 | 0 | 3.3827 × 10−16 | 1 | 1.5238 × 10−1 | 0 | 2.6397 × 10−5 | 1 | |
| Algorithm | Optimum Value | Optimal Cost | |||
|---|---|---|---|---|---|
| PSO | 46 | 26 | 12 | 47 | 9.9216 × 10−10 |
| DBO | 60 | 12 | 13 | 18 | 2.7265 × 10−8 |
| HBA | 54 | 12 | 37 | 57 | 8.8876 × 10−10 |
| MIHBA | 43 | 19 | 16 | 49 | 2.7009 × 10−12 |
| Algorithm | Optimum Value | Optimal Cost | |||
|---|---|---|---|---|---|
| PSO | 8.8652 × 10−1 | 4.3823 × 10−1 | 4.5933 × 101 | 1.3428 × 102 | 6.0978 × 103 |
| DBO | 9.8781 × 10−1 | 4.8827 × 10−1 | 5.1182 × 101 | 8.9237 × 101 | 6.3489 × 103 |
| HBA | 1.0888 × 100 | 5.4029 × 10−1 | 5.6377 × 101 | 5.4621 × 101 | 6.6714 × 103 |
| MIHBA | 7.9079 × 10−1 | 3.9089 × 10−1 | 4.0974 × 101 | 1.9109 × 102 | 5.9073 × 103 |
| Algorithm | Optimum Value | Optimal Cost | |
|---|---|---|---|
| PSO | 7.8489 × 10−1 | 4.1908 × 10−1 | 263.9078 |
| DBO | 7.9007 × 10−1 | 4.0433 × 10−1 | 263.8983 |
| HBA | 7.9240 × 10−1 | 3.9780 × 10−1 | 263.9059 |
| MIHBA | 7.8862 × 10−1 | 4.0840 × 10−1 | 263.8958 |
| Algorithm | Optimum Value | Optimal Cost | ||||||
|---|---|---|---|---|---|---|---|---|
| PSO | 3.6 | 0.7 | 17 | 8.3 | 8.3000 × 100 | 3.3522 × 100 | 5.5000 × 100 | 3.1977 × 103 |
| DBO | 3.6 | 0.7 | 17 | 8.3 | 8.3000 × 100 | 3.3522 × 100 | 5.2869 × 100 | 3.0560 × 103 |
| HBA | 3.6 | 0.7 | 17 | 8.3 | 7.7154 × 100 | 3.9000 × 100 | 5.2867 × 100 | 3.2093 × 103 |
| MIHBA | 3.6 | 0.7 | 17 | 7.3 | 7.7153 × 100 | 3.3502 × 100 | 5.2867 × 100 | 2.9945 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Li, T.; Liu, Q.; Huang, Y.; Song, H. A Multi-Strategy Improved Honey Badger Algorithm for Engineering Design Problems. Algorithms 2024, 17, 573. https://doi.org/10.3390/a17120573
Han T, Li T, Liu Q, Huang Y, Song H. A Multi-Strategy Improved Honey Badger Algorithm for Engineering Design Problems. Algorithms. 2024; 17(12):573. https://doi.org/10.3390/a17120573
Chicago/Turabian StyleHan, Tao, Tingting Li, Quanzeng Liu, Yourui Huang, and Hongping Song. 2024. "A Multi-Strategy Improved Honey Badger Algorithm for Engineering Design Problems" Algorithms 17, no. 12: 573. https://doi.org/10.3390/a17120573
APA StyleHan, T., Li, T., Liu, Q., Huang, Y., & Song, H. (2024). A Multi-Strategy Improved Honey Badger Algorithm for Engineering Design Problems. Algorithms, 17(12), 573. https://doi.org/10.3390/a17120573






