Abstract
We consider the problem of approximating the perimeter of an ellipse, for which there is no known finite formula, in the context of high-precision performance. Ellipses are broadly used in many fields, like astronomy, manufacturing, medical imaging, and geophysics. They are applied on large and nanoscales, and while numerical integration can be used to obtain precision measurements, having a finite formula can be used for modeling. We propose an iterative symbolic regression approach, utilizing the pioneering work of Ramanujan’s second approximation introduced in 1914 and a known Padé approximation, leading to good results for both low and high eccentricities. Our proposed model is also compared with a very comprehensive historical collection of different approximations collated by Stanislav Sýkora. Compared with the best-known approximations in this centuries-old mathematical problem, our proposed model performs at both extremities while remaining consistent in mid-range eccentricities, whereas existing models excel only at one extremity.
1. Introduction
It can be argued that the idea of establishing “precision machine learning” would not be considered a new endeavor for many scientists, as it has indeed been the aim of mathematicians over many centuries to give the best possible approximations of objects when there is no closed-form formula. For instance, precisely calculating elliptical perimeters without complex integrals has been a long-standing problem in mathematics. The accuracy of these approximations can be critical in astronomy, manufacturing, medical imaging, and geophysics calculations, such as the orbital mechanics of celestial bodies, where small errors can lead to significant deviations in downstream calculations or decisions, affecting everything from scientific research to industrial processes.
Beyond the motivation for greater precision for the theoretical sake of future unknown applications, a note of particular importance is the wide range of scales on which perimeter approximations are necessary. Applications scale from the astronomical order in orbital bodies to atomical in elliptical lens design. Approximations at these scales are also subject to data accuracy, for instance, when visually eliciting ellipse characteristics from images with limited resolution. As hardware improves over time, the viability of applying different potential approaches could also increase, and reassessment of available methods is necessary to maintain the state of the art.
1.1. The Perimeter of the Ellipse
It is well known that while the area, A, of an ellipse with major and minor semi-axes a and b, respectively, is given by ; in contrast, there is no such finite formula for the perimeter S when . An exact expression requires a formula to be written as an infinite series or the evaluation of an integral.
Following Sýkora [1,2], we are aware that many ellipse approximations have been categorized and benchmarked, namely into Keplerian, Padé, extreme, and algebraic categories. Sýkora uses the notation for the perimeter and gives the following formula:
where
is the eccentricity of the ellipse, and
is the complete elliptic integral of the second kind.
For more than 400 years, researchers such as Kepler, Euler, and Peano, among many others, have proposed approximations [3], a subject that was even covered in letters in the journal Nature over a century ago [4,5,6].
1.2. Ramanujan’s Approximations
In 1914 [7], Srinivasa Ramanujan first proposed two approximations of interest, given in Equations (1) and (2):
where
This second approximation, , certainly stood the test of time, and although it requires the computation of a square root, it is admired for its simplicity and precision. Ramanujan presented it as
where is about . It is well known that Ramanujan’s approximation underestimates the perimeter, and a detailed error analysis is now known thanks to M.B. Villarino [8].
1.3. Symbolic Regression and Learning from Data
Symbolic regression (SR) is a particular type of mathematical modeling from data that is aimed at discovering mathematical expressions that best fit a given dataset. The emphasis is also on trying to reduce the complexity of the models. Instead of assuming a specific model form (like linear or polynomial), symbolic regression searches through the space of mathematical expressions to find one that explains the data. This is often carried out using evolutionary algorithms, such as genetic programming, which iteratively build upon equations by combining mathematical operators, constants, and variables.
Symbolic regression demonstrates strong performance in scenarios with limited data, contrasting with artificial neural networks (ANNs), which typically require additional strategies for few-shot or few-sample learning (FSL) to function effectively in such conditions [9,10]. Unlike the opaque models ANNs generate, SR produces explicit mathematical equations that domain experts can readily analyze, facilitating detailed inspection of variable relationships within the data.
A key advantage of SR lies in its capacity to inform further investigation and guide subsequent data collection, as the relationship between the variables can be analyzed in the formulae. This is particularly relevant in physical phenomena, where low-order, simple functions often govern underlying models. SR’s ability to train on minimal samples, derive concise, interpretable formulae, and maintain robustness in the presence of measurement noise positions it as an effective method for identifying underlying models. These characteristics can lead to fundamental insights and discoveries within the data.
In this work, we configure TuringBot software [11], which utilizes a novel simulated annealing metaheuristic rather than an evolutionary approach to uncover models. Our use of this software is detailed further in later sections.
1.4. Structure of the Paper
The process for utilizing symbolic regression to uncover perimeter approximations is described in Section 2, including the iterative method using upper and lower bounds. The series of approximations uncovered are described in Section 3, where it is also benchmarked against Sýkora’s collection of ellipse approximations. We consider the properties of the residuals in high precision from a circle to ellipses with very large eccentricity. In the final section, Section 5, we make our final remarks and suggest potential downstream research.
2. Materials and Methods
We used the 2.16.1 version of TuringBot in our experimentation. We note its commercial nature and evolving updates, which suggest that the application will be more robust than an unsupported and unevolving academic software package for SR. Additionally, the multithreading software leverages multiple CPU cores, enabling parallel evaluations of candidate models. This increases efficiency and allows the software to explore a broader section of the solution space over time by exploring more potential solutions simultaneously.
TuringBot displays candidate formulas and provides errors according to the selected objective function. The software evolves and refines these formulas over multiple iterations. Formulas are ranked based on a Pareto frontier, providing multiple solutions. The user can select those of better accuracy or simplicity, balancing the resulting models’ interpretability and effectiveness. Due to the software’s commercial and proprietary nature, we are unable to provide exact details of the novel simulated annealing approach that produces and develops the candidate formulas [11].
The dataset defined in Table 1 was used as input to the software to produce the symbolic models. The mean square error was the objective function used to minimize, and all samples were used during exploration. Only the basic operators were permitted in the exploration: multiplication, division, addition, subtraction, and exponentiation. Only integer coefficients were considered in the produced models.

Table 1.
The table shows the absolute relative error for each approximation of an ellipse for different eccentricities within the training samples, where a varies but is constant. The smallest errors are in bold within each row.
Our results are based on a proposed method in which an iterative scheme of approximations is produced. We used symbolic regression and/or a known upper or lower bound at each step. Although the models were produced using the limited samples from Table 1, we evaluated them on uniformly sampled data in log space over the range and presented the results in plots with logarithmic scales on both axes.
The historical models curated by Sýkora, as well as the models produced by TuringBot, were subsequently re-implemented and re-evaluated in Mathematica at 200 points of decimal precision. When implementing the models from TuringBot at higher precision in Mathematica, the performance of some models declined and were excluded from consideration. We believe precision limitations within TuringBot led to this behavior, and it was something that affected only a few models that were generated in the last iteration of our approach.
Our Mathematica implementation validated the models from TuringBot and completed the approximations in Sýkora’s MATLAB implementation [1] by including S-class and algebraic equations in an independent implementation in an alternate language. We have made it available in the code repository accompanying this submission at https://github.com/impvau/ellipse (accessed 12 September 2024).
All Mathematica calculations were performed with a precision of 200 decimal places, including the “true” ellipse perimeter values computed with the EllipticE function. Using this EllipticE function allowed us to compute the exact perimeter values to the extent that we could compute the required integrals, which were subject to the numerical methods employed in this process. We confirmed that the computed values in Mathematica and MATLAB at 200 decimal places of accuracy were identical for all digits.
3. Results
This project started out of curiosity when one of the authors (PM) watched a YouTube video describing Equation (2). Arriving at Equation (8) using only the data for different values of a in Table 1 was relatively straightforward, so it is reasonable to give a more detailed rationale of the process involved since its simplicity has a certain beauty. Also, it may be potentially generalizable for other problems. Consequently, we first discuss the results of an approximation that can be obtained from Ramanujan’s second approximation. This defines the first iteration of our method and the first set of comparative results.
3.1. A New Asymptotic Bound Leads to a More Accurate Approximation for High Eccentricity
Ramanujan has not left any record on the rational process by which he proposed Equations (1) and (2) apart from mentioning that he used an “empirical” method (although his mastery in the use of continued fractions [12] may be behind it).
We propose here a new approximation; let be an upper bound defined as follows:
The model was produced using the samples in Table 1. We note that most a values are below 100, while the last six points range between 100 and to facilitate modeling the asymptotic behavior. Table 1 also shows approximation errors for key formulae mentioned in this section. Figure 1 shows the errors between and , while Figure 2 shows the errors where both axes are in a log scale and the functions are re-evaluated using 10,000 uniform points in log space between and with .
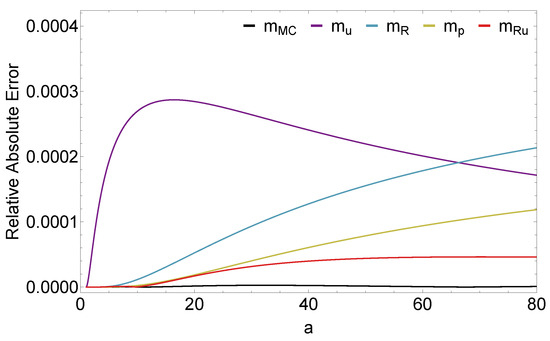
Figure 1.
Relative absolute error plot for the values in Table 1 that for a are between 1 and 80 while keeping . We compare the approximation of the upper bound model (Equation (5)) and our proposed model (Equation (12)). We observe a significant difference in the performance of , particularly for higher values of a.
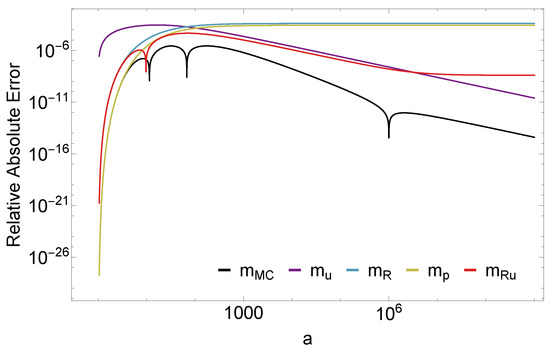
Figure 2.
Relative absolute error plot with log scale on the axes. We show the results for our upper bound model (Equation (5)), our best model (Equation (12)), and the other models listed in Table 1. The equations were produced using the samples from Table 1, which were then re-evaluated on 10,000 uniform values of a in the log space between and with . We observe strong performance from in both extremities of a relative to the other models.
Next, we take an iterative approach where we define the first iteration as
arising from the crude lower and upper bounds and , respectively.
Relying on the knowledge that has accumulated since 1914 to find an even better lower bound that can be used instead of Ramanujan’s second approximation, we now define as follows:
Once again, using TuringBot software, we find the following approximation:
3.2. Use of a Highly Accurate Padé Approximation Formula for Low Eccentricities
Another approximation that is more accurate than Ramanujan’s second approximation and exceptionally good for low eccentricity values is also known (and it is included in Table 1 for comparison). In line with previous proposals by Bronshtein (1964) and Jacobsen (1985) (covered in [3]), a Padé approximation-based equation for the ‘normalized’ perimeter (i.e., the perimeter divided by ) as a function of h is
Let us now analogously define as follows:
Once again, using symbolic regression and the TuringBot package, we have obtained a new approximation given by the following formula:
Utilizing , we obtain the following improved approximation, valid for any ellipse (except for a circle):
Once again, the integer coefficients for the formula for and its functional form were found via symbolic regression using the same software cited before with the values of a given in Table 1 and , as well as the corresponding exact solutions obtained via multiple precision calculations involving the integral definition of the perimeter. As a consequence, the values obtained for are also displayed in Table 1. It is clear now that maintains good asymptotic behavior for low a values, while the relative error for an extremely high eccentricity of is of the order of .
In this case, we searched for formulas that, in addition to the basic arithmetic functions of multiplication, division, addition, and subtraction, can also raise to a power. We used as variables the set , while we continued to only use integers as coefficients in the formulas.
The range of a values can be thought to be “measured in units of b” and covers a wide range of eccentricities in orbits around the Sun, including the comet Ikeya–Seki (C/1965 S1-A), as per https://theskylive.com/ikeyaseki-info (accessed on 12 September 2024), which has an eccentricity of 0.999915 and an a in units of b of approximately 76.7.
We note for the periodic comet called 103P/Hartley 2 (https://www.wikiwand.com/en/articles/103P/Hartley (accessed on 12 September 2024)), with an eccentricity of 0.694 and an a in units of b of approximately 1.39, has a relative error of the order of , thus maintaining the good approximation behavior of Equation (9), but for highly eccentric ellipses, clearly the introduction of our simple (Equation (5)) approximation formula gave a better asymptotic behavior. This motivated us to look more widely to see if other proposed approximations also do well for very eccentric ellipses.
4. Comparative Results with Sýkora’s Curated Collection of Approximations
Sýkora has put together an extensive collection of ellipse perimeter approximations and provides a classification into groups that share properties. Some approximations may fall into multiple categories (for instance, both Keplerian and Padé) and are explicitly classified as such in those circumstances.
We define in this section a few selected examples in each category of Sýkora’s collection, as well as all approximations from the S-class. A comprehensive list is provided in the code repository accompanying this submission, and later in Figure 3, Figure 4 and Figure 5, the nature of the residuals for each class can be seen. Note that Sýkora’s analysis considers the ratio of the semi-axes .
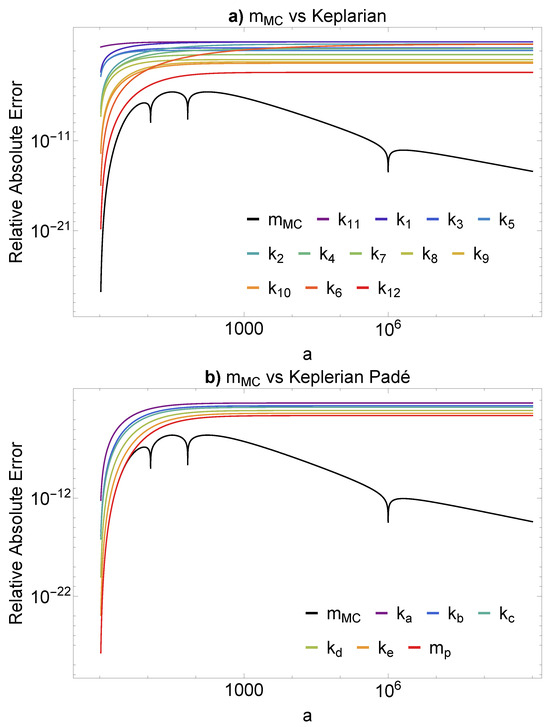
Figure 3.
Comparison of the Keplerian and Keplerian Padé equation classes in Sýkora’s analysis in subfigures (a) and (b), respectively. The proposed model (Equation (12)) appears in black in each subfigure, and the axes plot the log of the relative absolute error across the log space between a values between 1 and with .
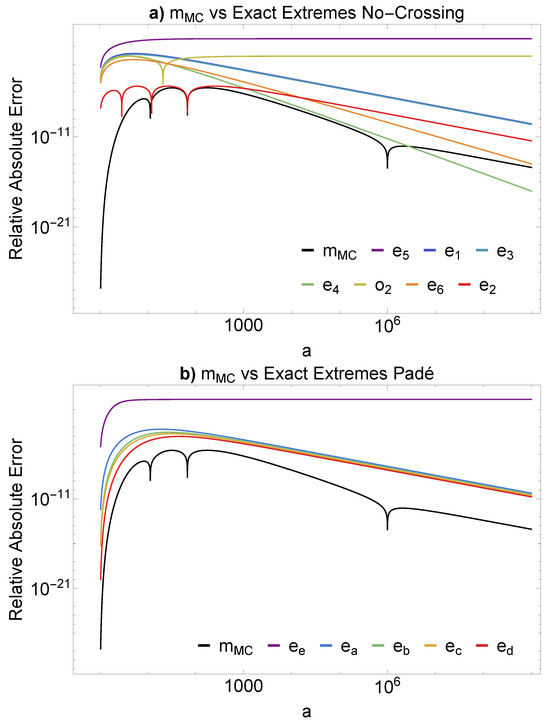
Figure 4.
Comparison of the Padé equation classes exact extremes no-crossing and exact extremes in Sýkora’s analysis in subfigures (a) and (b), respectively. The proposed model (Equation (12)) appears in black in each subfigure, and the axes plot the log of the relative absolute error across the log space between a values between 1 and with .
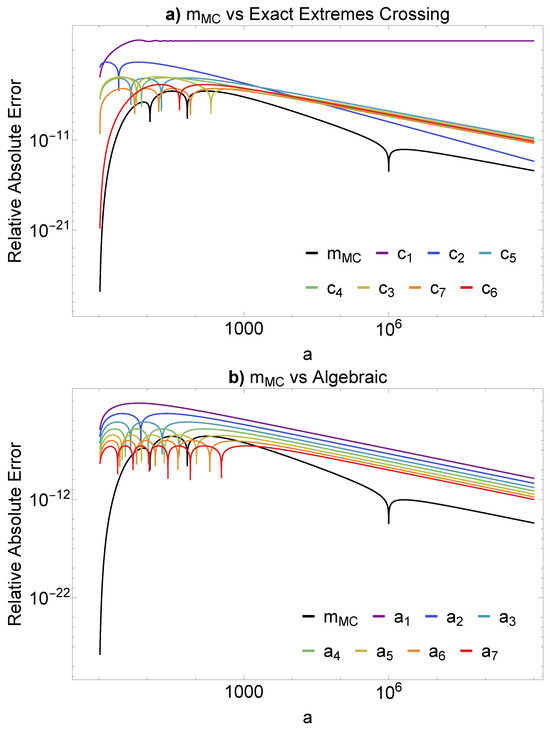
Figure 5.
Comparison of the exact extremes crossing and algebraic equation classes in Sýkora’s analysis given in subfigures (a) and (b), respectively. The proposed model (Equation (12)) appears in black in each subfigure, and the axes plot the log of the relative absolute error across the log space between a values between 1 and with .
4.1. Keplerian Equations
Keplerian approximations have been defined as approximations “whose relative error curves attain absolute maximum at (degenerate ellipses) and decay towards zero at (circles)”. Examples are given as follows:
4.2. Keplerian Padè Equations
Padé approximations are classified “by fractions , where n and m are the degrees of the polynomials in h appearing, respectively, in the nominator and denominator of the rational function”. Some examples are
4.3. Exact Extremes (No Crossing) Equations
“Exact extreme” approximations are exact for both and . Sýkora divides them into those with “crossing” or “no crossing”, where the latter means “ remains …” ( being the approximation to S). A few examples are given as follows:
4.4. Combined Padè Equations with Exact Extremes (No Crossing)
Examples of this class follow:
4.5. Exact Extremes and Crossing Equations
These are exact models where does not always remain either above or below .
4.6. Algebraic Equations
The following Sýkora “algebraic” approximations are those “which use only the four basic operations of the real numbers algebra”.
4.7. All S-Class Equations
The S-class approximations contain approximations identified after the prior classes’ classification and are limited to “a single square root evaluation”. These are the most performant approximations from Sýkora’s approximations regarding the maximum absolute relative error.
4.8. A Detailed Comparison of Results with the Best Performers in the S-Class of Sýkora’s Collection
Towards the end of our benchmarking study, we looked at other alternative proposals described by Sýkora. We have continued to group the existing formulas and compare them within the same range. Sýkora compares approaches by measuring the maximum relative absolute error in parts per unit (generally million or billion). These functions and categories are defined in the code repository accompanying this submission.
We have taken our best model produced in the prior sections and show the comparison to each category in Figure 3, Figure 4 and Figure 5, as well as Sýkora’s best performers (the S-class) in Figure 6.
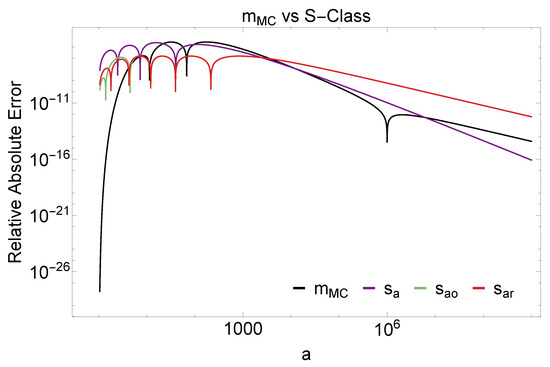
Figure 6.
Relative absolute error plot with log scale on the axes, comparing our equation (Equation (12)) with models from Sýkora’s S-class. The equations are evaluated on 10,000 uniform values of a in the log space between a = 1 and .
Sýkora’s analysis focuses on the maximum point of errors; however, we focus on consistency at the extremities and in the regions of critical practical performance () for astronomical importance. The categories in Figure 3, Figure 4 and Figure 5 show that the approach excels at approximating the extremities of a. We observe that we generally out-compete all categories, except for out-competing at very high a values, and notably, is the only method offering a close approximation at both extremities. In most circumstances, out-competes across the entire spectrum of a, except for the region before , where many methods outperform .
Interestingly, in the most competitive S-class comparison in Figure 6, we exclude , , and , which fail to achieve good performance when evaluated at high precision (see code repository accompanying this submission). The unoptimized Ahmedi is perhaps the closest to our approximation due to its performance at high a values, although it is not as competitive at low a values.
5. Discussion
Le Verrier’s 1846 work predicting Neptune due to perturbations in Uranus’s orbit is a famous example of the importance of mathematical modeling in scientific discovery [13]. Key orbital parameters, such as the semi-major axis and eccentricity, were central to his calculations, demonstrating how additional gravitational forces affect planetary paths. Considering that later work in [14] suggests that comparable accuracy can be achieved with less numerical calculation and given that we can easily perform computations directly from integral representations or series expansions with modern computers, we might ask ourselves then, “Why is this quest for high-precision approximations still relevant”?
In our case, we are motivated by the development of new methods for “precision machine learning” [15] since high-precision approximations are often crucial to scientific discovery. We are also motivated by the quest of finding approximations with simple models since sometimes we have functions that are defined via integral representations or series expansions; having a simple model can help if these computations need to be carried out for several values of parameters many times during simulations.
Given these motivations, the problem of approximating the ellipse’s perimeter seems to be an ideal test bed of new ideas and a challenging one with centuries of approximations given, and we hope our work encourages others to keep moving in the same direction.
Overall, this case study indicates that an iterative approach to creating high-performing approximations using symbolic regression can (at least sometimes) be achieved, given existing data, by recursively computing the upper and lower bounds of the function of interest interspersed with the computation of extra variables as in Equations (3) and (7) to be incrementally added to generate new and more precise bounding models. This procedure can be understood as a constructive heuristic approach to building a “network” of increasingly better approximations, but, in conjunction with many other connectionist approaches, it requires symbolic regression at different steps to build intermediate models, each with an increasing approximation.
In addition, we also found that minimization of the mean relative error may be useful to produce approximations that work well for a large range of parameters. The functional forms of Equations (8) and (9) suggests that continued fraction regression [16] using dynamic depth strategies [17] can be used to obtain more concise and precise approximations iteratively.
As a side note, the search process did not result in a simpler and/or equally fitting approximation than Equation (8), using symbolic regression, even when we used other ellipse characteristics such as the eccentricity or the semi-latus rectum. We note that nonlinear optimization may also be helpful to identify other values of , , and that can even improve the approximation for particular ranges of a measured in units of b that have specific applications. For example, in fitting planetary orbiting objects, a training set that uses the most typical values of a could possibly lead to other coefficient values that would better approximate for the particular range of interest.
Author Contributions
Conceptualization, P.M.; methodology, P.M. and A.C.; software, A.C.; validation, P.M. and A.C.; formal analysis, P.M. and A.C.; investigation, P.M. and A.C.; resources, P.M. and A.C.; data curation, P.M. and A.C.; writing—original draft preparation, P.M. and A.C.; writing—review and editing, P.M. and A.C.; visualization, A.C.; supervision, P.M.; project administration, P.M.; funding acquisition, P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Australian Research Council grant number [DP200102364].
Data Availability Statement
All data and software used to produce the data in these experiments are available in the software repositories at https://github.com/impvau/ellipse (accessed on 12 September 2024).
Acknowledgments
P.M. acknowledges a previous generous donation from the Maitland Cancer Appeal.
Conflicts of Interest
Author Andrew Ciezak was employed by the company Impervium Solutions. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sykora, S. Approximations of Ellipse Perimeters and of the Complete Elliptic Integral E(x). Review of known formulae. In Stan’s Library; Extra Byte: Castano Primo, Italy, 2005. [Google Scholar] [CrossRef]
- Nemes, G. A historic comment on ellipse perimeter approximations. In Stan’s Library; Extra Byte: Castano Primo, Italy, 2005. [Google Scholar] [CrossRef]
- Barnard, R.W.; Pearce, K.; Schovanec, L. Inequalities for the Perimeter of an Ellipse. J. Math. Anal. Appl. 2001, 260, 295–306. [Google Scholar] [CrossRef]
- Tomkys, H. Formula for the Perimeter of an Ellipse. Nature 1902, 65, 563. [Google Scholar] [CrossRef]
- Muir, T. Formula for the Perimeter of an Ellipse. Nature 1902, 66, 174–175. [Google Scholar] [CrossRef][Green Version]
- Rogers, R. Perimeter of an Ellipse. Nature 1920, 105, 8. [Google Scholar] [CrossRef]
- Ramanujan, S. Modular equations and approximations to π. Q. J. Math. Oxf. 1914, 45, 350–372. [Google Scholar]
- Villarino, M.B. A note on the accuracy of Ramanujan’s approximative formula for the perimeter of an ellipse. J. Inequal. Pure Appl. Math. 2006, 7, 21. [Google Scholar]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. 2021, 53, 63. [Google Scholar] [CrossRef]
- Lu, J.; Gong, P.; Ye, J.; Zhang, C. A survey on machine learning from few samples. Pattern Recognit. 2023, 139, 109480. [Google Scholar] [CrossRef]
- TuringBot. Documentation for TuringBot: Symbolic Regression Software. 2024. Available online: https://turingbotsoftware.com/documentation.html (accessed on 12 September 2024).
- Villarino, M.B. Ramanujan’s inverse elliptic arc approximation. Ramanujan J. 2014, 34, 157–161. [Google Scholar] [CrossRef][Green Version]
- Grosser, M. The Discovery of Neptune; Harvard University Press: Cambridge, MA, USA, 1962. [Google Scholar]
- Lyttleton, R.A. A short method for the discovery of Neptune. Mon. Not. R. Astron. Soc. 1958, 118, 551–559. [Google Scholar] [CrossRef][Green Version]
- Michaud, E.J.; Liu, Z.; Tegmark, M. Precision Machine Learning. Entropy 2023, 25, 175. [Google Scholar] [CrossRef]
- Sun, H.; Moscato, P. A Memetic Algorithm for Symbolic Regression. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2167–2174. [Google Scholar] [CrossRef]
- Moscato, P.; Ciezak, A.; Noman, N. Dynamic depth for analytic continued fraction regression. In Proceedings of the 2023 Annual Conference on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2023; pp. 520–528. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).