Algorithmic Aspects of Some Variations of Clique Transversal and Clique Independent Sets on Graphs

Abstract

This paper studies the maximum-clique independence problem and some variations of the clique transversal problem such as the $\left\{k\right\}$-clique, maximum-clique, minus clique, signed clique, and k-fold clique transversal problems from algorithmic aspects for k-trees, suns, planar graphs, doubly chordal graphs, clique perfect graphs, total graphs, split graphs, line graphs, and dually chordal graphs. We give equations to compute the $\left\{k\right\}$-clique, minus clique, signed clique, and k-fold clique transversal numbers for suns, and show that the $\left\{k\right\}$-clique transversal problem is polynomial-time solvable for graphs whose clique transversal numbers equal their clique independence numbers. We also show the relationship between the signed and generalization clique problems and present NP-completeness results for the considered problems on k-trees with unbounded k, planar graphs, doubly chordal graphs, total graphs, split graphs, line graphs, and dually chordal graphs.

1. Introduction

Every graph $G=(V,E)$ in this paper is finite, undirected, connected, and has at most one edge between any two vertices in G. We assume that the vertex set V and edge set E of G contain n vertices and m edges. They can also be denoted by $V\left(G\right)$ and $E\left(G\right)$. A graph $G^{\prime }=(V^{\prime },E^{\prime })$ is an induced subgraph of G denoted by $G\left[V^{\prime }\right]$ if $V^{\prime }\subseteq V$ and $E^{\prime }$ contains all the edge $(x,y)\in E$ for $x,y\in V^{\prime }$. Two vertices $x,y\in V$ are adjacent or neighbors if $(x,y)\in E$. The sets $N_G\left(x\right)=\{y\mid (x,y)\in E\}$ and $N_G\left[x\right]=N_G\left(x\right)\cup \left\{x\right\}$ are the neighborhood and closed neighborhood of a vertex x in G, respectively. The number $de{g}_G\left(x\right)=\left|N_G\left(x\right)\right|$ is the degree of x in G. If $de{g}_G\left(x\right)=k$ for every $x\in V$, then G is k-regular. Particularly, cubic graphs are an alternative name for 3-regular graphs.

A subset S of V is a clique if $(x,y)\in E$ for $x,y\in S$. Let Q be a clique of G. If $Q\cap Q^{\prime }\ne Q$ for any other clique $Q^{\prime }$ of G, then Q is a maximal clique. We use $C\left(G\right)$ to represent the set $\{C\mid C$ is a maximal clique of $G\}$. A clique $S\in C\left(G\right)$ is a maximum clique if $\left|S\right|\ge |S^{\prime }|$ for every $S^{\prime }\in C\left(G\right)$. The number $\omega \left(G\right)=max\left\{\right|S|\mid S\in C(G\left)\right\}$ is the clique number of G. A set $D\subseteq V$ is a clique transversal set (abbreviated as CTS) of G if $|C\cap D|\ge 1$ for every $C\in C\left(G\right)$. The number ${\tau }_C\left(G\right)=min\left\{\right|S|\mid S$ is a CTS of $G\}$ is the clique transversal number of G. The clique transversal problem (abbreviated as CTP) is to find a minimum CTS for a graph. A set $S\subseteq C\left(G\right)$ is a clique independent set (abbreviated as CIS) of G if $\left|S\right|=1$ or $\left|S\right|\ge 2$ and $C\cap C^{\prime }=\varnothing$ for $C,C^{\prime }\in S$. The number ${\alpha }_C\left(G\right)=max\left\{\right|S|\mid S$ is a CIS of $G\}$ is the clique independence number of G. The clique independence problem (abbreviated as CIP) is to find a maximum CIS for a graph.

The CTP and the CIP have been widely studied. Some studies on the CTP and the CIP consider imposing some additional constraints on CTS or CIS, such as the maximum-clique independence problem (abbreviated as MCIP), the k-fold clique transversal problem (abbreviated as k-FCTP), and the maximum-clique transversal problem (abbreviated as MCTP).

Definition 1 

([1,2]). Suppose that $k\in \mathbb{N}$ is fixed and G is a graph. A set $D\subseteq V\left(G\right)$ is a k-fold clique transversal set (abbreviated as k-FCTS) of G if $|C\cap D|\ge k$ for $C\in C\left(G\right)$. The number ${\tau }_C^k\left(G\right)=min\left\{\right|S|\mid S$ is a k-FCTS of $G\}$ is the k-fold clique transversal number of G. The k-FCTP is to find a minimum k-FCTS for a graph.

Definition 2 

([3,4]). Suppose that G is a graph. A set $D\subseteq V\left(G\right)$ is a maximum-clique transversal set (abbreviated as MCTS) of G if $|C\cap D|\ge 1$ for $C\in C\left(G\right)$ with $\left|C\right|=\omega \left(G\right)$. The number ${\tau }_M\left(G\right)=min\left\{\right|S|\mid S$ is an MCTS of $G\}$ is the maximum-clique transversal number of G. The MCTP is to find a minimum MCTS for a graph. A set $S\subseteq C\left(G\right)$ is a maximum-clique independent set (abbreviated as MCIS) of G if $\left|C\right|=\omega \left(G\right)$ for $C\in S$ and $C\cap C^{\prime }=\varnothing$ for $C,C^{\prime }\in S$. The number ${\alpha }_M\left(G\right)=max\left\{\right|S|\mid S$ is an MCIS of $G\}$ is the maximum-clique independence number of G. The MCIP is to find a maximum MCIS for a graph.

The k-FCTP on balanced graphs can be solved in polynomial time [2]. The MCTP has been studied in [3] for several well-known graph classes and the MCIP is polynomial-time solvable for any graph H with ${\tau }_M\left(H\right)={\alpha }_M\left(H\right)$ [4]. Assume that $Y\subseteq \mathbb{R}$ and $f:X\to Y$ is a function. Let $f\left(X^{\prime }\right)={\sum }_{x\in X}f\left(x\right)$ for $X^{\prime }\subseteq X$, and let $f\left(X\right)$ be the weight of f. A CTS of G can be expressed as a function f whose domain is $V\left(G\right)$ and range is $\{0,1\}$, and $f\left(C\right)\ge 1$ for $C\in C\left(G\right)$. Then, f is a clique transversal function (abbreviated as CTF) of G and ${\tau }_C\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is a CTF of $G\}$. Several types of CTF have been studied [4,5,6,7]. The following are examples of CTFs.

Definition 3. 

Suppose that $k\in \mathbb{N}$ is fixed and G is a graph. A function f is a $\left\{k\right\}$-clique transversal function (abbreviated as $\left\{k\right\}$-CTF) of G if the domain and range of f are $V\left(G\right)$ and $\{0,1,2,\dots ,k\}$, respectively, and $f\left(C\right)\ge k$ for $C\in C\left(G\right)$. The number ${\tau }_C^{\left\{k\right\}}\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is a $\left\{k\right\}$-CTF of $G\}$ is the $\left\{k\right\}$-clique transversal number of G. The $\left\{k\right\}$-clique transversal problem (abbreviated as $\left\{k\right\}$-CTP) is to find a minimum-weight $\left\{k\right\}$-CTF for a graph.

Definition 4. 

Suppose that G is a graph. A function f is a signed clique transversal function (abbreviated as SCTF) of G if the domain and range of f are $V\left(G\right)$ and $\{-1,1\}$, respectively, and $f\left(C\right)\ge 1$ for $C\in C\left(G\right)$. If the domain and range of f are $V\left(G\right)$ and $\{-1,0,1\}$, respectively, and $f\left(C\right)\ge 1$ for $C\in C\left(G\right)$, then f is a minus clique transversal function (abbreviated as MCTF) of G. The number ${\tau }_C^s\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is an SCTF of $G\}$ is the signed clique transversal number of G. The minus clique transversal number of G is ${\tau }_C^{-}\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is an MCTF of $G\}$. The signed clique transversal problem (abbreviated as SCTP) is to find a minimum-weight SCTF for a graph. The minus clique transversal problem (abbreviated as MCTP) is to find a minimum-weight MCTF for a graph.

Lee [4] introduced some variations of the k-FCTP, the $\left\{k\right\}$-CTP, the SCTP, and the MCTP, but those variations are dedicated to maximum cliques in a graph. The MCTP on chordal graphs is NP-complete, while the MCTP on block graphs is linear-time solvable [7]. The MCTP and SCTP are linear-time solvable for any strongly chordal graph G if a strong elimination ordering of G is given [5]. The SCTP is NP-complete for doubly chordal graphs [6] and planar graphs [5].

According to what we have described above, there are very few algorithmic results regarding the k-FCTP, the $\left\{k\right\}$-CTP, the SCTP, and the MCTP on graphs. This motivates us to study the complexities of the k-FCTP, the $\left\{k\right\}$-CTP, the SCTP, and the MCTP. This paper also studies the MCTP and MCIP for some graphs and investigates the relationships between different dominating functions and CTFs.

Definition 5. 

Suppose that $k\in \mathbb{N}$ is fixed and G is a graph. A set $S\subseteq V\left(G\right)$ is a k-tuple dominating set (abbreviated as k-TDS) of G if $|S\cap N_G\left[x\right]|\ge 1$ for $x\in V\left(G\right)$. The number ${\gamma }_{\times k}\left(G\right)=min\left\{\right|S|\mid S$ is a k-TDS of $G\}$ is the k-tuple domination number of G. The k-tuple domination problem (abbreviated as k-TDP) is to find a minimum k-TDS for a graph.

Notice that a dominating set of a graph G is a 1-TDS. The domination number $\gamma \left(G\right)$ of G is ${\gamma }_{\times 1}\left(G\right)$.

Definition 6. 

Suppose that $k\in \mathbb{N}$ is fixed and G is a graph. A function f is a $\left\{k\right\}$-dominating function (abbreviated as $\left\{k\right\}$-DF) of G if the domain and range of f are $V\left(G\right)$ and $\{0,1,2,\dots ,k\}$, respectively, and $f\left(N_G\left[x\right]\right)\ge k$ for $x\in V\left(G\right)$. The number ${\gamma }_{\left\{k\right\}}\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is a $\left\{k\right\}$-DF of $G\}$ is the $\left\{k\right\}$-domination number of G. The $\left\{k\right\}$-domination problem (abbreviated as $\left\{k\right\}$-DP) is to find a minimum-weight $\left\{k\right\}$-DF for a graph.

Definition 7. 

Suppose that G is a graph. A function f is a signed dominating function (abbreviated as SDF) of G if the domain and range of f are $V\left(G\right)$ and $\{-1,1\}$, respectively, and $f\left(N_G\left[x\right]\right)\ge 1$ for $x\in V\left(G\right)$. If the domain and range of f are $V\left(G\right)$ and $\{-1,0,1\}$, respectively, and $f\left(N_G\left[x\right]\right)\ge 1$ for $x\in V\left(G\right)$, then f is a minus dominating function (abbreviated as MDF) of G. The number ${\gamma }_s\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is an SDF of $G\}$ is the signed domination number of G. The minus domination number of G is ${\gamma }^{-}\left(G\right)=min\{f\left(V\left(G\right)\right)\mid f$ is an MDF of $G\}$. The signed domination problem (abbreviated as SDP) is to find a minimum-weight SDF for a graph. The minus domination problem (abbreviated as MDP) is to find a minimum-weight MDF for a graph.

Our main contributions are as follows.

1.

We prove in Section 2 that ${\gamma }^{-}\left(G\right)={\tau }_C^{-}\left(G\right)$ and ${\gamma }_s\left(G\right)={\tau }_C^s\left(G\right)$ for any sun G. We also prove that ${\gamma }_{\times k}\left(G\right)={\tau }_C^k\left(G\right)$ and ${\gamma }_{\left\{k\right\}}\left(G\right)={\tau }_C^{\left\{k\right\}}\left(G\right)$ for any sun G if $k>1$.

2.

We prove in Section 3 that ${\tau }_C^{\left\{k\right\}}\left(G\right)=k{\tau }_C\left(G\right)$ for any graph G with ${\tau }_C\left(G\right)={\alpha }_C\left(G\right)$. Then, ${\tau }_C^{\left\{k\right\}}\left(G\right)$ is polynomial-time solvable if ${\tau }_C\left(G\right)$ can be computed in polynomial time. We also prove that the SCTP is a special case of the generalized clique transversal problem [8]. Therefore, the SCTP for a graph H can be solved in polynomial time if the generalized transversal problem for H is polynomial-time solvable.

3.

We show in Section 4 that ${\gamma }_{\times k}\left(G\right)={\tau }_C^k\left(G\right)$ and ${\gamma }_{\left\{k\right\}}\left(G\right)={\tau }_C^{\left\{k\right\}}\left(G\right)$ for any split graph G. Furthermore, we introduce $H_1$-split graphs and prove that ${\gamma }^{-}\left(H\right)={\tau }_C^{-}\left(H\right)$ and ${\gamma }_s\left(H\right)={\tau }_C^s\left(H\right)$ for any $H_1$-split graph H. We prove the NP-completeness of SCTP for split graphs by showing that the SDP on $H_1$-split graphs is NP-complete.

4.

We show in Section 5 that ${\tau }_C^{\left\{k\right\}}\left(G\right)$ for a doubly chordal graph G can be computed in linear time, but the k-FCTP is NP-complete for doubly chordal graphs as $k>1$. Notice that the CTP is a special case of the k-FCTP and the $\left\{k\right\}$-CTP when $k=1$, and thus ${\tau }_C\left(G\right)={\tau }_C^1\left(G\right)={\tau }_C^{\left\{1\right\}}\left(G\right)$ for any graph G.

5.

We present other NP-completeness results in Section 6 and Section 7 for k-trees with unbounded k and subclasses of total graphs, line graphs, and planar graphs. These results can refine the “borderline” between P and NP for the considered problems and graphs classes or their subclasses.

2. Suns

In this section, we give equations to compute ${\tau }_C^{\left\{k\right\}}\left(G\right)$, ${\tau }_C^k\left(G\right)$, ${\tau }_C^s\left(G\right)$, and ${\tau }_C^{-}\left(G\right)$ for any sun G and show that ${\tau }_C^{\left\{k\right\}}\left(G\right)={\gamma }_{\left\{k\right\}}\left(G\right)$, ${\tau }_C^k\left(G\right)={\gamma }_{\times k}\left(G\right)$, ${\tau }_C^s\left(G\right)={\gamma }_s\left(G\right)$, and ${\tau }_C^{-}\left(G\right)={\gamma }^{-}\left(G\right)$.

Let $p\in \mathbb{N}$ and G be a graph. An edge $e\in E\left(G\right)$ is a chord if e connects two non-consecutive vertices of a cycle in G. If C has a chord for every cycle C consisting of more than three vertices, G is a chordal graph. A sun G is a chordal graph whose vertices can be partitioned into $W=\{w_i\mid 1\le i\le p\}$ and $U=\{u_i\mid 1\le i\le p\}$ such that (1) W is an independent set, (2) the vertices $u_1,u_2,\dots ,u_p$ of U form a cycle, and (3) every $w_i\in W$ is adjacent to precisely two vertices $u_i$ and $u_j$, where $j\equiv i+1$ (mod p). We use $S_p=(W,U,E)$ to denote a sun. Then, $\left|V\right(S_p\left)\right|=2p$. If p is odd, $S_p$ is an odd sun; otherwise, it is an even sun. Figure 1 shows two suns.

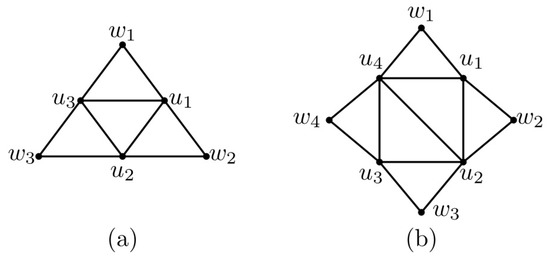
Figure 1. (a) The sun $S_3$. (b) A sun $S_4$.

Lemma 1. 

For any sun $S_p=(W,U,E)$, ${\tau }_C^2\left(S_p\right)=p$ and ${\tau }_C^3\left(S_p\right)=2p$.

Proof. 

It is straightforward to see that U is a minimum 2-FCTS and $W\cup U$ is a minimum 3-FCTS of $S_p$. This lemma therefore holds. □

Lemma 2. 

Suppose that $k\in \mathbb{N}$ and $k>1$. Then, ${\tau }_C^{\left\{k\right\}}\left(S_p\right)=\lceil pk/2\rceil$ for any sun $S_p=(W,U,E)$.

Proof. 

Let $i,j\in \{1,2,\dots p\}$ such that $j\equiv i+1$ (mod p). Since every $w_i\in W$ is adjacent to precisely two vertices $u_i,u_j\in U$, $N_{S_p}\left[w_i\right]=\{w_i,u_i,u_j\}$ is a maximal clique of $S_p$. By contradiction, we can prove that there exists a minimum $\left\{k\right\}$-CTF f of $S_p$ such that $f\left(w_i\right)=0$ for $w_i\in W$. Since $f\left(N_{S_p}\left[w_i\right]\right)\ge k$ for $1\le i\le p$, we have

$${\tau }_C^{\left\{k\right\}}\left(S_p\right)=\sum _{i=1}^{p}f\left(u_i\right)=\frac{{\sum }_{i=1}^{p}f\left(N_{S_p}\left[w_i\right]\right)}{2}\ge \frac{pk}{2}.$$

Since ${\tau }_C^{\left\{k\right\}}\left(S_p\right)$ is a nonnegative integer, ${\tau }_C^{\left\{k\right\}}\left(S_p\right)\ge \lceil pk/2\rceil$.

We define a function $h:W\cup U\to \{0,1,\dots ,k\}$ by $h\left(w_i\right)=0$ for every $w_i\in W$, $h\left(u_i\right)=\lceil k/2\rceil$ for $u_i\in U$ with odd index i and $h\left(u_i\right)=\lfloor k/2\rfloor$ for every $u_i\in U$ with even index i. Clearly, a maximal clique Q of $S_n$ is either the closed neighborhood of some vertex in W or a set of at least three vertices in U. If $Q=N_{S_p}\left[w_i\right]$ for some $w_i\in W$, then $h\left(Q\right)=\lceil k/2\rceil +\lfloor k/2\rfloor =k$. Suppose that Q is a set of at least three vertices in U. Since $k\ge 2$, $h\left(Q\right)\ge 3·\lfloor k/2\rfloor \ge k$. Therefore, h is a $\left\{k\right\}$-CTF of $S_p$. We show the weight of h is $\lceil pk/2\rceil$ by considering two cases as follows.

Case 1: p is even. We have

$$h\left(V\left(S_p\right)\right)=\sum _{i=1}^{p}h\left(u_i\right)=\frac{p}{2}·\left(\lceil k/2\rceil +\lfloor k/2\rfloor \right)=\frac{pk}{2}.$$

Case 2: p is odd. We have

$$h\left(V\left(S_p\right)\right)=\sum _{i=1}^{p}h\left(u_i\right)=\frac{(p-1)}{2}·k+\lceil k/2\rceil =\lceil pk/2\rceil .$$

Following what we have discussed above, we know that h is a minimum $\left\{k\right\}$-CTF of $S_n$ and thus ${\tau }_C^{\left\{k\right\}}\left(S_p\right)=\lceil pk/2\rceil$. □

Lemma 3. 

For any sun $S_p=(W,U,E)$, ${\tau }_C^{-}\left(S_p\right)={\tau }_C^s\left(S_p\right)=0.$

Proof. 

For $1\le i\le p$, $N_{S_p}\left[w_i\right]$ is a maximal clique of $S_p$. Let h be a minimum SCTF of $S_p$. Then, ${\tau }_C^s\left(S_p\right)=h\left(V\left(S_p\right)\right)$. Note that $h\left(N_{S_p}\left[w_i\right]\right)\ge 1$ for $1\le i\le p$. We have

$$h\left(V\left(S_p\right)\right)=\sum _{i=1}^{p}h\left(N_{S_p}\left[w_i\right]\right)-\sum _{i=1}^{p}h\left(u_i\right)\ge p-\sum _{i=1}^{p}h\left(u_i\right).$$

Since ${\sum }_{i=1}^{p}h\left(u_i\right)\le p$, we have ${\tau }_C^s\left(S_p\right)\ge 0$. Let f be an SCTF of $S_p$ such that $f\left(u_i\right)=1$ and $f\left(w_i\right)=-1$ for $1\le i\le p$. The weight of f is 0. Then f is a minimum SCTF of $S_p$. Hence, ${\tau }_C^{-}\left(S_p\right)=0$ and ${\tau }_C^s\left(S_p\right)=0$. The proof for ${\tau }_C^{-}\left(G\right)=0$ is analogous to that for ${\tau }_C^s\left(G\right)=0$. □

Theorem 1 

(Lee and Chang [9]). Let $S_p$ be a sun. Then,

(1)

${\gamma }^{-}\left(S_p\right)={\gamma }_s\left(S_p\right)=0$;

(2)

${\gamma }_{\left\{k\right\}}\left(S_p\right)=\lceil pk/2\rceil$;

(3)

${\gamma }_{\times 1}\left(S_p\right)=\lceil p/2\rceil$, ${\gamma }_{\times 2}\left(S_p\right)=p$ and ${\gamma }_{\times 3}\left(S_p\right)=2p$.

Corollary 1. 

Let$S_p$be a sun. Then,

(1)

${\gamma }^{-}\left(S_p\right)={\tau }_C^{-}\left(S_p\right)={\gamma }_s\left(S_p\right)={\tau }_C^s\left(S_p\right)=0$;

(2)

${\gamma }_{\left\{k\right\}}\left(S_p\right)={\tau }_C^{\left\{k\right\}}\left(S_p\right)=\lceil pk/2\rceil$ for $k>1$;

(3)

${\gamma }_{\times 2}\left(S_p\right)={\tau }_C^2\left(S_p\right)=p$ and ${\gamma }_{\times 3}\left(S_p\right)={\tau }_C^3\left(S_p\right)=2p$.

Proof. 

The corollary holds by Lemmas 1–3 and Corollary 1. □

3. Clique Perfect Graphs

Let $\mathcal{G}$ be the set of all induced subgraphs of G. If ${\tau }_C\left(H\right)={\alpha }_C\left(H\right)$ for every $H\in \mathcal{G}$, then G is clique perfect. In this section, we study the $\left\{k\right\}$-CTP for clique perfect graphs and the SCTP for balanced graphs.

Lemma 4. 

Let G be such a graph that ${\tau }_C\left(G\right)={\alpha }_C\left(G\right)$. Then, ${\tau }_C^{\left\{k\right\}}\left(G\right)=k{\tau }_C\left(G\right)$.

Proof. 

Assume that D is a minimum CTS of G. Then, $\left|D\right|={\tau }_C\left(G\right)$. Let $x\in V\left(G\right)$ and let f be a function whose domain is $V\left(G\right)$ and range is $\{0,1,\dots ,k\}$, and $f\left(x\right)=k$ if $x\in D$; otherwise, $f\left(x\right)=0$. Clearly, f is a $\left\{k\right\}$-CTF of G. We have ${\tau }_C^{\left\{k\right\}}\left(G\right)\le k{\tau }_C\left(G\right)$.

Assume that f is a minimum-weight $\left\{k\right\}$-CTF of G. Then, $f\left(V\left(G\right)\right)={\tau }_C^{\left\{k\right\}}\left(G\right)$ and $f\left(C\right)\ge k$ for every $C\in C\left(G\right)$. Let $S=\{C_1,C_2,\dots ,C_{\ell }\}$ be a maximum CIS of G. We know that $\left|S\right|=\ell ={\alpha }_C\left(G\right)$ and ${\sum }_{i=1}^{\ell }f\left(C_i\right)\le f\left(V\left(G\right)\right)$. Therefore, $k{\tau }_C\left(G\right)=k{\alpha }_C\left(G\right)=k\ell \le {\sum }_{i=1}^{\ell }f\left(C_i\right)\le f\left(V\left(G\right)\right)={\tau }_C^{\left\{k\right\}}\left(G\right)$. Following what we have discussed above, we know that ${\tau }_C^{\left\{k\right\}}\left(G\right)=k{\tau }_C\left(G\right)$. □

Theorem 2. 

If a graph G is clique perfect, ${\tau }_C^{\left\{k\right\}}\left(G\right)=k{\tau }_C\left(G\right)$.

Proof. 

Since G is clique perfect, ${\tau }_C\left(G\right)={\alpha }_C\left(G\right)$. Hence, the theorem holds by Lemma 4. □

Corollary 2. 

The $\left\{k\right\}$-CTP is polynomial-time solvable for distance-hereditary graphs, balanced graphs, strongly chordal graphs, comparability graphs, and chordal graphs without odd suns.

Proof. 

Distance-hereditary graphs, balanced graphs, strongly chordal graphs, comparability graphs, and chordal graphs without odd suns are clique perfect, and the CTP can be solved in polynomial time for them [10,11,12,13,14]. The corollary therefore holds. □

Definition 8. 

Suppose that R is a function whose domain is $C\left(G\right)$ and range is $\{0,1,\dots ,\omega (G\left)\right\}$. If $R\left(C\right)\le \left|C\right|$ for every $C\in C\left(G\right)$, then R is a clique-size restricted function (abbreviated as CSRF) of G. A set $D\subseteq V\left(G\right)$ is an R-clique transversal set (abbreviated as R-CTS) of G if R is a CSRF of G and $|D\cap C|\ge R\left(C\right)$ for every $C\in C\left(G\right)$. Let ${\tau }_R\left(G\right)=min\left\{\right|D|\mid D$ is an R-CTS of $G\}$. The generalized clique transversal problem (abbreviated as GCTP) is to find a minimum R-CTS for a graph G with a CSRF R.

Lemma 5. 

Let G be a graph with a CSRF R. If $R\left(C\right)=\lceil \left(\right|C|+1)/2\rceil$ for every $C\in C\left(G\right)$, then ${\tau }_C^s\left(G\right)=2{\tau }_R\left(G\right)-n$.

Proof. 

Assume that D is a minimum R-CTS of G. Then, $\left|D\right|={\tau }_R\left(G\right)$. Let $x\in V\left(G\right)$ and let f be a function of G whose domain is $V\left(G\right)$ and range is $\{-1,1\}$, and $f\left(x\right)=1$ if $x\in D$; otherwise, $f\left(x\right)=-1$. Since $|D\cap C|\ge \lceil \left(\right|C|+1)/2\rceil$ for every $C\in C\left(G\right)$, there are at least $\lceil \left(\right|C|+1)/2\rceil$ vertices in C with the function value 1. Therefore, $f\left(C\right)\ge 1$ for every $C\in C\left(G\right)$, and f is an SCTF of G. Then, ${\tau }_C^s\left(G\right)\le 2{\tau }_R\left(G\right)-n$.

Assume that h is a minimum-weight SCTF of G. Clearly, $h\left(V\left(G\right)\right)={\tau }_C^s\left(G\right)$. Since $h\left(C\right)\ge 1$ for every $C\in C\left(G\right)$, C contains at least $\lceil \left(\right|C|+1)\rceil /2$ vertices with the function value 1. Let $D=\{x\mid h(x)=1,x\in V(G\left)\right\}$. The set D is an R-CTS of G. Therefore, $2{\tau }_R\left(G\right)-n\le 2\left|D\right|-n={\tau }_C^s\left(G\right)$. Hence, we have ${\tau }_C^s\left(G\right)=2{\tau }_R\left(G\right)-n$. □

Theorem 3. 

The SCTP on balanced graphs can be solved in polynomial time.

Proof. 

Suppose that a graph G has n vertices $v_1,v_2,\dots ,v_n$ and ℓ maximal cliques $C_1,C_2,\dots ,C_{\ell }$. Let $i\in \{1,2,\dots ,\ell \}$ and $j\in \{1,2,\dots ,n\}$. Let M be an $\ell \times n$ matrix such that an element $M(i,j)$ of M is one if the maximal clique $C_i$ contains the vertex $v_j$, and $M(i,j)=0$ otherwise. We call M the clique matrix of G. If the clique matrix M of G does not contain a square submatrix of odd order with exactly two ones per row and column, then M is a balanced matrix and G is a balanced graph. We formulae the GCTP on a balanced graph G with a CSRF R as the following integer programming problem:

$$\left.\begin{array}{cc}\mathrm{minimize}\hfill & \sum _{i=1}^n{x}_i\hfill \\ & \\ \mathrm{subject} \mathrm{to}\hfill & MX\ge \mathcal{C}\hfill \end{array}\right\}$$

where $\mathcal{C}=(R\left(C_1\right),R\left(C_2\right),\dots ,R\left(C_{\ell }\right))$ is a column vector and $X=(x_1,x_2,\dots ,x_n)$ is a column vector such that $x_i$ is either 0 or 1. Since the matrix M is balanced, an optimal 0–1 solution of the integer programming problem above can be found in polynomial time by the results in [15]. By Lemma 5, we know that the SCTP on balanced graphs can be solved in polynomial time. □

4. Split Graphs

Let G be such a graph that $V\left(G\right)=I\cup C$ and $I\cap C=\varnothing$. If I is an independent set and C is a clique, G is a split graph. Then, every maximal of G is either C itself, or the closed neighborhood $N_G\left[x\right]$ of a vertex $x\in I$. We use $G=(I,C,E)$ to represent a split graph. The $\left\{k\right\}$-CTP, the k-FCTP, the SCTP, and the MCTP for split graphs are considered in this section. We also consider the $\left\{k\right\}$-DP, the k-TDP, the SDP, and the MDP for split graphs.

For split graphs, the $\left\{k\right\}$-DP, the k-TDP, and the MDP are NP-complete [16,17,18], but the complexity of the SDP is still unknown. In the following, we examine the relationships between the $\left\{k\right\}$-CTP and the $\left\{k\right\}$-DP, the k-FCTP and the k-TDP, the SCTP and the SDP, and the MCTP and the MDP. Then, by the relationships, we prove the NP-completeness of the SDP, the $\left\{k\right\}$-CTP, the k-FCTP, the SCTP, and the MCTP for split graphs. We first consider the $\left\{k\right\}$-CTP and the k-FCTP and show in Theorems 4 and 5 that ${\tau }_C^k\left(G\right)={\gamma }_{\times k}\left(G\right)$ and ${\tau }_C^{\left\{k\right\}}\left(G\right)={\gamma }_{\left\{k\right\}}\left(G\right)$ for any split graph G. Chordal graphs form a superclass of split graphs [19]. The cardinality of $C\left(G\right)$ is at most n for any chordal graph G [20]. The following lemma therefore holds trivially.

Lemma 6. 

The k-FCTP, the $\left\{k\right\}$-CTP, the SCTP, and the MCTP for chordal graphs are in NP.

Theorem 4. 

Suppose that $k\in \mathbb{N}$ and $G=(I,C,E)$ is a split graph. Then, ${\tau }_C^k\left(G\right)={\gamma }_{\times k}\left(G\right)$.

Proof. 

Let S be a minimum k-FCTS of G. Consider a vertex $y\in I$. By the structure of G, $N_G\left[y\right]$ is a maximal clique of G. Then, $|S\cap N_G\left[y\right]|\ge k$. We now consider a vertex $x\in C$. If $C\notin C\left(G\right)$, then there exists a vertex $y\in I$ such that $N_G\left[y\right]=C\cup \left\{y\right\}$. Clearly, $N_G\left[y\right]\subseteq N_G\left[x\right]$ and $|S\cap N_G\left[x\right]|\ge |S\cap N_G\left[y\right]|\ge k$. If $C\in C\left(G\right)$, then $|S\cap N_G\left[x\right]|\ge |S\cap C|\ge k$. Hence, S is a k-TDS of G. We have ${\gamma }_{\times k}\left(G\right)\le {\tau }_C^k\left(G\right)$.

Let D be a minimum k-TDS of G. Recall that the closed neighborhood of every vertex in I is a maximal clique. Then, D contains at least k vertices in the maximal clique $N_G\left[y\right]$ for every vertex $y\in I$. If $C\notin C\left(G\right)$, D is clearly a k-FCTS of G. Suppose that $C\in C\left(G\right)$. We consider three cases as follows.

Case 1: $y\in I\backslash D$. Then, $|D\cap C|\ge |D\cap N_G\left(y\right)|\ge k$. The set D is a k-FCTS of G.

Case 2: $y\in I\cap D$ and $x\in N_G\left(y\right)\backslash D$. Then, the set $D^{\prime }=(D\backslash \left\{y\right\})\cup \left\{x\right\}$ is still a minimum k-TDS and $|D^{\prime }\cap C|\ge |D^{\prime }\cap N_G\left(y\right)|\ge k$. The set $D^{\prime }$ is a k-FCTS of G.

Case 3: $I\subseteq D$ and $N_G\left[y\right]\subseteq D$ for every $y\in I$. Then, $|D\cap C|\ge |D\cap N_G\left(y\right)|\ge k-1$. Since $C\in C\left(G\right)$, there exists $x\in C$ such that $y\notin N_G\left(x\right)$. If $N_G\left(x\right)\cap I=\varnothing$, then $N_G\left[x\right]=C$ and $|D\cap C|=|D\cap N_G\left[x\right]|\ge k$. Otherwise, let $y^{\prime }\in N_G\left(x\right)\cap I$. Then, $x\in D$ and $|D\cap C|\ge |D\cap N_G\left(y\right)|+1\ge k$. The set D is a k-FCTS of G.

By the discussion of the three cases, we have ${\tau }_C^k\left(G\right)\le {\gamma }_{\times k}\left(G\right)$. Hence, we obtain that ${\gamma }_{\times k}\left(G\right)\le {\tau }_C^k\left(G\right)$ and ${\tau }_C^k\left(G\right)\le {\gamma }_{\times k}\left(G\right)$. The theorem holds for split graphs. □

Theorem 5. 

Suppose that $k\in \mathbb{N}$ and $G=(I,C,E)$ is a split graph. Then, ${\tau }_C^{\left\{k\right\}}\left(G\right)={\gamma }_{\left\{k\right\}}\left(G\right)$.

Proof. 

We can verify by contradiction that G has a minimum-weight $\left\{k\right\}$-CTF f and a minimum-weight $\left\{k\right\}$-DF g of G such that $f\left(y\right)=0$ and $g\left(y\right)=0$ for every $y\in I$. By the structure of G, $N_G\left[y\right]\in C\left(G\right)$ for every $y\in I$. Then, $f\left(N_G\left[y\right]\right)\ge k$ and $g\left(N_G\left[y\right]\right)\ge k$. Since $f\left(y\right)=0$ and $g\left(y\right)=0$, $f\left(N_G\left(y\right)\right)\ge k$ and $g\left(N_G\left(y\right)\right)\ge k$.

For every $y\in I$, $N_G\left(y\right)\subseteq C$ and $f\left(C\right)\ge f\left(N_G\left(y\right)\right)\ge k$. For every $x\in C$, $f\left(N_G\left[x\right]\right)\ge f\left(C\right)\ge k$. Therefore, the function f is also a $\left\{k\right\}$-DF of G. We have ${\gamma }_{\left\{k\right\}}\left(G\right)\le {\tau }_C^{\left\{k\right\}}\left(G\right)$. We now consider $g\left(C\right)$ for the clique C. If $C\notin C\left(G\right)$, the function g is clearly a $\left\{k\right\}$-CTF of G. Suppose that $C\in C\left(G\right)$. Notice that g is a $\left\{k\right\}$-DF and $g\left(y\right)=0$ for every $y\in I$. Then, $g\left(C\right)=g\left(N_G\left[x\right]\right)\ge k$ for any vertex $x\in C$. Therefore, g is also a $\left\{k\right\}$-CTF of G. We have ${\tau }_C^{\left\{k\right\}}\left(G\right)\le {\gamma }_{\left\{k\right\}}\left(G\right)$. Following what we have discussed above, we know that ${\tau }_C^{\left\{k\right\}}\left(G\right)={\gamma }_{\left\{k\right\}}\left(G\right)$. □

Corollary 3. 

The $\left\{k\right\}$-CTP and the k-FCTP are NP-complete for split graphs.

Proof. 

The corollary holds by Theorems 4 and 5 and the NP-completeness of the $\left\{k\right\}$-DP and the k-TDP for split graphs [16,18]. □

A graph G is a complete if $C\left(G\right)=\left\{V\right(G\left)\right\}$. Let G be a complete graph and let $x\in V\left(G\right)$. The vertex set $V\left(G\right)$ is the union of the sets $\left\{x\right\}$ and $V\left(G\right)\backslash \left\{x\right\}$. Clearly, $\left\{x\right\}$ is an independent set and $V\left(G\right)\backslash \left\{x\right\}$ is a clique of G. Therefore, complete graphs are split graphs. It is easy to verify the Lemma 7.

Lemma 7. 

If G is a complete graph and$k\in \mathbb{N}$, then

(1)

${\tau }_C^k\left(G\right)={\gamma }_{\times k}\left(G\right)=k$ for $k\le n$;

(2)

${\tau }_C^{\left\{k\right\}}\left(G\right)={\gamma }_{\left\{k\right\}}\left(G\right)=k$;

(3)

${\tau }_C^{-}\left(G\right)={\gamma }^{-}\left(G\right)=1$;

(4)

${\tau }_C^s\left(G\right)={\gamma }_s\left(G\right)=\left\{\begin{array}{cc}1\hfill & if n is odd;\hfill \\ 2\hfill & otherwise.\hfill \end{array}\right.$

For split graphs, however, the signed and minus domination numbers are not necessarily equal to the signed and minus clique transversal numbers, respectively. Figure 2 shows a split graph G with ${\tau }_C^s\left(G\right)={\tau }_C^{-}\left(G\right)=-3$. However, ${\gamma }_s\left(G\right)={\gamma }^{-}\left(G\right)=1$. We therefore introduce $H_1$-split graphs and show in Theorem 6 that their signed and minus domination numbers are equal to the signed and minus clique transversal numbers, respectively. $H_1$-split graphs are motivated by the graphs in [17] for proving the NP-completeness of the MDP on split graphs. Figure 3 shows an $H_1$-split graph.

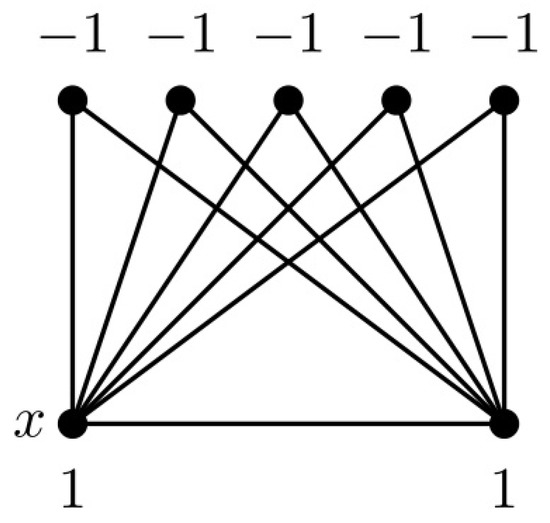
Figure 2. A split graph G with ${\tau }_C^s\left(G\right)={\tau }_C^{-}\left(G\right)=-3$.

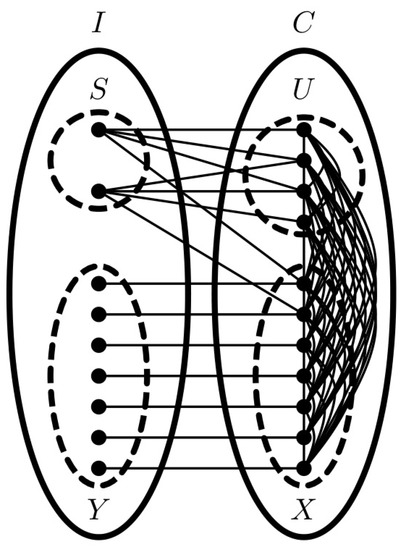
Figure 3. A split graph G with one of its partitions indicated.

Definition 9. 

Suppose that$G=(I,C,E)$is a split graph with$3p+3\ell +2$vertices. Let U, S, X, and Y be pairwise disjoint subsets of$V\left(G\right)$such that$U=\{u_i\mid 1\le i\le p\}$,$S=\{s_i\mid 1\le i\le \ell \}$,$X=\{x_i\mid 1\le i\le p+\ell +1\}$, and$Y=\{y_i\mid 1\le i\le p+\ell +1\}$. The graph G is an$H_1$-split graph if$V\left(G\right)=U\cup S\cup X\cup Y$and G entirely satisfies the following three conditions.

(1)

$I=S\cup Y$ and $C=U\cup X$.

(2)

$N_G\left(y_i\right)=\left\{x_i\right\}$ for $1\le i\le p+\ell +1$.

(3)

$|N_G\left(s_i\right)\cap U|=3$ and $N_G\left(s_i\right)\cap X=\left\{x_i\right\}$ for $1\le i\le \ell$.

Theorem 6. 

For any $H_1$-split graph $G=(I,C,E)$, ${\tau }_C^s\left(G\right)={\gamma }_s\left(G\right)$ and ${\tau }_C^{-}\left(G\right)={\gamma }^{-}\left(G\right)$.

Proof. 

We first prove ${\tau }_C^s\left(G\right)={\gamma }_s\left(G\right)$. Let $G=(I,C,E)$ be an $H_1$-split graph. As stated in Definition 9, I can be partitioned into $S=\{s_i\mid 1\le i\le \ell \}$ and $Y=\{y_i\mid 1\le i\le p+\ell +1\}$, and C can be partitioned into $U=\{u_i\mid 1\le i\le p\}$ and $X=\{x_i\mid 1\le i\le p+\ell +1\}$. Assume that f is a minimum-weight SDF of G. For each $y_i\in Y$, $|N_G\left[y_i\right]|=2$ and $y_i$ is adjacent to only the vertex $x_i\in X$. Then, $f\left(x_i\right)=f\left(y_i\right)=1$ for $1\le i\le p+\ell +1$. Since $C=U\cup X$ and $\left|U\right|=p$, we know that $f\left(C\right)=f\left(U\right)+f\left(X\right)\ge (-p)+(p+\ell +1)\ge \ell +1$. Notice that $f\left(N_G\left[y\right]\right)\ge 1$ and $N_G\left[y\right]\in C\left(G\right)$ for every $y\in I$. Therefore, f is also an SCTF of G. We have ${\tau }_C^s\left(G\right)\le {\gamma }_s\left(G\right)$.

Assume that h is a minimum-weight SCTF of G. For each $y_i\in Y$, $|N_G\left[y_i\right]|=2$ and $y_i$ is adjacent to only the vertex $x_i\in X$. Then, $h\left(x_i\right)=h\left(y_i\right)=1$ for $1\le i\le p+\ell +1$. Consider the vertices in I. Since $N_G\left[y\right]\in C\left(G\right)$ for every $y\in I$, $h\left(N_G\left[y\right]\right)\ge 1$. We now consider the vertices in C. Recall that $C=U\cup X$. Let $u_i\in U$. Since $\left|U\right|=p$ and $\left|S\right|=\ell$, we know that $h\left(N_G\left[u_i\right]\right)=h\left(U\right)+h\left(X\right)+h(N_G\left[u_i\right]\cap S)\ge (-p)+(p+\ell +1)+(-\ell )\ge 1$. Let $x_i\in X$. Then, $h\left(N_G\left[x_i\right]\right)=h\left(U\right)+h\left(X\right)+h\left(y_i\right)+h\left(s_i\right)\ge (-p)+(p+\ell +1)+1-1\ge \ell +1$. Therefore, h is also an SDF of G. We have ${\gamma }_s\left(G\right)\le {\tau }_C^s\left(G\right)$.

Following what we have discussed above, we have ${\tau }_C^s\left(G\right)={\gamma }_s\left(G\right)$. The proof for ${\tau }_C^{-}\left(G\right)={\gamma }^{-}\left(G\right)$ is analogous to that for ${\tau }_C^s\left(G\right)={\gamma }_s\left(G\right)$. Hence, the theorem holds for any $H_1$-split graphs. □

Theorem 7. 

The SDP on $H_1$-split graphs is NP-complete.

Proof. 

We reduce the (3,2)-hitting set problem to the SDP on $H_1$-split graphs. Let $U=\{u_i\mid 1\le i\le p\}$ and let $\mathcal{C}=\{C_1,C_2,\dots ,C_{\ell }\}$ such that $C_i\subseteq U$ and $|C_i|=3$ for $1\le i\le \ell$. A (3,2)-hitting set for the instance $(U,\mathcal{C})$ is a subset $U^{\prime }$ of U such that $|C_i\cap U^{\prime }|\ge 2$ for $1\le i\le \ell$. The (3,2)-hitting set problem is to find a minimum (3,2)-hitting set for any instance $(U,\mathcal{C})$. The (3,2)-hitting set problem is NP-complete [17].

Consider an instance $(U,\mathcal{C})$ of the (3,2)-hitting set problem. Let $S=\{s_i\mid 1\le i\le \ell \}$, $X=\{x_i\mid 1\le i\le p+\ell +1\}$, and $Y=\{y_i\mid 1\le i\le p+\ell +1\}$. We construct an $H_1$-split graph $G=(I,C,E)$ by the following steps.

(1)

Let $I=S\cup Y$ be an independent set and let $C=U\cup X$ be a clique.

(2)

For each vertex $s_i\in S$, a vertex $u\in U$ is connected to $s_i$ if $u\in C_i$.

(3)

For $1\le i\le p+\ell +1$, the vertex $y_i$ is connected to the vertex $x_i$.

(4)

For $1\le i\le \ell$, the vertex $s_i$ is connected to the vertex $x_i$.

Let ${\tau }_h(3,2)$ be the minimum cardinality of a (3,2)-hitting set for the instance $(U,\mathcal{C})$. Assume that $U^{\prime }$ is a minimum (3,2)-hitting set for the instance $(U,\mathcal{C})$. Then, $|U^{\prime }|={\tau }_h(3,2)$. Let f be a function whose domain is $V\left(G\right)$ and range is $\{-1,1\}$, and $f\left(v\right)=1$ if $v\in X\cup Y\cup U^{\prime }$ and $f\left(v\right)=-1$ if $v\in S\cup (U\backslash U^{\prime })$. Clearly, f is an SDF of G. We have ${\gamma }_s\left(G\right)\le 2(p+\ell +1)+|U^{\prime }|-\ell -(p-|U^{\prime }\left|\right)=p+\ell +2{\tau }_h(3,2)+2$.

Assume that f is minimum-weight SDF of G. For each $y_i\in Y$, $|N_G\left[y_i\right]|=2$ and $y_i$ is adjacent to only the vertex $x_i\in X$. Then, $f\left(x_i\right)=f\left(y_i\right)=1$ for $1\le i\le p+\ell +1$. For any vertex $v\in X\cup Y\cup U$, $f\left(N_G\left[v\right]\right)\ge 1$ no matter what values the function f assigns to the vertices in U or in S. Consider the vertices in S. By the construction of G, $de{g}_G\left(s_i\right)=4$ and $|N_G\left[s_i\right]|=5$ for $1\le i\le \ell$. There are at least three vertices in $N_G\left[s_i\right]$ with the function value 1. If $f\left(N_G\left[s_i\right]\right)=5$, then there exists an SDF g of G such that $g\left(s_i\right)=-1$ and $g\left(v\right)=f\left(v\right)$ for every $v\in V\left(G\right)\backslash \left\{s_i\right\}$. Then, $g\left(V\right(G\left)\right)<f\left(V\right(G\left)\right)$. It contradicts the assumption that the weight of f is minimum. Therefore, there exists a minimum-weight SDF h of G such that $h\left(s_i\right)=-1$ for $1\le i\le \ell$. Notice that $N_G\left(s_i\right)=C_i\cup \left\{x_i\right\}$ for $1\le i\le \ell$. There are at least two vertices in $C_i$ with the function value 1. Then, the set $U^{\prime }=\{u\in U\mid h\left(u\right)=1\}$ is a (3,2)-hitting set for the instance $(U,\mathcal{C})$. We have $p+\ell +2{\tau }_h(3,2)+2\le p+\ell +2\left|U^{\prime }\right|+2={\gamma }_s\left(G\right)$.

Following what we have discussed above, we know that ${\gamma }_s\left(G\right)=p+\ell +2{\tau }_h(3,2)+2$. Hence, the SDP on $H_1$-split graphs is NP-complete. □

Corollary 4. 

The SCTP and the MCTP on split graphs are NP-complete.

Proof. 

The corollary holds by Theorems 6 and 7 and the NP-completeness of the MDP on split graphs [17]. □

5. Doubly Chordal and Dually Chordal Graphs

Assume that G is a graph with n vertices $x_1,x_2,\dots ,x_n$. Let $i\in \{1,2,\dots ,n\}$ and let $G_i$ be the subgraph $G[V\left(G\right)\backslash \{x_1,x_2,\dots x_{i-1}\}]$. For every $x\in V\left(G_i\right)$, let $N_i\left[x\right]=\{y\mid y\in (N_G\left[x\right]\backslash \{x_1,x_2,\dots ,x_{i-1}\})\}$. In $G_i$, if there exists a vertex $x_j\in N_i\left[x_i\right]$ such that $N_i\left[x_k\right]\subseteq N_i\left[x_j\right]$ for every $x_k\in N_i\left[x_i\right]$, then the ordering $(x_1,x_2,\dots ,x_n)$ is a maximum neighborhood ordering (abbreviated as MNO) of G. A graph G is dually chordal [21] if and only if G has an MNO. It takes linear time to compute an MNO for any dually chordal graph [22]. A graph G is a doubly chordal graph if G is both chordal and dually chordal [23]. Lemma 8 shows that a dually chordal graph is not necessarily a chordal graph or a clique perfect graph. Notice that the number of maximal cliques in a chordal graph is at most n [20], but the number of maximal cliques in a dually chordal graph can be exponential [24].

Lemma 8. 

For any dually graph G, ${\tau }_C\left(G\right)={\alpha }_C\left(G\right)$, but G is not necessarily clique perfect or chordal.

Proof. 

Brandstädt et al. [25] showed that the CTP is a particular case of the clique r-domination problem and the CIP is a particular case of the clique r-packing problem. They also showed that the minimum cardinality of a clique r-dominating set of a dually chordal graph G is equal to the maximum cardinality of a clique r-packing set of G. Therefore, ${\tau }_C\left(G\right)={\alpha }_C\left(G\right)$.

Assume that H is a graph obtained by connecting every vertex of a cycle $C_4$ of four vertices $x_1,x_2,x_3,x_4$ to a vertex $x_5$. Clearly, the ordering $(x_1,x_2,x_3,x_4,x_5)$ is an MNO and thus H is a dually chordal graph. The cycle $C_4$ is an induced subgraph of H and does not have a chord. Moreover, ${\tau }_C\left(H\right)={\alpha }_C\left(H\right)=1$, but ${\tau }_C\left(C_4\right)=2$ and ${\alpha }_C\left(C_4\right)=1$. Hence, a dually chordal graph is not necessarily clique perfect or chordal. □

Theorem 8. 

Suppose that $k\in \mathbb{N}$ and $k>1$. The k-FCTP on doubly chordal graphs is NP-complete.

Proof. 

Suppose that G is a chordal graph. Let H be a graph such that $V\left(H\right)=V\left(G\right)\cup \left\{x\right\}$ and $E\left(H\right)=E\left(G\right)\cup \left\{\right(x,y)\mid y\in V(G\left)\right\}$. Clearly, H is a doubly chordal graph and we can construct H from G in linear time.

Assume that S is a minimum $(k-1)$-FCTS of G. By the construction of H, each maximal clique of H contains the vertex x. Therefore, $S\cup \left\{x\right\}$ is a k-FCTS of H. Then ${\tau }_C^k\left(H\right)\le {\tau }_C^{k-1}\left(G\right)+1$.

By contradiction, we can verify that there exists a minimum k-FCTS D of H such that $x\in D$. Let $S=D\backslash \left\{x\right\}$. Clearly, S is a $(k-1)$-FCTS of G. Then ${\tau }_C^{k-1}\left(G\right)\le {\tau }_C^k\left(H\right)-1$. Following what we have discussed above, we have ${\tau }_C^k\left(H\right)={\tau }_C^{k-1}\left(G\right)+1$. Notice that ${\tau }_C\left(G\right)={\tau }_C^1\left(G\right)$ and the CTP on chordal graphs is NP-complete [14]. Hence, the k-FCTP on doubly chordal graphs is NP-complete for doubly chordal graphs. □

Theorem 9. 

For any doubly chordal graph G, ${\tau }_C^{\left\{k\right\}}\left(G\right)$ can be computed in linear time.

Proof. 

The clique r-dominating problem on doubly chordal graphs can be solved in linear time [25]. The CTP is a particular case of the clique r-domination problem. Therefore, the CTP on doubly chordal graphs can also be solved in linear time. By Lemmas 4 and 8, the theorem holds. □

6. k-Trees

Assume that G is a graph with n vertices $x_1,x_2,\dots ,x_n$. Let $i\in \{1,2,\dots ,n\}$ and let $G_i$ be the subgraph $G[V\left(G\right)\backslash \{x_1,x_2,\dots x_{i-1}\}]$. For every $x\in V\left(G_i\right)$, let $N_i\left[x\right]=\{y\mid y\in (N_G\left[x\right]\backslash \{x_1,x_2,\dots ,x_{i-1}\})\}$. If $N_i\left[x_i\right]$ is a clique for $1\le i\le n$, then the ordering $(x_1,x_2,\dots ,x_n)$ is a perfect elimination ordering (abbreviated as PEO) of G. A graph G is chordal if and only if G has a PEO [26]. A chordal graph G is a k-tree if and only if either G is a complete graph of k vertices or G has more than k vertices and there exists a PEO $(x_1,x_2,\dots ,x_n)$ such that $N_i\left[x_i\right]$ is a clique of k vertices if $i=n-k+1$; otherwise, $N_i\left[x_i\right]$ is a clique of $k+1$ vertices for $1\le i\le n-k$. Figure 4 shows a 2-tree with the PEO $(v_1,v_2,\dots ,v_{13})$.

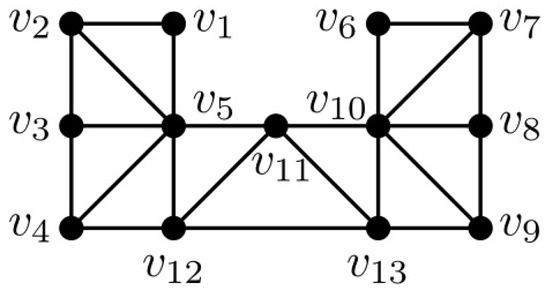
Figure 4. A 2-tree H.

In [3], Chang et al. showed that the MCTP is NP-complete for k-trees with unbounded k by proving $\gamma \left(G\right)={\tau }_M\left(G\right)$ for any k-tree G. However, Figure 4 shows a counterexample that disproves $\gamma \left(G\right)={\tau }_M\left(G\right)$ for any k-tree G. The graph H in Figure 4 is a 2-tree with the perfect elimination ordering $(v_1,v_2,\dots ,v_{13})$. The set $\{v_5,v_{10}\}$ is the minimum dominating set of H and the set $\{v_5,v_{10},v_{11}\}$ is a minimum MCTS of H. A modified NP-completeness proof is therefore desired for the MCTP on k-tree with unbounded k.

Theorem 10. 

The MCTP and the MCIP are NP-complete for k-trees with unbounded k.

Proof. 

The CTP and the CIP are NP-complete for k-trees with unbounded k [8]. Since every maximal clique in a k-tree is also a maximum clique [27], an MCTS is a CTS and an MCIS is a CIS. Hence, the MCTP and the MCIP are NP-complete for k-trees with unbounded k. □

Theorem 11. 

The SCTP is NP-complete for k-trees with unbounded k.

Proof. 

Suppose that $k_1\in \mathbb{N}$ and G is a $k_1$-tree with $\left|V\left(G\right)\right|>k_1$. Let $C\left(G\right)=\{C_1,C_2,\dots ,C_{\ell }\}$. Since G is a $k_1$-tree, $|C_i|=k_1+1$ for $1\le i\le \ell$.

Let Q be a clique with $k_1+1$ vertices. Let H be a graph such that $V\left(H\right)=V\left(G\right)\cup Q$ and $E\left(H\right)=E\left(G\right)\cup \left\{\right(x,y)\mid x,y\in Q\}\cup \left\{\right(x,y)\mid x\in Q,y\in V(G\left)\right\}$. Let $X_i=C_i\cup Q$ be a clique for $1\le i\le \ell$. Clearly, $C\left(H\right)=\{X_i\mid 1\le i\le \ell \}$. Let $k_2=2k_1+1$. Then, H is a $k_2$-tree and $|X_i|=k_2+1=2k_1+2$ for $1\le i\le \ell$. Clearly, we can verify that there exists a minimum-weight SCTF h of H of such that $h\left(x\right)=1$ for every $x\in Q$. Then, $C_i=X_i\backslash Q$ contains at least one vertex x with $h\left(x\right)=1$ for $1\le i\le \ell$. Let $S=\{x\mid x\in V(H)\backslash Q$ and $h\left(x\right)=1\}$. Then, S is a CTS of G. Since ${\tau }_C^s\left(H\right)=\left|Q\right|+2\left|S\right|-\left|V\left(G\right)\right|$, we have $\left|Q\right|+2{\tau }_C\left(G\right)-\left|V\left(G\right)\right|\le {\tau }_C^s\left(H\right)$.

Assume that D is a minimum CTS of G. Let f be a function of H whose domain is $V\left(H\right)$ and range is $\{-1,1\}$, and (1) $f\left(x\right)=1$ for every $x\in Q$, (2) $f\left(x\right)=1$ for every $x\in D$, and (3) $f\left(x\right)=-1$ for every $x\in V\left(G\right)\backslash D$. Each maximal clique of H has at least $k_1+2$ vertices with the function value 1. Therefore, f is an SCTF. We have ${\tau }_C^s\left(H\right)\le \left|Q\right|+2{\tau }_C\left(G\right)-\left|V\left(G\right)\right|$. Following what we have discussed above, we know that ${\tau }_C^s\left(H\right)=\left|Q\right|+2{\tau }_C\left(G\right)-\left|V\left(G\right)\right|$. The theorem therefore holds by the NP-completeness of the CTP for k-trees [8]. □

Theorem 12. 

Suppose that $\kappa \in \mathbb{N}$ the κ-FCTP is NP-complete on k-trees with unbounded k.

Proof. 

Assume that $k_1\in \mathbb{N}$ and G is a $k_1$-tree with $\left|V\left(G\right)\right|>k_1$. Let H be a graph such that $V\left(H\right)=V\left(G\right)\cup \left\{x\right\}$ and $E\left(H\right)=E\left(G\right)\cup \left\{\right(x,y)\mid y\in V(G\left)\right\}$. Clearly, H is a $(k_1+1)$-tree and we can construct H in linear time. Following the argument analogous to the proof of Theorem 8, we have ${\tau }_C^{\kappa }\left(H\right)={\tau }_C^{\kappa -1}\left(G\right)+1$. The theorem therefore holds by the NP-completeness of the CTP for k-trees [8]. □

Theorem 13. 

The SCTP and κ-FCTP problems can be solved in linear-time for k-trees with fixed k.

Proof. 

Assume that $\kappa \in \mathbb{N}$ and G is a graph. The $\kappa$-FCTP is the GCTP with the CSRF R whose domain is $C\left(G\right)$ and range is $\left\{\kappa \right\}$. By Lemma 5, ${\tau }_C^s\left(G\right)$ can be obtained from the solution to the GCTP on a graph G with a particular CSRF R. Since the GCTP is linear-time solvable for k-trees with fixed k [8], the SCTP and $\kappa$-FCTP are also linear-time solvable for k-trees with fixed k. □

7. Planar, Total, and Line Graphs

In a graph, a vertex x and an edge e are incident to each other if e connects x to another vertex. Two edges are adjacent if they share a vertex in common. Let G and H be graphs such that each vertex $x\in V\left(H\right)$ corresponds to an edge $e_x\in E\left(G\right)$ and two vertices $x,y\in V\left(H\right)$ are adjacent in H if and only if their corresponding edges $e_x$ and $e_y$ are adjacent in G. Then, H is the line graph of G and denoted by $L\left(G\right)$. Let $H^{\prime }$ be a graph such that $V\left(H^{\prime }\right)=V\left(G\right)\cup E\left(G\right)$ and two vertices $x,y\in V\left(H^{\prime }\right)$ are adjacent in H if and only if x and y are adjacent or incident to each other in G. Then, $H^{\prime }$ is the total graph of G and denoted by $T\left(G\right)$.

Lemma 9 

([28]). The following statements hold for any triangle-free graph G.

(1)

Every maximal clique of $L\left(G\right)$ is the set of edges of G incident to some vertex of G.

(1)

Two maximal cliques in $L\left(G\right)$ intersect if and only if their corresponding vertices (in G) are adjacent in G.

Theorem 14. 

The MCIP is NP-complete for any 4-regular planar graph G with the clique number 3.

Proof. 

Since $\left|C\right(G\left)\right|=O\left(n\right)$ for any planar graph G [29], the MCIP on planar graphs is in NP. Let $\mathcal{G}$ be the class of triangle-free, 3-connected, cubic planar graphs. The independent set problem remains NP-complete even when restricted to the graph class $\mathcal{G}$ [30]. We reduce this NP-complete problem to the MCIP for 4-regular planar graphs with the clique number 3 as follows.

Let $G\in \mathcal{G}$ and $H=L\left(G\right)$. Clearly, we can construct H in polynomial time. By Lemma 9, we know that H is a 4-regular planar graph with $\omega \left(H\right)=3$ and each maximal clique is a triangle in H.

Assume that $D=\{x_1,x_2,\dots ,x_{\ell }\}$ is an independent set of G of maximum cardinality. Since $G\in \mathcal{G}$, $de{g}_G\left(x\right)=3$ for every $x\in V\left(G\right)$. Let $e_{i_1},e_{i_2},e_{i_3}\in E\left(G\right)$ have the vertex $x_i$ in common for $1\le i\le \ell$. Then, $e_{i_1},e_{i_2},e_{i_3}$ form a triangle in H. Let $C_i$ be the triangle formed by $e_{i_1},e_{i_2},e_{i_3}$ in H for $1\le i\le \ell$. For each pair of vertices $x_j,x_k\in D$, $x_j$ is not adjacent to $x_k$ in G. Therefore, $C_j$ and $C_k$ in H do not intersect. The set $\{C_1,C_2,\dots ,C_{\ell }\}$ is an MCIS of H. We have $\alpha \left(G\right)\le {\alpha }_M\left(H\right)$.

Assume that $S=\{C_1,C_2,\dots ,C_{\ell }\}$ is a maximum MCIS of H. Then, each $C_i\in S$ is a triangle in H. Let $C_i$ be formed by $e_{i_1},e_{i_2},e_{i_3}$ in H for $1\le i\le \ell$. Then, $e_{i_1},e_{i_2},e_{i_3}$ are incident to the same vertex in G. For $1\le i\le \ell$, let $e_{i_1},e_{i_2},e_{i_3}\in E\left(G\right)$ have the vertex $x_i$ in common. For each pair of $C_j,C_k\in S$, $C_j$ and $C_k$ do not intersect. Therefore, $x_j$ is not adjacent to $x_k$ in G. The set $\{x_1,x_2,\dots ,x_{\ell }\}$ is an independent set of G. We have ${\alpha }_M\left(H\right)\le \alpha \left(G\right)$.

Hence, $\alpha \left(G\right)={\alpha }_M\left(H\right)$. For $k\in \mathbb{N}$, we know that $\alpha \left(G\right)\ge k$ if and only if ${\alpha }_M\left(G\right)\ge k$. □

Corollary 5. 

The MCIP is NP-complete for line graphs of triangle-free, 3-connected, cubic planar graphs.

Proof. 

The corollary holds by the reduction of Theorem 14. □

Theorem 15. 

The MCIP problem is NP-complete for total graphs of triangle-free, 3-connected, cubic planar graphs.

Proof. 

Since $\left|C\right(G\left)\right|=O\left(n\right)$ for a planar graph G, the MCIP on planar graphs is in NP. Let $\mathcal{G}$ be the classes of traingle-free, 3-connected, cubic planar graphs. The independent set problem remains NP-complete even when restricted to the graph class $\mathcal{G}$ [30]. We reduce this NP-complete problem to MCIP for for total graphs of triangle-free, 3-connected, cubic planar graphs. as follows

Let $G\in \mathcal{G}$ and $H=T\left(G\right)$. Clearly, we can construct H in polynomial time. By Lemma 9, we can verify that H is a 6-regular graph with $\omega \left(H\right)=4$.

Assume that $D=\{x_1,x_2,\dots ,x_{\ell }\}$ is an independent set of G of maximum cardinality. Since $G\in \mathcal{G}$, $de{g}_G\left(x\right)=3$ for every $x\in V\left(G\right)$. Let $e_{i_1},e_{i_2},e_{i_3}\in E\left(G\right)$ have the vertex $x_i$ in common. Then, $x_i,e_{i_1},e_{i_2},e_{i_3}$ form a maximum clique in H. Let $C_i$ be the maximum clique formed by $x_i,e_{i_1},e_{i_2},e_{i_3}$ in H for $1\le i\le \ell$. For each pair of vertices $x_j,x_k\in D$, $x_j$ is not adjacent to $x_k$ in G. Therefore, $C_j$ and $C_k$ in H do not intersect. The set $\{C_1,C_2,\dots ,C_{\ell }\}$ is an MCIS of H. We have $\alpha \left(G\right)\le {\alpha }_M\left(H\right)$.

Assume that $S=\{C_1,C_2,\dots ,C_{\ell }\}$ is a maximum MCIS of H. By the construction of H, each $C_i\in S$ is formed by three edge-vertices in $E\left(G\right)$ and their common end vertex in $V\left(G\right)$. Let $x_i\in V$ and $e_{i_1},e_{i_2},e_{i_3}\in E\left(G\right)$ in H such that $C_i$ is formed by $v_i,e_{i_1},e_{i_2},e_{i_3}$ for $1\le i\le \ell$. For each pair of $C_j,C_k\in C$, $C_j$ and $C_k$ do not intersect. Therefore, $x_j$ is not adjacent to $x_k$ in G. The set $\{x_1,x_2,\dots ,x_{\ell }\}$ is an independent set of G. We have ${\alpha }_M\left(H\right)\le \alpha \left(G\right)$.

Hence, $\alpha \left(G\right)={\alpha }_M\left(H\right)$. For $k\in \mathbb{N}$, we know that $\alpha \left(G\right)\ge k$ if and only if ${\alpha }_M\left(H\right)\ge k$. □