Unstructured Uncertainty Based Modeling and Robust Stability Analysis of Textile-Reinforced Composites with Embedded Shape Memory Alloys
Abstract
1. Introduction
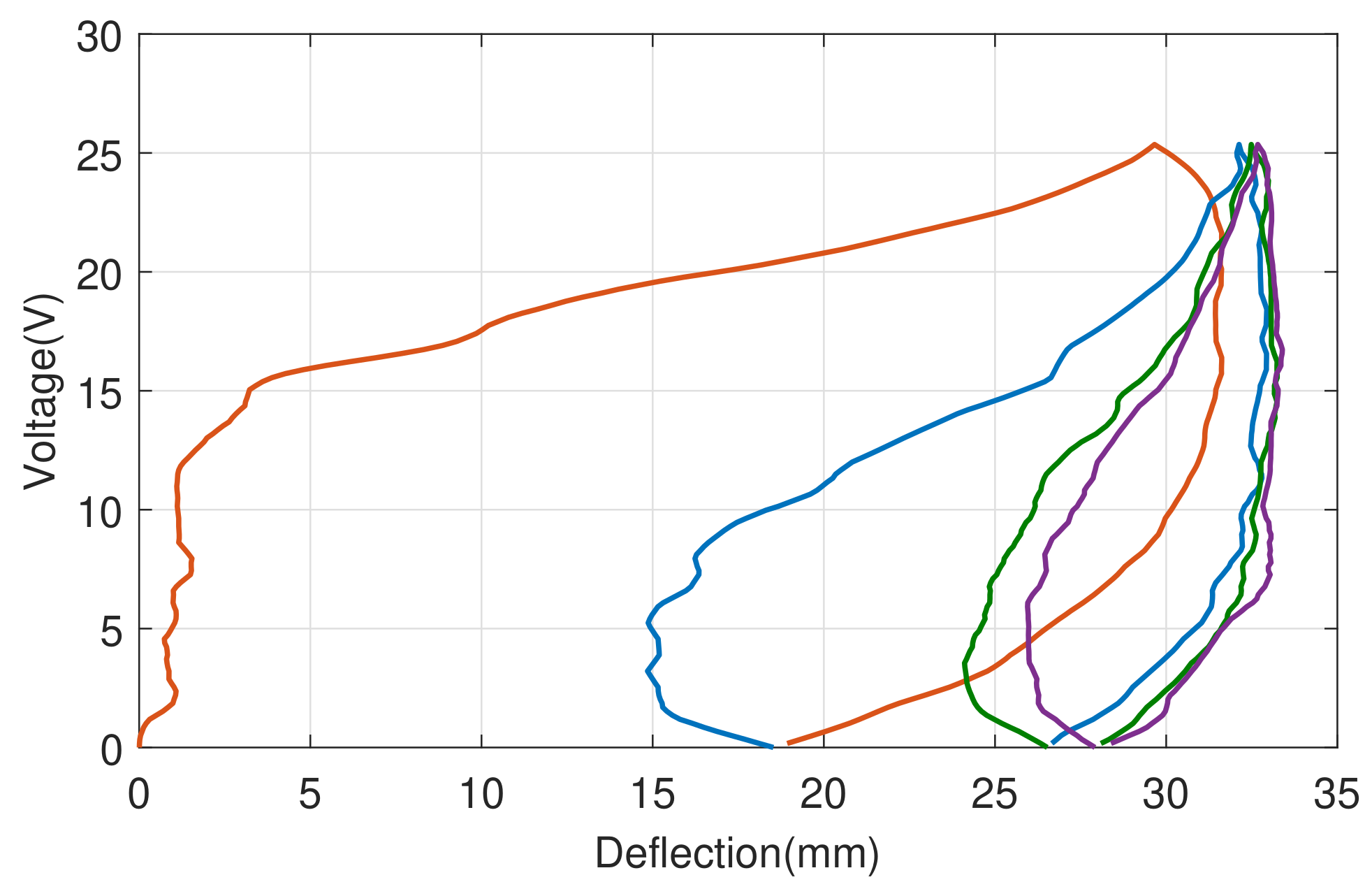
2. System Description
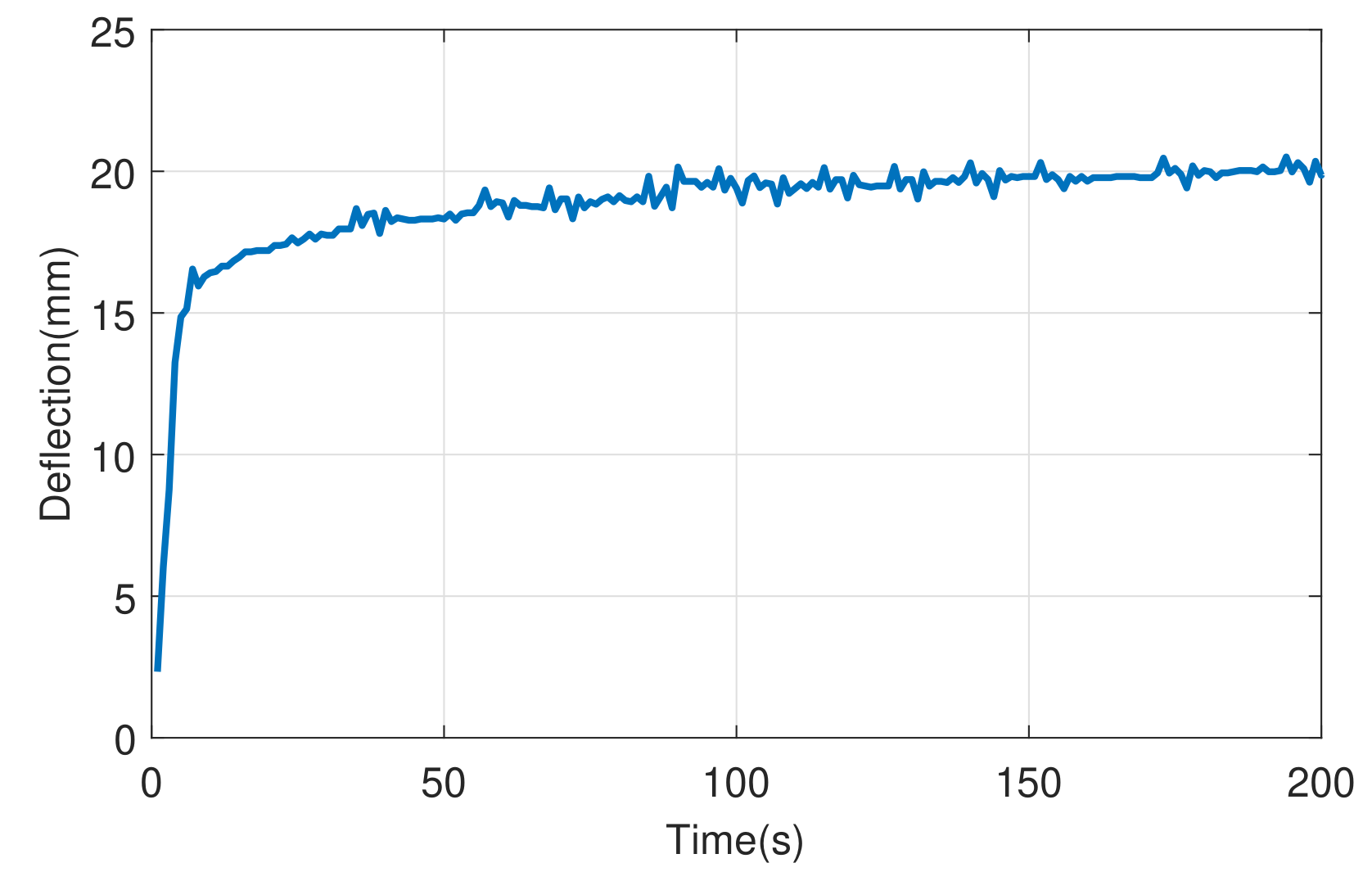
3. Model Identification
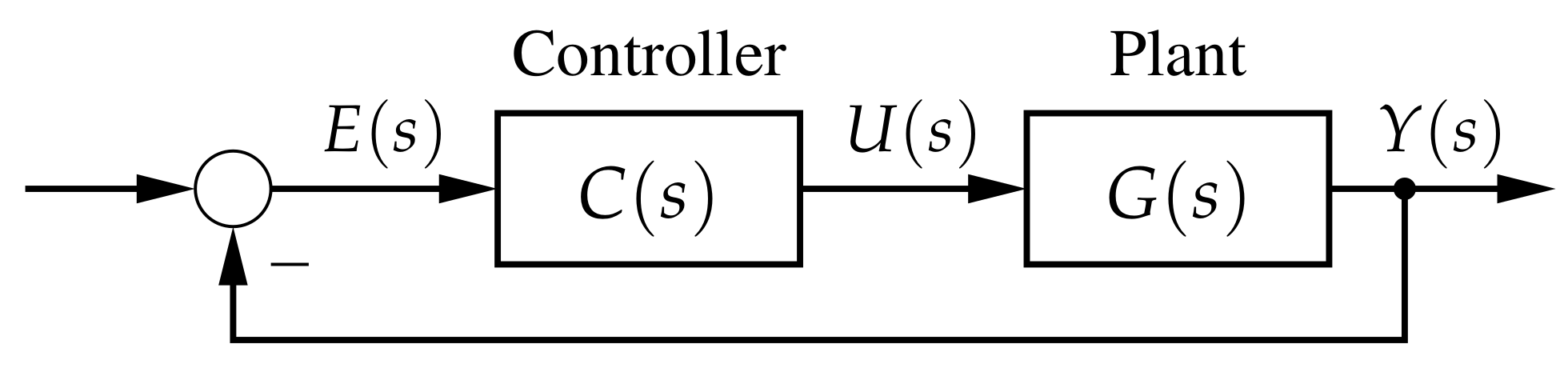
4. Classical Controller Design
5. Robust Control
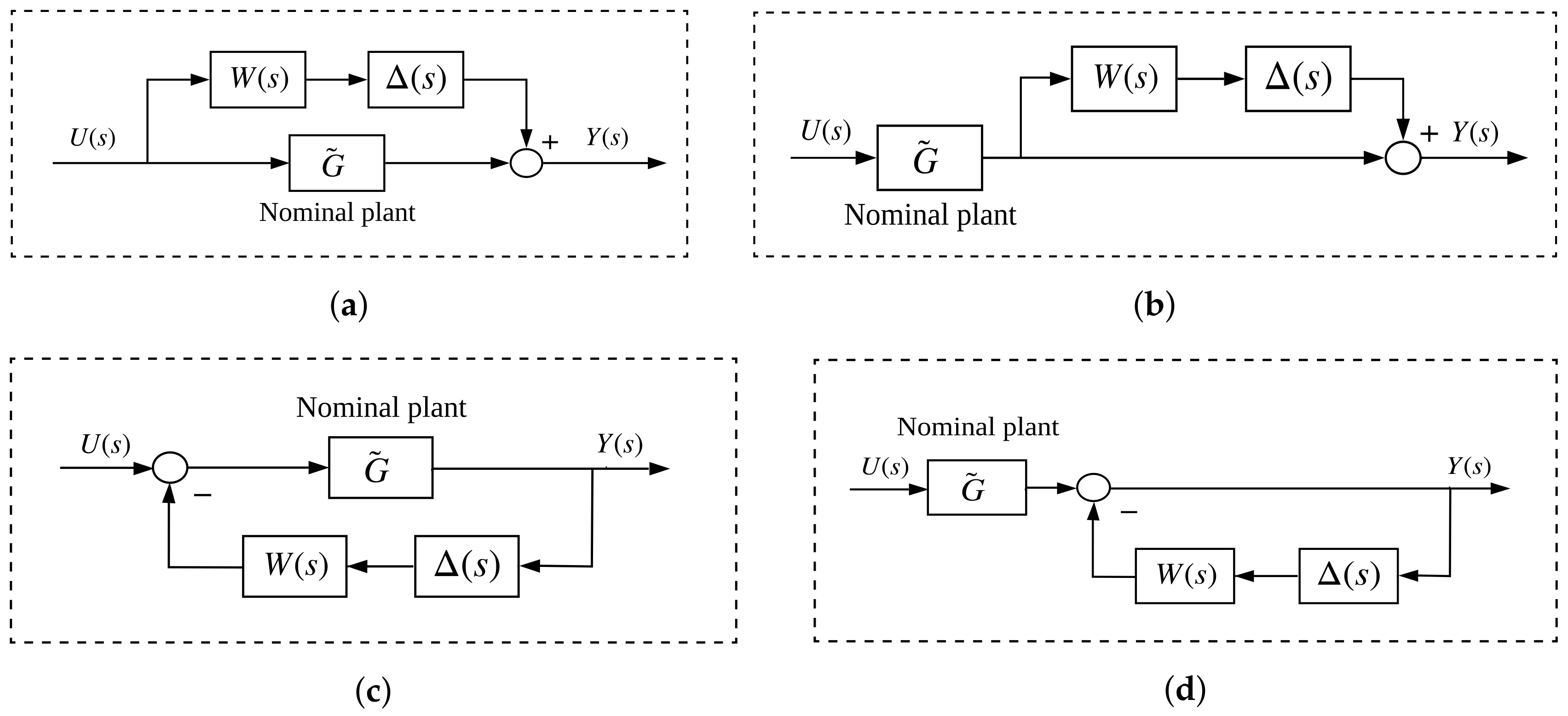
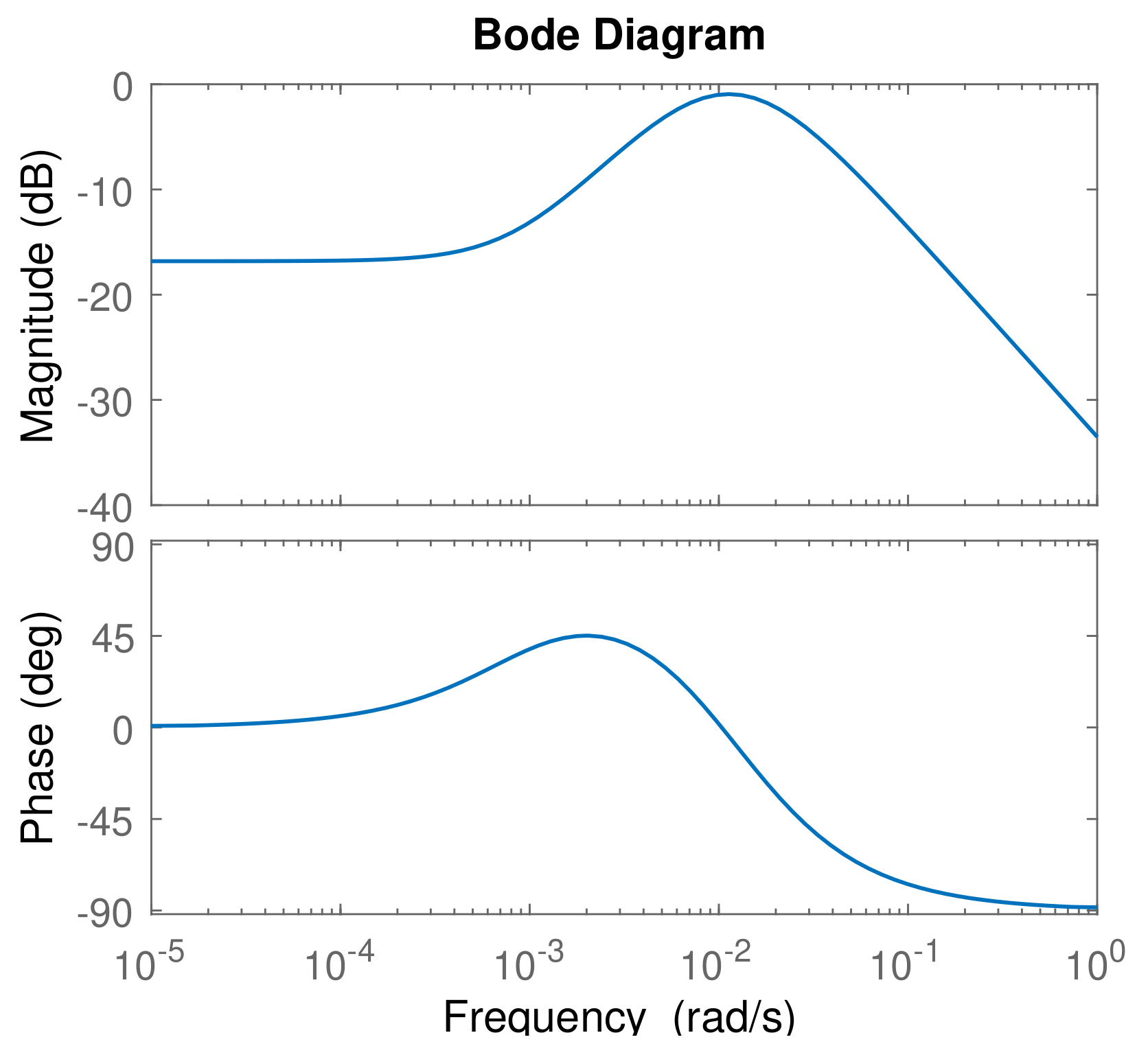
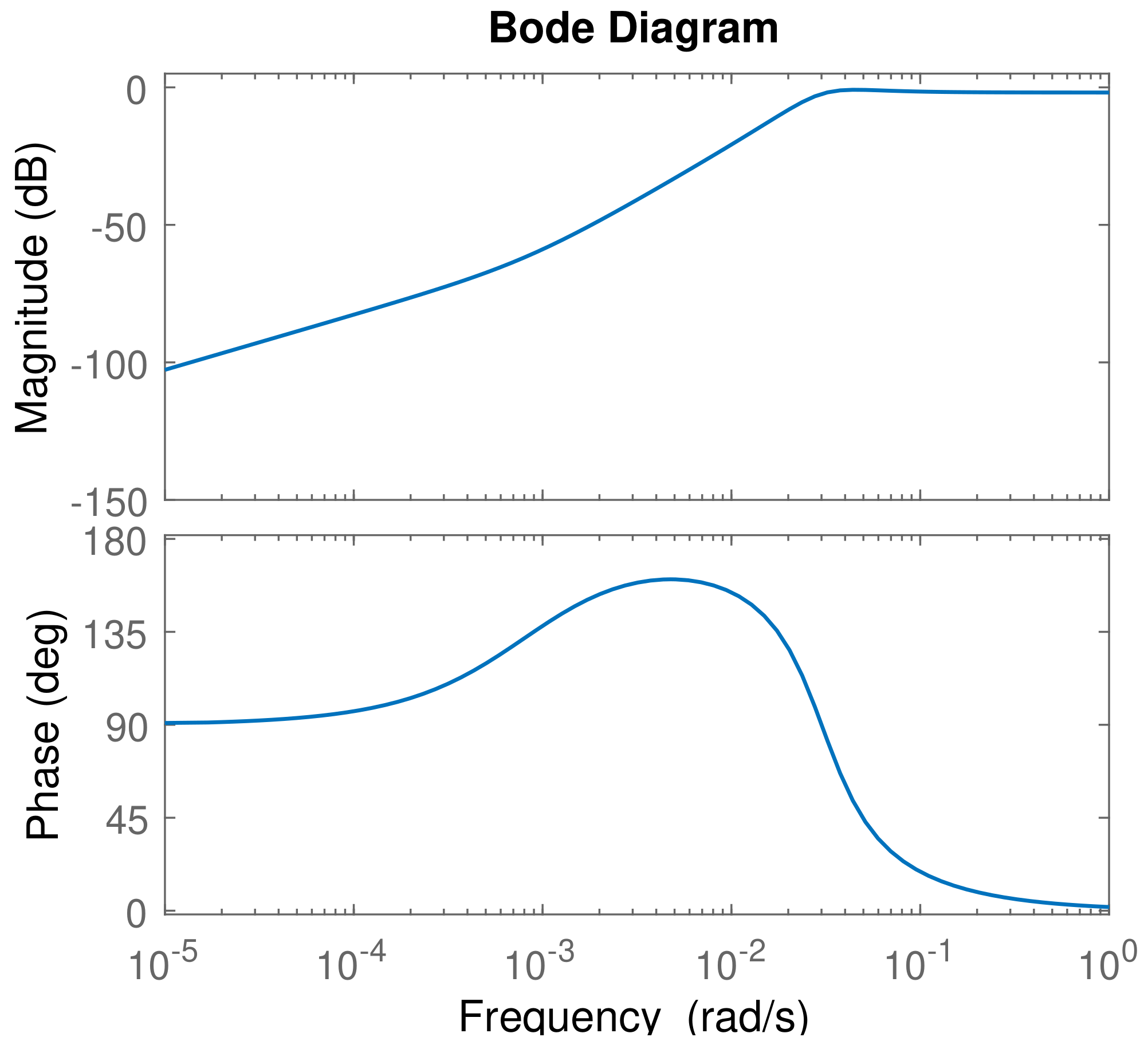
5.1. Uncertainty Models
- Additive Uncertainty
- Multiplicative Uncertainty
- Feedback Uncertainty
- Multiplicative Feedback Uncertainty
- Multiplicative Uncertainty
- Feedback Uncertainty
- Multiplicative Feedback Uncertainty
5.2. Robust Stability Analysis
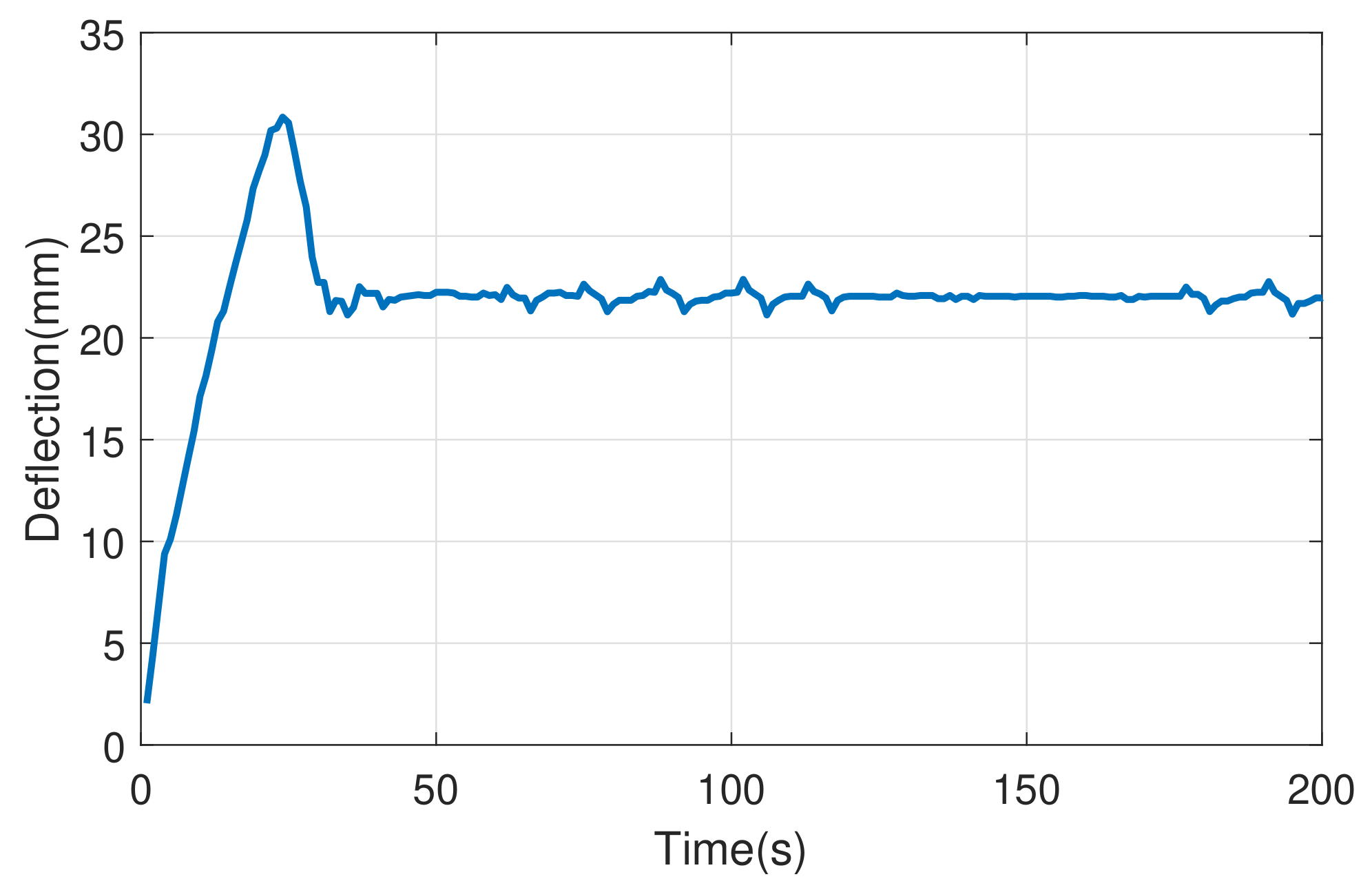
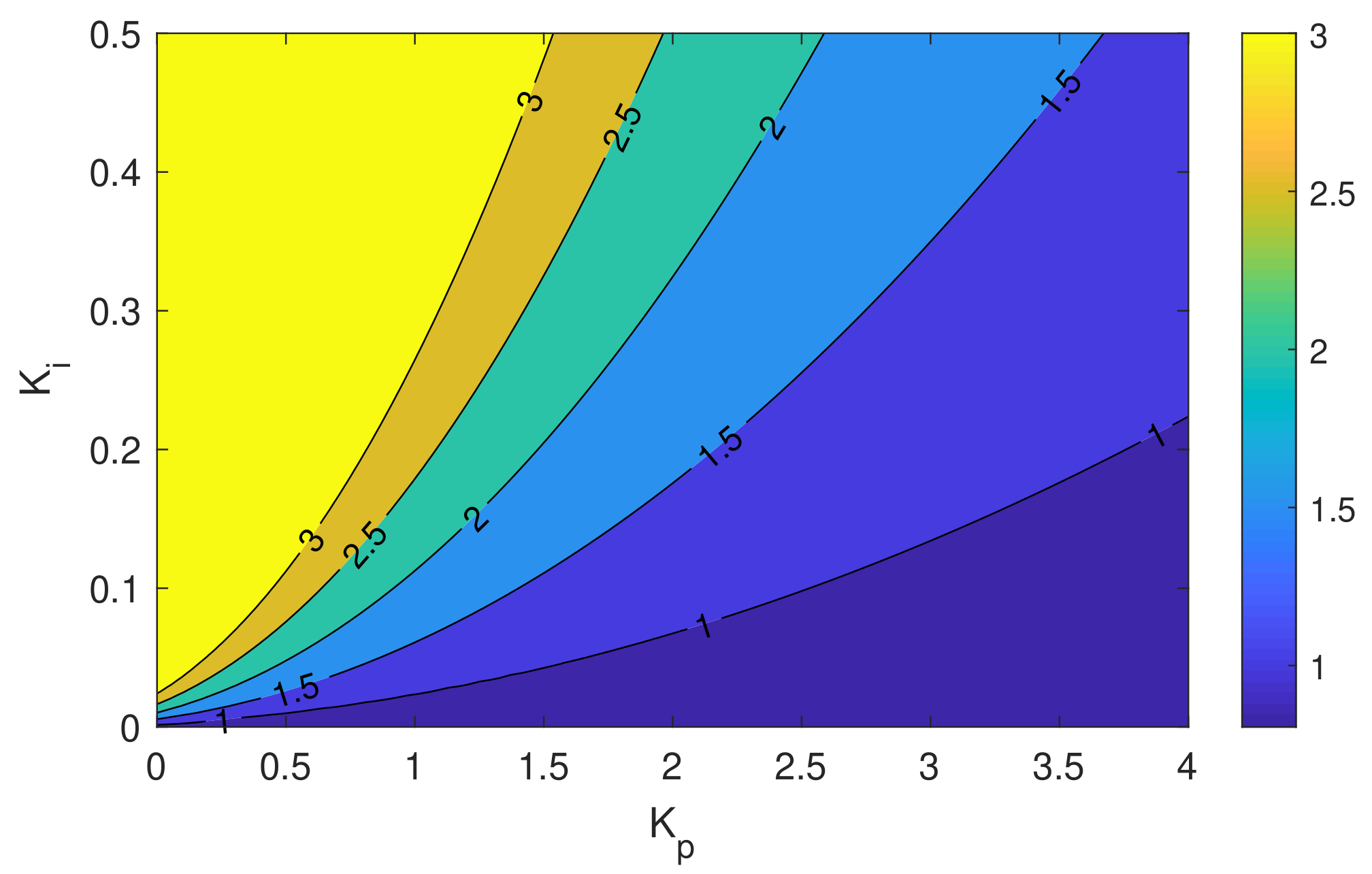
5.3. Robust PI Control
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hughes, J.; Culha, U.; Giardina, F.; Guenther, F.; Rosendo, A.; Iida, F. Soft manipulators and grippers: A review. Front. Robot. AI 2016, 3, 69. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft robotics: Review of fluid-driven intrinsically soft devices; manufacturing, sensing, control, and applications in human-robot interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Siddika, A.; Al Mamun, M.A.; Alyousef, R.; Amran, Y.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 100798. [Google Scholar] [CrossRef]
- Naser, M.; Hawileh, R.; Abdalla, J. Fiber-reinforced polymer composites in strengthening reinforced concrete structures: A critical review. Eng. Struct. 2019, 198, 109542. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.; Pua, G.; Jawaid, M.; Islam, M.S. A review on natural fiber reinforced polymer composite and its applications. Int. J. Polym. Sci. 2015, 2015, 243947. [Google Scholar] [CrossRef]
- Sohn, J.W.; Kim, G.W.; Choi, S.B. A state-of-the-art review on robots and medical devices using smart fluids and shape memory alloys. Appl. Sci. 2018, 8, 1928. [Google Scholar] [CrossRef]
- González García, C.; Meana Llorián, D.; Pelayo García-Bustelo, B.C.; Cueva Lovelle, J.M. A review about smart objects, sensors, and actuators. Int. J. Interact. Multimed. Artif. Intell. 2017, 4, 7–10. [Google Scholar] [CrossRef]
- Shian, S.; Bertoldi, K.; Clarke, D.R. Dielectric elastomer based “grippers” for soft robotics. Adv. Mater. 2015, 27, 6814–6819. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.; Lee, J.; Ahn, K.K. Continuous nonsingular terminal sliding-mode control of shape memory alloy actuators using time delay estimation. IEEE/ASME Trans. Mechatronics 2014, 20, 899–909. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Sreekumar, M.; Nagarajan, T.; Singaperumal, M.; Zoppi, M.; Molfino, R. Critical review of current trends in shape memory alloy actuators for intelligent robots. Ind. Robot. Int. J. 2007, 34, 285–294. [Google Scholar] [CrossRef]
- Tanaka, K.; Nagaki, S. A thermomechanical description of materials with internal variables in the process of phase transitions. Ingenieur-Archiv 1982, 51, 287–299. [Google Scholar] [CrossRef]
- Liang, C.; Rogers, C.A. One-dimensional thermomechanical constitutive relations for shape memory materials. J. Intell. Mater. Syst. Struct. 1997, 8, 285–302. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Preisach, F. Über die magnetische Nachwirkung. Z. Phys. 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Brokate, M.; Sprekels, J. Hysteresis operators. In Hysteresis and Phase Transitions; Springer: Berlin/Heidelberg, Germany, 1996; pp. 22–121. [Google Scholar]
- Al Janaideh, M.; Rakheja, S.; Su, C.Y. A generalized Prandtl–Ishlinskii model for characterizing the hysteresis and saturation nonlinearities of smart actuators. Smart Mater. Struct. 2009, 18, 045001. [Google Scholar] [CrossRef]
- Ljung, L. Perspectives on system identification. Annu. Rev. Control. 2010, 34, 1–12. [Google Scholar] [CrossRef]
- Isermann, R.; Münchhof, M. Identification of Dynamic Systems—An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Keshtkar, N.; Röbenack, K.; Fritzsche, K. Position Control of Textile-Reinforced Composites by Shape Memory Alloys. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 442–447. [Google Scholar]
- Cherif, C.; Hickmann, R.; Nocke, A.; Schäfer, M.; Röbenack, K.; Wießner, S.; Gerlach, G. Development and testing of controlled adaptive fiber-reinforced elastomer composites. Text. Res. J. 2018, 88, 345–353. [Google Scholar] [CrossRef]
- STMicroelectronics. L298; Dual Full-Bridge Driver–Datasheet; STMicroelectronics: Geneva, Switzerland, 2000. [Google Scholar]
- Sharp. GP2Y0A41SK0F, Distance MEasuring Sensor Unit, Measuring Distance: 4 to 30 Cm, Analog Output Type; Datasheet; Sharp: Osaka, Japan, 2011; Available online: https://global.sharp/products/device/lineup/data/pdf/datasheet/gp2y0a41sk_e.pdf (accessed on 14 January 2020).
- Röbenack, K. Mobile Robotics with Arduino: Design and Programming; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2018. [Google Scholar]
- Kurniawan, A. Getting Started with Matlab Simulink and Arduino; PE Press: Prešov, Slovakia, 2013. [Google Scholar]
- Hespanha, J.P. Linear Systems Theory, 2nd ed.; Princeton University Press: Princeton, NJ, USA; Exford, UK, 2018. [Google Scholar]
- Ljung, L. System Identification Toolbox™; The MathWorks, Inc.: Natick, MA, USA, 2012. [Google Scholar]
- O’Dwyer, A. Handbook of PI and PID cOntroller Tuning Rules; Imperial College Press: London, UK, 2009. [Google Scholar]
- Datta, A.; Ho, M.T.; Bhattacharyya, S.P. Structure and Synthesis of PID Controllers; Springer: London, UK, 2000. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Workman, M.L. Digital Control of Dynamic Systems, 3rd ed.; Addison-Wesley: Menlo Park, CA, USA, 1998. [Google Scholar]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Matušů, R.; Prokop, R.; Pekař, L. Parametric and unstructured approach to uncertainty modeling and robust stability analysis. Int. J. Math. Model. Methods Appl. Sci. 2011, 5, 1011–1018. [Google Scholar]
- Reinschke, K. Lineare Regelungs- und Steuerungstheorie, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2014. (In German) [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshtkar, N.; Röbenack, K. Unstructured Uncertainty Based Modeling and Robust Stability Analysis of Textile-Reinforced Composites with Embedded Shape Memory Alloys. Algorithms 2020, 13, 24. https://doi.org/10.3390/a13010024
Keshtkar N, Röbenack K. Unstructured Uncertainty Based Modeling and Robust Stability Analysis of Textile-Reinforced Composites with Embedded Shape Memory Alloys. Algorithms. 2020; 13(1):24. https://doi.org/10.3390/a13010024
Chicago/Turabian StyleKeshtkar, Najmeh, and Klaus Röbenack. 2020. "Unstructured Uncertainty Based Modeling and Robust Stability Analysis of Textile-Reinforced Composites with Embedded Shape Memory Alloys" Algorithms 13, no. 1: 24. https://doi.org/10.3390/a13010024
APA StyleKeshtkar, N., & Röbenack, K. (2020). Unstructured Uncertainty Based Modeling and Robust Stability Analysis of Textile-Reinforced Composites with Embedded Shape Memory Alloys. Algorithms, 13(1), 24. https://doi.org/10.3390/a13010024





