An Improved Multiobjective Particle Swarm Optimization Based on Culture Algorithms
Abstract
:1. Introduction
2. Preliminary
2.1. Cultural Algorithms
2.2. Multiobjective Optimization Problems
s.t.g(x) ≤ 0, h(x) = 0
2.3. Particle Swam Optimization
| Algorithm 1. The Procedure of Particle Swarm Optimization (PSO) |
| (1) Calculate the fitness function of each particle. |
| (2) Update p and p. |
| (3) Update the velocity and position of each particle. |
| (4) If the stop criterion is not met, go to (1), else p is the best position |
3. The Proposed Algorithm
3.1. Three Kinds of Knowledge Based on Population
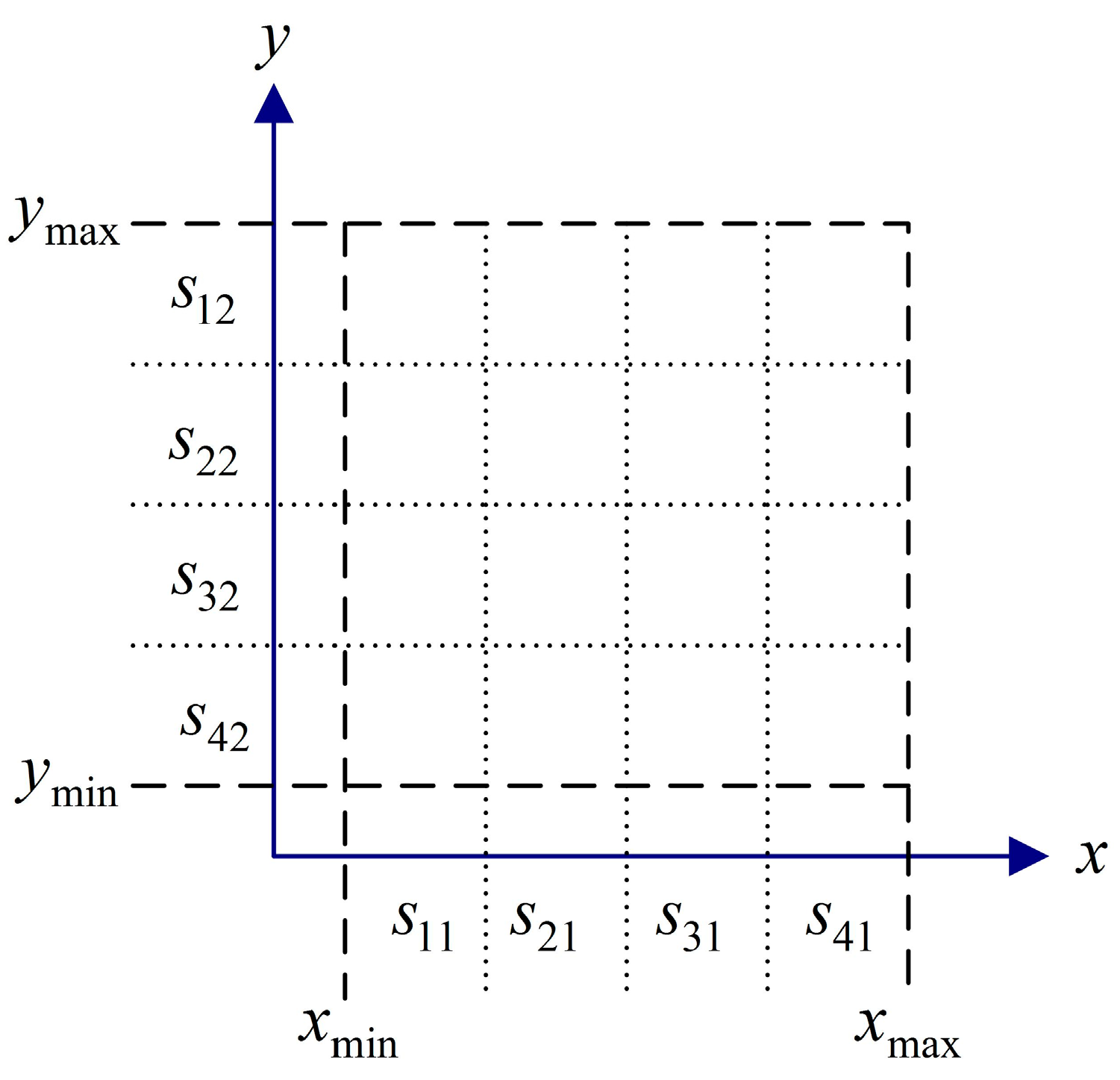
3.2. Personal Guide
| Algorithm 2. The Detailed Procedure of A Personal Guide |
| For the d-th dimension of the i-th particle, |
| (1) bn+1 = max({pbestid|i = 1, 2, …, n}); |
| b1 = min({pbestid|i = 1, 2, …, n}); |
| bi = b1 + (bn+1 – b1)·(i – 1)/n, i = 2, 3, …, n |
| (2) si = rand(bi, bi+1); |
| (3) Replace x with si and get a new particle |
| (4) If the newly generated particle dominates xi, then it replaces xi; break; |
| if not, the newly generated particle is discarded |
3.3. Global Guide
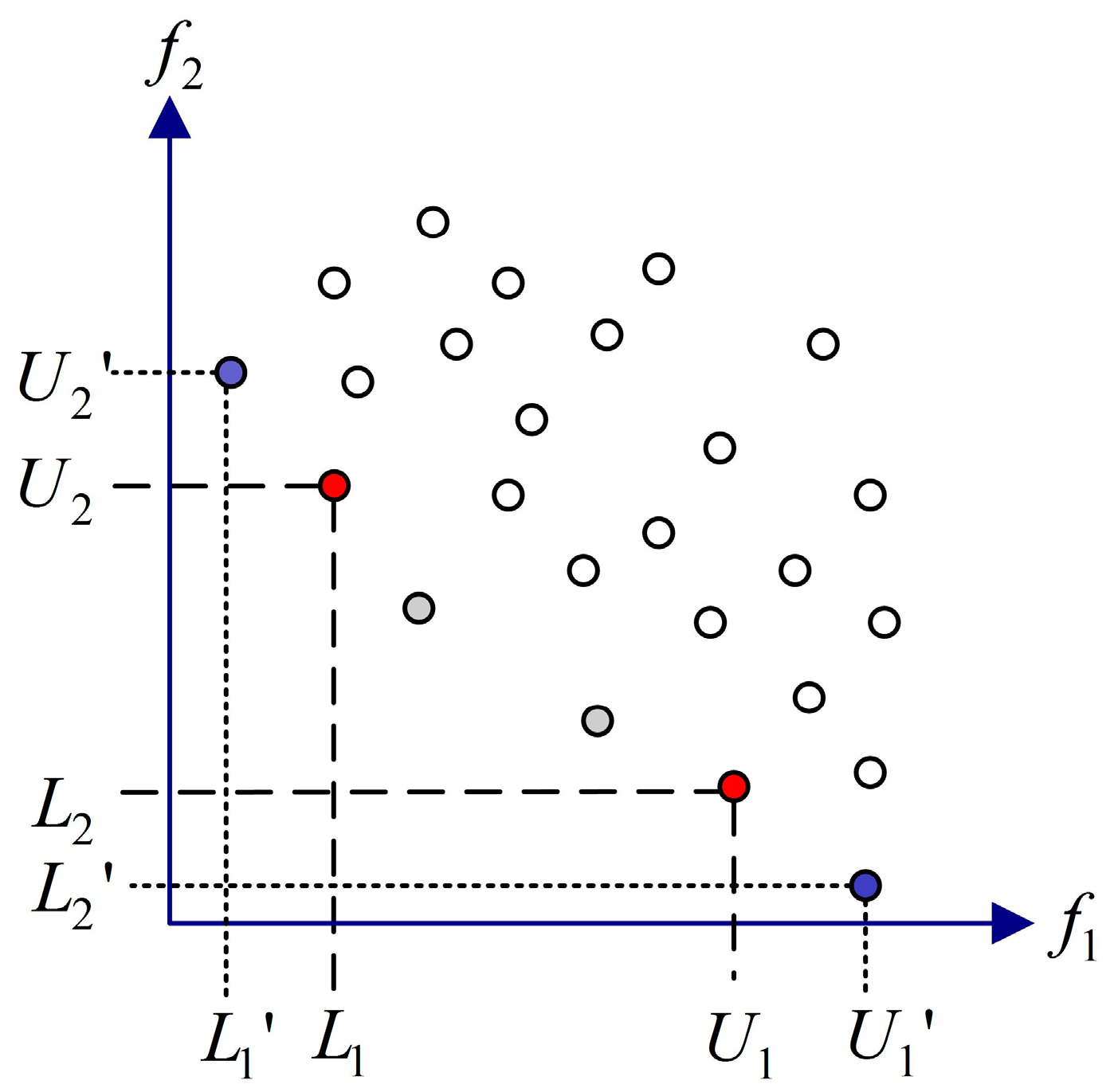
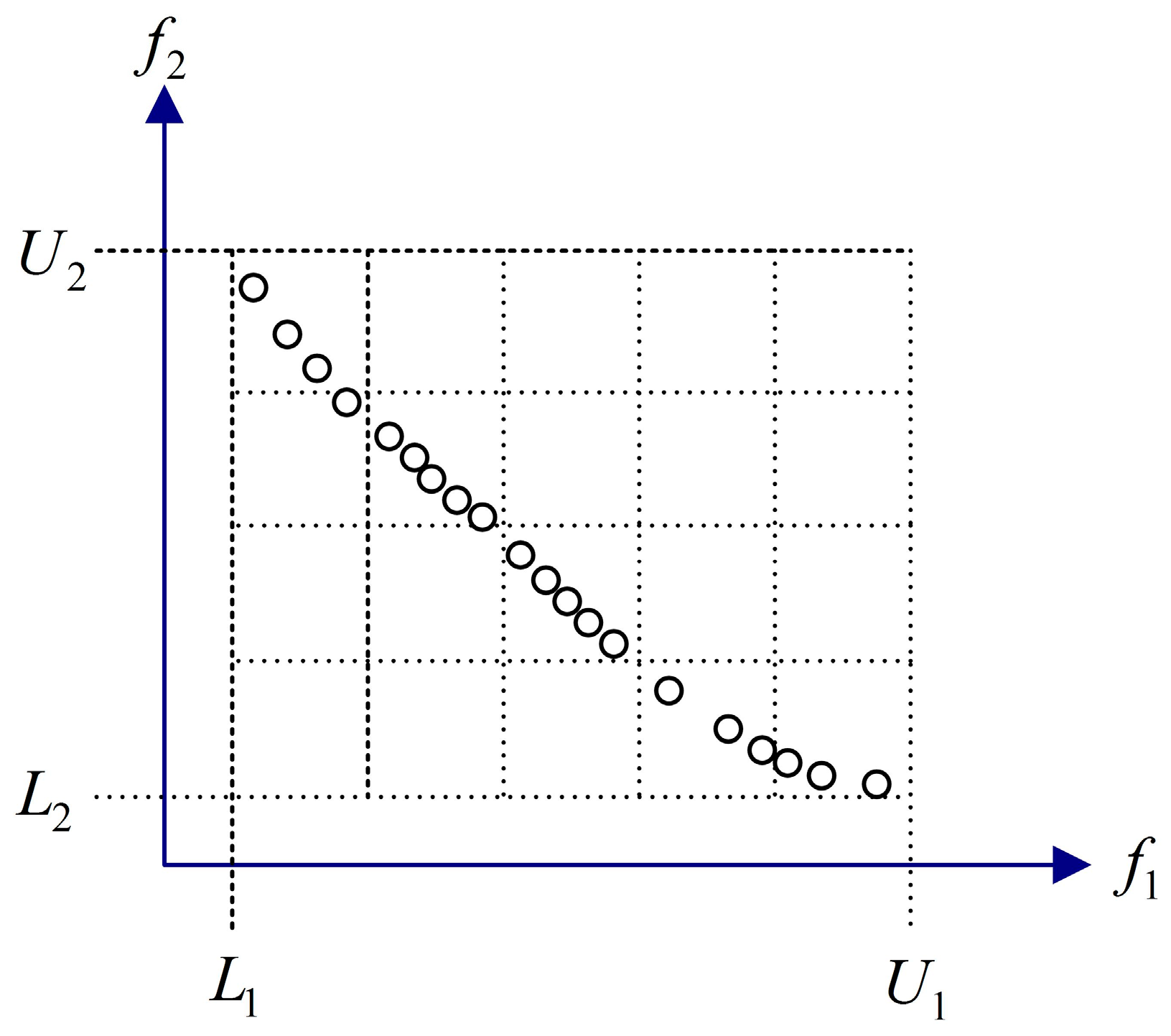
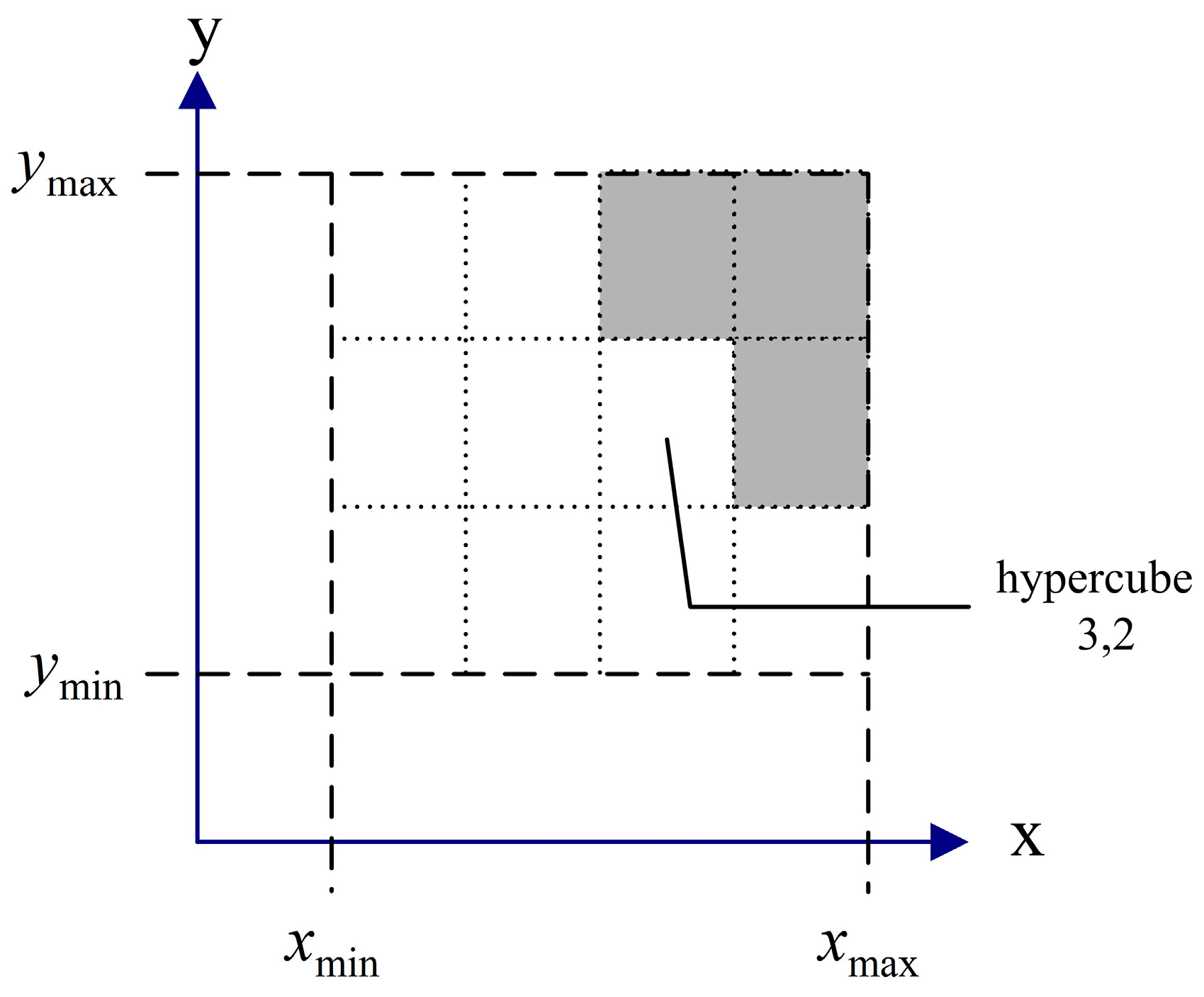
3.4. Dominate Criteria Based on the Hypercube
3.5. Mutation Operator
3.6. Updating the Repository
| Algorithm 3. The Update Function of the Dominance Archive |
| Suppose element f’ is a new element that is to be judged whether to enter the repository (rep). |
| (1) Input rep, f |
| (2) If ¬f’ rep:hypercube(f)hypercube(f’) then rep = rep∪{f}E |
| (3) If f’:hypercube(f’) = hypercube(f)∩fε + f’ then rep = rep∪{f}f’ |
| (4) If ¬f’:hypercube(f’) = hypercube(f)∪hypercube(f’)hypercube(f), then rep = rep∪{f} |
| (5) Output rep |
4. Experiments
4.1. Quantitative Performance Evaluations
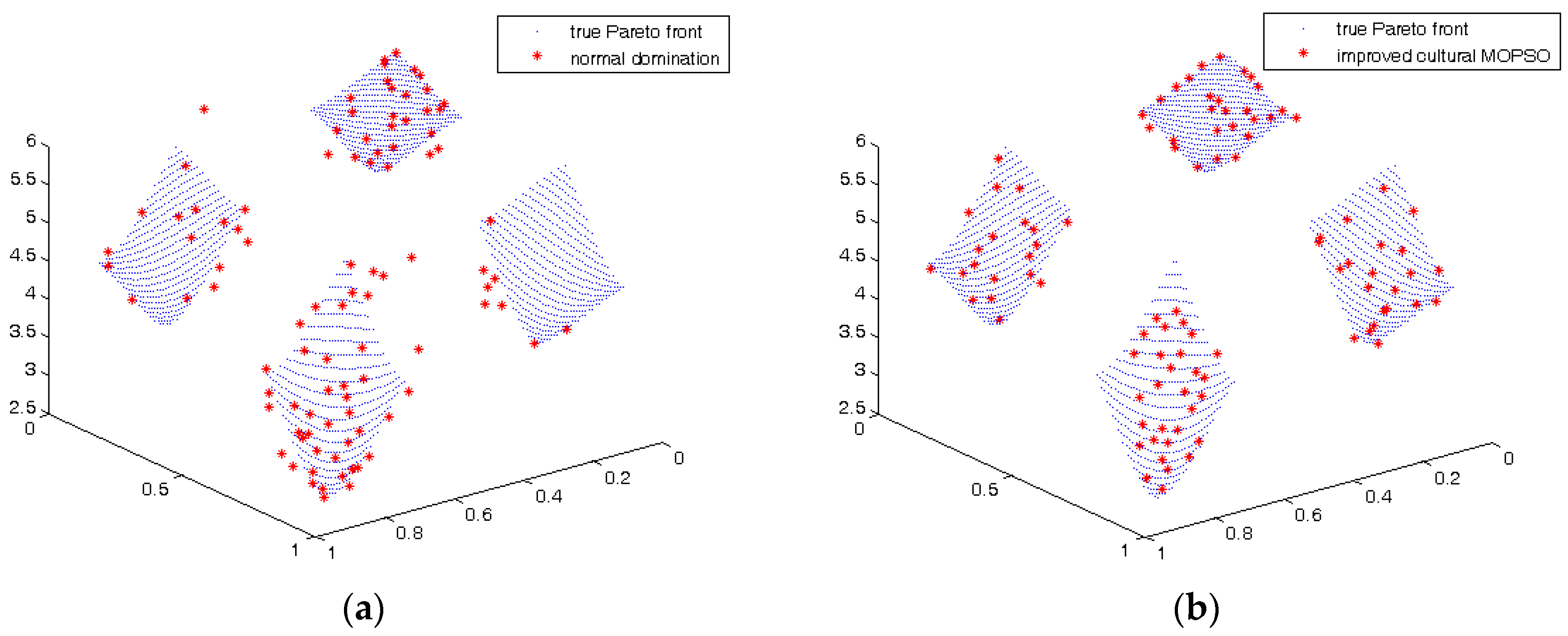
4.2. Comparison of the Results Using Hypercube-Based -Domination and Normal Domination Hypervolume
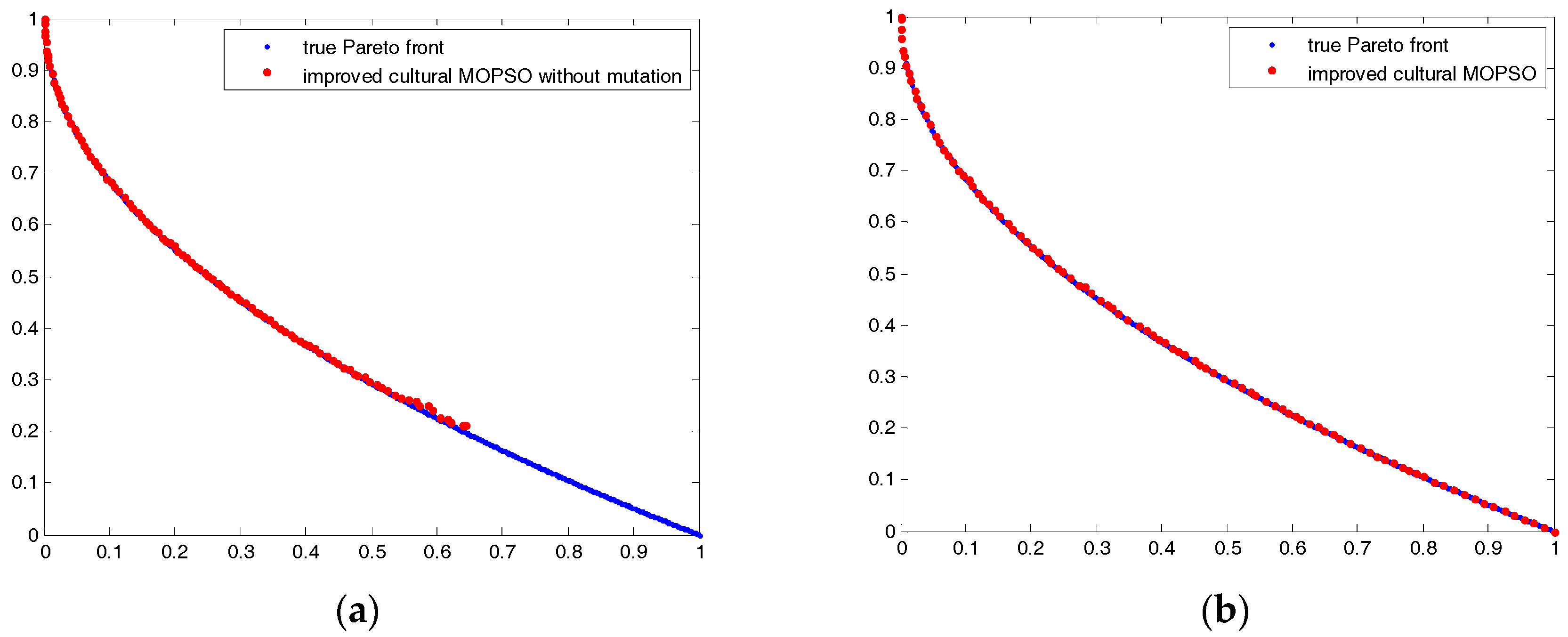
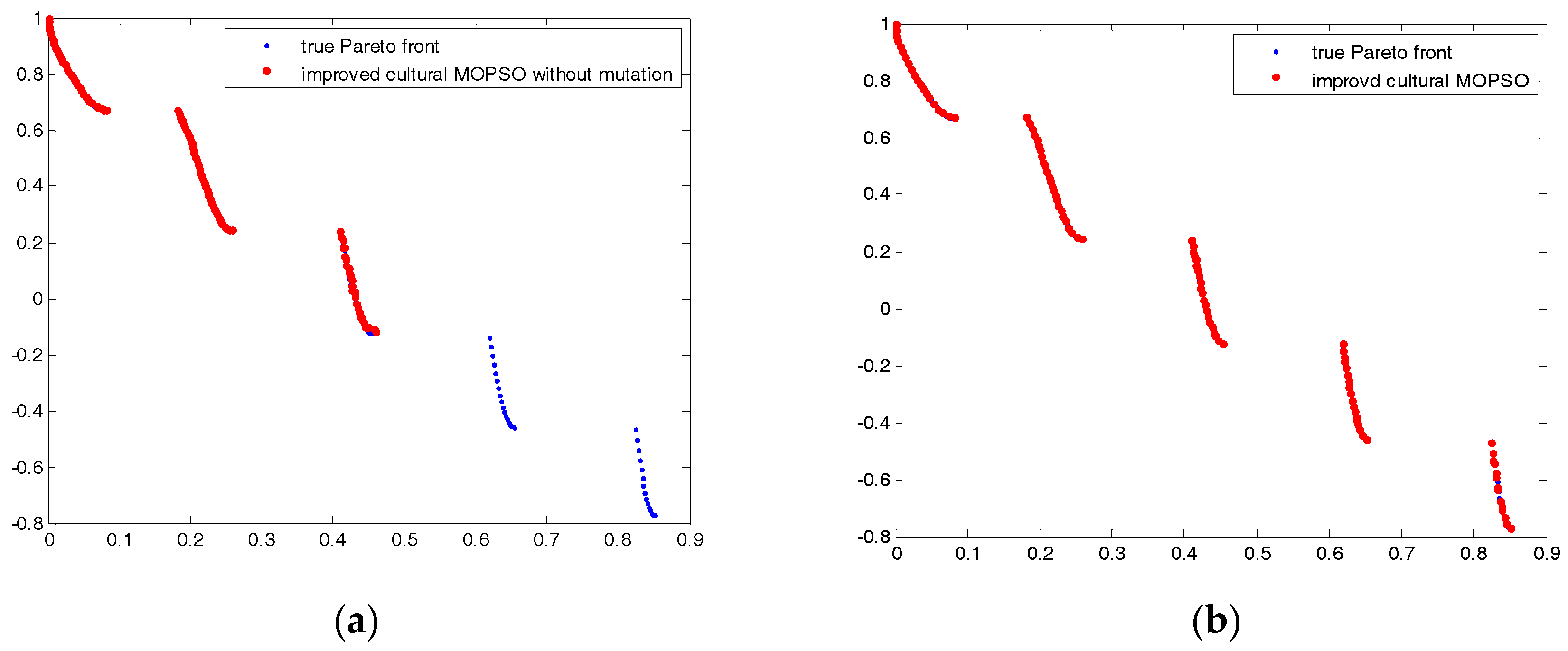
4.3. Comparison of the Result with and without the Mutation Operator
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, T.; Jiao, L.; Ma, W.; Ma, J.; Shang, R. A new quantum-Behaved particle swarm optimization based on cultural evolution mechanism for multiobjective problems. Appl. Soft Comput. 2016, 46, 267–283. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: Nsga-ii. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. Spea2: Improving the strength pareto evolutionary algorithm. In Proceedings of the Evolution Methods Design Optimization Control Applications Industrial Problems, Zurich, Switzerland, 1 May 2002. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lechuga, M.S. Mopso: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12 May 2002. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multi-Objective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Liu, H.; Gu, F.; Zhang, Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. Evol. Comput. 2014, 18, 450–455. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Raquel, C.R.; Naval, P.C. An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005. [Google Scholar]
- Pulido, G.T.; Coello, C.A.C. Using clustering techniques to improve the performance of a particle swarm optimizer. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Seattle, WA, USA, 26–30 June 2004. [Google Scholar]
- Mostaghim, S.; Teich, J. Strategies for finding good local guides in multi-Objective particle swarm optimization (MOPSO). In Proceedings of the IEEE Swarm Intelligence Symposium (SIS 2003), Los Alamitos, CA, USA, 26 April 2003; IEEE Computer Society Press: Indianapolis, IN, USA, 2003. [Google Scholar] [CrossRef]
- Branke, J.; Mostaghim, S. About Selecting the Personal Best in Multi-Objective Particle Swarm Optimization. In Proceedings of the Parallel Problem Solving From Nature (PPSN Ix) International Conference, Reykjavik, Iceland, 9–13 September 2006. [Google Scholar]
- Coello, C.A.C.; Becerra, R.L. Evolutionary multiobjective optimization using a cultural algorithm. In Proceedings of the Swarm Intelligence Symposium, Indianapolis, IN, USA, 24 April 2003. [Google Scholar]
- Daneshyari, M.; Yen, G.G. Cultural-Based multiobjective particle swarm optimization. IEEE Trans. Syst. Man Cybern. 2011, 41, 553–567. [Google Scholar] [CrossRef] [PubMed]
- Daneshyari, M.; Yen, G.G. Constrained Multiple-Swarm Particle Swarm Optimization within a Cultural Framework. IEEE Trans. Syst. Man Cybern. 2012, 42, 475–490. [Google Scholar] [CrossRef]
- Daneshyari, M.; Yen, G.G. Cultural-Based particle swarm for dynamic optimisation problems. Int. J. Syst. Sci. 2011, 43, 1–21. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K. Combining Convergence and Diversity in Evolutionary Multiobjective Optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef] [PubMed]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Tang, L.; Wang, X. A Hybrid Multiobjective Evolutionary Algorithm for Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2013, 17, 20–45. [Google Scholar] [CrossRef]
- Yu, G. Multi-Objective estimation of Estimation of Distribution Algorithm based on the Simulated binary Crossover. J. Converg. Inf. Technol. 2012, 7, 110–116. [Google Scholar]
- Hadka, D.; Reed, P. Borg: An Auto-Adaptive Many-Objective Evolutionary Computing Framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef] [PubMed]
- Gee, S.B.; Arokiasami, W.A.; Jiang, J. Decomposition-Based multi-Objective evolutionary algorithm for vehicle routing problem with stochastic demands. Soft Comput. 2016, 20, 3443–3453. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Ding, Z. A bare-Bones multi-Objective particle swarm optimization algorithm for environmental/economic dispatch. Inf. Sci. 2012, 192, 213–227. [Google Scholar] [CrossRef]
- Hu, W.; Yen, G.G.; Zhang, X. Multiobjective particle swarm optimization based on Pareto entropy. Ruan Jian Xue Bao/J. Softw. 2014, 25, 1025–1050. (In Chinese) [Google Scholar]
- Peng, B.; Reynolds, R.G. Cultural algorithms: Knowledge learning in dynamic environments. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 1751–1758. [Google Scholar]
- Coello, C.A.C.; Veldhuizen, D.A.V.; Lamont, G.B. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Kluwer Academic Publishers: New York, NY, USA, 2007; pp. 1–19. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Li, L.M.; Lu, K.D.; Zeng, G.Q.; Wu, L.; Chen, M.-R. A novel real-Coded population-Based extremal optimization algorithm with polynomial mutation: A non-Parametric statistical study on continuous optimization problems. Neurocomputing 2016, 174, 577–587. [Google Scholar] [CrossRef]
- Chen, Y.; Zou, X.; Xie, W. Convergence of multi-Objective evolutionary algorithms to a uniformly distributed representation of the Pareto front. Inf. Sci. 2011, 181, 3336–3355. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Ratnaweera, A.; Halgamuge, S.; Watson, H.C. Self-Organizing hierarchical particle swarm optimizer with time-Varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective Optimization Using Evolutionary Algorithms—A Comparative Case Study. In Proceedings of the Conference on Parallel Problem Solving from Nature (PPSN V), Amsterdam, The Netherlands, 27–30 September 1998; Agoston, E.E., Thomas, B., Marc, S., Schwefel, H.-P., Eds.; Springer: Berlin /Heidelberg, Germany, 1998. [Google Scholar]


| Test Functions | MOPSO | IC MOPSO | Cultural MOQPSO | Cultural MOPSO | NSGA-II | CD MOPSO | |
|---|---|---|---|---|---|---|---|
| ZDT1 | mean | 5.56 × 10−1 | 8.73 × 10−1 | 8.42 × 10−1 | 8.66 × 10−1 | 8.11 × 10−1 | 8.74 × 10−1 |
| standard deviation (std) | 9.03 × 10−2 | 5.38 × 10−3 | 8.01 × 10−2 | 7.00 × 10−3 | 8.46 × 10−3 | 4.76 × 10−3 | |
| p-value | 8.42 × 10−2 | 3.72 × 10−2 | 8.82 × 10−5 | 6.65 × 10−40 | 6.25 × 10−1 | ||
| ZDT2 | mean | 2.88 × 10−1 | 5.38 × 10−1 | 4.72 × 10−1 | 4.20 × 10−1 | 1.20 × 10−1 | 5.37 × 10−1 |
| std | 1.19 × 10−1 | 7.88 × 10−3 | 1.07 × 10−1 | 1.91 × 10−1 | 2.22 × 10−2 | 6.43 × 10−3 | |
| p-value | 1.69 × 10−16 | 1.40 × 10−3 | 1.31 × 10−5 | 6.53 × 10−66 | 8.25 × 10−1 | ||
| ZDT3 | mean | 1.00 | 1.01 | 9.39 × 10−1 | 7.61 × 10−1 | 7.60 × 10−1 | 1.01 |
| std | 5.17 × 10−3 | 4.01 × 10-3 | 1.43 × 10−1 | 4.00 × 10−1 | 1.31 × 10−2 | 4.37 × 10−3 | |
| p-value | 1.72 × 10−7 | 0.0110 | 1.35 × 10−3 | 2.35 × 10−66 | 8.76 × 10−1 | ||
| ZDT4 | mean | 0.00 | 8.71 × 10−1 | 8.67 × 10-1 | 0.00 | 3.66 × 10−1 | 0.00 |
| std | 0.00 | 6.08 × 10−3 | 5.18 × 10−3 | 0.00 | 1.77 × 10−1 | 0.00 | |
| p-value | 1.80 × 10−118 | 1.59 × 10−2 | 1.80 × 10−118 | 1.80 × 10−118 | 1.80 × 10−118 | ||
| ZDT6 | mean | 4.94 × 10−1 | 5.04 × 10−1 | 4.65 × 10−1 | 5.03 × 10−1 | 0.00 | 5.05 × 10−1 |
| std | 7.43 × 10−3 | 4.88 × 10−3 | 1.12 × 10−1 | 7.63 × 10−3 | 0.00 | 5.77 × 10−3 | |
| p-value | 5.97 × 10−08 | 6.31 × 10−2 | 8.61 × 10−1 | 3.40 × 10−110 | 8.76 × 10−1 | ||
| DTLZ1 | mean | 0.00 | 1.30 | 1.30 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 2.02 × 10−3 | 3.07 × 10−3 | 0.00 | 0.00 | 0.00 | |
| p-value | 2.90 × 10−156 | 6.44 × 10−1 | 2.90 × 10−156 | 2.90 × 10−156 | 2.90 × 10−156 | ||
| DTLZ2 | mean | 6.74 × 10-1 | 7.15 × 10−1 | 4.27 × 10−1 | 2.46 × 10−1 | 6.93 × 10−1 | 7.20 × 10−1 |
| std | 1.50 × 10−2 | 9.74 × 10−3 | 2.41 × 10−2 | 1.26 × 10−2 | 8.35 × 10−3 | 8.12 × 10−3 | |
| p-value | 4.76 × 10−18 | 3.83 × 10−54 | 1.33 × 10−78 | 3.17 × 10−13 | 3.85 × 10−2 | ||
| DTLZ3 | mean | 0.00 | 7.16 × 10−1 | 7.15 × 10−1 | 0.00 | 0.00 | 0.00 |
| std | 0.00 | 7.63 × 10−3 | 9.61 × 10−3 | 0.00 | 0.00 | 0.00 | |
| p-value | 8.20 × 10−108 | 9.47 × 10−1 | 8.20 × 10−108 | 8.20 × 10−108 | 8.20 × 10−108 | ||
| DTLZ4 | mean | 6.82 × 10−1 | 7.29 × 10−1 | 5.46 × 10−1 | 1.67 × 10−1 | 6.65 × 10−1 | 7.22 × 10−1 |
| std | 1.56 × 10−2 | 7.45 × 10−3 | 5.70 × 10−2 | 6.76 × 10−2 | 3.11 × 10−2 | 8.74 × 10−3 | |
| p-value | 1.55 × 10−21 | 9.53 × 10−25 | 6.11 × 10−47 | 9.22 × 10−16 | 8.66 × 10−4 | ||
| DTLZ5 | mean | 4.34 × 10−1 | 4.39 × 10−1 | 4.35 × 10−1 | 2.43 × 10−1 | 4.38 × 10−1 | 4.38 × 10−1 |
| std | 6.21 × 10−3 | 4.94×10−3 | 8.00 × 10−3 | 4.96 × 10−3 | 5.74 × 10−3 | 5.86 × 10−3 | |
| p-value | 1.65 × 10−3 | 3.72 × 10−2 | 2.13 × 10−77 | 5.64 × 10−1 | 3.14 × 10−1 | ||
| DTLZ6 | mean | 4.29 × 10−1 | 4.40×10−1 | 4.21 × 10−1 | 2.36 × 10−1 | 0.00 | 4.39 × 10−1 |
| std | 6.99 × 10−3 | 5.97×10−3 | 7.53 × 10−3 | 2.81 × 10−2 | 0.00 | 6.85 × 10−3 | |
| p-value | 1.43 × 10−8 | 5.64 × 10−15 | 3.58 × 10−43 | 9.89 × 10−102 | 6.28 × 10−1 | ||
| DTLZ7 | mean | 1.27 | 1.43 | 1.21 | 5.44 × 10−1 | 1.47 × 10−1 | 1.38 |
| std | 2.93 × 10−2 | 3.20 × 10−2 | 4.10 × 10−2 | 8.36 × 10−2 | 4.43 × 10−2 | 4.25 × 10−2 | |
| p-value | 1.19 × 10−28 | 2.91 × 10−31 | 1.98 × 10−51 | 5.57 × 10−73 | 5.54 × 10−6 | ||
| Better/similar/worse | 12/0/0 | 9/3/0 | 11/1/0 | 11/1/0 | 5/6/1 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Zhu, H. An Improved Multiobjective Particle Swarm Optimization Based on Culture Algorithms. Algorithms 2017, 10, 46. https://doi.org/10.3390/a10020046
Jia C, Zhu H. An Improved Multiobjective Particle Swarm Optimization Based on Culture Algorithms. Algorithms. 2017; 10(2):46. https://doi.org/10.3390/a10020046
Chicago/Turabian StyleJia, Chunhua, and Hong Zhu. 2017. "An Improved Multiobjective Particle Swarm Optimization Based on Culture Algorithms" Algorithms 10, no. 2: 46. https://doi.org/10.3390/a10020046
APA StyleJia, C., & Zhu, H. (2017). An Improved Multiobjective Particle Swarm Optimization Based on Culture Algorithms. Algorithms, 10(2), 46. https://doi.org/10.3390/a10020046






