Optimization of Microwave-Based Heating of Cellulosic Biomass Using Taguchi Method

1. Introduction

2. Methods

2.1. Microwave-Based Heating Device

This study used a closed pressure vessel as a heat receiver, in which the microwave-based heating system consists of a microwave-based heating cavity and a control system. Four temperature sensors were installed to monitor temperature variations. The experiment employed the Taguchi method to determine the effect of the water volume of the closed vessel, the heating power and Pennisetum purpureum heating mass of the closed pressure vessel, in order to ascertain the optimal parameters of the factors, and to find out the effects of the parameters on the heating quality and variation in characteristics of the parameters.

After the optimal heating conditions were determined, the experiment was performed, and the input power and output (temperature) data were recorded. Next, the system identification method was used to construct the equation that conforms to the actual system.

The microwave-based heating device used in this study is a SAMPO RE-115M type, which was modified as required by the experiment. The measuring equipment is shown in Figure 1.

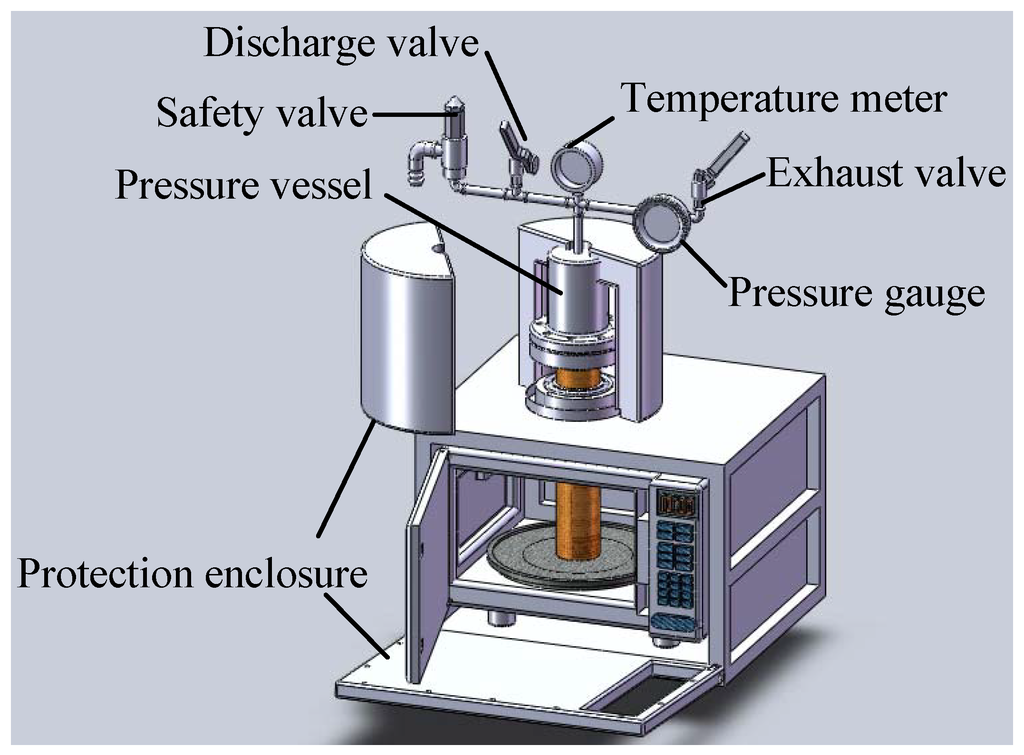
Figure 1. Microwave-based heating device and measuring equipment.

2.2. Taguchi Method

In pretreatment with steam explosion, the main operating conditions affecting the product composition include temperature and processing time [16], while improper treatment may affect the subsequent catalysis of the cellulase enzyme and the alcoholic fermentation [17]. This study heated lignocellulose (Pennisetum purpureum) to 190 °C [10], and used the optimal combination of parameters, as determined by the Taguchi method, to reduce the parameter combination variations.

The Taguchi method can improve product quality by reducing the impact of factor variations, while using orthogonal arrays to reduce experiment frequency. Firstly, signal to noise ratio (S/N) is determined in terms of quality characteristics; secondly, S/N is used to evaluate the quality characteristics of different parameter combinations, and predict the optimal parameter combination; finally, verification experiments are conducted to show that the predicted combination can reduce the parameter variations and achieve the quality characteristics. The Taguchi method flow is as shown in Figure 2.

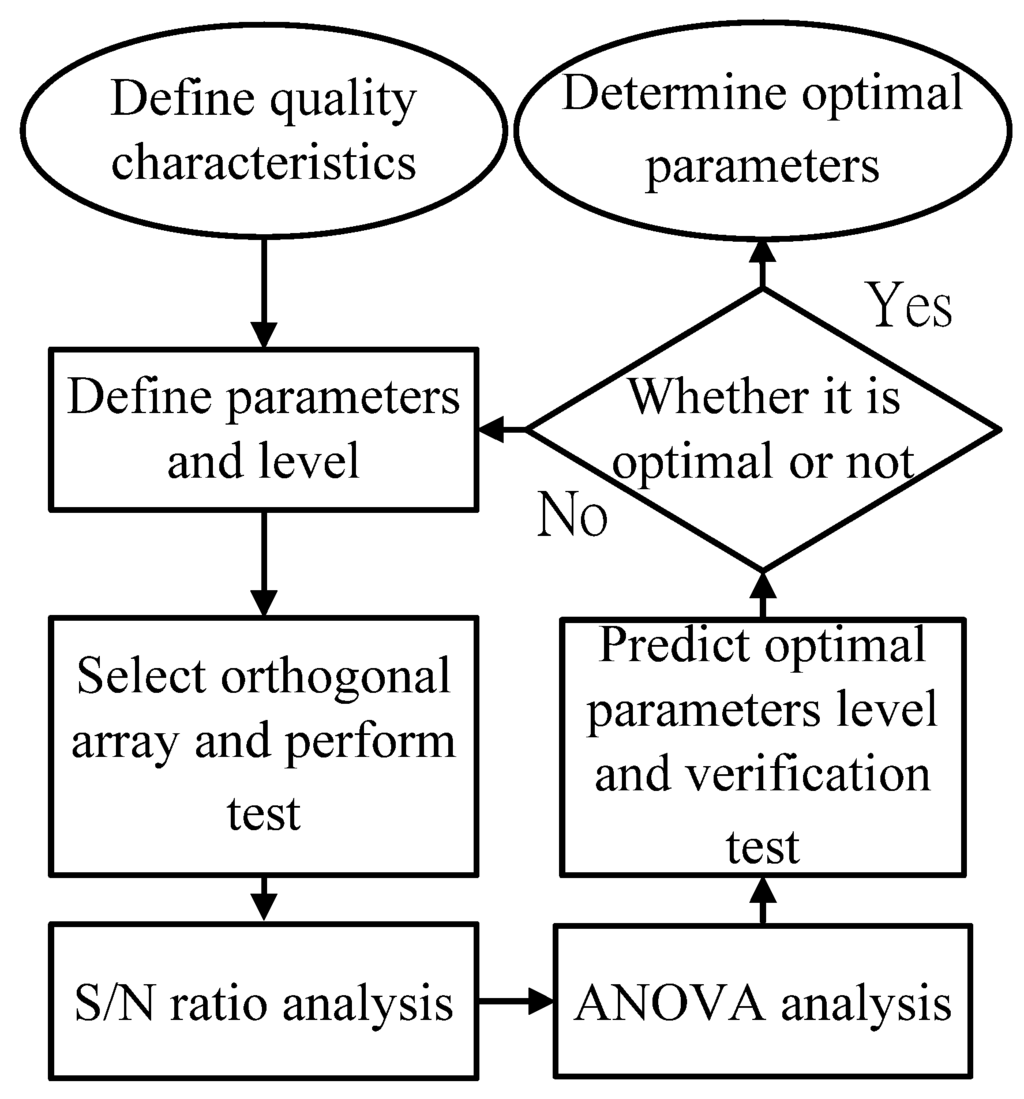
Figure 2. Taguchi method flow.

2.2.1. Define Quality Characteristics

In the experimental design of the Taguchi method, objective functions need to be identified to properly express the quality characteristics. This study shows how to make the vessel in a microwave-based heating device reach a specified temperature of 190 °C in the shortest time by changing the set parameters [10]. As required, it is better to heat the object to 190 °C with microwave-based heating within a short time. Thus, smaller-the-better is used as the method for calculating the experimental results of the quality characteristics. The S/N ratio for smaller-the-better is defined in Equation (1).

(1)

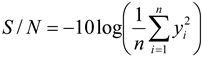where, y_i is the value of the i experiment in each group, and n is the frequency of experiment in each group.

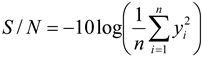
The microwave-based heating device in this experiment is 1 kW, and the input power of the cavity is set to 100%, 70%, and 50%. The working state diagram is as shown in Figure 3.

Figure 3. State diagram of microwave-based heating power.

2.2.2. Define Parameters and Level

For any product or process, a relational diagram of quality characteristics is plotted, as shown in Figure 4 [18,19], and such quality characteristics represent the response values to be discussed. The parameters affecting quality characteristics can be divided into signal factors, control factors, and interference factors. The signal factor and response value have input and output relations, and thus, the signal factor is the input of electric power; the control factor is an important factor of quality characteristics’ optimization. The control factors include the water volume of the vessel, heating power setting, and Pennisetum purpureum mass. The interference factor is an uncontrolled parameter, which cannot be determined for a special case, and is represented by heat loss. The parameter levels of the control factors in this study are as shown in Table 1.

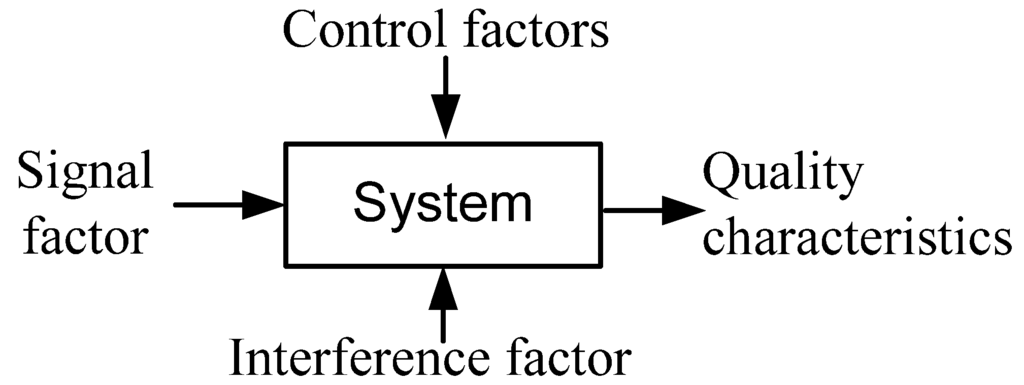
Figure 4. State diagram of microwave-based heating power.

Table 1. Level of control factor parameters.

Table 1. Level of control factor parameters.

Description	Level 1	Level 2	Level 3
Water volume of vessel (mL)	100	150	200
Power setting (kW)	0.5	0.7	1
Pennisetum purpureum mass (g)	5	10	15

2.3. System Identification

The system identification inputs the signal of the actual system to deduce an approximate difference equation, or differential equation, to construct a system mathematical model. This study applied microwave-based heating to the pretreatment of biomass material, with water and Pennisetum purpureum in the vessel. If the model is constructed using a physical method, in addition to the electric power converted into the microwave gain, microwave distribution in the heating cavity, as well as the speed of water molecules absorbing microwave energy, should be considered. It is too complex to use a general differential equation for model construction; thus, the system has to be considered as a black box. Input and output signals were used to construct the approximate difference equation or differential equation through system identification [20,21]. The system identification flow is as shown in Figure 5.

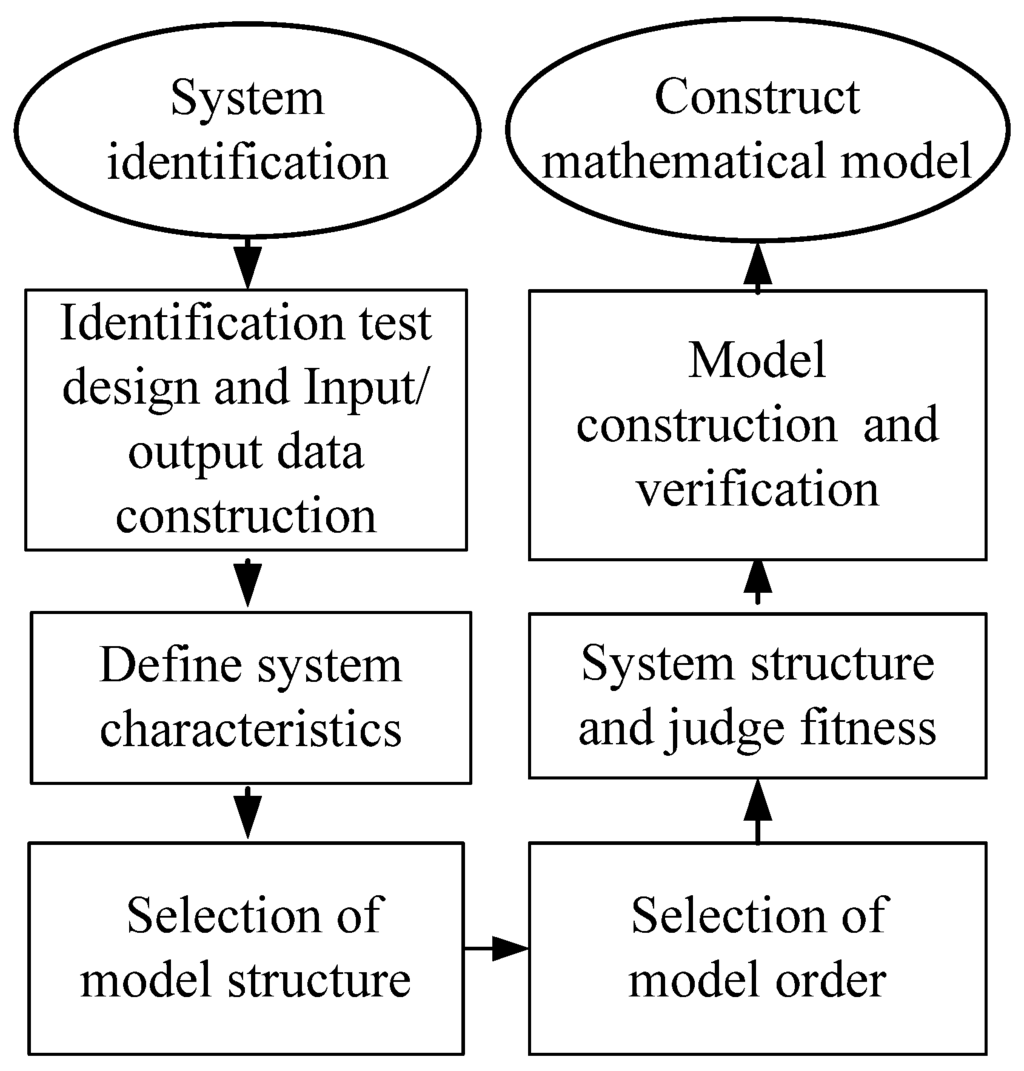
Figure 5. System identification flow chart.

3. Results and Discussion

3.1. Parameter Optimization Experiment Using the Taguchi Method

3.1.1. Orthogonal Arrays

With the orthogonal arrays in the Taguchi method, it is intended to use a low number of experiments to obtain useful statistical information. The representation method for orthogonal arrays is La (n^w), where L is the Latin squares of the orthogonal array, a is the number of experiments, n is the number of factor levels, and w is the number of control factors. In selecting orthogonal arrays, the total degrees of freedom of the control factors must first be calculated. One factor has three levels, and the degree of freedom is two (number of levels −1 = dofj). In this experiment, the number of levels is three control factors, and the total degree of freedom is 8 (dof_T = a − 1 = m), which defines that the number of experiments using the selected orthogonal arrays should not be smaller than eight. The orthogonal array planning and the experimental data of L₉(3³) experiment are as listed in Table 2.

Table 2. L₉(3³) orthogonal arrays.

Table 2. L₉(3³) orthogonal arrays.

No.	Water volume (mL)	Power setting (kW)	Pennisetum purpureum mass(g)	Heating time (min)	S/N ratio (db)
1	1	1	1	27.5	−28.787
2	1	2	2	46	−33.255
3	1	3	3	55	−34.807
4	2	1	2	36	−31.126
5	2	2	3	48	−33.625
6	2	3	1	33.76	−30.568
7	3	1	3	44	−32.869
8	3	2	1	42	−32.465
9	3	3	2	38	−31.596

3.1.2. Analyze Mean Value

The S/N ratio in the experiment can be calculated, which is then used to create a response table and plot a response diagram. The influence of the factors on the system can be calculated using the data in Table 2 to create the response table and plot the response diagram of the factors. The response value of the S/N ratio of each factor is calculated in Equation (2), and the calculated data are shown in Table 3.

(2)

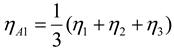where, η_A1 is the response value of S/N ratio of 1 level of factor A, η₁, η₂ and η₃ is the response value of S/N ratio of No.1, No.2, No.3 respectively.

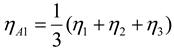
• Average S/N for A (water volume of vessel):
• average S/N for A1 = [(−28.787) + (−33.255) + (−34.807)]/3 = −32.28
• average S/N for A2 = [(−31.126) + (−33.625) + (−30.568)]/3 = −31.77
• average S/N for A3 = [(−32.869) + (−32.465) + (−31.596)]/3 = −32.31
• Average S/N for B (heating power):
• average S/N for B1 = [(−28.787) + (−31.126) + (−32.869)]/3 = −30.93
• average S/N for B2 = [(−33.255)+(−33.625) + (−32.465)]/3 = −33.11
• average S/N for B3 = [(−34.807) + (−30.568) + (−31.596)]/3 = −32.32
• Average S/N for C (Pennisetum purpureum):
• average S/N for C1 = [(−28.787) + (−30.568) + (−32.465)]/3 = −30.61
• average S/N for C2 = [(−33.255) + (−31.126) + (−31.596)]/3 = −32.99
• average S/N for C3 = [(−34.807) + (−33.625) + (−32.869)]/3 = −33.77

The quality characteristic is the smaller-the-better, thus, the quality characteristics are better when the experimental result of the S/N ratio is closer to zero. Based on the results in Table 3 and Figure 6, the optimal parameter level can be predicted as the water volume of the vessel is 150 mL, heating power is 0.5 kW, and mass of Pennisetum purpureum is 5 g. The optimal parameter combination of the microwave-based heating is A2 B1 C1. Based on the response in Table 3, the degree of contribution of the parameters to the system can be calculated. The calculation method is to subtract the S/N maximum level of each factor from the S/N ratio of the minimum level of each factor. The contribution degree of parameters is C > B > A.

Table 3. Integration results of response in Taguchi experiments.

Table 3. Integration results of response in Taguchi experiments.

Level	Water volume(A)	Power setting(B)	Pennisetum purpureum mass (C)
1	−32.28	−30.93	−30.61
2	−31.77	−33.11	−32.99
3	−32.31	−32.32	−33.77
Effect	0.54	2.18	3.16
Rank	3	2	1

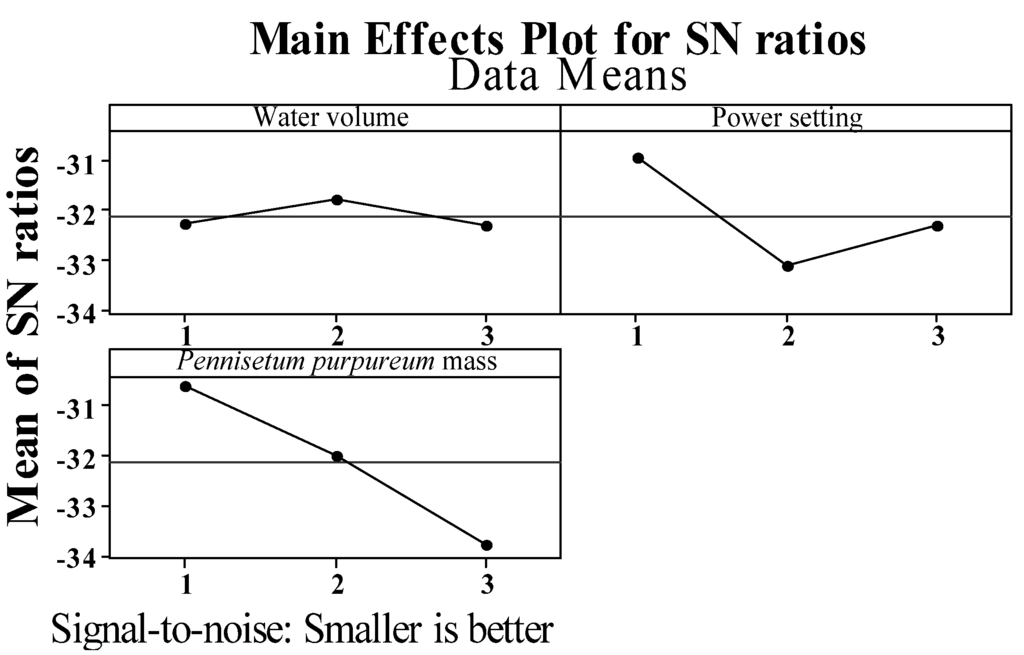
Figure 6. Response diagram of Taguchi experiments.

3.1.3. Analyze Variance

The main text paragraph Analysis of Variance (ANOVA) aims to evaluate experimental errors, and the F-ratio method is used to identify the influential degree of each factor [22]. The factor is significant when the F-ratio is greater than the smallest F-ratio in the confidence level. The factors in which the F-ratio is smaller than the minimum value are used for pooling experimental errors. The response value of the S/N ratio of ANOVA for each factor is calculated by the error degree of freedom (dof_e), sum of square (SS) of variance, total SS of variance, SS of individual variance, SS of variance error, variance of variable j, error of variance, F-ratio [23]. The calculated data are shown in Table 4.

The minimum value of the F-ratio is four when the confidence level is below 80%. The values in which the F-ratio is smaller than four are pooled errors, as shown in Table 5. As can be seen, the water volume and heating power are pooled errors when the confidence level is below 80%, and the significant factor is the mass of Pennisetum purpureum.

Table 4. Analysis of Variance (ANOVA).

Table 4. Analysis of Variance (ANOVA).

Source	dof	SS	V	F-ratio
Water volume	2	0.549	0.275	0.17
Heating power	2	7.362	3.681	2.25
Pennisetum purpureum mass	2	15.059	7.529	4.61
Error	2	3.267	1.633	–
Total	8	26.237	–	–

Table 5. ANOVA after pooling of errors.

Table 5. ANOVA after pooling of errors.

Source	dof	SS	V	F-ratio
Water volume	Pooled
Heating power	Pooled
Pennisetum purpureum mass	2	15.059	7.529	4.04
Error	6	11.178	1.863	–
Total	8	26.237	–	–

3.1.4. Verification Test

In the verification test, the Taguchi method applies a confidence interval to verify whether the parameter level is optimal, and determines the confidence interval of the predicted value of the optimal parameter level as well as the confidence interval of the actual value. If the two intervals overlap, the optimal parameter level proposed by the Taguchi experiment is confident.

Based on the response table and response diagram, an optimal parameter level combination can be predicted. As shown in Figure 6, the optimal parameter level combination is A2B1C1. The predicted optimal parameter level combination is tested, and the S/N is calculated using the results of the test. The S/N ratio of the optimal parameter level combination is then calculated using the equation for S/N the smaller-the-better. Finally, the reliability of parameter optimization is tested when the confidence level is below 80% [18,22]. An 80% confidence interval range of the experimental parameter level is presented by Equation (3); the confidence interval of the predicted value of the optimal parameter level is shown in Equation (4). The results are shown in Table 6 and Figure 7.

(3)

(4)

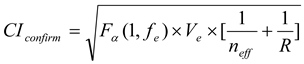
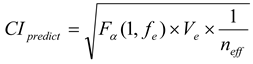where, α denotes 0.2, f_e denotes degree of freedom of F-ratio, n_eff denotes experiment number n/(1 + average degree of freedom of significant factor), and R denotes test number, F_α(1, f_e) = 2.07.

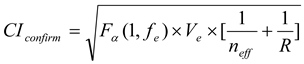
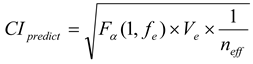
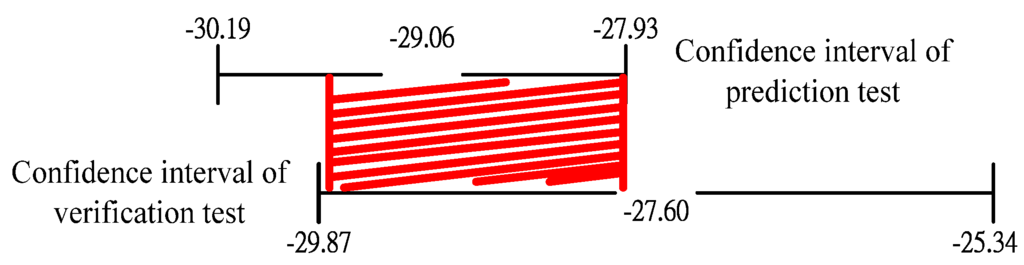
Figure 7. Relation between confidence intervals of predicted value and actual value.

Table 6. Comparison of predicted value and actual value of A2B1C1.

Table 6. Comparison of predicted value and actual value of A2B1C1.

Value	S/N ratio	Heating time (min)
Predicted value	−29.06	27.23
Actual value	−27.60	24

Based on Table 6, the S/N ratio of the predicted value is −29.06, and the S/N ratio of the actual value is −27.60. The S/N of the actual value is closer to zero in each experiment, meaning that the parameter level can reduce variation. In the verification test, the confidence interval of the predicted value and the verification test overlaps, and it can be verified that A2B1C1 is the optimal parameter level combination.

3.2. Building Parametric Model Using System Identification

3.2.1. Identification Test Design

The water in a closed vessel is heated in a microwave. The dynamic response of the temperature rise is directly related to the power consumption as is shown in Figure 8, thus, the consumed power and water temperature changes are used as input and output signals for the system identification. Due to the long heating time, the sampling intervals of the experiment data are one minute.

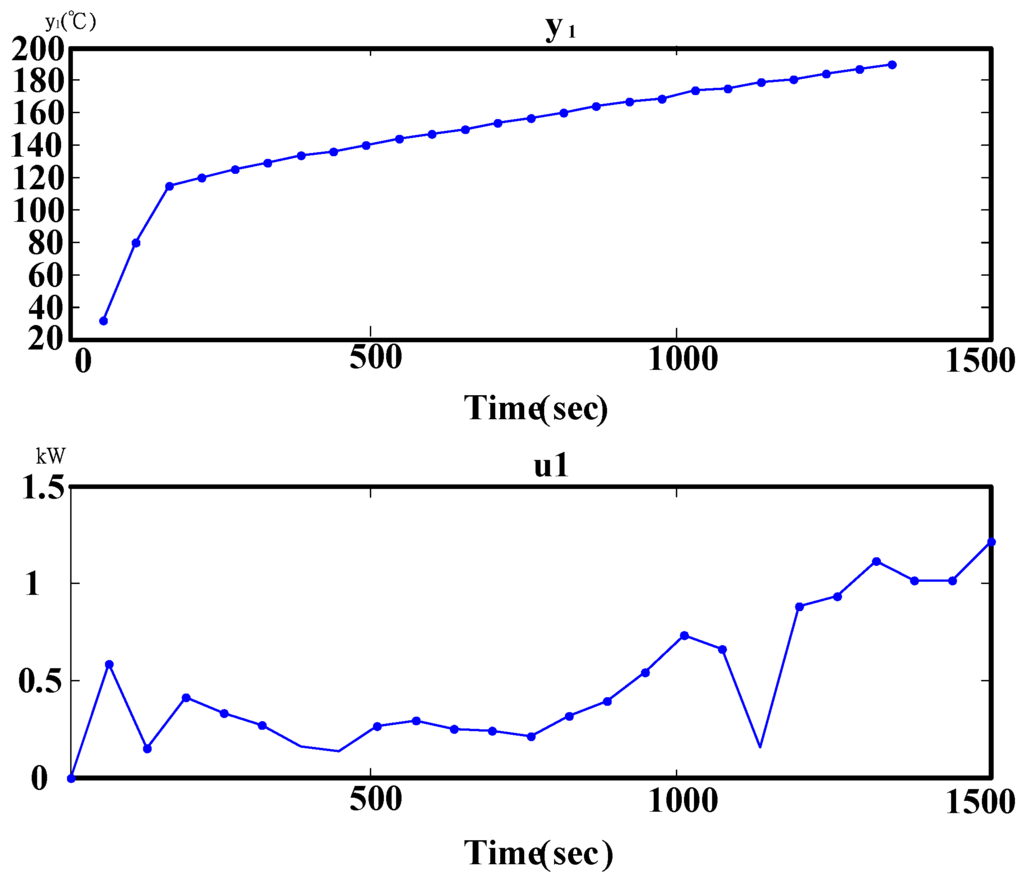
Figure 8. Dynamic response of actual system input and output.

3.2.2. Define System Characteristics

This paper defines the microwave-based heating system as SISO (single-input single-output), a linear time-invariant system, where the input signal and initial state of the system can determine the output signal. It is a deterministic system. The actual system is a continuous-time system; however, the samples of the system input and output signals are discrete values. For this reason, the system is defined as discrete-time system in identification. Based on the defined characteristics, a parametric model is used for system identification. The parametric model uses finite parameters to describe the dynamic characteristics of the system [20].

3.2.3. Selection of Model Structure

When selecting the model structure, a model approximate to the characteristics of the actual system is preferred. In addition, generated or added positions for system operations or noise measurements should be considered. If the system characteristics are not clear, several types of models can be used to identify the unknown system, and optimal identification results are used as the reference [21]. This study used ARX, OE (Output Error), BJ (Box and Jenkins), and PEM (Polynominal Error Mode) for identification.

3.2.4. Selection of Model Order

First, 4SID (SubSpace-base State Space Model Identification Method) is used to determine the optimal noise model order from the input and output data [20]. The 4SID is an effective system identification method used to identify a state space model using input and output data [24], where the analysis result is partial to one order, as shown in Figure 9 and the noise model order is one. Next, MATLAB is used for system identification, with the results shown in Table 7. Apart from the goodness of fit, FPE (Final Prediction Error) and Loss Function are used to identify the fitness of the model [20,21]. The smaller the values of FPE and the loss function are, the higher is the fitness. Thus, the system structure of an eight-order ARX model is selected.

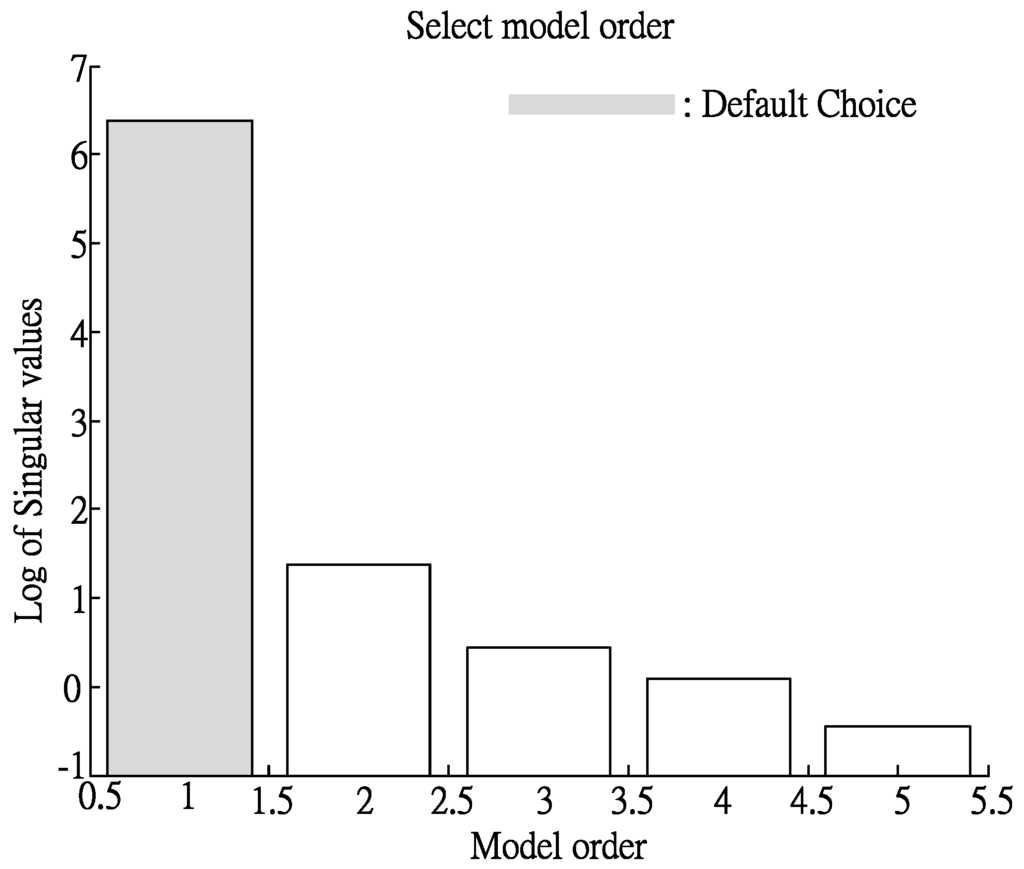
Figure 9. Order of optimal noise model using 4SID (SubSpace-base State Space Model Identification Method).

Table 7. Identification results from the models.

Table 7. Identification results from the models.

Model	Order	Goodness of fit (%)	Final Prediction Error	Loss Function
ARX	7	98.84	0.059	0.211
ARX	8	99.13	0.039	0.177
OE	6	95.69	0.143	0.633
OE	7	97.31	0.042	0.335
BJ	3	98.64	0.165	0.73
PEM	1	98.2	0.875	1.39

3.2.5. System Structure

The energy transmission process can be used to analyze the system structure. The energy transmission of the microwave-based heating is as shown in Figure 10, where electric energy produces microwaves through a magnetron. The gain can be regarded as B(q). After microwaves are produced, their distribution in the cavity is uneven, and the heating efficiency of the microwave is affected. The factors are considered as external interference e(k), and 1/A(q) is the gain from the temperature change after the water molecules absorb microwave energy. Thus, ARX of similar structures are used for identification. The energy transmission of the microwave-based heating device and system structure are as shown in Figure 11.

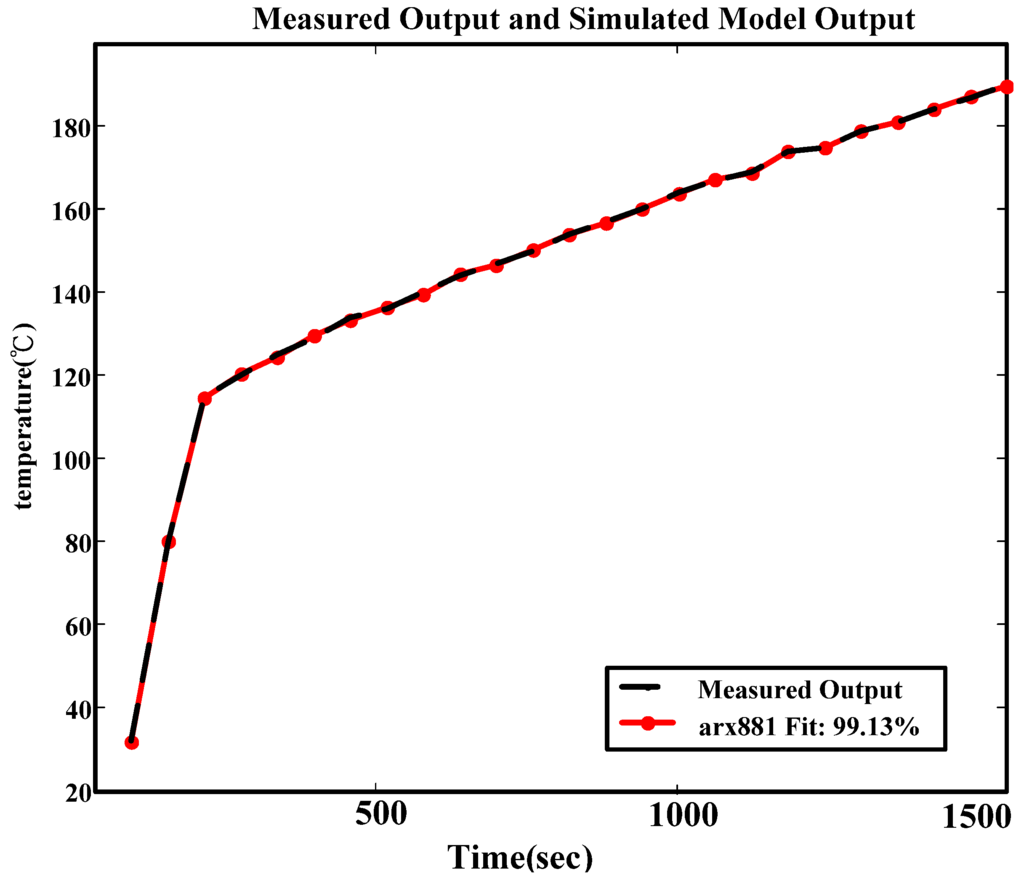
Figure 10. Simulated dynamic response of actual system and ARX881.

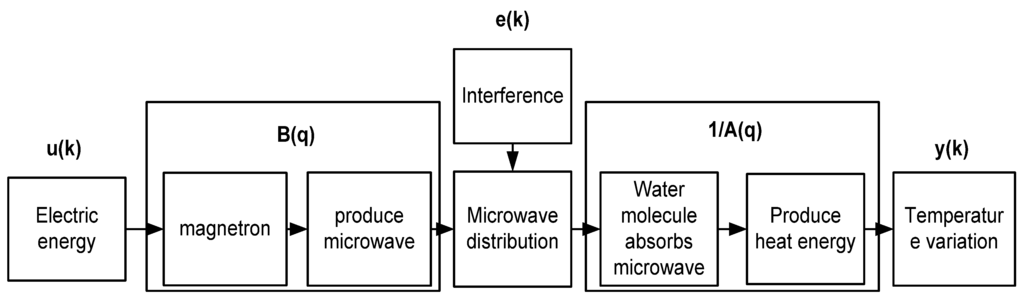
Figure 11. Relation between microwave energy transmission and system structure.

3.2.6. Model Construction and Verification

Identification is conducted when the noise parameter of the above selected ARX in one order (ARX881), and Equation (5) can be obtained. Fit, loss function, and FPE are 99.13, 0.039, and 0.177, respectively, and the fitness of the model is very high. Next, residual analysis is conducted for ARX881 [20,21]. The result of the residual analysis for ARX881 is better that than of other models, as shown in Figure 12. The divergence is smaller, and the accuracy of ARX881 is better. In terms of fit, loss function, FPE, uncertainty, and results from the residential analysis, ARX881 is most similar to the system structure. Figure 13 shows the block diagram of ARX, and the difference equation is shown in Equation (5).

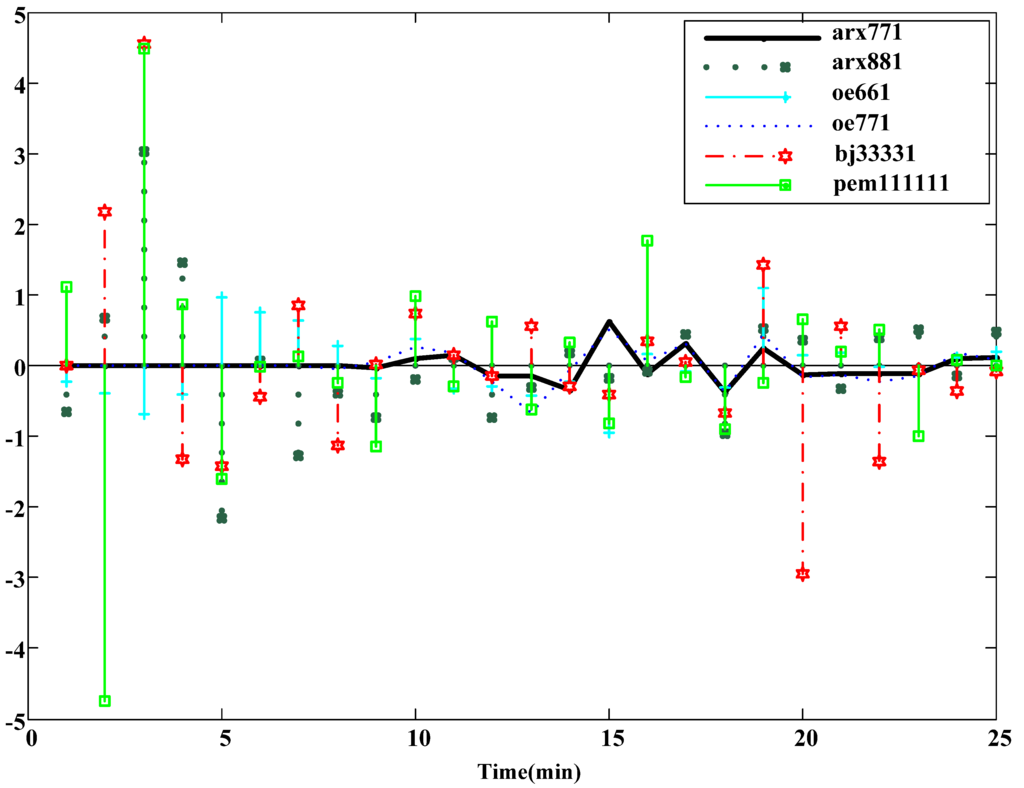
Figure 12. Results of residual analysis of the models.

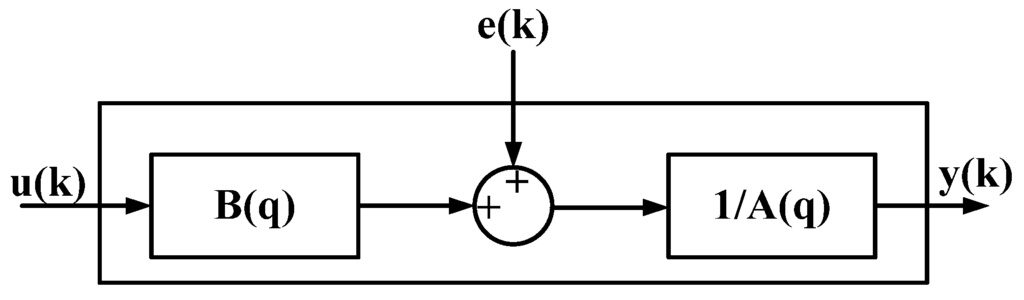
Figure 13. ARX block diagram.

(5)

where

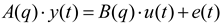
A(q) = 1 + 0.896q⁻¹ − 1.116q⁻² − 1.065q⁻³ − 0.4614q⁻⁴ + 0.3194q⁻⁵ + 0.6206q⁻⁶ − 0.3411q⁻⁷ + 1.07838q⁻⁸

B(q) = −3.162q⁻¹ − 0.1285q⁻² − 2.53q⁻³ − 1.255q⁻⁴ + 0.2473q⁻⁵ − 4.274q⁻⁶ + 7.583q⁻⁷ − 1.422q⁻⁸

4. Discussion

5. Conclusions

References

1. Inayat, A.; Ahmad, M.M.; Yusup, S.; Mutalib, M.I.A. Biomass steam gasification with in-situ CO₂ capture for enriched hydrogen gas production: A reaction kinetics modelling approach. Energies 2010, 3, 1472–1484. [Google Scholar] [CrossRef]
2. Dalgaard, T.; Jorgensen, U.; Olesen, J.E.; Jensen, E.S.; Kristensen, E.S. Looking at biofuels and bioenergy. Science 2006, 312, 1743–1748. [Google Scholar] [CrossRef] [PubMed]
3. Mason, W.H. Process and apparatus for disintegration of wood and the like. U.S. Patent 1,578,609, 30 March 1926. [Google Scholar]
4. Wyman, C.E.; Dale, B.E.; Elander, R.T.; Holtzapple, M.; Ladisch, M.R.; Lee, Y.Y. Comparative sugar recovery data from laboratory scale application of leading pretreatment technologies to corn stover. Bioresour. Technol. 2005, 96, 2026–2032. [Google Scholar] [CrossRef] [PubMed]
5. Mason, W.H. Apparatus for process of explosion fibration of lignocellulose material. U.S. Patent 1,665,618, 10 January 1928. [Google Scholar]
6. Binod, P.; Satyanagalakshmi, K.; Sindhu, R.; Janu, K.U.; Sukumaran, R.K.; Pandey, A. Short duration microwave assisted pretreatment enhances the enzymatic saccharification and fermentable sugar yield from sugarcane bagasse. J. Renew. Energy 2012, 37, 109–116. [Google Scholar] [CrossRef]
7. Azuma, J.; Tananka, F.; Koshijima, T. Enhancement of enzymatic suceptibility of lignocellulosic wastes by microwave irradiation. J. Ferment. Technol. 1984, 64, 377–384. [Google Scholar]
8. Jones, D.A.; Lelyveld, T.P.; Mavrofidis, S.D.; Kingman, S.W.; Miles, N.J. Microwave heating applications in environmental engineering—A review. Resour. Conserv. Recycl. 2002, 34, 75–90. [Google Scholar] [CrossRef]
9. Budarin, V.L.; Clark, J.H.; Lanigan, B.A.; Shuttleworth, P.; Macquarrie, D.J. Microwave assisted decomposition of cellulose: A new thermochemical route for biomass exploitation. Bioresour. Technol. 2010, 10, 3776–3779. [Google Scholar] [CrossRef]
10. Hu, Z.; Wen, Z. Enhancing enzymatic digestibility of SwitchGrass by microwave-assisted Alkali pretreatment. Biochem. Eng. J. 2008, 38, 369–378. [Google Scholar] [CrossRef]
11. Chen, W.H.; Tu, Y.J.; Sheen, H.K. Disruption of sugarcane bagasse lignocellulosic structure by means of dilute sulfuric acid pretreatment with microwave-assisted heating. J. Appl. Energy 2011, 88, 2726–2734. [Google Scholar] [CrossRef]
12. Zhao, X.; Song, Z.; Liu, H.; Li, Z.; Li, L.; Ma, C. Microwave pyrolysis of corn stalk bale: A promising method for direct utilization of large-sized biomass and syngas production. J. Anal. Appl. Pyrolysis 2010, 89, 87–94. [Google Scholar] [CrossRef]
13. Zhu, S.; Wu, Y.; Yu, Z.; Chen, Q.; Wu, G.; Yu, F.; Wang, C.; Jin, S. Microwave-assisted alkali pre-treatment of wheat straw and its enzymatic hydrolysis. Biosyst. Eng. 2006, 94, 437–442. [Google Scholar] [CrossRef]
14. Gabhane, J.; Prince William, S.P.M.; Vaidya, A.N.; Mahapatra, K.; Chakrabarti, T. Influence of heating source on the efficacy of lignocellulosic pretreatment—A cellulosic ethanol perspective. Biomass Bioenergy 2011, 35, 96–102. [Google Scholar] [CrossRef]
15. Shi, J.; Pu, Y.; Yang, B.; Ragauskas, A.; Wyman, C.E. Comparison of microwaves to fluidized sand baths for heating tubular reactors for hydrothermal and dilute acid batch pretreatment of corn stover. Bioresour. Technol. 2011, 102, 5952–5961. [Google Scholar] [CrossRef] [PubMed]
16. Chum, H.L.; Johnson, D.K.; Black, S.K.; Overend, R.P. Pretreatment-catalyst effects and the combined severity parameter. Appl. Biochem. Biotechnol. 1990, 24–25, 1–14. [Google Scholar] [CrossRef] [PubMed]
17. Xu, J.; Chen, H.Z.; Kadar, Z.; Thomsen, A.B.; Schmidt, J.E.; Peng, H.D. Optimization of microwave pretreatment on wheat straw for ethanol production. J. Biomass Bioenergy 2011, 35, 3859–3864. [Google Scholar] [CrossRef]
18. Taguchi, G.; Jugulum, R. The Mahalanobis-Taguchi Strategy: A Pattern Technology System; John Wiley & Sons Inc.: New York, NY, USA, 2002. [Google Scholar]
19. Kuehl, R.O. Design of Experiments: Statistical Principles of Research Design and Analysis; Cengage Learning Inc.: Belmont, CA, USA, 1999. [Google Scholar]
20. Ljung, L. System Identification, Theory for the User; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
21. Giri, F.; Bai, E.W. Block-Oriented Nonlinear System Identification; Springer-Verlag: London, UK, 2010. [Google Scholar]
22. Torng, C.C.; Chou, C.U.; Liu, H.R. Applying quality engineering technique to improve wastewater treatment. J. Ind. Technol. 1999, 15, 1–7. [Google Scholar]
23. Roy, R. A Primer on the Taguchi Method; Society of Manufacturing Engineers: Dearborn, MI, USA, 2010. [Google Scholar]
24. Rodriguez Vasquez, J.R.; Rivas Perez, R.; Sotomayor Moriano, J.; Peran Gonzalez, J.R. System identification of steam pressure in a fire-tube boiler. Comput. Chem. Eng. 2008, 32, 2839–2848. [Google Scholar] [CrossRef]