Compression Techniques for Real-Time Control and Non-Time-Critical Big Data in Smart Grids: A Review

Abstract

Significant amounts of data need to be transferred in order to optimize the operation of power grids. The development of advanced metering and control infrastructure ensures a growth in the amount of data transferred within smart grids. Data compression is a strategy to reduce the burden. This paper presents current challenges in the field of time-series data compression. This paper’s novel contribution is the division of data in smart grids to real-time data used for control purposes and big data sets used for non-time-critical analysis of the system. Both of these two applications have different requirements for effective compression. Currently used algorithms are listed and described with their advantages and drawbacks for both of these applications. Details needed for the implementation of an algorithm were also provided. Comprehensive analysis and comparison are intended to facilitate the design of a data compression method tailored for a particular application. An important contribution is the description of the influence of data compression methods on cybersecurity, which is one of the major concerns in modern power grids. Future work includes the development of adaptive compression methods based on artificial intelligence, especially machine learning and quantum computing. This review will offer a solid foundation for the research and design of data compression methods.

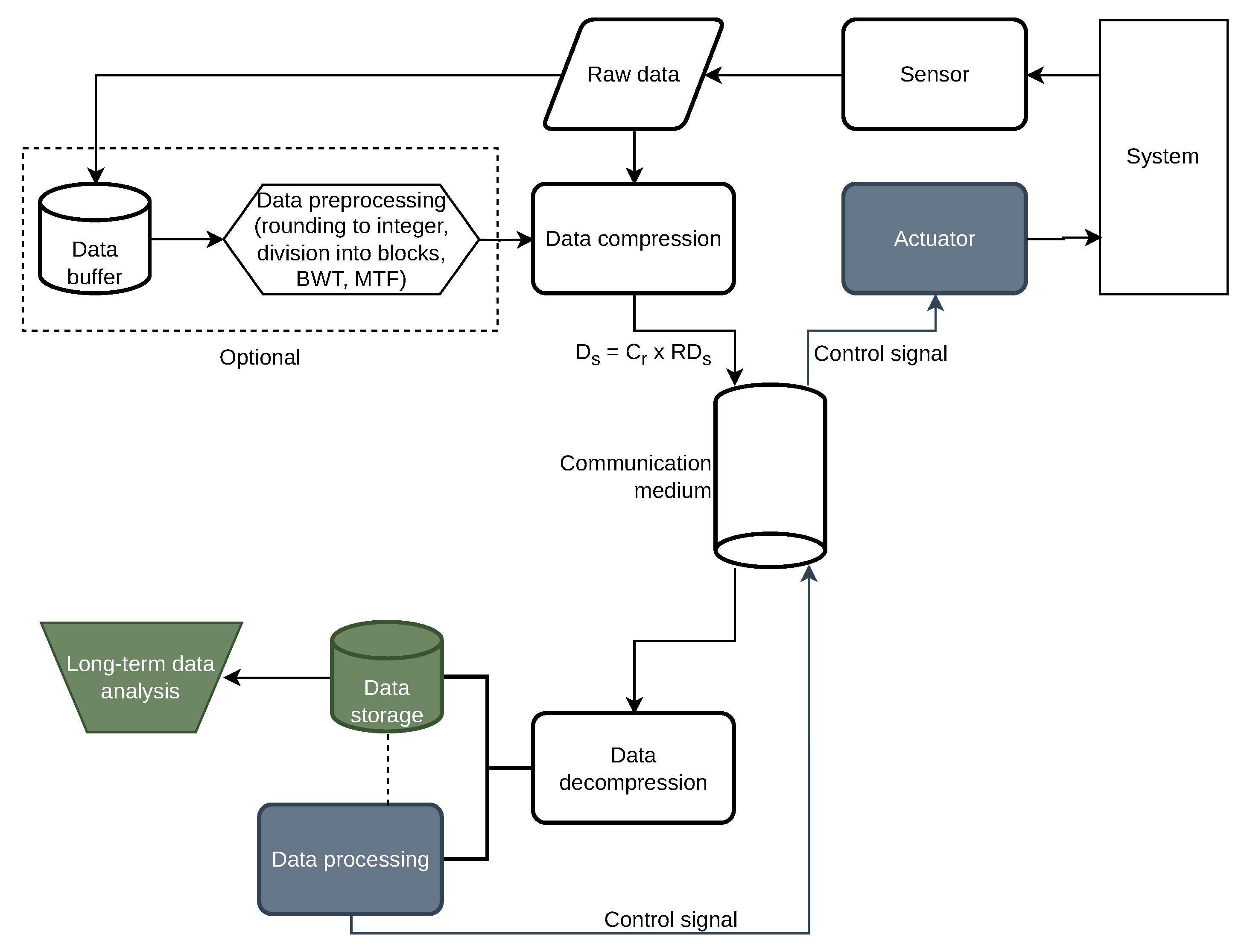
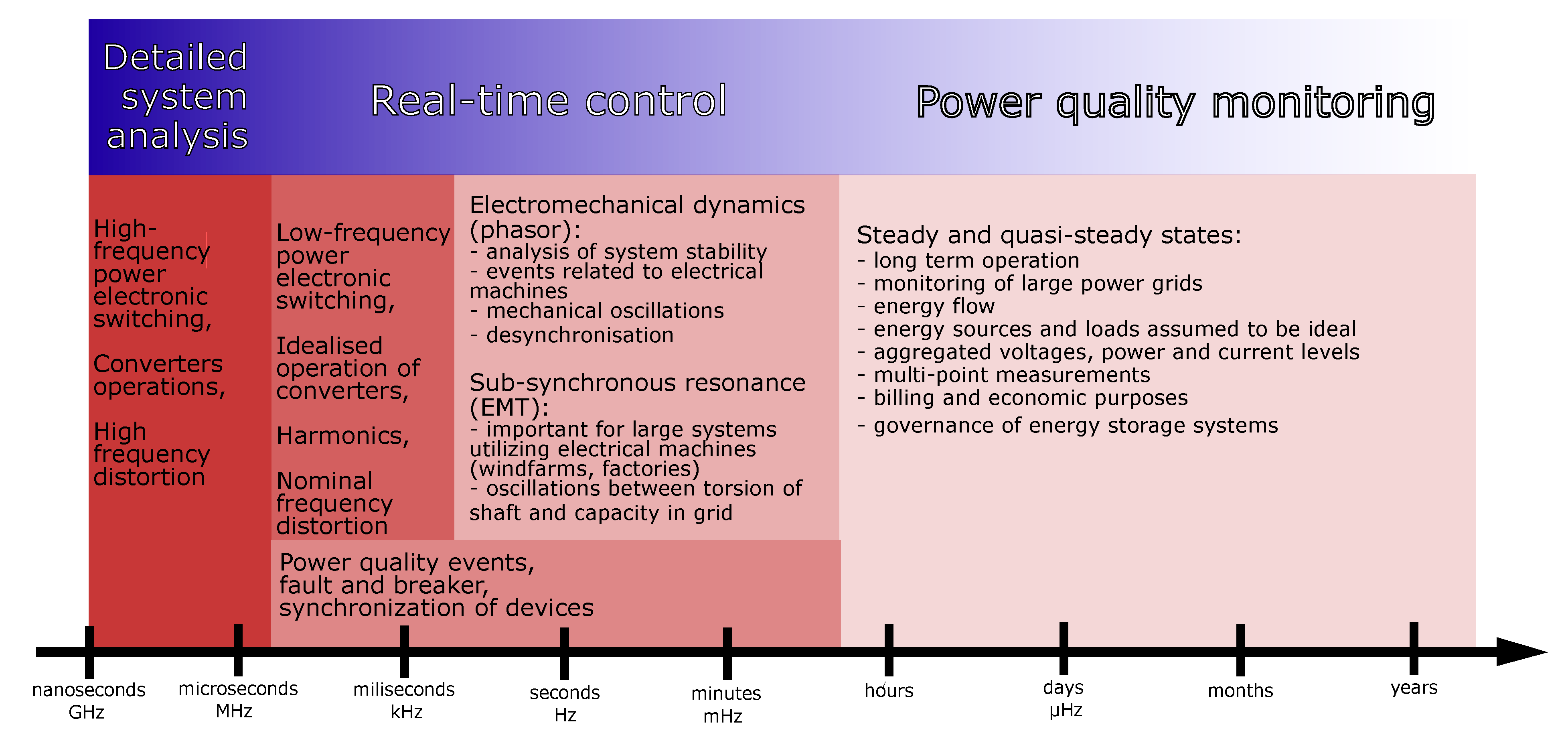
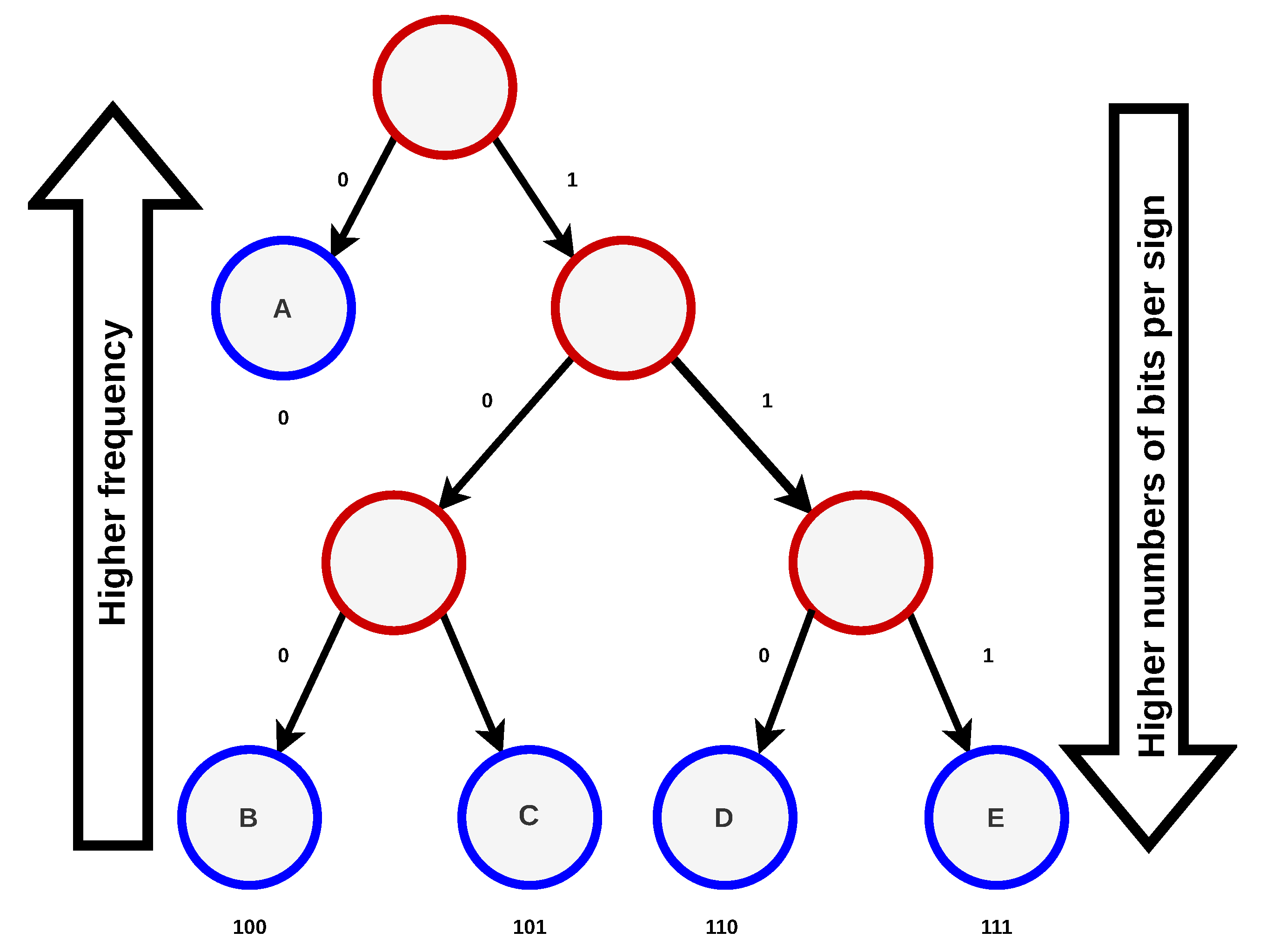
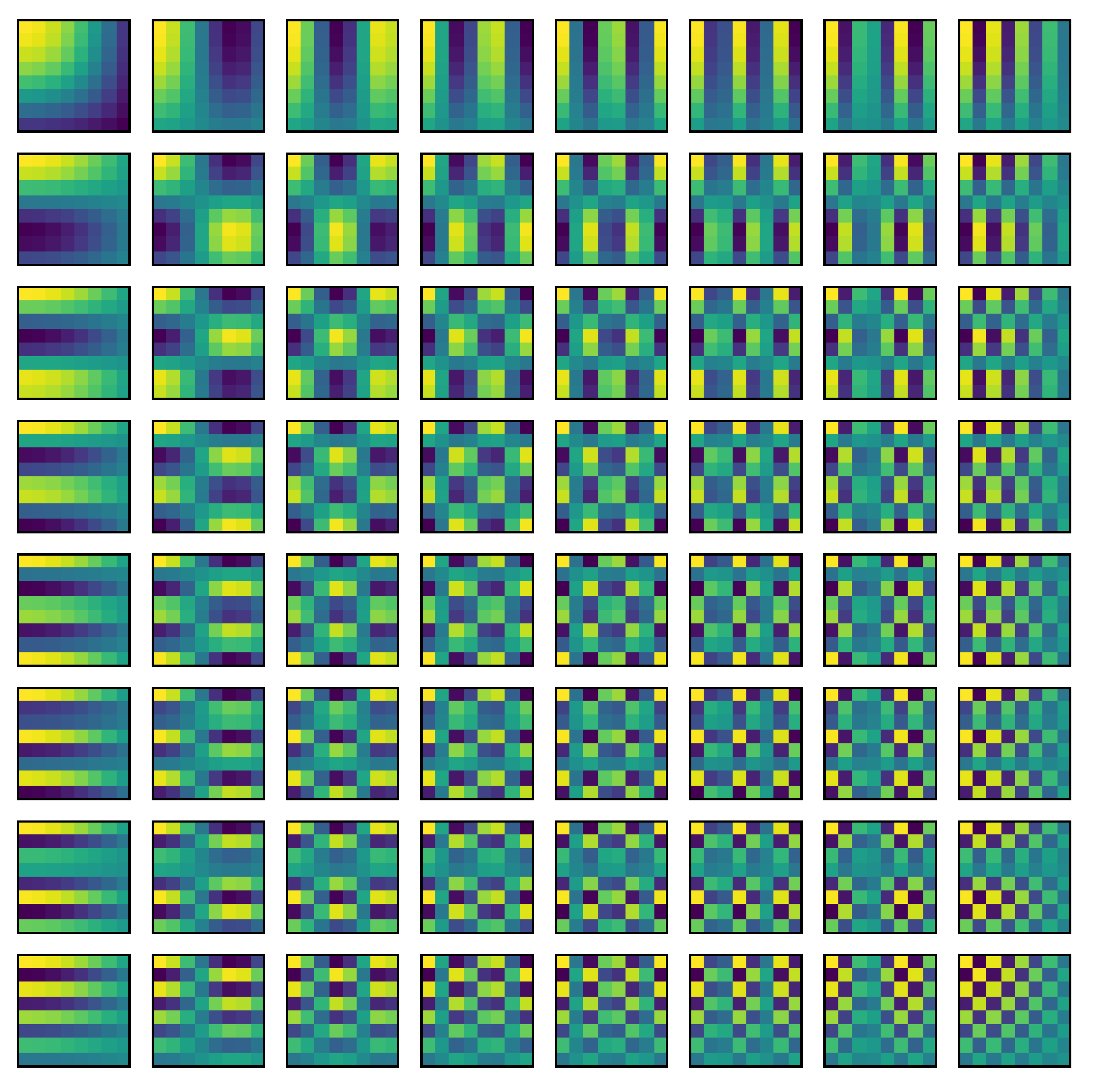
1. Introduction

Efficient management of the power grid requires the operator to possess accurate information about the state of the system in as many points as possible, in order to have a precise input to control the system. A way to carry this out is to develop measurement infrastructure, add new measurement points, increase time and amplitude resolution, increase communication bandwidth, and use modern computation systems or modern actuators with faster reaction time and less disturbance introduced to the action of the system [1]. Implementing any of these actions requires incurring costs. At the same time, consumers expect energy to have the lowest possible price, especially in modern and developed markets, which allow energy trade by allowing many entities to trade in it. According to control theory, the role of a measurement system is to gather data about the state of a controlled system and supply it to the controller, which analyzes the data, extracts information from them and commands the actuator to act accordingly. The typical data acquisition and control system is presented in Figure 1.

One of the main challenges in the development of modern power grids is ensuring a sufficient supply of measurement data [2]. Given the inherent periodicity exhibited by signals within power grids, the process of compressing signal data emerges as a favorable approach to increase the throughput of the communication system and efficiently manage the required disk space. Data compression methods are very popular in domains such as image (JPEG, GIF, PNG, WebP), video (H.264, H.265, VP9) or audio (MP3, AAC, Opus) processing, as well as general information-to-data ratio optimization (ZIP, Gzip, LZ77, LZ78). This review article presents popular techniques and methods used to compress time series in power grids. The goal of this article is to provide information on popular components of data compression methods, to be a guide for the selection of appropriate methods and a resource for gathering knowledge about the topic. This article also presents an overview of recent research on data compression in smart grids. A novel contribution of this work is defining two areas (

Table 1. Data types in distributed measurement systems in smart grids with crucial requirements for data compression.

Data Type	Properties	Example of Application	Compression Requirements
Non-time critical power quality data	Large datasets, aggregated data, data content defined by norms and legislation	Electrical grid data collected by power quality meters, energy consumption data used for billing purposes, Wide Area Measurement System, Large Scale Phasor Measurement	Maximizing compression ratio, low data degradation, preserving data crucial for the application, scalability for large data sets
Real time control systems is Smart Grid	Constant stream of data, transients reporting, high resolution	Islanding protection, overvoltage and overcurrent protection, transient detection, short-circuit protection	low-latency, preservation of data crucial for application, low computational complexity, operation on blocks of data

) of application of data compression techniques in the smart grid:

• Static—compressing data at rest, or data that can be transferred without crucial time constraints. An example can be the storage of 24 h of measurements in order to perform disturbance trend analysis, consumption analysis, etc.
• Dynamic—compressing data in transit that have to be transferred under exigent timing constraints. An example of this application can be data that needs to be registered, transmitted, and processed within a few milliseconds in systems like short-circuit, over voltage, over current, or islanding protection.

The IEEE Standard for Synchrophasor Measurements for Power Systems (IEEE Std. C37.118.1-2018) [3] and the IEC/IEEE Communication Networks and Systems for Power Utility Automation: Precision time protocol profile for utility automation (IEC/IEEE 61850-9-3) [4] are two normative documents that provide precise timing constraints for real-time communication in smart grids [5,6].

• Sub-microsecond level synchronization: According to IEEE Std C37.118.1-2018, the synchronization protocol should provide clock synchronization on the order of a microsecond. This means that the communication system should be able to maintain synchronization to a level of precision that is a few microseconds.
• Timeliness: IEEE Std C37.118.1-2018 also specifies that the communication system should be able to deliver data and control signals within a few milliseconds to ensure the safety and reliability of the smart grid.
• Precision time protocol profile for utility automation: IEC/IEEE 61850-9-3 specifies the precision time protocol (PTP) profile for utility automation. PTP is a network protocol for clock synchronization, which can be used to synchronize the clocks of devices in the smart grid to a few microseconds.

Prioritization of data is a crucial issue in mission-critical systems like power grid control. Real-time data, which include information on current energy consumption, grid status, and equipment performance, may need to be prioritized over historical data for immediate decision-making. Historical data, such as long-term consumption patterns and equipment maintenance records, can be stored and analyzed separately. Critical data, such as information related to system faults, security breaches, or emergency situations, should be given the highest priority. Noncritical data, like routine monitoring information, can be processed with lower priority. Data related to load forecasting and prediction models may require special attention for accurate energy planning. Operational data, such as real-time grid conditions and equipment status, are essential for efficient management [7]. Segregation of measurement data is a crucial matter in data-intensive environments. In power grids, data are segregated using rule-based segregation or time-series analysis. Rule-based systems define criteria to categorize data into different priority levels. Rules can be based on factors such as data source, urgency, and criticality. Time-series analysis techniques distinguish between real-time data and historical trends. Algorithms such as ARIMA (AutoRegressive Integrated Moving Average) can help in forecasting and segregating data. More recently, edge computing architecture and machine learning techniques were introduced in order to improve the quality and efficiency of data segregation. Machine learning algorithms automatically categorize and prioritize data based on historical patterns and real-time conditions. Clustering algorithms can group similar data for efficient processing. Edge computing uses data processing locally at the source, reducing the need to transmit large volumes of raw data. Edge devices can perform initial data segregation and send only relevant information to central systems [8].

2. Data in Power Systems

The popularity of data compression methods grew along with the popularization of distributed computing and data storage systems since it reduced the ratio between the cost and benefit of such systems. In many fields, data compression is a fundamental part of their development. Complex and data-demanding information, such as audio or video files, has been a subject of data compression study for a long time. Real-time applications, such as bilateral voice transmission, also exist in cellular technology. In the domain of power systems, data compression was a niche topic most of the time, but the recent rise in the complexity of modern power systems, along with the need for detailed measurements, calls for optimization of data transfer [9]. The types of information that must be known about the system to be managed precisely are presented in Figure 2.

Using such a large amount of data makes data compression methods an attractive choice to increase system efficiency.

Data utilized for real-time control usually need to be compressed with methods that allow low-latency streaming and quick access to the data [10]. However, in most cases, the aggregated data that describe power quality in the system is not time critical and, therefore, can be compressed with methods that do not meet demanding time constraints but offer a higher compression ratio or lower computational efficiency instead [11].

Based on the principle of operation, data compression methods can be divided into two categories—lossy and lossless.

2.1. Lossless

Lossless compression algorithms are designed to preserve all the information contained in the original data. This means that when the data are compressed using these methods, they can be later decompressed to obtain an exact replica of the original data without loss or distortion [12]. Lossless compression methods often rely on the concept of entropy, which is a measure of the information content in the data. The basic idea is to identify and exploit patterns, redundancy, and statistical properties within the data to represent them more efficiently [13]. The most common techniques that are used to compress data without any losses are based on statistical encoding in order to reduce the entropy in the signal [14], thus reducing the quantity of the data or on dictionary methods, which replace repetitive data with shorter codes [15].

2.2. Lossy

Lossy data compression methods are techniques used to reduce the size of digital data by selectively removing some information that is considered less essential or perceptually less significant [16]. These methods are commonly employed in applications such as image and audio compression [17,18]. Due to that fact, most of the methods used in industry are based on deep analysis of human senses like sight and hearing and designed in a way to primarily lose the information that is less important to the receiver (like color-related information in JPEG, due to the fact that the human eye has more rod cells than cone cells, which makes information related to shape more crucial than information related to color to human receivers or frequencies bordering on the audible range in MP3 since they are less notable by humans) [19,20]. In lossy compression, the primary objective is to achieve high compression ratios by eliminating redundant or less important details. This involves quantization, where the data values are rounded or mapped to a smaller set of values. The discarded information is irretrievable during decompression, making lossy compression unsuitable for applications where data fidelity is critical, such as undertaking high-impact decisions about the state of the power grid. The key challenge in lossy compression is to achieve a balance between achieving significant compression while minimizing perceptual degradation [21]. While lossy compression offers substantial size reduction, it is crucial to use it judiciously in scenarios where slight data loss is acceptable. Historically, most lossy data compression methods were developed for the information received by humans, like video, audio, or image. In most cases, the information from the power grid does not need to be directly understood by humans, rather than by other IoT devices [22]. Direct transfer of methods from different domains should be carried out with caution. Lossy data compression methods are also specific to their application, which creates a field of data compression methods that should be tailored to be received and processed by machines, not by humans. The development of a lossy data compression method requires a deep knowledge of the system and the information contained in the data, which makes lossy compression algorithms harder to implement, but may offer a more optimized smart grid supervision system in the end [23].

3. Algorithms Used in Smart Grid Data Compression

Within the domain of information theory and data compression, two fundamental concepts, source coding [24] and entropy coding [25,26], play a pivotal role in optimizing data representation and transmission (Table 2). Source coding, often termed data compression or signal compression, serves as the foundation for reducing the size of datasets while preserving their essential information [27]. This process involves eliminating redundant details and superfluous information. For example, the ubiquitous Huffman coding technique assigns variable-length codes to characters in a text document based on their frequency of occurrence [28]. The most frequently used values receive shorter codes, resulting in efficient compression of text data.

Entropy coding, on the other hand, represents a specialized subset of source coding that delves into the statistical properties and probabilities inherent in the data source. It takes advantage of principles from information theory and probability theory to optimize compression efficiency. For example, arithmetic coding is an entropy coding method that encodes data based on its cumulative probability distribution [29]. By assigning shorter codes to more likely symbols, compression ratios are achieved that approach the entropy of the data source [30]. This is particularly valuable in lossless compression applications, such as event-related data compression, where exact reconstruction is essential.

Source coding methods such as Run-Length Encoding (RLE) can efficiently reduce the size of binary images by encoding consecutive runs of identical bytes as a single value [31]. Meanwhile, entropy coding techniques, including Huffman coding or arithmetic coding, further compress the data by exploiting the statistical properties of sample values. In essence, source coding and entropy coding represent essential tools in the data compression toolkit, each offering unique strategies to optimize the representation and transmission of information, with applications spanning from text and images to audio and video data [27,32].

3.1. Run-Length Encoding (RLE)

Run-Length Encoding (RLE) is a lossless compression algorithm used in power grid signals analysis to efficiently represent time-series data from voltage and current sensors [33]. During the encoding phase, consecutive identical values in the signal are compressed into a single value and a count, reducing storage and transmission requirements (Algorithm 1). The compressed data, accompanied by relevant metadata, is stored or transmitted [34]. In the decoding phase, the original signal is reconstructed for analysis, allowing identification of voltage variations, transient events, and patterns of interest in the power grid. RLE is a simple algorithm; thus, it can be implemented at a low resource cost [35].

Algorithm 1 Run-Length Encoding (RLE)
$compressed\_output\leftarrow$ “”	▹ Initialize the compressed output string
$current\_character\leftarrow input\left[0\right]$	▹ Initialize the current character
$count\leftarrow 1$	▹ Initialize the count to 1
for $i\leftarrow 1$ to $\mathrm{length}\left(input\right)-1$ do
if $input\left[i\right]=current\_character$ then
$count\leftarrow count+1$
else
$compressed\_output\leftarrow compressed\_output+current\_character+count$
$current\_character\leftarrow input\left[i\right]$
$count\leftarrow 1$
end if
end for
$compressed\_output\leftarrow compressed\_output+current\_character+count$	▹ Append the character with counter
return $compressed\_output$

Sliding-Window Run-Length Encoding (SW-RLE) is an extended version of the classic Run-Length Encoding (RLE) algorithm, specifically designed for scenarios where consecutive identical values are encountered within a sliding window of data in a time series sequence, as often occurs in the context of power grids signals analysis (Algorithm 2). SW-RLE operates in two distinct phases [36].

During the encoding phase, a fixed-size sliding window is used to traverse the time-series data. Within this window, a count variable is initialized to 1, and a result buffer is used to accumulate the encoded data. At each position of the sliding window, a comparison is made between the values within the window. If all values within the window are identical, the count is incremented to represent the consecutive run of identical values. In cases where variations exist within the window, the value within the window and its count are appended to the result buffer. This process continues as the sliding window moves forward, covering all data in the time series. The result buffer eventually holds the compressed data, effectively representing consecutive identical values within the sliding window.

The decoding phase, on the other hand, starts at the beginning of the encoded data. An output buffer is initialized to store the decoded signal. The encoded data are then iterated through, processing pairs of values (element, count). For each pair, the element is appended to the output buffer count times, effectively reconstructing the original time-series data. This decoding process continues until the end of the encoded data is reached, producing the final output buffer with the uncompressed time-series data.

In the domain of analysis of power grid signals, SW-RLE is particularly valuable when analyzing sliding windows of continuous signals, where localized patterns and anomalies are of interest [37]. The adaptability of SW-RLE allows the adjustment of sliding window sizes to capture patterns of different durations, making it versatile for various analysis requirements. Importantly, SW-RLE preserves the integrity of the original data within the sliding windows, ensuring that no localized information is lost during the compression and decoding processes. This makes it a powerful tool for focused and localized analysis within the broader context of power grid signals.

Algorithm 2 Sliding-Window Run-Length Encoding (SWRLE)
$compressed\_output\leftarrow$ “”	▹ Initialize the compressed output string
$windowStart\leftarrow 0$	▹ Initialize the start of the sliding window
while $windowStart<\mathrm{length}\left(input\right)$ do
$windowEnd\leftarrow min(windowStart+windowSize,\mathrm{length}(input\left)\right)$	▹ Window end
$subsequence\leftarrow input[windowStart:windowEnd]$	▹ Get the subsequence
$runLength\leftarrow 1$
for $i\leftarrow 1$ to $\mathrm{length}\left(subsequence\right)-1$ do
if $subsequence\left[i\right]=subsequence[i-1]$ then
$runLength\leftarrow runLength+1$
else
$compressed\_output\leftarrow compressed\_output+subsequence[i-1]+runLength$
$runLength\leftarrow 1$
end if
end for
$compressed\_output\leftarrow compressed\_output+subsequence\left[\mathrm{length}\right(subsequence)-1]+runLength$
$windowStart\leftarrow windowStart+\mathrm{length}\left(subsequence\right)$	▹ Move the sliding window
end while
return $compressed\_output$

3.2. Huffman Coding

Huffman coding, a widely used data compression technique, also finds application in power grid signal compression [38]. It begins by collecting time-series data from power grid sensors, and then, based on the data’s frequency distribution, constructs a Huffman tree that assigns shorter binary codes to common signal values and longer codes to less frequent ones (Figure 3). This tailored encoding significantly reduces data size. The compressed data, along with information about the Huffman tree structure, are stored or transmitted efficiently. During decoding, the Huffman tree is utilized to reconstruct the original signal values, preserving data accuracy for critical power grid applications, including grid monitoring and fault detection.

Huffman coding can significantly reduce repetitive data size, which is useful in the domain of power grids [39]. The algorithm works efficiently with large datasets, which makes it a good choice for compressing large datasets. For streaming time-critical data, the choice of dictionary (binary tree) is crucial, since frequent changes in the dictionary increase the load on the communication channel and might result in low or even negative compression ratio [40].

3.3. Lempel–Ziv–Welch

The LZW algorithm (Algorithm 3) works by reading a sequence of symbols, grouping them into strings, and converting the strings into codes. The codes take less space than the strings they replace, achieving compression [41]. The algorithm uses a code table, with 4096 as a common choice for the number of table entries. Codes 0–255 in the code table are always assigned to represent single bytes of the input file. As the encoding continues, LZW identifies repeated sequences in the data and adds them to the code table [42].

Algorithm 3 Lempel–Ziv–Welch algorithm steps

P = first input character while not end of input stream do     C = next input character     if $P+C\in$ string table then         $P=P+C$     else         output the code for P         add $P+C$ to the string table         $P=C$     end if end while output code for P

LZW takes advantage of short patterns. Due to the fact that power grids function in a periodic mode, this can be a useful way to compress data from a power grid [39]. This algorithm can also facilitate the observation of the power grid with periodic disturbances, because a sequence of samples may follow the same model if they register a distortion caused by the same reason [43].

3.4. Discrete Cosine Transform (DCT)

The discrete cosine transform (DCT) is extensively used in power systems data compression. Data from power systems, such as electrical quantities such as voltage, current, and power, often have a high-frequency component [44]. DCT can be used to compress these data by transforming them into the frequency domain, where the high-frequency components can be discarded if they do not contribute significantly to the overall data [45].

Due to its nature, data processed by DCT have more applications than sole compression:

• Data compression: DCT can be used to compress the data of the power system before storage or transmission. For example, the DCT can be used to compress the voltage profile data, which is a sequence of voltage values at different points in time. By discarding the high-frequency components of the DCT, the data can be significantly compressed without significant loss of information.
• Signal processing: DCT can be used in signal processing in power systems. For example, it can be used in the analysis of electrical disturbances, where DCT can be used to transform disturbances into the frequency domain, making it easier to analyze and diagnose disturbances [46].
• Predictive analytics: DCT can be used in predictive analytics in power systems. For example, it can be used to predict future power system conditions based on historical data. By transforming historical data into the frequency domain using DCT, the predictive model can focus on the low-frequency components of the data, which are more likely to be relevant to predict future conditions [47].
• Control systems: DCT can be used in control systems in power systems. For example, it can be used in the control of power distribution systems, where DCT can be used to transform control signals into the frequency domain, making it easier to design and implement the control system.

In all these applications, DCT is used to transform the data into the frequency domain, where the high-frequency components can be discarded, thereby reducing the size of the data and improving the efficiency of data compression [48], signal processing, predictive analytics, and control systems in power systems [49]. The signal is represented as a weighted sum of subsignals (Figure 4), which is lossless, but initially offers little or no compression. The data obtained are quantized as a weighted sum of the DCT matrix, where the weights are lower for higher frequency components. This approach increases the further compression using techniques such as RLE. DCT can be used to amplify the compression ratio received from other algorithms such as wavelet transform [50].

3.5. Wavelet Transform

Wavelet transform is a powerful tool in data compression, especially in real-time systems. The process of wavelet transform involves separating the signal into different frequencies, which can then be compressed independently [51]. This is particularly useful in power-system-related data, where signals often exhibit low-frequency and high-frequency components [52].

The fast continuous wavelet transform (fCWT) is an open-source algorithm that separates scale-independent and scale-dependent operations, which is beneficial for real-time, high-quality, noise-resistant time-frequency analysis of nonstationary noisy signals [53].

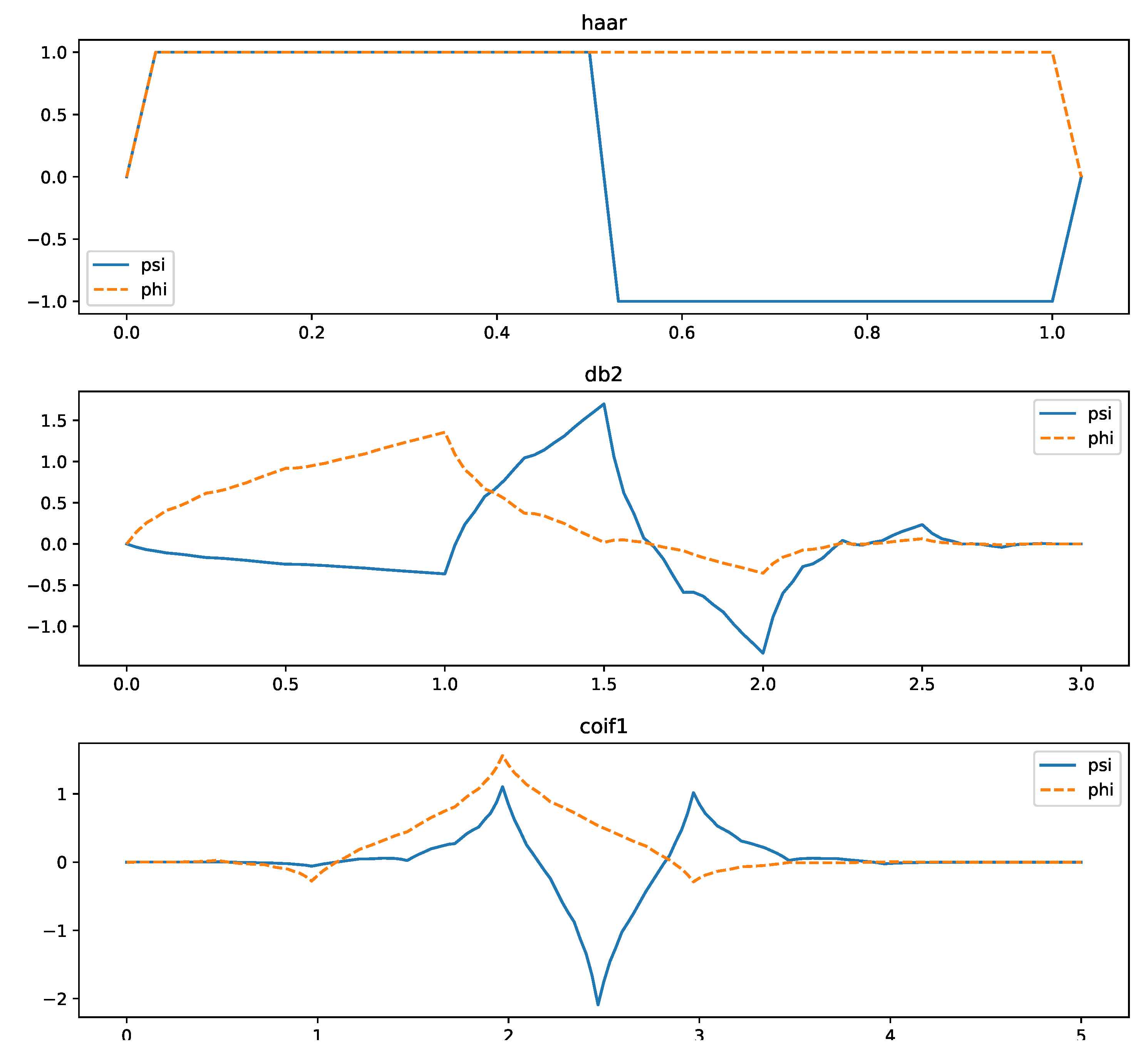
In power systems, a wavelet-based data compression method can be used to compress the recorded data of oscillations [54]. This method selects the optimal wavelet function and decomposition scale according to the criterion of the minimum compression distortion composite index (CDCI). The most popular wavelet functions are the Haar, Daubechies, and Coiflet families (Figure 5). This balances compression performance and reconstruction accuracy [55].

The wavelet function and decomposition scale can be selected directly according to the oscillation frequency, which is the most significant characteristic of oscillations. The amount of calculation in this method is much lower than that in methods that require compressing and reconstructing signals with all candidates of wavelets and scales. This makes the wavelet-based data compression method for oscillations in power systems particularly efficient [57]. In the wavelet-based data compression method, the window length of data to be processed at a time deserves careful consideration. The length of a window defines the compromise between compression ratios and distortion rates [58].

The compression ratio depends on the oscillation frequency and can almost reach the compression ratio limit of scale i. The distortion rate is on the order of ${10}^{-4}$ in general and is always no more than 2 × 10${}^{-3}$. The computational burden is not great for compression in storage.

Wavelet compression in general is a better solution for handling transients [59], which makes it more effective for unstable grids. It can be used as a component of the hybrid method, together with other algorithms, that work better for predictable periodic data, which is a common type of signal in stable power grids [21].

3.6. Differential Encoding

Differential encoding is a data compression technique that works by encoding the difference between consecutive data points rather than the data points themselves (Algorithm 4). This technique is particularly useful for time-series data where the values are often similar to those of their neighbors [60]. By encoding the differences, we can significantly reduce the amount of data that need to be stored, leading to more efficient storage and faster data retrieval [61].

The time complexity of this algorithm is O(n), where n is the number of data points. This is because we are performing a constant amount of work for each data point: calculating the difference and appending it to the list.

The space complexity of the algorithm is also O(n), since we are storing a new piece of data for each data point. However, the space required to store the encoded data is generally much less than the space required to store the original data, especially for time-series data with many similar consecutive values [62].

Algorithm 4 Differential encoding algorithm

Require: Time-series data D Ensure: Encoded data E  $E\leftarrow \varnothing$  $E\leftarrow E\cup D\left[1\right]$  for $i\leftarrow 2$ to n do      $E\leftarrow E\cup \left(D\right[i]-D[i-1\left]\right)$  end for

Differential encoding is frequently used in compressing data in stable systems, where consecutive values do not change much. The compression ratio may deteriorate in systems with a high disturbance ratio. Differential encoding is perfect for reducing the size of data in stable periods of operation, but it is unlikely to be an optimal solution to compress transients [40]. This algorithm, in general, can be used to improve the performance of real-time systems during stable periods of operation and to significantly improve the compression of non-time-critical data in the processing of large power-quality datasets.

3.7. Burrows–Wheeler Transform (BWT)

The Burrows–Wheeler transform (BWT) is a block-sorting data transformation algorithm that is used in data compression (Algorithm 5). It is not a standalone data compression method, however; it is being used as a component with different solutions to increase the performance of other data compression algorithms [63]. BWT rearranges the input data in a way that similar data elements are grouped together. This property of BWT is exploited in the Burrows–Wheeler transform compression (BWT-C) algorithm, which is a data compression algorithm that is particularly effective for data with long repetitive sequences [64].

Algorithm 5 Burrows–Wheeler transform (BWT)

Require: $string$ Ensure: $BWT\_string,last\_column\_index$  $rotations\leftarrow generate\_rotations\left(string\right)$  $sorted\_rotations\leftarrow sort\left(rotations\right)$  $BWT\_string\leftarrow concatenate(sorted\_rotations)$  $last\_column\_index\leftarrow find\_last\_column\_index(string,BWT\_string)$  return $BWT\_string,last\_column\_index$

In the context of power-system-related data, BWT-C could be particularly useful. Data from power systems often contain long sequences of similar values, such as multiple readings of the same power consumption or generation value. Using BWT, these similar values are grouped together, which can significantly reduce the size of the data. BWT can also be used for methods that compress and encrypt data sent in power grids [65].

The BWT-C algorithm works in several stages. First, the input data are transformed using the Burrows–Wheeler transform, which rearranges the data in such a way that similar data elements are grouped together [66]. This is carried out by sorting the input data according to the characters that follow each character in the data.

The transformed data are then compressed using a lossless compression algorithm, such as Run-Length Encoding (RLE) or move-to-front transform (MTF). These algorithms take advantage of the fact that similar values are grouped together in the transformed data to further compress the data [67].

Finally, the compressed data are encoded into a format that can be easily stored or transmitted [40]. This can be carried out using any suitable encoding method, such as Huffman coding or arithmetic coding [68].

The use of BWT-C in real-time systems is particularly interesting. In real-time systems, data are continuously generated, and it is necessary to compress these data in real time to avoid storage overflow or transmission delay. Using BWT-C, it is possible to compress large amounts of data from power systems in real time, making it suitable for use in real-time systems [69].

In conclusion, the Burrows–Wheeler transform can be used to compress data related to power systems by rearranging the data in such a way that similar values are grouped together [70]. This can significantly reduce the size of the data, making it suitable for use in real-time systems. The use of the Burrows–Wheeler transform in data compression is a complex process that involves several stages, but it can be highly effective when used correctly.

3.8. Move-to-Front (MTF) Encoding

Move-to-front transform (MTF) is a data encoding technique designed to enhance the performance of entropy encoding techniques of compression [71]. The MTF transform works by maintaining an ordered list of legal symbols (for example, a to z in case of English text) [72]. The process involves searching for the input character in the list, printing the position at which the character appears in the list, and then moving that character to the front of the list (Algorithm 6). This process is repeated until indexes for all input characters are obtained [73].

Algorithm 6 Move-to-front encoding (MTF)

Require: $input\_text,len\_text,list$ Ensure: $output\_arr$  for $i=0$ to $len\_text$ do     $output\_arr\left[i\right]\leftarrow search(input\_text[i],list)$     $moveToFront(output\_arr[i],list)$ end for return $output\_arr$

The MTF transform is particularly effective in reducing the entropy of a message by exploiting the local correlation of frequencies [74]. This means that letters recently used stay at the front of the list, resulting in a large number of small numbers such as “0” and “1” in the output if the use of letters exhibits local correlations [74].

However, not all data exhibit this type of local correlation. For some messages, the MTF transform may actually increase the entropy. However, an important use of the MTF transform is in Burrows–Wheeler transform-based compression. The Burrows–Wheeler transform is very good at producing a sequence that exhibits local frequency correlation from text and certain other special classes of data [63]. Compression benefits greatly from following up the Burrows–Wheeler transform with an MTF transform before the final step of entropy encoding [73].

One problem with the basic MTF transform is that it makes the same changes for any character, regardless of frequency, which can result in decreased compression, as characters that occur rarely may push frequent characters to higher values [75]. Due to the fact that there is a risk of negative compression, especially in grids with high distortion, proper algorithm calibration is needed. Various alterations and alternatives have been developed for this reason. One common change is to make it so that characters above a certain point can only be moved to a certain threshold [76]. Another is to make an algorithm that runs a count of each character’s local frequency and uses these values to choose the characters’ order at any point. Many of these transforms still reserve zero for repeat characters since these are often the most common in data after the Burrows–Wheeler transform. In the context of real-time systems operating in the domain of power grids, the MTF transform can be particularly useful in systems where data are frequently updated or where there is a high degree of local correlation in the data [77].

3.9. Real Time Compression—Prequisities

In general, selecting the right data compression method for a system is based on balancing compression ratio, data distortion, and computational complexity [78]. However, in the domain of power systems, data that are being used for non-time-critical purposes mostly focus on achieving a high compression ratio with low data distortion. Algorithm complexity is rarely a case for such an application, since long computing times are acceptable, for the gain of reduced communication medium usage. Real-time systems give much more constraints on the selected method [10,79].

• Understanding of the application domain: In power grid applications, a thorough understanding of data types, characteristics, and permissible loss in data fidelity is crucial for effective data compression [80]. Knowledge of the properties of the power system and the purpose of compressed data is crucial. The systems used to protect the grid shall not lose transient data that may lead to false negatives. Metrology devices that are used to monitor systems with constant distortion should be carefully analyzed before using methods that result in negative compression.
• Timing constraint analysis: Real-time power grid systems have stringent timing requirements. It is essential to analyze task scheduling, response time, and deadline constraints to select appropriate compression techniques. This is a complex parameter to analyze since it requires deep knowledge of the data being compressed and computational capabilities of metrological system [81].
• Compression algorithm selection: The choice of compression algorithms must consider the trade-off between compression ratio and computational overhead. Customized real-time compression algorithms may be necessary to optimize performance. Stream algorithms in most cases offer lower latency, but also a lower compression ratio. In the case of block algorithms, block size should be carefully considered in order not to violate real-time constraints due to the long time needed to fill the buffer [82].
• Hardware and software considerations: Hardware and software platforms play a vital role in compression [83]. Understanding their capabilities and limitations is crucial to selecting and implementing compression techniques. Many modern embedded systems offer hardware acceleration for selected data compression methods [84], which significantly improves their performance [83,85]. Some software platforms also implement data compression algorithms on the lower layers of their architecture, which makes their use easier and more efficient. Field-programmable gate arrays (FPGAs) are a frequent choice for low-level acceleration of data compression algorithms in power grids [86,87,88].
• Error detection and correction: Robust error detection and correction mechanisms are essential to ensure data integrity, especially in noisy power grid environments prone to transmission errors [89]. The exact meaning of error varies between applications, but in general, should be considered a violation of the purpose of the system. For systems reacting to transients reporting false detection or omitting the actual event, this can be considered an error from the functional point of view. For monitoring systems used for power quality analysis, a difference in aggregated samples from real values is the most critical measure of an error [90].
• Validation and testing: Rigorous validation and testing procedures, including worst-case execution time analysis and simulation, are essential to confirm that the compression scheme meets real-time requirements in power grid applications [91]. Due to the network nature of power grids, every device used shall be compliant with legislation. Validation of such systems is a complex, long, and costly process; hence, special effort should be carried out during the development phase in order to avoid test failure.
• Efficiency and reliability: Meeting these prerequisites forms a strong foundation for enhancing the efficiency and reliability of data compression in real-time power grid systems [92]. Many power systems are used in remote locations with limited ability to monitor their operations. The design of such systems should also take into account the long period of their usage, and compliance with other systems that can be used in the future in case of expansion of modernization of adjacent systems [93].

3.10. Error Resilience

In the context of power grids, error resilience in data compression algorithms is crucial for real-time systems. This is due to the high volume of data generated by power grids, which can lead to data congestion if not properly managed [94]. The data generated include information about power generation, transmission, and distribution, as well as information about potential faults and disturbances in the power grid.

One approach to managing these data is the use of real-time energy data compression strategies. These strategies aim to reduce data traffic by compressing meter data efficiently. This is particularly important in smart grid systems, which feature an advanced metering infrastructure (AMI) that automatically collects meter data from widely distributed sensors [95].

The proposed algorithm for real-time energy data compression combines several existing compression algorithms and operates from 2 to 10% more efficiently than previously published algorithms. This efficiency is crucial in real-time systems, where data must be processed and transmitted quickly to avoid delays and potential system failures.

In addition to data compression, the resilience of errors in power grid systems also involves the use of machine learning and artificial intelligence techniques for fault detection and diagnosis. These techniques can help identify and diagnose faults in the power grid in real time, allowing quick remediation and minimizing the impact of these faults on power grid operation [96].

For example, hybrid machine learning models can be used to improve the resilience of the power grid through real-time fault detection and remediation [97]. These models combine different machine learning techniques to improve the accuracy and efficiency of fault detection and diagnosis.

In addition, the resilience of a power grid can be measured using a Dynamic Inoperability Input-output Model (DIIM). DIIM reflects the ability of the power grid to deal with disturbances and changes in the equilibrium state through the restoration ability. This model can be used to measure the resilience of the power grid and to verify the effectiveness of the measures taken to improve the resilience of the power grid [98].

Forward error correction (FEC) is a method used in data communication to detect and correct errors that occur during data transmission. FEC works by adding redundant data to the original data before it is transmitted [99]. This redundant data are used to detect and correct errors that occur during transmission. If an error is detected, the redundant data are used to correct the error. This allows the original data to be reconstructed accurately, even if some of it was lost or corrupted during transmission [100,101].

Table 2. Comparison of compression algorithms for time-series databases.

Algorithm	Category	Real-Time Application Benefits	Real-Time Application Drawbacks	Non-Time-Critical Application Benefits	Non-Time-Critical Application Drawbacks	References
RLE	Lossless	Low computational complexity	Less efficient for block algorithms	Well performing on large datasets, good compression of datasets with multiple subsequent occurrences of the same symbol	Low compression ratio	[102]
Sliding-window RLE	Lossless	Block operation, low latency for streaming	Lower compression ratio	More predictable output data format, block division may reduce compression ratio	Block division may reduce compression ratio	[103,104]
Huffman Coding	Lossless	Variable length, efficient for compression of smooth time-series	Changes to the dictionary might deteriorate performance	Well performing on large datasets, efficient compression for repetitive patterns	Efficiency relies on the fixed dictionary, complex computation	[40]
LZW	Lossless	Efficient for block operation, availability of hardware acceleration	Requires proper definition of dictionary	Adaptation to the input data, efficient for frequently occurring patterns	The size of the dictionary can grow significantly for large datasets, adds computational complexity	[39]
DCT	Lossy or Lossless	Ability to lose frequency components irrelevant for the application, preprocessing of data	Improper parameters selection may result in the loss of relevant data	Concentration of most of the signal energy in few crucial coefficients	Blocking artifacts as a result of data quantization	[105]
Wavelet Transform	Lossy or Lossless	Preprocessing of transient data, lowering computational effort for the controller	Inefficient for smooth signals, complex computation, possible block artifacts	Efficient for compressing data with diverse patterns, multiresolution analysis, possibility of 2D representation of a large dataset useful for trends observation	Complex computation for large datasets, performance of the algorithm is very sensitive to the choice of parameters	[106,107]
Differential Encoding	Lossless, possible lossy	Low computational complexity, optimized for streamed data	Risk of error accumulation, sensitive to data variation	Low complexity and simple implementation, adaptable to trends	Risk of error accumulation, sensitive to data variation	[60,62]
BWT	Lossless	Preprocessing data blocks, enhancement of other algorithms, simple decompression	Added complexity, reduced benefit with distorted data	Efficient for compressing data with local patterns and repetitive sequences	Performance dependent on input data	[77]
MTF	Lossless	Preprocessing data blocks, enhancement of other algorithms	Variable compression ratio depending on the input	Simple implementation	Compression ratios may vary depending on the input data	[108]

Table 2. Comparison of compression algorithms for time-series databases.

Algorithm	Category	Real-Time Application Benefits	Real-Time Application Drawbacks	Non-Time-Critical Application Benefits	Non-Time-Critical Application Drawbacks	References
RLE	Lossless	Low computational complexity	Less efficient for block algorithms	Well performing on large datasets, good compression of datasets with multiple subsequent occurrences of the same symbol	Low compression ratio	[102]
Sliding-window RLE	Lossless	Block operation, low latency for streaming	Lower compression ratio	More predictable output data format, block division may reduce compression ratio	Block division may reduce compression ratio	[103,104]
Huffman Coding	Lossless	Variable length, efficient for compression of smooth time-series	Changes to the dictionary might deteriorate performance	Well performing on large datasets, efficient compression for repetitive patterns	Efficiency relies on the fixed dictionary, complex computation	[40]
LZW	Lossless	Efficient for block operation, availability of hardware acceleration	Requires proper definition of dictionary	Adaptation to the input data, efficient for frequently occurring patterns	The size of the dictionary can grow significantly for large datasets, adds computational complexity	[39]
DCT	Lossy or Lossless	Ability to lose frequency components irrelevant for the application, preprocessing of data	Improper parameters selection may result in the loss of relevant data	Concentration of most of the signal energy in few crucial coefficients	Blocking artifacts as a result of data quantization	[105]
Wavelet Transform	Lossy or Lossless	Preprocessing of transient data, lowering computational effort for the controller	Inefficient for smooth signals, complex computation, possible block artifacts	Efficient for compressing data with diverse patterns, multiresolution analysis, possibility of 2D representation of a large dataset useful for trends observation	Complex computation for large datasets, performance of the algorithm is very sensitive to the choice of parameters	[106,107]
Differential Encoding	Lossless, possible lossy	Low computational complexity, optimized for streamed data	Risk of error accumulation, sensitive to data variation	Low complexity and simple implementation, adaptable to trends	Risk of error accumulation, sensitive to data variation	[60,62]
BWT	Lossless	Preprocessing data blocks, enhancement of other algorithms, simple decompression	Added complexity, reduced benefit with distorted data	Efficient for compressing data with local patterns and repetitive sequences	Performance dependent on input data	[77]
MTF	Lossless	Preprocessing data blocks, enhancement of other algorithms	Variable compression ratio depending on the input	Simple implementation	Compression ratios may vary depending on the input data	[108]

4. Compression and Security

In the past, many data transmission channels in power grids were isolated and thus physically inaccessible to the attacker. In such systems, the security of the data was not considered. At present, many measurement systems work in the IoT network, utilizing mediums and infrastructure available to other entities. This raises concerns about data security. Compression algorithms are not neutral for security. The application of data compression influences the security properties of the systems in various ways.

4.1. Data Transmission Efficiency

Data compression is often used to reduce the size of files or data for more efficient transmission over networks. Smaller data sizes mean faster transmission times and reduced bandwidth usage. In a cybersecurity context, this efficiency is crucial to maintaining a secure and responsive network. Faster transmission can contribute to faster response times in the detection and prevention of security threats.

4.2. Network Security

Compressed data can impact how security devices, such as firewalls and intrusion detection systems, analyze network traffic. Some security tools may struggle to inspect compressed data effectively, potentially allowing malicious content to pass undetected. Attackers may use compression to obfuscate their payloads and make it harder for security systems to identify and block malicious activities.

4.3. Data Integrity

Compression algorithms, if not implemented or configured properly, can introduce vulnerabilities that attackers might exploit. Poorly designed compression algorithms may lead to data corruption or even facilitate certain types of attacks, such as compression-based attacks like the CRIME (Compression Ratio Info-leak Made Easy) attack, which targets the compression used in SSL/TLS protocols.

4.4. Storage Security

In storage environments, compressed data are commonly used to optimize storage space. However, security concerns arise if the compression algorithm is not secure. If an attacker can manipulate compressed data in a way that exploits vulnerabilities in the decompression process, it could lead to security breaches. Properly securing compressed data during storage is essential to maintain the confidentiality and integrity of sensitive information.

4.5. Secure File Transfer

In secure file transfer protocols, compression is often integrated to optimize data transfer times. However, the security of the compression algorithm and its implementation becomes paramount in ensuring the confidentiality and integrity of the transferred data. Encryption techniques are introduced to change the data before transfer in order to preserve the privacy of parties participating in communication [109] or protect the confidentiality of the data from adversaries. In many cases, the transmitted measurement data has the form of a 2D graphic, which is compressed using image codecs [110]. In such cases, it is crucial to compress data with preservation of the quality suitable for further data processing and maintain security properties of encryption [111].

4.6. Attack Scenarios Exploiting Compression Methods

Data compression bring benefit in the form of more efficient communication; however, changing the properties of data may expose the system to exploitation.

• Side-channel security of smart meter data compression techniques. In this scenario, attackers exploit side-channel information to compromise the security of smart meters leveraging data compression techniques. By analyzing patterns such as power consumption, bus load, and temperature of systems processing compressed data, adversaries can gain insight into power consumption patterns, potentially revealing sensitive information about occupants’ behavior or activities [112,113]. Unauthorized access to detailed information on power usage could lead to privacy breaches, enabling malicious entities to deduce occupancy patterns and habits or even identify periods of low security on a premise.
• Joint adversarial example and false data injection attacks for state estimation in power systems. Adversaries generate adversarial examples in compressed data sent for state estimation in power systems [114,115]. Additionally, false data injection attacks can involve injecting compressed or manipulated data into the system [116,117]. These attacks can compromise the accuracy of state estimation algorithms, leading to incorrect assessments of the state of the power system [118]. Misleading state estimates can result in improper control actions [119], potentially causing disruptions, overloads, or cascading failures in the power grid. This could lead to severe operational challenges, affecting the reliability and stability of the entire power system [120].
• Adversarial attacks and defenses for deep learning-based unmanned aerial vehicles (UAVs). Smart grids increasingly use UAVs for monitoring and maintenance. Adversarial attacks on the data compression techniques used in UAV communications can involve manipulating compressed data to deceive or disrupt the operation of these vehicles [121]. This might include altering sensor data or compromising communication channels [122]. Adversarial attacks on UAVs can lead to incorrect or delayed information, affecting decision-making processes in power grid management. This could potentially disrupt critical tasks such as infrastructure inspection, maintenance, or emergency response.
• Data integrity attacks on smart grid communication channels. Attackers exploit vulnerabilities in compression algorithms to manipulate or corrupt compressed data during transmission [123]. This can involve injecting false information, altering control signals, or disrupting communication channels between various components of the smart grid. Compromised data integrity can lead to incorrect decision-making in power grid control systems.
• Eavesdropping on compressed communication channels. Adversaries may eavesdrop on compressed communication channels within the smart grid. By intercepting and analyzing compressed data, attackers can gain insight into sensitive information, including control commands, grid configurations, or operational strategies [124]. Unauthorized access to critical information can allow attackers to plan more sophisticated and targeted attacks on the power grid, potentially leading to service disruptions, financial losses, or even physical damage to the infrastructure.

4.7. Influence on Entropy

Both data compression and cryptography focus on the modification of the message entropy; however, their point is the opposite. The goal of cryptography is to increase the entropy of the data, while the goal of compression is to reduce the entropy of the data. Through encryption, cryptography aims to transform data into a more unpredictable and seemingly random form, making it difficult for unauthorized parties to decipher without the appropriate key. Cryptography and compression serve opposite purposes in terms of data entropy. Cryptography seeks to make data more unpredictable and secure, while compression seeks to make data more efficient and space-saving by reducing redundancy and, consequently, lowering entropy. It is important to take security into account during the development of the data compression strategy.

5. Future Work

A future trend in the development of data compression techniques in smart grids could be the integration of machine learning and artificial intelligence (AI) to improve the efficiency and adaptability of these techniques.

Machine learning algorithms can be used to analyze patterns in data, which can help in the development of more efficient compression algorithms. Machine learning algorithms excel at uncovering intricate patterns and relationships within complex datasets. In the realm of data compression for smart grids, these algorithms can be trained to recognize the significance of different data segments. For example, in power systems, machine learning can identify critical aspects of electrical signals that must be preserved for accurate analysis. Subsequently, this insight aids in the development of more sophisticated compression algorithms that selectively retain essential information while efficiently compressing less critical data. This approach helps mitigate computational complexity and storage requirements [125].

Artificial intelligence can also be used to optimize the parameters of compression algorithms in real time, based on the characteristics of the data and the requirements of the system [95,126]. Artificial intelligence, particularly through the use of advanced algorithms, can optimize compression processes dynamically in real time. This adaptability is crucial in smart grid scenarios where the nature of the data and system requirements can vary. AI algorithms can continuously assess factors such as the urgency of data transmission, the available bandwidth in communication channels, and the specific needs of the system. By adjusting compression parameters on the fly, AI ensures that the compression process is aligned with the dynamic demands of the smart grid environment. This adaptability improves the overall efficiency of the data compression system.

Another potential trend is the use of quantum computing for data compression. Quantum computing has the potential to significantly speed up the compression and decompression processes, which could be particularly beneficial for handling large volumes of data in smart grids. However, this would require significant advancements in quantum computing technology [127]. Quantum computing introduces a paradigm shift in data compression by leveraging the principles of quantum mechanics. The inherent parallelism and superposition capabilities of quantum bits (qubits) can significantly speed up compression and decompression processes. In the context of smart grids, this translates to faster and more efficient handling of large volumes of data. Quantum computing has the potential to revolutionize the processing of complex datasets, which makes it particularly advantageous for the high-throughput requirements of smart grids. However, it is essential to note that the practical implementation of quantum computing in this domain necessitates substantial advancements in quantum technology, including error correction and scalability.

Finally, the development of more advanced data compression techniques that can handle different types of data and different levels of compression could also be a future trend. For example, techniques that can handle lossless and lossy compression or that can adapt the level of compression based on the characteristics of the data [128].

6. Summary

The primary objective of this paper was to draw attention to a major problem for automation, measurement, and control of power systems in the imminent future. The focal point of our investigation was the advancements made in the realm of compression techniques applied to electric signals. We delved into the existing developments in this area and shed light on the critical need for robust compression methodologies tailored for smart grid applications.

The most popular algorithms were described with application details. The paper focused on two different ways of handling data in power grids—large datasets, used for non-time-critical analysis, like power quality reports or monthly billing of the electricity consumers, and real-time data transfer, for time-critical purposes like islanding protection or circuit breakers. The advantages and drawbacks of selected data compression algorithms were presented in the application for both of these purposes.

In addition to emphasizing the current state of electric signal compression techniques, the paper underscored the necessity of introducing powerful compression methods to address the specific challenges posed by smart grid applications. As our world becomes increasingly interconnected, the demand for efficient and secure data transmission in smart grids grows substantially. Here, the synergy between cybersecurity and data compression becomes particularly noteworthy.

The relationship between cybersecurity and data compression in the context of smart grids lies at the intersection of efficient data handling and the securing of critical information. Although compression contributes to optimizing data transmission and storage, it introduces considerations for cybersecurity. Ensuring the confidentiality, integrity, and availability of compressed data becomes paramount, given the potential vulnerabilities that can be exploited by malicious actors. Therefore, future research efforts in this domain should focus not only on improving compression techniques but also on fortifying the cybersecurity measures associated with compressed data.

Addressing these research challenges is crucial to pave the way toward the development of novel and cost-effective devices. Reducing the amount of data transferred will facilitate the development of smart sensing, monitoring, metering, diagnosis, and protection systems in the next generation of electric power systems: smart grids. By addressing these challenges at the intersection of compression technologies and cybersecurity, we can propel the advancement of resilient and secure solutions for the evolving landscape of power systems.

The article aims to highlight the pressing challenges in the automation, measurement, and control of power systems, focusing on the need for robust compression techniques tailored for smart grid applications. The paper explores existing advancements in compression methods for electric signals, addressing two main aspects of power grid data handling: large datasets for non-time-critical analysis and real-time data transfer for time-sensitive operations.

The popular compression algorithms, including the discrete cosine transform, wavelet transform, differential encoding, Burrows–Wheeler transform, and move-to-front encoding, are described with their application details. The advantages and drawbacks of these algorithms are discussed in the context of handling both large datasets and real-time applications in power grids.

The article emphasizes the importance of introducing powerful compression methods to meet the specific challenges posed by smart grid applications. As the world becomes more interconnected, the demand for efficient and secure data transmission in smart grids increases substantially. The article highlights the intersection of cybersecurity and data compression, underlining the need to ensure the confidentiality, integrity, and availability of compressed data. Future research efforts are suggested to focus on fortifying cybersecurity measures associated with compressed data, in addition to improving compression techniques.

Addressing these research challenges is crucial for the development of novel and cost-effective devices, facilitating advancements in smart sensing, monitoring, metering, diagnosis, and protection systems in the next generation of electric power systems: smart grids. The article envisions the advancement of resilient and secure solutions to meet the evolving landscape of power systems.