Heat Transfer Analysis for Combustion under Low-Gradient Conditions in a Small-Scale Industrial Energy Systems
Abstract
:1. Introduction
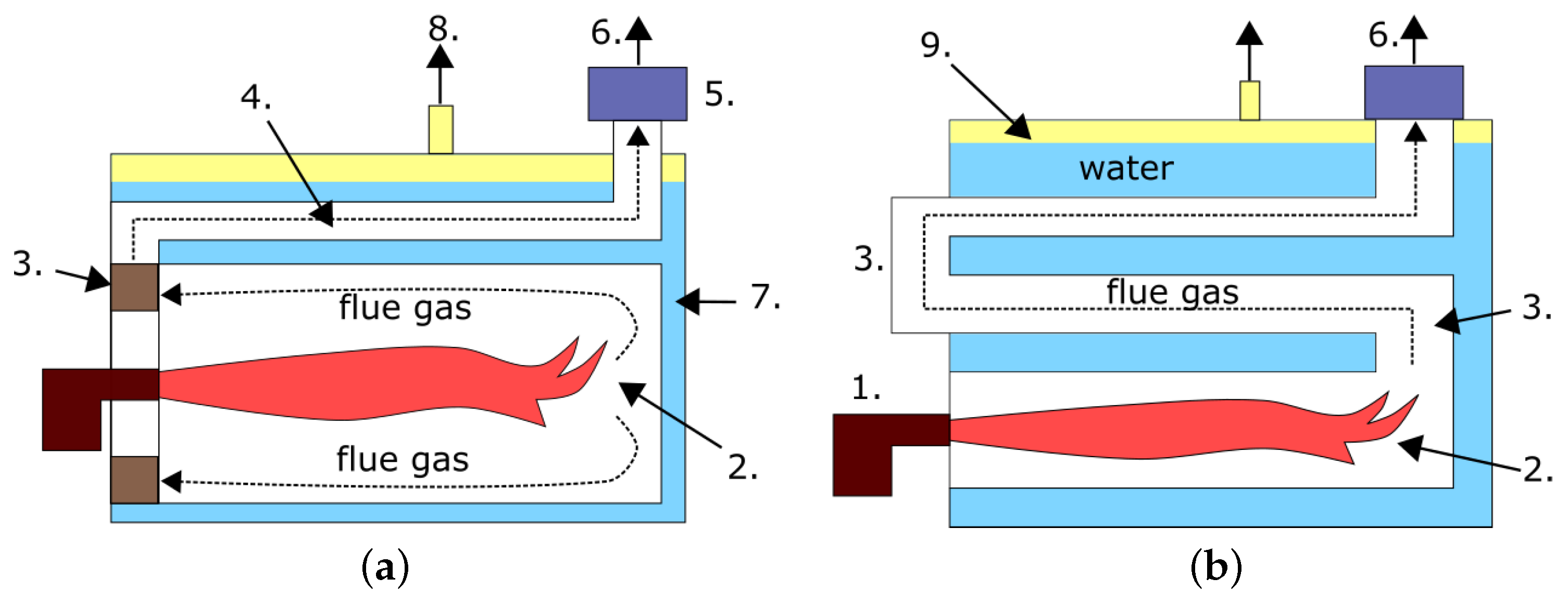
2. Construction and Operation Principle of Fire-Tube Boiler
3. Numerical Analysis
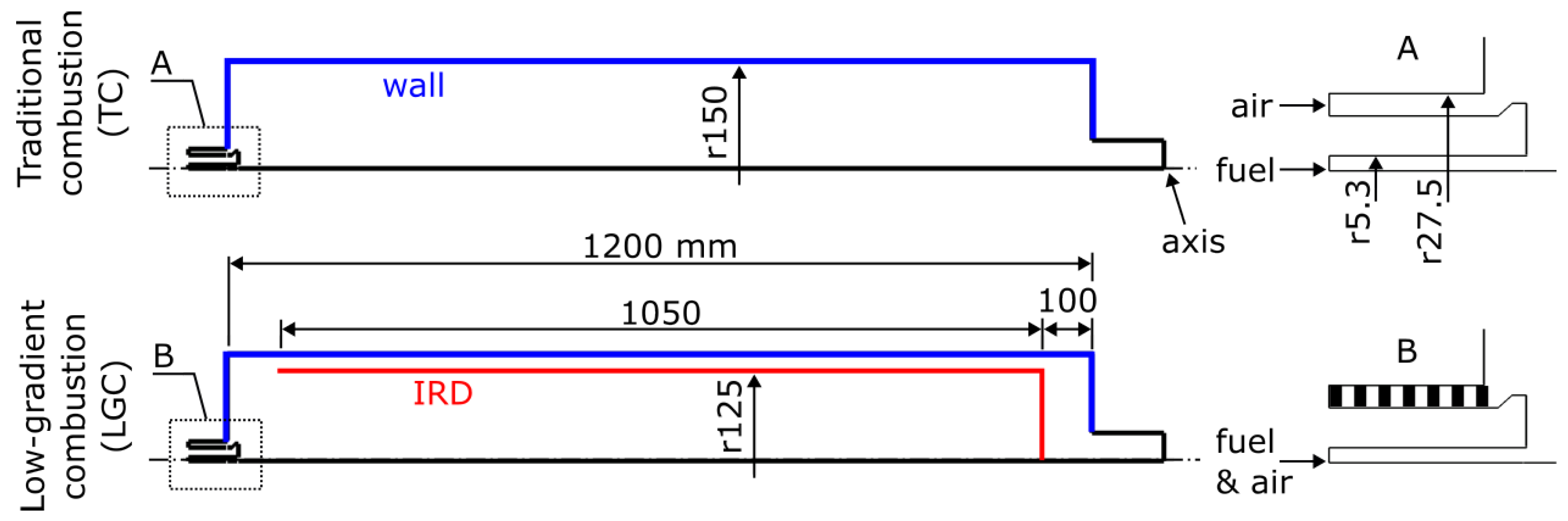
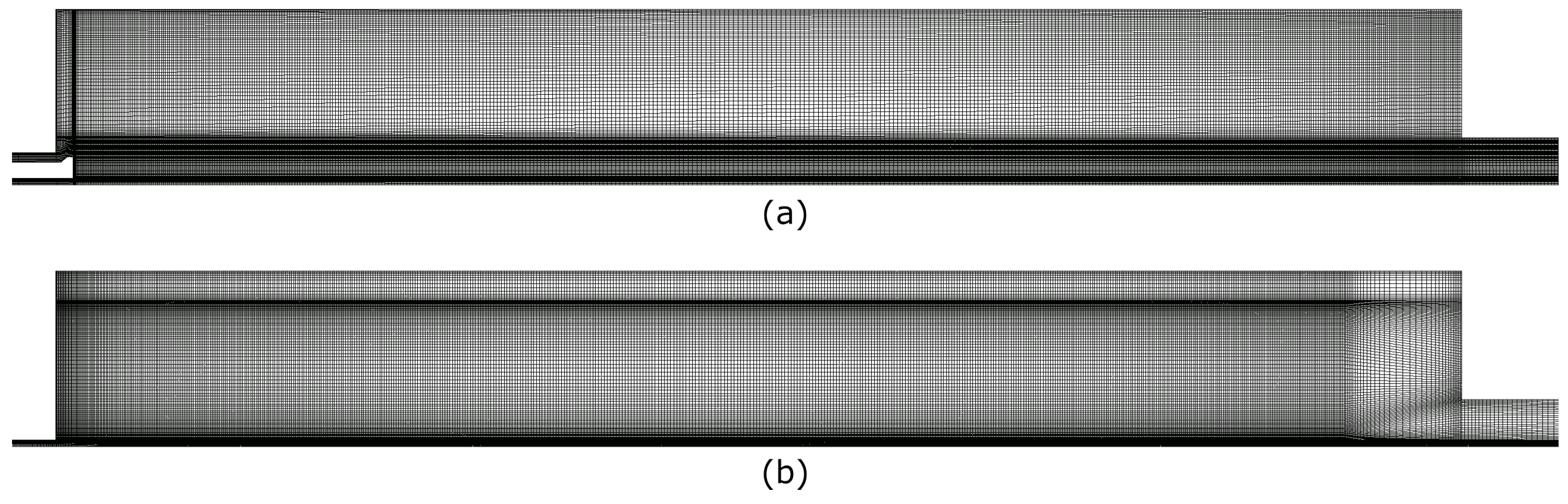
3.1. Computational Domains and Numerical Meshes
3.2. General Setup of the Numerical Model
3.3. Validation—Reference Results
4. Results and Discussion
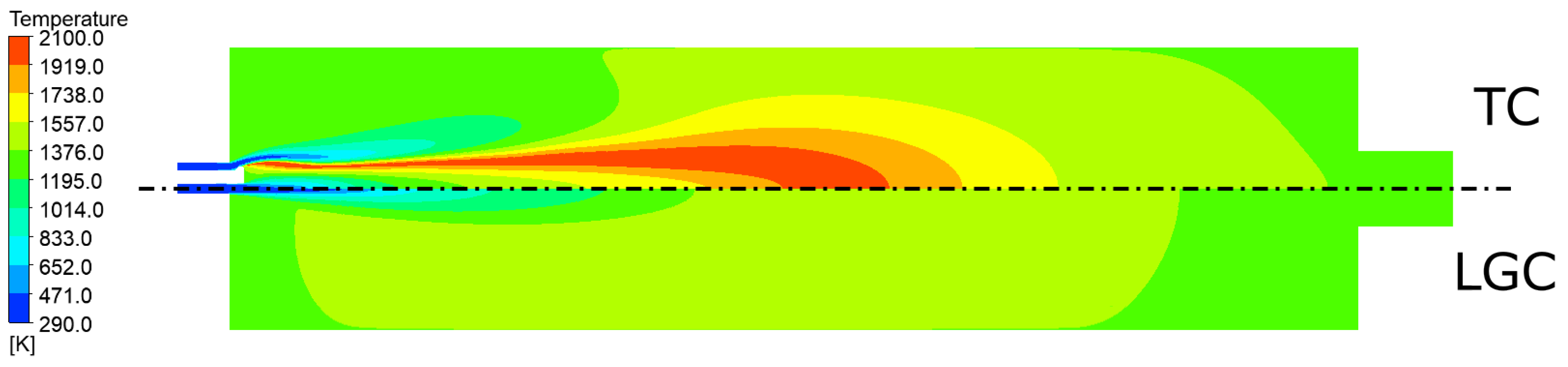
4.1. High Heat Extraction Conditions
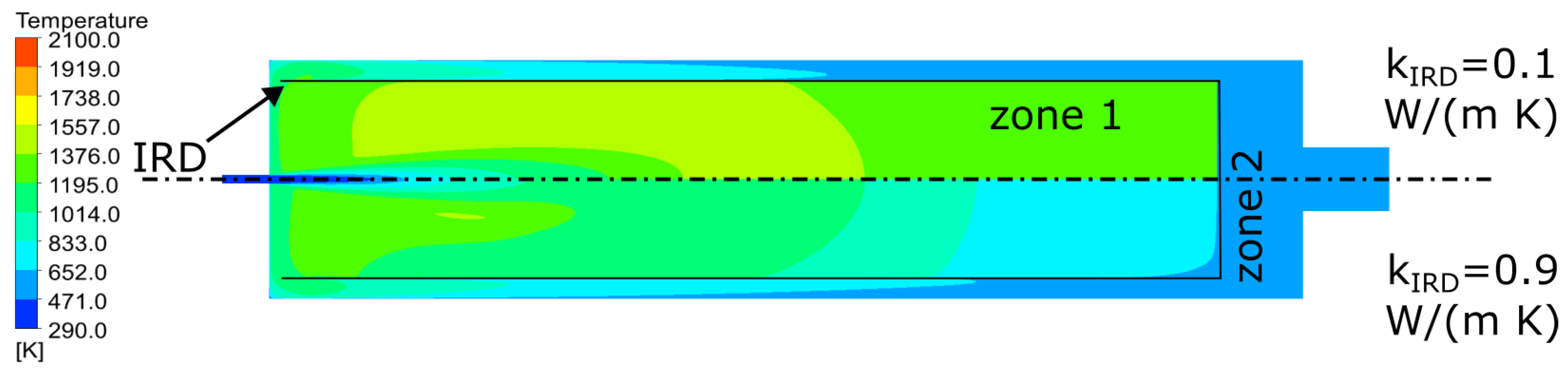
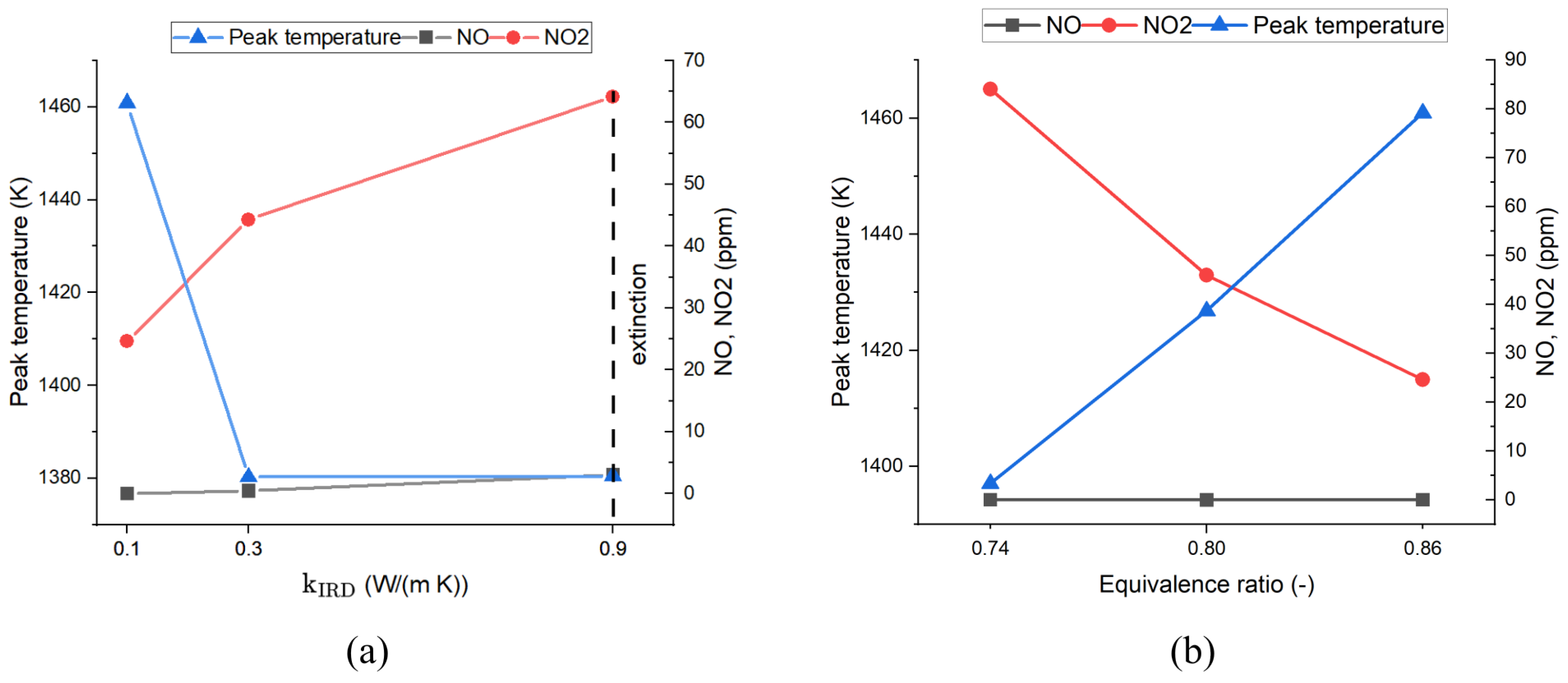
4.2. Impact of the IRD on Combustion and Emissions
4.3. Heat Transfer with the IRD
5. Conclusions
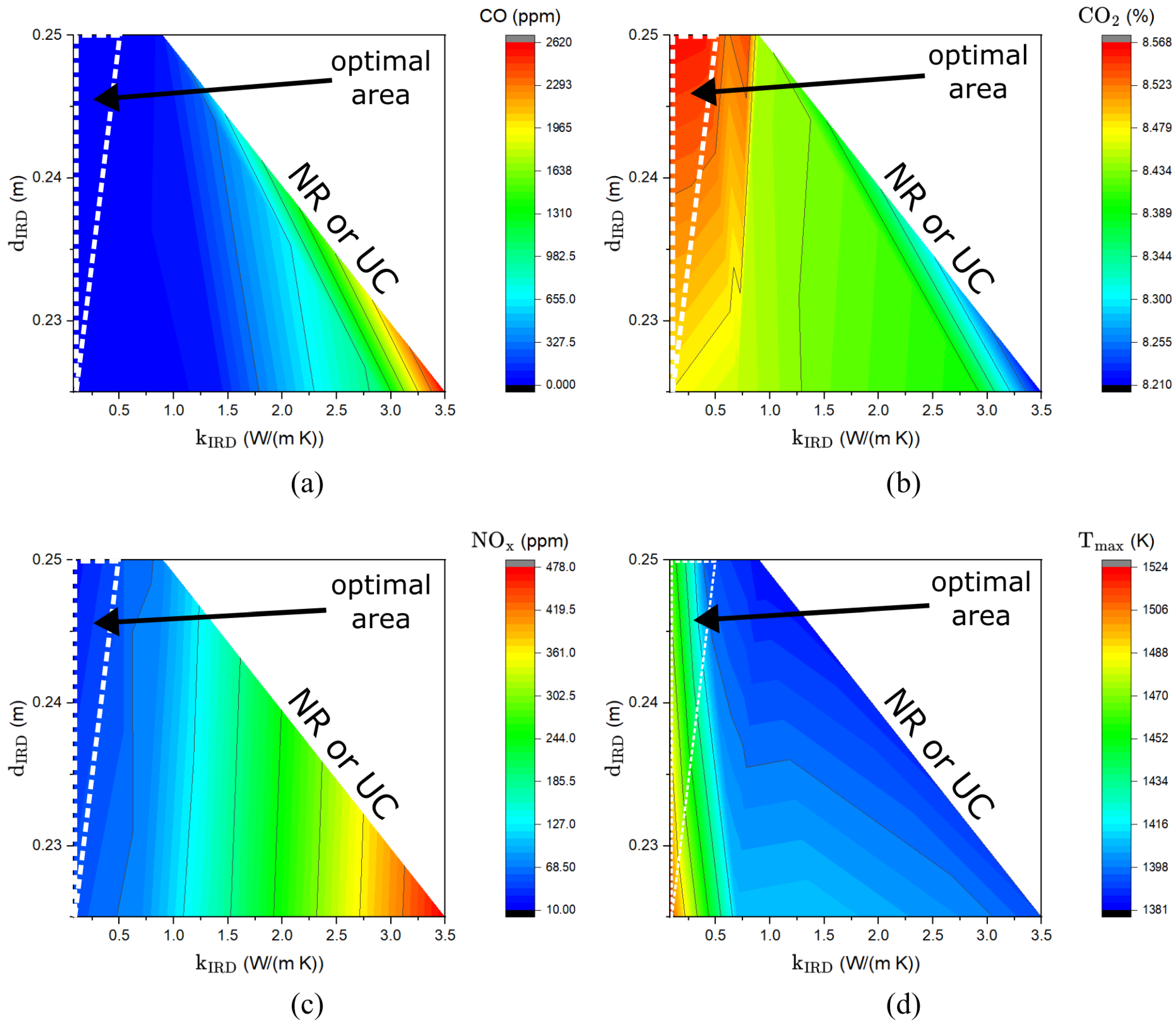
- Heat extraction efficiency is, indeed, capped at 88% after IRD introduction, regardless of IRD thermal conductivity and diameter . Also, critical = 0.9 W/(m·K) at = 0.25 m, beyond which combustion goes extinct, has been confirmed.
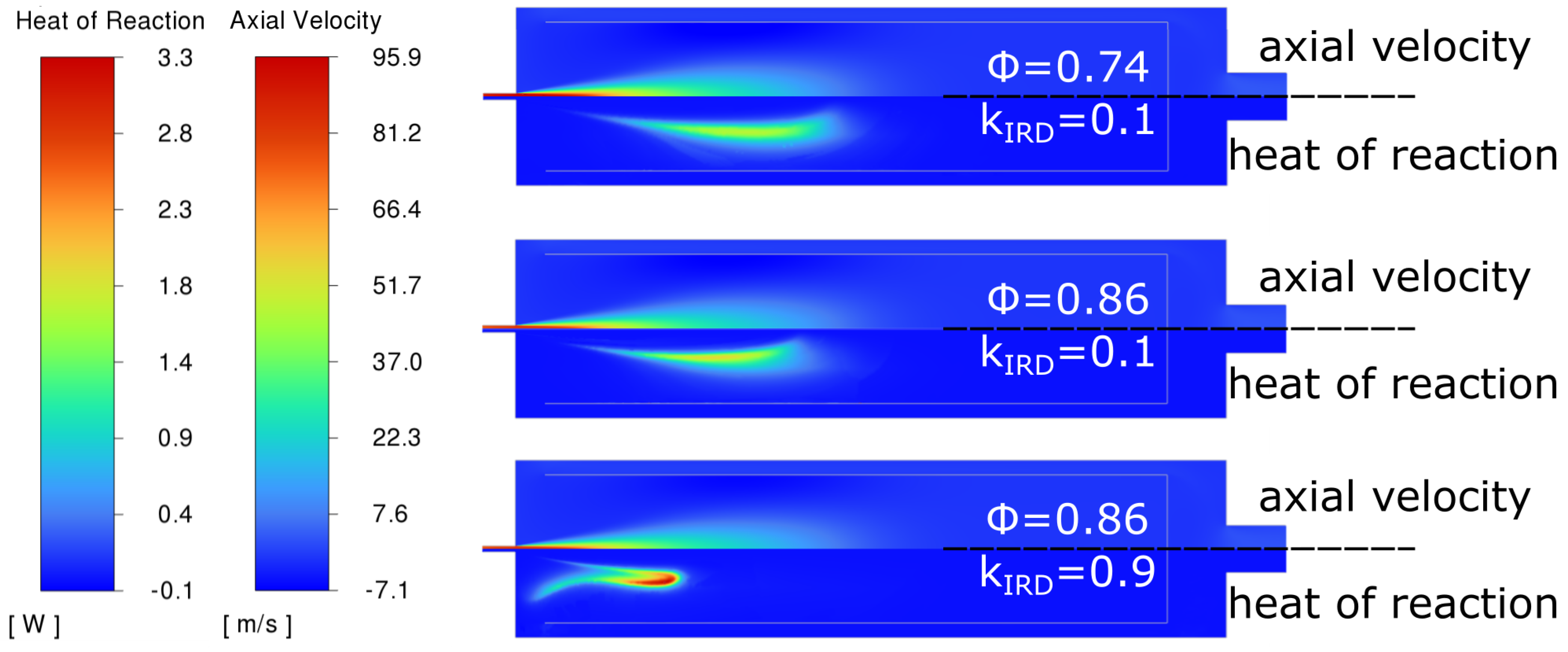
- Along with increasing (past 1 W/(m·K)), the temperature decreases within the combustion chamber. As a result, NO emission grows rapidly far above NO and NO emissions put together. The resulting total NO emission exceeds 150 ppm.
- IRD diameter lowered from 0.25 to 0.225 (by 10%) shifts critical towards higher values (from 0.9 W/(m·K) to at least 3.5 W/(m·K)). Consistent combustion extinction was observed even for low = 0.1 after increase in the diameter from 0.25 to 0.275.
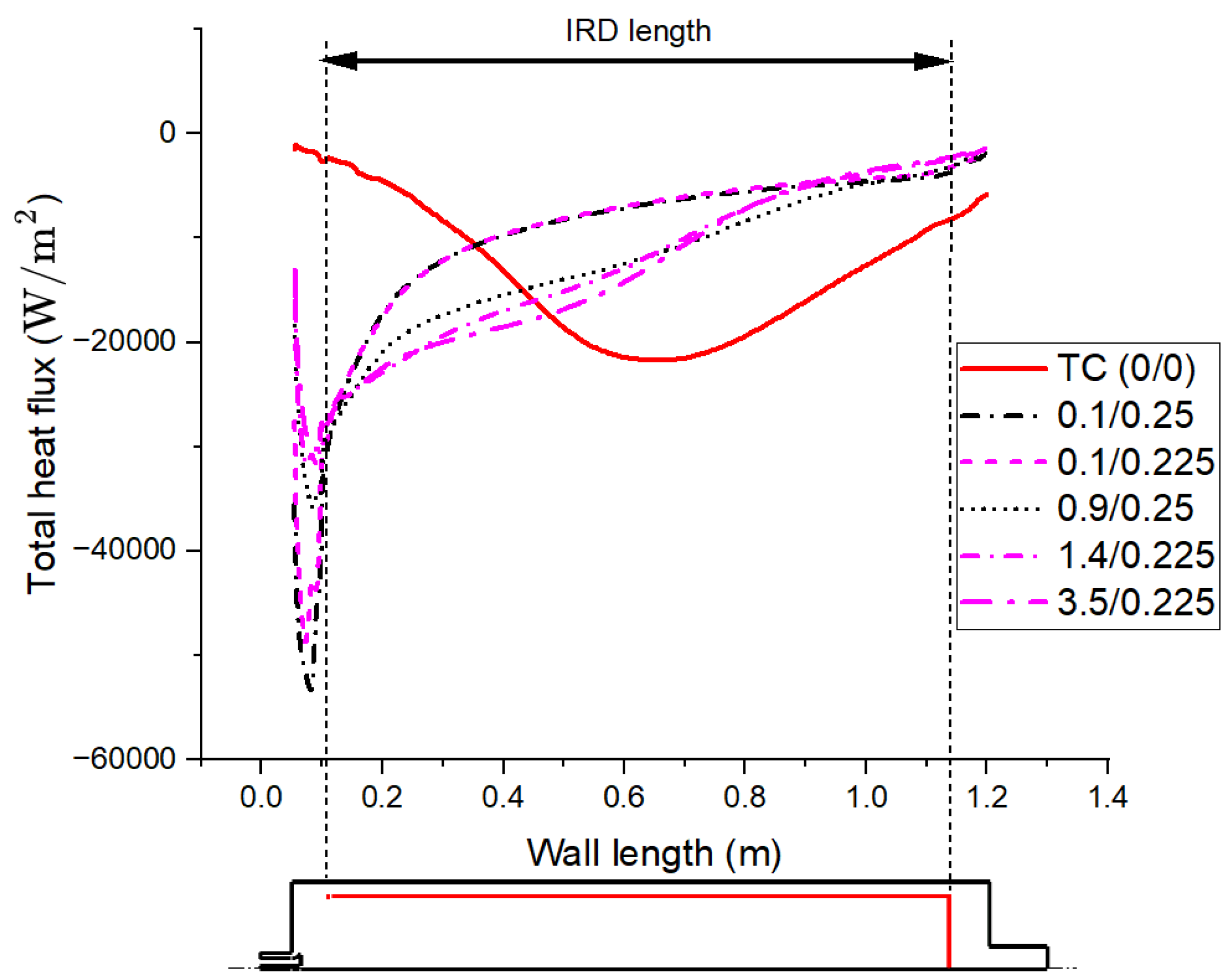
- Heat flux distribution at the external wall changes drastically after switching from TC to IRD-enhanced LGC. In TC mode, the distribution takes the shape of a bell curve (symmetrical to some extent), while in IRD-LGC, a steep gradient and extremum ahead of the IRD is noticeable, with a gradual decrease downstream. Additionally, LGC heat extraction efficiency (in addition to being fixed at 88%) is approximately 10% higher than TC heat extraction efficiency.
- Taking into account the serious impact of the IRD on CO and NO emissions, it should be very carefully designed in terms of material and its geometry to avoid excessive pollution and risk of flame extinction.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LGC | Low-Gradient Combustion |
| MILD | Moderate or Intense Low-oxygen Dilution |
| HiTAC | High-Temperature Air Combustion |
| HPAC | Highly Preheated Air Combustion |
| CFC | Colorless Distributed Combustion |
| FLOX | Flameless Oxidation |
| FC | Flameless Combustion |
| IRD | Internal Recirculation Device |
| BC | Boundary Condition |
| TC | Traditional Combustion (or conventional combustion) |
| EDC | Eddy Dissipation Concept |
| DO | Discrete Ordinates |
| WSGGM | Weighted-Sum-of-Gray-Gases Model |
| EXP | Experiment(al) |
| CFD | Computational Fluid Dynamics (or numerical) |
References
- Morelli, A.; Tognoli, M.; Ghidoni, A.; Najafi, B.; Rinaldi, F. Reduced FV modelling based on CFD database and experimental validation for the thermo-fluid dynamic simulation of flue gases in horizontal fire-tubes. Int. J. Heat Mass Transf. 2022, 194, 123033. [Google Scholar] [CrossRef]
- Aguilar Vizcarra, D.; Esenarro, D.; Rodriguez, C. Three steps mixed (Fire tube–water tube) vertical boiler to optimize thermal performance. Fluids 2021, 6, 93. [Google Scholar] [CrossRef]
- Kilic, G.; Sungur, B.; Topaloglu, B.; Ozcan, H. Experimental analysis on the performance and emissions of diesel/butanol/biodiesel blended fuels in a flame tube boiler. Appl. Therm. Eng. 2018, 130, 195–202. [Google Scholar] [CrossRef]
- Gutiérrez Ortiz, F.J. Modeling of fire-tube boilers. Appl. Therm. Eng. 2011, 31, 3463–3478. [Google Scholar] [CrossRef]
- Beyne, W.; Lecompte, S.; Ameel, B.; Daenens, D.; Van Belleghem, M.; De Paepe, M. Dynamic and steady state performance model of fire tube boilers with different turn boxes. Appl. Therm. Eng. 2019, 149, 1454–1462. [Google Scholar] [CrossRef]
- Ferrarini, L.; Rastegarpour, S.; Landi, A. Experimental model validation and predictive control strategy for an industrial fire-tube boiler. Therm. Sci. Eng. Prog. 2022, 36, 101482. [Google Scholar] [CrossRef]
- Habib, M.A.; Ben-Mansour, R.; Badr, H.M.; Ahmed, S.F.; Ghoniem, A.F. Computational fluid dynamic simulation of oxyfuel combustion in gas-fired water tube boilers. Comput. Fluids 2012, 56, 152–165. [Google Scholar] [CrossRef]
- Batrakov, P.A. The Nitrogen Oxide Formation Studying at Natural Gas Combustion in Non-circular Profile Furnaces of Fire-tube Boilers. Procedia Eng. 2016, 152, 144–150. [Google Scholar] [CrossRef]
- Mansir, I.B.; Ben-Mansour, R.; Habib, M.A. Oxy-fuel combustion in a two-pass oxygen transport reactor for fire tube boiler application. Appl. Energy 2018, 229, 828–840. [Google Scholar] [CrossRef]
- Habib, M.A.; Nemitallah, M.A. Design of an ion transport membrane reactor for application in fire tube boilers. Energy 2015, 81, 787–801. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.; Ye, H. CFD simulation of syngas combustion in a two-pass oxygen transport membrane reactor for fire tube boiler application. Energies 2021, 14, 7348. [Google Scholar] [CrossRef]
- Sungur, B.; Topaloglu, B.; Ozcan, H. Effects of nanoparticle additives to diesel on the combustion performance and emissions of a flame tube boiler. Energy 2016, 113, 44–51. [Google Scholar] [CrossRef]
- Tognoli, M.; Najafi, B.; Rinaldi, F. Dynamic modelling and optimal sizing of industrial fire-tube boilers for various demand profiles. Appl. Therm. Eng. 2018, 132, 341–351. [Google Scholar] [CrossRef]
- Tognoli, M.; Najafi, B.; Marchesi, R.; Rinaldi, F. Dynamic modelling, experimental validation, and thermo-economic analysis of industrial fire-tube boilers with stagnation point reverse flow combustor. Appl. Therm. Eng. 2019, 149, 1394–1407. [Google Scholar] [CrossRef]
- Buczyński, R.; Uryga-Bugajska, I.; Tokarski, M. Recent advances in low-gradient combustion modelling of hydrogen fuel blends. Fuel 2022, 328, 125265. [Google Scholar] [CrossRef]
- Cavaliere, A.; De Joannon, M. Mild combustion. Prog. Energy Combust. Sci. 2004, 30, 329–366. [Google Scholar] [CrossRef]
- Weber, R.; Mancini, M. On scaling and mathematical modelling of large scale industrial flames. J. Energy Inst. 2020, 93, 43–51. [Google Scholar] [CrossRef]
- Wiinning, J.A.; Wiinning, J.G. Flameless Oxidation to Reduce Thermal No-Formation. Prog. Energy Combust. Sci. 1997, 23, 81–94. [Google Scholar] [CrossRef]
- Wang, F.; Li, P.; Mi, J.; Shu, Z. A novel method to improve stability of MILD combustion in a highly heat-extracted furnace. Fuel 2021, 292, 120315. [Google Scholar] [CrossRef]
- Sayadzadeh, M.E.; Samani, M.R.; Toghraie, D.; Emami, S.; Eftekhari, S.A. Numerical study on pollutant emissions characteristics and chemical and physical exergy analysis in Mild combustion. Energy 2023, 278, 128001. [Google Scholar] [CrossRef]
- Tu, Y.; Su, K.; Liu, H.; Wang, Z.; Xie, Y.; Zheng, C.; Li, W. MILD combustion of natural gas using low preheating temperature air in an industrial furnace. Fuel Process. Technol. 2017, 156, 72–81. [Google Scholar] [CrossRef]
- Galletti, C.; Parente, A.; Derudi, M.; Rota, R.; Tognotti, L. Numerical and experimental analysis of NO emissions from a lab-scale burner fed with hydrogen-enriched fuels and operating in MILD combustion. Int. J. Hydrog. Energy 2009, 34, 8339–8351. [Google Scholar] [CrossRef]
- Mardani, A.; Karimi Motaalegh Mahalegi, H. Hydrogen enrichment of methane and syngas for MILD combustion. Int. J. Hydrog. Energy 2019, 44, 9423–9437. [Google Scholar] [CrossRef]
- Xu, S.; Tu, Y.; Huang, P.; Luan, C.; Wang, Z.; Shi, B.; Liu, H.; Liu, Z. Effects of wall temperature on methane MILD combustion and heat transfer behaviors with non-preheated air. Appl. Therm. Eng. 2020, 174, 115282. [Google Scholar] [CrossRef]
- Luan, C.; Xu, S.; Shi, B.; Tu, Y.; Liu, H.; Li, P.; Liu, Z. Re-Recognition of the MILD Combustion Regime by Initial Conditions of Tin and XO2 for Methane in a Nonadiabatic Well-Stirred Reactor. Energy Fuels 2020, 34, 2391–2404. [Google Scholar] [CrossRef]
- Xu, S.; Tian, Z.; Tian, S.; Xi, L.; Tu, Y.; Liu, H. Sustainability of hydrogen-enriched methane MILD combustion over a wide range of hydrogen-blending ratios in a strongly heat-extracted well-stirred reactor. Fuel 2024, 357, 130035. [Google Scholar] [CrossRef]
- Mohammadzadeh Pormehr, F.; Zabetian Targhi, M. Deflector design to improve internal gas recirculation in a MILD combustion laboratory furnace. Fuel 2024, 360, 130542. [Google Scholar] [CrossRef]
- Andalia, W.; Pramadhony; Arita, S. Physical properties analysis of gases emission of blend biodiesel burning process in a fire tube boiler. Int. J. Geomate 2019, 17, 266–272. [Google Scholar] [CrossRef]
- Kalyan, P.S.P.; Deshpande, A. CFD simulation of fuel/flue gas section of the fire tube steam boiler system. In Proceedings of the World Congress on Mechanical, Chemical, and Material Engineering, Virtual, 16–18 August 2020; Avestia Publishing: Orléans, ON, Canada, 2020; pp. 1–9. [Google Scholar] [CrossRef]
- El-Mahallawy, F.M.; Mahdi Ali, E.; El-Asfouri, A.S.; Ibrahim, H.A. Combustion and heat transfer characteristics in boilers with asymmetrical reversed flow flame tube. Exp. Therm. Fluid Sci. 2003, 27, 417–430. [Google Scholar] [CrossRef]
- Shu, Z.; Wang, F.; Dai, C.; Si, J.; Wang, B.; Mi, J. Characteristics of Nitric-Oxide Emissions from Traditional Flame and MILD Combustion Operating in a Laboratory-Scale Furnace. J. Therm. Sci. 2020, 29, 868–883. [Google Scholar] [CrossRef]
- Çengel, Y.A. Heat Transfer: A Practical Approach, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2007. [Google Scholar]
- Arghode, V.K.; Gupta, A.K. Role of thermal intensity on operational characteristics of ultra-low emission colorless distributed combustion. Appl. Energy 2013, 111, 930–956. [Google Scholar] [CrossRef]
- Smoot, L.D. Fundamentals of Coal Combustion: For Clean and Efficient Use; Elsevier: Amsterdam, The Netherlands, 1993; p. 755. [Google Scholar]
- Szkarowski, A. Spalanie Gazów—Teoria, Praktyka, Ekologia, 2nd ed.; Wydawnictwo WNT: Warszawa, Poland, 2014. [Google Scholar]
- Glarborg, P.; Miller, J.A.; Ruscic, B.; Klippenstein, S.J. Modeling nitrogen chemistry in combustion. Prog. Energy Combust. Sci. 2018, 67, 31–68. [Google Scholar] [CrossRef]
- Wilk, R.K. Low-Emission Combustion, 1st ed.; Wydawnictwo Politechniki Ślaskiej: Gliwice, Poland, 2002. [Google Scholar]
- Rönnberg, K.; Duwig, C. Heat transfer and associated coherent structures of a single impinging jet from a round nozzle. Int. J. Heat Mass Transf. 2021, 173, 121197. [Google Scholar] [CrossRef]
- Devahdhanush, V.S.; Mudawar, I. Critical Heat Flux of Confined Round Single Jet and Jet Array Impingement Boiling. Int. J. Heat Mass Transf. 2021, 169, 120857. [Google Scholar] [CrossRef]
- Gurgul, S.; Fornalik-Wajs, E. On the Measure of the Heat Transfer Performance of RANS Turbulence Models in Single Round Jet Impingement. Energies 2023, 16, 7236. [Google Scholar] [CrossRef]
- Angelino, M.; Di Venuta, I.; Boghi, A.; Petracci, I.; Gori, F. Further results on the mean mass transfer and fluid flow in a turbulent round jet. Int. Commun. Heat Mass Transf. 2023, 141, 106568. [Google Scholar] [CrossRef]
- Di Venuta, I.; Boghi, A.; Angelino, M.; Petracci, I.; Gori, F. Numerical simulation and self-similarity of the mean mass transfer in turbulent round jets. Int. Commun. Heat Mass Transf. 2021, 122, 105146. [Google Scholar] [CrossRef]
- Angioletti, M.; Nino, E.; Ruocco, G. CFD turbulent modelling of jet impingement and its validation by particle image velocimetry and mass transfer measurements. Int. J. Therm. Sci. 2005, 44, 349–356. [Google Scholar] [CrossRef]
- Xie, M.; Tu, Y.; Peng, Q. Numerical study of NH3/CH4 MILD combustion with conjugate heat transfer model in a down-fired lab-scale furnace. Appl. Energy Combust. Sci. 2023, 14, 100144. [Google Scholar] [CrossRef]
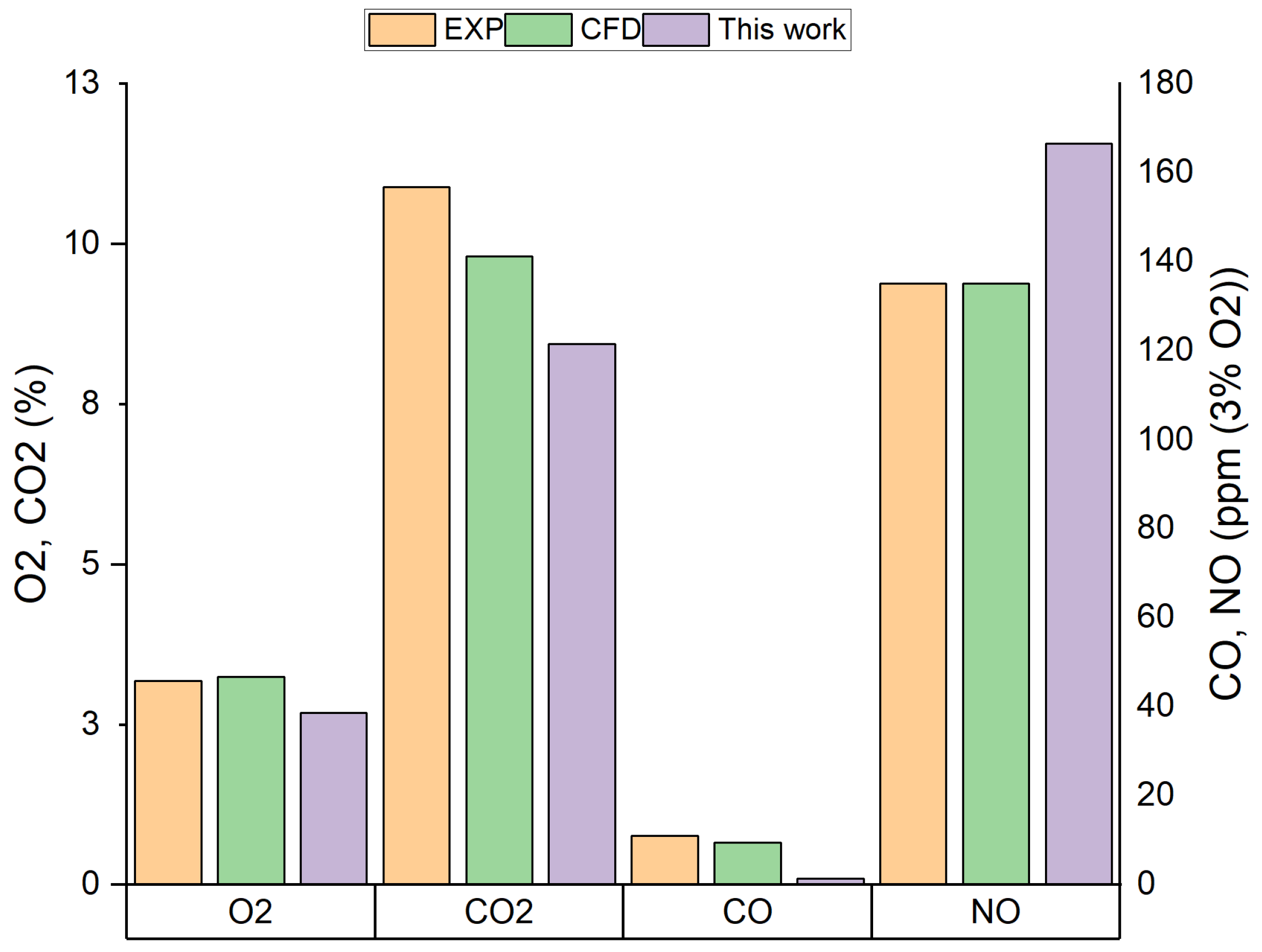
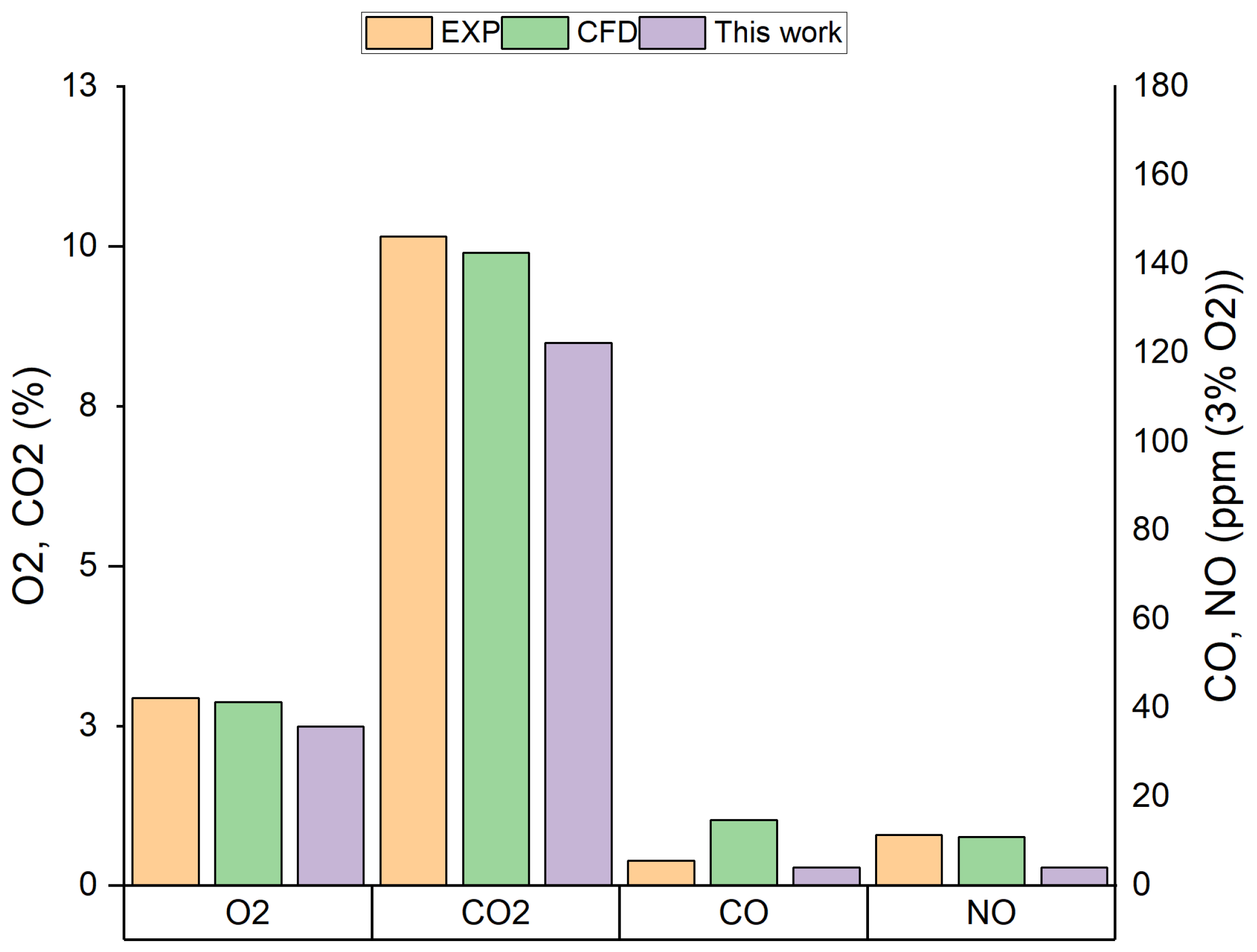



| Wall BC | O | CO | CO | NO | NO | NO * |
|---|---|---|---|---|---|---|
| % | % | ppm | ppm | ppm | ppm | |
| 2.7 | 8.4 | 1.3 | 162.1 | 0.4 | 162.5 | |
| 2.8 | 8.4 | 48.5 | 142.4 | 23.7 | 166.1 |
| Quantity Name | Baseline Case | Case 2 | Case 3 |
|---|---|---|---|
| Equivalence ratio, -: | 0.86 | 0.80 | 0.74 |
| , -: | 57,500 | 61,500 | 66,000 |
| Turb. intensity, %: | 4.1 | 4.0 | 4.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokarski, M.; Buczyński, R. Heat Transfer Analysis for Combustion under Low-Gradient Conditions in a Small-Scale Industrial Energy Systems. Energies 2024, 17, 186. https://doi.org/10.3390/en17010186
Tokarski M, Buczyński R. Heat Transfer Analysis for Combustion under Low-Gradient Conditions in a Small-Scale Industrial Energy Systems. Energies. 2024; 17(1):186. https://doi.org/10.3390/en17010186
Chicago/Turabian StyleTokarski, Mieszko, and Rafał Buczyński. 2024. "Heat Transfer Analysis for Combustion under Low-Gradient Conditions in a Small-Scale Industrial Energy Systems" Energies 17, no. 1: 186. https://doi.org/10.3390/en17010186
APA StyleTokarski, M., & Buczyński, R. (2024). Heat Transfer Analysis for Combustion under Low-Gradient Conditions in a Small-Scale Industrial Energy Systems. Energies, 17(1), 186. https://doi.org/10.3390/en17010186






