Grid Synchronization of a Seven-Phase Wind Electric Generator Using d-q PLL

Abstract

The evolving multiphase induction generators (MPIGs) with more than three phases are receiving prominence in high power generation systems. This paper aims at the development of a comprehensive model of the wind turbine driven seven-phase induction generator (7PIG) along with the necessary power electronic converters and the controller for grid interface. The dynamic model of the system is developed in MATLAB/Simulink (R2015b, The MathWorks, Inc., Natick, MA, USA). A synchronous reference frame phase-locked loop (SRFPLL) system is incorporated for grid synchronization. The modeling aspects are detailed and the system response is observed for various wind velocities. The effectiveness of the seven phase induction generator is demonstrated with the fault tolerant capability and high output power with reduced phase current when compared to the conventional 3-phase wind generation scheme. The response of the PLL is analysed and the results are presented.

1. Introduction

Electric power generation gained by exploring the use of renewable energy sources is a viable solution for reducing the dependency on fast depleting fossil fuels and to adhere to environmentally friendly conditions [1]. Among all existing non-conventional sources, wind has latent qualities that can be utilized to meet the heaping energy demand [2]. Self-excited induction generators (SEIGs) are usually deployed for wind energy conversion systems in standalone applications with their inherent characteristics as mentioned in [3,4]. Later they also operated in a grid connected mode for distributed power generation in hybrid micro grids [5]. However, they are suitable for low and medium power applications [4]. Multiphase induction generator (MPIG) with more than three phases is a potential contender which combines the advantages of MPIG with SEIG technologies to yield an efficient, reliable, and fault tolerant machine that has diverse applications [6,7,8,9]. Multiphase systems can be employed for different applications, such as offshore energy harvesting, electrical vehicles, electric ship propulsion, and aircrafts. The earlier proposed research works describe the supremacy of multiphase machines for obtaining a better reliable performance [10,11,12,13,14,15,16,17,18,19,20,21,22].

As a consequence, MPIG research has evoked interest among researchers in the recent past which has culminated into gradual but steady progress in this field. However, the available literature suggests that finite modeling approaches should be implemented for MPIG analysis.

The d-q model of the six phase induction generator with a dual stator and single rotor has been presented in many papers [23,24,25,26]. The performance of the six phase dual stator induction generator has been investigated in [25,26,27]. Dynamic analysis of the six phase induction generator for standalone wind power generation was investigated in [28], while steady state performance analysis of the machine, and its experimental validation have been carried out in [29,30,31].

The most challenging requirement for wind electric systems is the low voltage ride through capability that requires generators to remain connected during grid faults and to contribute to the system recovery. Unbalanced voltage conditions and dips in the grid can have significant negative effects on the performance of induction generators. These effects can decrease the lifetime of sensitive components in the wind energy converter in the long term and in extreme cases, they can cause damage and tripping of the system, leading to violation of the grid code requirements [32,33,34,35].

The grid integration of wind electric generators (WEG) is a critical aspect in the planning of a wind power generation system. The variation in production and higher intermittency of wind generation makes it difficult for grid integration. Hence it is necessary to provide the appropriate synchronization techniques such that the system maintains constant frequency and voltage to ensure stable and reliable operation of the grid [36,37]. A good synchronization method must detect the frequency and phase angle variations proficiently in order to reduce the harmonics and disturbances for safe operation of the grid. Further simple implementation and cost decides the reliability of the synchronization schemes [38]. The power transfer between distributed generation and the grid is enhanced by a good synchronization method. Earlier known zero crossing detectors have adverse power quality issues in a weak grid. Nowadays, phase-locked loop (PLL) is one of the generally used techniques and it controls the distributed power generation system and other applications. Several types of PLL are analysed in [37,38]. This paper aims to develop a PLL based grid connected seven phase WEG where PLL enables the frequency and voltage synthesis.

A d-q model of the seven-phase induction generator (7PIG) with the stator windings phase shifted by 51.42° is developed. A simulation is carried out to study the performance under varying wind velocities. The voltage build up process is shown. The generator voltage, current, and power output is presented under varying load conditions. The reliability of the machine under a fault condition is examined with one or two phases open. The results are compared with the three phase generator. The power electronic interface, namely the seven phase rectifier, boost converter, and the three phase neutral point clamped (NPC) inverter are simulated for varying modulation indices and the results are explored. The synchronous reference frame (SRF) PLL is designed to track the phase angle and frequency. The PLL response analyses various grid conditions such as unbalanced grid voltages, voltage sags, line to line (LL) faults, and line to line ground faults (LLG), and the results are explored.

2. Proposed System Description

Figure 1 shows the proposed multiphase AC power system for wind power application. The grid connected seven phase wind generation system considered for the study, consists of a wind turbines that is driven by a 7PIG through a gearbox. The generated seven phase AC output is rectified by the seven phase rectifier and filtered by an LC filter. The filtered and boosted DC output voltage is injected through a three phase inverter to the grid with proper synchronization through SRF PLL. The inverter is controlled using the synchronous d-q reference frame approach. The phase lock loop technique that is incorporated synchronizes the inverter and the grid. The high frequency ripple at the inverter is filtered. The filtered output of the inverter is fed into the grid through a step-up transformer.

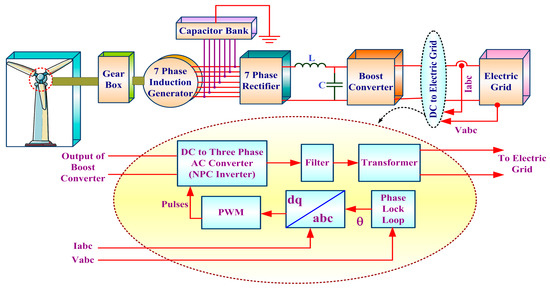
Figure 1. Seven Phase Grid Connected Wind Electric Generator.

3. Modeling of System Components

The mathematical modeling of the seven phase wind generator components, namely the wind turbine, seven phase induction generator, seven phase rectifier, and three phase inverter and PLL are discussed in the following sections.

3.1. Wind Turbine

The following equation defines the power output of the wind turbine, which is the aerodynamic power developed on the main shaft of the wind turbine:

$$P_{tur}=0.5\rho A{C}_p(\lambda ){V_w}^3,$$

(1)

C_p is a dimensionless power coefficient that depends on the wind speed and constructional characteristics of the wind turbine. For the wind turbine used in this study, the following form approximates C_p as a function of $\lambda$ known as the tip-speed ratio, which depends on the rotor speed of the turbine and the wind speed.

$$C_p=0.5\left(\frac{116}{{\lambda }_1}-0.4\beta -5\right)e^{\frac{-16.5}{{\lambda }_1}},$$

(2)

$$\lambda =\frac{R{\omega }_{tur}}{V_w},$$

(3)

$${\lambda }_1=\frac{1}{\frac{1}{\left(\lambda +0.089\right)}-\frac{0.035}{({\beta }^3+1)}},$$

(4)

where, ${\rho }_{tur}$: Air density (kg/m³); $V_w$—wind speed (m/s); R—Radius of the wind turbine rotor (m); A—Area swept out by the turbine blades (m²); C_p: power coefficient defined by Equation (2); λ—Tip speed ratio given by Equation (3); ${\omega }_{tur}$: angular rotor speed of the turbine (rad/s); $\beta$: The blade pitch angle (degree).

3.2. 7PIG Model

A 7PIG has seven stator windings sinusoidally distributed with a phase displacement of 51.4° (360°/7) and the rotor is short circuited for the squirrel cage induction machine. The 7P induction machine operating as a generator is represented as a two phase equivalent circuit. The ds-qs represent the stator direct and quadrature axes and dr-qr represents the rotor direct and quadrature axes. The transformation of the seven phase stationary reference frame variables to a two phase stationary reference frame is given by Equation (5). The assumptions made in modeling 7PIG are the same as those given in [8,39,40,41]. The modeling of 7PIG is carried out using a d-q equivalent circuit, as shown in Figure 2 [39,40,41].

$$\left[\begin{array}{c}{V}_{qs}\\ V_{ds}\\ V_{xs}\\ V_{ys}\\ .\\ V_{os}\end{array}\right]=\left[\begin{array}{cccccc}1& \cos \alpha & \cos 2\alpha & \cos 3\alpha & .& \cos n\alpha \\ 0& \sin \alpha & \sin 2\alpha & \sin 3\alpha & .& \sin n\alpha \\ 1& \cos 2\alpha & \cos 4\alpha & \cos 6\alpha & .& \cos 2n\alpha \\ 0& \sin 2\alpha & \sin 4\alpha & \sin 6\alpha & .& \sin 2n\alpha \\ .& .& .& .& .& .\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& .& \frac{1}{\sqrt{2}}\end{array}.\right]X\left[\begin{array}{c}{V}_a\\ V_b\\ V_c\\ V_d\\ .\\ V_n\end{array}\right],$$

(5)

where α = 2π/n; n = number of phases; s and r represent stator and rotor quantities, respectively; d-q represents a direct and quadrature axis.

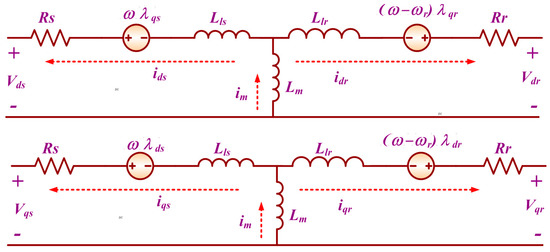
Figure 2. d-q-axis Equivalent Circuit of Seven-Phase Induction Generator (7PIG).

Equations (5) and (6) define the stator side voltages

$$V_{qs}=-R_s{i}_{qs}+\omega {\lambda }_{ds}+p{\lambda }_{qs},$$

(6)

$$V_{ds}=-R_s{i}_{ds}-\omega {\lambda }_{qs}+p{\lambda }_{ds},$$

(7)

Equations (7) and (8) define the rotor side voltages

$$V_{qr}=R_r{i}_{qr}+\left(\omega -{\omega }_r\right){\lambda }_{dr}+p{\lambda }_{qr},$$

(8)

$$V_{dr}=R_r{i}_{dr}-\left(\omega -{\omega }_r\right){\lambda }_{qr}+p{\lambda }_{dr},$$

(9)

The voltage equations for dynamic performance analysis under balanced conditions are represented in a stationary reference frame (ω = 0). The rotor side voltages V_qr and V_dr are zero for the squirrel cage induction generators. The rotor side quantities are referred to as stator reference frame. The flux linkage expression as a function of the current is given by Equations (10)–(15).

$${\lambda }_{qs}=-L_{ls}{i}_{qs}+L_m\left(i_{qr}-i_{qs}\right),$$

(10)

$${\lambda }_{ds}=-L_{ls}{i}_{ds}+L_m\left(i_{dr}-i_{ds}\right),$$

(11)

$${\lambda }_{qr}=L_{lr}{i}_{qr}+L_m\left(i_{qr}-i_{qs}\right),$$

(12)

$${\lambda }_{dr}=L_{lr}{i}_{dr}+L_m\left(i_{dr}-i_{ds}\right),$$

(13)

$${\lambda }_{dm}={\mathrm{L}}_{\mathrm{m}}\left(i_{ds}+i_{dr}\right),$$

(14)

$${\lambda }_{qm}={\mathrm{L}}_{\mathrm{m}}\left(i_{qs}+i_{qr}\right),$$

(15)

The leakage inductance of the stator and rotor are assumed to be constant. The degree of magnetic saturation decides the magnetizing inductance L_m and it is a non-linear function of the magnetizing current, which is given by the following equation

$${\mathrm{I}}_m=\sqrt{{\left(i_{qr}+i_{qs}\right)}^2+{\left(i_{dr}+i_{ds}\right)}^2},$$

(16)

The non-linear piecewise relationship between the magnetizing inductance and the current (L_m, i_m) is given by

$${\mathrm{L}}_m=\{\begin{array}{l}0.012726,0\le i_m<25.944\\ 1.94597/\left(i_m+117.6\right),25.944\le i_m<51.512\\ 1.79031/\left(i_m+61.2\right),52.512\le i_m<73.8\\ 1.41566/\left(i_m+46.296\right),73.8\le i_m<85.872\\ 2.67838/\left(i_m+31.608\right),i_m\ge 85.872\end{array},$$

(17)

The developed electromagnetic torque of the 7PIG is defined by

$$T_g=-\frac{7}{2}\left(\frac{P}{2}\right)L_m\left(i_{qs}{i}_{dr}-i_{ds}{i}_{qr}\right),$$

(18)

A negative (-ve) sign indicates generation action.

$$L_r=L_{lr}+L_m,$$

(19)

$$L_s=L_{ls}+L_m,$$

(20)

3.3. Modeling of the Shunt Capacitor and Load

The modeling equations of the voltage and current of the excitation capacitor and the load in the d-q-axis are given by Equations (21)–(26)

$$p{V}_{qs}=\left(\frac{1}{C}\right)i_{cqs}-\omega V_{ds},$$

(21)

$$p{V}_{ds}=\left(\frac{1}{C}\right)i_{cds}+\omega V_{qs},$$

(22)

$$i_{cqs}=i_{qs}-i_{Rqs},$$

(23)

$$i_{cds}=i_{ds}-i_{Rds},$$

(24)

$$i_{Rqs}=\frac{V_{qs}}{R},$$

(25)

$$i_{Rds}=\frac{V_{ds}}{R},$$

(26)

The 7P voltages are transformed to 2P using Equation (27).

$$\begin{array}{l}{V}_a=V_{qs}\cos {\theta }_e+V_{ds}\sin {\theta }_e\\ V_b=V_{qs}\cos ({\theta }_e-\alpha )+V_{ds}\sin ({\theta }_e-\alpha )\\ V_c=V_{qs}\cos ({\theta }_e-2\alpha )+V_{ds}\sin ({\theta }_e-2\alpha )\\ V_d=V_{qs}\cos ({\theta }_e-3\alpha )+V_{ds}\sin ({\theta }_e-3\alpha )\\ V_e=V_{qs}\cos ({\theta }_e-4\alpha )+V_{ds}\sin ({\theta }_e-4\alpha )\\ V_f=V_{qs}\cos ({\theta }_e-5\alpha )+V_{ds}\sin ({\theta }_e-5\alpha )\\ V_g=V_{qs}\cos ({\theta }_e-6\alpha )+V_{ds}\sin ({\theta }_e-6\alpha )\end{array}\},$$

(27)

4. DC Link Converter

The power electronics based interface system, namely the DC link converter, involves a seven phase rectifier, three phase inverter, and a DC-DC boost converter. The uncontrolled seven phase rectifier converts the seven phase AC output of the generator to DC and is boosted by the boost converter.

4.1. Seven Phase Diode Bridge Rectifier

A variable magnitude, the variable frequency voltage at the seven phase induction generator terminal, is converted to DC using a seven-phase diode bridge rectifier [42,43,44,45]. The voltage V_rec at the output is given by Equation (28) in terms of the peak phase voltage V_ds of the generator. The LC filter reduces the output voltage ripple of the seven phase rectifier.

$$V_{rec}=\frac{1}{(2\pi /14)}{\displaystyle \underset{-\pi /14}{\overset{\pi /14}{\int }}1.949V_{ds}\cos (\omega }t)d(\omega t),$$

(28)

$$V_{rec}=1.932V_{ds},$$

(29)

4.2. DC-DC Boost Converter

A DC-DC boost converter (Figure 3) steps up the input voltage depending on the duty ratio, inductor, and capacitor values [40]. The output voltage of the boost converter is given by

$$V_{dc}=\frac{V_{rec}}{1-\delta },$$

(30)

where, V_rec—Input voltage from the seven phase rectifier; δ—Duty cycle of the switch. The inductance and capacitance are determined using Equations (31) and (32).

$$\mathrm{Inductance},L=\frac{R*\delta {(1-\delta )}^2}{2*f_S}(\mathrm{Henry}),$$

(31)

$$\mathrm{Capacitance},\mathrm{C}\ge \frac{{\mathrm{V}}_{\mathrm{O}}*\delta }{f_S*\Delta {\mathrm{V}}_{\mathrm{O}}*R}(\mathrm{Farad}),$$

(32)

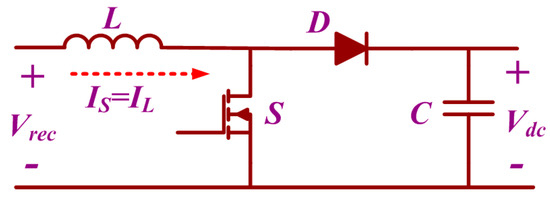
Figure 3. Power Circuit of Boost Converter.

4.3. Three Level Neutral Point Clamped Inverter

The DC input is given to this inverter from the DC/DC converter (Figure 3) and the three phase, three level output obtained is given to the grid through a step-up transformer. The modulation index of the reference signal is varied to control the output voltage of the inverter and is given by Equation (33)

$${\mathrm{Modulation}\mathrm{Index},\mathrm{M}}_{\mathrm{a}}=\frac{V_m}{\raisebox{1ex}{$V_{dc}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},$$

(33)

where, V_m—Peak value of the Phase voltage (V); V_dc—Input Input DC voltage/Output of the Boost converter.

5. Grid Interface Using PLL

The effective power transfer between the grid and the source can be realized by the efficient synchronization technique. The most familiar method is tracking of the phase angle using the PLL which synchronizes the voltage and frequency of a given reference and output signal. A phase detector, loop filter, and voltage controlled oscillator (VCO) together make a basic PLL system, wherein the phase detector generates an error signal by comparing the reference and output signal. The harmonics of the error signal are eliminated by the loop filter. Depending on the output of the loop filter, the VCO generates the output signal. The basic structure of the PLL circuit is shown in Figure 4. A linear PLL is usually used in a single phase system, whereas a three phase system employs an SRF PLL or otherwise a d-q PLL.

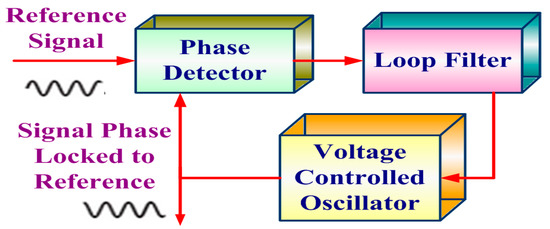
Figure 4. Basic Phase Locked Loop (PLL) Structure.

Synchronous Reference Frame (SRF/d-q) PLL

In the synchronous frame PLL, Clarke’s transformation [39] is applied to the three-phase voltage vector to transform abc to the αβ stationary reference frame. Park’s transformation changes αβ to the d-q rotating frame, as shown in Figure 5. The feedback loop controls the angular position of the d-q reference, making the q-axis component zero in the steady state. The d-axis will be the voltage amplitude during steady state conditions.

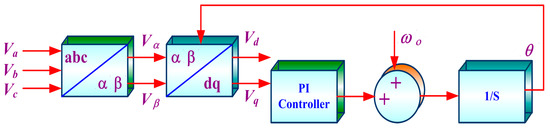
Figure 5. Synchronous Reference Frame (SRF)/d-q PLL Structure.

The d- and q-axis components are defined by the following equation under balanced conditions.

$$\left[\begin{array}{l}{V}_d\\ V_q\end{array}\right]=\left[\begin{array}{ll}\cos \widehat{\theta }& \sin \widehat{\theta }\\ -\sin \widehat{\theta }& \cos \widehat{\theta }\end{array}\right]\left[\begin{array}{l}U\cos \theta \\ U\sin \theta \end{array}\right]=\left[\begin{array}{l}U\cos (\theta -\widehat{\theta })\\ U\sin (\theta -\widehat{\theta })\end{array}\right],$$

(34)

where U, $\theta$—amplitude and phase of the input signal; $\widehat{\theta }$—PLL output; and V_d, V_q are the d- and q-axis components.

The phase is denoted by the q-axis and the amplitude in steady state is denoted by the d-axis error. The generalized voltage vector under unbalanced utility conditions (without voltage harmonics) is represented by

$$V=V_{+}+V_{-}+V_0,$$

(35)

The positive, negative, and zero sequence components are represented by subscripts +, −, and 0. The αβ component using Clarke’s transformation is given by

$$V_{\alpha \beta \gamma }=\left[\begin{array}{l}{V}_{\alpha }\\ V_{\beta }\\ V_{\gamma }\end{array}\right]=T_{\alpha \beta /abc}\left[\begin{array}{l}{V}_a\\ V_b\\ V_c\end{array}\right],$$

(36)

$$T_{\alpha \beta /abc}=\frac{2}{3}\left[\begin{array}{ccc}1& \frac{-1}{2}& \frac{-1}{2}\\ 0& \frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right],$$

(37)

The zero-sequence component is neglected as it is on the γ-axis. The expression of the voltage vector on the αβ-plane is:

$$V_{\alpha \beta }=T_{\alpha \beta /abc}(V_{+}+V_{-})=\left[\begin{array}{l}{U}_{+}\cos {\theta }_{+}+U_{-}\cos {\theta }_{-}\\ U_{+}\sin {\theta }_{+}+U_{-}\sin {\theta }_{-}\end{array}\right],$$

(38)

The αβ frame is transformed to the d-q frame using Park’s transformation.

$$V_{dq}=T_{dq/\alpha \beta }{V}_{\alpha \beta }=\left[\begin{array}{l}{U}_{+}\cos ({\theta }_{+}-\widehat{\theta })+U_{-}\cos ({\theta }_{-}-\widehat{\theta })\\ U_{+}\sin ({\theta }_{+}-\widehat{\theta })+U_{-}\sin ({\theta }_{-}-\widehat{\theta })\end{array}\right]=\left[\begin{array}{l}{U}_{+}+U_{-}\cos (2\omega t)\\ U_{+}-U_{-}\sin (2\omega t)\end{array}\right],$$

(39)

$$T_{dq/\alpha \beta }=\left[\begin{array}{ll}\cos \widehat{\theta }& \sin \widehat{\theta }\\ -\sin \widehat{\theta }& \cos \widehat{\theta }\end{array}\right],$$

(40)

ω is the angular frequency of the voltage vector and $\widehat{\theta }={\theta }_{+}={\theta }_{-}=\omega t$.

6. Simulation Result

The modeling equations of the various system components are simulated with the parameters given in Appendix A. The individual component models are analysed and integrated to study the performance of the seven phase wind electric generator. The simulation results are discussed in the following sections.

6.1. Wind Turbine

A 250 kW wind turbine is simulated using the Equations (1)–(4) for various wind speeds and rotational speeds. Figure 6 shows the power curves of the wind turbine at various wind speeds. The rated power of 250 kW is achieved at the rated wind speed of 15 m/s and 40 rpm. The wind turbine produces the maximum power at various rotational speeds for the different wind speeds.

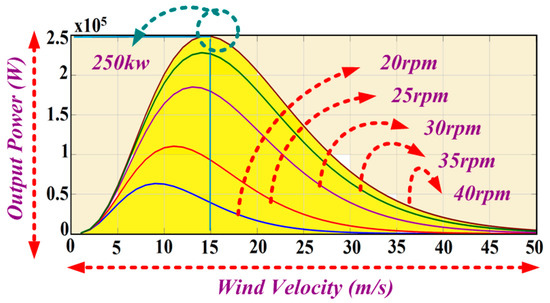
Figure 6. Wind Turbine Power Output vs. Wind Velocity (Wind Speed).

6.2. Seven Phase Induction Generator

The mathematical equations represented by Equations (5)–(27) are used to develop a mathematical model of the seven phase induction generator from the d-q equivalent circuit shown in Figure 2. The performance of 7PIG is investigated under various operating conditions.

The rated speed of 1018 rpm with the excitation capacitance of 2332 µF is given as the input to the generator and the voltage and current of the 7PIG are obtained at no load and are presented in Figure 7. The self-excitation process begins at time t = 0, and the stator voltage builds and the steady state value of 419 V (peak) and a current of about 165 A is reached at t = 2.2 s with the phases mutually displaced by 51.4° (2π/n).

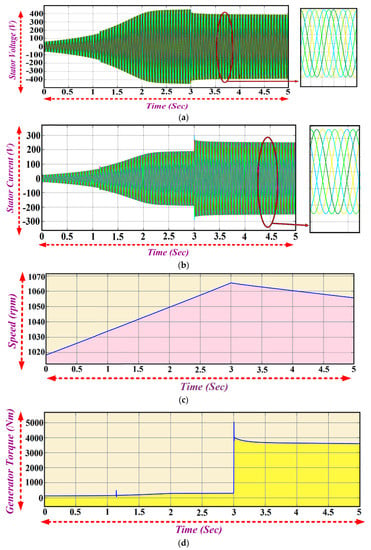
Figure 7. 7PIG (a) Output Voltage; (b) Current; (c) Generator speed; (d) Generator Torque.

The 7PIG is loaded at t = 3 s with the excitation capacitance held constant at 2332 µF. At t = 3 s, the terminal voltage of the stator is reduced from 419 volts to 386 volts and the current increases from 165 A to 241 A. The steady state is reached at t = 2 s as shown in Figure 7a,b. The generated torque and speed of the generator are represented in Figure 7c,d which show that for increasing the load, the speed of the generator decreases with an increase in the torque. The line voltages of the seven phase induction generator varies for the adjacent (V_ab = 0.8676 V_m) and non-adjacent sides (V_ac = 1.5629 V_m) and (V_ad = 1.949 V_m), which is clearly illustrated using the results shown in the Figure 8a–c.

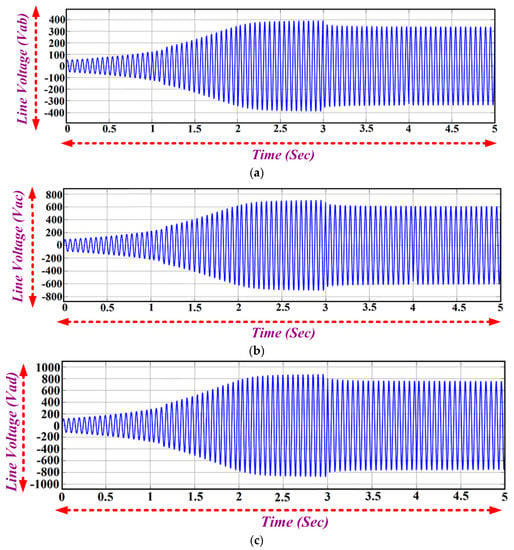
Figure 8. Generated Line Voltage of 7PIG Adjacent Side and Non Adjacent Side (a) V_ab; (b) V_ac; (c) V_ad.

6.3. Fault Tolerant Operation of 7PIG

The most important ability of the multiphase phase generator is that it continues to operate even after the fault occur in one (or more) phase(s), whereas three-phase machines can hardly continue their operation. Under the faulty conditions, the additional degrees of freedom available in MPIG are efficiently used for the post fault operating strategy. One-, two-phases are open circuited V_c, V_c and V_d at t = 3 s for the seven phase induction generator for the investigation test. It is clear from the obtained numerical results by Figure 9 and Figure 10 that the generator continues to operate with the reduced phase current in amplitude for continuous propagation under open circuit faulty conditions.

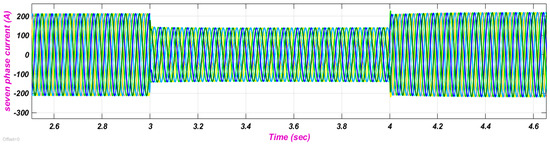
Figure 9. Fault Current of 7PIG with One Phase Open (V_c).

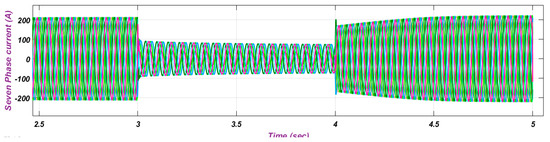
Figure 10. Fault Current of 7PIG with Two Phases Open (V_c and V_d).

The performance of the seven phase induction generator is compared with the three phase generator in terms of generating voltage and current. The per phase voltage of the three phase and seven phase system remains the same whereas the current per phase is reduced, as clearly shown in Figure 11a,b.

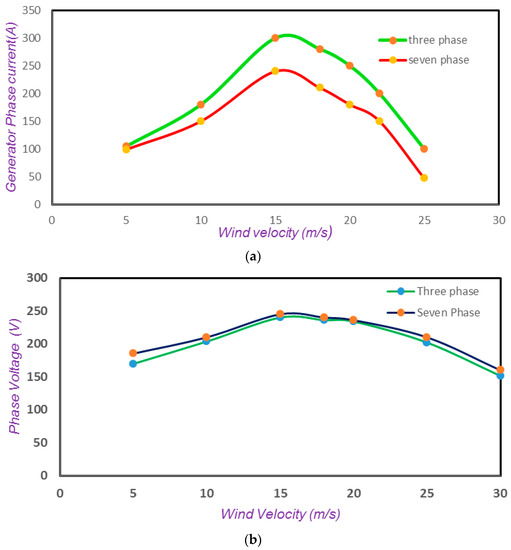
Figure 11. (a) Seven Phase Current vs. Three Phase Current for Varying Wind Velocity; (b) Three Phase Voltage vs. Seven Phase Voltage.

6.4. DC Link Converter

The generated seven phase AC output is fed as an input to the seven phase rectifier which converts AC to DC. The rectified DC output voltage feeds the boost converter. The boost converter output voltage and current of 845 V and 279 A is achieved, as shown in Figure 12a,b.

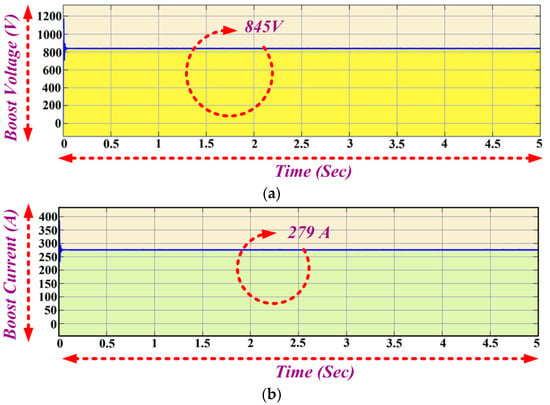
Figure 12. (a) Boost Voltage; (b) Boost Current.

6.5. Grid Integration

The grid tied inverter is the power electronic converter that converts the DC signal into AC, but with the appropriate synchronizing techniques. It is basically used in the integration of renewable energy to the utility line. The magnitude and phase of the inverter voltage should be the same as that of the grid and its output frequency should be equal to the grid frequency for proper grid synchronization. The output phase voltage of the inverter is 365 V (peak) and a current of about 508 V (peak) is achieved at a 0.85 modulation index with a DC input of 845 V as shown in Figure 13 and Figure 14. The line voltage of the inverter is given by Figure 15.

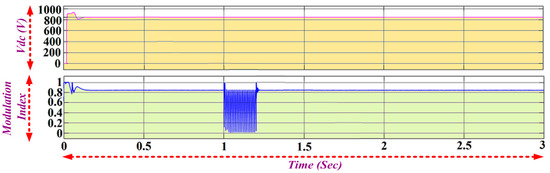
Figure 13. Vdc and Modulation Index.

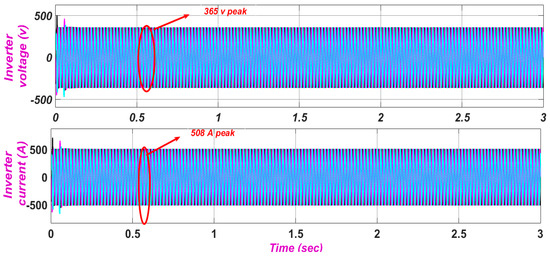
Figure 14. Inverter Output Voltage and Inverter Current.

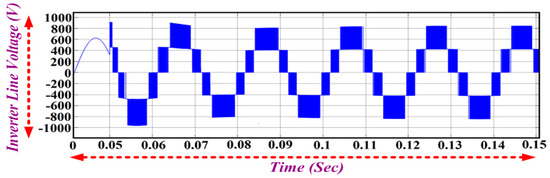
Figure 15. Inverter Line Voltage.

The d- and q-axis voltage of the d-q PLL and frequency tracking is shown in Figure 16. The voltage and current drawn by the load connected at the point of common coupling is shown in Figure 17. The grid voltage and current are shown in Figure 18. The power injected into the grid is about 196 kW, which is shown in Figure 19.

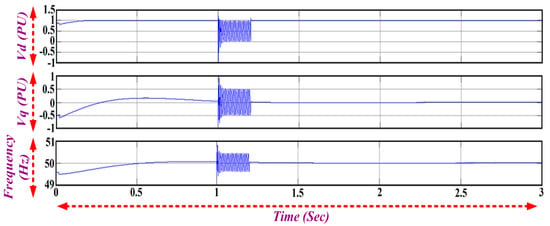
Figure 16. Graph of V_d, V_q, and Frequency.

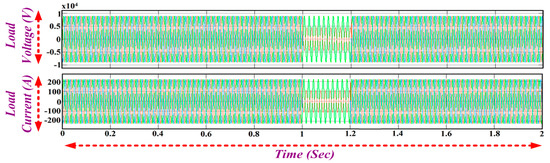
Figure 17. Load Voltage and Load Current.

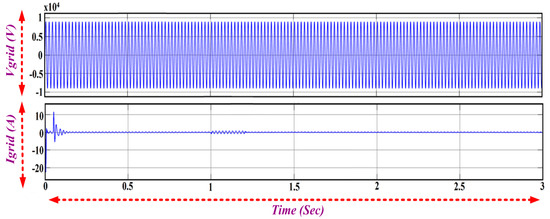
Figure 18. Grid Voltage (Vgrid) and Grid Current (Igrid).

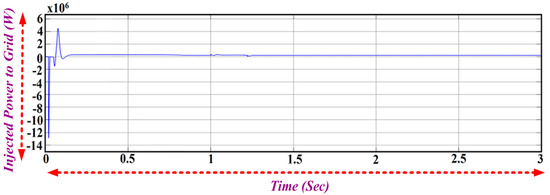
Figure 19. Power injected into the Grid.

6.6. SRF PLL Performance under Various Grid Conditions

The grid is subjected to different fault conditions to investigate the performance of the SRF PLL. Figure 20a shows the frequency and phase detection variation during a line to line fault. It is clear from the figure that phases B and C are in phase with each other and their magnitude is less than phase A, whereas the magnitude of phase of B and C are zero during a line to line ground fault as shown in Figure 21a. The voltages of the d-q-axis also vary, as it contains second harmonic ripples as given by Equation (35), which is illustrated by Figure 20b and Figure 21b.

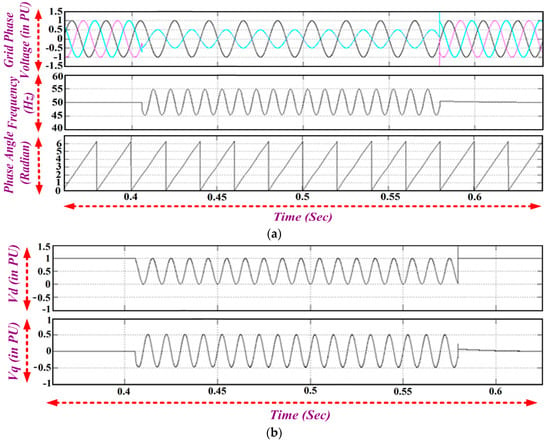
Figure 20. (a) Frequency and Phase Angle Variation during a Line to Line Fault; (b) q-axis and d-axis Voltage Magnitude during a Line to Line Fault.

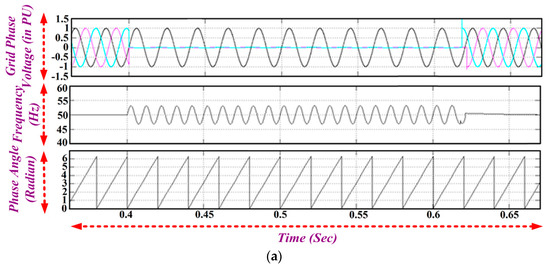
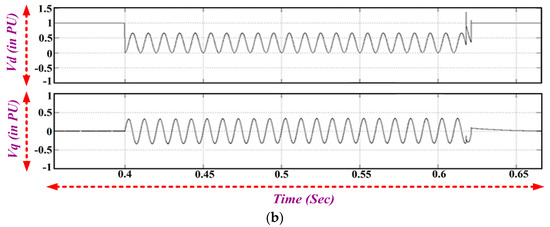
Figure 21. (a) Frequency and Phase Angle Variation during a Line-Line ground LLG Fault; (b) q-axis and d-axis Voltage Magnitude during a LLG Fault.

During unbalanced grid voltage condition, the sinusoidal nature of the q-axis voltage component affects the output of the PI controller. Therefore, the PI controller generates a sinusoidal error signal, angular frequency is shown in Figure 22a,b, which is similar to that of the line to line fault.

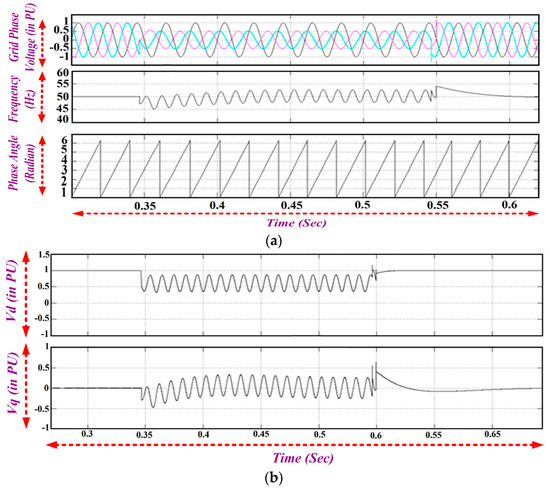
Figure 22. (a) Frequency and Phase Detection Variation during Unbalanced Grid Voltages; (b) q-axis and d-axis Voltage Magnitude during Unbalanced Grid Voltages.

The SRF PLL performance during voltage sag is shown in Figure 23a,b. Voltage sag occurs in the grid such that the magnitude of all phase voltages are equal and their magnitudes are 50% of the nominal voltage. It is noticed that it does not cause any oscillations in the frequency and the d-q voltages. Balanced voltage sag does not affect PLL tracking. However, a sudden change in the magnitude causes a dip in the estimated frequency of d-q PLL, and later it tracks the phase angle of the grid voltages.

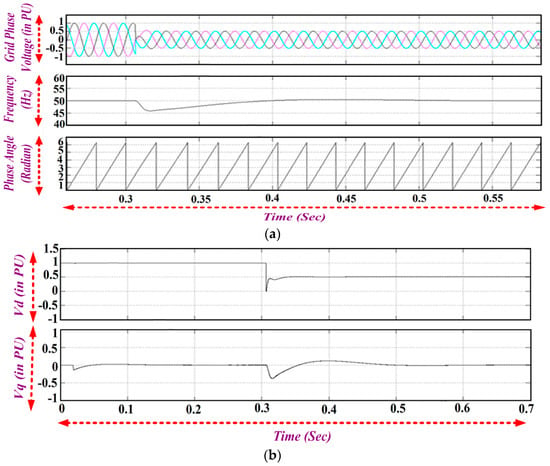
Figure 23. (a) Frequency and Phase Detection Variation during Voltage Sag; (b) q-axis and d-axis Voltage Magnitude during Voltage Sag.

7. Conclusions

In this article, a comprehensive model of a wind driven 7PIG in grid connected mode was developed using the two axis d-q equivalent circuit. A seven phase wind electric generator is integrated using the individual system components and the performance of the seven phase wind electric generator is analysed for varying wind speed [46]. A synchronous reference frame PLL incorporated for the grid interface is simulated and analysed. The enhanced performance of 7PIG is evaluated through the fault tolerant capability and high output power with reduced current per phase when compared with the three phase model. The performance of SRF-PLL incorporated in the grid connected seven phase wind electric generator was analysed for various operating grid conditions. The use of multiphase machines along with the PLL synchronization of the grid increases the reliability of the WEG. Notably by the possibility of achieving post-fault disturbance free operation provided by the seven phase machine, as well as the constant voltage and frequency operation enabled by the d-q PLL.