Analysis of Magnetic Field Measurements for Indoor Positioning †
Abstract
:1. Introduction
- A magnetic field acquisition system was developed using the Arduino Pro Mini and the LSM9DS1. The RLOWESS smoothing filter was proposed to eliminate the effects of noise, distortion, and outliers in the raw MF measurements.
- Static tests, trajectory tests, and rotational tests were designed to investigate the magnetic characteristics of the heterogeneous smartphone.
- Calibration tests of heterogeneous smartphones were carried out to demonstrate the potential of smartphone calibration in solving the heterogeneous device problem of MF.
- Classification tests of heterogeneous smartphones were performed to show the feasibility of magnetic field positioning.
2. Related Work
3. Magnetometer Measurement Model
4. Analysis of the MF Characterisctics
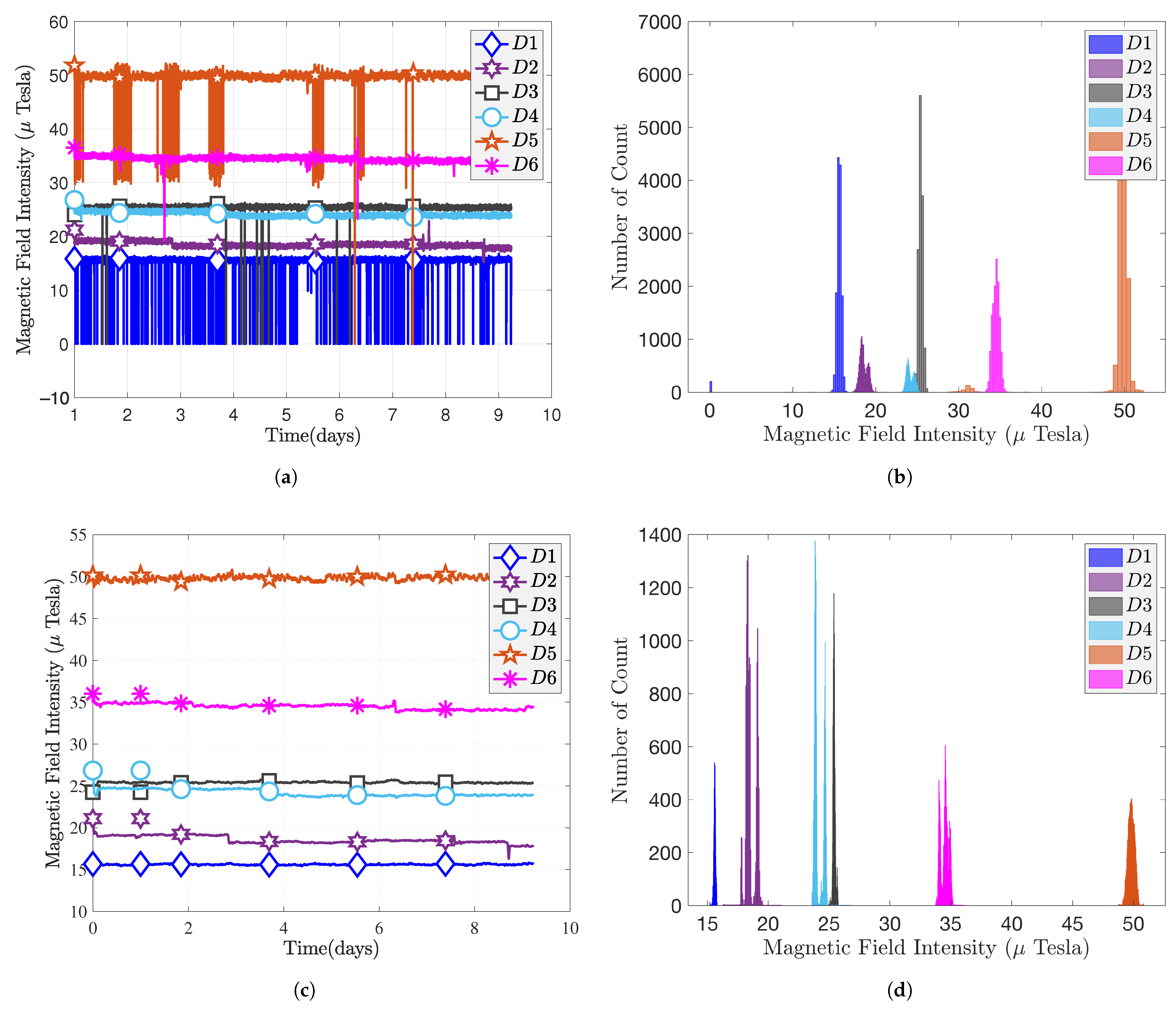
4.1. Statistical Tests with Heterogeneous Smartphones
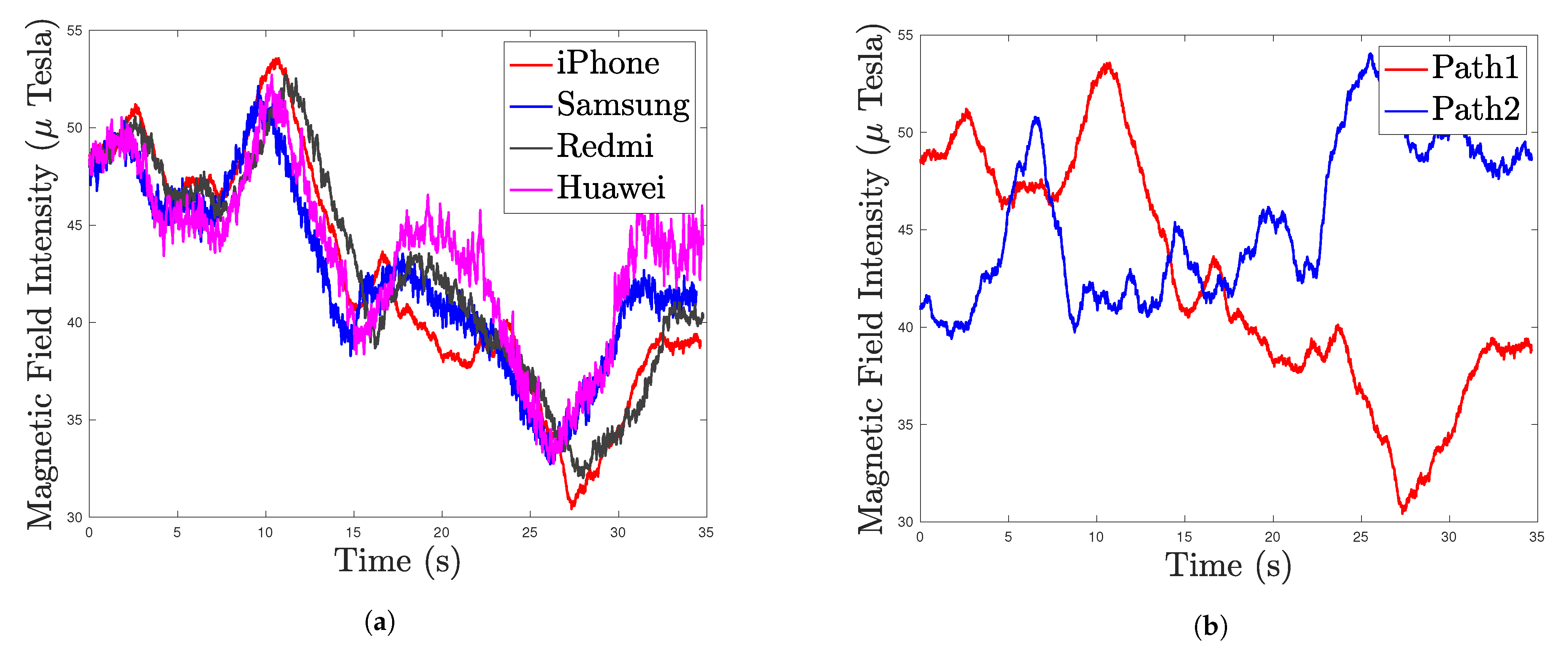
4.2. Trajectory Test with Heterogeneous Smartphone
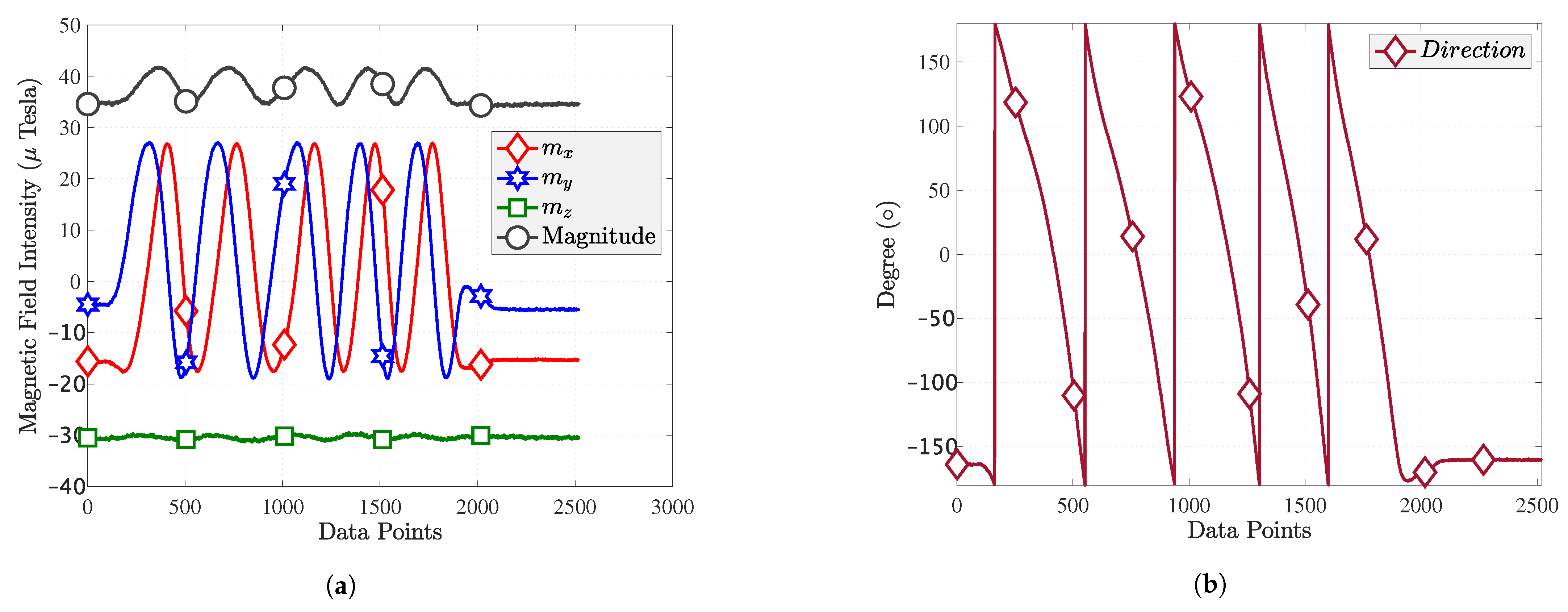
4.3. Rotation Test
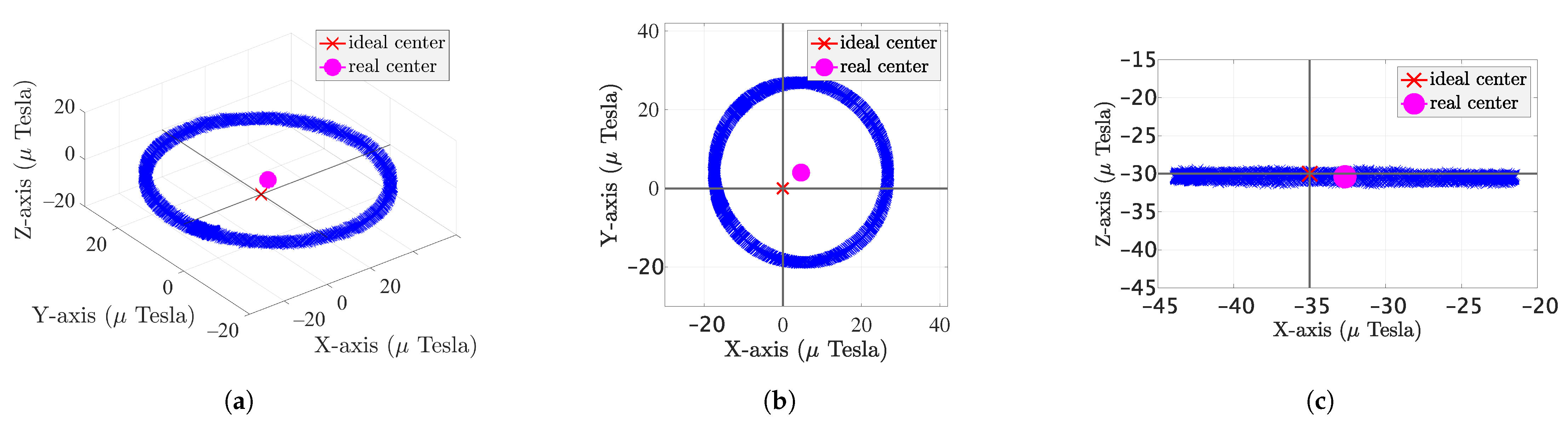
4.4. Static Tests with Magnetometer
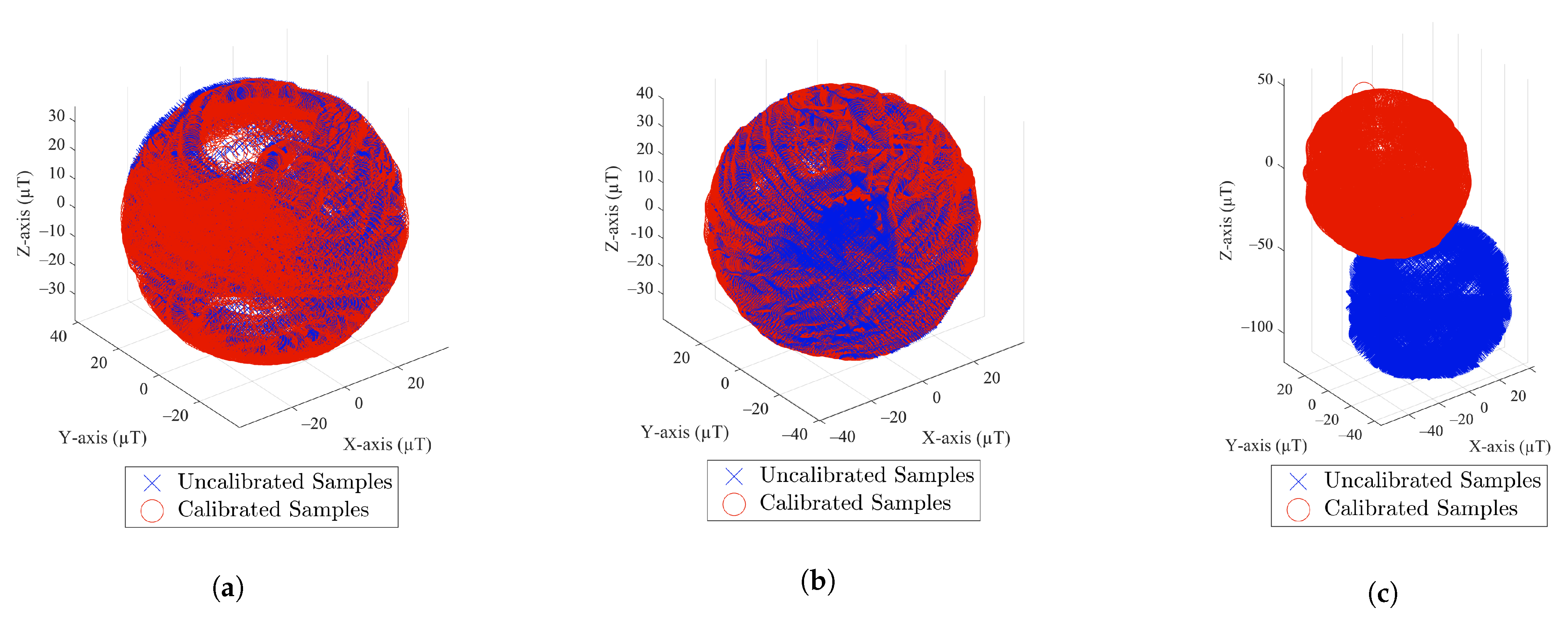
5. Calibration of Magnetic Field
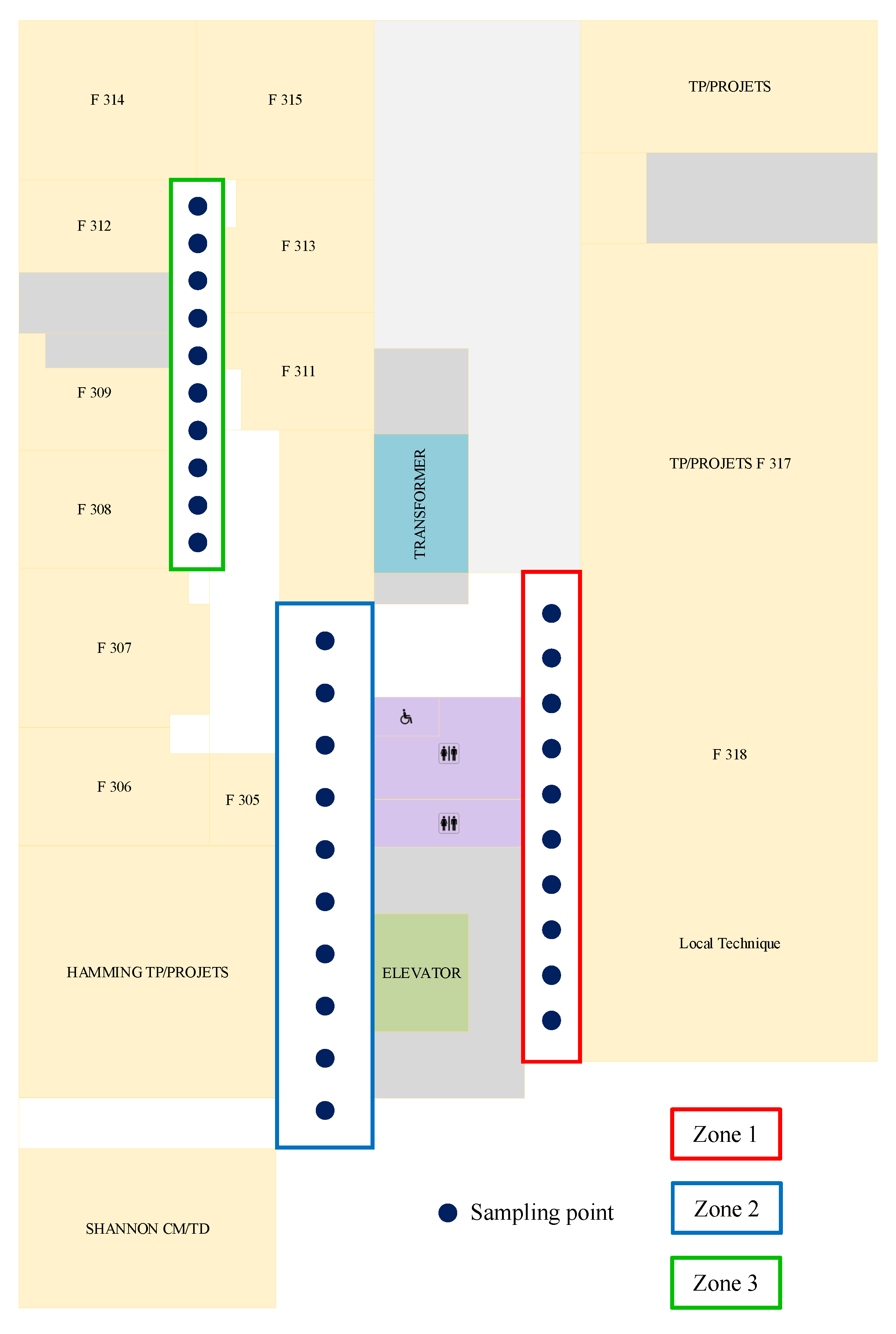
6. Classification Test with Calibration
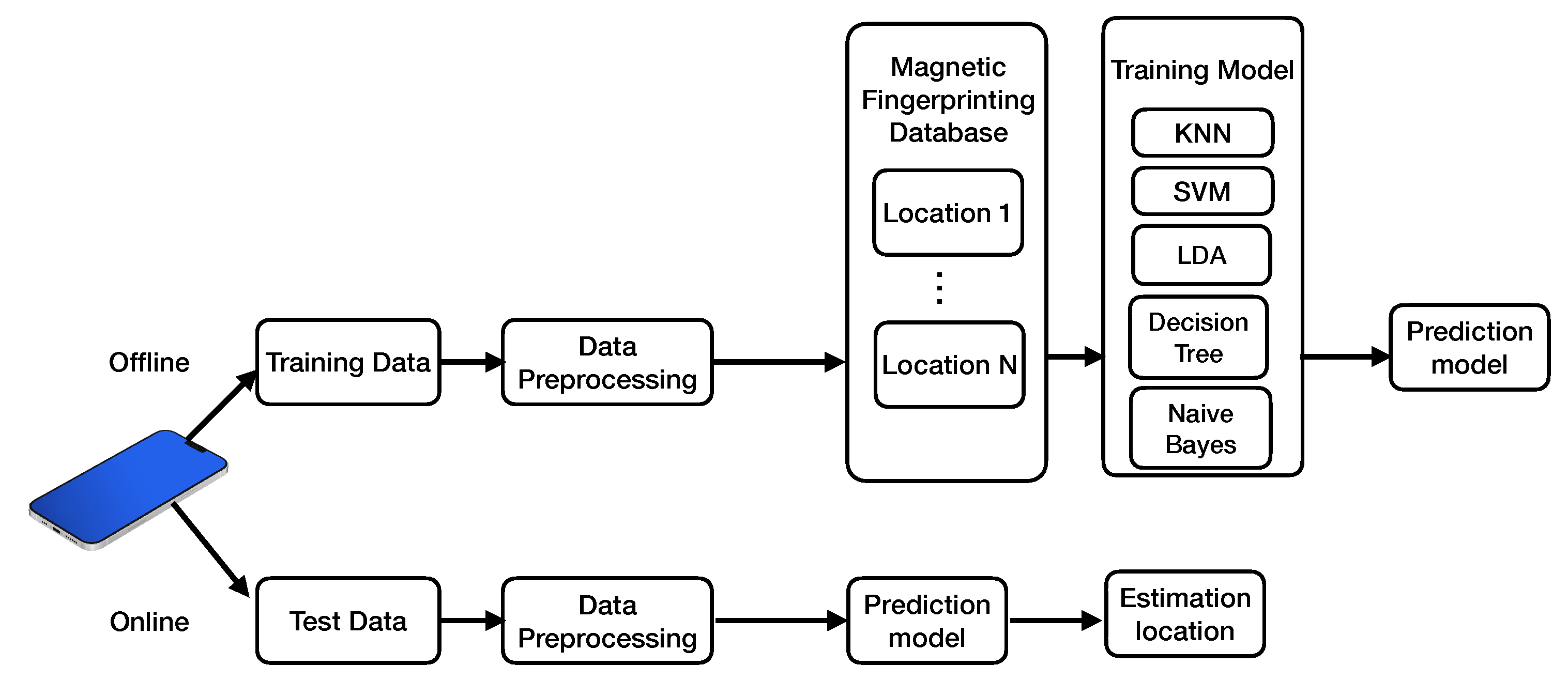
6.1. Data Pre-Processing
6.2. Machine Learning Methods Used for Classification
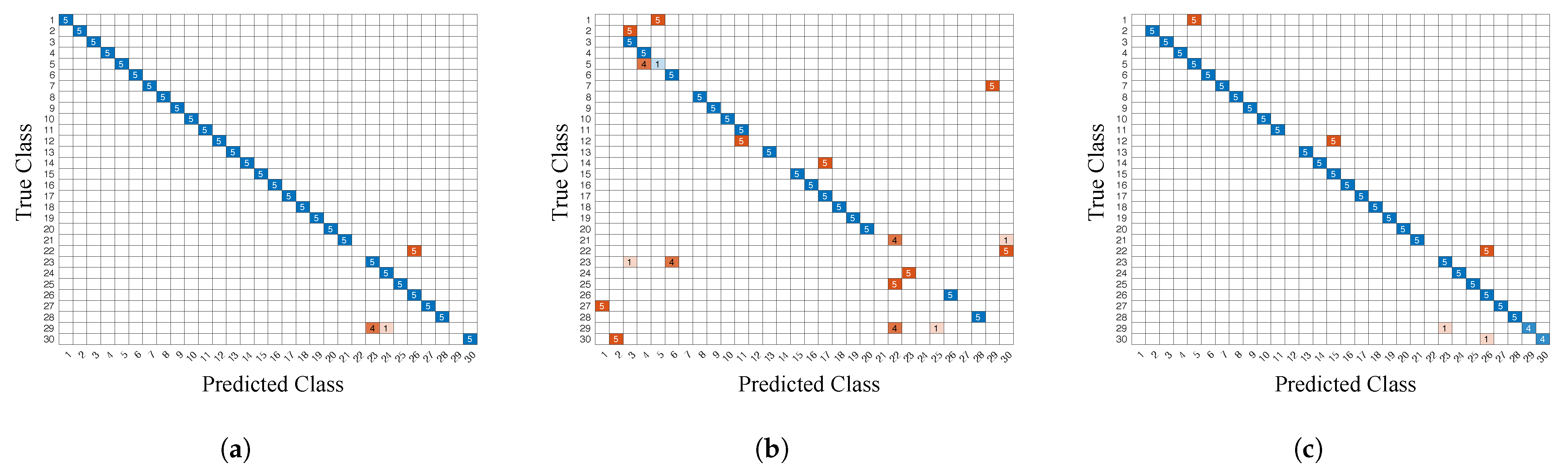
6.3. Classification Result
7. Conclusions
- Firstly, the use of MF data requires the processing of device heterogeneity. The magnetometers with different specifications used by smartphone manufacturers result in different MF measurements. Hence, MF fingerprinting would require the use of smartphones/magnetometers which have similar characteristics to ensure the efficiency of such a positioning approach.
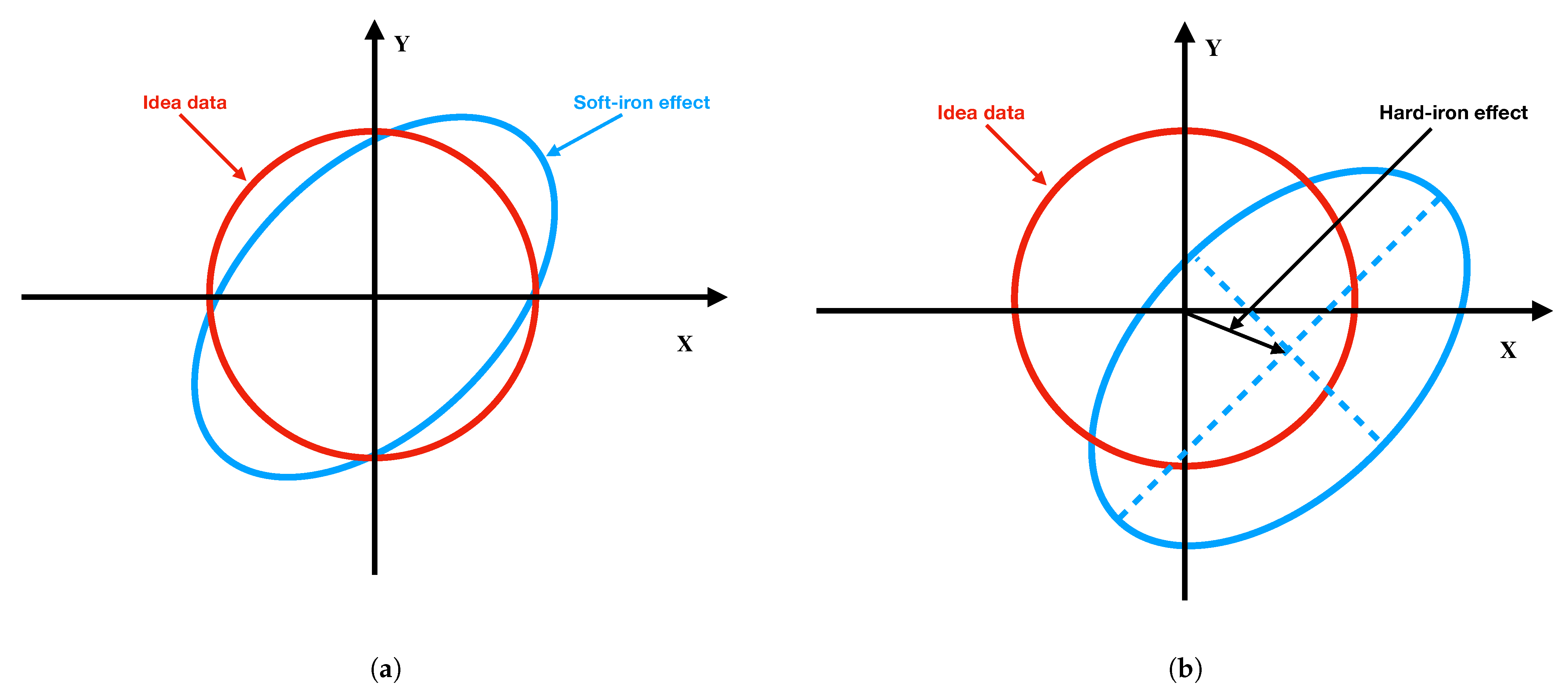
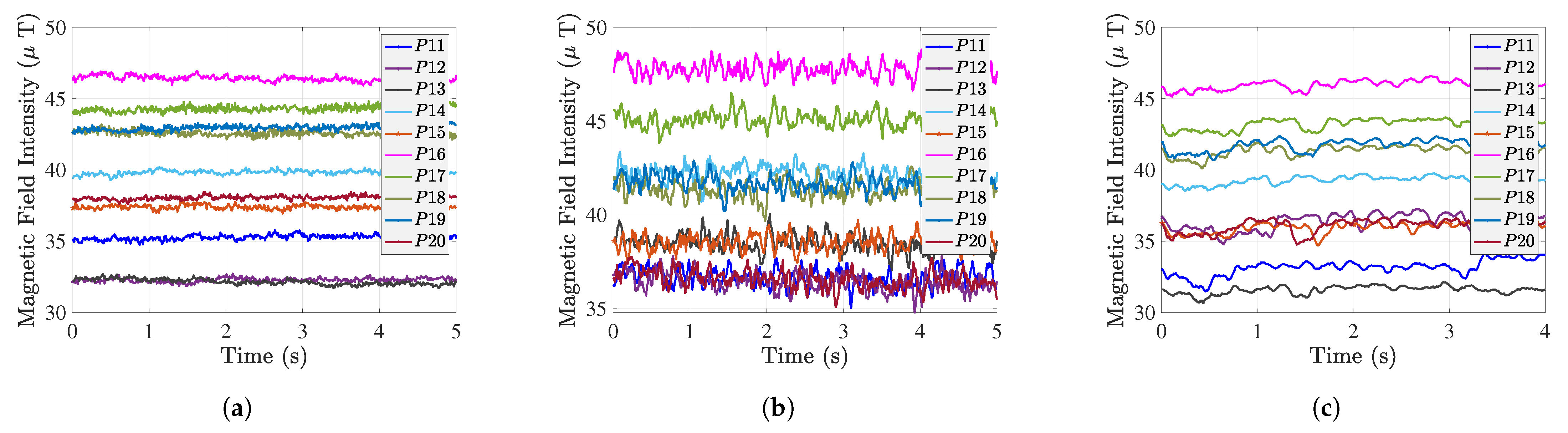
- Data pre-processing is necessary in order to exploit the MF data. This includes filtering out the outliers that affect the magnetometer measurements (in this work, we propose the RLOWESS algorithm to smooth the MF measurements). It also includes the calibration of the magnetometer, which is necessary to eliminate soft and hard iron influences.
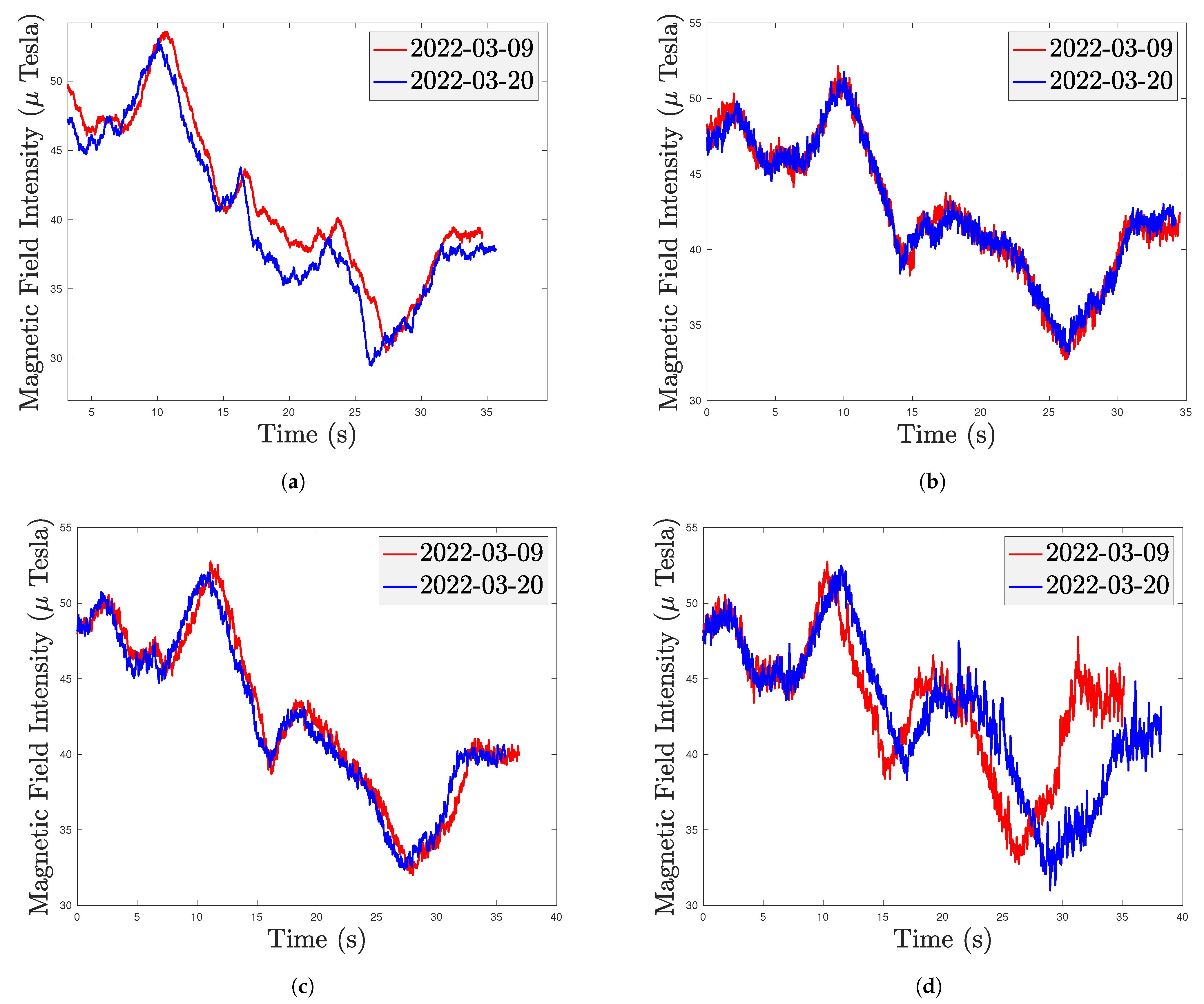
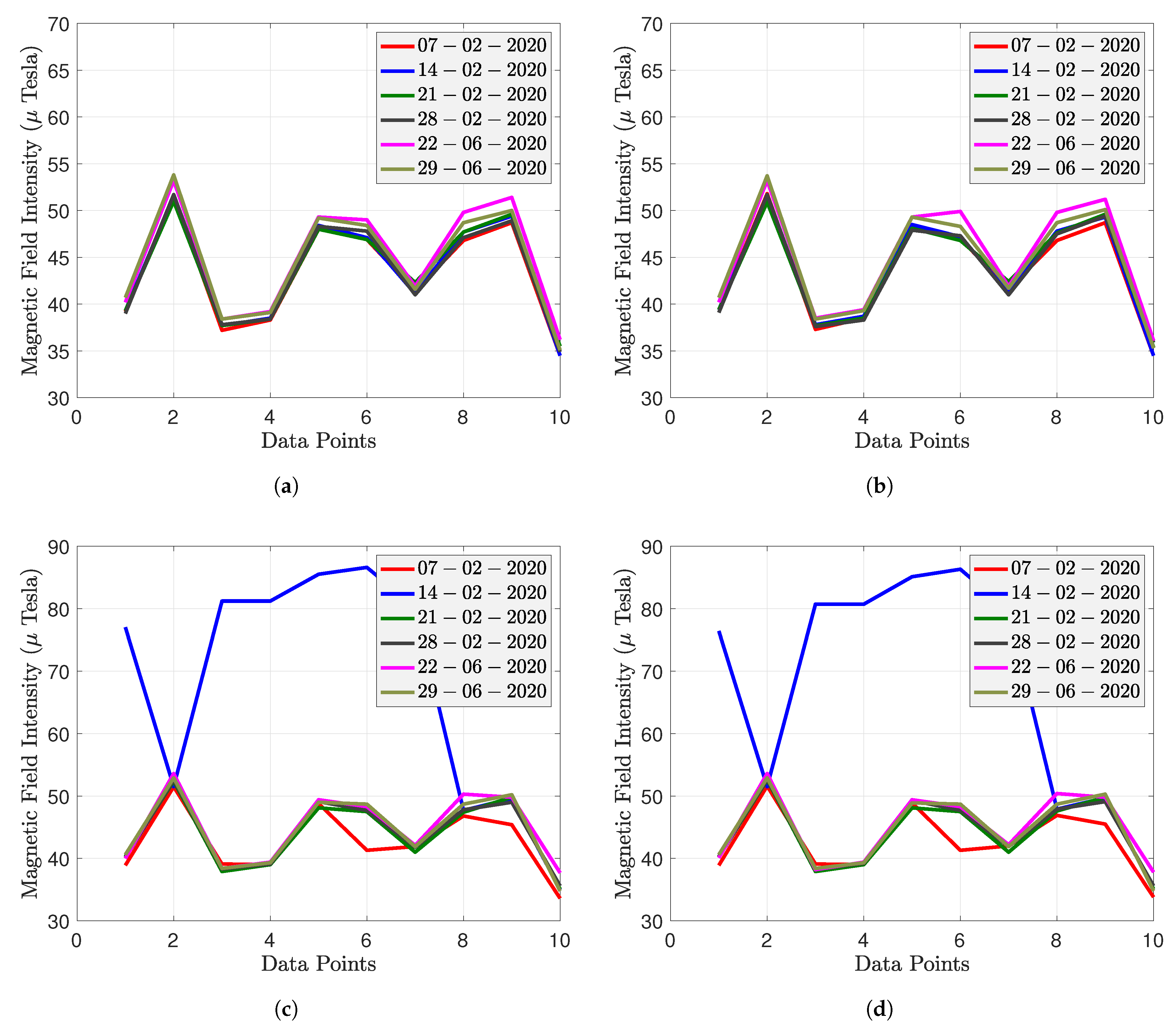
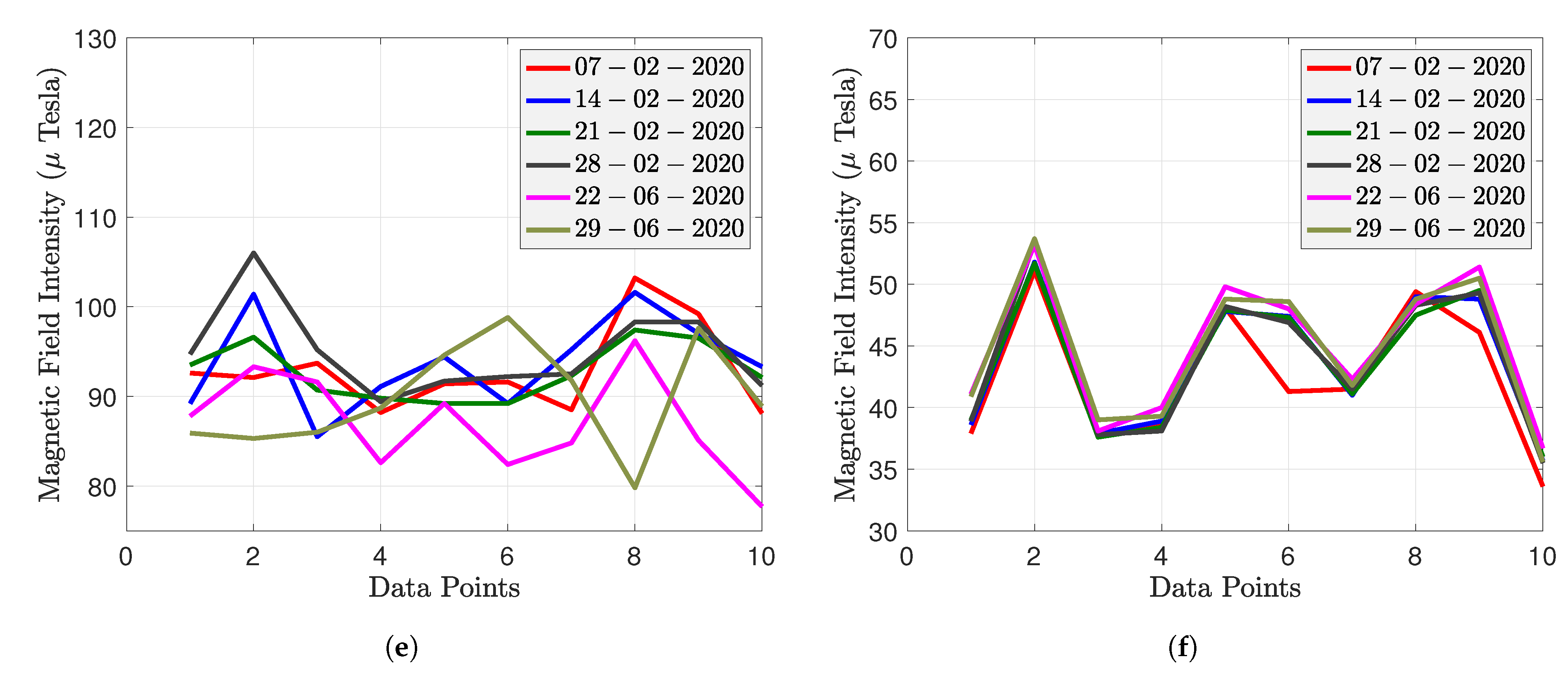
- The magnetic signatures of heterogeneous smartphones on the same path have the same pattern but do not overlap. As the X and Y axes of the magnetic field are direction-dependent, the MF intensity of the smartphone fluctuates as it rotates around the Z axis, which is challenging for magnetic field map construction.
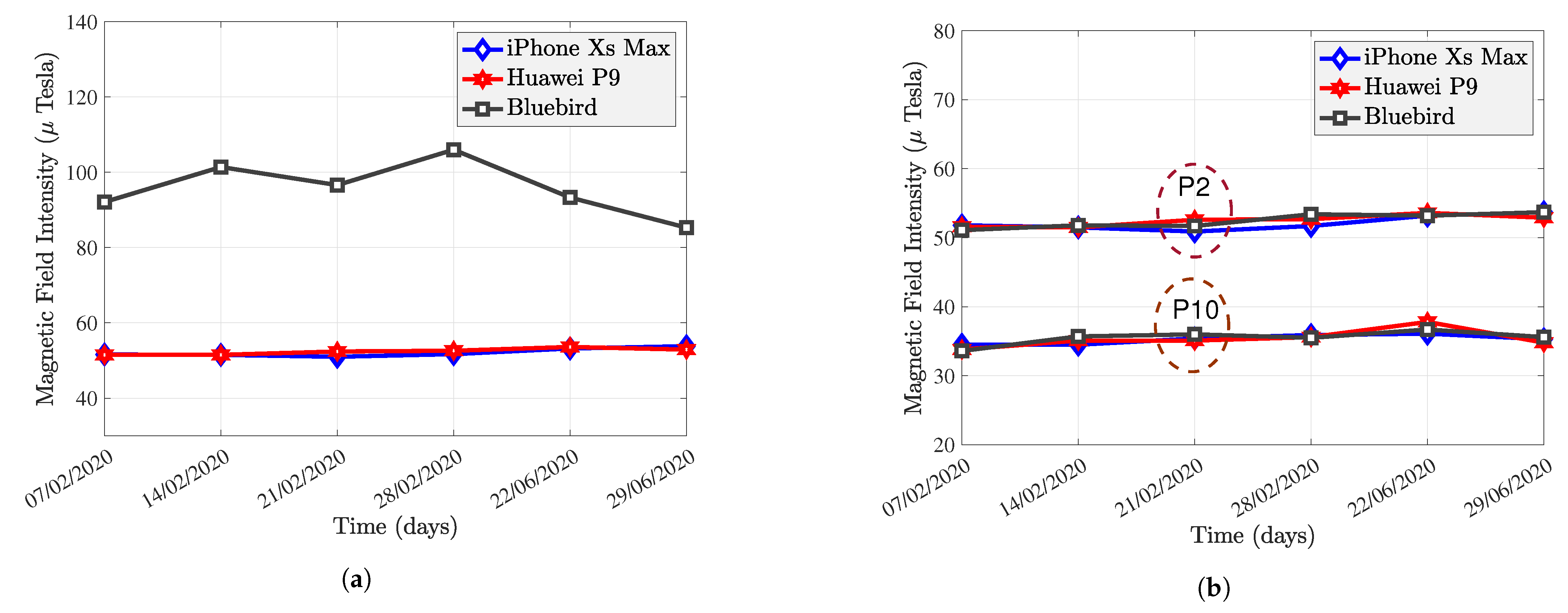
- Calibration tests were carried out with different smartphones in specific locations at given dates. It was found that the calibration parameters of the smartphones depend only on its specifications and not on the environment. There is no need to re-estimate the calibration transform periodically or for different locations.
- The MF collected by one smartphone is calibrated as a fingerprint database, and other smartphones can use this MF fingerprint database for positioning. This method can somewhat solve the MF positioning problem of heterogeneous devices. However, we can still see that the positioning accuracy of heterogeneous devices is significantly lower than that of homogeneous devices.
- Interference sources may enhance the specificity of local MF fingerprints (e.g., proximity to fridges, lifts, metal doors). In the above experiment, the Huawei P9’s positioning accuracy was significantly higher in zone 2 than in the other two zones.
- Despite these challenges, MF data can be used as a complementary method to improve the positioning accuracy of hybrid positioning solutions (e.g., in combination with Wi-Fi, Bluetooth, etc.).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MarketAndMarket. Indoor Location Market. [EB/OL]. Available online: https://www.marketsandmarkets.com/Market-Reports/indoor-location-market-989.html (accessed on 20 July 2021).
- Schiller, J.; Voisard, A. Location-Based Services; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Basiri, A.; Lohan, E.S.; Moore, T.; Winstanley, A.; Peltola, P.; Hill, C.; Amirian, P.; e Silva, P.F. Indoor location based services challenges, requirements and usability of current solutions. Comput. Sci. Rev. 2017, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Chan, S.H.G. Wi-Fi fingerprint-based indoor positioning: Recent advances and comparisons. IEEE Commun. Surv. Tutor. 2015, 18, 466–490. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, Y.; Striegel, A. Face-to-face proximity estimation using bluetooth on smartphones. IEEE Trans. Mob. Comput. 2013, 13, 811–823. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, Z.; Markham, A.; Trigoni, N.; Ren, Y. Does BTLE measure up against WiFi? A comparison of indoor location performance. In Proceedings of the European Wireless 2014—20th European Wireless Conference, Barcelona, Spain, 14–16 May 2014; pp. 1–6. [Google Scholar]
- Sun, Z.; Purohit, A.; Chen, K.; Pan, S.; Pering, T.; Zhang, P. Pandaa: Physical arrangement detection of networked devices through ambient-sound awareness. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September 2011; pp. 425–434. [Google Scholar]
- Huang, W.; Xiong, Y.; Li, X.Y.; Lin, H.; Mao, X.; Yang, P.; Liu, Y. Shake and walk: Acoustic direction finding and fine-grained indoor localization using smartphones. In Proceedings of the IEEE INFOCOM 2014—IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 370–378. [Google Scholar]
- Kuo, Y.S.; Pannuto, P.; Hsiao, K.J.; Dutta, P. Luxapose: Indoor positioning with mobile phones and visible light. In Proceedings of the 20th Annual International Conference on Mobile Computing and Networking, Maui, HI, USA, 7–11 September 2014; pp. 447–458. [Google Scholar]
- Yang, Z.; Wang, Z.; Zhang, J.; Huang, C.; Zhang, Q. Wearables can afford: Light-weight indoor positioning with visible light. In Proceedings of the 13th Annual International Conference on Mobile Systems, Applications, and Services, Florence, Italy, 18–22 May 2015; pp. 317–330. [Google Scholar]
- Chung, J.; Donahoe, M.; Schmandt, C.; Kim, I.J.; Razavai, P.; Wiseman, M. Indoor location sensing using geo-magnetism. In Proceedings of the 9th International Conference on Mobile Systems, Applications, and Services, Bethesda, MD, USA, 28 June–1 July 2011; pp. 141–154. [Google Scholar]
- He, S.; Shin, K.G. Geomagnetism for smartphone-based indoor localization: Challenges, advances, and comparisons. ACM Comput. Surv. (CSUR) 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Haverinen, J.; Kemppainen, A. A global self-localization technique utilizing local anomalies of the ambient magnetic field. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3142–3147. [Google Scholar]
- Xie, H.; Gu, T.; Tao, X.; Ye, H.; Lv, J. MaLoc: A practical magnetic fingerprinting approach to indoor localization using smartphones. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 243–253. [Google Scholar]
- IndoorAtlas. IndoorAtlas. [EB/OL]. Available online: https://www.indooratlas.com/ (accessed on 10 July 2021).
- Order, F. Find & Order. [EB/OL]. Available online: https://findnorder.com/ (accessed on 8 July 2021).
- Qi, J.; Liu, G.P. A robust high-accuracy ultrasound indoor positioning system based on a wireless sensor network. Sensors 2017, 17, 2554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, F.; Liu, J.; Yin, Y.; Wang, W.; Hu, D.; Chen, P.; Niu, Q. Survey on WiFi-based indoor positioning techniques. IET Commun. 2020, 14, 1372–1383. [Google Scholar] [CrossRef]
- Mainetti, L.; Patrono, L.; Sergi, I. A survey on indoor positioning systems. In Proceedings of the 2014 22nd International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 17–19 September 2014; pp. 111–120. [Google Scholar]
- Mazhar, F.; Khan, M.G.; Sällberg, B. Precise indoor positioning using UWB: A review of methods, algorithms and implementations. Wirel. Pers. Commun. 2017, 97, 4467–4491. [Google Scholar] [CrossRef]
- Singh, J.; Raza, U. Passive visible light positioning systems: An overview. In Proceedings of the Workshop on Light Up the IoT, London, UK, 21 September 2020; pp. 48–53. [Google Scholar]
- Koyuncu, H.; Yang, S.H. A survey of indoor positioning and object locating systems. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2010, 10, 121–128. [Google Scholar]
- Wu, Y.; Zhu, H.B.; Du, Q.X.; Tang, S.M. A survey of the research status of pedestrian dead reckoning systems based on inertial sensors. Int. J. Autom. Comput. 2019, 16, 65–83. [Google Scholar] [CrossRef]
- Ouyang, G.; Abed-Meraim, K. A Survey of Magnetic-Field-Based Indoor Localization. Electronics 2022, 11, 864. [Google Scholar] [CrossRef]
- Finlay, C.C.; Maus, S.; Beggan, C.; Bondar, T.; Chambodut, A.; Chernova, T.; Chulliat, A.; Golovkov, V.; Hamilton, B.; Hamoudi, M.; et al. International geomagnetic reference field: The eleventh generation. Geophys. J. Int. 2010, 183, 1216–1230. [Google Scholar]
- Ashraf, I.; Zikria, Y.B.; Hur, S.; Park, Y. A Comprehensive Analysis of Magnetic Field Based Indoor Positioning With Smartphones: Opportunities, Challenges and Practical Limitations. IEEE Access 2020, 8, 228548–228571. [Google Scholar] [CrossRef]
- Li, B.; Gallagher, T.; Dempster, A.G.; Rizos, C. How feasible is the use of magnetic field alone for indoor positioning. In Proceedings of the IEEE 2012 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, NSW, Australia, 13–15 November 2012; pp. 1–9. [Google Scholar]
- Li, B.; Gallagher, T.; Rizos, C.; Dempster, A.G. Using geomagnetic field for indoor positioning. J. Appl. Geod. 2013, 7, 299–308. [Google Scholar] [CrossRef]
- Frassl, M.; Angermann, M.; Lichtenstern, M.; Robertson, P.; Julian, B.J.; Doniec, M. Magnetic maps of indoor environments for precise localization of legged and non-legged locomotion. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 913–920. [Google Scholar]
- Shu, Y.; Bo, C.; Shen, G.; Zhao, C.; Li, L.; Zhao, F. Magicol: Indoor localization using pervasive magnetic field and opportunistic WiFi sensing. IEEE J. Sel. Areas Commun. 2015, 33, 1443–1457. [Google Scholar] [CrossRef]
- Ashraf, I.; Hur, S.; Park, Y. Enhancing Performance of Magnetic Field Based Indoor Localization Using Magnetic Patterns from Multiple Smartphones. Sensors 2020, 20, 2704. [Google Scholar] [CrossRef]
- Ashraf, I.; Kang, M.; Hur, S.; Park, Y. MINLOC: Magnetic field patterns-based indoor localization using convolutional neural networks. IEEE Access 2020, 8, 66213–66227. [Google Scholar] [CrossRef]
- Lee, S.; Chae, S.; Han, D. ILoA: Indoor localization using augmented vector of geomagnetic field. IEEE Access 2020, 8, 184242–184255. [Google Scholar] [CrossRef]
- Vandermeulen, D.; Vercauteren, C.; Weyn, M.; Vandermeulen, D. Indoor localization using a magnetic flux density map of a building. In Proceedings of the International Conference on Ambient Computing, Applications, Services and Technologies, Porto, Portugal, 29 September–3 October 2013; pp. 42–49. [Google Scholar]
- Luo, H.; Zhao, F.; Jiang, M.; Ma, H.; Zhang, Y. Constructing an indoor floor plan using crowdsourcing based on magnetic fingerprinting. Sensors 2017, 17, 2678. [Google Scholar] [CrossRef] [Green Version]
- Pei, L.; Zhang, M.; Zou, D.; Chen, R.; Chen, Y. A survey of crowd sensing opportunistic signals for indoor localization. Mob. Inf. Syst. 2016, 2016, 4041291. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Chen, Q.; Yang, L.T.; Chao, H.C. Indoor smartphone localization via fingerprint crowdsourcing: Challenges and approaches. IEEE Wirel. Commun. 2016, 23, 82–89. [Google Scholar] [CrossRef]
- Ayanoglu, A.; Schneider, D.M.; Eitel, B. Crowdsourcing-based magnetic map generation for indoor localization. In Proceedings of the IEEE 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–8. [Google Scholar]
- Chen, L.; Wu, J.; Yang, C. MeshMap: A magnetic field-based indoor navigation system with crowdsourcing support. IEEE Access 2020, 8, 39959–39970. [Google Scholar] [CrossRef]
- Gao, C.; Harle, R. Semi-automated signal surveying using smartphones and floorplans. IEEE Trans. Mob. Comput. 2017, 17, 1952–1965. [Google Scholar] [CrossRef] [Green Version]
- Vallivaara, I.; Haverinen, J.; Kemppainen, A.; Röning, J. Simultaneous localization and mapping using ambient magnetic field. In Proceedings of the 2010 IEEE Conference on Multisensor Fusion and Integration, Salt Lake City, UT, USA, 5–7 September 2010; pp. 14–19. [Google Scholar]
- Wahlström, N.; Kok, M.; Schön, T.B.; Gustafsson, F. Modeling magnetic fields using Gaussian processes. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3522–3526. [Google Scholar]
- Akai, N.; Ozaki, K. Gaussian processes for magnetic map-based localization in large-scale indoor environments. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4459–4464. [Google Scholar]
- Solin, A.; Kok, M.; Wahlström, N.; Schön, T.B.; Särkkä, S. Modeling and interpolation of the ambient magnetic field by Gaussian processes. IEEE Trans. Robot. 2018, 34, 1112–1127. [Google Scholar] [CrossRef] [Green Version]
- Kok, M.; Solin, A. Scalable magnetic field SLAM in 3D using Gaussian process maps. In Proceedings of the IEEE 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 1353–1360. [Google Scholar]
- Wang, H.; Sen, S.; Elgohary, A.; Farid, M.; Youssef, M.; Choudhury, R.R. No need to war-drive: Unsupervised indoor localization. In Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services, Low Wood Bay Lake District, UK, 25–29 June 2012; pp. 197–210. [Google Scholar]
- Abdelnasser, H.; Mohamed, R.; Elgohary, A.; Alzantot, M.F.; Wang, H.; Sen, S.; Choudhury, R.R.; Youssef, M. SemanticSLAM: Using environment landmarks for unsupervised indoor localization. IEEE Trans. Mob. Comput. 2015, 15, 1770–1782. [Google Scholar] [CrossRef]
- Shang, J.; Gu, F.; Hu, X.; Kealy, A. Apfiloc: An infrastructure-free indoor localization method fusing smartphone inertial sensors, landmarks and map information. Sensors 2015, 15, 27251–27272. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Zheng, Y.; Li, Z.; Li, M.; Shen, G. Iodetector: A generic service for indoor outdoor detection. In Proceedings of the 10th ACM Conference on Embedded Network Sensor Systems, Toronto, ON, Canada, 6–9 November 2012; pp. 113–126. [Google Scholar]
- Elhamshary, M.; Youssef, M.; Uchiyama, A.; Yamaguchi, H.; Higashino, T. TransitLabel: A crowd-sensing system for automatic labeling of transit stations semantics. In Proceedings of the 14th Annual International Conference on Mobile Systems, Applications, and Services, Singapore, 26–30 June 2016; pp. 193–206. [Google Scholar]
- Subbu, K.P.; Gozick, B.; Dantu, R. Indoor localization through dynamic time warping. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 1639–1644. [Google Scholar]
- Perez-Navarro, A.; Montoliu, R.; Torres-Sospedra, J.; Conesa, J. Magnetic field as a characterization of wide and narrow spaces in a real challenging scenario using dynamic time warping. In Proceedings of the IEEE 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–8. [Google Scholar]
- Wang, Q.; Luo, H.; Zhao, F.; Shao, W. An indoor self-localization algorithm using the calibration of the online magnetic fingerprints and indoor landmarks. In Proceedings of the IEEE 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–8. [Google Scholar]
- Chen, J.; Ou, G.; Peng, A.; Zheng, L.; Shi, J. A hybrid dead reckon system based on 3-dimensional dynamic time warping. Electronics 2019, 8, 185. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Yang, X.; Yin, Y.; Gao, S.; Niu, Q. Smartphone-based indoor localization with integrated fingerprint signal. IEEE Access 2020, 8, 33178–33187. [Google Scholar] [CrossRef]
- Hoang, M.T.; Zhu, Y.; Yuen, B.; Reese, T.; Dong, X.; Lu, T.; Westendorp, R.; Xie, M. A soft range limited K-nearest neighbors algorithm for indoor localization enhancement. IEEE Sens. J. 2018, 18, 10208–10216. [Google Scholar] [CrossRef] [Green Version]
- Bottou, L.; Lin, C.J. Support vector machine solvers. Large Scale Kernel Mach. 2007, 3, 301–320. [Google Scholar]
- Wu, Z.; Xu, Q.; Li, J.; Fu, C.; Xuan, Q.; Xiang, Y. Passive indoor localization based on csi and naive bayes classification. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1566–1577. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Nessa, A.; Adhikari, B.; Hussain, F.; Fernando, X.N. A survey of machine learning for indoor positioning. IEEE Access 2020, 8, 214945–214965. [Google Scholar] [CrossRef]
- Galván-Tejada, C.E.; García-Vázquez, J.P.; Brena, R.F. Magnetic field feature extraction and selection for indoor location estimation. Sensors 2014, 14, 11001–11015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Y.; Dou, Z.; Jiang, Q.; Hou, Z. Basmag: An optimized HMM-based localization system using backward sequences matching algorithm exploiting geomagnetic information. IEEE Sens. J. 2016, 16, 7472–7482. [Google Scholar] [CrossRef]
- Kwak, M.; Hamm, C.; Park, S.; Kwon, T.T. Magnetic Field based Indoor Localization System: A Crowdsourcing Approach. In Proceedings of the IEEE 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–8. [Google Scholar]
- Zhao, H.; Wang, Z. Motion measurement using inertial sensors, ultrasonic sensors, and magnetometers with extended kalman filter for data fusion. IEEE Sens. J. 2011, 12, 943–953. [Google Scholar] [CrossRef]
- Xie, H.; Gu, T.; Tao, X.; Ye, H.; Lu, J. A reliability-augmented particle filter for magnetic fingerprinting based indoor localization on smartphone. IEEE Trans. Mob. Comput. 2015, 15, 1877–1892. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Nie, J.; Lin, L. Magnetic-based indoor localization using smartphone via a fusion algorithm. IEEE Sens. J. 2019, 19, 6477–6485. [Google Scholar] [CrossRef]
- Robertson, P.; Frassl, M.; Angermann, M.; Doniec, M.; Julian, B.J.; Puyol, M.G.; Khider, M.; Lichtenstern, M.; Bruno, L. Simultaneous localization and mapping for pedestrians using distortions of the local magnetic field intensity in large indoor environments. In Proceedings of the IEEE International Conference on Indoor Positioning and Indoor Navigation, Montbeliard, France, 28–31 October 2013; pp. 1–10. [Google Scholar]
- Wang, X.; Zhang, C.; Liu, F.; Dong, Y.; Xu, X. Exponentially weighted particle filter for simultaneous localization and mapping based on magnetic field measurements. IEEE Trans. Instrum. Meas. 2017, 66, 1658–1667. [Google Scholar] [CrossRef]
- Ashraf, I.; Hur, S.; Park, Y. Application of deep convolutional neural networks and smartphone sensors for indoor localization. Appl. Sci. 2019, 9, 2337. [Google Scholar] [CrossRef] [Green Version]
- Ashraf, I.; Hur, S.; Park, Y. mPILOT-magnetic field strength based pedestrian indoor localization. Sensors 2018, 18, 2283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashraf, I.; Hur, S.; Shafiq, M.; Kumari, S.; Park, Y. GUIDE: Smartphone sensors-based pedestrian indoor localization with heterogeneous devices. Int. J. Commun. Syst. 2019, 32, e4062. [Google Scholar] [CrossRef]
- Sun, D.; Wei, E.; Yang, L.; Xu, S. Improving Fingerprint Indoor Localization Using Convolutional Neural Networks. IEEE Access 2020, 8, 193396–193411. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Z.; Mao, S. DeepML: Deep LSTM for indoor localization with smartphone magnetic and light sensors. In Proceedings of the 2018 IEEE international conference on communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Bae, H.J.; Choi, L. Large-scale indoor positioning using geomagnetic field with deep neural networks. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Jang, H.J.; Shin, J.M.; Choi, L. Geomagnetic field based indoor localization using recurrent neural networks. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Liu, T.; Wu, T.; Wang, M.; Fu, M.; Kang, J.; Zhang, H. Recurrent neural networks based on LSTM for predicting geomagnetic field. In Proceedings of the 2018 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Bali, Indonesia, 20–21 September 2018; pp. 1–5. [Google Scholar]
- Bhattarai, B.; Yadav, R.K.; Gang, H.S.; Pyun, J.Y. Geomagnetic field based indoor landmark classification using deep learning. IEEE Access 2019, 7, 33943–33956. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Z.; Chen, J.; Fourati, H.; Li, R. Fast complementary filter for attitude estimation using low-cost MARG sensors. IEEE Sens. J. 2016, 16, 6997–7007. [Google Scholar] [CrossRef]
- Ahmed, H.; Tahir, M. Accurate attitude estimation of a moving land vehicle using low-cost MEMS IMU sensors. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1723–1739. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Yang, G.Z. Calibration of miniature inertial and magnetic sensor units for robust attitude estimation. IEEE Trans. Instrum. Meas. 2013, 63, 711–718. [Google Scholar] [CrossRef]
- Kok, M.; Schön, T.B. Magnetometer calibration using inertial sensors. IEEE Sens. J. 2016, 16, 5679–5689. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Wu, Y.; Hu, X.; Wu, M. Calibration of three-axis magnetometer using stretching particle swarm optimization algorithm. IEEE Trans. Instrum. Meas. 2012, 62, 281–292. [Google Scholar] [CrossRef]
- Kok, M.; Hol, J.D.; Schön, T.B. Using inertial sensors for position and orientation estimation. arXiv 2017, arXiv:1704.06053. [Google Scholar]
- Phyphox. Phyphox Sensor Database. [EB/OL]. Available online: https://phyphox.org/sensordb/ (accessed on 16 May 2022).
- Matyunin, N.; Wang, Y.; Arul, T.; Kullmann, K.; Szefer, J.; Katzenbeisser, S. Magneticspy: Exploiting magnetometer in mobile devices for website and application fingerprinting. In Proceedings of the 18th ACM Workshop on Privacy in the Electronic Society, London, UK, 11 November 2019; pp. 135–149. [Google Scholar]
- Matzka, J.; Chulliat, A.; Mandea, M.; Finlay, C.; Qamili, E. Geomagnetic observations for main field studies: From ground to space. Space Sci. Rev. 2010, 155, 29–64. [Google Scholar] [CrossRef]
- Le Grand, E.; Thrun, S. 3-axis magnetic field mapping and fusion for indoor localization. In Proceedings of the 2012 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Hamburg, Germany, 13–15 September 2012; pp. 358–364. [Google Scholar]
- Angermann, M.; Frassl, M.; Doniec, M.; Julian, B.J.; Robertson, P. Characterization of the indoor magnetic field for applications in localization and mapping. In Proceedings of the IEEE 2012 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, NSW, Australia, 13–15 November 2012; pp. 1–9. [Google Scholar]
- STMicroelectronics. LSM9DS1 Datasheet. [EB/OL]. Available online: https://www.st.com/resource/en/datasheet/lsm9ds1.pdf (accessed on 22 March 2022).
- Arduino. Adafruit LSM9DS1 Accelerometer + Gyro + Magnetometer 9-DOF Breakout. [EB/OL]. Available online: https://learn.adafruit.com/adafruit-lsm9ds1-accelerometer-plus-gyro-plus-magnetometer-9-dof-breakout/arduino-code (accessed on 27 March 2022).
- Robert, C.; William, C.; Irma, T. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Soken, H.E. A survey of calibration algorithms for small satellite magnetometers. Measurement 2018, 122, 417–423. [Google Scholar] [CrossRef]
- Wu, Y.; Shi, W. On calibration of three-axis magnetometer. IEEE Sens. J. 2015, 15, 6424–6431. [Google Scholar] [CrossRef] [Green Version]
- Ozyagcilar, T. Calibrating an eCompass in the Presence of Hard- and Soft-Iron Interference. [EB/OL]. Available online: https://www.nxp.com/docs/en/application-note/AN4246.pdf (accessed on 2 March 2022).
- Salamah, A.H.; Tamazin, M.; Sharkas, M.A.; Khedr, M. An enhanced WiFi indoor localization system based on machine learning. In Proceedings of the IEEE 2016 International conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–8. [Google Scholar]
- Chan, T.F. An improved algorithm for computing the singular value decomposition. ACM Trans. Math. Softw. (TOMS) 1982, 8, 72–83. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control 1981, 4, 70–77. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, 4, 580–585. [Google Scholar] [CrossRef]
- Li, T.; Zhu, S.; Ogihara, M. Using discriminant analysis for multi-class classification: An experimental investigation. Knowl. Inf. Syst. 2006, 10, 453–472. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Zhou, R.; Lu, X.; Zhao, P.; Chen, J. Device-free presence detection and localization with SVM and CSI fingerprinting. IEEE Sens. J. 2017, 17, 7990–7999. [Google Scholar] [CrossRef]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar]


| Positioning Technology | Coverage Range | Positioning Accuracy | Advantages | Disadvantages |
|---|---|---|---|---|
| Ultrasound [17] | ∼10 m | Meters |
|
|
| Wi-Fi [18] | ∼35 m | 5 m∼15 m |
|
|
| Bluetooth [19] | ∼10 m | 1∼5 m |
|
|
| UWB [20] | Few meters | 10∼30 cm |
|
|
| Visible light [21] | Line of sight condition | 10 cm∼2m |
|
|
| Vision (camera) [22] | Line of sight condition | 0.01∼1 m |
|
|
| Inertial navigation [23] | Hundreds of meters | 2 m |
|
|
| Magnetic field [24] | ∼ | 1∼5 m |
|
|
| Smartphone | System Version | Magnetometer Model | Sensor Vendor | Description |
|---|---|---|---|---|
| Huawei P9 | Android 8.0 | AK09911 | AKM |
|
| Redmi Note 10 Pro | Android 11 | AK0991x | AKM |
|
| Samsung S9 | Android 9.0 | AK09916C | AKM |
|
| Bluebird | Android 6.0 | Mmc3416x | MEMSIC |
|
| iPhone Xs Max | iOS 15.3.1 | ∼ | ∼ | ∼ |
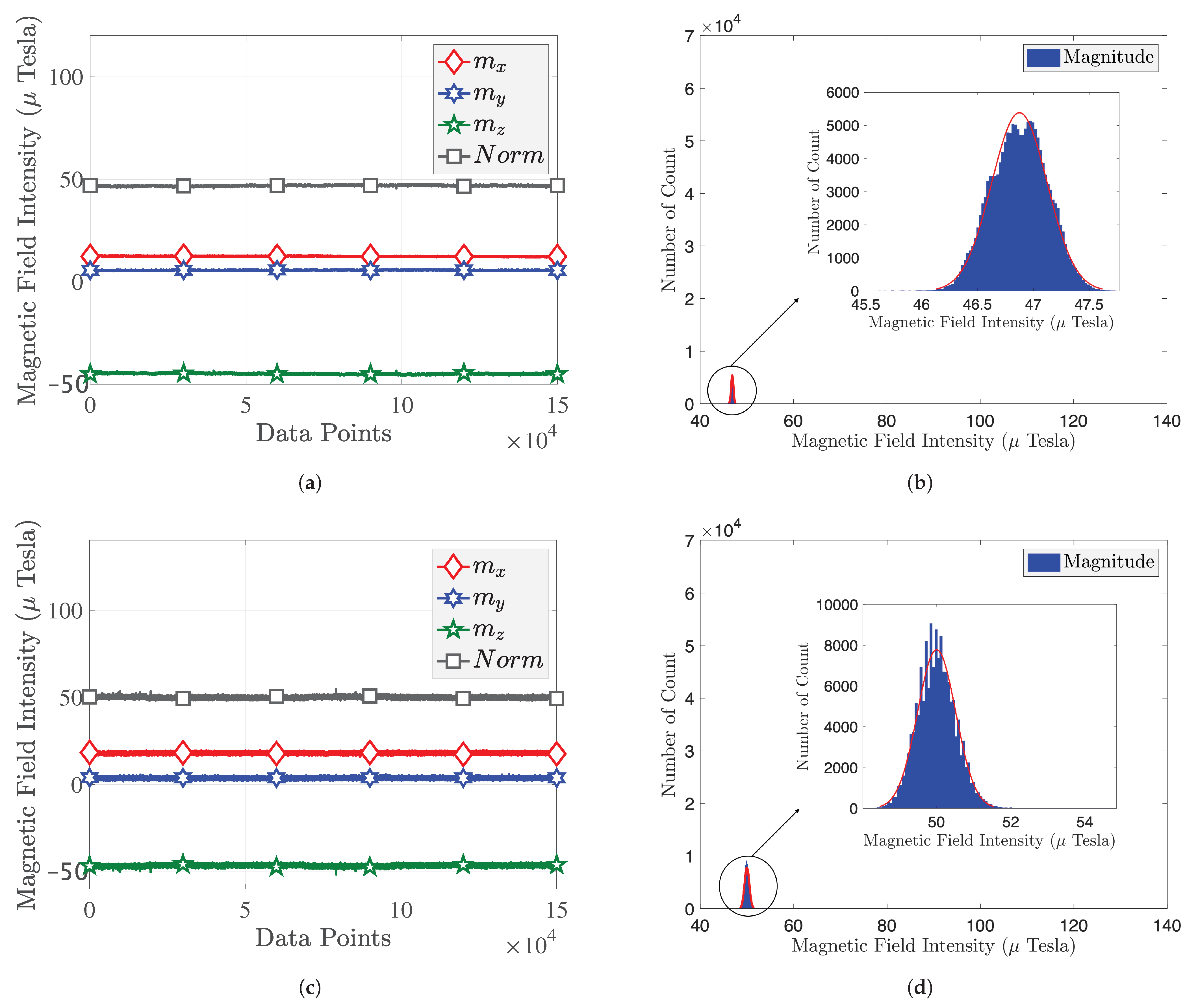
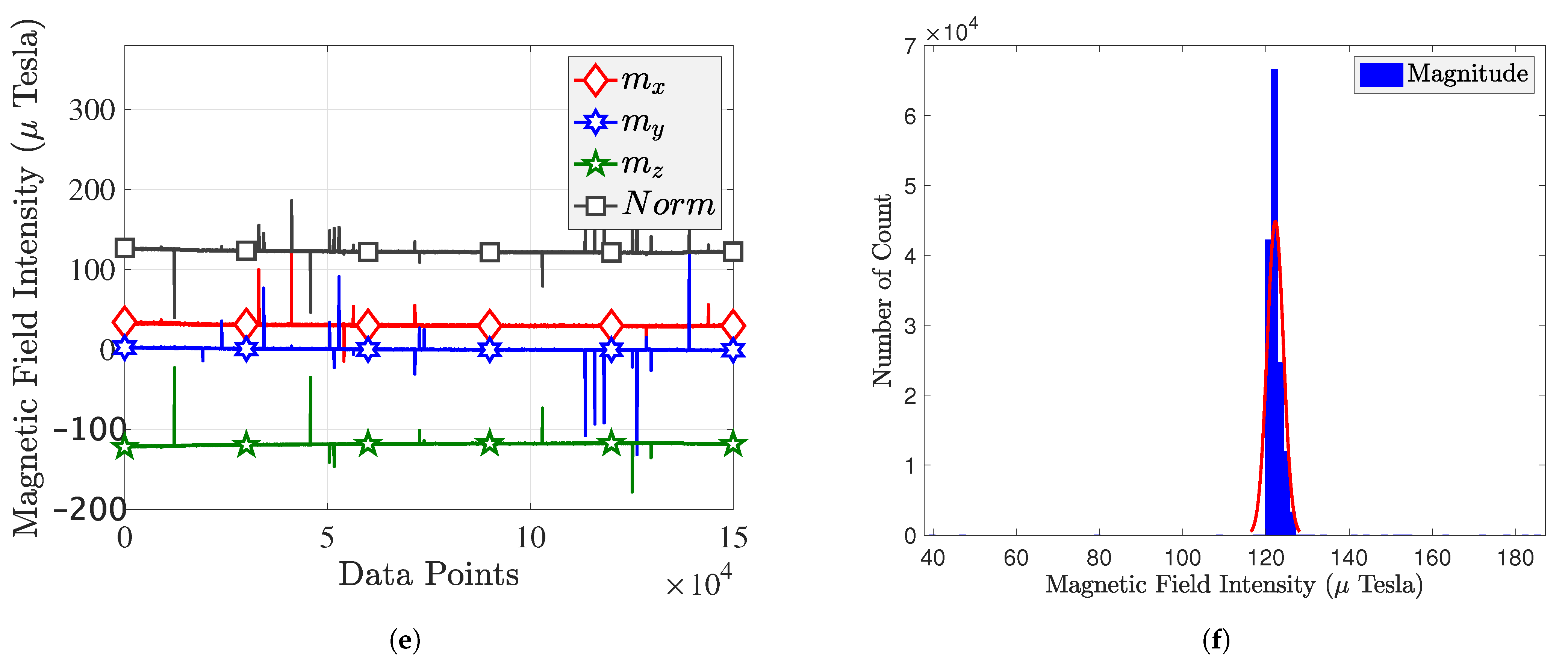
| Time | Device | Mean | Std | Kurtosis | Skewness |
|---|---|---|---|---|---|
| 22 January 2021 | iPhone Xs Max | 46.87 | 0.25 | 2.72 | −0.06 |
| Huawei P9 | 50.00 | 0.52 | 3.87 | 0.32 | |
| Bluebird | 122.24 | 1.94 | 506.21 | −0.04 | |
| 4 February 2021 | iPhone Xs Max | 47.63 | 0.37 | 3.09 | −0.62 |
| Huawei P9 | 49.01 | 0.53 | 3.97 | 0.37 | |
| Bluebird | 125.19 | 1.79 | 1764.79 | 12.33 |
| D1 | D2 | D3 | D4 | D5 | D6 | |
|---|---|---|---|---|---|---|
| Original MF Variance | 3.67 | 0.24 | 0.74 | 0.20 | 8.03 | 0.20 |
| Filtered MF Variance | 0.01 | 0.19 | 0.01 | 0.16 | 0.07 | 0.11 |
| Smartphone | KNN | Decision Tree | Naive Bayes | Discriminant Analysis | SVM |
|---|---|---|---|---|---|
| iPhone | 93.3% | 76.7% | 76.7% | 88.0% | 86.0% |
| Huawei | 53.3% | 40.7% | 40.7% | 42.7% | 52.0% |
| Bluebird | 88.7% | 82.0% | 82.0% | 89.3% | 88.0% |
| Smartphone | KNN | Decision Tree | Naive Bayes | Discriminant Analysis | SVM |
|---|---|---|---|---|---|
| Huawei | 59.3% | 53.3% | 53.3% | 47.3% | 46.0% |
| Bluebird | 59.3% | 44.7% | 44.7% | 55.3% | 55.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, G.; Abed-Meraim, K. Analysis of Magnetic Field Measurements for Indoor Positioning. Sensors 2022, 22, 4014. https://doi.org/10.3390/s22114014
Ouyang G, Abed-Meraim K. Analysis of Magnetic Field Measurements for Indoor Positioning. Sensors. 2022; 22(11):4014. https://doi.org/10.3390/s22114014
Chicago/Turabian StyleOuyang, Guanglie, and Karim Abed-Meraim. 2022. "Analysis of Magnetic Field Measurements for Indoor Positioning" Sensors 22, no. 11: 4014. https://doi.org/10.3390/s22114014
APA StyleOuyang, G., & Abed-Meraim, K. (2022). Analysis of Magnetic Field Measurements for Indoor Positioning. Sensors, 22(11), 4014. https://doi.org/10.3390/s22114014






