Optimization of a Low-Power Chemoresistive Gas Sensor: Predictive Thermal Modelling and Mechanical Failure Analysis
Abstract
1. Introduction
2. Modeling of the Microheaters
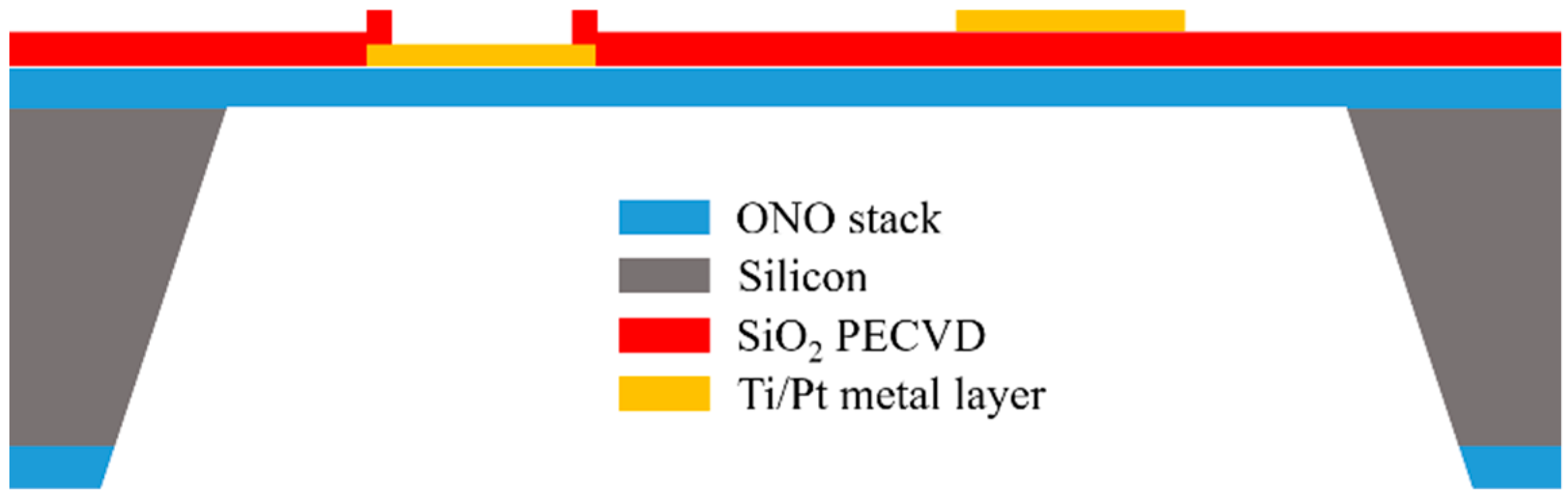
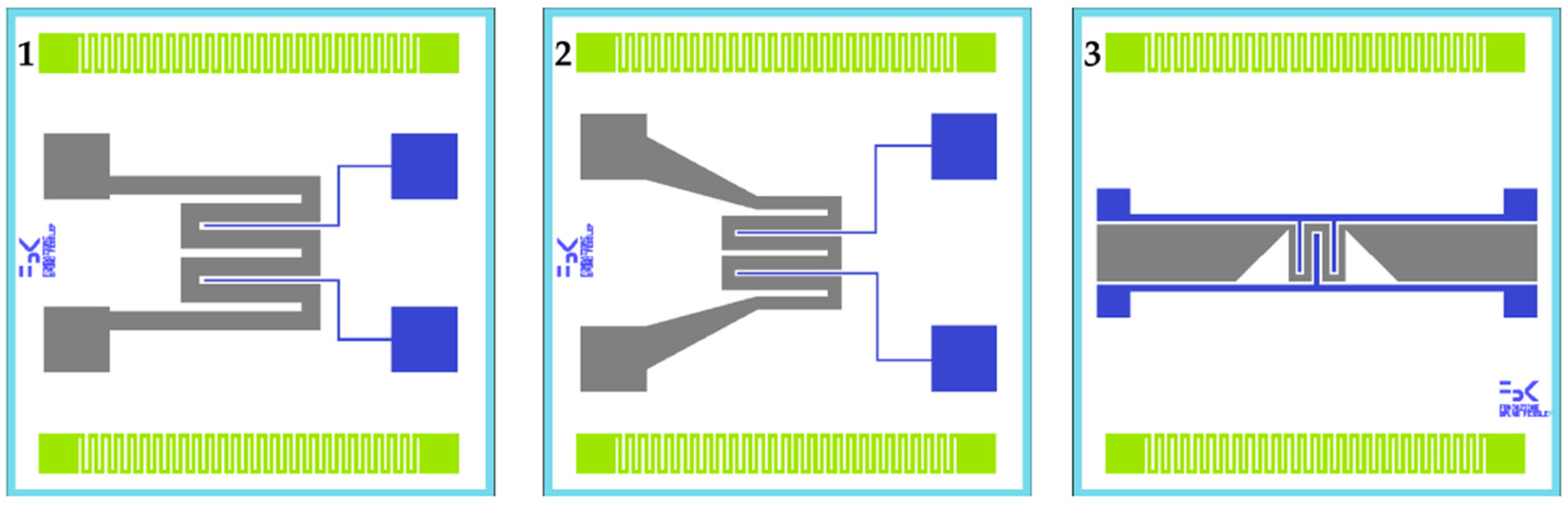
2.1. Structure of the Microheaters
2.2. Thermal Model
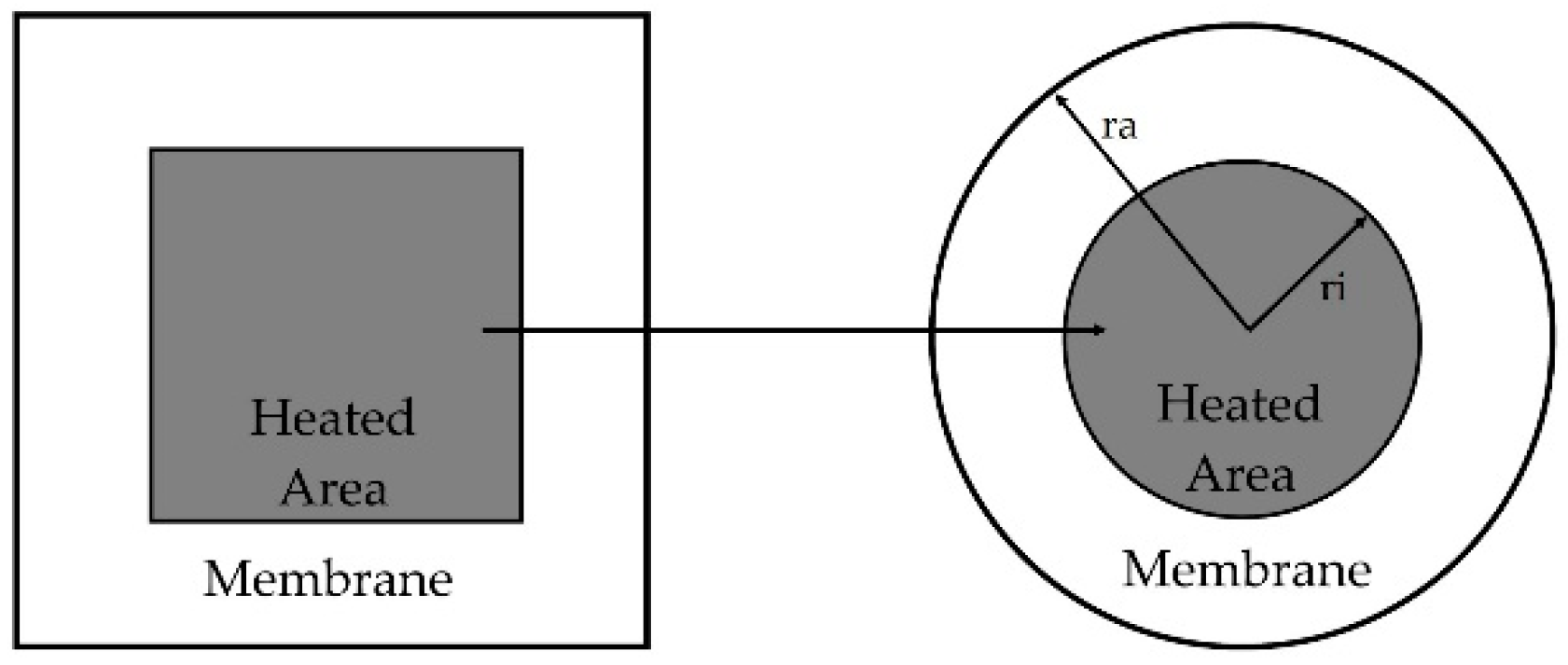
2.2.1. Membrane Heat Losses
2.2.2. Air Heat Losses
3. Materials and Methods
4. Results and Discussion
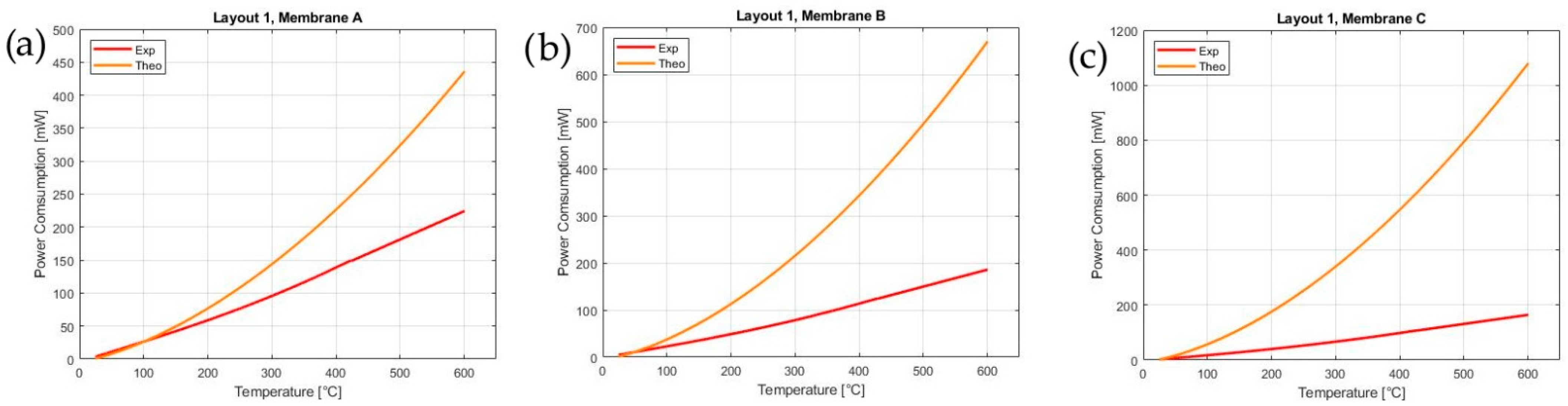
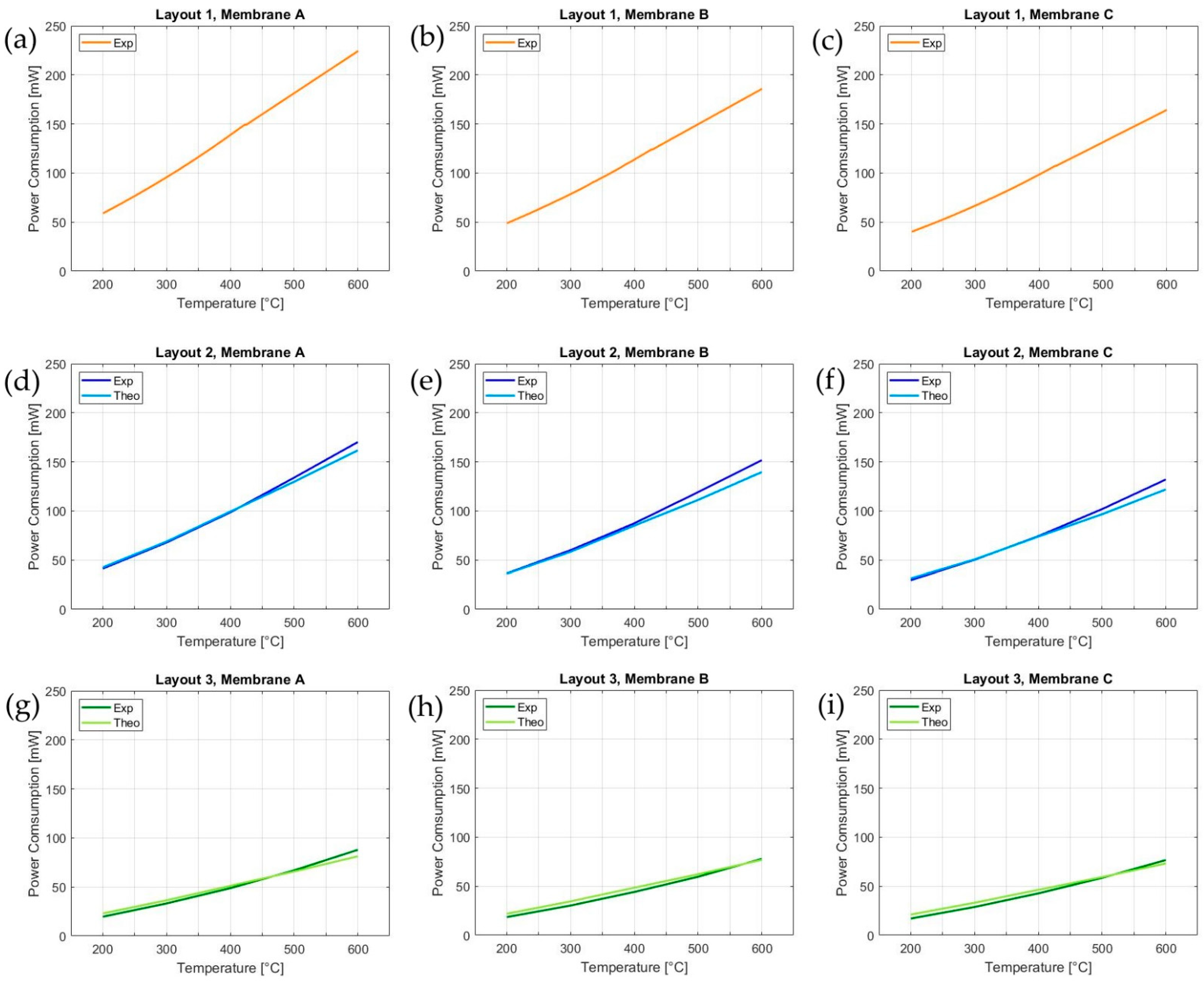
4.1. Thermal Model for Power Consumption Evaluation
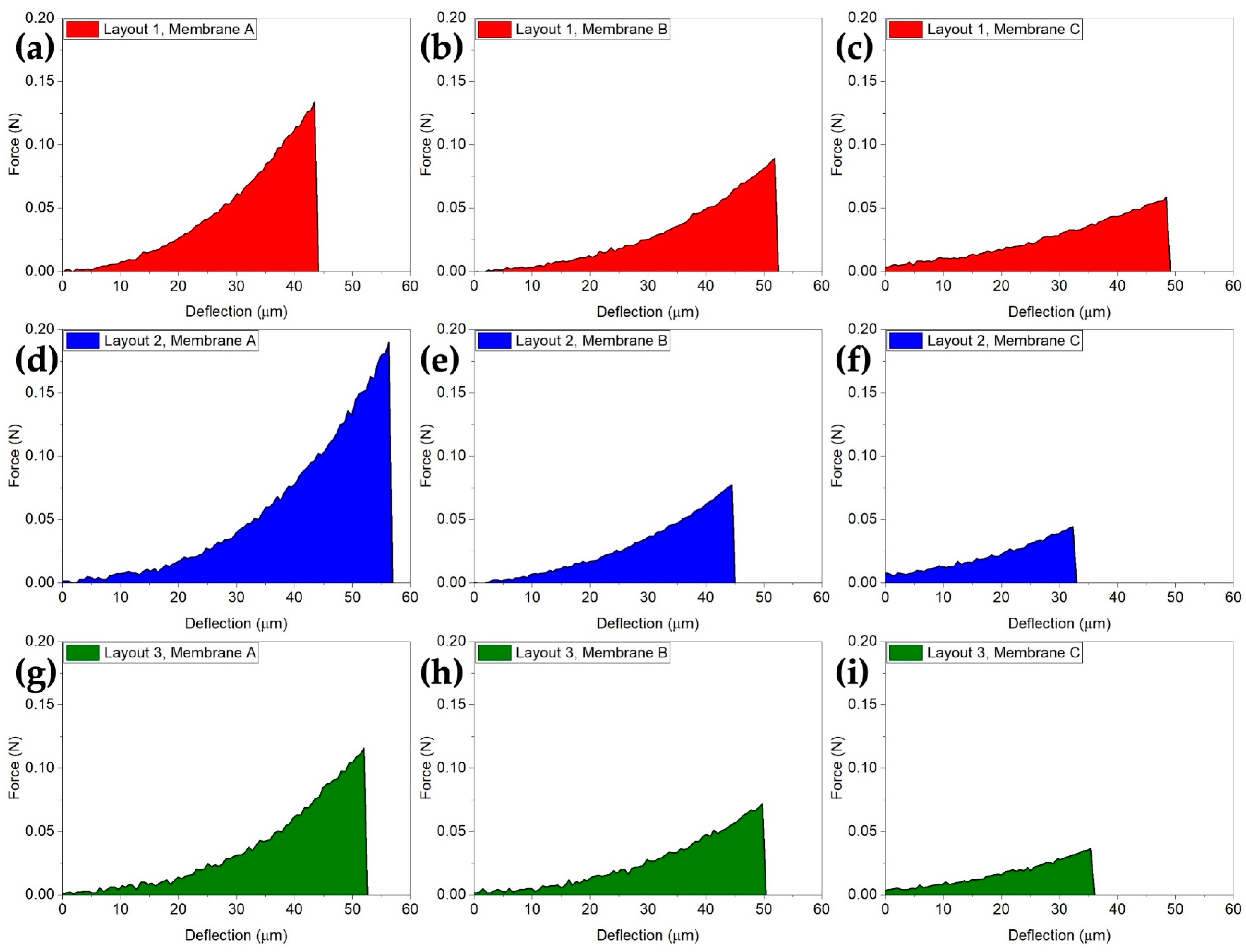
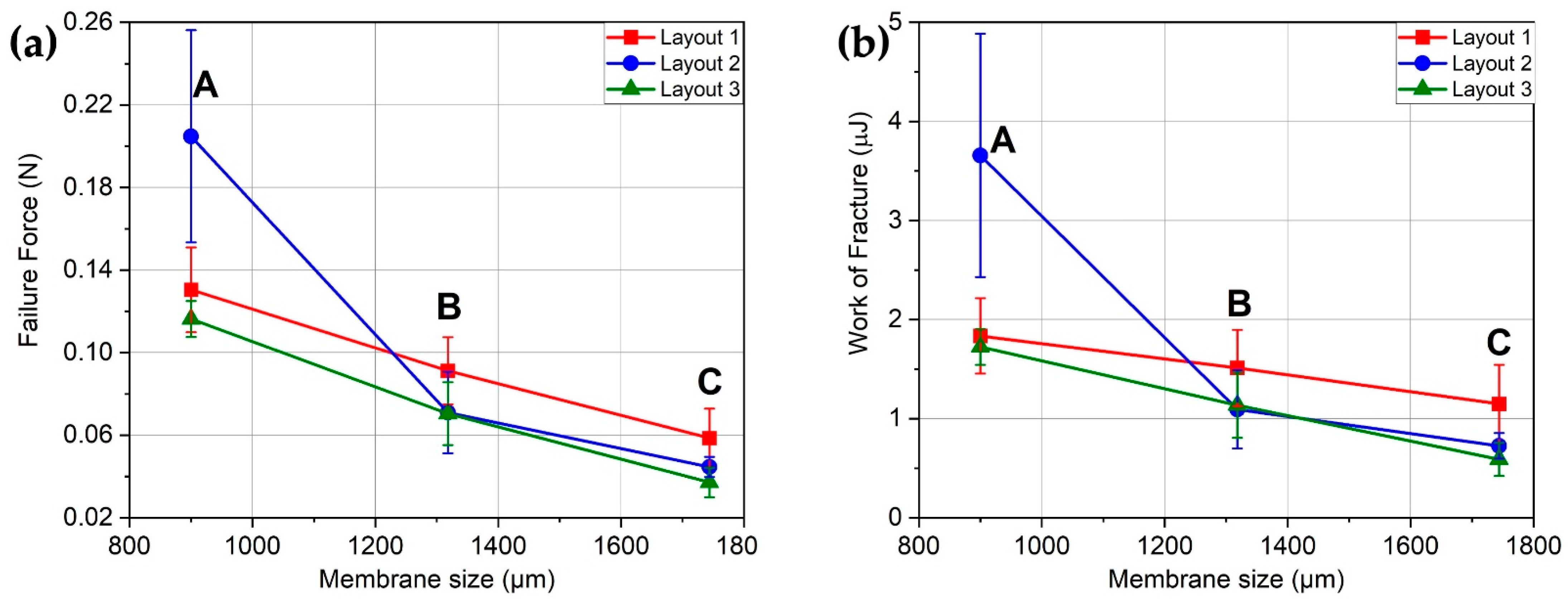
4.2. Mechanical Failure Analysis
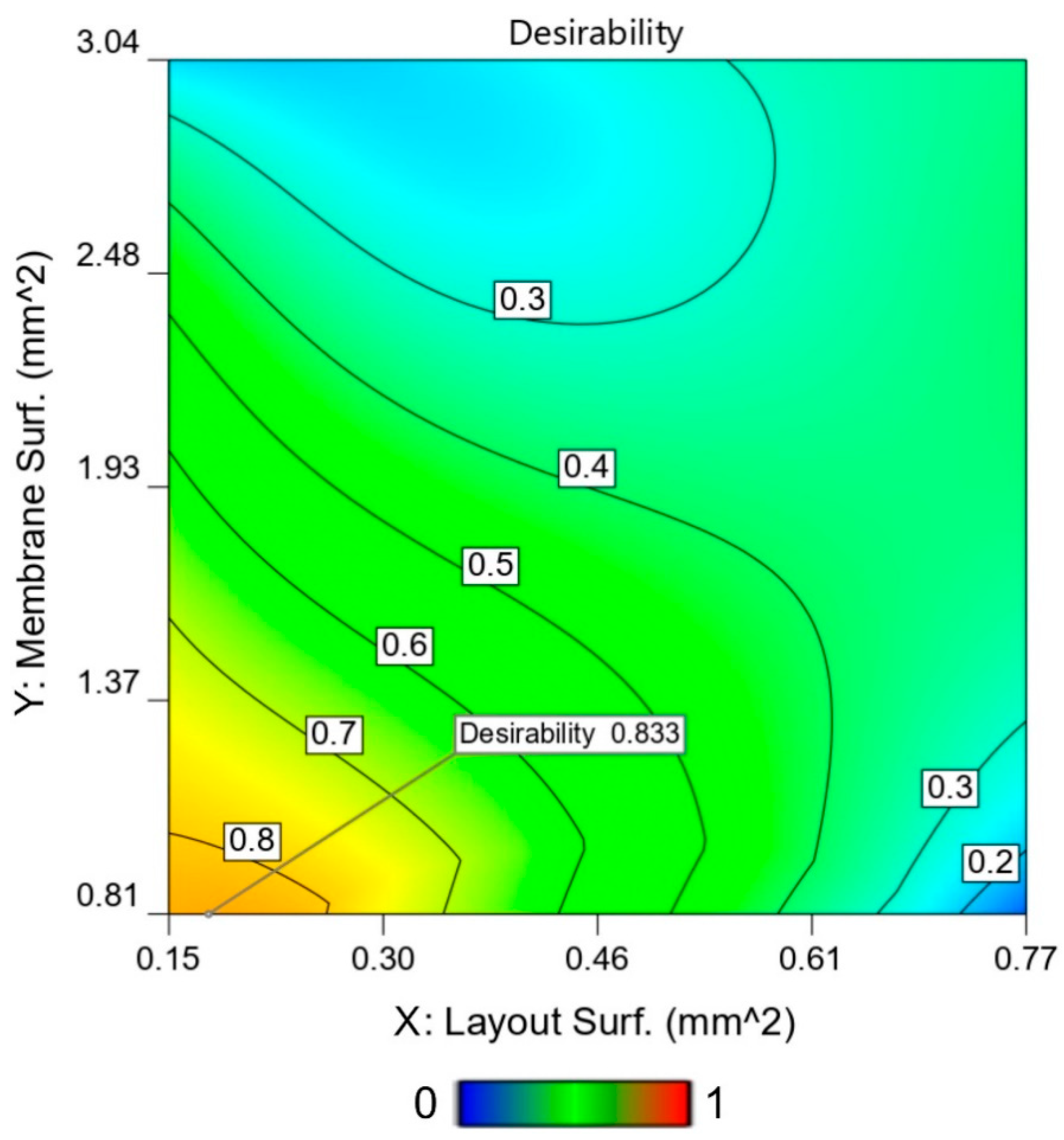
4.3. Statistical Model for the Cross-Correlation of Thermal and Mechanical Analyses
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Santer, B.D.; Taylor, K.E.; Wigley, T.M.L.; Penner, J.E.; Jones, P.D.; Cubasch, U. Towards the detection and attribution of an anthropogenic effect on climate. Clim. Dyn. 1995, 12, 77–100. [Google Scholar] [CrossRef]
- Soloman, S. Sensors Handbook, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Kind, T.; Fiehn, O. Advances in structure elucidation of small molecules using mass spectrometry. Bioanal. Rev. 2010, 2, 23–60. [Google Scholar] [CrossRef]
- De Gouw, J.; Warneke, C. Measurements of volatile organic compounds in the earth’s atmosphere using proton-transfer-reaction mass spectrometry. Mass Spectrom. Rev. 2007, 26, 223–257. [Google Scholar] [CrossRef]
- Isacsson, U.; Wettermark, G. Chemiluminescence in analytical chemistry. Anal. Chim. Acta 1974, 68, 339–362. [Google Scholar] [CrossRef]
- Werle, P.; Slemr, F.; Maurer, K.; Kormann, R.; Mücke, R.; Jänker, B. Near- and mid-infrared laser-optical sensors for gas analysis. Opt. Laser Eng. 2002, 37, 101–114. [Google Scholar] [CrossRef]
- Comini Elisabetta Faglia, G.; Sberveglieri, G. (Eds.) Solid State Gas Sensing; Springer Science & Business Media: New York, NY, USA, 2008; Volume 20. [Google Scholar]
- Hunter, G.W.; Akbar, S.; Bhansali, S.; Daniele, M.; Erb, P.D.; Johnson, K.; Liu, C.-C.; Miller, D.; Oralkan, O.; Hesketh, P.J.; et al. Editors′ Choice-Critical Review—A Critical Review of Solid State Gas Sensors. J. Electrochem. Soc. 2020, 167, 037570. [Google Scholar] [CrossRef]
- Neri, G. First fifty years of chemoresistive gas sensors. Chemosensors 2015, 3, 1–20. [Google Scholar] [CrossRef]
- Rackauskas, S.; Barbero, N.; Barolo, C.; Viscardi, G. ZnO nanowire application in chemoresistive sensing: A review. Nanomaterials 2017, 7, 381. [Google Scholar] [CrossRef] [PubMed]
- Neri, G.; Leonardi, S.G.; Latino, M.; Donato, N.; Baek, S.; Conte, D.E.; Russo, P.A.; Pinna, N. Sensing behavior of SnO2/reduced graphene oxide nanocomposites toward NO2. Sens. Actuators B Chem. 2013, 179, 61–68. [Google Scholar] [CrossRef]
- Kumar, V.; Mirzaei, A.; Bonyani, M.; Kim, K.-H.; Kim, H.W.; Kim, S.S. Advances in electrospun nanofiber fabrication for polyaniline (PANI)-based chemoresistive sensors for gaseous ammonia. Trends Analyt. Chem. 2020, 129, 115938. [Google Scholar] [CrossRef]
- Bertoni, C.; Naclerio, P.; Viviani, E.; Dal Zilio, S.; Carrato, S.; Fraleoni-Morgera, A. Nanostructured p3ht as a promising sensing element for real-time, dynamic detection of gaseous acetone. Sensors 2019, 19, 1296. [Google Scholar] [CrossRef] [PubMed]
- Willa, C.; Yuan, J.; Niederberger, M.; Koziej, D. When nanoparticles meet poly(ionic liquid)s: Chemoresistive CO2 sensing at room temperature. Adv. Funct. Mater. 2015, 25, 2537–2542. [Google Scholar] [CrossRef]
- Gaiardo, A.; Fabbri, B.; Giberti, A.; Guidi, V.; Bellutti, P.; Malagù, C.; Valt, M.; Pepponi, G.; Gherardi, S.; Zonta, G.; et al. ZnO and Au/ZnO thin films: Room-temperature chemoresistive properties for gas sensing applications. Sens. Actuators B Chem. 2016, 237, 1085–1094. [Google Scholar] [CrossRef]
- Gaiardo, A.; Fabbri, B.; Guidi, V.; Bellutti, P.; Giberti, A.; Gherardi, S.; Vanzetti, L.; Malagù, C.; Zonta, G. Metal sulfides as sensing materials for chemoresistive gas sensors. Sensors 2016, 16, 296. [Google Scholar] [CrossRef]
- Giberti, A.; Fabbri, B.; Gaiardo, A.; Guidi, V.; Malagù, C. Resonant photoactivation of cadmium sulfide and its effect on the surface chemical activity. Appl. Phys. Lett. 2014, 104, 222102. [Google Scholar] [CrossRef]
- Zonta, G.; Astolfi, M.; Casotti, D.; Cruciani, G.; Fabbri, B.; Gaiardo, A.; Gherardi, S.; Guidi, V.; Landini, N.; Valt, M.; et al. Reproducibility tests with zinc oxide thick-film sensors. Ceram. Int. 2020, 46, 6847–6855. [Google Scholar] [CrossRef]
- Srinivasan, P.; Ezhilan, M.; Kulandaisamy, A.J.; Babu, K.J.; Rayappan, J.B.B. Room temperature chemiresistive gas sensors: Challenges and strategies—A mini review. J. Mater. Sci. Mater. Electron. 2019, 30, 15825–15847. [Google Scholar] [CrossRef]
- Joshi, N.; Hayasaka, T.; Liu, Y.; Liu, H.; Oliveira, O.N.; Lin, L. A review on chemiresistive room temperature gas sensors based on metal oxide nanostructures, graphene and 2D transition metal dichalcogenide. Microchim. Acta 2018, 185, 213. [Google Scholar] [CrossRef]
- Hashtroudi, H.; MacKinnon, I.D.R.; Shafiei, M. Emerging 2D hybrid nanomaterials: Towards enhanced sensitive and selective conductometric gas sensors at room temperature. J. Mater. Chem. C 2020, 8, 13108–13126. [Google Scholar] [CrossRef]
- Gaiardo, A.; Fabbri, B.; Giberti, A.; Valt, M.; Gherardi, S.; Guidi, V.; Malagù, C.; Bellutti, P.; Pepponi, G.; Casotti, D.; et al. Tunable formation of nanostructured SiC/SiOC core-shell for selective detection of SO2. Sens. Actuators B Chem. 2020, 305, 127485. [Google Scholar] [CrossRef]
- Guidi, V.; Fabbri, B.; Gaiardo, A.; Gherardi, S.; Giberti, A.; Malagù, C.; Zonta, G.; Bellutti, P. Metal sulfides as a new class of sensing materials. Procedia. Eng. 2015, 120, 138–141. [Google Scholar] [CrossRef]
- Dey, A. Semiconductor metal oxide gas sensors: A review. Mat. Sci. Eng. B Adv. 2018, 229, 206–217. [Google Scholar] [CrossRef]
- Degler, D. Trends and advances in the characterization of gas sensing materials based on semiconducting oxides. Sensors 2018, 18, 3544. [Google Scholar] [CrossRef] [PubMed]
- Fabbri, B.; Valt, M.; Parretta, C.; Gherardi, S.; Gaiardo, A.; Malagù, C.; Mantovani, F.; Strati, V.; Guidi, V. Correlation of gaseous emissions to water stress in tomato and maize crops: From field to laboratory and back. Sens. Actuators B Chem. 2020, 303, 127227. [Google Scholar] [CrossRef]
- Zonta, G.; Anania, G.; Astolfi, M.; Feo, C.; Gaiardo, A.; Gherardi, S.; Giberti, A.; Guidi, V.; Landini, N.; Palmonari, C.; et al. Chemoresistive sensors for colorectal cancer preventive screening through fecal odor: Double-blind approach. Sens. Actuators B Chem. 2019, 301, 127062. [Google Scholar] [CrossRef]
- Zonta, G.; Anania, G.; de Togni, A.; Gaiardo, A.; Gherardi, S.; Giberti, A.; Guidi, V.; Landini, N.; Palmonari, C.; Ricci, L.; et al. Use of Gas Sensors and FOBT for the Early Detection of Colorectal Cancer. Sens. Actuators B Chem. 2018, 262, 884–891. [Google Scholar] [CrossRef]
- Piedrahita, R.; Xiang, Y.; Masson, N.; Ortega, J.; Collier, A.; Jiang, Y.; Li, K.; Dick, R.P.; Lv, Q.; Hannigan, M.; et al. The next generation of low-cost personal air quality sensors for quantitative exposure monitoring. Atmos. Meas. Tech. 2014, 7, 3325–3336. [Google Scholar] [CrossRef]
- Gaiardo, A.; Zonta, G.; Gherardi, S.; Malagù, C.; Fabbri, B.; Valt, M.; Vanzetti, L.; Landini, N.; Casotti, D.; Cruciani, G.; et al. Nanostructured SmFeO3 gas sensors: Investigation of the gas sensing performance reproducibility for colorectal cancer screening. Sensors 2020, 20, 5910. [Google Scholar] [CrossRef]
- Bagolini, A.; Gaiardo, A.; Crivellari, M.; Demenev, E.; Bartali, R.; Picciotto, A.; Valt, M.; Ficorella, F.; Guidi, V.; Bellutti, P. Development of MEMS MOS gas sensors with CMOS compatible PECVD inter-metal passivation. Sens. Actuators B Chem. 2019, 292, 225–232. [Google Scholar] [CrossRef]
- Ochiwa Shinichi (Fuji Electric Co Ltd.). Gas Sensor. Japanese Patent Number JPH03248054, 6 November 1991. [Google Scholar]
- Martinelli, G.; Carotta, M.C.; Ferroni, M.; Sadaoka, Y.; Traversa, E. Screen-printed perovskite-type thick films as gas sensors for environmental monitoring. Sens. Actuators B Chem. 1999, 55, 99–110. [Google Scholar] [CrossRef]
- Simon, I.; Bârsan, N.; Bauer, M.; Weimar, U. Micromachined metal oxide gas sensors: Opportunities to improve sensor performance. Sens. Actuators B Chem. 2001, 73, 1–26. [Google Scholar] [CrossRef]
- Ma, H.; Du, Y.; Wei, M.; Ding, E.; Lin, L. Silicon microheater based low-power full-range methane sensing device. Sens. Actuators A 2019, 295, 70–74. [Google Scholar] [CrossRef]
- Lahlalia, A.; Filipovic, L.; Selberherr, S. Modeling and Simulation of Novel Semiconducting Metal Oxide Gas Sensors for Wearable Devices. IEEE Sens. J. 2018, 18, 1960–1970. [Google Scholar] [CrossRef]
- Hwang, W.-J.; Shin, K.-S.; Roh, J.-H.; Lee, D.-S.; Choa, S.-H. Development of micro-heaters with optimized temperature compensation design for gas sensors. Sensors 2011, 11, 2580–2591. [Google Scholar] [CrossRef] [PubMed]
- Belmonte, J.C.; Puigcorbé, J.; Arbiol, J.; Vilà, A.; Morante, J.R.; Sabaté, N.; Gràcia, I.; Cané, C. High-temperature low-power performing micromachined suspended micro-hotplate for gas sensing applications. Sens. Actuators B Chem. 2006, 114, 826–835. [Google Scholar] [CrossRef]
- Bhattacharyya, P. Technological journey towards reliable microheater development for MEMS gas sensors: A review. IEEE Trans. Device Mat. Reliab. 2014, 14, 589–599. [Google Scholar] [CrossRef]
- Prajesh, R.; Jain, N.; Agarwal, A. Low power highly sensitive platform for gas sensing application. Microsyst. Technol. 2016, 22, 2185–2192. [Google Scholar] [CrossRef]
- Baranov, A.; Spirjakin, D.; Akbari, S.; Somov, A. Optimization of power consumption for gas sensor nodes: A survey. Sens. Actuator A Phys. 2015, 233, 279–289. [Google Scholar] [CrossRef]
- Hille, P.; Strack, H. A heated membrane for a capacitive gas sensor. Sens. Actuators A 1992, 32, 321–325. [Google Scholar] [CrossRef]
- Sberveglieri, G.; Hellmich, W.; Müller, G. Silicon hotplates for metal oxide gas sensor elements. Microsyst. Technol. 1997, 3, 183–190. [Google Scholar] [CrossRef]
- Iwaki, T.; Covington, J.A.; Udrea, F.; Ali, S.Z.; Guha, P.K.; Gardner, J.W. Design and simulation of resistive SOI CMOS micro-heaters for high temperature gas sensors. J. Phys. Conf. Ser. 2005, 15, 27–32. [Google Scholar] [CrossRef]
- Lee, S.M.; Dyer, D.C.; Gardner, J.W. Design and optimisation of a high-temperature silicon micro-hotplate for nanoporous palladium pellistors. Microelectron. Eng. 2003, 34, 115–126. [Google Scholar] [CrossRef]
- Fung, S.K.H.; Tang, Z.; Chan, P.C.H.; Sin, J.K.O.; Cheung, P.W. Thermal analysis and design of a micro-hotplate for integrated gas-sensor applications. Sens. Actuators A 1996, 54, 482–487. [Google Scholar] [CrossRef]
- Zhang, K.L.; Chou, S.K.; Ang, S.S. Fabrication, modeling and testing of a thin film Au/Ti microheater. Int. J. Therm. Sci. 2007, 46, 580–588. [Google Scholar] [CrossRef]
- USDOD. Test Method Standard: Microcircuits, Military Standard 883K; USDOD: Washington, DC, USA, 2017.
- Srikar, V.T.; Spearing, S.M. A critical review of microscale mechanical testing methods used in the design of microelectromechanical systems. Exp. Mech. 2003, 43, 238–247. [Google Scholar] [CrossRef]
- Vlassak, J.J.; Nix, W.D. A new bulge test technique for the determination of Young’s modulus and Poisson’s ratio of thin films. J. Mater. Res. 1992, 7, 3242–3249. [Google Scholar] [CrossRef]
- Gaspar, J.; Ruther, P.; Paul, O. Mechanical characterization of thin-film composites using the load-deflection response of multilayer membranes-elastic and fracture properties. Mater. Res. Soc. Symp. Proc. 2006, 977. [Google Scholar] [CrossRef]
- Fitzgerald, A.M.; Pierce, D.M.; Benedikt, Z. “Predicting reliability of silicon MEMS.” Reliability, Packaging, Testing, and Characterization of MEMS/MOEMS and Nanodevices IX; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7592. [Google Scholar]
- Jadaan, O.M.; Nemeth, N.N.; Bagdahn, J.; Sharpe, W.N. Probabilistic Weibull behavior and mechanical properties of MEMS brittle materials. J. Mater. Sci. 2003, 38, 4087–4113. [Google Scholar]
- Barsan, N.; Schweizer-Berberich, M.; Göpel, W. Fundamental and practical aspects in the design of nanoscaled SnO2 gas sensors: A status report. Fresenius J. Anal. Chem. 1999, 365, 287–304. [Google Scholar] [CrossRef]
- Vasiliev, A.A.; Pisliakov, A.V.; Sokolov, A.V.; Polovko, O.V.; Samotaev, N.N.; Kujawski, W.; Rozicka, A.; Guarnieri, V.; Lorencelli, L. Gas sensor system for the determination of methane in water. Procedia. Eng. 2014, 87, 1445–1448. [Google Scholar] [CrossRef]
- Available online: https://cmm.fbk.eu/en/research/mnf-micro-nano-facility/ (accessed on 27 December 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Bucciarelli, A.; Reddy Chandraiahgari, C.; Adami, A.; Mulloni, V.; Lorenzelli, L. Precise Dot Inkjet Printing Thought Multifactorial Statistical Optimization of the Piezoelectric Actuator Waveform. Flex. Print. Electron. 2020, 5, 045002. [Google Scholar] [CrossRef]
- Bucciarelli, A.; Muthukumar, T.; Kim, J.S.; Kim, W.K.; Quaranta, A.; Maniglio, D.; Khang, G.; Motta, A. Preparation and Statistical Characterization of Tunable Porous Sponge Scaffolds Using UV Cross-Linking of Methacrylate-Modified Silk Fibroin. ACS Biomater. Sci. Eng. 2019, 5, 6374–6388. [Google Scholar] [CrossRef] [PubMed]
- Bucciarelli, A.; Chiera, S.; Quaranta, A.; Yadavalli, V.K.; Motta, A.; Maniglio, D. A Thermal-Reflow-Based Low-Temperature, High-Pressure Sintering of Lyophilized Silk Fibroin for the Fast Fabrication of Biosubstrates. Adv. Funct. Mater. 2019, 29, 1901134. [Google Scholar] [CrossRef]
- Bucciarelli, A.; Adami, A.; Chandaiahgari, C.R.; Lorenzelli, L. Multivariable Optimization of Inkjet Printing Process of Ag Nanoparticle Ink on Kapton. In Proceedings of the 2020 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Manchester, UK, 16–19 August 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Edwards, R.L.; Coles, G.; Sharpe, W.N. Comparison of tensile and bulge tests for thin-film silicon nitride. Exp. Mech. 2004, 44, 49–54. [Google Scholar] [CrossRef]
- Carrera, E.; Ciuffreda, A. A unified formulation to assess theories of multilayered plates for various bending problems. Compos. Struct. 2005, 69, 271–293. [Google Scholar] [CrossRef]
- Hussein Al-Tholaia, M.M.; Al-Gahtani, H.J. RBF-Based Meshless Method for Large Deflection of Elastic Thin Rectangular Plates with Boundary Conditions Involving Free Edges. Math. Probl. Eng. 2016, 2016, 6489375. [Google Scholar] [CrossRef]
- Dai, Z.; Xu, L.; Duan, G.; Li, T.; Zhang, H.; Li, Y.; Cai, W. Fast-response, sensitivitive and low-powered chemosensors by fusing nanostructured porous thin film and IDEs-microheater chip. Sci. Rep. 2013, 3, 1669. [Google Scholar] [CrossRef]
- Walden, P.; Kneer, J.; Knobelspies, S.; Kronast, W.; Mescheder, U.; Palzer, S. Micromachined hotplate platform for the investigation of ink-jet printed, functionalized metal oxide nanoparticles. J. Microelectromech. Syst. 2015, 24, 1384–1390. [Google Scholar] [CrossRef]
- Viricelle, J.P.; Rivière, B.; Pijolat, C. Optimization of SnO2 screen-printing inks for gas sensor applications. J. Eur. Ceram. Soc. 2005, 25, 2137–2140. [Google Scholar] [CrossRef]
- Vincenzi, D.; Butturi, M.A.; Guidi, V.; Carotta, M.C.; Martinelli, G.; Guarnieri, V.; Pignatel, G.U. Development of a low-power thick-film gas sensor deposited by screen-printing technique onto a micromachined hotplate. Sens. Actuators B Chem. 2001, 77, 95–99. [Google Scholar] [CrossRef]
- Puigcorbé, J.; Vogel, D.; Michel, B.; Vilà, A.; Gràcia, I.; Cané, C.; Morante, J.R. Thermal and mechanical analysis of micromachined gas sensors. J. Micromech. Microeng. 2003, 13, 548–556. [Google Scholar] [CrossRef]
- Udrea, F.; Gardner, J.W.; Setiadi, D.; Covington, J.A.; Dogaru, T.; Lu, C.C.; Milne, W.I. Design and simulations of SOI CMOS micro-hotplate gas sensors. Sens. Actuators B Chem. 2001, 78, 180–190. [Google Scholar] [CrossRef]
- Gaiardo, A.; Demenev, E.; Bellutti, P.; Dolci, C.; Maestrini, A.; Antonelli, F.; Miotto, V. New Chemoresistive Gas Sensor Arrays for Outdoor Air Quality Monitoring: A Combined R&D and Outreach Activities. In ECS Meeting Abstracts; IOP Publishing: Bristol, UK, 2020; p. 2203. [Google Scholar]
- Suárez, J.I.; Arroyo, P.; Lozano, J.; Herrero, J.L.; Padilla, M. Bluetooth gas sensing module combined with smartphones for air quality monitoring. Chemosphere 2018, 205, 618–626. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Jiang, Y.; Tai, H.; Liu, B.; Duan, Z.; Yuan, Z.; Pan, H.; Xie, G.; Du, X.; Su, Y. An integrated flexible self-powered wearable respiration sensor. Nano Energy 2019, 63, 103829. [Google Scholar] [CrossRef]



| Group | Factor X-Area Layout (mm2) | Factor Y-Area Membrane (mm2) |
|---|---|---|
| 1 | 0.15 | 0.81 |
| 2 | 0.15 | 1.74 |
| 3 | 0.15 | 3.01 |
| 4 | 0.56 | 0.81 |
| 5 | 0.56 | 1.74 |
| 6 | 0.56 | 3.01 |
| 7 | 0.77 | 0.81 |
| 8 | 0.77 | 1.74 |
| 9 | 0.77 | 3.01 |
| T (°C) | a(T) | b(T) |
|---|---|---|
| 200 | 0.001839 | 1.303 |
| 300 | 0.001590 | 1.296 |
| 400 | 0.001794 | 1.249 |
| 500 | 0.001742 | 1.234 |
| 600 | 0.001825 | 1.213 |
| Membrane | Layout 1 | Layout 2 | Layout 3 |
|---|---|---|---|
| A | 95% | 69% | 18% |
| B | 44% | 32% | 9% |
| C | 25% | 18% | 5% |
| Membrane Layout | Membrane Size | Estimate Percentage of Broken MH (%) |
|---|---|---|
| 1 | A | ~0 |
| 1 | B | ~0 |
| 1 | C | 37 |
| 2 | A | ~0 |
| 2 | B | 2 |
| 2 | C | 100 |
| 3 | A | ~0 |
| 3 | B | 1 |
| 3 | C | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaiardo, A.; Novel, D.; Scattolo, E.; Crivellari, M.; Picciotto, A.; Ficorella, F.; Iacob, E.; Bucciarelli, A.; Petti, L.; Lugli, P.; et al. Optimization of a Low-Power Chemoresistive Gas Sensor: Predictive Thermal Modelling and Mechanical Failure Analysis. Sensors 2021, 21, 783. https://doi.org/10.3390/s21030783
Gaiardo A, Novel D, Scattolo E, Crivellari M, Picciotto A, Ficorella F, Iacob E, Bucciarelli A, Petti L, Lugli P, et al. Optimization of a Low-Power Chemoresistive Gas Sensor: Predictive Thermal Modelling and Mechanical Failure Analysis. Sensors. 2021; 21(3):783. https://doi.org/10.3390/s21030783
Chicago/Turabian StyleGaiardo, Andrea, David Novel, Elia Scattolo, Michele Crivellari, Antonino Picciotto, Francesco Ficorella, Erica Iacob, Alessio Bucciarelli, Luisa Petti, Paolo Lugli, and et al. 2021. "Optimization of a Low-Power Chemoresistive Gas Sensor: Predictive Thermal Modelling and Mechanical Failure Analysis" Sensors 21, no. 3: 783. https://doi.org/10.3390/s21030783
APA StyleGaiardo, A., Novel, D., Scattolo, E., Crivellari, M., Picciotto, A., Ficorella, F., Iacob, E., Bucciarelli, A., Petti, L., Lugli, P., & Bagolini, A. (2021). Optimization of a Low-Power Chemoresistive Gas Sensor: Predictive Thermal Modelling and Mechanical Failure Analysis. Sensors, 21(3), 783. https://doi.org/10.3390/s21030783







