1. Introduction
Maritime transport plays a key role in the global trade with nearly 80% of commodity volumes and 70% of commodity values being transported by sea [
1]. The increasing transport volume leads not only to rapidly growing vessel dimensions but also to an increase of traffic densities especially in coastal areas and port entrances. Here reliable and accurate navigational information is required to avoid situations that could compromise the safety of the ship, crew, and the environment. Currently, Global Navigation Satellite Systems (GNSSs), and particularly GPS, are the main source for the provision of absolute position, navigation, and precise time (PNT) information for maritime navigation. A large number of systems and functionalities onboard a vessel, such as the Electronic Chart Display and Information System (ECDIS), the Automatic Identification System (AIS), and the Automatic Track Control just to name a few, are strongly dependent on the provision of accurate PNT information. Furthermore, as first conceptual studies and demonstration projects have been started with the aim to development fully autonomous vessels [
2], the need for accurate and reliable PNT will increase even further in the future.
This dependency on GNSS has raised serious concerns on the vulnerability of the navigation process [
3,
4]. As the GNSS signals are very weak (≈–125 dBm) when arriving to the receivers on the Earth’s surface, they become relatively susceptible to possible radio interference. Currently, a noticeable increase in intentional and unintentional radio frequency interference (RFI) in GNSS bands is observed. The act of intentionally directing powerful electromagnetic waves toward a victim’s receiver aiming to deny its operations is called jamming [
5]. Especially the availability of cheap jamming devices such as Personal Privacy Devices (PPDs) has been widely recognized as a real threat to GNSS applications. One of a typical jammer’s application scenario is to dodge the unwanted tracking, e.g., as used in illegal fishing or by the drivers working overlong hours. In Newark, NJ, USA, the operation of an aviation ground-based augmentation system was disturbed by a PPD jammer used by a truck driver, regularly passing a road close to the airport [
6]. Just recently, an international measurement campaign studying radio frequency interference (RFI) in the L1/E1 and L5/E5a bands on a container vessel was performed [
7]. This study reports how frequent RFI events occur, even making the GNSS service unavailable in some cases. Moreover, South Korea has also repeatedly reported jamming attacks from North Korea, heavily affecting the maritime transport [
8].
The International Maritime Organization (IMO) recognized the importance of resilient onboard provision of PNT data, and the development of Guidelines for an onboard PNT (data processing) unit has been identified as supplementary and necessary. The German Aerospace Center (DLR) has developed a concept for such a PNT unit [
9] and was actively involved in the development of a corresponding guideline at the IMO, which has been finally approved in June 2017 by the IMO [
10]. The basic idea behind the concept of the PNT data processing unit is to develop a scalable approach for a combined and harmonized usage of all available onboard sensors using the methods of multi-sensor and information fusion.
In general, one can distinguish three main groups of solutions that can be used for mitigation of GNSS jamming. Within the methods of the first group, the impact of jamming is mitigated inside the GNSS receiver by techniques such as adaptive notch filtering, pulse blanking, or adaptive beamforming using a multi-antenna GNSS receiver [
11,
12,
13]. Within the second group, alternative terrestrial radio navigation systems are employed to enable a position determination independently from GNSS. However, after the decommission of LORAN-C (eLoran) in the US as well as in Europe, no global operational backup exists anymore. For maritime application, the so-called R-Mode (R-Ranging) is currently being developed as a terrestrial backup system. Here existing signals of opportunity of globally available maritime infrastructure such as MF radio beacons and ashore AIS stations will be used as possible ranging sources [
14]. A first experimental testbed for R-Mode will be established in the R-Mode Baltic project (2017–2020) in the western part of the Baltic Sea [
15]. Finally, within the third group, the positioning information from the GNSS receiver is combined within a multi-sensor fusion scheme with independent onboard sensors such as inertial sensors, a speed log, or a gyrocompass. Such hybrid navigation systems enable PNT determination even in cases where GNSS information are either not available or not sufficient for a complete solution.
The present paper focuses on an example from the third group, where a classical inertial measurement unit (IMU)/GNSS sensor fusion scheme is augmented with a Doppler velocity log (DVL). Although the benefits of integrated IMU/GNSS navigation systems have already been demonstrated for marine applications [
16], a performance test of such a multi-sensor system under real jamming conditions on a vessel is still missing. Typically, the GNSS outage is only emulated by switching the GNSS signals off instantaneously, whereas within a real jamming scenario a complete GNSS outage is only the final stage after a slow degradation of GNSS signal reception. The crucial point is the correct description of the GNSS measurement error statistics under jamming conditions. Whenever the GNSS noise model assumptions are violated, the Kalman filter (KF) could behave suboptimally and therefore could result in inferior performance compared to that which is often demonstrated using pure simulated data. Typically, it is expected that the jamming leads to an increased range noise and might even result in failures in signal tracking loops. Therefore, the characterization of GNSS pseudorange errors statistics under jamming conditions is a prerequisite of using an IMU/DVL/GNSS integration in a real jamming scenario.
The rest of the paper is organized as follows. In
Section 2, a brief overview of existing work on jamming experiments and the application of hybrid navigation systems for maritime applications is given. The details of the applied GNSS/IMU/DVL unscented KF are given in
Section 3 and are followed by the description of the experimental setup of the measurement campaign in
Section 4. The results are presented and discussed in
Section 5, and a summary and outlook for future work are provided in
Section 6.
2. Previous Work
The emerging of safety-critical applications subject to accurate GNSS positioning and timing, such as autonomous cars or assisted landing, has urged the GNSS community into identifying jamming as one of the major menaces [
17,
18,
19]. Thus, lately there have been numerous studies related to detecting and counteracting the impact of jamming attacks. In [
20], the performance of a broad range of consumer grade GPS receivers under the interference of a low cost PPD is analyzed. The test was carried out for a static scenario within a confined space, where the performance of the receiver in terms of positioning accuracy and solution availability was analyzed for both the jamming-free and jamming scenarios of different intensities. Surprisingly, the tested receivers coped properly with the interference during the light jamming attack (with a jamming-to-signal ratio of 15 dB) with only a marginal influence on the quality of the position solution. However, during the severe jamming attack (jamming-to-noise-ratio of 25 dB), the availability of the position solution was reduced by more than
, while the positioning accuracy heavily degraded. It appears that jamming merely introduces additional noise in the measured pseudoranges, while the positioning degradation occurs under powerful interference due to the loss of satellite signal track and a consequent poor satellite geometry.
A series of works addressing the impact of jamming attacks on the maritime navigation has been recently presented. For example, a trial was conducted on the East coast of United Kingdom using a professional L1 band jammer [
21]. This study evaluated the jamming impact on the safety of maritime navigation and the quality of on-shore services such as vessel traffic management. The lack of GNSSs triggers numerous alarms and failures of interfaces (like the ECDIS) on the bridge of the vessel, causing discomfort to a vessel crew that additionally needs to face the challenge of quickly reverting to traditional means of navigation. This study nicely underlines the necessity for a backup for GNSS-based positioning on board a vessel.
Subsequently, a jamming experiment was carried out in the north of Norway using a broadband (bandwidth ≈ 60 MHz) jammer, centered at GPS L1 frequency and affecting the GLONASS primary frequencies [
22]. The main experimental finding was that GLONASS G1 tracking remained more resistant to jamming than GPS L1. This finding could, however, have been caused by the fact that GLONASS G1 frequencies lie at the edge of the reported jammer bandwidth, and the effective jammer-to-signal power in that band could already be significantly lower than for GPS L1. The primary output of the work was the suggestion for the maritime community to update their GNSS receivers to modern multi-constellation and multi-frequency ones. While this might be a solution for some type of jammers, currently, there are already PPD jammers on the market being able to jam all relevant GNSS frequencies.
One of the typical approaches to bridge short GNSS outages is to combine GNSS information with that from an inertial measurement unit (IMU). The inertial sensors measure the relative state of the object with respect to the inertial navigation frame and have distinct advantages, such as being self-contained, immune to interference, and highly dynamical. Unfortunately, these systems provide only incremental information and the integration outputs drift over time when no external reference is provided [
23]. An early work [
16] assessed the potential application of IMU/GNSS integration for maritime navigation using a loosely coupled KF. A collection of IMUs of different grade was employed to characterize the position drift over time of the hybrid navigation system when the GNSS service was artificially disabled. Although the performance of the inertial sensors was relatively good, the authors concluded that, despite the tangible advantages from the usage of IMU, inertial sensors still could not be considered as a primary backup to GNSS due to their fast position drift even when high-priced navigation sensors are employed. This statement is corroborated by our recent work [
24], where the performance of a hybrid IMU/GNSS system in maritime applications was also evaluated, including modern affordable tactical grade MEMS inertial sensors.
Another sensor typically used in maritime applications is the Doppler velocity log (DVL). When mounted on a vessel, the sensor faces the sea floor and can provide very accurate velocity information of the vessel with respect to the sea floor [
25] for scenarios up to a certain depth. The working principle of a DVL is rather simple. Firstly, an oscillating acoustic signal is sent out along each of the transducer axes. From the frequency shift between the emitted and the returned signal, the velocity along each of the transducer axis is determined. Despite being commonly mounted on marine vehicles ranging from large ships to small autonomous underwater vehicles (AUVs), there is a scarcity of academic resources concerning the specifics and functionality of DVLs [
26]. The combined usage of DVL and IMU have been reported in a number of works [
27,
28,
29] for the navigation AUVs, although only in few works has it been applied to merchant vessels [
30], and none have reported the performance of a hybrid IMU/GNSS/DVL navigation system. In a previous work [
31], the performance of the navigation solution fusing IMU, GNSS, and DVL was demonstrated on a maritime scenario. However, the performance characterization under actual GNSS jamming conditions has not yet been realized.
3. Methods
The proposed hybrid navigation system employs the recursive Bayesian estimation (RBE) framework to combine the outputs of several sensors in order to obtain a single navigation solution. The RBE methods deal with the problem of estimating the changing-in-time state of the system applying a priori information about the underlying system dynamics and the observations from the sensors. The probabilistic paradigm has been widely applied to navigation and tracking problems, given its ability to accommodate inaccurate models as well as imperfect sensors [
32].
In general, any RBE cycle is performed in two steps:
Prediction: The a priori probability is calculated from the last a posteriori probability using the available process model.
Correction: The a posteriori probability is calculated from the a priori probability using the measurement model and the current measurements.
Among the multiple RBE methods, the Kalman filter (KF) is probably the most well-known solution for the navigation problem. The original KF provides an optimal solution when the models are linear and the probabilities are Gaussian. However, when dealing with nonlinearities in the models, as is often the case for positioning problems, nonlinear extensions of KF such as the extended KF (EKF) or the unscented KF (UKF) can be used. In the case of the EKF, the nonlinear models are linearized around the most recent state estimate, while in the UKF the probability distribution is approximated using a set of deterministically chosen (non-randomly sampled) points in the state space, where every sample is assigned a particular fixed weight. This set of points conserves the Gaussian properties of the distribution under nonlinear transformations [
33].
Although the EKF has been for a long time considered as a
de facto standard for tracking applications [
34], the UKF has emerged as an alternative, claiming even higher accuracy and robustness for nonlinear models [
35]. The UKF employs the statistical linearization techniques and implements the scaled unscented transform (UT), where carefully selected samples of the state are propagated through the actual nonlinear functions. Then, the mean and covariance are recalculated back from the propagated points, yielding more accurate results compared to a conventional linearization routine. Although in the presented work we have adopted UKF as a core estimation framework, similar results are expected if the estimation process would have been formulated with an EKF with sufficiently high update rate [
36].
In general, the navigation filter is formulated as a nonlinear estimation problem for the system governed by the following stochastic models:
where
is the state vector of length
n,
is the vector of observations of length
m,
is the control input,
is a zero mean process noise vector, and
is the observation noise vector. The
and
are the dynamic models for the state propagation and measurement model, respectively. Here the noises neither have to be additive nor have to be of the same dimensionality as
or
.
In our work, the vector
describing the state of the vessel in a 3D space can be expressed as
where
q represents the attitude quaternion from the vessel local to the the earth-centered, earth-fixed (ECEF) frames,
v and
p are the 3D velocity and position in the ECEF frame, and
and
are the accelerometer and gyroscope offsets. Finally, for tightly coupled IMU/GNSS integration schemes, the state has to be augmented with GPS receiver clock offset
and clock offset rate
. Further, GNSS clock offsets can be added to the estimated state if a multi-constellation GNSS scenario is considered.
Effective and accurate attitude estimation can be considered as a key component of almost any higher performance navigation system. Within our implementation, we have explicitly addressed a challenge of attitude estimation by separating the attitude part (quaternion) and the vector part of the estimated kinematic state. In the present work, we chose a unit quaternion as the attitude parametrization due to its computational efficiency, low redundancy, and absence of singularity. The unit quaternion, although consisting of four numbers, is deprived of one degree of freedom due to its unit norm constraint and, therefore, requires a special treatment within the framework of the UKF [
37]. Except for the interesting part of quaternion handling, the rest of the process model follows a classical strapdown inertial mechanization approach for higher performance systems [
23] and is formulated in the ECEF frame.
There are several options to construct the measurement models depending on the configuration of the filter. For a
loosely coupled approach, a snapshot least-square adjustment is applied to estimate the position and velocity of the vessel. In the case of a classical code-based GNSS positioning, a time-of-arrival concept is employed to determine the receiver position from the measured code pseudoranges of the satellites in view. The positioning principle is based on solving a geometric problem from the measured ranges to the set of visible satellites with known coordinates [
38]. The ionosphere corrections are estimated using the Klobuchar empirical model, while the Saastamonien model is applied for estimating the tropospheric corrections. Similarly, the Doppler shift of the GNSS signals can be used to compute the velocity and the clock offset rate of the receiver.
Note that at least four satellites have to be visible in order to solve explicitly for both the position and the velocity in loosely coupled architecture. If there are fewer than four satellites visible at a given epoch, no solution can be found and the GNSS measurement step of the loosely coupled filter has to be skipped. An alternative approach, also known as
tightly coupled integration, avoids the intermediate snapshot position and velocity solutions by applying the code or Doppler measurements directly in the measurement models of the filter. This strategy puts no inherent restrictions on the number of satellites available and even fewer than four available measurements could still be employed to constrain, at least partially, the possible drift of the estimated position. The same holds for the Doppler GNSS measurements, which can be combined with the GNSS code-ranges to enforce a radial velocity measurement over each available link. The mathematical model to relate the pseudorange
and the pseudorange rate
to the state estimate is as follows:
where the superscript
j refers to the
GNSS tracked satellite,
is the unit line-of-sight vector between the satellite and the receiver,
represents the baseline between the IMU and the GNSS antenna expressed in the vessel body frame,
c stands for the speed of light,
and
I gather the tropospheric and ionospheric effects, respectively, and
is the angular rate of the vehicle expressed in the vessel body frame. The operation ⊗ refers to quaternion multiplication. For more details on quaternion conventions and a comprehensive explanation on quaternion algebra, the authors recommend consulting [
39].
In the case of a loosely coupled integration, an equivalent position solution error covariance can be calculated by using the geometry matrix from the iterated LS solution and a corresponding weight matrix, where the weights are assigned following the assumptions regarding the quality of each link. A simplification, commonly used in practice (and which we actually assume within the equivalent design of the tightly coupled architecture) is that the measurements from the different satellites are uncorrelated. The measurement weighting matrix can then be constructed as an inverse of the diagonal measurement noise covariance matrix. As the GNSS Doppler measurements are usually of a relatively high quality, a constant noise assumption can be easily adopted with an equivalent circular covariance approximation for Doppler LS solution in a loosely coupled configuration.
Finally, the DVL measurement model can be considered as the X–Y velocity measurement in the coordinate frame of the sensor including the lever arm compensation with respect to the IMU. In addition to the actual 2D velocity measurement, a constraint along the body vertical axis of the vessel can be employed (velocity projection in the body frame) as one can assume the vertical velocity to be zero on average. The constraint has been implemented within the UKF framework as so-called “pseudo-measurement” by extending the true sensor measurement with a third component, setting the measurement to zero with some associated measurement noise. This vertical velocity measurement significantly decreases the vertical position drift by reducing it from being cubic in time to becoming quasi-linear in time. The measurement model for the DVL speed observation
is expressed as
where
refers to the baseline between the IMU and the DVL positions within the local ship frame.
Naturally, for lower-cost IMUs the navigation performance is strongly degraded due to a fast accumulation of the errors caused by sensor noises, biases, scale factor errors, etc. Moreover, for non-augmented IMU/GNSS system (e.g., a system without the magnetometer, a gyrocompass, or multiple GNSS antennas), the attitude and some of the inertial sensor errors become weakly observable, and the ability of the system to effectively estimate them is strongly conditioned on the dynamics of the vessel. For these reasons, the baseline observations (non-collinear vector measurements) were incorporated from three spatially distributed GNSS antennas to ensure that the attitude drift is constrained when baseline measurements are available. Recall that the attitude integration is the first integral of three subsequent integrals, which constitute the strapdown inertial mechanization and the attitude errors start to dominate the other error sources relatively fast. A baseline observation is considered to be valid if the RTK-based baseline determination between two antennas resulted in a fixed integer ambiguity solution; therefore, up to three baseline observations can be incorporated into the measurement model at each epoch depending on the quality of the RTK solutions. Here, baseline estimation is realized in a loosely coupled manner, following the methodology presented in [
40]. Nonetheless, heading determination can be also tightly coupled to the positioning problem for a higher exploitation of redundant information [
41]. The advantage of a direct baseline vector observation model is that the heading becomes observable even with a single observation of non-vertical baseline (i.e., the baseline non-collinear with the local Earth gravity vector). Note that both pitch and roll angles are effectively observable via the coupling of the position measurements with the Earth gravity and only the heading information cannot be directly determined with a single GNSS antenna for typically limited vessel dynamics.
4. Setup and Measurement Campaign
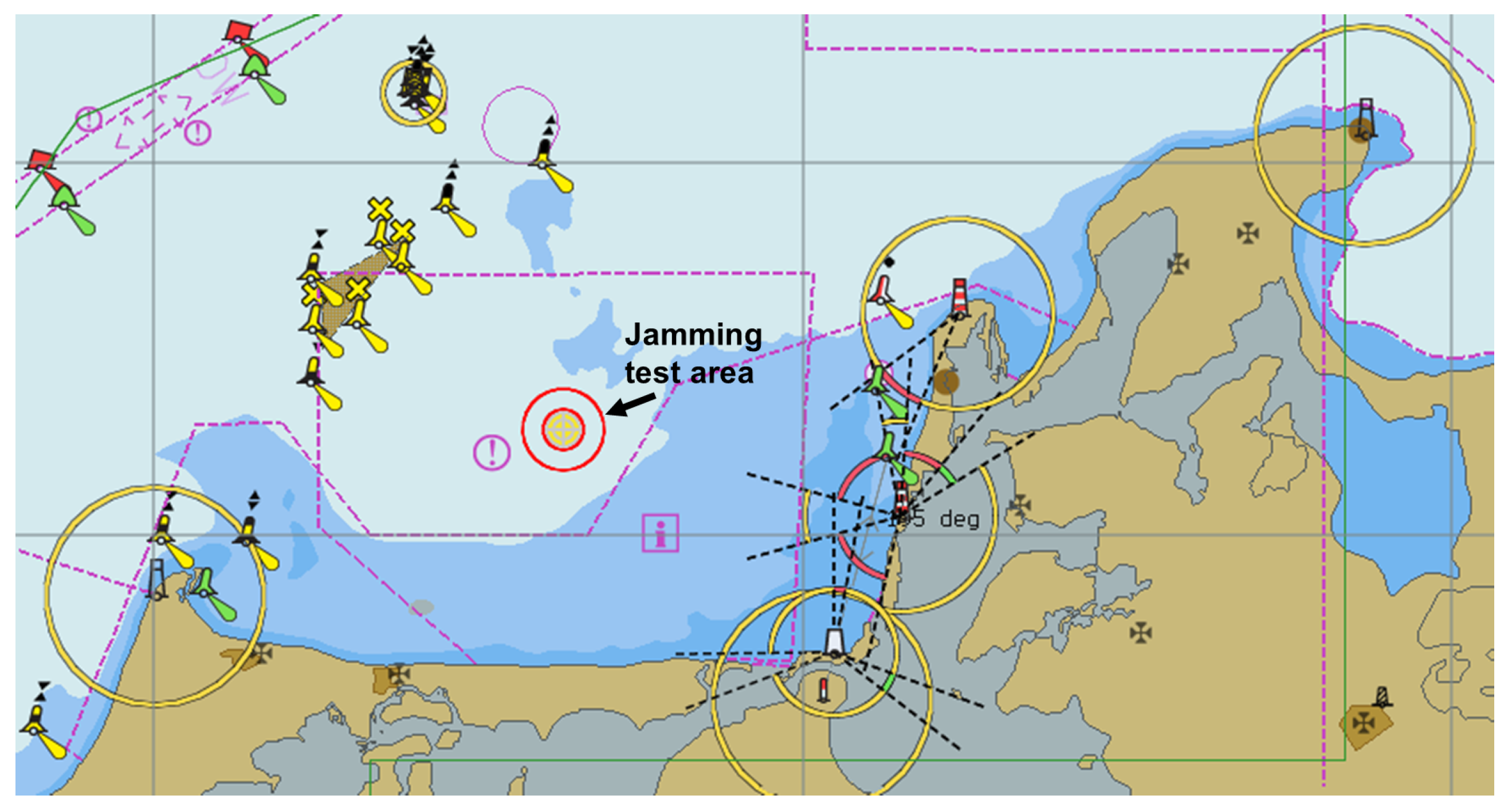
In order to enable experimental jamming tests under real life maritime conditions, the DLR in cooperation with the German Federal Network Agency has allocated a civilian maritime GNSS jamming testbed in the Baltic Sea. The test area is located approximately 10 km North of the Darß Peninsula (see
Figure 1). The measurement campaign took place in November 2015. A PPD jammer (WolvesFleet 212G, output power: 2 W) was mounted on the monkey deck of the tugboat AARON (length 26 m, beam 8 m) (see
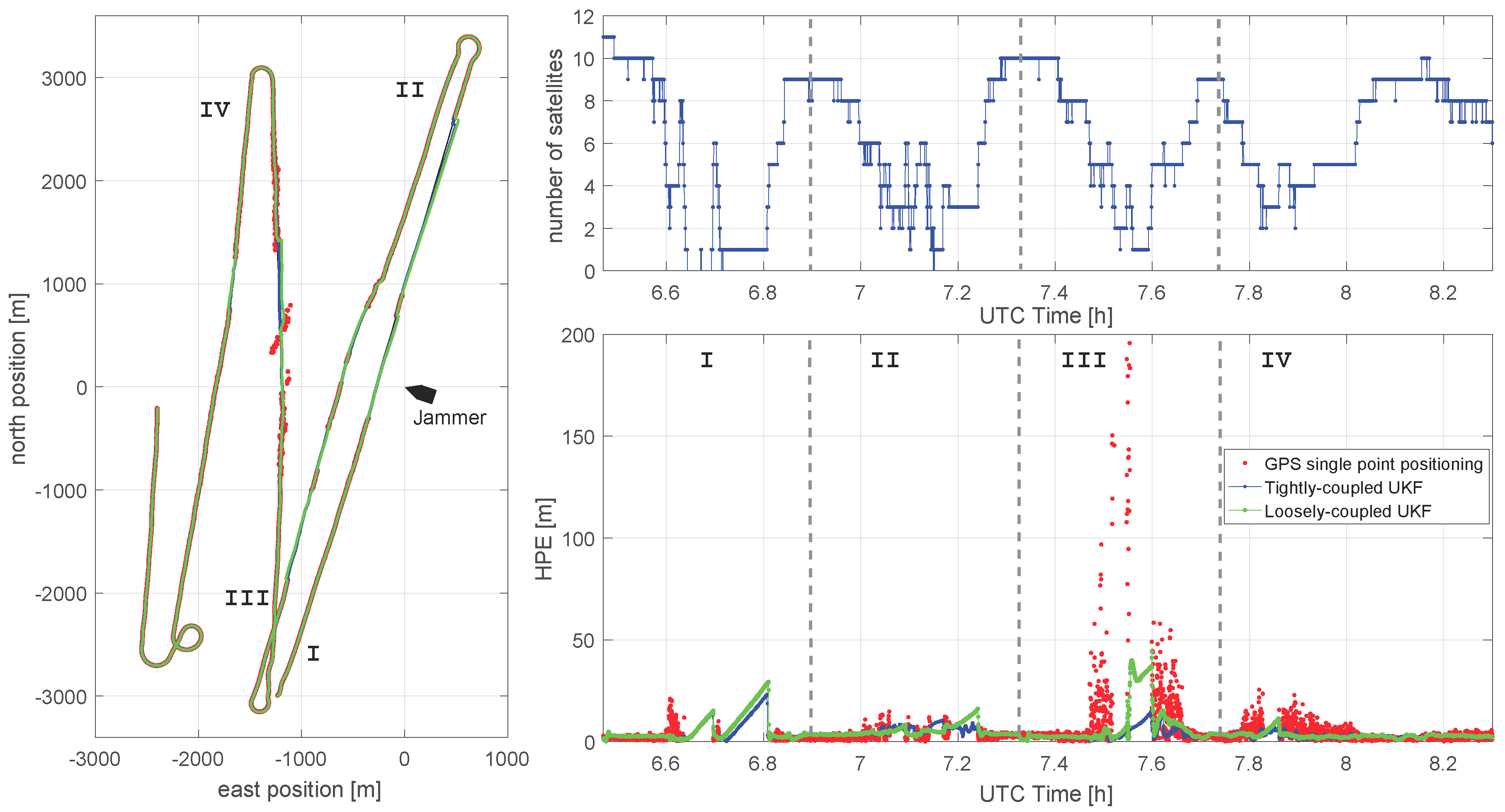
Figure 2). During the campaign, the AARON was anchored in the center of the jamming test area, keeping a fixed position and heading. Due to waves (wave height: 1–2 m), the roll and pitch angle of the vessel varied significantly.
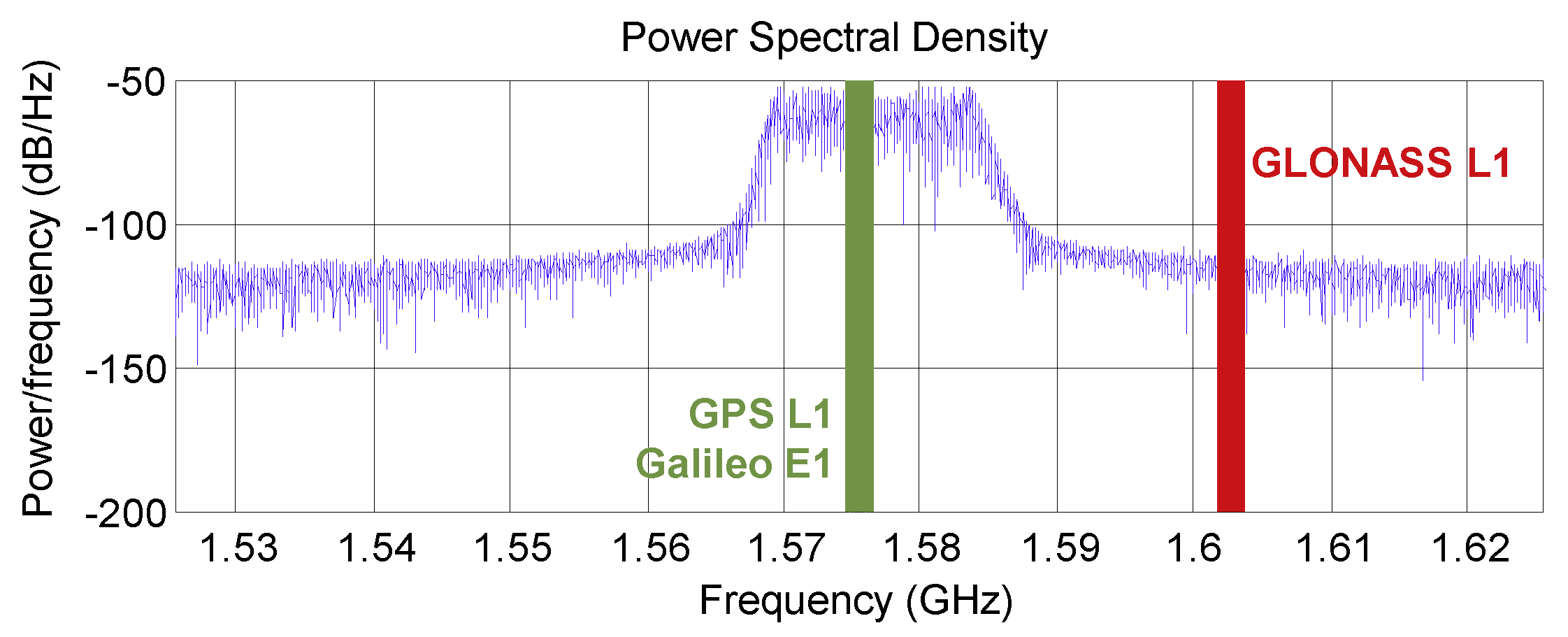
The applied PPD jammer was sweeping a continuous wave signal with an update rate of ∼ 10
around the GPS L1 frequency covering a bandwidth of 17 MHz (see
Figure 3) affecting both GPS L1 and Galileo E1 signal tracking, while GLONASS L1 mainly remained unaffected. This allowed us to use GLONASS for the calculation of a Precise Point Positioning (PPP) reference trajectory using RTKLib software [
42] even in the direct vicinity of the jammer.
The measurement equipment was installed on BALTIC TAUCHER II, the multipurpose research and diving vessel (length 29 m, beam 7 m, see
Figure 4), which was navigated around the tugboat AARON with a maximum speed of 8 knots and a distance to the jammer varying from ∼50 m to 4000 m. The vessel was equipped with three separate dual frequency GNSS receivers (type: Javad Delta, antenna type: navXperience 3G+C maritime), a FOG IMU (type Imar IMU FCAI, list of specifications at [
43]), a gyrocompass, and a DVL (type: Furuno DS 60, list of specifications at [
44]). All relevant sensor measurements were provided either directly via Ethernet or via serial to Ethernet adapter to a Box PC where the measurements were processed in real-time and in parallel stored in a SQlite3 database along with the corresponding time stamps. The described setup enables record and replay functionality for further processing of the original sensor data. The system consists of a highly modular hardware platform and a Real-Time software Framework implemented in ANSI - C
++ as described in [
45].
6. Summary
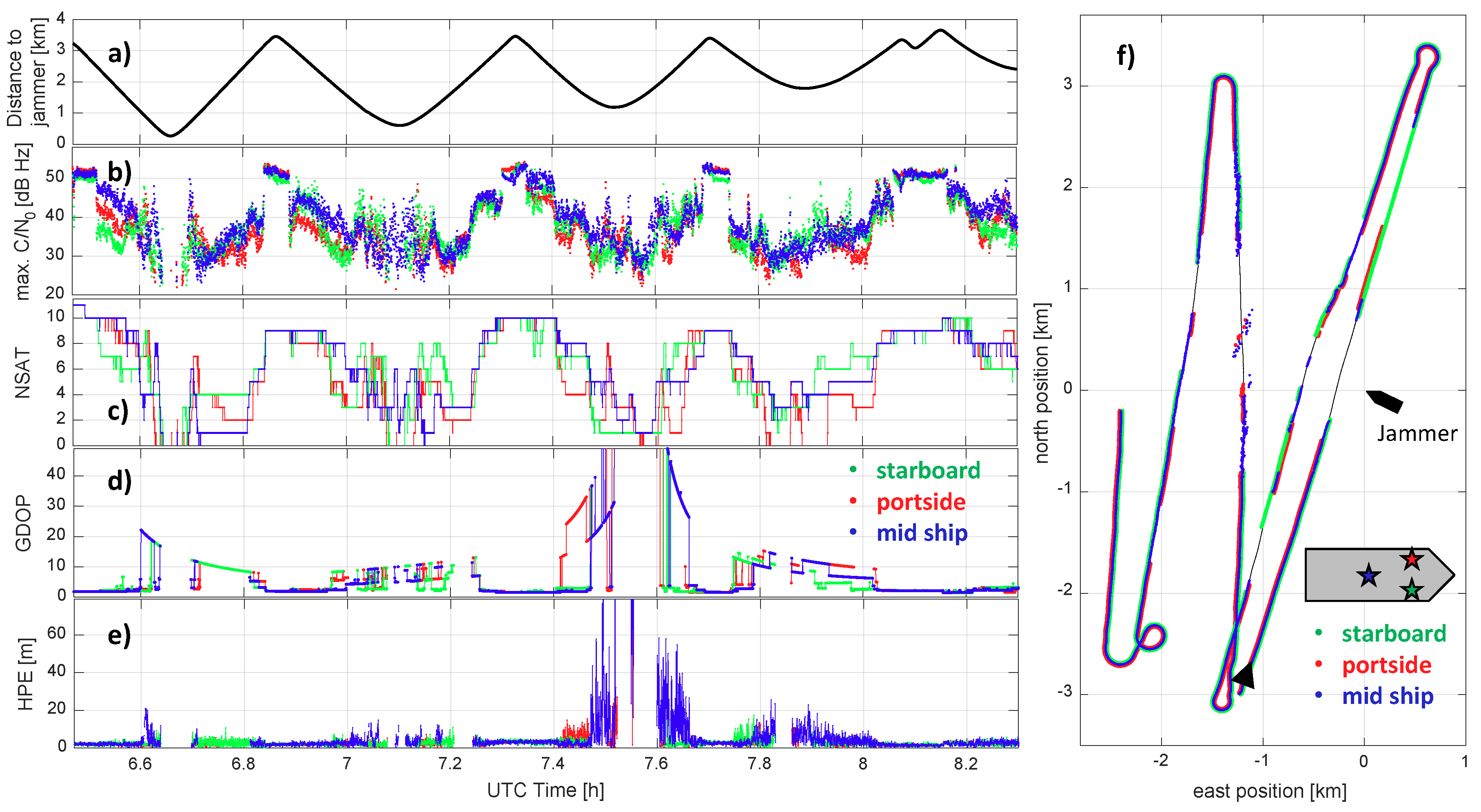
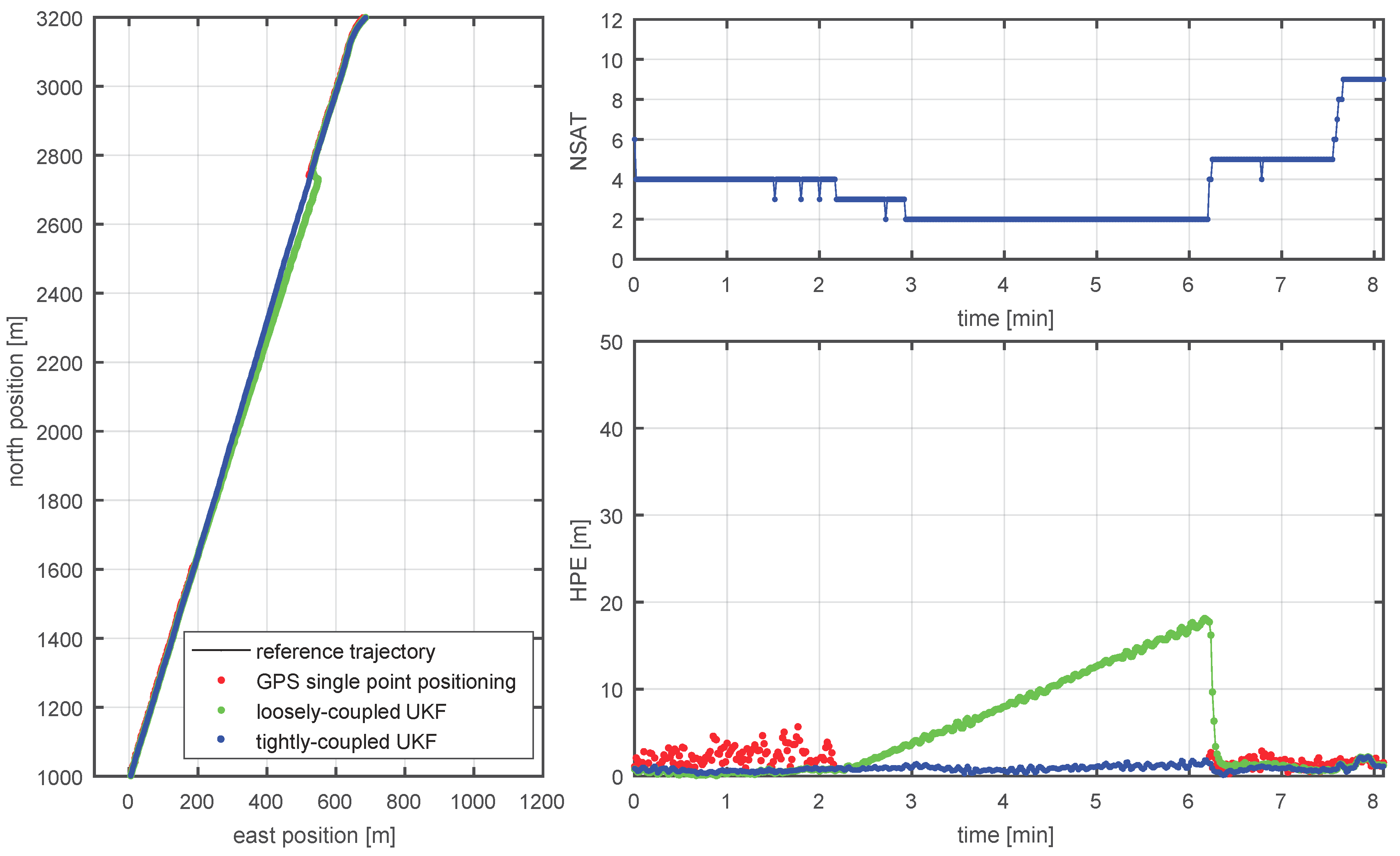
In this paper, a hybrid navigation system is introduced using GNSS, inertial, and DVL measurements. For the first time, such a hybrid navigation system was evaluated in a real maritime jamming scenario. For the measurement campaign conducted in the civilian jamming testbed in the Baltic Sea, a Personal Privacy Device (PPD) jammer was installed on a moored vessel. A second vessel, equipped with three separately placed GNSS antennas and receivers, an inertial measurement unit (IMU), and a Doppler velocity log (DVL) passed the jammer several times with varying distances. The influence of the jammer on the three antennas varied significantly, with the GPS single point positioning being partially disrupted up to a distance of approximately 3 km and corresponding positioning errors up to 200 m.
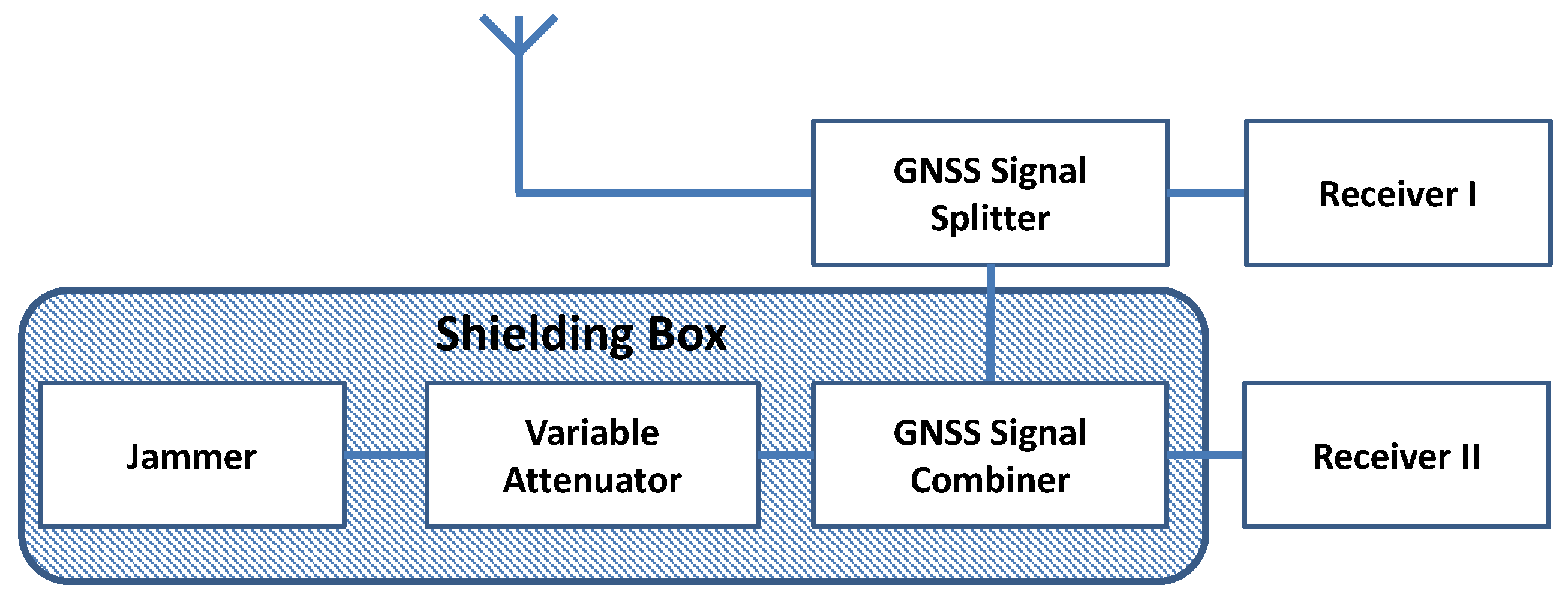
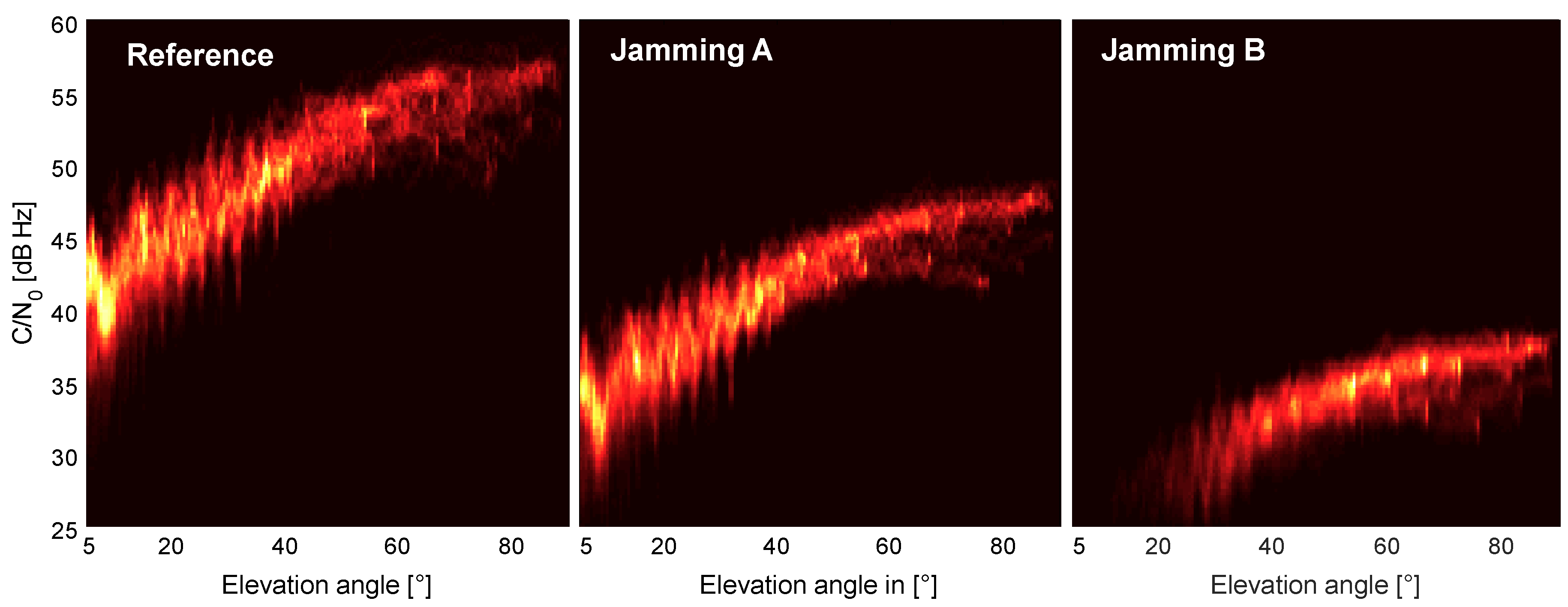
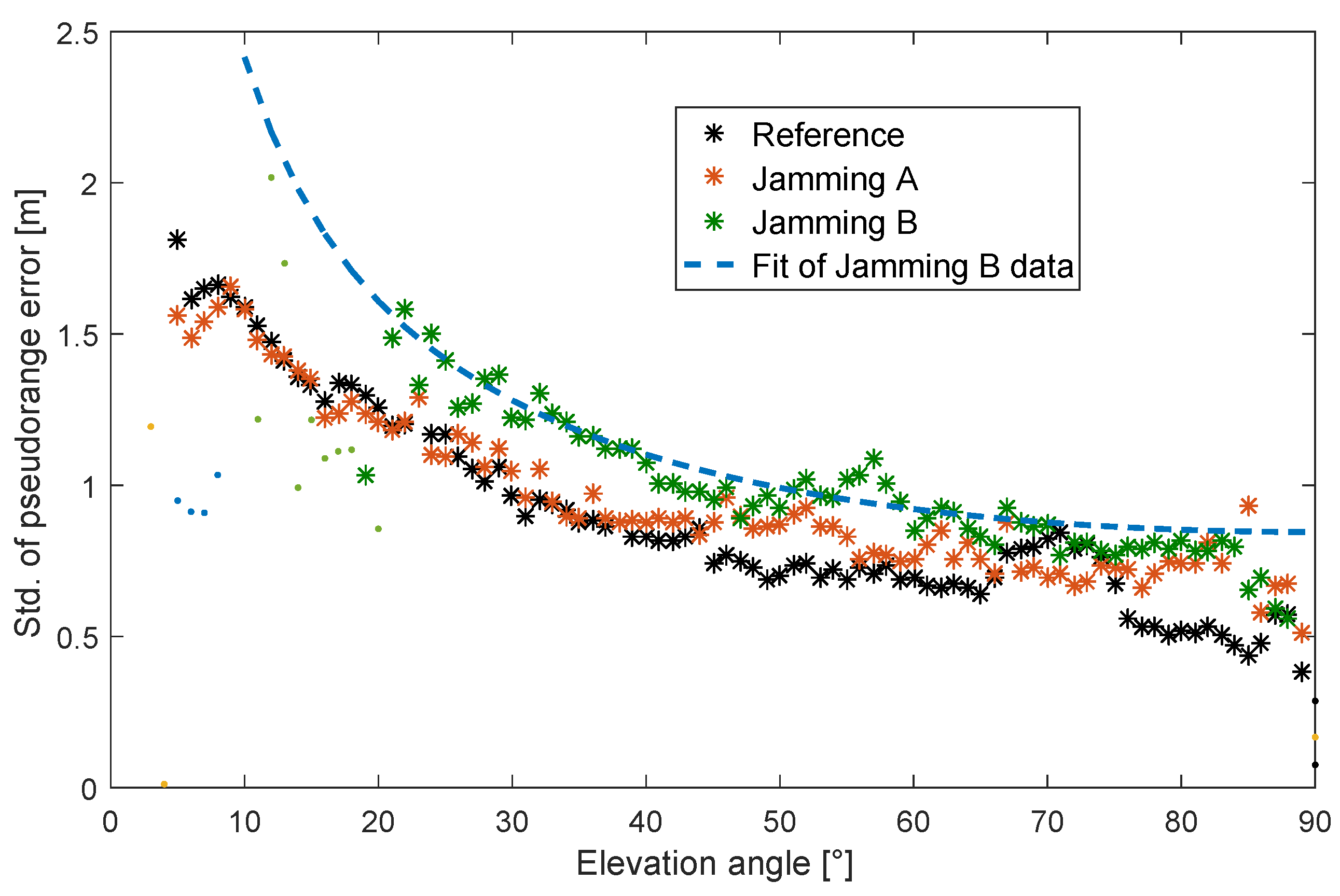
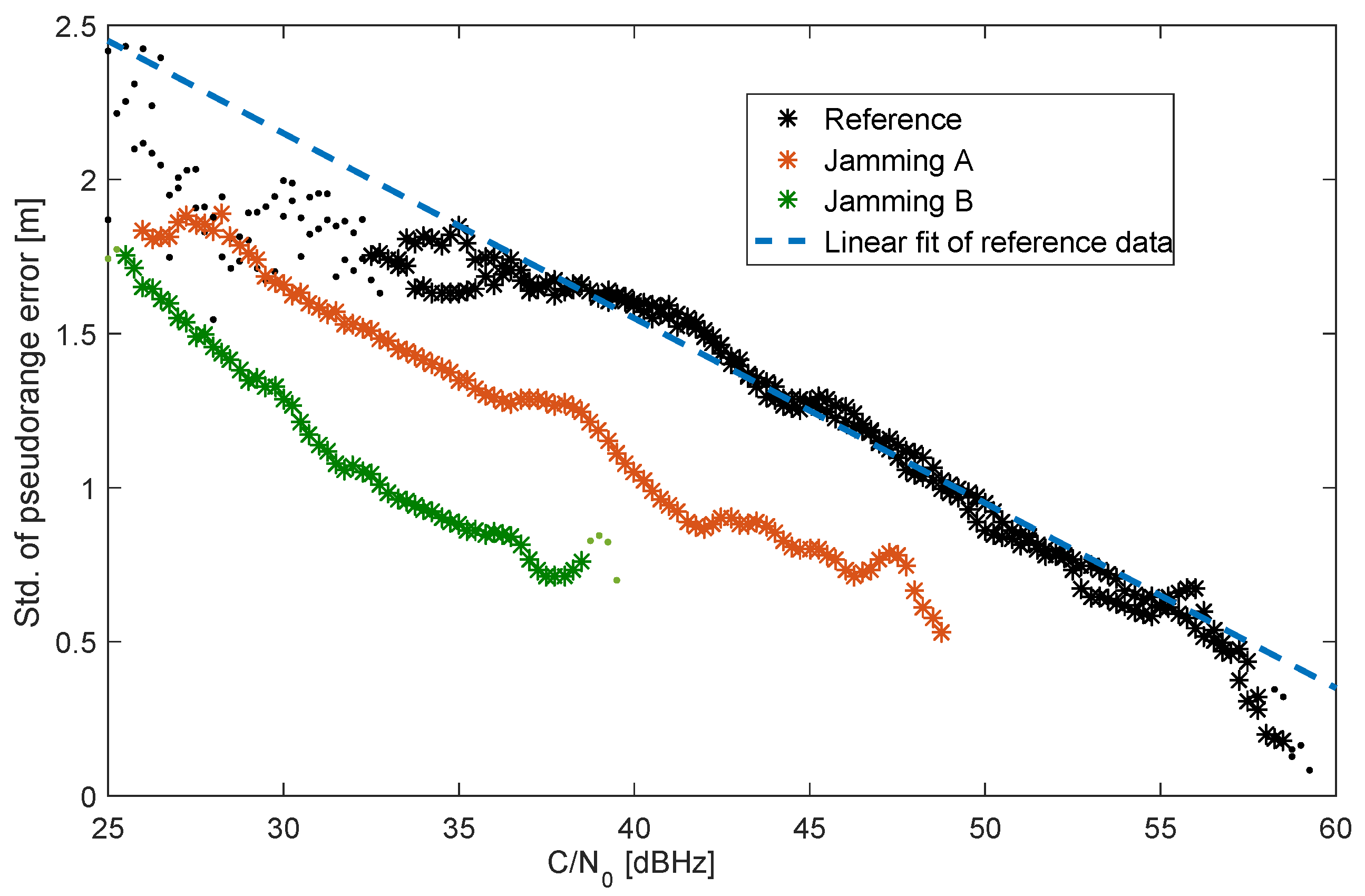
A successful usage of GPS pseudorange measurements under challenging jamming conditions is only possible if the measurements still follow assumed test statistics within the sensor fusion algorithm. In order to determine the pseudorange error statistic under a jammed condition, a lab experiment was performed, where the output of a GNSS antenna was merged with the signal of an attenuated PPD jammer before being fed to a GNSS receiver. The analysis of this experiment shows that, as expected, the carrier-to-noise density (CN0) decreases with increasing jamming power, and the number of tracked satellites is therefore significantly reduced. Unexpected is the fact that the standard deviation of the pseudorange error is only slightly increased by the jammer. A CN0-based variance model, which is typically assumed to be the best model, substantially overestimates the error in the presence of a jammer. Out of this analysis, a standard elevation-based noise model or even a constant noise model appear to be good candidates for the application in the sensor fusion scheme.
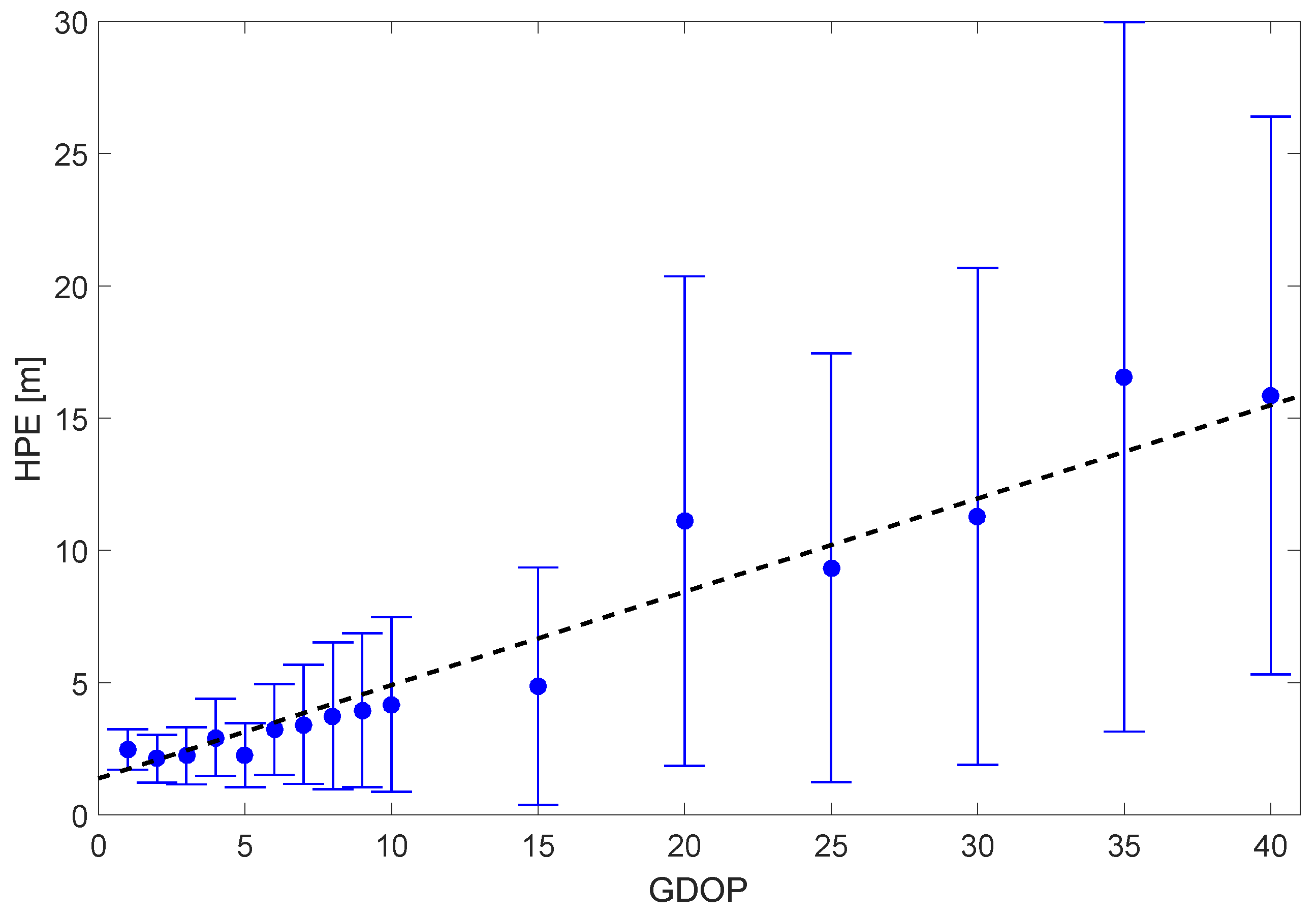
The evaluation of the proposed IMU/GNSS/DVL UKF within the challenging jamming scenario confirmed the superior performance of the tightly coupled approach when compared to the loosely coupled scheme. Here, the advantage of the tightly coupled UKF is mainly due to a direct usage of the measurements in the segments affected by the jamming, where the number of tracked satellite drops partially below four. Due to the usage of the DVL, the filter shows only a linear position drift during complete GPS outages. This can be seen as a substantial advantage when compared to classical GNSS/IMU integration, where the positioning error grows cubically in time due to triple integration of the gyroscope errors in a strapdown navigation system. The analysis of the different weighting schemes for the GPS pseudorange measurements inside the UKF yielded rather small differences between the approaches. The best performance was achieved using the elevation-based variance model and, therefore, confirms the results of the lab experiment. The maximum horizontal position error of less than 30 meters of the tightly coupled IMU/GNSS/DVL UKF for the challenging jamming environment is small enough to successfully support most of the maritime applications.
Future work will deal with the reduction of the observed constant linear drift of 5 m/min by trying to align better the DVL and GNSS compass or, alternatively, considering a constant alignment error within the estimator. Additionally, the simultaneous usage of the measurements from all three antennas and the performance of the filter with available stable reference clock will be explored. With respect to the pseudorange error model in the vicinity of jammer, we will extend the lab experiment in order to calibrate an error model based on both the elevation and carrier-to-noise density ratio. Finally, an appropriate error model for the GNSS Doppler measurements needs to be developed.