Design and Simulation of an Integrated Wireless Capacitive Sensors Array for Measuring Ventricular Pressure
Abstract
1. Introduction
2. Integrated Wireless System Description
2.1. Implantable LC Sensor Set
2.2. External Coil
3. Results and Discussion
3.1. Capacitive Array
3.2. Inductive Coupling Link
3.2.1. Internal Dual-Layer Coil Model
3.3.2. External Coil
3.3.3. Magnetic Coupling Link Model
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Peng, Y.; Wang, T.; Jiang, W.; Liu, X.; Wen, X.; Wang, G. Modeling and Optimization of Inductively Coupled Wireless Bio-Pressure Sensor System Using the Design of Experiments (DOE) Method. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 8, 65–72. [Google Scholar]
- Guyton, A.C.; Hall, J. Textbook of Medical Physiology, 4th ed.; Saunders: Philadelphia, PA, USA; London, UK; Toronto, ON, Canada, 1971. [Google Scholar]
- Collins, C. Miniature passive pressure transensors for implanting in the eye. IEEE Trans. Biomed. Eng. 1967, 14, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Rosengren, L.; Rangsten, P.; Bäcklund, Y.; Hok, B.; Svedbergh, B.; Selen, G. A system for passive implantable pressure sensors. In Proceedings of the 8th International Solid-State Sensors and Actuators, Yokohama, Japan, 7–10 June 1993; pp. 588–591. [Google Scholar]
- Olsen, E.R.; Collins, C.C.; Loughborough, W.F.; Richards, V.; Adams, J.E.; Pinto, D.W. Intracranial pressure measurement with a miniature passive implanted pressure transensor. Am. J. Surg. 1967, 113, 727–729. [Google Scholar] [CrossRef]
- Wise, K.D.; Clark, S.K. Diaphragm formation and pressure sensitivity in batch-fabricated silicon pressure sensors. In Proceedings of the 1978 International Electron Devices Meeting, Washington, DC, USA, 4–6 December 1978; pp. 96–99. [Google Scholar]
- Lee, Y.S.; Wise, K.D. A batch-fabricated silicon capacitive pressure transducer with low temperature sensitivity. IEEE Trans. Electron Devices 1982, 29, 42–48. [Google Scholar] [CrossRef]
- Chatzandroulis, S.; Tsoukalas, D.; Neukomm, P.A. A miniature pressure system with a capacitive sensor and a passive telemetry link for use in implantable applications. J. Microelectromech. Syst. 2000, 9, 18–23. [Google Scholar] [CrossRef]
- Park, E.C.; Yoon, J.B.; Yoon, E. Hermetically sealed inductor–capacitor (LC) resonator for remote pressure monitoring. Jpn. J. Appl. Phys. 1998, 37, 7124–7128. [Google Scholar] [CrossRef]
- Takahata, K.; DeHennis, A.; Wise, K.D.; Gianchandani, Y.B. A wireless microsensor for monitoring flow and pressure in a blood vessel utilizing a dual-inductor antenna stent and two pressure sensors. Int. Conf. Micro ElectroMech. Syst. 2004, 17, 216–219. [Google Scholar]
- DeHennis, A.; Wise, K.D. A fully-integrated multisite pressure sensor for wireless arterial flow characterization. Dig. N. Am. Sens. Actuator Microsyst. Workshop 2004, 15, 168–171. [Google Scholar] [CrossRef]
- Información General Sobre Hipertensión en el Mundo. Available online: http://apps.who.int/iris/bitstream/handle/10665/87679/WHO_DCO_WHD_2013.2_spa.pdf;jsessionid=CA28E7F834B1972192D25482E211BCBC?sequence=1 (accessed on 15 March 2018).
- Banegas, J.R.; Ruilope, L.M. Mortality study from the Spanish Registry of ABPM. An appeal for the transition of ABPM to clinical practice. Hipertensión y Riesgo Cardiovascular 2018, 97–100. [Google Scholar] [CrossRef] [PubMed]
- Campos, C.N.; Lucia, H.C. Hipertensión en adultos mexicanos: Prevalencia, diagnóstico y tipo de tratamiento. Salud Pública de México 2018, 6. [Google Scholar] [CrossRef]
- Maria, T.L. Burden of hypertension as a cardiovascular risk factor. Revista Médica Clínica Los Condes 2015, 26, 156–163. [Google Scholar]
- Lanzarini, L.; Fontana, A.; Campana, C.; Klersy, C. Two simple echo-Doppler measurements can accurately identify pulmonary hypertension in the large majority of patients with chronic heart failure. J. Heart Lung Transplant. 2005, 24, 745–754. [Google Scholar] [CrossRef] [PubMed]
- Hugo, E.V.; Pablo, F.C.; Roberto, A.F.; Mario, A.A.; Milton, E.A.; Carlos, C.D.; Robert, C.B. Comparison of a Radiofrequency-Based Wireless Pressure Sensor to Swan-Ganz Catheter and Echocardiography for Ambulatory Assessment of Pulmonary Artery Pressure in Heart Failure. J. Am. Coll. Cardiol. 2007, 50, 2375–2382. [Google Scholar] [CrossRef]
- Ogedegbe, G.; Pickering, T. Principles and Techniques of Blood Pressure Measurement. Cardiol. Clin. 2010, 28, 571–586. [Google Scholar] [CrossRef] [PubMed]
- Fonarow, G.C.; Stevenson, L.W.; Walden, J.A.; Livingston, N.A.; Steimle, A.E.; Hamilton, M.A.; Moriguchi, J.; Tillisch, J.H.; Woo, M.A. Impact of comprehensive heart failure management program on hospital readmission and functional status of patients with advanced heart failure. J. Am. Coll. Cardiol. 1997, 30, 725–732. [Google Scholar] [CrossRef]
- Fonarow, G.C.; Chelimsky-Fallick, C.; Stevenson, L.W.; Luu, M.; Hamilton, M.A.; Moriguchi, J.D.; Tillisch, J.H.; Walden, J.A.; Albanese, E. Effect of direct vasodilation with hydralazine versus angiotensin-converting enzyme inhibition with captopril on mortality in advanced heart failure: The HyC trial. J. Am. Coll. Cardiol. 1992, 19, 842–850. [Google Scholar] [CrossRef]
- Stevenson, L.W.; Tillish, T.H. Maintenance of cardiac output with normal filling pressures in patients with dilated heart failure. Circulation 1986, 74, 1303–1308. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, M.A.; Allen, M.G.; Kroh, J.; White, J. Flexible wireless passive pressure sensors for biomedical applications. In Proceedings of the Technical Digest Solid-State Sensor, Actuator, and Microsystems Workshop, Hilton Head Island, SC, USA, 4–8 June 2006; pp. 37–42. [Google Scholar]
- CardioMEMSTM. Available online: https://www.accessdata.fda.gov/cdrh_docs/pdf10/p100045c.pdf (accessed on 21 February 2018).
- Clausen, I.; Glott, T. Development of Clinically Relevant Implantable Pressure Sensors: Perspectives and Challenges. Sensors 2014, 14, 17686–17702. [Google Scholar] [CrossRef] [PubMed]
- CardioMEMS, CardioMEMS, Inc. Announces FDA Clearance of the EndoSureä Wireless AAA Pressure Measurement System for Measuring Intrasac Pressure during Thoracic Aortic Aneurysm (TAA) Repair. Available online: http://www.cardiomems.com/content.asp?display=news&view=9 (accessed on 21 February 2018).
- Host, J.F.; Hasan, A. Role of telephone monitoring in patients with chronic heart failure: Theory and practical implications. Smart Homecare Technol. TeleHealth 2014, 2, 1–12. [Google Scholar]
- Pandey, A.C.; Kheder, K.; Pelter, M.; Srivastava, A.V.; Heywood, J.T.; Mohan, R. Reducing Days in the Hospital with Cardiomems Device in Patients with Left Ventricular Assist Device. J. Heart Lung Transplant. 2018, 37, S280–S281. [Google Scholar] [CrossRef]
- Rodrigo, B. Revolucionando el tratameinto de la insuficiencia cardíaca descubriendo CardioMEMSTM: Descubriendo CardoMEMST. Insuficiencia Cardíaca 2015, 10, 141–148. [Google Scholar]
- Abraham, W.T.; Stevenson, L.W.; Bourge, R.C.; Lindenfeld, J.A.; Bauman, J.G.; Adamson, P.B.; CHAMPION Trial Study Group. Sustained efficacy of pulmonary artery pressure to guide adjustment of chronic heart failure therapy: Complete follow-up results from the CHAMPION randomised trial. Lancet 2016, 387, 453–461. [Google Scholar] [CrossRef]
- Ahmed, D. RVSP—Right Ventricular Systolic Pressure: MyHeart. Available online: https://myheart.net/articles/rvsp-right-ventricular-systolic-pressure/ (accessed on 1 June 2018).
- Takahata, K.; DeHennis, A.; Wise, K.D.; Gianchandani, Y.B. A micromachined antenna stent for wireless monitoring of implantable microsensors. In Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; pp. 3360–3363. [Google Scholar]
- DeHennis, A.D.; Wise, K.D. A fully integrated multisite pressure sensor for wireless arterial flow characterization. J. Microelectromech. Syst. 2006, 15, 678–685. [Google Scholar] [CrossRef]
- CardioMEMS. Available online: http://www.cardiomems.com (accessed on 1 June 2018).
- Allen, M.G. Micromachined endovascularly-implantable wireless aneurysm pressure sensors: From concept to clinic Transducers. In Proceedings of the 13th International Conference on Solid-State Sensors, Actuators and Microsystems, Seoul, Korea, 5–9 June 2005; pp. 275–278. [Google Scholar]
- Hamilton, M.A.; Stevenson, L.W.; Child, J.S.; Moriguchi, J.D.; Walden, J.; Woo, M. Sustained reduction in valvular regurgitation and atrial volumes with tailored vasodilator therapy in advanced congestive heart failure secondary to dilated (ischemic or idiopathic) cardiomyopathy. Am. J. Cardiol. 1991, 67, 259–263. [Google Scholar] [CrossRef]
- Harvey, S.; Stevens, K.; Harrison, D.; Young, D.; Brampton, W.; McCabe, C.; Singer, M.; Rowan, K. An evaluation of the clinical and cost-effectiveness of pulmonary artery catheters in patient management in intensive care: A systematic review and a randomized controlled trial. Health Technol Assess. 2006, 10, 1–133. [Google Scholar] [CrossRef]
- Merchant, F.M.; Dec, G.W.; Singh, J.P. Implantable sensors for heart failure. Circ. Arrhythm. Electrophysiol. 2010, 3, 657–667. [Google Scholar] [CrossRef] [PubMed]
- Adamson, P.B.; Magalski, A.; Braunschweig, F.; Bohm, M.; Reynolds, D.; Steinhaus, D.; Luby, A.; Linde, C.; Ryden, L.; Cremers, B.; et al. Ongoing right ventricular hemodynamics in heart failure: Clinical value of measurements derived from an implantable monitoring system. J. Am. Coll. Cardiol. 2003, 41, 565–571. [Google Scholar] [CrossRef]
- Magalski, A.; Adamson, P.; Gadler, F.; Boehm, M.; Steinhaus, D.; Reynolds, D.; Vlach, K.; Linde, C.; Cremers, B.; Sparks, B.; et al. Continuous ambulatory right heart pressure measurements with an implantable hemodynamic monitor: A multicenter, 12-month follow-up study of patients with chronic heart failure. J. Card. Fail. 2002, 8, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Adamson, P.B.; Kjellstrom, B.; Braunschweig, F.; Magalski, A.; Linde, C.; Kolodiezj, A.; Cremers, B.; Bennett, T. Ambulatory hemodynamic monitoring from an implanted device: Components of continuous 24-h pressures that correlate to supine resting conditions and acute right heart catheterization. Congest. Heart Fail. 2006, 12, 14–19. [Google Scholar] [CrossRef] [PubMed]
- Mondritzki, T.; Boehme, P.; White, J.; Park, J.W.; Hoffmann, J.; Vogel, J.; Kolkhof, P.; Walsh, S.; Sandner, P.; Bischoff, E.; et al. Remote Left Ventricular Hemodynamic Monitoring Using a Novel Intracardiac Sensor. Circ. Cardiovasc. Interv. 2018, 11, e006258. [Google Scholar] [CrossRef] [PubMed]
- Mosterd, A.; Azadas, A.W. Epidemiología clínica de la insuficiencia cardíaca. Heart 2007, 93, 1137–1146. [Google Scholar] [CrossRef] [PubMed]
- Zile, M.R.; Bennett, T.D.; John, S.M.; Cho, Y.K.; Adamson, P.B.; Aaron, M.F.; Aranda, J.M.; Braham, W.T.; Smart, F.W.; Stevenson, L.W.; et al. Transición de la insuficiencia cardíaca crónica compensada a la descompensada aguda: Información fisiopatológica obtenida de la monitorización continua de las presiones intracardíacas. Circulation 2008, 118, 1433–1441. [Google Scholar] [CrossRef] [PubMed]
- Lang, R.M.; Badano, L.P.; Mor-Avi, V.; Afilalo, J.; Armstrong, A.; Ernande, L. Recomendaciones para la Cuantificación de las Cavidades Cardíacas por Ecografía en Adultos: Actualización de la Sociedad Americana de Ecocardiografía y de la Asociación Europea de Imagen Cardiovascular. Available online: http://www.ecosiac.org/files/GUIA_011.pdf (accessed on 1 June 2018).
- Rendón-Nava, A.; Díaz-Méndez, J.; Nino-de-Rivera, L.; Calleja-Arriaga, W.; Gil-Carrasco, F.; Díaz-Alonso, D. Study of the Effect of Distance and Misalignment between Magnetically Coupled Coils for Wireless Power Transfer in Intraocular Pressure Measurement. Sci. World J. 2014, 2014, 692434. [Google Scholar] [CrossRef] [PubMed]
- Díaz, D. Caracterización y Modelado de Sensores Capacitivos para Aplicaciones Médicas. Ph.D. Thesis, Instituto Nacional de Astrofísica, Óptica y Electrónica, Puebla, Mexico, 2015. [Google Scholar]
- Díaz, D.; Mario, M.M.; Carlos, Z.; Joel, M.; Wilfrido-Calleja, A.; Juan-Carlos, C.; Luis-Niño, R.; Volodymir, P.; Felix, G.; Angel, G.; et al. Hermetic capacitive pressure sensors for biomedical applications. Microelectron. Int. 2016, 33, 79–86. [Google Scholar] [CrossRef]
- Carrasco, F.; Alonso, D.; Niño-de-Rivera, L. Biocompatibility and implant of a less invasive intraocular pressure sensor. Microelectron. Eng. 2016, 159, 32–37. [Google Scholar] [CrossRef]
- Chen, P.J.; Saati, S.; Varma, S.; Humayun, M.S.; Tai, Y.C. Wireless intraocular pressure sensing using microfabricated minimally invasive flexible-coiled LC sensor implant. J. Microelectromechan. Syst. 2010, 19, 721–734. [Google Scholar] [CrossRef]
- Chen, P.J.; Rodger, D.; Saati, S.; Humayun, M.S.; Tai, Y.C. Microfabricated Implantable Parylene-Based Wireless Passive Intraocular Pressure Sensors. J. Microelectromech. Syst. 2018, 17, 1342–1351. [Google Scholar] [CrossRef]
- Hannan, M.A.; Mutashar, S.; Samad, S.A.; Hussain, A. Energy harvesting for the implantable biomedical devices: Issues and challenges. Biomed. Eng. Online 2014, 13, 79. [Google Scholar] [CrossRef] [PubMed]
- Finkenzeller, K. RFID Handbook: Fundamentals and Applications in Contactless Smart Cards and Identification, 2nd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Ko, W.H.; Wang, Q. Touch mode capacitive pressure sensors. Sens. Actuators A Phys. 1999, 75, 242–251. [Google Scholar] [CrossRef]
- Yamamoto, S.; Nakao, O.; Nishimura, H. Touch mode capacitive pressure sensor for passive tire monitoring system. Proc. IEEE Sens. 2002, 2, 1582–1586. [Google Scholar]
- Timoshenko, S.P.; Woinowsky, K.S. Theory of Plates and Shells, 2nd ed.; Mc-Graw-Hill Book: New York, NY, USA, 1959. [Google Scholar]
- Islam, A.; Islam, S. Design of multi-spiral solenoidal inductor for inductive power transfer in biomedical applications. In Proceedings of the 27th Annual Review of Progress in Applied Computational Electromagnetics, Williamsburg, VA, USA, 27–31 March 2011; pp. 369–374. [Google Scholar]
- Zhao, J. A new calculation for designing multilayer planar spiral inductors. EDN 2010, 29, 37–40. [Google Scholar]
- Chiang, C.; Klin, C.; Ju, M. An implantable capacitive pressure sensor for biomedical applications. Sens. Actuators A Phys. 2007, 134, 382–388. [Google Scholar] [CrossRef]
- Mutashar, S.; Hannan, M.A.; Samad, S.A.; Hussain, A. Analysis and optimization of spiral circular inductive coupling link for bio-implanted applications on air and within human tissue. Sensors 2014, 14, 11522–11541. [Google Scholar] [CrossRef] [PubMed]
- Mutashar, S.; Hannan, M.A.; Samad, S.A.; Hussain, A. Efficiency Improvement of Wireless Power Transmission for Bio-Implanted Devices. Int. J. Med. Health Biomed. Bioeng. Pharm. Eng. 2013, 7. [Google Scholar] [CrossRef]
- Hmida, G.B.; Ghariani, H.; Samet, M. Design of wireless power and data transmission circuits for implantable biomicrosystem. Biotechnol. J. 2007, 6, 153–164. [Google Scholar]
- Rahko, P.S. Evaluation of the skin-to-heart distance in the standing adult by two-dimensional echocardiography. J. Am. Soc. Echocardiogr. 2008, 21, 761–764. [Google Scholar] [CrossRef] [PubMed]
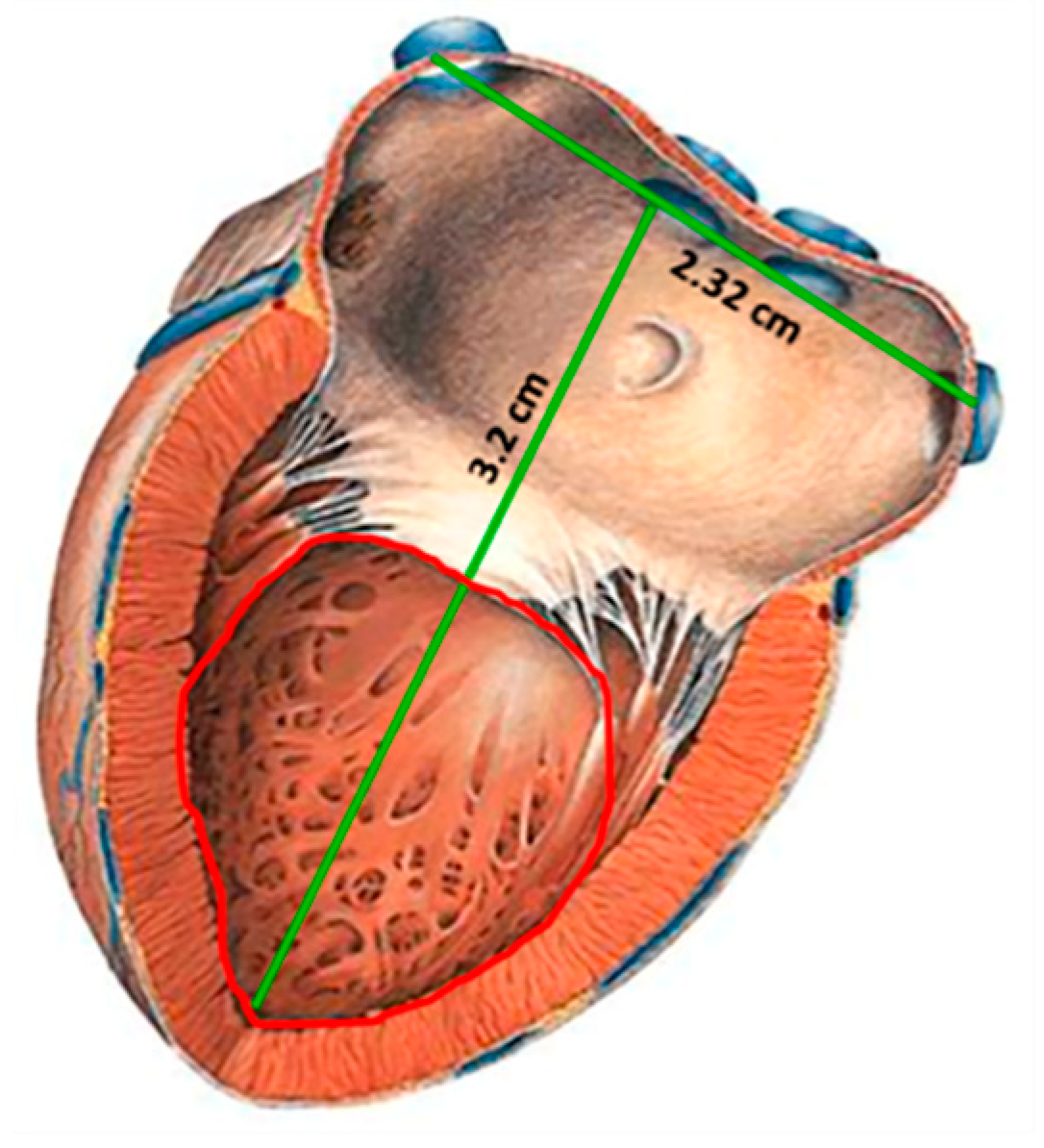
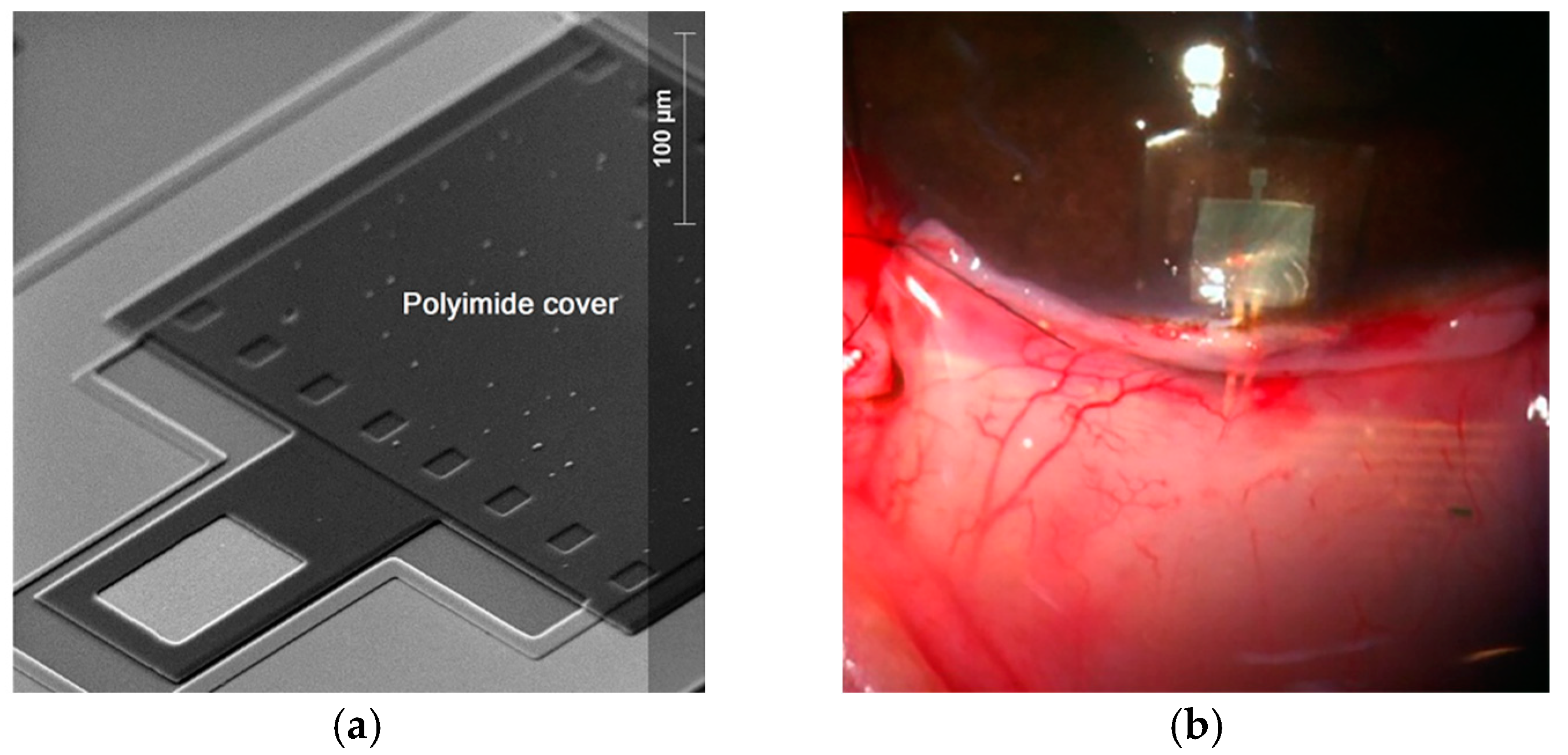
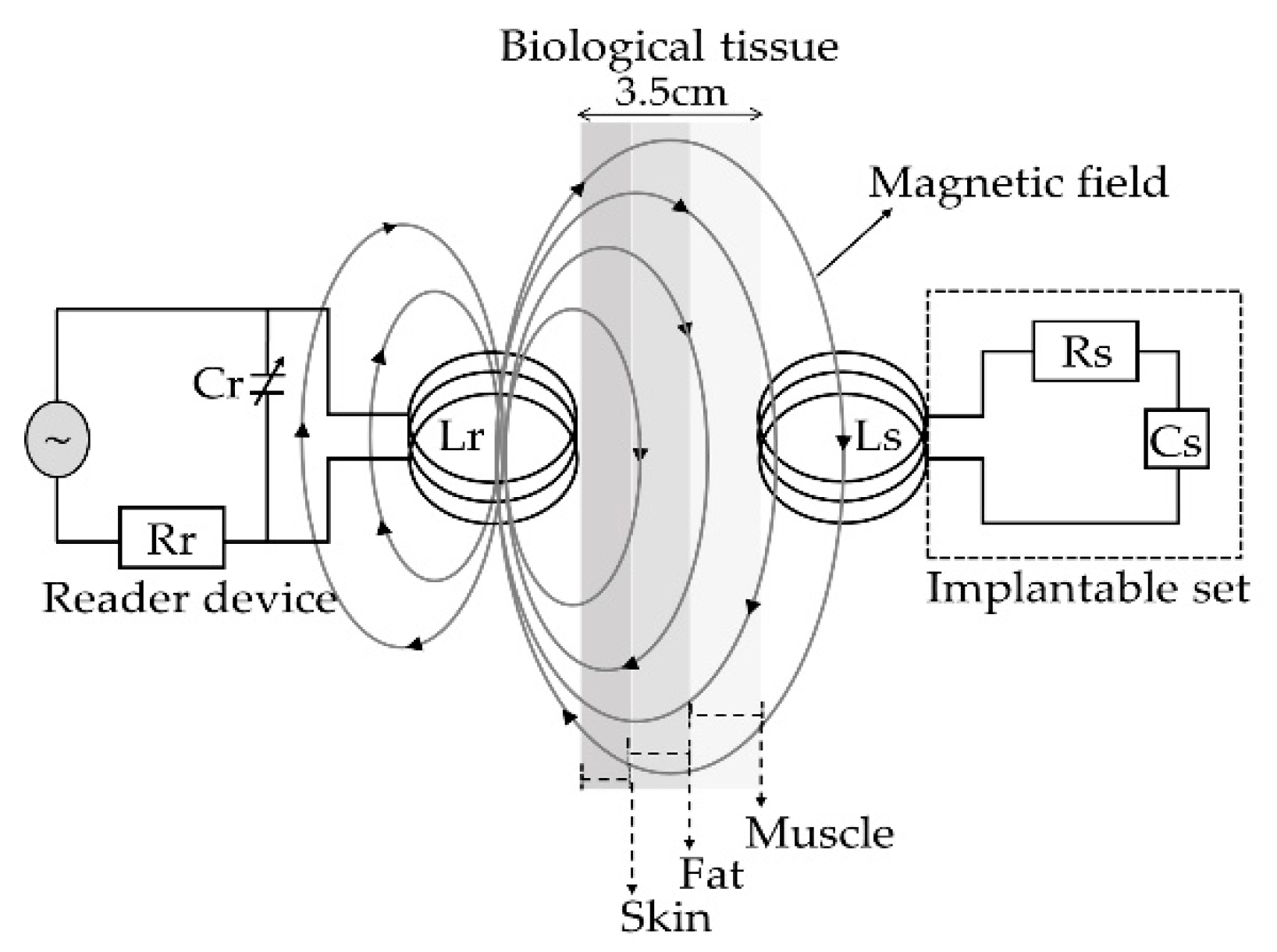
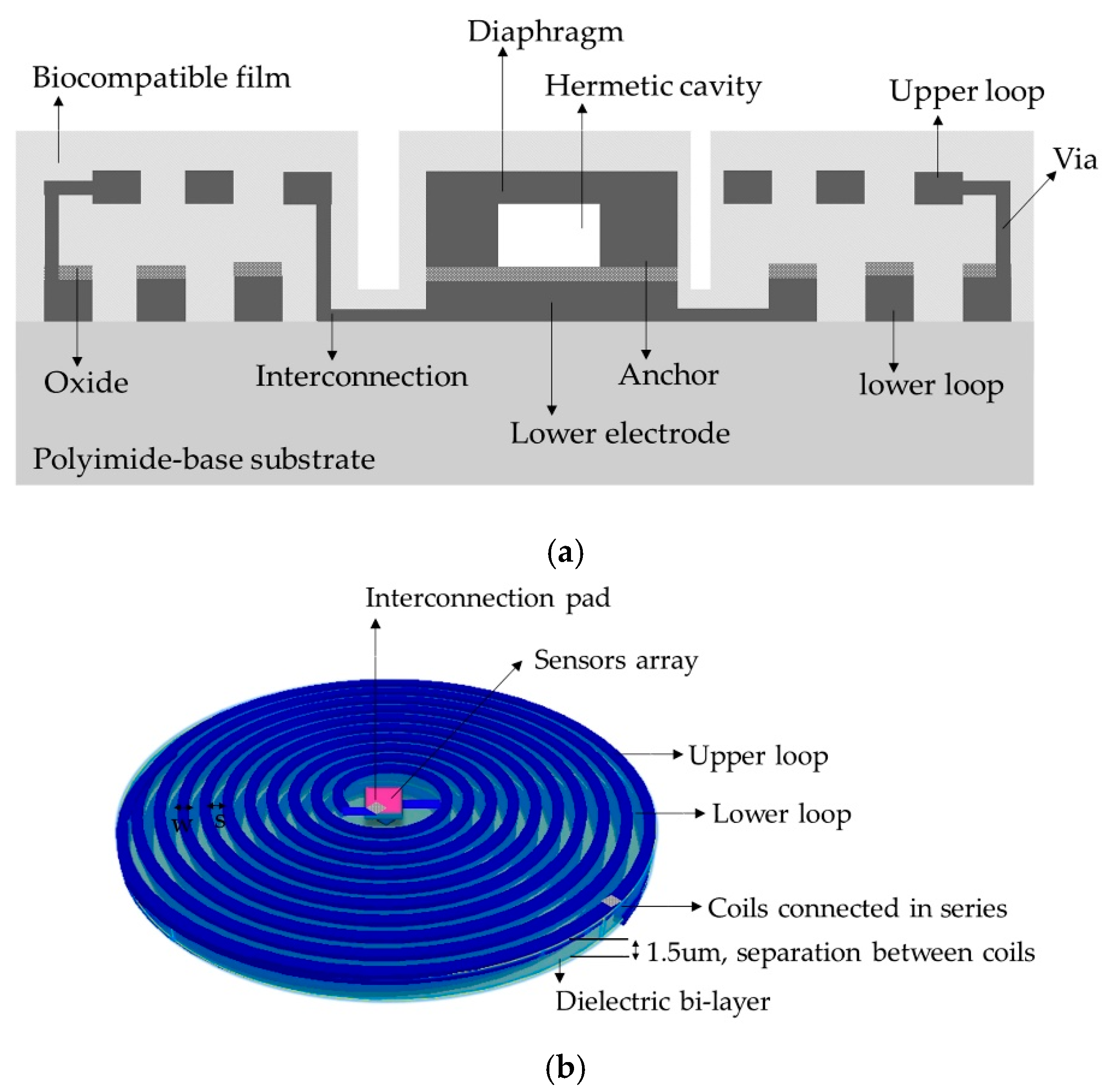

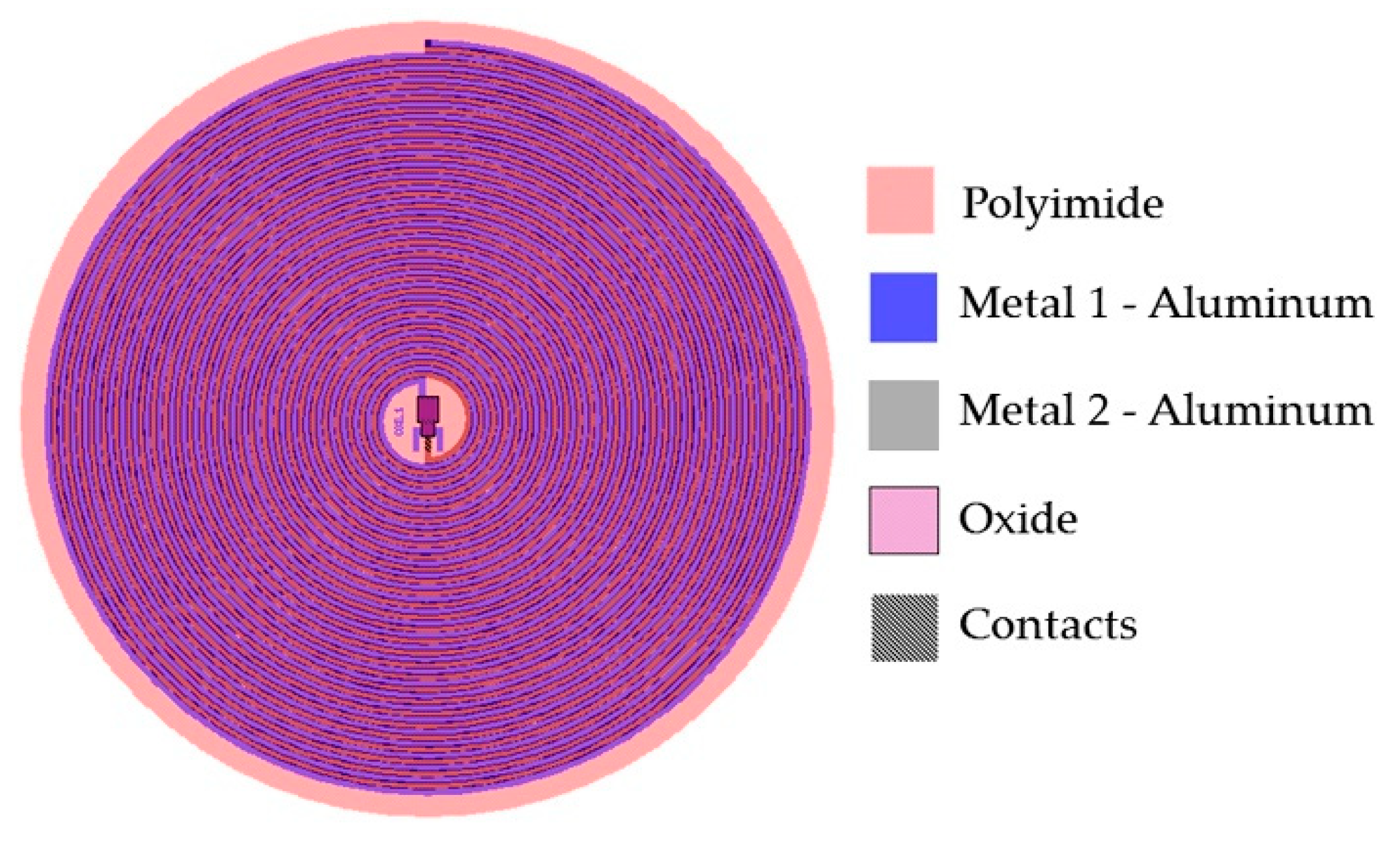
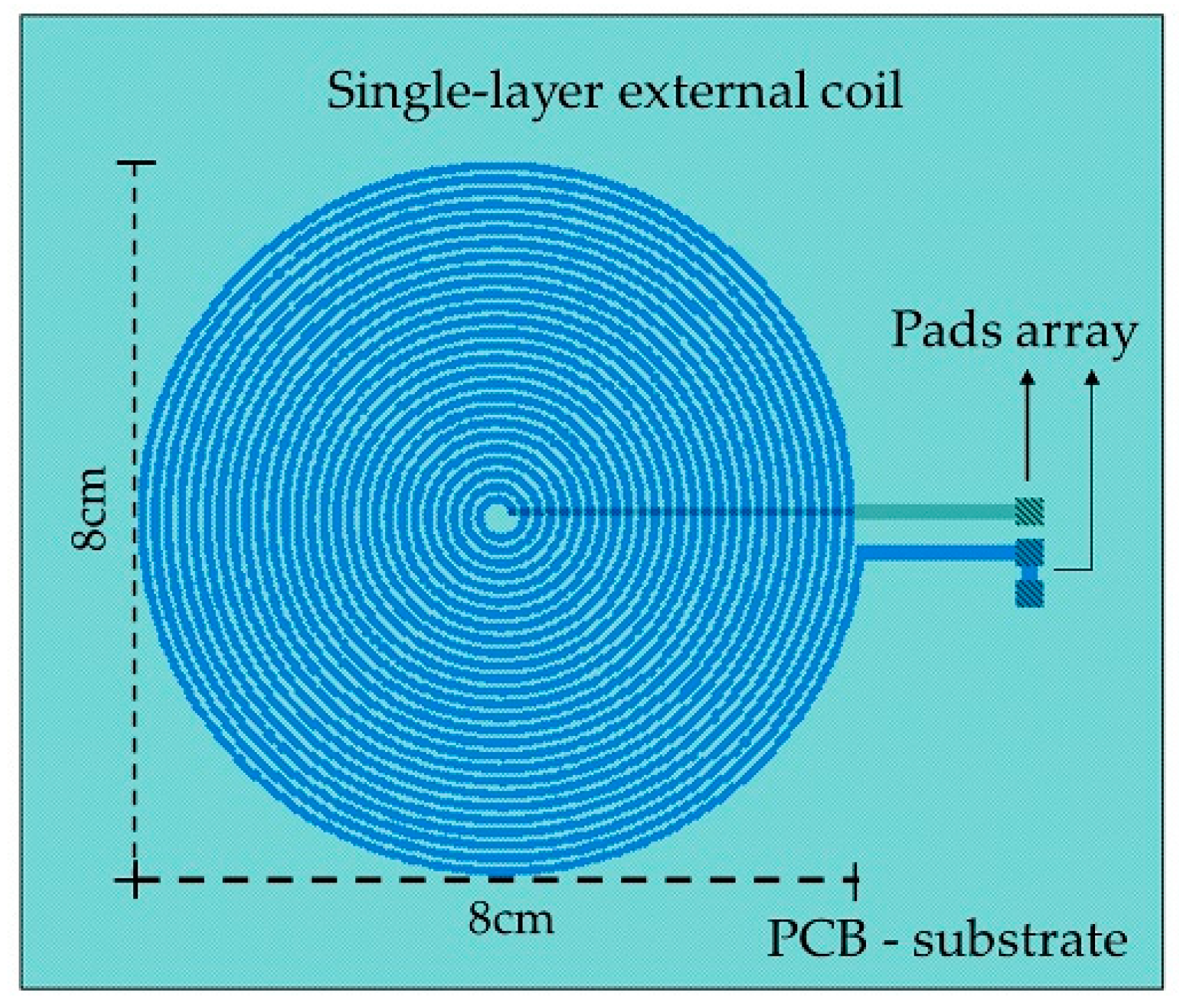
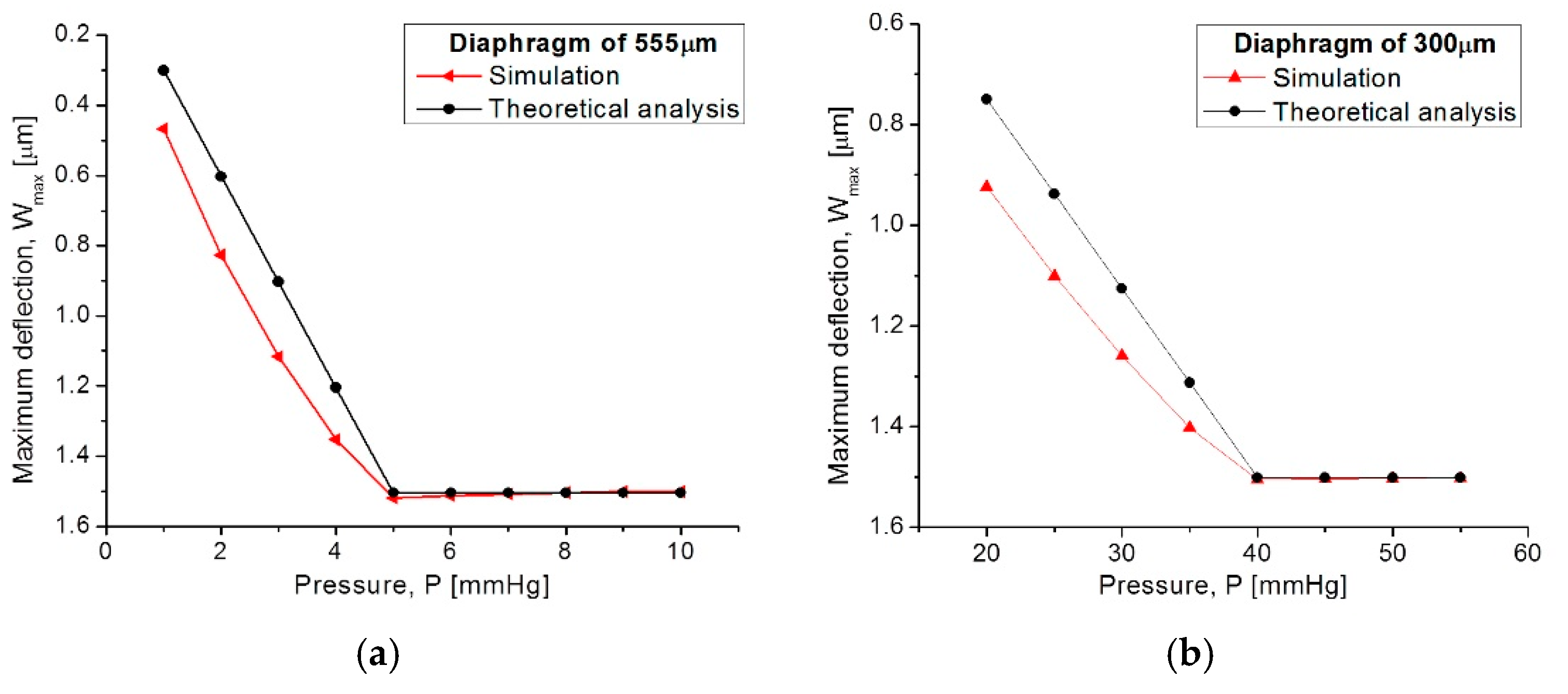
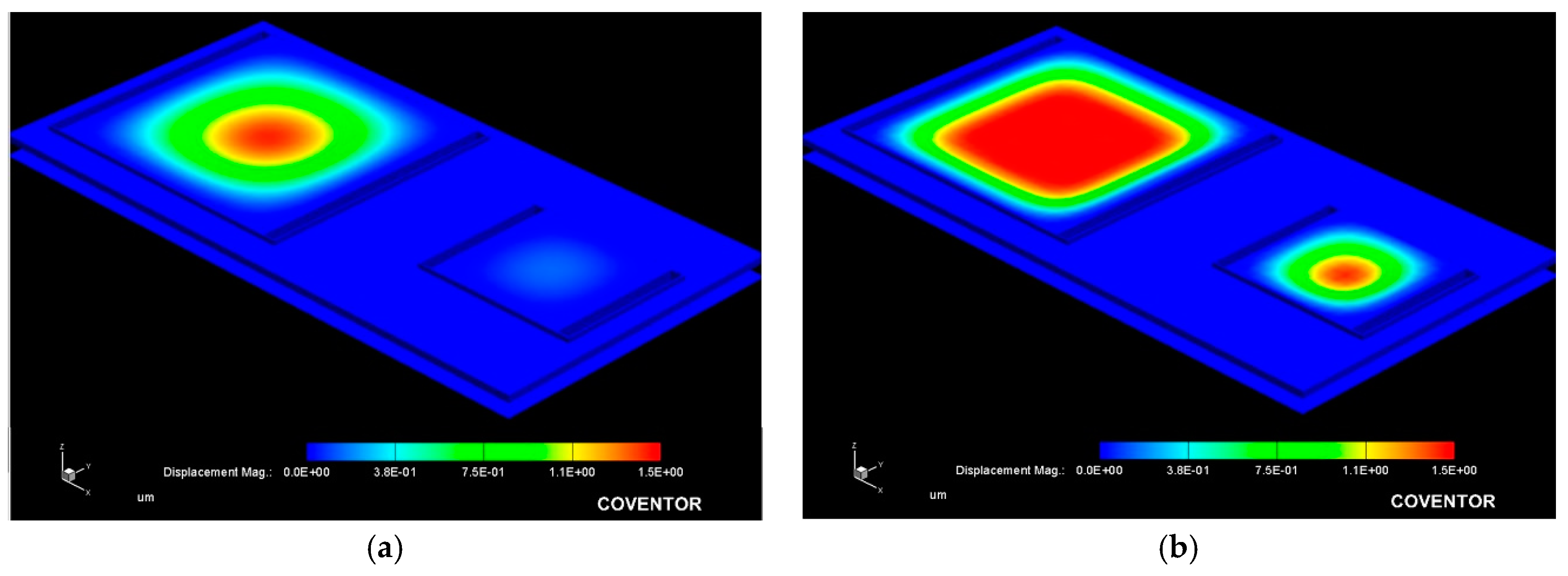
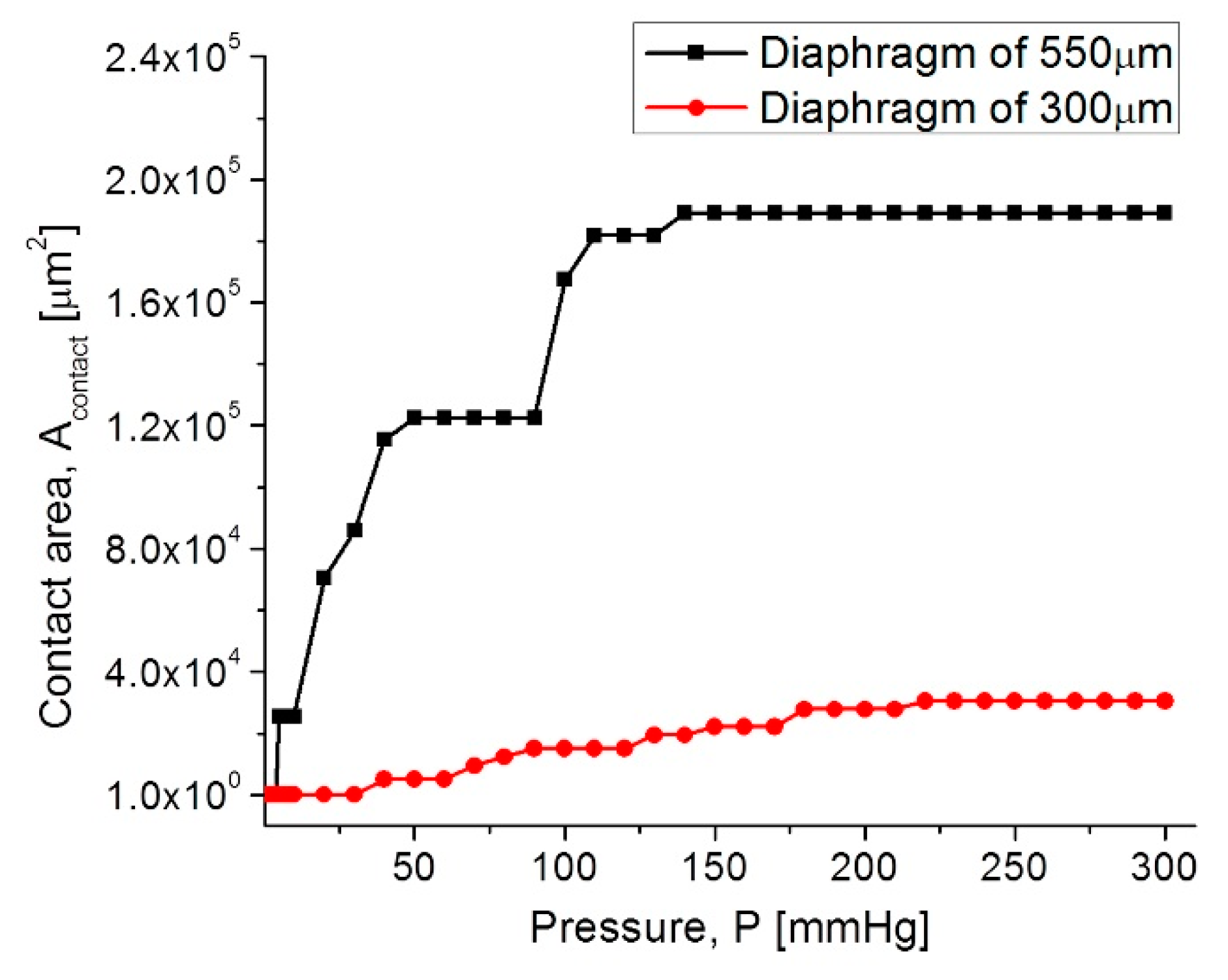
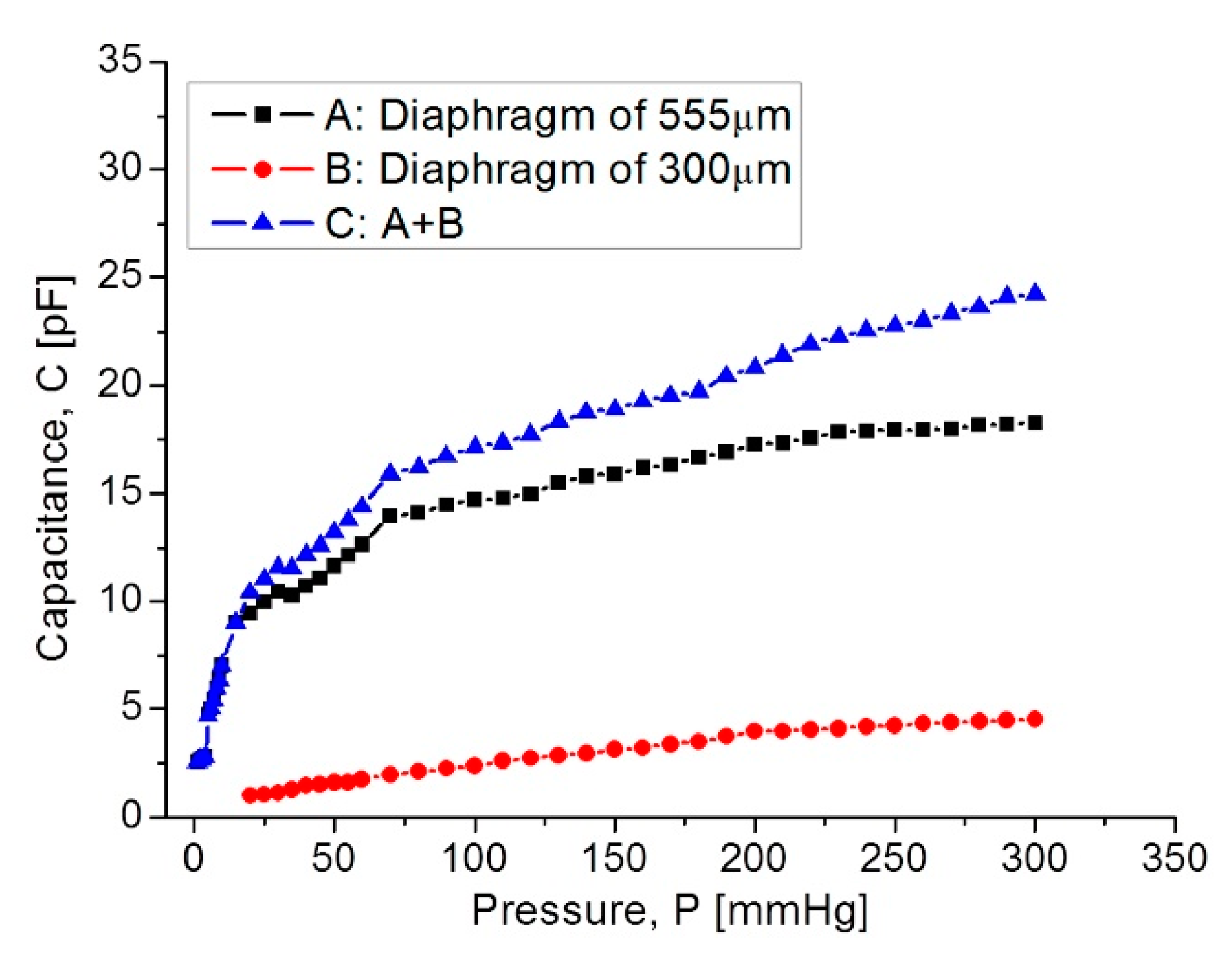
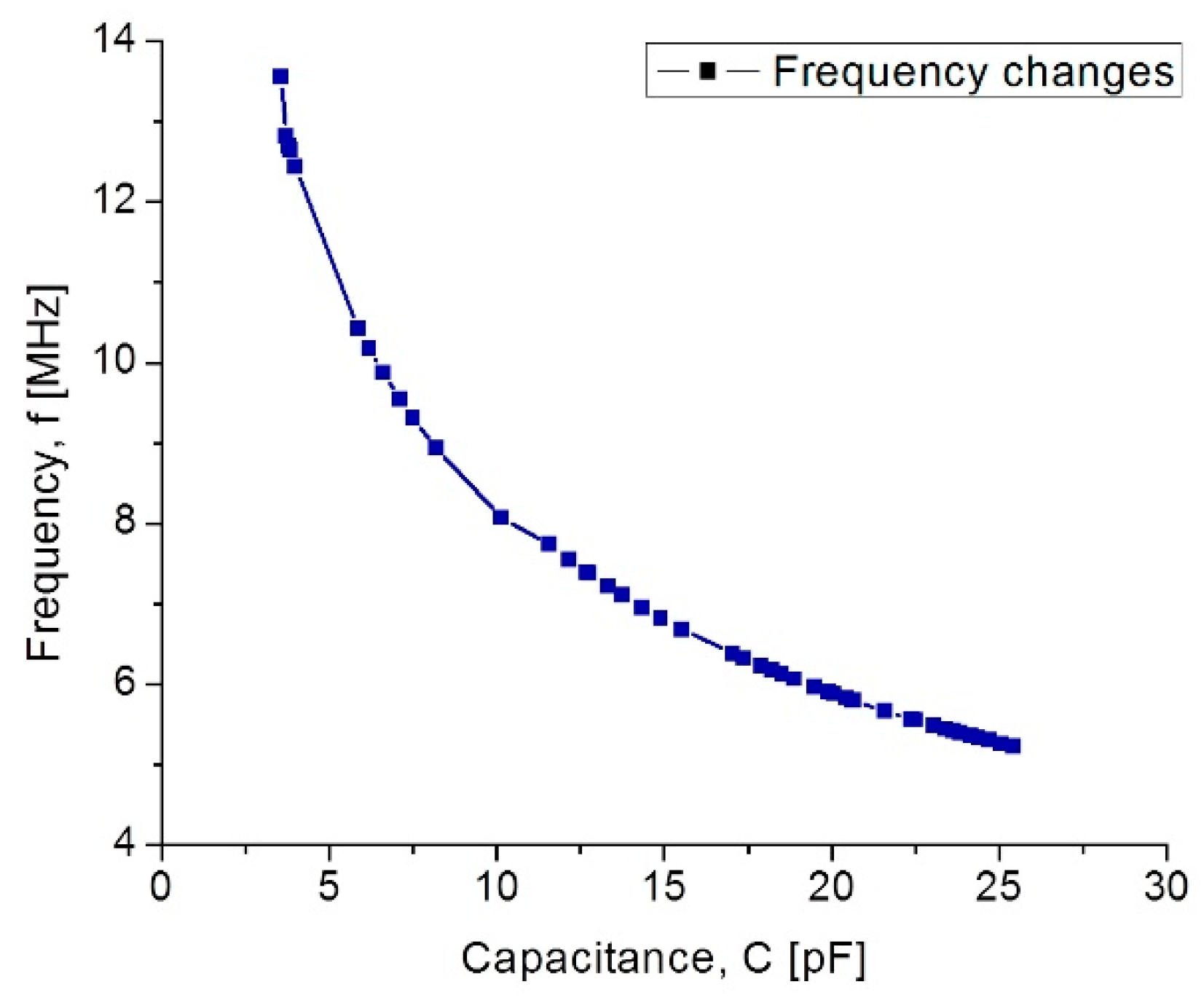
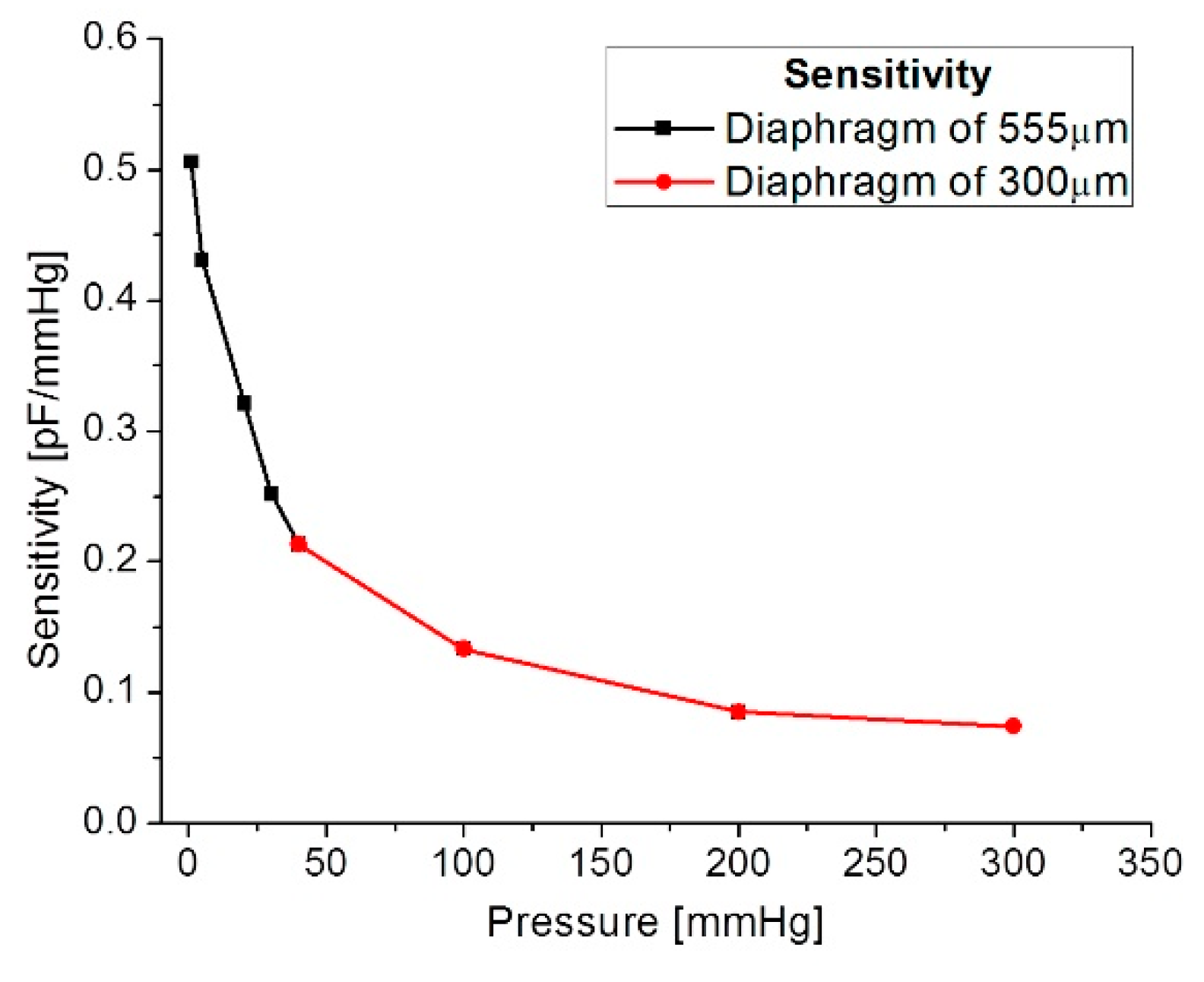
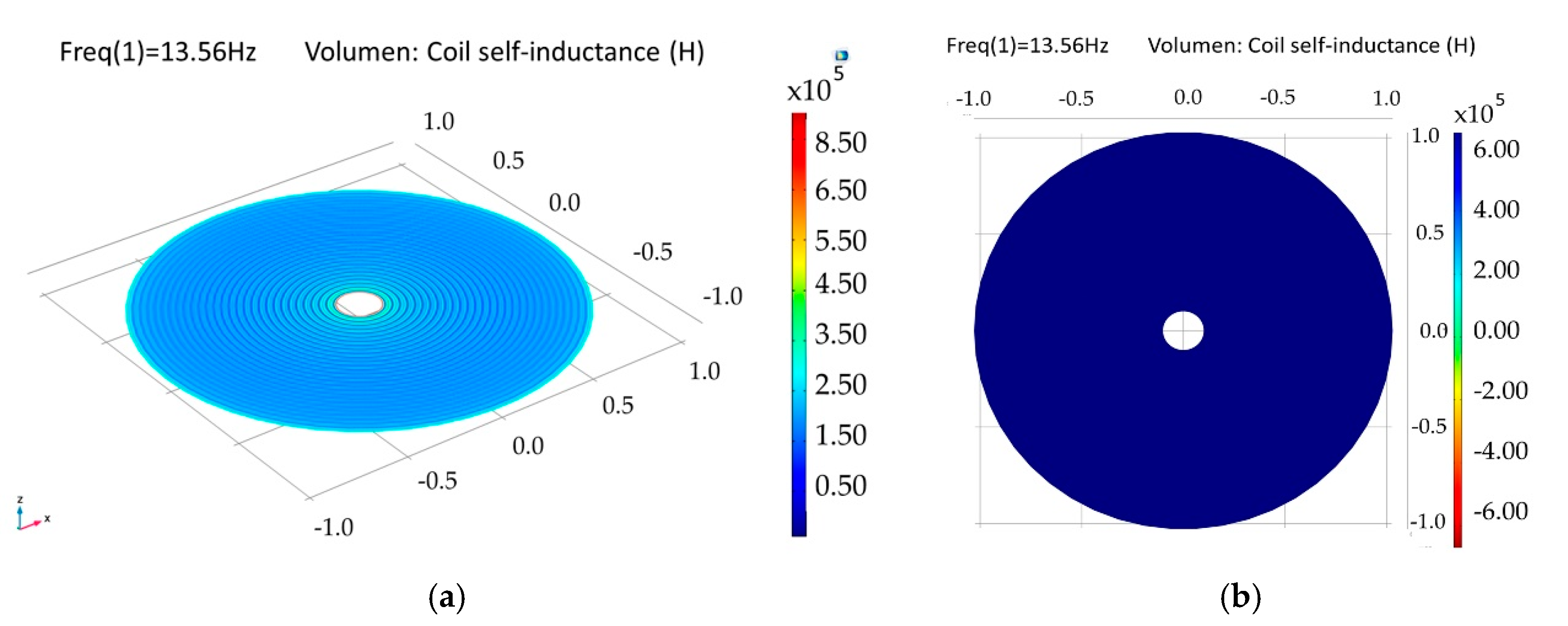
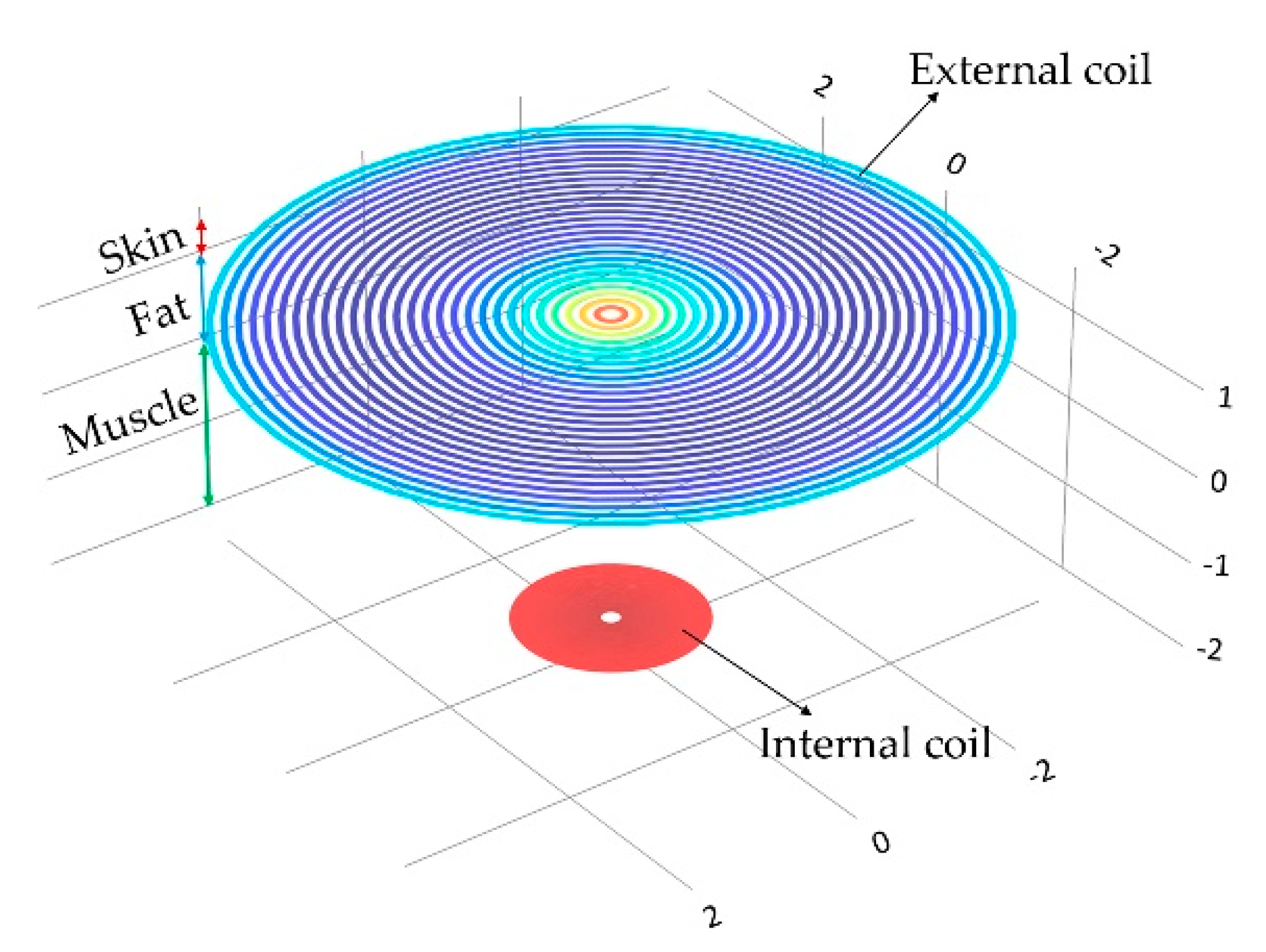
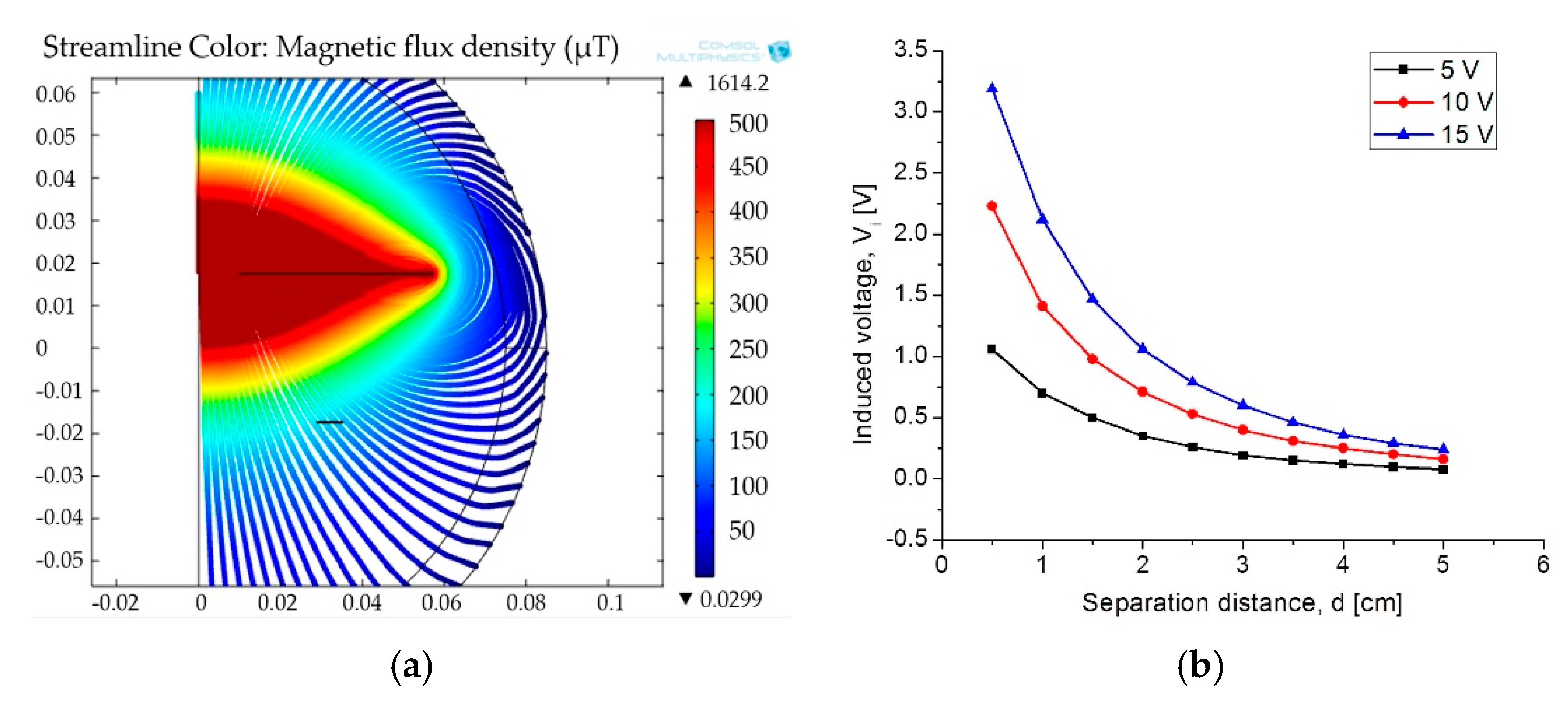
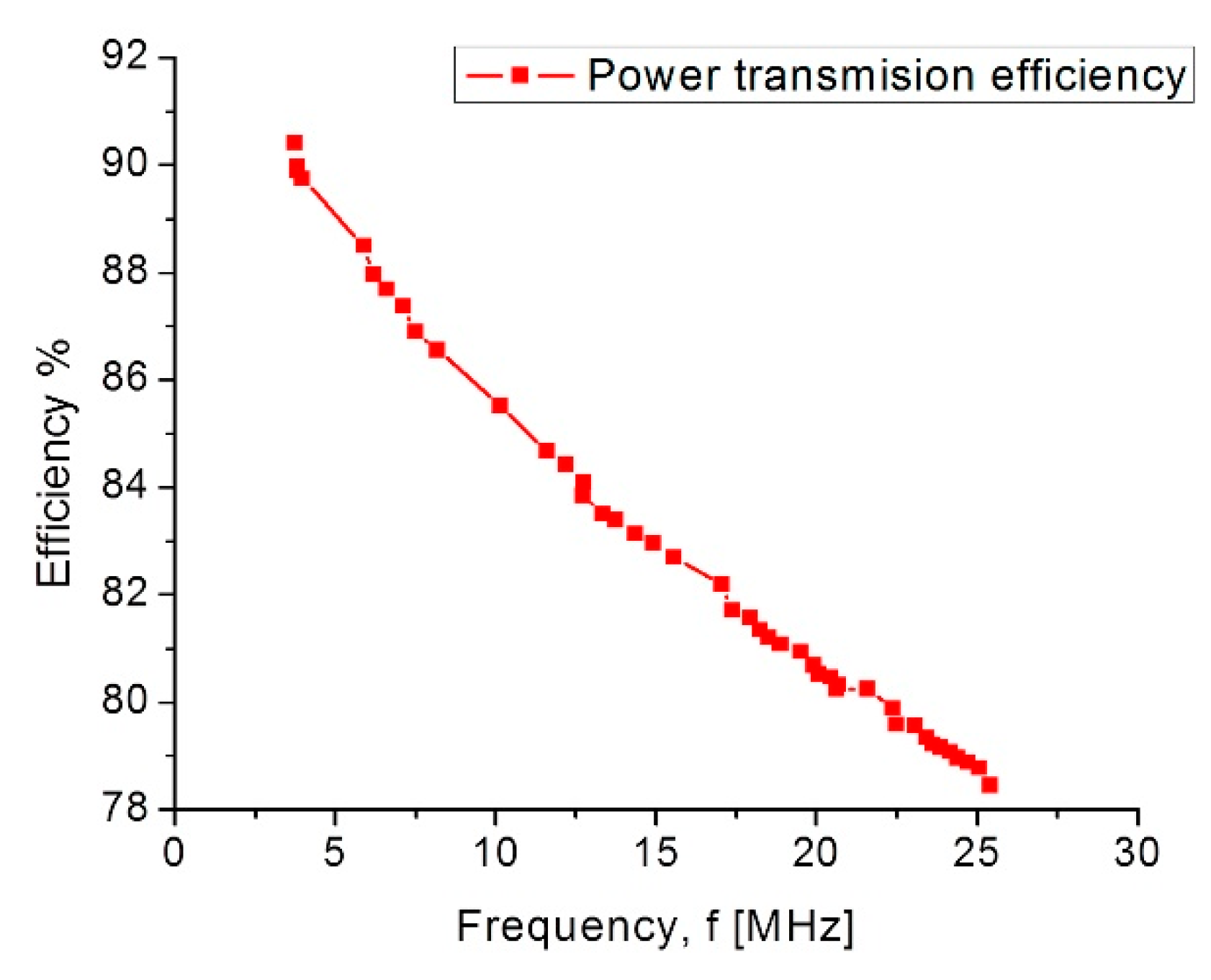
| Parameters | Symbol | Structure 1 | Structure 2 |
|---|---|---|---|
| Contact pressure | PTocuh | 5 mmHg | 40 mmHg |
| Maximum operating pressure | PMax | 200 mmHg | 300 mmHg |
| Lateral length of the diaphragm | a | 555 µm | 300 µm |
| Thickness of the lower electrode | tElow | 2 µm | 2 µm |
| Thickness of the top electrode | tEtop | 1 µm | 1 µm |
| Thickness of the biocompatible film | tBio | 1.5 µm | 1.5 um |
| Air gap | Wmax | 1.5 µm | 1.5 µm |
| Oxide thickness | toxi | 0.2 µm | 0.2 µm |
| Sensor capacitance at zero pressure | Cp0 | 1.9 pF | 0.51 pF |
| Quantity | Symbol | Internal Coil | External Coil |
|---|---|---|---|
| Internal diameter | Din | 2 mm | 2 mm |
| External diameter | Dout | 2 cm | 8 cm |
| Width of the metal lines | w | 160 µm | 700 µm |
| Space between turns | s | 160 µm | 700 µm |
| Thickness of the metal lines | h | 2 µm y 1 µm | 35 µm |
| Number of turns | N | 28 each loop | 27 |
| Length | l | 1.14 m | 1.7 m |
| Operating frequency | fs | 13.56 MHz | |
| Self-Inductance | L | 20.05 µH | 21.29 µH |
| Electric resistance | R | 309 Ω | 4 Ω |
| Quality factor | Q | 8 | 591 |
| Load resistance | Rload | 3 kΩ | --- |
| Radiation distance | X | 3.5 cm | |
| Coupling coefficient | k | 0.054 | |
| Mutual inductance | M | 2.5 µH | |
| Power transmission efficiency | η | 90% | |
| Parameters | Lower Loop | Upper Loop | Binding |
|---|---|---|---|
| Electrical resistance | 77 Ω | 158 Ω | 259 Ω |
| Self-inductance | 6.68 µH | 6.68 µH | 21.12 µH |
| Quality Factor | 17 | 8.3 | 9.1 |
| Internal coupling factor 1 | 0.99 | ||
| Internal mutual inductance 1 | 6.67 µH | ||
| Model | Thickness (cm) | Conductivity (Sm−1) | Relative Permittivity | Wavelength (m) |
|---|---|---|---|---|
| Dry skin | 0.5 | 0.23802 | 285.25 | 2.26 |
| Wet skin | 0.38421 | 177.13 | 2.87 | |
| Fat | 1 | 0.030354 | 11.827 | 11.11 |
| Muscle | 2 | 0.62818 | 138.44 | 3.24 |
| Parameters | Symbol | Value |
|---|---|---|
| Resonance frequency | 13.56 MHz | |
| Mutual inductance | 3.38 µH | |
| Magnetic flux density | 150 µT | |
| Coupling efficiency | 0.054 | |
| Radiation distance | 3.5 cm | |
| Power transmission efficiency | 90.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Sebastián, N.; Díaz-Alonso, D.; Renero-Carrillo, F.J.; Villa-Villaseñor, N.; Calleja-Arriaga, W. Design and Simulation of an Integrated Wireless Capacitive Sensors Array for Measuring Ventricular Pressure. Sensors 2018, 18, 2781. https://doi.org/10.3390/s18092781
Hernández-Sebastián N, Díaz-Alonso D, Renero-Carrillo FJ, Villa-Villaseñor N, Calleja-Arriaga W. Design and Simulation of an Integrated Wireless Capacitive Sensors Array for Measuring Ventricular Pressure. Sensors. 2018; 18(9):2781. https://doi.org/10.3390/s18092781
Chicago/Turabian StyleHernández-Sebastián, Natiely, Daniela Díaz-Alonso, Francisco Javier Renero-Carrillo, Noé Villa-Villaseñor, and Wilfrido Calleja-Arriaga. 2018. "Design and Simulation of an Integrated Wireless Capacitive Sensors Array for Measuring Ventricular Pressure" Sensors 18, no. 9: 2781. https://doi.org/10.3390/s18092781
APA StyleHernández-Sebastián, N., Díaz-Alonso, D., Renero-Carrillo, F. J., Villa-Villaseñor, N., & Calleja-Arriaga, W. (2018). Design and Simulation of an Integrated Wireless Capacitive Sensors Array for Measuring Ventricular Pressure. Sensors, 18(9), 2781. https://doi.org/10.3390/s18092781





