Abstract
The coupled cluster based linear response theory which is applicable to the direct calculation of atomic and molecular properties are presented and applied to compute the ionization potentials and excitation energies of light and moderately heavy atoms. The effect of electron correlation on the ground and excited states is studied using Hartree-Fock, Dirac-Fock and approximate two-component relativistic spinors.
Keywords:
Standard Model; Model space; Kinetic balance; Variational collapse; HF; DF; RESC; CCM and CCLRT 1 Introduction
The study of physical and chemical processes in atomic and molecular systems containing heavy elements is of great importance both experimentally and theoretically. Aside from their obvious relevance to understanding the chemistry of compounds containing heavy atoms, these studies can provide a quantitative estimate of relativistic contributions, kinematic effects, and a probe for physics that departs from the predictions of the standard model. The twin facts that heavy atom compounds contain many electrons and that the behavior of these electrons must be treated relativistically introduce severe impediments to accurate theoretical treatments of systems con-taining heavy atoms. Rigorous relativistic electronic structure methods begin by forgoing the Schro¨dinger equation in favor of the Dirac equation. The concomitant size of the matrices to be manipulated and the number of two-electron integrals to be evaluated in the Dirac equation have forced the introduction of various approximate method to describe the electronic structure of heavy atom polyatomics by either restricting the number of electrons to be treated explicitly or by converting the relativistic problem into a combination of a non-relativistic many electron problem, a perturbative treatment of the relativistic corrections, and/or both.
The most widely used approximate relativistic scheme for describing heavy atom systems is the effective core potential (ECP) method, where the core electrons are represented by suitable functions and where only the valence electrons are treated explicitly. Recently Motegi et al. have proposed a somewhat less approximate relativistic scheme (RESC) [1] for generating relativistic spinors. The RESC method proceeds by eliminating the small component portion of the relativistic Hamiltonian from the four-component Dirac equation through a suitable transformation.
In this article, we illustrate the efficacy of the RESC scheme by comparing the ionization poten-tials (IPs) and excitation energies (EEs) obtained from the coupled cluster based linear response theory (CC-LRT) [2,3,4,5,6,7,8,9,10] with Hartree-Fock, RESC, and four-component Dirac-Fock orbitals.
2 Coupled Cluster Based Linear Response Theory
In CC-LRT approach, one begins with the ground state function |Ψ0⟩, written in the coupled cluster form
where the cluster operator T consists of various hole-particle excitations from the closed-shell function φ0, taken as the vacuum. The ionized/excited state Ψk bare generated from the ground state by the action of ionization/ excitation operator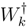 
, and the corresponding energy ωk are obtained from an equation of the form [2,3,4,5,6,7]:
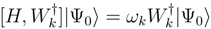
|Ψ0⟩ = exp(T)|φ0⟩
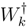, and the corresponding energy ωk are obtained from an equation of the form [2,3,4,5,6,7]:
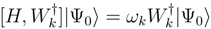
In non-orthogonally spin-adapted formulation of CC-LRT, both T and 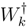are expressed as a linear combination of various spin-free hole-particle excitations operators, written in normal-order. Thus, for example, for single and double excitations, one has operators like
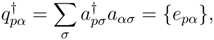and
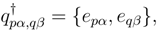respectively.
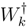are expressed as a linear combination of various spin-free hole-particle excitations operators, written in normal-order. Thus, for example, for single and double excitations, one has operators like
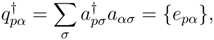
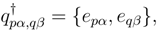
The curly brackets in eqs. (3) and (4) stand for normal ordering. The labels α, β and p, q signify hole and particle orbitals, respectively, and σ denotes spin labels. The operators T and 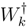are expressed as
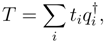and
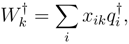respectively, for excitation process. The cluster operators 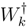s for ionization and electron attach-ment processes are expressed as
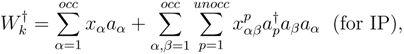and
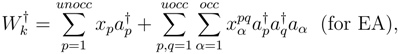respectively.
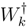are expressed as
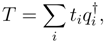
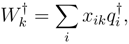
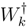s for ionization and electron attach-ment processes are expressed as
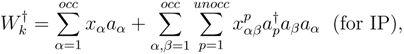
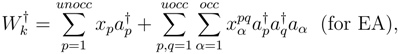
Since T and 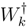commute, premultiplying eq. (2) by exp(−T) we get the following equation of motion (EOM):
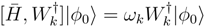with
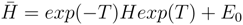where E0 is the ground state energy. Projecting eq.(9) on to the biorthogonal space 
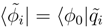, we get
where
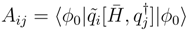and Xk denotes the columns of xk. Since T is anti-Hermitian, eq. (10) leads to a non-Hermitian operator 
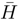and the associated matrix A.
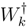commute, premultiplying eq. (2) by exp(−T) we get the following equation of motion (EOM):
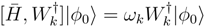
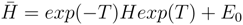
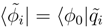, we get
AXk = ωk Xk,
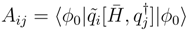
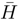and the associated matrix A.3 Results
In the present work, we have used the truncation scheme T = T1 + T2 for computing Ψ0. The excited/ionized states Ψk are generated by the action of 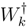where the excitation/ionization operator 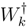is truncated at 2h-2p level for EE, 2h-1p for IP, and 1h-2p for EA processes, respectively. To avoid variational collapse in the DF procedure, we impose kinetic balance condition and relativistic boundary conditions on the basis spinors. Since the expression for kinetic balance condition is simple for uncontracted Gaussian/Slater functions, we use uncontracted Gaussian basis to gener-ate the Hartree-Fock(HF), RESC and Dirac-Fock (DF)orbitals. While the HF and RESC orbitals are obtained from GAMESS [11] code, the DF orbitals are generated from the code developed in our laboratory. Note that in the present RESC scheme, only the one electron integral corrections are added. A more accurate treatment can be achieved by means of relativistically averaged basis set which incorporates the two- electron integral corrections. However, the RESC corrections to two-electron is beyond the scope of the present work.
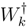where the excitation/ionization operator 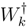is truncated at 2h-2p level for EE, 2h-1p for IP, and 1h-2p for EA processes, respectively. To avoid variational collapse in the DF procedure, we impose kinetic balance condition and relativistic boundary conditions on the basis spinors. Since the expression for kinetic balance condition is simple for uncontracted Gaussian/Slater functions, we use uncontracted Gaussian basis to gener-ate the Hartree-Fock(HF), RESC and Dirac-Fock (DF)orbitals. While the HF and RESC orbitals are obtained from GAMESS [11] code, the DF orbitals are generated from the code developed in our laboratory. Note that in the present RESC scheme, only the one electron integral corrections are added. A more accurate treatment can be achieved by means of relativistically averaged basis set which incorporates the two- electron integral corrections. However, the RESC corrections to two-electron is beyond the scope of the present work.The basis sets used in the computation of IPs and EEs are displayed in Table 1. Figure 1 plots the absolute difference in the ground state energy obtained from CC calculation using DF, HF, and RESC orbitals with respect to atomic number (Z), i.e.,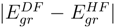 
and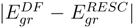 
versus the atomic number. The present work shows that the ground energy obtained from HF orbital is less than that obtained from the RESC and DF orbitals. Figure 1 also demonstrates that while 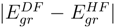increases with increasing atomic number, 
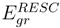remains quite close to 
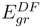over the entire range. The fact that 
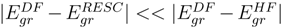for the ground state clearly demonstrates that dominant relativistic corrections can be incorporated through RESC scheme.
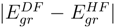and 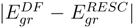versus the atomic number. The present work shows that the ground energy obtained from HF orbital is less than that obtained from the RESC and DF orbitals. Figure 1 also demonstrates that while 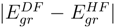increases with increasing atomic number, 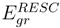remains quite close to 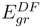over the entire range. The fact that 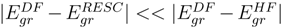for the ground state clearly demonstrates that dominant relativistic corrections can be incorporated through RESC scheme.Table 2 compares the ionization potentials (IPs) obtained from CCLRT-IP method using HF, DF, and RESC orbitals with the experiment [12]. Table 2 shows that the average deviation (absolute) of the computed IPs with HF, RESC and DF orbitals are 1.269%, 0.576% and 0.552%, respectively. Table 2 further demonstrates that the accuracy of computed IPs with HF orbitals deteriorates with increasing atomic number (Z) as anticipated. The fact that IPs obtained using RESC orbitals are quite close to those obtained from DF orbitals suggests that relativistic effects can be introduced efficiently via RESC scheme.
Table 1.
Basis set used in the computation IPs and EEs.
| System | Basis set | Ref. |
| Be | 16s9p5d1f | [15] |
| B | 16s10p5d1f | [15] |
| C | 14s10p4d1f | [15] |
| Ne | 13s9p5d2f | [16] |
| Ar | 20s13p4d2f | [17] |
| Rb | 15s12p8d2f | [18] |
| Cs | 15s12p8d2f | [18] |
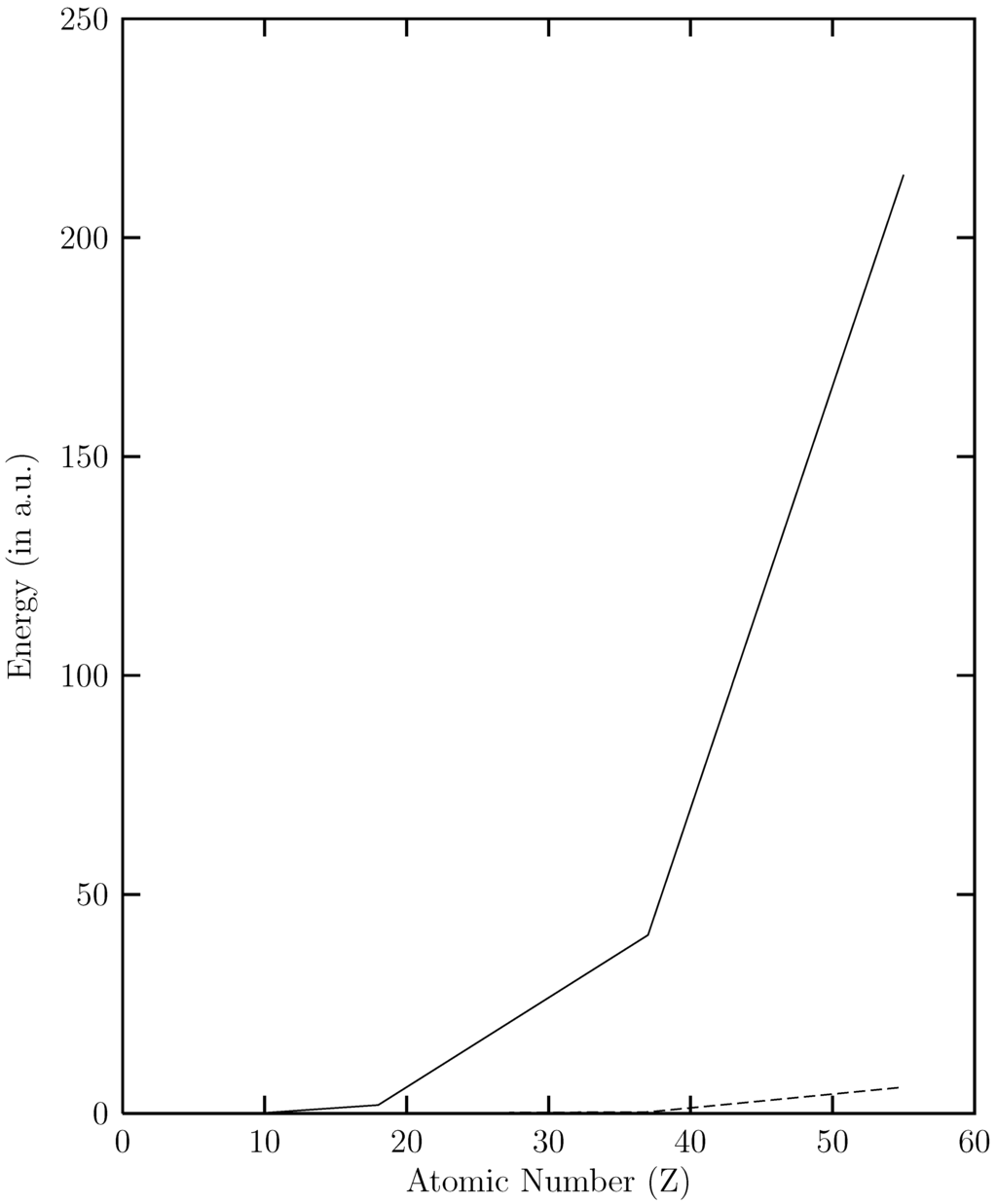
Figure 1.
Plot of 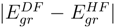(solid line) and 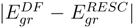(dotted line) versus the atomic number (Z).
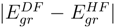(solid line) and 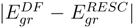(dotted line) versus the atomic number (Z).
Table 2.
Ionization Potentials (in eV) of Be, B, C++, Ne, Ar, Rb, and Cs obtained from CCLRT-IP method using Hartree-Fock (HF), RESC, and Dirac-Fock (DF) orbitals.
| System | CCLRT | Experiment [12] | ||
| HF | RESC | DF | ||
| Be | 9.315 | 9.316 | 9.322 | 9.322 |
| B | 8.222 | 8.220 | 8.223 | 8.298 |
| B+ | 25.134 | 25.140 | 25.146 | 25.155 |
| C+ | 24.292 | 24.289 | 24.289 | 24.383 |
| Ne | 21.240 | 21.262 | 21.633 | 21.564 |
| Ar | 15.656 | 15.638 | 15.898 | 15.759 |
| Rb | 4.074 | 4.141 | 4.185 | 4.177 |
| Cs | 3.735 | 3.889 | 3.960 | 3.894 |
| Average Error | 1.269% | 0.576% | 0.552% | |
Table 3 compares the CCLRT valence electron removal energies of B, C+, Rb, and Cs atom with the experiment [12]. It is evident from Table 3 that the average error in computed valence electron removal energies with HF orbitals is large compared to those obtained from RESC and DF orbitals. Table 3 also indicates that the computed valence electron removal energies of C+(2P1/2), Rb(2S1/2), and Cs(2S1/2) states are quite off from the experiment. However, this is purely a basis inadequacy problem. Using larger basis (with more d and f) this difference can be reduced significantly [13]. Since, the main motivation of this work is to assess the relative accuracy of different choice of orbitals, we use limited but same basis for all three cases.
In Table 4, we compare the excitations energies of Be, B+, and C++ obtained from CCLRT-EE method using HF and RESC orbitals with the experiment. Table 4 shows that the average and RMS errors are slightly less for EE obtained from the HF orbitals than those computed with RESC orbitals. Since the systems investigated here are not heavy, it is difficult at this stage to assess the efficacies of the RESC scheme. However, based on the previous results (displayed in Table 2 and Table 3), we strongly believe that the accuracy of estimated EEs from HF orbitals will deteriorate with increasing atomic number. Moreover, studies on alkali metal halides (NaCl, NaBr, KCl, RbCl etc.) suggest that the RESC orbitals offers more accurate estimate of ionization potentials, electron affinities, and dissociation energies than the HF orbitals [14] for systems containing heavy elements.
Table 3.
Valence electron removal energies (in cm−1) of B, C+, Rb, and Cs obtained from CCLRT-EA method using Hartree-Fock (HF), RESC, and Dirac-Fock (DF) orbitals.
| System | Dominant | CCLRT | Experiment [12] | ||
| Configuration | HF | RESC | DF | ||
| B | [Be]2p(2P3/2) | 66322 | 66946 | ||
| [Be]3s(2S1/2) | 26787 | 26790 | 26723 | 26890 | |
| [Be]4s(2S1/2) | 11829 | 11830 | 11789 | 11921 | |
| C+ | [Be]2p(2P3/2) | 195903 | 196723 | ||
| [Be]3p(2P1/2) | 64551 | 64934 | |||
| [Be]3p(2P3/2) | 64786 | 64783 | 64780 | 64923 | |
| Rb | [Kr]6s(2S1/2) | 10963 | 11242 | 11260 | 13557 |
| [Kr]5p(2P1/2) | 20804 | 21112 | |||
| [Kr]5p(2P3/2) | 20481 | 20500 | 20577 | 20874 | |
| Cs | [Xe]7s(2S1/2) | 9067 | 9854 | 9960 | 12872 |
| [Xe]6p(2P1/2) | 19741 | 20229 | |||
| [Xe]6p(2P3/2) | 19215 | 19265 | 19309 | 19674 | |
| Average Error | 7.754% | 6.534% | 6.397% | ||
4 Discussion
The coupled cluster based linear response theory is presented and applied to compute ionization potentials and excitation energies for light atoms. In this work, we investigate the effect of electron correlation on the ground and excited states using HF, DF and RESC orbitals. The present work demonstrates that dominant relativistic corrections can be incorporated through RESC scheme. The present work further demonstrates that for heavy elements accuracy of the properties computed with HF orbitals is much less than those obtained from DF and RESC orbitals. Since the two-electron integral corrections are not included in the present RESC scheme, comparison between the DF and RESC scheme is not perfect at this stage. A comparative study of DF orbitals versus RESC with relativistically averaged basis set which incorporates the two-electron integral corrections will be more appropriate. Research in this direction is in progress.
Table 4.
Singlet state excitation energies (in cm−1) of Be, B+ and C++ obtained from CCLRT-EE using Hartree-Fock (HF) and RESC orbitals.
| System | Dominant | CCLRT | Experiment [12] | |
| Configuration | HF | RESC | ||
| Be | [He]2s3s(1S) | 54657 | 54665 | 54662 |
| [He]2s2p(1P ) | 42806 | 42819 | 42565 | |
| [He]2s3p(1P ) | 60418 | 60429 | 60187 | |
| [He]2s4s(1S) | 65222 | 65230 | 65245 | |
| [He]2s5s(1S) | 70107 | 70115 | 69332 | |
| B+ | [He] 2s2p(1P ) | 73993 | 74052 | 73397 |
| [He] 2p2(1D) | 104338 | 104449 | 102362 | |
| [He] 2p2(1S) | 129283 | 129368 | 127622 | |
| [He] 2s3s(1S) | 138333 | 138396 | 137622 | |
| [He] 2s3p(1P ) | 144079 | 144131 | 144103 | |
| [He] 2p2(1D) | 156856 | 156907 | 154687 | |
| [He] 2s4s(1S) | 167801 | 167845 | 167936 | |
| [He] 2s4p(1P ) | 171322 | 171374 | 170591 | |
| C++ | [He] 2s2p(1P ) | 103254 | 103411 | 102351 |
| [He] 2p2(1D) | 148668 | 148966 | 145875 | |
| [He] 2s3s(1S) | 185593 | 185883 | 182520 | |
| Average Error | 0.82% | 0.87% | ||
References
- Nakajima, T.; Suzumura, T.; Hirao, K. Chem. Phys. Letts. 1999, 304, 271.Suzumura, T.; Nakajima, T.; Hirao, K. Int. J. Quantum Chem. 1999, 75, 757. [CrossRef]Nakajima, T.; Koga, K.; Hirao, H. J. Chem. Phys. 2001, 112, 10142.Motegi, K.; Nakajima, T.; Hirao, K.; Seijo, L. J. Chem. Phys. 2001, 114, 6000.
- Mukherjee, D.; Mukherjee, P.K. Chem. Phys. 1979, 37, 327.
- Ghosh, S.; Bhattacharyya, S.N.; Mukherjee, D. Chem. Phys. 1982, 72, 961.
- Adnan, S.S.Z.; Bhattacharyya, S.N.; Mukherjee, D. Mol. Phys. 1982, 39, 519.
- Adnan, S.S.Z.; Bhattacharyya, S.N.; Mukherjee, D. Chem. Phys. Letts. 1982, 85, 204.
- Mukhopadhayay, S.; Chaudhuri, R.K.; Mukhopadhyay, D.; Mukherjee, D. Chem. Phys. Letts. 1990, 173, 181.
- Kundu, B.; Mukherjee, D. Chem. Phys. Letts. 1991, 179, 468. [CrossRef]
- Monkhorst, H.J. Int. J. Quantum Chem. 1977, S11, 421.Dalgaard, E.; Monkhorst, H.J. Phys. Rev. 1983, A 28, 1217. [CrossRef]
- Sekino, H.; Bartlett, R.J. Int. J. Quantum Chem. 1984, S 18, 255. [CrossRef]Greetsen, J.; Rittby, M.; Bartlett, R.J. Chem. Phys. Lett. 1989, 164, 57.
- Koch, H.; Jensen, H.J.A.; Jorgensen, P.; Helgaker, T. J. Chem. Phys. 1990, 93, 3345.Koch, H.; Jorgensen, P. J. Chem. Phys. 1990, 93, 3333.
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; Windus, T.L.; Dupuis, M.; Montgomery, J.A. J. Comput. Chem. 1993, 14, 1347. [CrossRef]
- Moore, C.E. Atomic Energy Levels. In Natl. Bur. Standard, Ref. Data Ser., Natl. Bur. Stand.; (U.S.) Circ. No. 35; U.S. GPO: Washington, D. C., 1971; Vol 1. [Google Scholar]
- Chaudhuri, R.K.; Sahoo, B.K.; Das, B.P.; Merlitz, H.; Mahapatra, U.S.; Mukherjee, D. J. Chem. Phys. (in press).
- Nayak, M.K.; Chaudhuri, R.K. (to be submitted).
- Maroulis, G.; Bishop, D.M. J. Phys. B 1985, 18, 3653. [CrossRef]
- Maroulis, G.; Bishop, D.M. Chem. Phys. Letts. 1985, 114, 182. [CrossRef]
- Schmidt, M.W.; Ruedenberg, K. J. Chem. Phys. 1979, 71, 3951. Exponents for the Ar polarization functions are constructed from their p exponents.
- Godbout, N.; Salahub, D.R.; Andzelm, J.; Wimmer, E. Can. J. Chem. 1992, 70, 560. Rb basis is generated by adding exponents to Godbout et al. basis set. The same basis set is used for Cs atom.
©2003 by MDPI, Basel, Switzerland. Reproduction for noncommercial purposes permitted.