Abstract
We construct a 2-categorical extension of the relative entropy functor of Baez and Fritz, and show that our construction is functorial with respect to vertical morphisms. Moreover, we show such a ‘2-relative entropy’ satisfies natural 2-categorial analogues of convex linearity, vanishing under optimal hypotheses, and lower semicontinuity. While relative entropy is a relative measure of information between probability distributions, we view our construction as a relative measure of information between channels.
Keywords:
2-category; Bayesian inference; discrete memoryless channel; functor; information theory; relative entropy; synthetic probability MSC:
primary 94A17; secondary 18A05; 62F15
1. Introduction
Let X and Y be finite sets which are the input and output alphabets of a discrete memoryless channel with probability transition matrix , representing the probability of the output y given the input x. Every input x then determines a probability distribution on Y which we denote by , so that for all and . The channel together with the choice of a prior distribution p on X will be denoted , and such data then determine a distribution on given by . Given a second channel with prior distribution q on X, the chain rule for relative entropy says that the relative entropy is given by
As the RHS of (1) involves precisely the datum of the channels f and g together with the prior distributions p and q, we view the quantity as a relative measure of information between the channels and . In particular, since from a Bayesian perspective may be thought of as the amount of information gained upon discovering that the assumed prior distribution p is actually q, it seems only natural to think of as the amount of information gained upon learning that the assumed channel is actually the channel .
To make such a Bayesian interpretation more precise, we build upon the work of Baez and Fritz [1], who formulated a type of Bayesian inference as a process (including a set of conditional hypotheses on the outcome of the process), which given a prior distribution p on X yields distributions r on Y and q on X in such a way that the relative entropy has an operational meaning as a quantity associated with a Bayesian updating with respect to the process . (Here, X may be thought of more generally as the set of possible states of some system to be measured, while Y may be thought of as the possible outcomes of the measurement.) Baez and Fritz then proved that up to a constant multiple, the map on such processes given by
is the unique map satisfying the following axioms.
- Functoriality: Given a composition of processes ,
- Convex Linearity: Given a collection of processes indexed by the elements of a finite probability space ,
- Vanishing Under Optimal Hypotheses: If the conditional hypotheses associated with a process are optimal, then
- Continuity: The map is lower semi-continuous.
While Baez and Fritz facilitated their exposition using the language of category theory [2], knowing that a category consists of a class of objects together with a class of composable arrows (i.e., morphisms) between objects is all that is needed for an appreciation of their construction. From such a perspective, the aforementioned processes are morphisms in a category , and the relative entropy assignment given by (2) is then a map from morphisms in to .
In what follows, we elevate the construction of Baez and Fritz to the level of 2-categories (or more precisely, double categories), whose 2-morphisms may be viewed as certain processes between processes, or rather, processes which connect one channel to another. In particular, in Section 2, we formally introduce the category introduced by Baez and Fritz, and then, in Section 3, we review their functorial characterization of relative entropy using . In Section 4, we construct a category which is a 2-level extension of , and in Section 5, we define a convex structure on . In Section 6, we define a relative measure of information between channels which we refer to as conditional relative entropy, and show that it is convex linear and functorial with respect to vertical morphisms in . The conditional relative entropy is then used in Section 7 to define a relative entropy assignment on 2-morphisms via the chain rule as given by (1) (for more on the chain rule for relative entropy one may consult Chapter 2 of [3]). Moreover, we show that such a ‘2-relative entropy’ satisfies the natural 2-level analogues of axioms 1–4 as satisfied by the relative entropy map RE.
As abstract as a relative entropy of processes between processes may seem, Shannon’s Noisy Channel Coding Theorem—which is a cornerstone of information theory—is essentially a statement about transforming a noisy channel into a noiseless one via a sequence of codings and encodings. From such a viewpoint, information theory is fundamentally about processes (i.e., a sequence of codings and encodings), between processes (i.e., channels), and it is precisely this viewpoint with which we will proceed. Furthermore, there is a growing recent interest in axiomatic and categorical approaches to information theory [4,5,6,7,8,9,10,11,12,13], and the present work is a direct outgrowth of such activity.
2. The Category
In this section, we introduce the first-level structure of interest, which is the category introduced by Baez and Fritz [1]. Though we use the language of categories, knowing that a category consists of a class of composable arrows between a class of objects is sufficient for the comprehension of all categorical notions in this work.
Definition 1.
Let X and Y be finite sets. Adiscrete memoryless channel(or simplychannelfor short) associates every with a probability distribution on Y. In such a case, the sets X and Y are referred to as theset of inputsandset of outputsof the channel f, respectively, and is the probability of receiving the output y given the input x, which will be denoted by .
Definition 2.
If and are channels, then the composition is given by
for all and .
Remark 1.
If is a channel such that for every there exists a with , then such a y is necessarily unique given x, and as such, f may be identified with a function . In such a case, we say that the channel f ispure(ordeterministic), and from here on, we will not distinguish the difference between a pure channel and the associated function from its set of inputs to its set of outputs.
Definition 3.
If ★ denotes a set with a single element, then a channel is simply a probability distribution on X, and, in such a case, we will use to denote the probability of x as given by p for all . The pair is then referred to as a finite probability space.
Notation 1.
The datum of a channel together with a prior distribution on its set of inputs will be denoted .
Definition 4.
Let denote the category whose objects are finite probability spaces, and whose morphisms consist of the following data:
- A function such that ;
- A channel such that . In other words, is astochastic sectionof .
A morphism in is then summarized by a diagram of the form
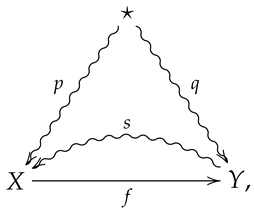 and a composition of morphisms in is obtained via function composition and composition of stochastic sections. In such a case, it is straightforward to show that a composition of stochastic sections is a stochastic section, etc. The morphism corresponding to diagram (3) will often be denoted .
and a composition of morphisms in is obtained via function composition and composition of stochastic sections. In such a case, it is straightforward to show that a composition of stochastic sections is a stochastic section, etc. The morphism corresponding to diagram (3) will often be denoted .

Remark 2.
Note that in diagram (3), a straight arrow is used for as f is a function, as opposed to a noisy channel.
Remark 3.
The operational interpretation of diagram (3) is as follows. The set X is thought of as the set of possible states of the system, and is then thought of as a measurement process, so that Y is then thought of as the set of possible states of some measuring apparatus. The stochastic section is then thought of as a set of hypotheses about the state of the system given a state of the measuring apparatus. In particular, is thought of as the probability the system was in state x given the state y of the measuring apparatus.
Definition 5.
If the stochastic section in diagram (3) is such that , then s will be referred to as anoptimal hypothesisfor .
Definition 6.
Let be a finite probability space, and let be a collection of channels with prior distributions indexed by X. Theconvex combinationof with respect to is the channel
where is the channel given by
with prior distribution given by
where is such that . Such a convex combination will be denoted .
3. The Baez and Fritz Characterization of Relative Entropy
We now recall the Baez and Fritz characterization of relative entropy in .
Definition 7.
Let be a finite probability space, and let
be a collection of morphisms in indexed by X. Theconvex combinationof with respect to is the morphism in corresponding to the diagram
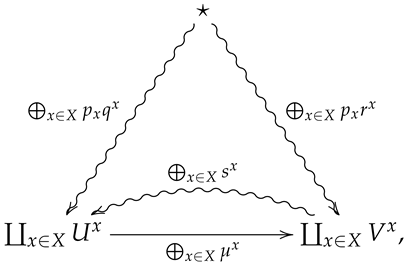 where for all .
where for all .

Definition 8.
Let be a morphism in , and let . Therelative entropyof is the non-negative extended real number given by
where is the relative entropy between the distributions p and r on X.
Definition 9.
Let be a map from the morphisms in to the extended non-negative reals .
- F is said to befunctorialif and only if for every composition of morphisms in we have
- F is said to beconvex linearif and only if for every convex combination of morphisms in we have
- F is said to bevanishing under optimal hypothesesif and only if for every morphism in with s an optimal hypothesis we have
- F is said to belower semicontinuousif and only if for every sequence of morphisms in converging to a morphism we have
Theorem 1
(The Baez and Fritz Characterization of Relative Entropy). Let be the collection of maps from the morphisms in to which are functorial, convex linear, vanishing under optimal hypotheses and lower semicontinuous. Then, the following statements hold.
- 1.
- The relative entropy is an element of ;
- 2.
- If , then for some non-negative constant .
4. The Category
In this section, we introduce the second-level structure of interest, namely, the double category , which is a 2-level extension of .
Definition 10.
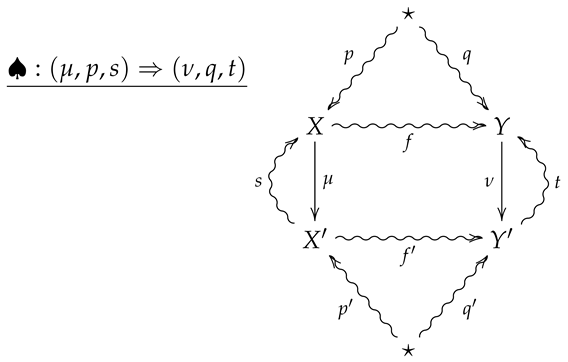
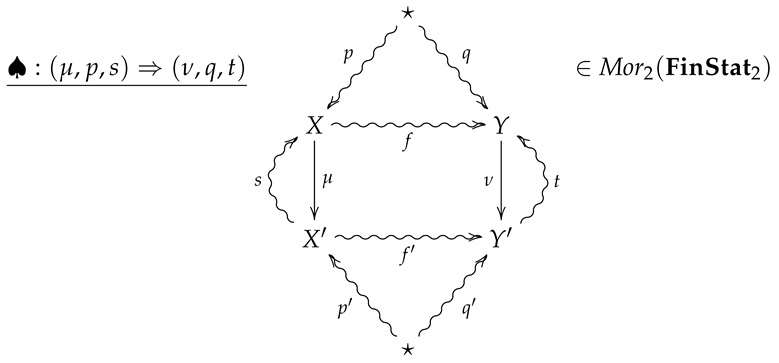
Let denote the 2-category whose objects and 1-morphisms coincide with those of , and whose 2-morphisms are constructed as follows. Given 1-morphisms
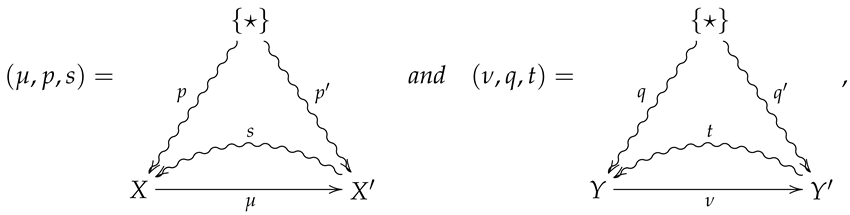 a 2-morphism consists of channels and such that
a 2-morphism consists of channels and such that
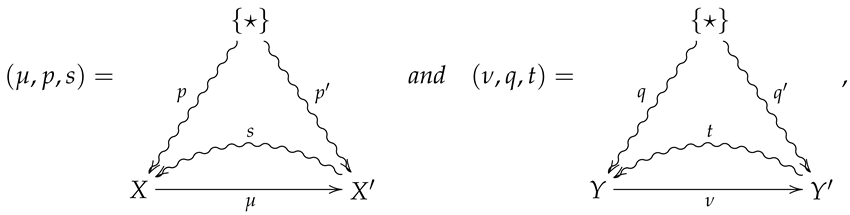
The 2-morphism may then be summarized by the following diagram.

Remark 4.
A crucial point is that in the above diagram, all arrows necessarily commute except for any compositions involving the the outer ‘wings’, s and t. For example, the compositions and need not be equal to p and f, respectively.
Remark 5.
Diagram (5) should be thought of as a flattened out pyramid, whose base is the inner square and whose vertex is obtained by the identification of the upper and lower stars in the diagram.
Remark 6.
For an operational interpretation of a 2-morphism in as given by diagram (5), one may consider X and Y as sample spaces associated with all possible outcomes of experiments and . As the sets X and Y are endowed with prior distributions p and q, the maps and are then random variables with values in and , and the stochastic sections s and t then represent conditional hypotheses about the outcomes of the measurements corresponding to μ and ν. The channels and then represent stochastic processes such that taking the measurement μ followed by results in the same process as first letting X evolve according to f and then taking the measurement ν.
Example 1.
For a real-life scenario which realizes a 2-morphism in , suppose two experimenters Alice and Bob are collaborating on a project to verify predictions of a theory. As such, Alice and her data analyst partner Alicia travel to a mountain in Brazil during a solar eclipse to perform experiments while Bob and and his data-analyst partner Bernie travel to a mountain in Montenegro at the same time for the same purpose. Alice and Bob will then perform experiments in their separate locations and hand their results over to Alicia and Bernie, who will then analyze the data to produce numerical results. At the end of each day, Alice will report her results to Bob over a noisy channel while Alicia will report her results to Bernie over a noisy channel, so that Bob and Bernie may compare their results with Alice and Alicia’s. We then summarize such a scenario with the following 2-morphism in :
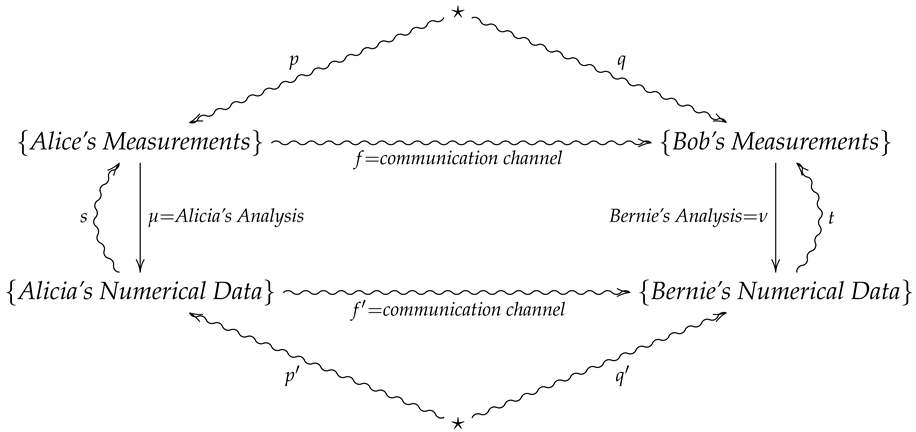

In diagram (6), p and q are assumed prior distributions on Alice and Bob’s measurements, while s and t are empirical conditional distributions on Alice and Bob’s measurements given the data outcomes of Alicia and Bernie’s analysis. Moreover, if the communication channel f is less reliable than , then the composition provides a Bayesian updating for the channel f.
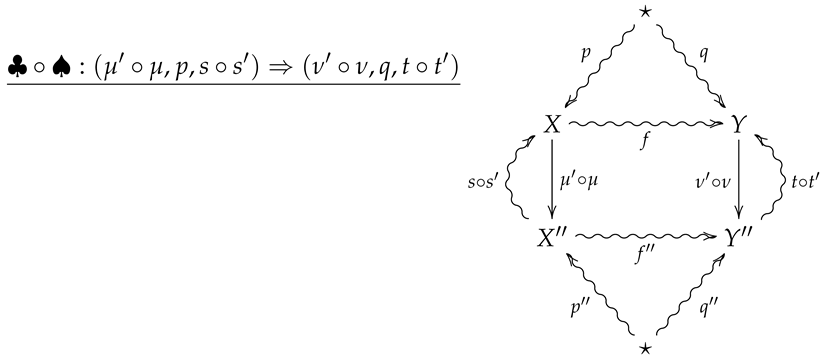
For vertical composition of 2-morphisms, suppose is the 2-morphism summarized by the following diagram.
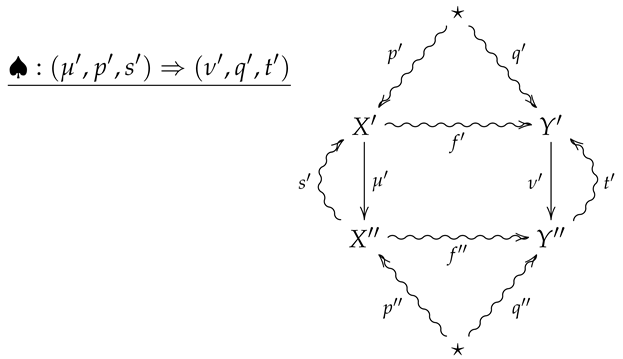
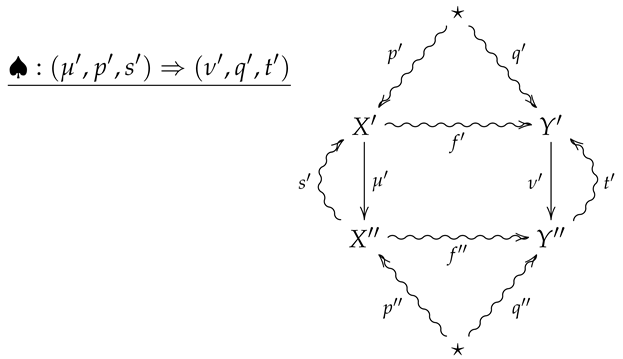
The vertical composition is then summarized by the following diagram.

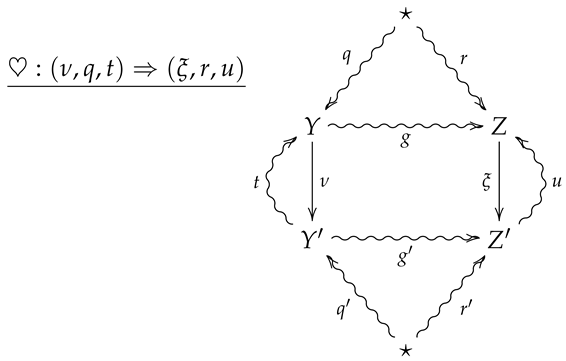
For horizontal composition, let be a 2-morphism summarized by the following diagram.

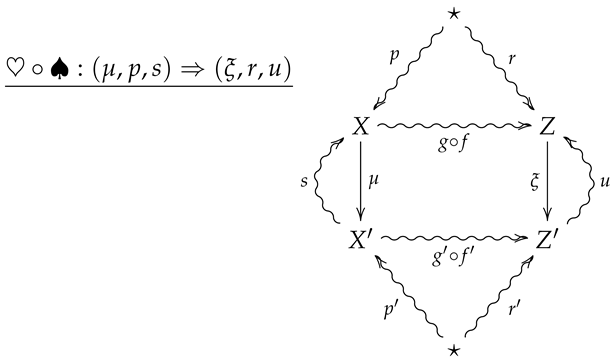
The horizontal composition is then summarized by the following diagram.

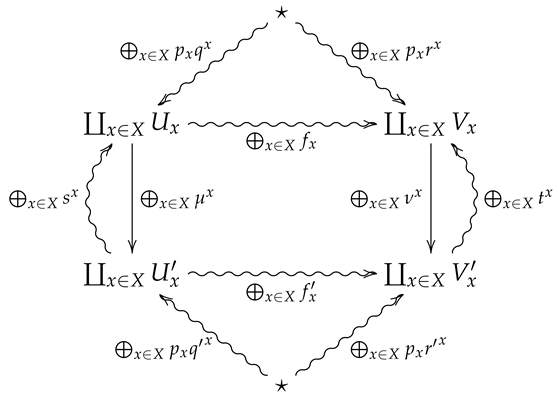
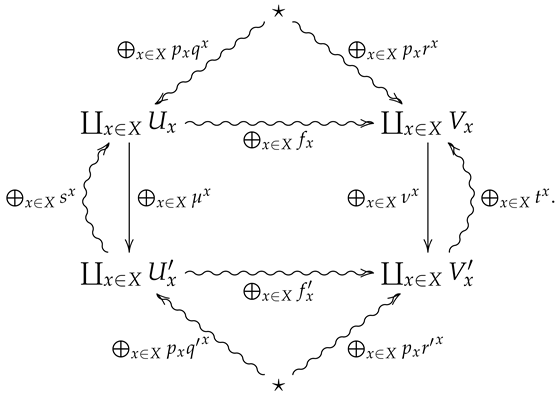
5. Convexity in
We now generalize the convex structure on morphisms in to 2-morphisms in . For this, let be a finite probability space, and let be a collection of 2-morphisms in indexed by X, where is summarized by the following diagram.
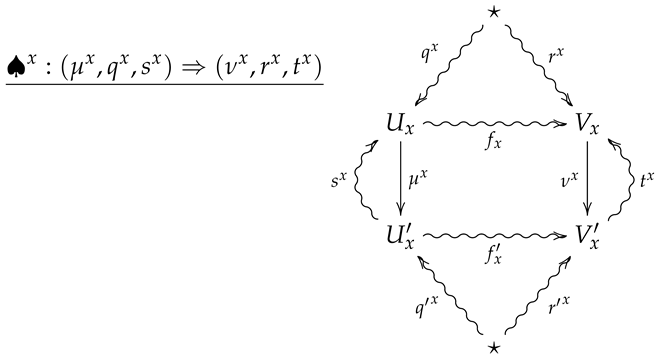

Definition 11.
Theconvex sum is the 2-morphism in summarized by the following diagram.

6. Conditional Relative Entropy in
We now introduce a measure of information associated with 2-morphisms in which we refer to as ‘conditional relative entropy’. The results proved in this section are essentially all lemmas for the results proved in the next section, where we introduce a 2-level extension of the relative entropy map RE, and show that it satisfies the 2-level analogues of the characterizing axioms of relative entropy.
Definition 12.
With every 2-morphism
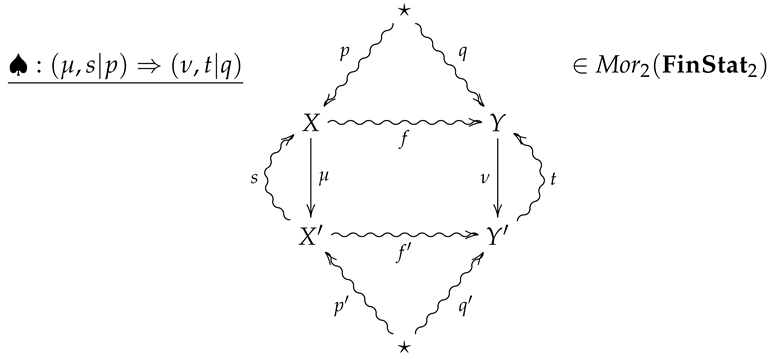 we associate the non-negative extended real number given by
where is the standard relative entropy. We refer to as the conditional relative entropy of ♠.
we associate the non-negative extended real number given by
where is the standard relative entropy. We refer to as the conditional relative entropy of ♠.

Remark 7.
We refer to as conditional relative entropy as its defining formula (7) is structurally similar to the defining formula for conditional entropy. In particular, if is a channel with prior distribution , then the conditional entropy is given by
where is the Shannon entropy of the distribution on Y.
Proposition 1.
Conditional relative entropy in is convex linear, i.e., if is a finite probability space and is a collection of 2-morphisms in indexed by X, then
Proof.
Suppose is summarized by the following diagram
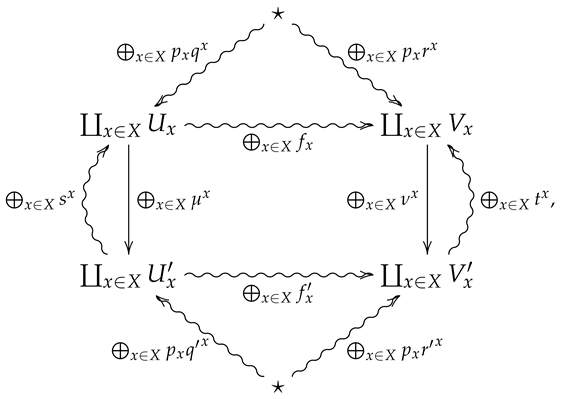 and let , , , and . We then have
as desired. □
and let , , , and . We then have
as desired. □

Theorem 2.
Conditional relative entropy in is functorial with respect to vertical composition, i.e., if is a vertical composition in , then .
Lemma 1.
Let be a composition of channels.
- 1.
- If f is a pure channel, then ;
- 2.
- If g is a stochastic section of a pure channel , then .
Proof.
The statements 1 and 2 follow immediately from the definitions of pure channel and stochastic section. □
Lemma 2.
Let ♠ be a 2-morphism in as summarized by the diagram
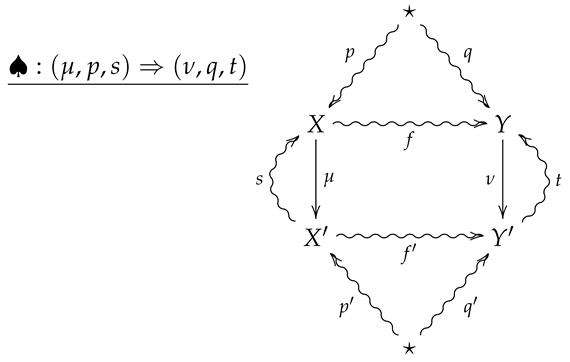 Then,
Then,

- 1.
- for all ;
- 2.
- for all .
Proof.
To prove item (1), let and . Then,
where the third equality follows from Lemma 1 since is a pure channel, and the fourth equality follows also from Lemma 1 since t is a stochastic section of a pure channel. We then have
as desired.
To prove item (2), the condition is equivalent to the equation for all and . In addition, since
and
it follows that , thus, for all and , it follows that for all . As such, we have
as desired. □
Proof of Theorem 2.
Suppose ♠ and ♣ are such that the vertical composition is summarized by the following diagram.
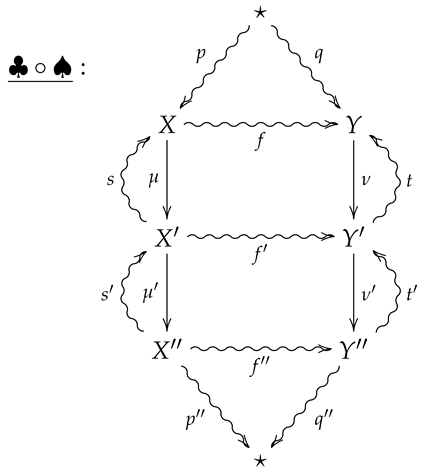 By item (1) in Lemma 2, we then have
and since t is a section of the pure channel , by item (2) of Lemma 1, it follows that for every we have
As such, we have
as desired (the second-to-last equality follows by item (1) of Lemma 2). □
By item (1) in Lemma 2, we then have
and since t is a section of the pure channel , by item (2) of Lemma 1, it follows that for every we have
As such, we have
as desired (the second-to-last equality follows by item (1) of Lemma 2). □

7. Relative Entropy in
In this section, we introduce a 2-level extension of the relative entropy map RE introduced by Baez and Fritz, and show that it satisfies the natural 2-level analogues of functoriality, convex linearity, vanishing under optimal hypotheses, and lower semicontinuity.
Definition 13.
With every 2-morphism
 we associate the non-negative extended real number given by
which we refer to as the 2-relative entropy of ♠. We note that the quantity appearing on the RHS of (8) is the relative entropy associated with the morphism in , so that
where is the standard relative entropy.
we associate the non-negative extended real number given by
which we refer to as the 2-relative entropy of ♠. We note that the quantity appearing on the RHS of (8) is the relative entropy associated with the morphism in , so that
where is the standard relative entropy.

Proposition 2.
2-Relative entropy is convex linear, i.e., if is a finite probability space and is a collection of 2-morphisms in indexed by X, then
Proof.
Suppose is summarized by the following diagram
 By Theorem 1, we know that the relative entropy RE is convex linear over 1-morphisms in , and by Proposition 1, we know conditional relative entropy is convex linear over 2-morphisms in , thus
We then have
as desired. □
By Theorem 1, we know that the relative entropy RE is convex linear over 1-morphisms in , and by Proposition 1, we know conditional relative entropy is convex linear over 2-morphisms in , thus
We then have
as desired. □

Theorem 3.
Relative entropy is functorial with respect to vertical composition, i.e., if is a vertical composition in , then .
Proof.
Suppose ♠ and ♣ are such that the vertical composition is summarized by the following diagram.
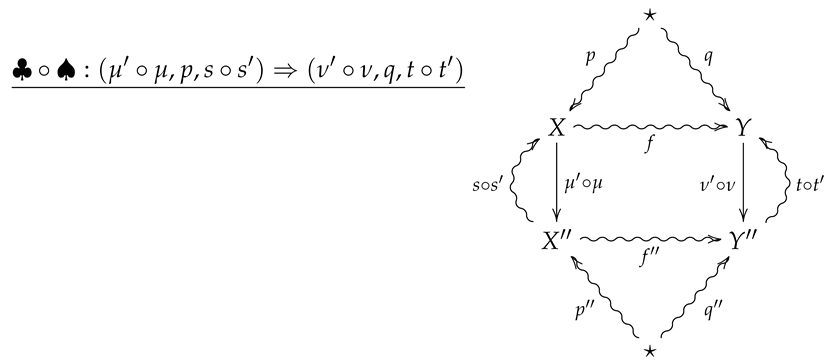 Then,
where the second equality follows from Theorems 1 and 2. □
Then,
where the second equality follows from Theorems 1 and 2. □

Proposition 3.
Let be a 2-morphism in , and suppose s and t are optimal hypotheses for and as (defined in Definition 5). Then, .
Proof.
Since s and t are optimal hypotheses, it follows that , from which the proposition follows. □
Proposition 4.
The 2-relative entropy is lower semicontinuous.
Proof.
Since the 2-relative entropy is a linear combination of 1-level relative entropies, and 1-level relative entropies are lower semicontinuous by Theorem 1, it follows that is lower semicontinuous. □
8. Conclusions, Limitations and Future Research
In this work, we have constructed a 2-categorical extension of the relative entropy functor RE of Baez and Fritz [1], yielding a new measure of information which we view as a relative measure of information between noisy channels. Moreover, we show that our construction satisfies natural 2-level analogues of functoriality, convex linearity, vanishing under optimal hypotheses and lower semicontinuity. As the relative entropy functor of Baez and Fritz is uniquely characterized by such properties, it is only natural to question if our 2-level extension of RE is also uniquely characterized by the 2-level analogues of such properties. It would also be interesting to investigate alternative versions of 2-morphisms in where the 2-morphisms are less restrictive, such as where the base pyramid of a 2-morphism is not assumed to be commutative. While taking the 2-relative entropy associated with such morphisms would not be functorial, such less restrictive morphisms would provide more flexibility for potential applications. Finally, as there are many other categories of interest with respect to information theory [8,14,15], it would be interesting to investigate 2-level extensions of such categories as well.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Baez, J.C.; Fritz, T. A Bayesian characterization of relative entropy. Theory Appl. Categ. 2014, 29, 422–457. [Google Scholar]
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Baez, J.C.; Fritz, T.; Leinster, T. A characterization of entropy in terms of information loss. Entropy 2011, 13, 1945–1957. [Google Scholar] [CrossRef]
- Coecke, B.; Fritz, T.; Spekkens, R. A mathematical theory of resources. Inform. Comput. 2016, 250, 59–86. [Google Scholar] [CrossRef] [Green Version]
- Faddeev, D.K. On the concept of entropy of a finite probabilistic scheme. Uspekhi Mat. Nauk 1956, 11, 227–231. [Google Scholar]
- Fong, B. Causal Theories: A Categorical Perspective on Bayesian Networks. Master’s Thesis, University of Oxford, Oxford, UK, 2012. [Google Scholar]
- Fritz, T. A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics. Adv. Math. 2020, 370, 107239. [Google Scholar] [CrossRef]
- Fullwood, J. An axiomatic characterization of mutual information. arXiv 2021, arXiv:2108.12647. [Google Scholar]
- Fullwood, J.; Parzygnat, A.P. The Information Loss of a Stochastic Map. Entropy 2021, 23, 1021. [Google Scholar] [CrossRef] [PubMed]
- Leinster, T. A short characterization of relative entropy. J. Math. Phys. 2019, 60, 023302. [Google Scholar] [CrossRef] [Green Version]
- Leinster, T. Entropy and Diversity: The Axiomatic Approach; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Parzygnat, A.P. A functorial characterization of von Neumann entropy. IHÉS prépublications. arXiv 2020, arXiv:2009.07125. [Google Scholar]
- Cho, K.; Jacobs, B. Disintegration and Bayesian inversion via string diagrams. Math. Struct. Comput. Sci. 2019, 29, 938–971. [Google Scholar] [CrossRef] [Green Version]
- Golubtsov, P.V. Information transformers: Category-theoretical structure, informativeness, decision-making problems. Hadron. J. Suppl. 2004, 19, 375–424. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).