An Improved Chaotic Optimization Algorithm Applied to a DC Electrical Motor Modeling

Abstract

The chaos-based optimization algorithm (COA) is a method to optimize possibly nonlinear complex functions of several variables by chaos search. The main innovation behind the chaos-based optimization algorithm is to generate chaotic trajectories by means of nonlinear, discrete-time dynamical systems to explore the search space while looking for the global minimum of a complex criterion function. The aim of the present research is to investigate the numerical properties of the COA, both on complex optimization test-functions from the literature and on a real-world problem, to contribute to the understanding of its global-search features. In addition, the present research suggests a refinement of the original COA algorithm to improve its optimization performances. In particular, the real-world optimization problem tackled within the paper is the estimation of six electro-mechanical parameters of a model of a direct-current (DC) electrical motor. A large number of test results prove that the algorithm achieves an excellent numerical precision at a little expense in the computational complexity, which appears as extremely limited, compared to the complexity of other benchmark optimization algorithms, namely, the genetic algorithm and the simulated annealing algorithm.

1. Introduction

A chaotic systems is a complex system that shows sensitivity to initial conditions, such as an economy, a stock market, the earth’s weather system, the behavior of water boiling on a stove, migratory patterns of birds, the spread of vegetation across a continent, an astronomical or a social system. In such systems, any uncertainty—no matter how small—in the beginning will produce rapidly escalating errors in the prediction of the system’s future behavior. To make an accurate prediction of the long-term behavior of such systems, the initial conditions must be known in their entirety and to an infinite level of accuracy. Even very simple or small systems can exhibit very complex behaviors. Typical features of chaotic systems include [1]:

• Nonlinearity: A linear system cannot be chaotic; therefore, only nonlinear systems may evolve in time forming chaotic trajectories.
• Determinism: A chaotic system is deterministic, as it does not include any random or stochastic element. Given an initial state for the system, it evolves according to deterministic rules. Chaos theory is the study of nonlinear dynamics, in which seemingly random events are actually predictable from deterministic equations.
• Sensitivity to initial conditions: Small changes in the initial state of a chaotic system may lead to radically different trajectories (this is commonly referred to as the ”butterfly effect”).
• Irregularity: Hidden order including a large or infinite number of unstable periodic trajectories forms the infrastructure of irregular chaotic systems. Chaos refers to an apparent lack of order in a system that nevertheless obeys particular laws or rules.
• Long-term unpredictability: Long-term prediction of a trajectory of a chaotic system is extremely hard due to its sensitivity to initial conditions, which can be known only up to a finite degree of precision.

Historically, the study of chaos started in mathematics and physics and expanded into engineering, as well as into information and social sciences. Information entropy is tightly related to chaoticity in real-world discrete-time sequences, as underlined, for example, in Hagmair et al. [2]. There exist different kinds of potential commercial and industrial applications of chaotic systems, which, for simplicity, are classified into stabilization, synthesis, and analysis [3]. A typical application of chaotic systems is found in the secure transmission of information, where a meaningful message is superimposed to a chaotic signal that makes it non-understandable to someone who neither knows the system that produces the chaotic trajectory nor its initial state. To decode the received signal, it is necessary to synchronize the chaotic oscillators at the transmitter and at the receiver [4].

In the present research study, chaotic systems are applied to constrained global optimization of possibly non-smooth, nonlinear complex functions of several variables. Although non-conventional optimization techniques based on stochastic methods have a long hystory (see, for example, [5]), optimization techniques based on chaos theory have been less investigated.

The present study took its moves from the seminal contribution [6] that proposed how to optimize complex functions by chaos search. The main idea behind the resulting chaos-based optimization algorithm (COA) [6] is to generate chaotic trajectories by means of nonlinear dynamical systems to explore the search space while looking for the global minimum of a complex criterion function. The main reasons to choose a chaotic search over a deterministic search may be summarized as follows:

• The criterion function to optimize may be non-smooth and non-differentiable, hence, standard search methods such as gradient steepest descent may not be applied in its optimization.
• A chaotic system may produces complex, non-repeating trajectories that hardly visit the same state more than once, hence a chaos-based search algorithm is able to visit the whole space efficiently while looking for the optimal configuration.
• A multivariate criterion function may include a large number of variables to optimize simultaneously, therefore, a simple mechanism to generate multivariate candidate solutions over a high-dimensional search space makes the search algorithm fast and easy to implement.

Despite its success in the optimization of complex functions, to the best of our knowledge, the potentiality of the chaos-based optimization algorithm has only been marginally investigated in the literature [7,8]. The aim of the present research study is to investigate the numerical properties of the COA, both on complex optimization test-functions from the literature and on a real-world problem, in order to contribute to the understanding of its global-search features. Through a large number of tests and numerical evaluations, it was found that the algorithm may be further fine-tuned in order to improve its numerical precision at a little expense in computational complexity, which is nevertheless extremely limited, compared to the complexity of other optimization algorithms, namely, the genetic algorithm and the simulated annealing algorithm.

The present paper is organized as follows. Section 2 summarizes the chaos-based optimization algorithm and tests a number of possible chaotic maps over a large number of test functions drawn from the specialized literature. Section 2 also suggests a fine-tuning of the original COA algorithm and compares the modified algorithm with the genetic algorithm and the simulated-annealing based optimization algorithm. Section 3 illustrates the performances of the refined COA algorithm in the modeling of a direct-current electrical motor. Section 4 concludes the paper.

2. The Chaos-Based Optimization Algorithm and Its Fine-Tuning

Traditional algorithms are unable to solve some optimization problems since these algorithms can get trapped into local minima or need too much search time. The properties of chaotic systems allow the development of an efficient chaos-based optimization algorithm. Unlike traditional stochastic optimization algorithms that escape from local minima by accepting some sub-optimal solutions according to a certain probability, the COA’s search takes advantage of chaotic motions’ regularity. A chaotic movement can go through every state in a definite area thanks to its own regularity and every state is obtained only once.

This Section illustrates the chaos-based optimization algorithm in Section 2.1 and describes in Section 2.2 several chaotic maps, which are indispensable for the development and the implementation of the COA; it also shows in Section 2.3 the performances of the COA in the optimization of a large set of benchmark functions. The results obtained from the large set of test experiments suggest a refinement of the original chaos-based optimization method, which is explained and numerically tested in Section 2.4. Section 2.5 presents a comparison between the refined COA and both the genetic optimization algorithm and the simulated-annealing-based optimization algorithm.

2.1. The Chaos-Based Optimization Algorithm

If a given optimization problem is described by a criterion $f:{\mathbb{R}}^n\to \mathbb{R}$ and the constraints that it is subjected to prescribe its variables $x_i$ to belong to specified intervals, the optimization problem can be described as $minf\left(x_i\right)$, $i=1,\dots ,n$, subjected to $a_i\le x_i\le b_i$, with $a_i,b_i\in \mathbb{R}$. In the COA, thanks to the carrier wave method, the optimization variables follow the trajectories of specific chaotic functions whose ergodic areas are sized according to the constraints of the problem. The COA is outlined as follows:

• Generate n chaotic variables $x_{i,k}$ from the same nonlinear chaotic oscillator, where the index i denotes the variable’s index and k denotes a discrete-time index. There will be n initial states $x_{i,0}$ that are chosen very close one to another (for instance $0.1$, $0.1001$, $0.1002$). These initial states, because of chaotic systems properties, will give rise to completely different trajectories.
• Launch the first carrier wave: This method allows us to obtain the optimization variables with the amplification of the ergodic areas of the n chaotic variables by the equation $x_{i,k}^{\prime }=c_i+d_i{x}_{i,k}$, where $c_i$ and $d_i$ denote amplification constants. Perform the rough search: Let ${\overline{x}}_i^{\prime }=x_{i,0}$, calculate the value of the objective function f at the initial state and save its value $\overline{f}=f\left(x_{i,0}\right)$. Then start to iterate over the time k: Increase the time-index (iteration counter) k, generate a new attempted solution $x_{i,k}^{\prime }$, calculate the value of the objective function $f=f(x_{i,k}^{\prime })$ and evaluate the solution: If $f\le \overline{f}$ then set $\overline{f}=f$ and ${\overline{x}}_i^{\prime }=x_{i,k}^{\prime }$. Continue with the iteration until $\overline{f}$ does not improve in $K_1$ search steps, where the integer constant $K_1$ determines the complexity of the search method. The first carrier wave will produce a rough solution $({\overline{x}}_1^{\prime },{\overline{x}}_2^{\prime },\dots ,{\overline{x}}_n^{\prime })$.
• Launch the second carrier wave: The second carrier wave explores the search space in a narrower interval around the rough solution, in fact, the trajectories of the optimization variables are generated according to the rule $x_{i,k}^{\prime \prime }={\overline{x}}_i^{\prime }+e_i+f_i{x}_{i,k}$, where the $x_{i,k}$ denote again the states of n discrete-time chaotic systems, while $e_i$ and $f_i$ are the new amplification constants to perform the search within small ergodic areas around ${\overline{x}}_i^{\prime }$. Perform the fine search: Start to iterate over the time k: Increase the time-index k, generate a new attempted solution $x_{i,k}^{\prime \prime }$, calculate the value of the objective function $f=f(x_{i,k}^{\prime \prime })$ and evaluate the solution: If $f\le \overline{f}$ then set $\overline{f}=f$ and ${\overline{x}}_i^{\prime \prime }=x_{i,k}^{\prime \prime }$. Continue with the iteration until $\overline{f}$ does not improve in $K_2$ search iterations.
• The process ends and the values of parameters $({\overline{x}}_1^{\prime \prime },{\overline{x}}_2^{\prime \prime },\dots ,{\overline{x}}_n^{\prime \prime })$, together with the criterion value $\overline{f}$, will be the best approximation of the global solution of the given optimization problem as found by the chaos-based optimization algorithm.

2.2. Chaotic Maps

To generate the carrier waves, the COA makes use of a chaotic map that controls the features of the chaotic system used to generate the variables that are essential for the optimization.

There are some known universal properties of the chaotic maps, for instance:

• They may present different kinds of attractors: An attractor is a set of numerical values towards which a dynamical system evolves after a sufficiently long time. A set of numerical values can be defined as an attractor if the trajectories that are related to them stay close to each other even if they are slightly perturbed.
• They may present different values of the Lyapunov coefficient: This coefficient measures how much the system’s orbits are dependent from the initial state. Specifically, the Lyapunov coefficient measures the average parting speed of two orbits that are initially close and then drift apart.

Four chaotic maps have been surveyed. The characteristics that are more interesting for the optimization problem are the state’s trajectory variation (assuming that the initial states $x_{i,0}$ are very close to each other) and the ergodic area of each chaotic system, which is measured by pooling numerically the distribution of its states.

• Logistic map. The “logistic map” is a second order polynomial function, described by:

  $$x_{k+1}=r{x}_k(1-x_k),k=0,1,2,3,\dots ,$$

  (1)

  where r is the control parameter. It is supposed that $0\le x_0\le 1$ and that $0\le r\le 4$. The Equation (1) represents a discrete-time, deterministic dynamical system without any stochastic interference. The long-term behavior of said system cannot be predicted because it changes completely as the control parameter r varies. In particular, when $r=4$, the system becomes chaotic. As we can see in Figure 1, from $k>10$, two waves originating from very close initial states start to behave in a different way and the system’s initial information is completely lost. It may be observed that the values generated by the logistic map are condensed around its ergodic area’s bounds, which are 0 and 1.
  

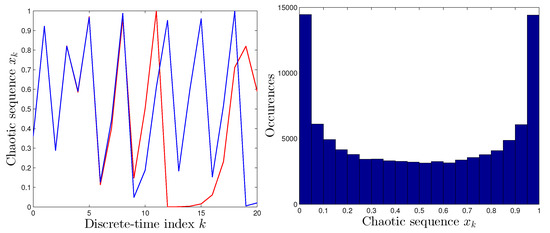  Figure 1. Logistic map. Left-hand panel: Comparison between system’s output with two different initial conditions. (The wave with initial value $x_0=0.1$ is represented by the red line and the other with initial value $x_0=0.1001$ by the blue line.) Right-hand panel: Occurrence histogram of the values of the states of the dynamical system (1).
• Quadratic map. The “quadratic map” arose as the real-valued version of the Mandelbrot set complex map and is described by:

  $$x_{k+1}=x_k^2-c,k=0,1,2,3,\dots ,$$

  (2)

  where the constant c is the control parameter. For $c=-2$, the system acquires interesting complicated dynamics. The ergodic area is included between $-2$ and 2, as may be readily observed in Figure 2.
  

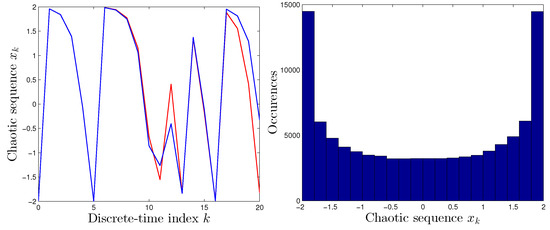  Figure 2. Quadratic map. Left-hand panel: Comparison between system’s output with two different, albeit very close, initial conditions. Right-hand panel: Occurrence histogram of the values of the states of the dynamical system (2).
• Tent map. The “tent map” is defined by the following dynamical system:

  $$x_{k+1}=\{\begin{array}{ccc}\mu x_k\hfill & \mathrm{if}\hfill & x_k<\frac{1}{2},\hfill \\ \mu (1-x_k)\hfill & \mathrm{if}\hfill & x_k\ge \frac{1}{2},\hfill \end{array}$$

  (3)

  where $\mu$ is the control parameter and $k=0,1,2,3,\dots$. For $\mu \ge 1.5$, the waves start to show bifurcations. The value that has been used in the tests is $\mu =1.9999$. Unlike the two previous maps, the tent map has an uniform distribution in its ergodic area $[0,1]$, as it may be readily appreciated in Figure 3.
  

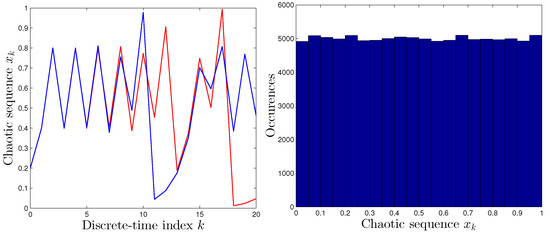  Figure 3. Tent map. Left-hand panel: Comparison between system’s output with two different, although very close, initial conditions. Right-hand panel: Occurrence histogram of the values of the states of the dynamical system (3).
• Sine map. The “sine map” gives rise to the following discrete-time dynamical system:

  $$x_{k+1}=\lambda \sin \left(\pi x_k\right),k=0,1,2,3,\dots ,$$

  (4)

  where $\lambda$ denotes the control parameter. This map generates a unique bifurcations diagram, symmetrical under both plane’s axis $\lambda ,x$. The value that has been used in the tests is $\lambda =1$. Figure 4 shows the behavior of the sine map and that its ergodic area is again $[0,1]$.
  

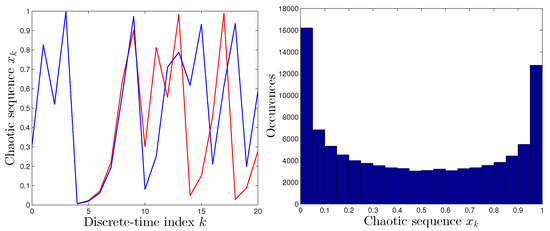  Figure 4. Sine map. Left-hand panel: Comparison between system’s output with two different initial conditions, very close to one another. Right-hand panel: Occurrence histogram of the values of the states of the dynamical system (4).

2.3. Optimization of Test Functions

Seven benchmark functions have been taken into consideration to test and to further develop the COA. These functions are usually used in the literature [9] because they show a wide spectrum of characteristics, namely, they give rise to continuous/discontinuous, convex/nonconvex, unimodal/multimodal, quadratic/nonquadratic optimization problems.

• F1: Generalized Rosenbrock function. This function of n variables is defined as

  $$f_1\left(x\right)=\sum _{i=1}^{n-1}\left(100{(x_i^2-x_{i+1})}^2+{(1-x_i)}^2\right).$$

  (5)
  It was proposed by Rosenbrock in 1960 and is commonly used to test optimization algorithms since, for $n=2$, the search for the minimum is problematic in its parabolic area $x_2=x_1^2$; furthermore, it becomes multimodal for $n>3$. The constraints and the global minimum of the generalized Rosenbrock function are recalled in the Table 1 and its graphical rendering is given in the Figure 5.
  Table 1. Constraints and global minimum of the generalized Rosenbrock function (benchmark function “F1”) for the case of $n=2$ independent variables.

  Constraints	Global Minimum
  $-2\le x_i\le 2$	$f_1^{★}=0$;    $x_i^{★}=1$

  

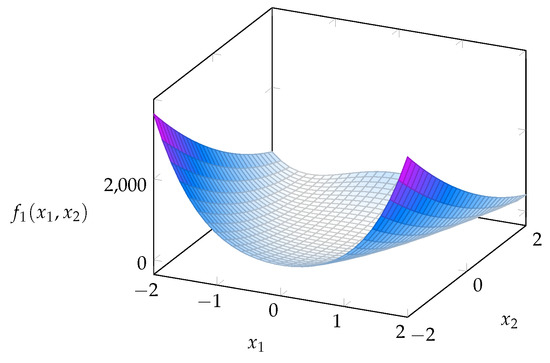  Figure 5. Rendering of the generalized Rosenbrock function (benchmark function “F1”) for the case of $n=2$ independent variables.
• F2: Parabolic function. This function is defined as

  $$f_2\left(x\right)=\sum _{i=1}^n{x}_i^2.$$

  (6)
  It was introduced to test optimization by genetic adaptive systems. The global minimum is not difficult to find because it is the only minimum of the function, but it can provide some information about the precision of the algorithm. The constraints that this optimization problem is subjected to are $-5.12\le x_i\le 5.12$.
• F3: Goldstein–Price function. This function is defined as

  $$\begin{array}{ccc}{f}_3\left(x\right)\hfill & =& (1+{(x_1+x_2+1)}^2(19-14x_1+3x_1^2-14x_2+6x_1{x}_2+3x_2^2))\times \hfill \\ & & ((30+{(2x_1-3x_2)}^2)(18-32x_1+12x_1^2+48x_2-36x_1{x}_2+27x_2^2)).\hfill \end{array}$$

  (7)
  The Goldstein–Price Function only has two variables but it exhibits several local minima. The constraints and the global minimum of this function within the considered domain are recalled in the Table 2, while its graphical rendering is given in the Figure 6.
  Table 2. Constraints and global minimum of the Goldstein–Price function (benchmark function “F3”).

  Constraints	Global Minimum
  $-2\le x_i\le 2$	$f_3^{★}=-1.0156\times {10}^5$;    $x_1^{★}=-1.7693$, $x_2^{★}=-2$

  

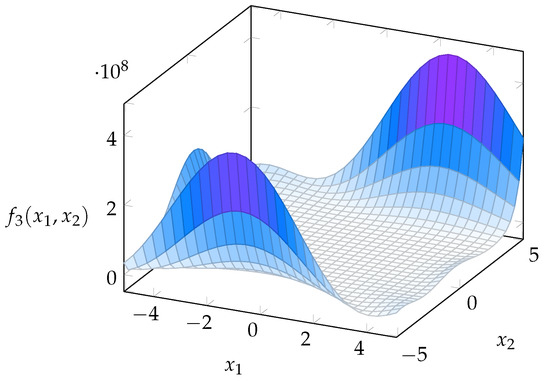  Figure 6. Rendering of the Goldstein–Price function (benchmark function “F3”).
• F4: Schaffer function. This function is defined as

  $$f_4\left(x\right)=0.5-\left(\frac{{\sin }^2\sqrt{x_1^2+x_2^2}-0.5}{{\left[1+0.001(x_1^2+x_2^2)\right]}^2}\right).$$

  (8)
  The Schaffer function (number 4) is quite interesting because its global minimum is not unique, but it is given by all the points situated on a circumference with a well-defined radius $r^{*}$. The constraints and the global minimum (in terms of radius) of this function are recalled in the Table 3 and its graphical rendering is given in the Figure 7.
  Table 3. Constraints and global minimum of the Schaffer function (benchmark function “F4”).

  Constraints	Global Minimum
  $-4\le x_i\le 4$	$f_4^{★}=0.0025$;    $r^{*}=1.5692$

  

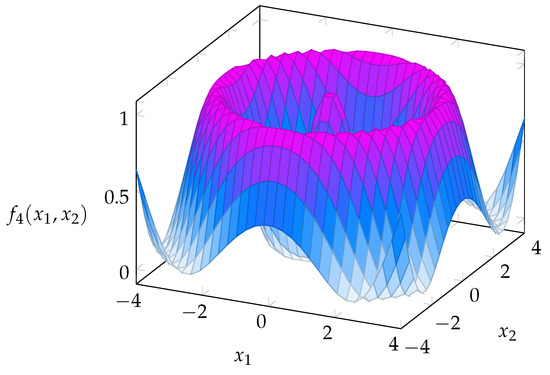  Figure 7. Rendering of the Schaffer function (benchmark function “F4”).
• F5: Step function. This function is defined as

  $$f_5\left(x\right)=\sum _{i=1}^n⎣x_i⎦,$$

  (9)

  where the symbol $⎣·⎦$ denotes rounding down to the nearest integer. This function tests an optimization algorithm’s ability to overcome discontinuities. The constraints and the global minimum of this function are recalled in Table 4 and its graphical rendering is given in Figure 8. Since there is not any unique global minimum, an optimization algorithm is supposed to stop when $x_i\le -5$.
  Table 4. Constraints and global minimum of the “step” function (benchmark function “F5”) for the case of $n=2$ independent variables.

  Constraints	Global Minimum
  $-5.1\le x_i\le 5.1$	$f_5^{★}=-12$;    $x_i^{★}\le -5$

  

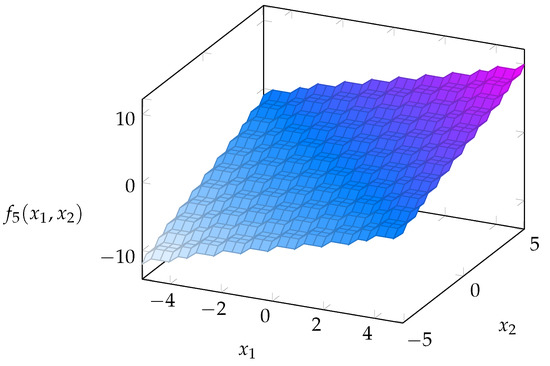  Figure 8. Rendering of the “step” function (benchmark function “F5”) for the case of $n=2$ independent variables.
• F6: Normalized Schwefel function. This function is defined as

  $$f_6\left(x\right)=-\frac{1}{n}\sum _{i=1}^n{x}_i\sin \left(\sqrt{|x_i|}\right).$$

  (10)
  The Schwefel Function has its global minimum far away from the best local minimum: For this reason, optimization algorithms could converge on a wrong direction. The constraints and the global minimum of this function are recalled in the Table 5 and its graphical rendering is given in Figure 9.
  Table 5. Constraints and global minimum of the Schwefel function (benchmark function “F6”) for the case of $n=2$ independent variables.

  Constraints	Global Minimum
  $-512\le x_i\le 512$	$f_6^{★}=-418.982887$;    $x_i^{★}=420.968746$

  

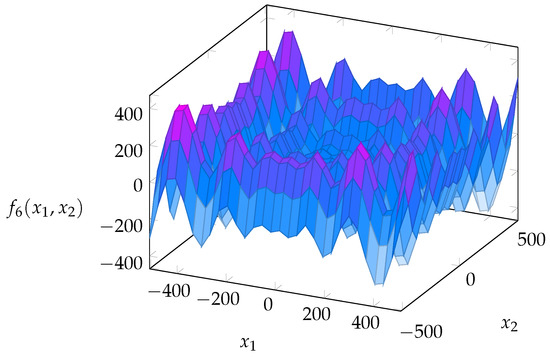  Figure 9. Rendering of the Schwefel function (benchmark function “F6”) for the case of $n=2$ independent variables.
• F7: Rastring function. This function of n independent variables is defined as

  $$f_7\left(x\right)=10n+\sum _{i=1}^n\left(x_i^2-10\cos \left(2\pi x_i\right)\right).$$

  (11)
  The Rastring function is an example of a nonlinear, multimodal function. Its optimization is considered as a complicated problem because of its extended search space and its several local minima. The constraints and the global minimum of this function are recalled in Table 6 and its graphical rendering is given in the Figure 10.
  Table 6. Constraints and global minimum of the Rastring function (benchmark function “F7”) for the case of $n=2$ independent variables.

  Constraints	Global Minimum
  $-5\le x_i\le 5$	$f_7^{★}=0$;    $x_i^{★}=0$

  

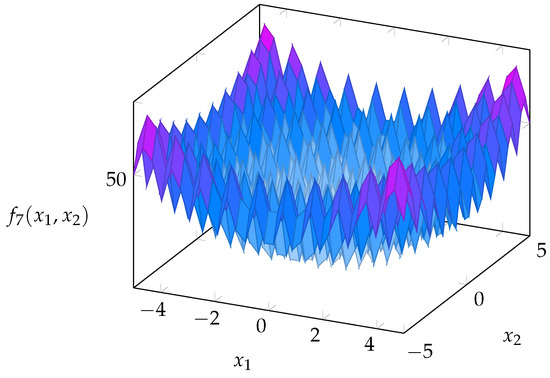  Figure 10. Rendering of the Rastring function (benchmark function “F7”) for the case of $n=2$ independent variables.

The COA algorithm has been tested over the above seven benchmark functions, initially with only the first carrier wave and subsequently with the full algorithm. All the recalled four types of chaotic maps have been used to generate the optimization variables trajectories. The parameters of the algorithm are recalled below for the convenience of the reader:

• $K_1$: Stop criterion for the “rough search”.
• $K_2$: Stop criterion for the “fine search”.
• $c_i$, $d_i$: Amplifiers for the first carrier wave.
• $e_i$, $f_i$: Amplifiers for the second carrier wave.

We recall that the amplifiers $c_i,d_i$ are constants that allow the chaotic maps’ ergodic areas to adapt to the specific search intervals (constraints) of the test function s. In the following tables, the figure Total Loops stands for the number of iterations taken to run and Error is the percentage distance (compared to the search interval) from the coordinates of the global minimum. The rough search has been run several times for all the functions and for all the chaotic maps with $K_1=100,200,400,600,800,1000$. Only the results that correspond to an error under 10% and a limited number of Total Loops have been reported.

Table 7 illustrates the results obtained by applying a rough search to the benchmark functions F1 and F2 with $n=2$ variables.

Table 7. Results of the application of a rough search (only first carrier wave) on the benchmark functions F1 and F2.

F1				F2
Map	${\mathbf{K}}_{\mathbf{1}}$	Total Loops	Error	Map	${\mathbf{K}}_{\mathbf{1}}$	Total Loops	Error
Logistic	400	553	7.90%	Logistic	100	100	2.00%
Quadratic	1000	3210	3.50%	Quadratic	100	100	2.00%
Sine	100	108	9.80%	Sine	100	100	2.00%
Tent	100	108	8.00%	Tent	100	100	2.00%

Only the quadratic map achieves a reasonable value but with too many iterations. With regard to the function F2, the algorithm, during the first 100 loops, could not find any better results than the initial states (that have been set at $x_{1,0}=0.1$ and $x_{2,0}=0.1001$).

Table 8 illustrates the results obtained by applying a rough search to the benchmark functions F3 and F4 with $n=2$ variables. F3 function’s error is overall low, the logistic map is the one that exhibits better results. The optimization of the F4 function could be resolved by an infinite number of points that belongs to the circumference of radius $r^{*}=1.5692$. Even in this case, the quadratic map needs the highest number of iterations.

Table 8. Results of the application of a rough search (only first carrier wave) on the benchmark functions F3 and F4.

F3				F4
Map	${\mathbf{K}}_{\mathbf{1}}$	Total Loops	Error	Map	${\mathbf{K}}_{\mathbf{1}}$	Total Loops	Error
Logistic	100	133	1.75%	Logistic	100	100	0.00%
Quadratic	600	1431	0.20 %	Quadratic	100	3526	0.00 %
Sine	400	632	1.60%	Sine	800	141	0.00%
Tent	400	826	1.80%	Tent	100	114	0.00%

The algorithm could easily overcome the discontinuity of the F5 function and it could find immediately values lower than $-5$, therefore it is not necessary to show the relative table.

Table 9 illustrates the results obtained by applying a rough search to the benchmark functions F6 and F7 with $n=2$ variables. The results about the optimization of the functions F6 and F7 do not provide any further information about the algorithm’s behavior but they confirm its excellent optimization ability.

Table 9. Results of the application of a rough search (only first carrier wave) on the benchmark functions F6 and F7.

F6				F7
Map	${\mathbf{K}}_{\mathbf{1}}$	Total Loops	Error	Map	${\mathbf{K}}_{\mathbf{1}}$	Total Loops	Error
Logistic	600	1010	1.26%	Logistic	100	100	2.00%
Quadratic	100	177	2.60 %	Quadratic	400	588	9.90 %
Sine	600	1067	2.00%	Sine	100	100	2.00%
Tent	800	1516	4.00%	Tent	100	116	1.80%

In summary, the logistic map is the chaotic map that allows the first carrier wave to obtain better outcomes, namely, lower number of Total Loops, stop criterion to about 200 iterations and a final value close to any global minimum (in the worst case, with an Error of 8%). Moreover, the tent map provide good results. The quadratic map proves to be the worst in almost all tests (the cause may be its ergodic area included between $-2$ and 2). As it can be seen, the rough search does not need a high value of $K_1$; in fact, since the initial search area is rather wide, increasing the number of Total Loops does not always imply a proportional Error’s reduction.

It is now worth recalling that the amplifiers $e_i,f_i$ of the second carrier wave are the algorithm’s most important parameters because they influence substantially its precision. These parameters are problem-dependent: specific constants were used, that could modify the ergodic area of the chaotic waves. In some cases, this area was changed to be 3% of the total search area, in others it was change to 2% or 8%. Thanks to its good performance during the “rough search”, the logistic map was used to guide the second carrier wave. The amplifiers were calculated in the following way:

$$e_i=-\epsilon |{\alpha }_i|,f_i=2\epsilon |{\beta }_i-{\alpha }_i|,$$

(12)

where ${\alpha }_i$ and ${\beta }_i$ are, respectively, the lower bound and the upper bound of the constraints that were associated to the variable $x_i$, $\epsilon$ is the area’s shrinkage percentage (for example, 2% or 3% or 8%).

Several tests were effected by changing at every test the stopping parameter $K_2$. The obtained results are displayed in Table 10. In the table, ${\overline{x}}_1$ and ${\overline{x}}_2$ denote the values found by the COA, whereas P is a precision index that shows the ratio between the errors’ average on the individual variables and a normalization constant proportional to the width of the search area, namely:

$$P=\frac{{\sum }_{i=1}^n|{\overline{x}}_i-x_i^{*}|}{{\sum }_{i=1}^n|{\beta }_i-{\alpha }_i|}.$$

(13)

Table 10. Results of the application of a fine search (both first and second carrier waves) on the benchmark functions F1–F7.

Benchmark Functions	Coordinates of GlobalMinimum	${\mathbf{K}}_{\mathbf{2}}$	Total Loops	${\overline{\mathbf{x}}}_{\mathbf{1}}$	${\overline{\mathbf{x}}}_{\mathbf{2}}$	P
F1	$x_i^{★}=1$	200	1032	$1.0268$	$1.0534$	$1.0547\times {10}^{-2}$
		2000	4500	0.9996	0.9976	$3.7846\times {10}^{-4}$
F2	$x_i^{★}=0$	1000	1568	$-0.0010$	$-0.0094$	$5.4751\times {10}^{-4}$
		2000	7806	0.0006	0.0002	$3.2104\times {10}^{-5}$
F3	$x_1^{★}=-1.7693$	100	1228	$-1.7707$	$-1.9999$	$1.2678\times {10}^{-4}$
	$x_2^{★}=-2.0000$	20,000	60,013	$-1.7963$	$-2.0000$	$1.8475\times {10}^{-24}$
F4	$r^{*}=1.5692$	200	538	0.7312	1.3886	$1.6854\times {10}^{-27}$
F5	$x_i^{★}\le -5$	100	137	$-5.0356$	$-5.0939$	-
F6	$x_i^{★}=420.9687$	100	1239	421.1416	420.9193	$1.1557\times {10}^{-4}$
		15,000	34,855	420.9656	420.9927	$1.3554\times {10}^{-5}$
F7	$x_i^{★}=0$	500	1068	$-0.0010$	$-0.0094$	$5.9844\times {10}^{-4}$
		2100	7606	$-0.0005$	0.0001	$3.2575\times {10}^{-5}$

In all experiments, $n=2$ variables were chosen.

The results pertaining to some selected values of the parameters $K_2$ are included in the table to point out the precision that can be obtained with either a low or a high number of iterations. The substantial Error of the “rough search” affects the performance of the “fine search” applied to the F1 function, which is the most troublesome for both stopping criteria. Therefore, it is important to use, for the purpose of optimization, a limited neighborhood for the second search. The values of the performance index P lay between ${10}^{-5}$ and ${10}^{-4}$ in most cases, which proves the quality of the chaos-based optimization algorithm. It can be seen that almost for all functions, excluding F4 and F5, the values ${\overline{x}}_1$ and ${\overline{x}}_2$ are close to the coordinates of the global minimum but only after a relatively large number of iterations.

2.4. Fine-Tuning of the COA Method (R-COA)

Specific problems that have dozens of variables in their objective functions or dynamic systems that need the resolution of differential equations could see their computing time exponentially increased by an high number of iterations. In the present research, to avoid the need for a large number of iterations, it has been proposed the introduction of a third carrier wave, which corresponds to an additional search stage, hereafter denoted as refined search. The whole refined chaos-based optimization algorithm (R-COA) may be outlined as follows:

• Generation of chaotic variables.
• Launch the first carrier wave and perform the rough search (identical to that of the COA).
• Launch the second carrier wave and perform the fine search (identical to that of the COA).
• Launch the third carrier wave: It is described by the equation $x_{i,k}^{\prime \prime \prime }={\overline{x}}_i^{\prime \prime }+g_i+h_i{x}_{i,k}$, where ${\overline{x}}_i^{\prime \prime }$ is the current best solution as found by the second carrier wave, $g_i$ and $h_i$ are new amplification constants that allow the search in small ergodic areas around ${\overline{x}}_i^{\prime \prime }$, and $x_{i,k}$ is a new chaotic wave. Perform the refined search: Start to iterate over the time k, increase the time-index (iteration counter) k, generate a new attempted solution $x_{i,k}^{\prime \prime \prime }$, calculate the value of the objective function $f=f(x_{i,k}^{\prime \prime \prime })$ and evaluate the solution: If $f\le \overline{f}$, then set $\overline{f}=f$ and ${\overline{x}}_i^{\prime \prime \prime }=x_{i,k}^{\prime \prime \prime }$. Continue with the iteration until $\overline{f}$ does not improve in $K_3$ search loops.
• The process ends and the parameter values $({\overline{x}}_1^{\prime \prime \prime },{\overline{x}}_2^{\prime \prime \prime },\dots ,{\overline{x}}_n^{\prime \prime \prime })$ together with the criterion value $\overline{f}$ will be the best global solution to the optimization problem, as found by the refined COA.

For the new analysis of the test functions, a lower value of the constant $K_2$ was used. In addition, different $K_3$ values were tried. The amplifiers $g_i,h_i$ are defined as:

$$g_i=-\delta |{\alpha }_i|,h_i=2\delta |{\beta }_i-{\alpha }_i|,$$

(14)

where $\delta$ represents the shrinkage percentage of analyzed area (2.5%, 1.5% or 0.5%).

The obtained results are displayed in Table 11. In the table, ${\overline{x}}_1$ and ${\overline{x}}_2$ again denot the values found by the R-COA, whereas P is the precision index defined before. Comparing the results displayed in Table 11 with the results displayed in Table 10, it can be noticed that the COA endowed with a third carrier wave always achieves a better (or comparable) precision, albeit with a lower number of Total Loops, than its original version. The values ${\overline{x}}_i$ found by the algorithm, excluded the ones pertaining to the F6 function (since it has a wide search interval), displays an error in the fourth or fifth decimal digit.

Table 11. Results of the application of a refined search (first, second and third carrier waves) on the benchmark functions F1–F3, F6, F7 (Since the functions F4 and F5 did not need a better optimization, they were not tested with the new algorithm).

Benchmark Functions	Coordinates of Global Minimum	${\mathbf{K}}_{\mathbf{3}}$	Total Loops	${\overline{\mathbf{x}}}_{\mathbf{1}}$	${\overline{\mathbf{x}}}_{\mathbf{2}}$	P
F1	$x_i^{★}=1$	1000	2812	0.9999	1.0008	$1.0657\times {10}^{-4}$
F2	$x_i^{★}=0$	300	851	0.0000	0.0001	$5.7872\times {10}^{-7}$
F3	$x_1^{★}=-1.7693$	800	2705	$-1.7691$	$-1.9999$	$1.3514\times {10}^{-5}$
	$x_2^{★}=-2.0000$
F6	$x_i^{★}=420.9687$	600	1884	420.9641	420.9719	$3.2198\times {10}^{-6}$
F7	$x_i^{★}=0$	100	438	0.0002	0.0005	$5.7785\times {10}^{-5}$

Table 12 displays the values $\overline{f}$ of the test function achieved by the refined COA: The differences between the value found by the optimization algorithm and the actual minimum are around ${10}^{-4}$ and ${10}^{-5}$.

Table 12. Values of the test functions resulting from the application of a refined search (first, second and third carrier waves) on the benchmark functions F1–F3, F6, F7. (The functions F4 and F5 were not tested).

Test Functions	Global Minimum	$\overline{\mathbf{f}}$
F1	0	$8.9131\times {10}^{-5}$
F2	0	$1.0032\times {10}^{-6}$
F3	$-1.0156\times {10}^5$	$-1.0154\times {10}^5$
F6	$-418.9828$	$-418.9829$
F7	0	$5.2471\times {10}^{-5}$

2.5. Comparison with the Genetic and the Simulated-Annealing Algorithms

The performances of the chaos-based optimization algorithm R-COA have been compared with those exhibited by Genetic Algorithm and Simulated Annealing algorithm.

Genetic algorithms (GAs) are computer programs that mimic the processes of biological evolution in order to solve problems and to model evolutionary systems (see, e.g., [10,11], for an overview). The continuing performance improvements of computational systems has made them attractive for some types of optimization. In particular, genetic algorithms work well on mixed continuous/discrete combinatorial problems. GAs are less susceptible to getting stuck at local optima than gradient search methods, although they tend to be computationally expensive. To run a genetic algorithm, one must represent a solution to a given problem as a genome (or chromosome) and the quality of an individual in relation to a given optimization problem is measured by a fitness function. The genetic algorithm then creates a population of solutions and applies genetic operators such as mutation and crossover to evolve the solutions in order to find the best ones. Although it is not guaranteed that a GA will find a global optimal solution, in general, a GA is able to find good solutions within an acceptable time span. Genetic algorithms present several parameters to set and operators to tune in order to optimize their optimization performances. In the present research, the GA solver of MATLAB’s Global Optimization Toolbox (version 2015a) was utilized maintaining without changes its already optimized options. See, e.g., [12], for a recent application to system identification and [13] for an application to magnetic resonance image segmentation.

Simulated annealing (SA) is a method for finding a good (albeit not necessarily optimal) solution to an optimization problem [14]. Simulated annealing’s strength is that it avoids getting caught at local optima, namely, at solutions that are better than any others nearby, and yet are not the global optima. In fact, generally speaking, an optimization algorithm searches for the best solution by generating a random initial solution and “exploring” the area nearby: If a neighboring solution is better than the current one, then it moves to it, otherwise the algorithm stays put. This basic mechanism can lead to situations where it gets stuck at a sub-optimal place. Simulated annealing injects some sort of randomness into the basic mechanism to escape local optima early in the process without getting off when an optimal solution is nearby. The simulated annealing algorithm used in the experiments is the one implemented within MATLAB (version 2015a). See, e.g., [15] for an application to indoor wireless local area network (WLAN) localization.

These algorithms were run 10 times on independent trials. Table 13 shows the results obtained by comparing the R-COA algorithm and the simulated annealing algorithm, while Table 14 shows the results obtained by comparing the COA algorithm and the genetic algorithm. In particular, for the SA and the GA, the tables show the average values $⟨x_i⟩$ over the independent trials and the standard deviation of the found global minimum’s coordinates, the average number of iterations required to converge and the number of times that the SA or the GA algorithm achieved convergence.

Table 13. Results of a comparison between the refined COA and the SA (Simulated Annealing Algorithm) on the benchmark functions F1–F7.

Function	Refined COA		Simulated Annealing
	Estimates	Total Loops	Average Estimates	Standard Deviation	Average Iterations	Convergence
F1	${\overline{x}}_1=0.9999$	2812	$⟨x_1⟩=1.0329$	0.1038	1407	10
	${\overline{x}}_2=1.0008$		$⟨x_2⟩=1.0771$	0.2240
F2	${\overline{x}}_1=0.0000$	851	$⟨x_1⟩=0.0000$	0.0000	1011	10
	${\overline{x}}_2=0.0001$		$⟨x_2⟩=0.0000$	0.0000
F3	${\overline{x}}_1=-1.7961$	2705	$⟨x_1⟩=-1.7693$	0.0000	1011	10
	${\overline{x}}_2=-1.9999$		$⟨x_2⟩=-2.0000$	0.0000
F4	$\overline{r}=1.5692$	538	$⟨r⟩=1.5688$	0.0010	1639	10
F5	${\overline{x}}_i\le -5$	137	$⟨x_i⟩\le -5$	0.0000	1011	10
F6	${\overline{x}}_1=420.9641$	1884	$⟨x_1⟩=109.1471$	218.5777	2437	0
	${\overline{x}}_2=420.9719$		$⟨x_2⟩=7.9124$	189.6553
F7	${\overline{x}}_1=0.0002$	438	$⟨x_1⟩=-0.0963$	0.3159	2167	8
	${\overline{x}}_2=0.0005$		$⟨x_2⟩=0.0979$	0.3152

Table 14. Results of a comparison between the refined COA and the GA (Genetic Algorithm) on the benchmark functions F1–F7.

Function	Refined COA		Genetic Algorithm
	Estimates	Total Loops	Average Estimates	Standard Deviation	Average Iterations	Convergence
F1	${\overline{x}}_1=0.9999$	2812	$⟨x_1⟩=0.8822$	0.0974	1392	10
	${\overline{x}}_2=1.0008$		$⟨x_2⟩=0.7867$	0.1745
F2	${\overline{x}}_1=0.0000$	851	$⟨x_1⟩=0.0000$	0.0000	1011	10
	${\overline{x}}_2=0.0001$		$⟨x_2⟩=0.0000$	0.0000
F3	${\overline{x}}_1=-1.7961$	2705	$⟨x_1⟩=0.6067$	1.2464	1186	3
	${\overline{x}}_2=-1.9999$		$⟨x_2⟩=-0.4933$	0.7942
F4	$\overline{r}=1.5692$	538	$⟨r⟩=1.5692$	0.0000	1040	10
F5	${\overline{x}}_i^{*}\le -5$	137	$⟨x_i⟩\le -5$	0.0000	1010	10
F6	${\overline{x}}_1=420.9641$	1884	$⟨x_1⟩=204.4482$	123.3547	1324	0
	${\overline{x}}_2=420.9719$		$⟨x_2⟩=150.4521$	126.5412
F7	${\overline{x}}_1=0.0002$	438	$⟨x_1⟩=-0.0995$	0.3146	1040	8
	${\overline{x}}_2=0.0005$		$⟨x_2⟩=0.1990$	0.4195

When tested over the functions F1–F5, the SA always converges towards the global minimum and obtains the exact solution for the benchmark functions F2, F3 and F5 (as it can be seen from the values of the standard deviation). For the functions F1, F4 and F7, the SA is less accurate than the R-COA, moreover, the average number of iterations for five functions out of seven is higher than the number of total loops required by the R-COA. The search for the test function F6 did not converge (the algorithm probably was trapped in a local minima due to the large search’s area).

GA’s results are worse compared with those of SA, even if, generally, the number of iterations is lower. The GA algorithm, not only does not always converge when tested with the benchmark functions F6 and F7, but for seven times out of ten, with F3, it achieves values that lay far apart from the global minimum. GA and R-COA exhibit the same accuracy for the problem F4. The number of Total Loops is higher than the average number of iterations only in two cases.

In conclusion, the chaos optimization algorithm exhibits two important properties that distinguish it from the optimization algorithms commonly invoked in the scientific literature:

• Convergence: The chaos-based optimization algorithm always converges towards the global minimum since: (a) it does not use variables related to probability; and (b) it is able to examine the whole search area, thanks to its mapping action;
• Low computation time: Since it does not utilize gradient’s calculation to evaluate the tendency of the objective function, it exhibits a computational complexity equal to $\mathsf{\Theta }\left(n\right)$ (the notation $\mathsf{\Theta }\left(f\right(n\left)\right)$ (commonly referred to as “big-Theta of $f\left(n\right)$”) is used to define the computational complexity of a problem: It expresses how fast an algorithm temporal cost increases as a function of The problem size n).

2.6. Generic Refined Chaos-Based Optimization Algorithm

The chaos-based algorithm, similar to other optimization algorithms, has parameters (ergodic areas’ amplifiers and stopping criteria) that must be adapted according to the faced problem. It was possible to model these parameters in order to create a generic algorithm, thanks to the large amount of data that were collected during the above tests.

The Euclidean distance between the minimum approximately found at the end of the rough search and the actual global minimum could be considered as a circle’s radius. This radius represents the sub-area where the second carrier wave will perform a second search. The same measure can be used for the fine search and the third carrier wave. Some general values were found while comparing all the sub-areas (regarded as a percentage of the total search area) and their relative stopping criteria. These values allow solving a generic optimization problem, even if it will perform less efficiently than a R-COA tailored to a specific problem.

The suggested amplifiers for the second carrier wave are:

$$e_i=-\sqrt{{\displaystyle \frac{0.025d_i^2}{\pi }}},f_i=2\left|e_i\right|,$$

(15)

and the suggested amplifiers for the third carrier wave are:

$$g_i=-\sqrt{{\displaystyle \frac{0.00015d_i^2}{\pi }}},h_i=2\left|g_i\right|,$$

(16)

where the $d_i$’s are the amplifiers for the first carrier wave. The stopping criteria are:

$$K_1=400,K_2=500.$$

(17)

Table 15 shows the outcomes of the optimization performed by the generic R-COA versus the results obtained with a specific R-COA. The global minimum’s coordinates are, in general, less accurate compared with those of specific R-COA (except for the first function). Moreover, the number of Total Loops is higher. However, since the error stays confined to the third or fourth decimal digit, the results can be considered acceptable.

Table 15. Results of a comparison between the specific refined COA and the generic refined COA on the benchmark functions F1–F7.

Functions	Specific Refined COA		Generic Refined COA
	Estimates	Total Loops	$\mathbf{Estimates}$	Total Loops
F1	${\overline{x}}_1=0.9999$	2812	${\overline{x}}_1=1.0014$	2055
	${\overline{x}}_2=1.0008$		${\overline{x}}_2=1.0026$
F2	${\overline{x}}_1=0.0000$	851	${\overline{x}}_1=-0.0001$	2055
	${\overline{x}}_2=0.0001$		${\overline{x}}_2=0.0009$
F3	${\overline{x}}_1=-1.7961$	2705	${\overline{x}}_1=-1.7695$	5283
	${\overline{x}}_2=-1.9999$		${\overline{x}}_2=-1.9998$
F4	$\overline{r}=1.5692$	538	$\overline{r}=1.5694$	2055
F6	${\overline{x}}_1=420.9641$	1884	${\overline{x}}_1=421.0366$	3662
	${\overline{x}}_2=420.9719$		${\overline{x}}_2=420.8288$
F7	${\overline{x}}_1=0.0002$	438	${\overline{x}}_1=0.0001$	2105
	${\overline{x}}_2=0.0005$		${\overline{x}}_2=0.0009$

3. Application to the Modeling of a Direct-Current Electrical Motor

The refined chaos-based optimization algorithm was applied to a real-world physical problem, namely, the estimation of the electro-mechanical parameters of a model of a direct-current (DC) electrical motor.

Direct-current motors found wide applications in industrial systems because they are easy to control and to model. For analytic control system design and optimization, a precise model of a DC motor may be desirable, since the specifications provided by the motor manufacturer may not be considered adequate, especially for cheaper DC motors which tend to exhibit relatively large tolerances in their electrical and mechanical parameters [16].

The present section recalls the fundamental equations describing the electro-mechanical dynamics of a direct-current electrical motor in Section 3.1. Section 3.2 casts the identification of the parameters of a DC motor model as an optimization problem. Section 3.3 describes and comments the results about the motor’s parameters identification when the motor is driven by a step signal.

3.1. Direct-Current Electrical Motors

Figure 11 shows an electro-mechanical model of a DC electrical motor. It is assumed that the stator has only a pair of polar expansions, characterized by an inductance $L_e$ associated to its relative winding and by a resistance $R_e$ associated to conductor’s leakage. The analytic equation that describes the stator-equivalent electrical circuit is:

$$v_e\left(t\right)=L_e\frac{d{i}_e\left(t\right)}{dt}+R_e{i}_e\left(t\right),$$

(18)

where $i_e$ denotes the stator current intensity. Likewise, it is assumed that the rotor has only a pair of polar expansions, characterized by an inductance $L_a$ and by a resistance $R_a$. Furthermore, the model takes into account the electromotive force’s effect, e, that correspond to an induced voltage proportional to the rotation speed. The following equation describes the rotor’s electrical circuit:

$$v_a\left(t\right)=L_a\frac{d{i}_a\left(t\right)}{dt}+R_a{i}_a\left(t\right)+e\left(t\right),$$

(19)

where $i_a$ denotes the rotor current intensity. According to the physical properties of the motor, while the motor rotates with angular velocity ${\omega }_m$, a proportional electromotive force is generated in the armature circuit, whose intensity is given by

$$e\left(t\right)=K{\omega }_m\left(t\right),$$

(20)

where K is a proportionality constant whose value depends on the physical design of the DC motor.

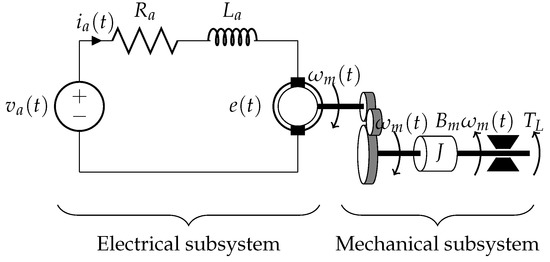
Figure 11. An electro-mechanical model of the direct-current electrical motor (we assumed no angular speed change after gear).

Whenever an electrical current of intensity $i_a$ flows through the rotor winding, magnetic attraction/repulsion forces appear between the stator’s and rotor’s windings, which cause the motor shaft to rotate. The magnetic field inside the motor transfers a mechanical torque to the drive shaft. If we denote the rotor inertia by J, the viscous friction constant by $B_m$ and the torque load applied to the drive shaft by $T_L$ (that is supposed to be constant), the equation relating the torque $T_m$ available at the drive shaft may be written as

$$T_m\left(t\right)=J{\displaystyle \frac{d{\omega }_m\left(t\right)}{dt}}+B_m{\omega }_m\left(t\right)+T_L.$$

(21)

3.2. Formulation of the Motor’s Parameters Identification as an Optimization Problem

To estimate, through an optimization algorithm, the values of the parameters of the above model of a DC motor, it is necessary to know its output values corresponding to a given input drive signal [17]. A DC motor was simulated by a Simulink model, assuming constant stator voltage, controlled by the armature voltage. Figure 12 shows the Simulink model block-diagram.

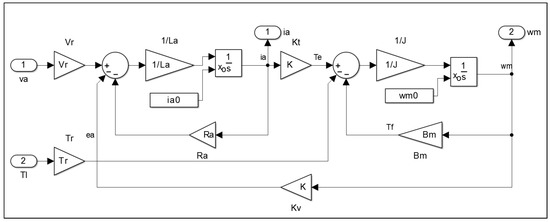
Figure 12. A Simulink model of an electrical direct-current motor with constant stator voltage.

The armature voltage $v_a$ is the only reference signal, whereas the constant load torque $T_L$ is regarded as a system disturbance. In the Simulink model, they are multiplied by $V_r$ and $T_r$, respectively, to amplify their values. In the two sections of the diagram that represent the electrical dynamics and the mechanical dynamics, there is an integrator block with initial conditions $i_{a0}$ and ${\omega }_{m0}$. The outputs of the model are the armature current $i_a$ and the angular speed ${\omega }_m$ of the drive shaft.

The state-space representation of the model is

$$\left\{\begin{array}{c}{\displaystyle \frac{d{i}_a\left(t\right)}{dt}}={\displaystyle \frac{v_a\left(t\right)-R_a{i}_a\left(t\right)-K{\omega }_m\left(t\right)}{L_a}},\hfill \\ {\displaystyle \frac{d{\omega }_m\left(t\right)}{dt}}={\displaystyle \frac{T_m\left(t\right)-B_m{w}_m\left(t\right)-T_L}{J}}.\hfill \end{array}\right.$$

(22)

The initial value of the armature current and of the angular speed of the drive shaft are $i_{a0}=22.8284$ A and ${\omega }_{m0}=122.3259$ rad/s.

A step input response was analyzed and its corresponding outputs are shown in Figure 13.

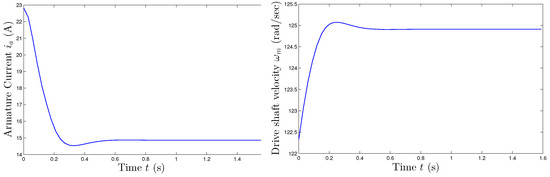
Figure 13. Example of output values of the model of a direct-current electrical motor driven by a step input voltage. Left-hand panel: Armature current $i_a$ versus time. Right-hand panel: Drive shaft angular velocity ${\omega }_m$ versus time.

To estimate the best values of the electro-mechanical parameters of a DC motor model, the problem is formulated in terms of model performance, to be optimized by means of the R-COA.

In [18], two performance criteria were tested, namely, a quadratic criterion and an absolute criterion. A comparison reported in the paper [18] reveals that the results obtained though the optimization of the quadratic criterion appear as better than those obtained by means of the absolute criterion. However, in the study [19], it was observed how these criteria perform nearly the same. In the present research, the following absolute criterion was selected as objective function:

$$C=\sum _{j=1}^D(k_a|i_{a,j}-i_{as,j}|+k_b|{\omega }_{m,j}-{\omega }_{ms,j}\left|\right),$$

(23)

where $i_{a,j}$ and ${\omega }_{m,j}$ represent the values of the variables computed by means of the Simulink model, upon time discretization, while $i_{as,j}$ and ${\omega }_{ms,j}$ denote the values of the variables obtained by the optimization algorithm, upon time discretization, at discrete-time step $j=1,2,\dots ,D$. The constants $k_a>0$ and $k_b>0$ are weights, which attribute a different importance to the error in the estimate of the armature current and to the error in the estimate of the drive shaft angular speed, that will be discussed later.

Table 16 shows the actual values of the electro-mechanical parameters of the considered DC motor.

Table 16. Application to DC motor model parameters estimation: Actual values of motor’s physical electro-mechanical parameters.

Parameter	Parameter Symbol	Parameter Value
Armature Resistance	$R_a$	0.6 $\mathsf{\Omega }$
Armature Inductance	${\mathbf{L}}_{\mathbf{a}}$	0.03 H
Viscous Friction	${\mathbf{B}}_{\mathbf{m}}$	0.1 N·m·s/rad
Rotor Inertia	$\mathbf{J}$	0.6 kg·m${}^2$/rad
Torque Coefficient	$\mathbf{K}$	1.85 V·s/rad
Torque Load	${\mathbf{T}}_{\mathbf{L}}$	15 N·m

When launching the R-COA, it is necessary to take into account that each parameter is constrained to lie in a given interval, summarized in Table 17. Therefore, the R-COA must adapt the ergodic areas of six chaotic waves to these constraints.

Table 17. Application to DC motor model parameters estimation: Search range for each parameter based on physical constrains.

Parameter	Parameter Symbol	Parameter Search Range
Armature Resistance	${\mathbf{R}}_{\mathbf{a}}$	0.1–0.8 ($\mathsf{\Omega }$)
Armature Inductance	${\mathbf{L}}_{\mathbf{a}}$	0.01–0.05 (H)
Viscous Friction	${\mathbf{B}}_{\mathbf{m}}$	0.05–0.5 (N·m·s/rad)
Rotor Inertia	$\mathbf{J}$	0.1–0.8 (kg·m${}^2$/rad)
Torque Coefficient	$\mathbf{K}$	1–2 (V·s/rad)
Torque Load	${\mathbf{T}}_{\mathbf{L}}$	10–20 (N·m)

3.3. Results for an Electrical Motor Driven by a Step Armature Voltage

In the first set of experiments, a reference step signal of 240 V of amplitude was applied as armature voltage. In this test condition, the velocity of the drive shaft ${\omega }_m$ rises until it reaches the steady-state value of $124.9103$ rad/s, while the armature current intensity decreases until it stabilizes at a value of $14.8600$ A. The transient lasts approximately $0.5$ second.

3.3.1. Separated Electrical and Mechanical Model Parameters Estimation

As a first test, only the electrical dynamics of the DC motor was considered as unknown, whereas the mechanical parameters were considered as exactly known. Namely, the armature resistance $R_a$ and armature inductance $L_a$ were taken as the only parameters to optimize for. In this test, the exact values of the torque load $T_L$ and of the torque coefficient K were made use of. In Table 18, the Error represents the difference between the value of the physical characteristic found by the algorithm and the value of the actual one, whereas the Total Error is the value of the objective function C in (23).

Table 18. Motor driven by a step armature voltage: Test on estimating the electrical model parameters only.

Carrier Wave	Total Loops	${\mathbf{R}}_{\mathbf{a}}$	Error	${\mathbf{L}}_{\mathbf{a}}$	Error	Total Error
First	202	0.6156	0.0156	0.0320	0.0020	1.1003
Second	953	0.6003	0.0003	0.0301	0.0001	0.0601

As a second test, only the mechanical dynamics of the DC motor was considered as unknown, whereas the electrical parameters were considered as exactly known. Namely, in the second case, the optimization variables are the viscous friction $B_m$ and the rotor inertia J. In this test, the exact values of the torque load $T_L$ and of the torque coefficient K were again made use of. In Table 19, the Error represents the difference between the value of the physical characteristic found by the algorithm and the value of the actual one, whereas the Total Error is the value of the objective function C in (23).

Table 19. Motor driven by a step armature voltage: Test on estimating the mechanical model parameters only.

Carrier Wave	Total Loops	${\mathbf{B}}_{\mathbf{m}}$	Error	J	Error	Total Error
First	272	0.0991	0.0009	0.6085	0.0085	1.0095
Second	432	0.0991	0.0009	0.6008	0.0008	0.0704

As can be readily seen in the above tables, the COA can obtain values that are very close to the actual ones, even without a refined search. The number of iterations needed to achieve such results appears as low.

3.3.2. Joint Electrical and Mechanical Model Parameters Estimation and Weights Analysis

In the definition of the absolute criterion C (23), the weights $k_a$ and $k_b$ are assigned to the armature current mismatch and to the drive shaft velocity mismatch, respectively. In the third test, different values for such weights were considered in order to achieve a joint electrical and mechanical model parameters estimation. In this test, the torque load $T_L$ was assumed equal to zero.

In Table 20, the parameters’ values are shown as obtained with both a low and an high number of iterations. In the latter case, it was evaluated the way that the quality of results improves while increasing the computation time. In the first two cases, even if slightly different results were obtained with few loops (521), it can be seen that both runs converge to the same values by increasing the iterations number. In the third case, the estimations are worse compared to the first two. Therefore, the values $k_a=1$ and $k_b=1$ will be used for the subsequent tests.

Table 20. Motor driven by a step armature voltage: Weights analysis for the joint electrical and mechanical model parameters estimation.

	Total Loops	${\mathbf{R}}_{\mathbf{a}}$	${\mathbf{L}}_{\mathbf{a}}$	${\mathbf{B}}_{\mathbf{m}}$	J	K	Total Error
Actual Value		0.6	0.03	0.1	0.6	1.85
${\mathbf{k}}_{\mathbf{a}}=\mathbf{1},{\mathbf{k}}_{\mathbf{b}}=\mathbf{1}$	521	0.5904	0.0295	0.0982	0.6388	1.8516	9.9568
	5229	0.5942	0.0312	0.1001	0.6503	1.8505	7.3798
${\mathbf{k}}_{\mathbf{a}}=\mathbf{1},{\mathbf{k}}_{\mathbf{b}}=\mathbf{0.5}$	521	0.6029	0.0295	0.1005	0.6521	1.8504	7.9601
	5229	0.5942	0.0312	0.1001	0.6503	1.8505	7.3798
${\mathbf{k}}_{\mathbf{a}}=\mathbf{1},{\mathbf{k}}_{\mathbf{b}}=\mathbf{2}$	582	0.5904	0.0295	0.0982	0.6399	1.8516	12.6972
	7143	0.5926	0.0321	0.1001	0.6503	1.8505	8.9209

As a side note, one might consider that the weights $k_a$ and $k_b$ may be regarded as constants that represent the measurements’ quality. For instance, if it is known in advance that the samples of the drive shaft’s velocity are affected by a measurement error, the Total Error could be reduced by modifying the constant $k_b$. That is to say, if it is known that a sensor is not particularly sophisticated or accurate, the weight related to the corresponding physical quantity could be adjusted. As a numerical example, Table 21 shows results obtained by adding a Gaussian noise drawn from a normal distribution to the drive shaft velocity and by adjusting the coefficient $k_b$. The Total Error obtained by setting $k_b=1$ increases drastically due to the noises added to measurements. By decreasing the weight $k_b$ by $70\%$ (namely, to $k_b=0.3$), the Total Error is reduced.

Table 21. Motor driven by a step armature voltage: Joint electrical and mechanical model parameters estimation in the presence of a disturbance on the drive shaft velocity measurements.

	Total Loops	${\mathbf{R}}_{\mathbf{a}}$	${\mathbf{L}}_{\mathbf{a}}$	${\mathbf{B}}_{\mathbf{m}}$	J	K	Total Error
Actual value		0.6	0.03	0.1	0.6	1.85
${\mathbf{k}}_{\mathbf{b}}=\mathbf{1}$	411	0.8000	0.0344	0.0703	0.2424	1.8328	139.2181
${\mathbf{k}}_{\mathbf{b}}=\mathbf{0.5}$	411	0.8000	0.0344	0.0703	0.2424	1.8328	139.2181
${\mathbf{k}}_{\mathbf{b}}=\mathbf{0.3}$	846	0.7993	0.0357	0.0888	0.5366	1.8010	114.2229

3.3.3. Full DC Motor Modeling

After the preliminary tests on modeling separated electrical/mechanical dynamics and after the evaluation of the criterion’s weights, the R-COA was used to obtain a solution to the full DC motor model’s parameter estimation. Several ergodic areas amplifiers were tested. Table 22 illustrates the best solutions found with a low and an high number of iterations.

Table 22. Motor driven by a step armature voltage: Full motor modeling results.

	Loops	${\mathbf{R}}_{\mathbf{a}}$	${\mathbf{L}}_{\mathbf{a}}$	${\mathbf{B}}_{\mathbf{m}}$	J	K	${\mathbf{T}}_{\mathbf{L}}$	Error	Parameter Error
Actual value		0.6	0.03	0.1	0.6	1.85	15
First carrier	1608	0.7693	0.0235	0.2053	0.7687	1.8285	13.5296	28.9436	5.1975
Second carrier	1766	0.6346	0.0339	0.0954	0.5253	1.8432	15.9757	18.0243	1.6334
Third carrier	1928	0.5594	0.0280	0.1004	0.5705	1.8551	15.5225	4.7574	0.9623
	4624	0.6274	0.3370	0.0992	0.5645	1.8465	15.6379	4.3600	1.0743

In the table, Total Error is defined as the sum of the differences between samples from the actual motors outputs and the outputs corresponding to the inferred parameters values. The Parameters Error is a performance index that allows one to evaluate the quality of the found parameters values and is defined as a weighted sum, namely

$$\mathrm{Param}.\mathrm{Error}=|R_a-R_{as}|+|B_m-B_{ms}|+10|J-J_s|+100|L_a-L_{as}|+\frac{1}{10}|T_L-T_{Ls}|.$$

(24)

Note that the weights of each term in the above sum were adjusted to balance the different values-ranges of the parameters.

The R-COA always converges towards the correct set of parameters, and the results are satisfactory. Comparing the obtained values of Total Error to the Parameters Error, two observations arise:

• These errors do not decrease proportionally: From the second and third carrier waves, the Parameters Error drops by $62.3$% and by $26.4$%, while the Total Error drops by $31.4$% and by $58.9$%.
• An improvement in the matching of the model responses to the actual responses does not always imply an improvement towards the correct parameters values. This may be due to the fact that there exists an infinite number of combinations of the parameters that correspond to the same model. In fact, from the state-space representation (22), it can be noticed that the model depends on a ratio between variables, namely, $L_a$ divides the electrical parameters while J divides the mechanical parameters: For this reason, infinite potential combinations are possible.

In Figure 14, a comparison between the response of the motor model, in terms of the armature current and of the velocity of the drive shaft, is shown. It is readily observed how the the steady-state responses, also reported in Table 23 for the convenience of the reader, look identical. The small differences of the two motors’ transient compose the Total Error.

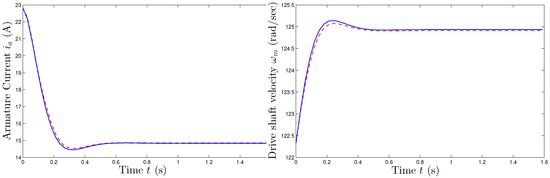
Figure 14. Motor driven by a step armature voltage: Comparison of the output curves. Blue-solid line: Actual motor response. Red-crosshatched line: Inferred motor model response.

Table 23. Motor driven by a step armature voltage: Actual steady-state values versus predicted values.

Armature Current		Drive Shaft Velocity
$i_a$	148,600	${\omega }_m$	1,249,102
$i_{as}$	148,379	${\omega }_{ms}$	1,249,340

3.3.4. Expansion of the Search Areas

To challenge the R-COA by increasing the problem’s difficulty, additional tests were conducted on expanded search areas of the electric motor’s physical characteristics compared to the ranges indicated in Table 17. Namely, in order to test the behavior of the R-COA when the search areas are badly estimated, the actual ranges were doubled and quadrupled, making them as indicated in Table 24. The R-COA always converges in spite of the enlarged search areas. The refined chaos-based optimization algorithm could find solutions that lay slightly apart from the actual ones and yet that minimize the absolute criterion. Table 25 presents the results of parameter estimation obtained after doubling the search areas, while Table 26 presents the results of parameter estimation obtained after quadrupling the search areas. Both Total and Parameters Error raise in the first and second carrier waves, while they decrease in the third one. If the number of iterations is quadrupled, the curves of the motor’s response get close to one another although the parameters’ precision does not improve. It can be observed that, even if the search areas increase, the number of iterations remains almost the same. In this case, the performance degrades, especially in the identification of the armature resistance $R_a$, with a minimum error of $0.0762$ on the actual value, and in the identification of the load torque $T_L$. The Total Error is $6.7405$, while in the previous tests did not exceed 5.

Table 24. Motor driven by a step armature voltage: Ranges for the parameters search areas doubled and quadrupled with respect to the values indicated in Table 17.

Constrains Expansion	${\mathbf{R}}_{\mathbf{a}}$	${\mathbf{L}}_{\mathbf{a}}$	${\mathbf{B}}_{\mathbf{m}}$	J	K	${\mathbf{T}}_{\mathbf{L}}$
Doubling	0.1–1.5	0.01–0.09	0.05–0.95	0.1–1.5	1–3	10–20
Quadrupling	0.1–2.9	0.01–0.17	0.05–1.85	0.1–2.9	1–5	10–50

Table 25. Motor driven by a step armature voltage: Results of parameters estimation by R-COA on doubled search areas.

	Total Loops	${\mathbf{R}}_{\mathbf{a}}$	${\mathbf{L}}_{\mathbf{a}}$	${\mathbf{B}}_{\mathbf{m}}$	J	K	${\mathbf{T}}_{\mathbf{L}}$	Total Error	Parameter Error
Actual value		0.6	0.03	0.1	0.6	1.85	15
First carrier	271	0.7077	0.0291	0.2256	0.3888	1.9174	11.6350	337.2882	10.7149
Second carrier	429	0.6041	0.0335	0.1051	0.6420	1.8668	15.9271	104.4469	4.9715
Third carrier	1531	0.5830	0.0306	0.1008	0.6645	1.8553	15.0930	12.6643	0.8976
	9037	0.6260	0.0297	0.0996	0.6589	1.8469	16.1967	4.7691	1.0058

Table 26. Motor driven by a step armature voltage: Results of parameters estimation by R-COA on quadrupled search areas.

	Total Loops	${\mathbf{R}}_{\mathbf{a}}$	${\mathbf{L}}_{\mathbf{a}}$	${\mathbf{B}}_{\mathbf{m}}$	J	K	${\mathbf{T}}_{\mathbf{L}}$	Total Error	Parameter Error
Actual value		0.6	0.03	0.1	0.6	1.85	15
First carrier	123	1.3366	0.1448	0.2094	0.8115	1.8609	16.45778	375.5978	22.2117
Second carrier	233	1.0405	0.0473	0.0959	0.2330	1.7996	16.1008	72.0653	7.0065
Third carrier	1349	0.5338	0.0312	0.0998	0.6371	1.8534	16.1937	24.6221	1.2778
	2582	0.7516	0.0429	0.0973	0.5987	1.8534	15.4716	6.7405	1.8114

The two panels of Figure 15 correspond to the values of the parameters reported in Table 25 and Table 26: The shown results seem to suggest that the more the search areas increases, the more the dynamics tend to differ, especially in the transient, while they always converge towards the same steady state.

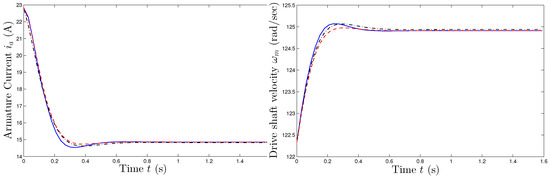
Figure 15. Motor driven by a step armature voltage: Comparison of responses corresponding to the values of the parameters reported in Table 25 and Table 26. Blue-solid lines: Actual response. Red-crosshatched line: Response corresponding to the values of the parameters inferred upon doubling the search areas. Black dot-dashed lines: Response corresponding to the values of the parameters inferred upon quadrupling the search areas.

3.4. Comparison with the Genetic Algorithm and the Simulated-Annealing Based Algorithm

As a last test, the solutions computed by means of the R-COA were compared to the solutions found by means of a Genetic Algorithm and a Simulated Annealing algorithm. Each optimization algorithm was run 10 times for each input type. Table 27 illustrates the average results. In particular, the bold-faced values are the best estimations for every parameter (e.g., for the Total loops, the parameter $R_a$ and the parameter $L_a$). In this way, it is also clear what algorithm performs the best on a particular parameter or figure.

Table 27. Estimation of a DC motor parameters: Comparison of the R-COA with the SA algorithm and the GA.

		Results
	Algorithm	R-COA	GA	SA
	Total Loops	4624	1578	9767
${\mathbf{R}}_{\mathbf{a}}$	0.6	0.6274	0.4048	0.3873
${\mathbf{L}}_{\mathbf{a}}$	0.03	0.0337	0.0183	0.0139
${\mathbf{B}}_{\mathbf{m}}$	0.1	0.0992	0.0511	0.0500
$\mathbf{J}$	0.6	0.5645	0.5147	0.4123
$\mathbf{K}$	1.85	1.8465	1.8508	1.8475
${\mathbf{T}}_{\mathbf{L}}$	15	15.6379	13.2203	14.8479
	Total Error	4.3600	204.1683	242.6949
	Parameter Error	1.0743	4.6403	6.1314

The GA is always able to keep the number of total loops low, whereas the SA algorithm in a few cases gets over 3000 iterations. On the other hand, the R-COA exhibits considerably reduced computing time. Quantitatively, it took about 120 min to run the GA- and SA-based experiments, while it took only 10 min to run the R-COA-based experiments (all the computer codes were written in MATLAB and were run on a 2.40 GHz, 4 GB RAM, Intel-based PC).

Genetic algorithm and Simulated Annealing Algorithm rarely converge towards the correct solution; in fact, R-COA’s Total Error is equal to the $5\%$ of the other two algorithms’ error. These two algorithms, due to the parameters’ imprecision, show a mean-square error, for every measurement, equal to $3.7808$ for the GA and equal to $4.4943$ for the SA.

Figure 16 illustrates the motor responses modeled by the three optimization algorithms.

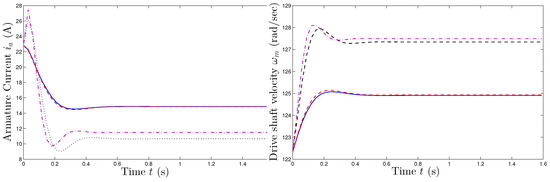
Figure 16. Estimation of a DC motor parameters: A comparison of motor responses between models instantiated with parameters estimated by the R-COA, GA and SA algorithm. In the two panels, the solid (blue) lines denote the expected responses, the crosshatched (red) lines denote the results corresponding to the R-COA-based optimization, the dashed (black) lines denote the results pertaining to the GA-based optimization, while the dot-dashed (purple) lines correspond to the SA-based optimization.

In general, COA and R-COA manage, on the one hand, to map the whole constrained area (maintaining a low computational complexity thanks to algorithm design) and, on the other hand, to explore gradually smaller sections by the chaotic wave mechanism that allow to refine the solution without getting lost in parameter space and in local minima. This can be an intuitive explanation of why it outperforms both GA and SA in the benchmark function analysis and in the motor modeling problem. For these reasons, chaotic methods have successfully been exploited in other areas, such as neural-network training, thanks to their excellent optimization abilities (see, for example, [20]).

4. Conclusions

The aim of the research endeavor summarized in the present paper was to investigate the COA, a global optimization algorithm based on the properties of chaotic waves.

The optimization features of the COA were first tested by means of a series of numerical experiments performed on seven benchmark functions, drawn from the scientific literature, that afforded getting an insight into the fundamental properties of this algorithm, which is based on the notion of two carrier waves. Such preliminary numerical tests also led to an interesting refinement that consisted in introducing a third carrier wave, which significantly improves the algorithm’s efficacy as it allows refining the solution at a little expense in terms of optimization loops.

The obtained R-COA algorithm was then applied to a real-world optimization problem, namely, a direct-current electric motor modeling. Several experiments were carried out, where the electrical and mechanical dynamics were analyzed separately or the search areas of the carrier waves were expanded. The same tests were performed using two different optimization algorithms: the genetic algorithm and the simulated annealing algorithm. The comparison with GA and SA highlights COA’s good features: convergence and low computing time.

It is important to emphasize that the effectiveness of COA and R-COA is highly related to the choice of its more important operator, the chaotic map. Further investigations could be carried out to find maps that would grant even better performances. Moreover, for future research, it could be interesting to carry out a more extensive study about both evolutionary strategies to set the ergodic areas’ amplifiers and about the extension of the modeling problem to control.