Modeling the Double Peak Phenomenon in Drug Absorption Kinetics: The Case of Amisulpride

Abstract

An interesting issue observed in some drugs is the “double peak phenomenon” (DPP). In DPP, the concentration-time (C-t) profile does not follow the usual shape but climbs to a peak and then begins to degrade before rising again to a second peak. Such a phenomenon is observed in the case of amisulpride, which is a second-generation antipsychotic. The aim of this study was to develop a model for the description of double peaks in amisulpride after oral administration. Amisulpride plasma C-t data were obtained from a 2 × 2 crossover bioequivalence study in 24 healthy adult subjects. A nonlinear mixed-effects modeling approach was applied in order to perform the analysis. Participants’ characteristics, such as demographics (e.g., body weight, gender, etc.), have also been investigated. A model for describing the double peak phenomenon was successfully developed. Simulations were run using this model to investigate the impact of significant covariates and recommend appropriate dosage regimens. For comparison purposes and to investigate the suitability of our developed model for describing the double peak phenomenon, modeling of previously published population pharmacokinetic models was also applied to the C-t data of this study.

1. Introduction

Amisulpride is a second-generation antipsychotic, a substituted benzamide derivative, and a highly selective antagonist of dopamine D2 and D3 receptors [1,2]. Amisulpride is commonly used for the treatment of acute and chronic schizophrenia [3,4,5,6]. The recommended dose to treat schizophrenia is 400–800 mg daily, with the starting dose being 200–400 mg daily, increasing to 800 mg daily, with 50–300 mg daily suggested for those experiencing predominantly negative symptoms [7]. The consensus guidelines consider amisulpride therapeutic drug monitoring as “strongly recommended” and its therapeutic reference ranges trough concentrations of 100–320 ng/mL, with a laboratory alert level of 640 ng/mL [8,9,10,11,12,13]. Nevertheless, high inter-individual variability of amisulpride kinetics has been observed in patients, and a considerable percentage of patients have concentration levels outside the reference range [13,14].

After oral administration, amisulpride concentration—time (C-t) profiles present two absorption peaks, one that occurs rapidly and reaches peak plasma concentration (Cmax) after 1 h, and a second between 3 and 4 h after administration [15,16,17]. Amisulpride shows relatively low bioavailability which can be attributed to its poor solubility at the relatively high pH of the small intestine, due to its weak basic nature (pKa 9.37) [18]. Low bioavailability can also be due to its strong affinity for the P-glycoprotein efflux pump [19]. Almost the entire amount of amisulpride is eliminated by the kidneys, without any hepatic metabolism or known interactions, has a plasma elimination half-life of approximately 12 h and a high renal clearance of 17–20 L/h suggesting additional renal secretion [20], possibly through the organic cation transport (OCT) system [21,22]. Therefore, there is little probability that CYP450 enzyme activity or metabolic enzyme gene polymorphisms will take place when using amisulpride [1]. In addition, amisulpride is a substrate for the organic ion transporters SLC22 that are found in the kidneys. This demonstrates that active renal secretion is most likely to be the primary route of elimination [21].

The disposition of amisulpride has previously been described by a two-compartment model [15,17,23,24]. Contrary to the previous studies, two recent studies reported that a one-compartment model can characterize amisulpride kinetics [25,26]. However, none of these studies is able to describe the biphasic absorption behavior of amisulpride which is reflected in the presence of double peaks in the C-t profile of the patients. The double peak phenomenon is one of the complexities that can appear in the absorption phase for orally administered drugs [27] and could have significant therapeutic and drug interaction implications, due to the underlying mechanism.

The aim of this study was initially to develop a model for the description of double peaks in amisulpride after oral administration. Covariates such as demographics (e.g., body weight, gender, etc.) have also been investigated. Following the development of the model and investigation of the covariate correlation, various dosage regimens were simulated in order to investigate C-t levels after multiple dosing and propose the most appropriate of them. In addition, simulations have been performed to explore the impact of significant covariates, such as body weight, on steady-state levels of amisulpride and examine the necessity of dose adjustment. For comparison purposes and to investigate the suitability of our developed model for describing the double peak phenomenon, previously published models were also examined for their applicability to the C-t data of this study.

2. Materials and Methods

2.1. Dataset

Amisulpride plasma concentration to time (C-t) data were obtained from a bioequivalence study that used a typical open-label, single-dose, two-period, two-sequence, balanced randomized crossover design, in healthy adult subjects under fasting conditions comparing two immediate-release oral products containing 400 mg amisulpride (amisulpride 400 mg f.c. tabs/Verisfield SA vs. 400 mg f.c. tabs Solian^® Sanofi). The study followed the International Conference on Harmonization’s Good Clinical Practice guidelines and was carried out in accordance with the principles of the Helsinki Declaration. An independent Ethics Committee examined and approved the study protocol. In addition, the Greek National Organization for Medicines approved the study protocol in accordance with local rules. Before enrolling in the study, each subject provided written informed consent. For this analysis, the pharmaceutical company (Verisfield SA) provided us with the individual C-t data (in blind form) and the covariates, and our study had nothing to do with the bioequivalence study or any other parts of the aforementioned study.

Twenty-four healthy subjects were included in the study; they ranged in age from 18 to 55, had a body mass index (BMI; calculated as the ratio: weight (Kg)/height (m²) between 18.5 and 30 Kg/m²), did not smoke, were not pregnant or nursing, and tested negative for drugs of abuse, alcohol, and HIV in urine tests. To guarantee the subjects’ health, they all had to undergo a series of tests and screenings, including a physical examination, ECG analysis, laboratory analyses, and a review of their medical histories.

All subjects were randomly allocated into two groups, orally receiving either one dose of the test product containing 400 mg amisulpride/Verisfield and the reference product containing 400 mg amisulpride Solian^® (Sanofi), with a washout period of at least 7 days between the two administrations. After an overnight fast, the medication was taken orally with about 240 mL of water. For each subject, 22 blood samples (each of 5.0 mL) were collected before the dose (0 h) and at 0.25, 0.5, 0.75, 1, 1.25, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 7, 8, 10, 12, 24, and 36 h after drug administration. After the appropriate sample preparation procedures, a validated HPLC method with a fluorescence detector was used to quantify amisulpride in plasma samples. The lower limit of quantification was 10 ng/mL and the calibration range was 10–1500 ng/mL.

2.2. Non-Linear Mixed Effect Modeling

2.2.1. General

The C-t data for amisulpride were analyzed using a nonlinear mixed-effects modeling strategy. The maximum likelihood estimators of the population parameters were estimated using the implemented stochastic approximation expectation maximization algorithm, with the stochastic (k1) and cooling (k2) iteration maximums set at 500 and 200, respectively, with automatic stopping rules and a single Markov chain. The final population parameters were determined by computing the objective function value with a Monte Carlo importance sampling approach. Monolix^TM 2021R2 (Lixoft^TM, Simulation Plus Inc., Lancaster, CA, USA) software was used for the entire modeling exercise.

2.2.2. Structural Model and Absorption Models

An initial stage involved determining how many compartments would be needed to adequately describe the amisulpride distribution. In order to investigate the double peak phenomenon, special focus was placed on the description of absorption. Initially, one-, two-, and three-compartment models with first-order elimination were examined. Secondly, since dual peaks were observed in the C–t profiles of subjects arising from absorption problems, conventional models proved inadequate to describe the complex recirculation kinetics of the drug. For this reason, several other absorption models were explored using previously published approaches assuming models with additional pre-absorption compartments, parallel absorption, delay functions, and their combination order to describe the double peaks (

Table 1. The development path of the model of amisulpride. Only a few of the most important models are shown among the many that have been tested.

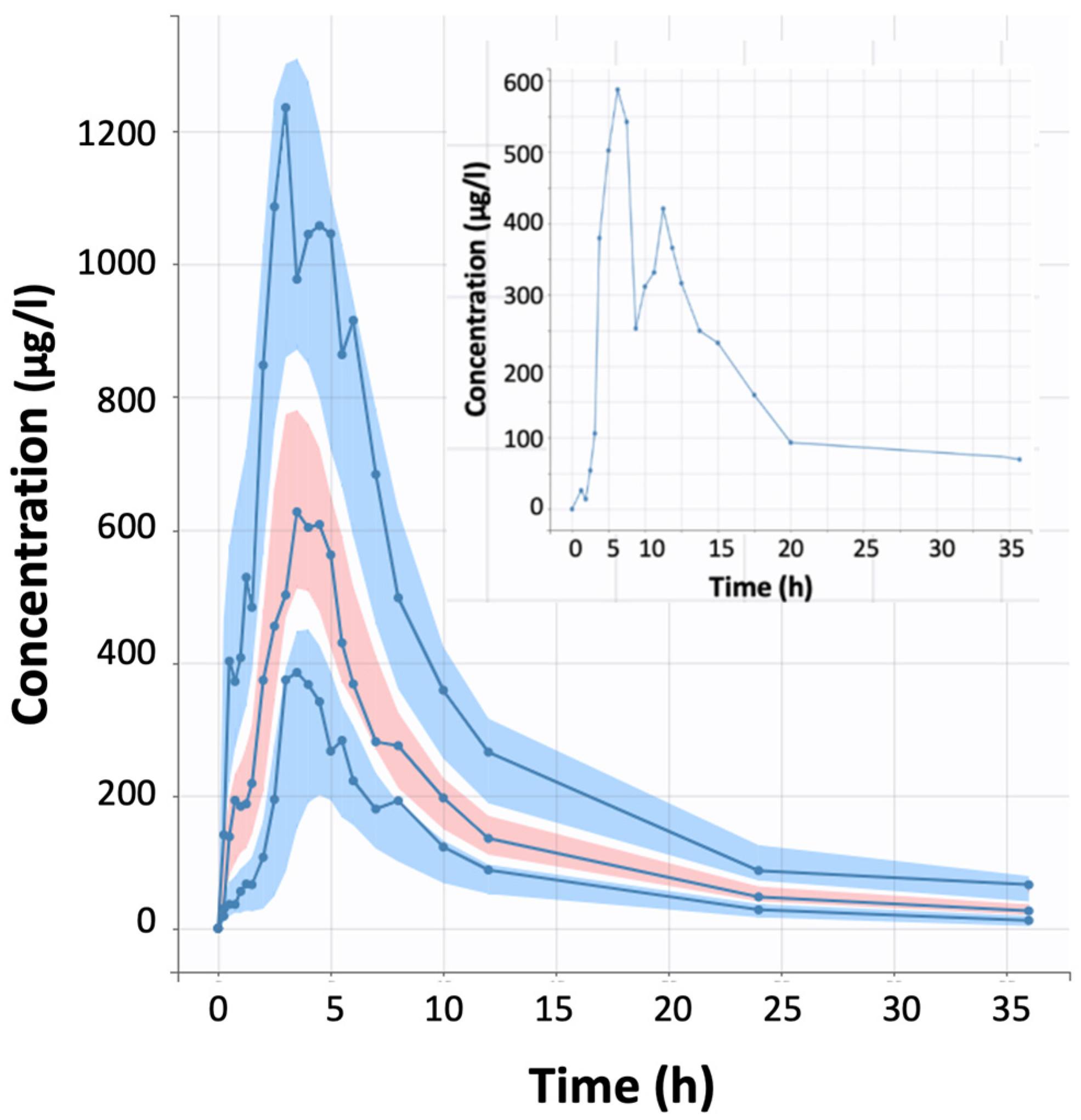
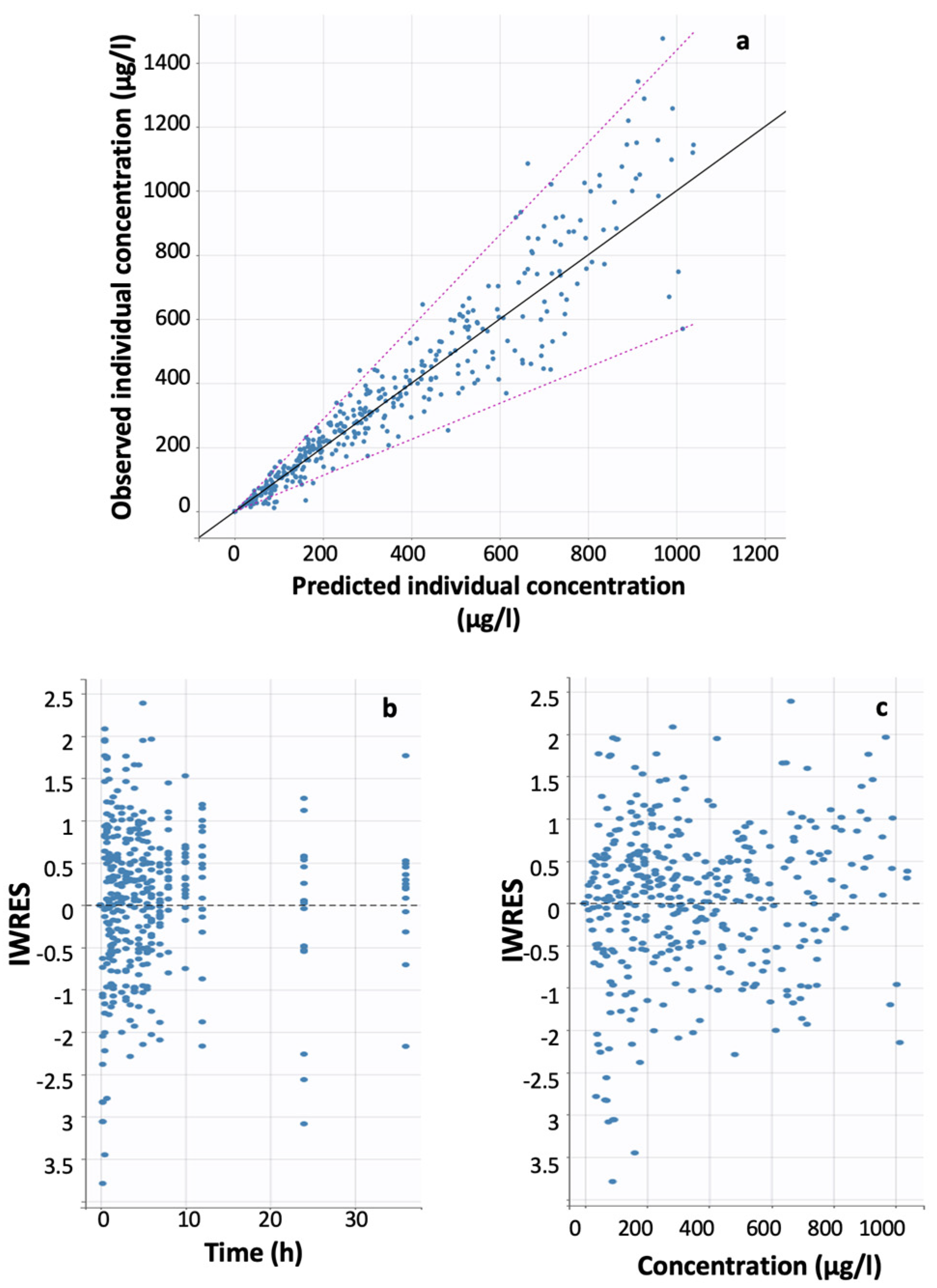
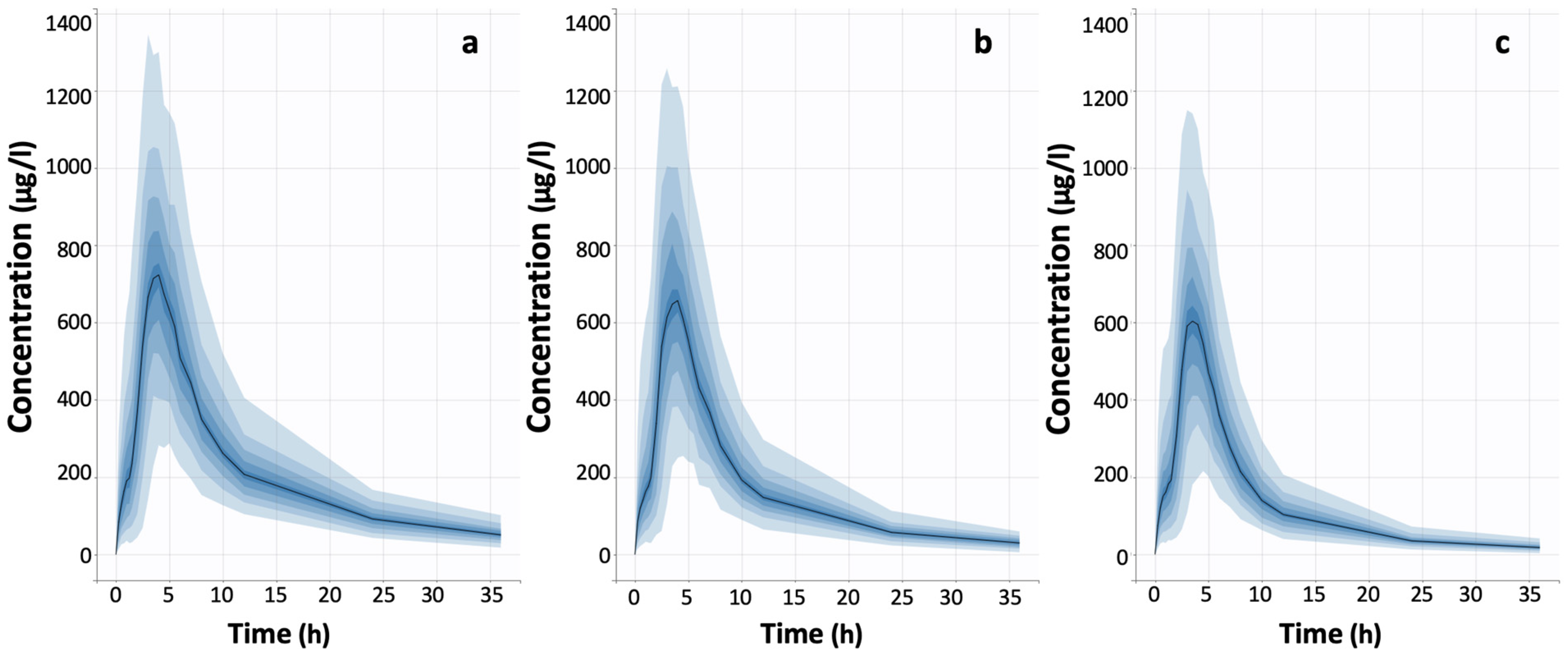
Model ID	Model Short Description	Statistical Criterion a
		−2LL	AIC	BIC
1	1-compartment model, first-order absorption	3642.7	3656.7	3663.31
2	1-compartment model, first-order absorption with lag time	3615.59	3633.59	3642.09
3	1-compartment model, first-order absorption, and transit compartment	3539.82	3561.82	3572.21
4	2-compartment model, first-order absorption	3572.16	3594.16	3604.55
5	2-compartment model, first-order absorption with lag time	3533.54	3559.54	3571.81
6	2-compartment model, first-order absorption, and transit compartment	3477.93	3507.93	3522.09
7	2-compartment, first-order absorption followed by first-order absorption	3574.6	3604.6	3618.76
8	2-compartment, first-order absorption followed by first-order absorption with lag time	3287.38	3321.38	3337.44
9	2-compartment, first-order absorption followed by zero-order absorption with lag time	3297.2	3331.2	3347.25
10	2-compartment model, zero-order absorption followed by first-order absorption with lag time	3348.72	3382.72	3398.78
11	3-compartment model, first-order absorption	3572.91	3602.91	3617.08
12	3-compartment model, first-order absorption with lag time	3533.13	3567.13	3583.18
13	3-compartment model, first-order absorption, and transit compartment	3486.41	3524.41	3542.35
14	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: body weight on V1/F (p = 0.28)	3286.95	3322.95	3339.95
15	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: body weight on V2/F (p = 0.68)	3286.11	3322.11	3339.11
16	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: age on CL/F (p = 0.53)	3285.61	3321.61	3338.61
17	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: gender on CL/F (p = 0.40) and body weight on CL/F (p = 0.00)	3279.23	3317.23	3335.18
18	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: age on CL/F (p = 0.48) and body weight on CL/F (p = 0.00)	3278.46	3316.46	3334.41
19	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: body weight on CL/F (p = 0.012)	3278.89	3314.89	3331.89
20	2-compartment, first-order absorption followed by first-order absorption with lag time Covariates: body weight on CL/F (p = 0.01) Correlations: Q/F and CL/F, ka1 and F	3254.61	3294.61	3313.5

^a −2LL, AIC and BIC are the −2 log-likelihood, Akaike information criterion and Bayesian information criterion, respectively. Key: F:, bioavailability fraction, V1/F: apparent volume of distribution, V2/F: apparent volume of distribution of the peripheral compartment, CL/F: apparent clearance, Q/F: apparent inter-compartment clearance.

) [28,29,30,31]. In particular, different first-order, first-order with a constant delay time (Tlag) which helps with delayed absorption profiles by describing drug absorption as a multi-step process represented by a chain of pre-systemic compartments, and first-order with transfer compartment kinetics were evaluated to determine the optimal absorption rate. The rate of change of the amount of drug in the nth compartment at time t (da_n/dt) is given by Equations (1)–(3):

$$\frac{{\mathrm{da}}_{\mathrm{n}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{tr}}{\mathrm{a}}_{\left(\mathrm{n}-1\right)}-{\mathrm{k}}_{\mathrm{tr}}{\mathrm{a}}_{\mathrm{n}}$$

(1)

where ${\mathrm{a}}_{\mathrm{n}}$ is the amount of drug in the nth compartment at time t, ${\mathrm{k}}_{\mathrm{tr}}$ refers to the transit rate constant, and n reflects the number of transit compartments. Using the approximation of Stirling $\mathrm{the} \mathrm{n}!\approx \sqrt{2\mathsf{\pi } }{\mathrm{n}}^{\mathrm{n}+0.5}{\mathrm{e}}^{-\mathrm{n}}$ and the number of compartments, then the analytical solution for ${\mathrm{a}}_{\mathrm{n}}$ becomes:

$${\mathrm{a}}_{\mathrm{n}}\left(\mathrm{t}\right)=\mathrm{Dose}·\mathrm{F}\frac{{\left({\mathrm{k}}_{\mathrm{tr}} \mathrm{t}\right)}^{\mathrm{n}}}{\mathrm{n}!}{\mathrm{e}}^{-{\mathrm{k}}_{\mathrm{tr}} \mathrm{t}}$$

(2)

Thus, the absorption compartment model is given by:

$$\frac{{\mathrm{dA}}_{\mathrm{a}}}{\mathrm{dt}}=\mathrm{Dose}·\mathrm{F}·{\mathrm{k}}_{\mathrm{tr}}\frac{{\left({\mathrm{k}}_{\mathrm{tr}} \mathrm{t}\right)}^{\mathrm{n}}{\mathrm{e}}^{-{\mathrm{k}}_{\mathrm{tr}} \mathrm{t}}}{\mathrm{n}!}-{ \mathrm{k}}_{\mathrm{a}}·{\mathrm{A}}_{\mathrm{a}}$$

(3)

By using this model, we can calculate an average time for amisulpride to travel from the first transit compartment to the absorption compartment [31]. In addition, dual absorption rates were tested with first-order followed by first-order, first-order followed by zero-order absorption, and zero-order followed by first-order. It is hypothesized that two distinct kinetic absorption processes are at work here. A model can be understood as the result of amisulpride solubility-limited absorption in the GI tract fluid if the first-order rate constant is related to the zero-order input parameters [32]. Using Monolix^TM encoding language Mlxtran, all models were represented as systems of ordinary differential equations. The initial parameter values were based on the literature [23,24,25,26].

The parameters were assumed to follow a lognormal distribution, while inter-individual variability was modeled using an exponential distribution. Each parameter’s random effect (η) has a normal distribution with a mean of 0 and an estimated variance of ω². Furthermore, the objective function and the comparison of goodness-of-fit plots were used to evaluate several error models of residual variability. These models included constant, proportional, and mixed constant and proportional models.

In addition to choosing a suitable baseline model, we also investigated how different covariates affected the resulting model parameters. Demographic factors such as age, height, weight, and body mass index (BMI) were included, as were laboratory data taken at the time of the screenings. Covariate analyses were performed utilizing both forward and backward selection steps. Allometric and linear tests, with and without transformation to a “mean” value, were used to assess the significance of continuous factors. The apparent volume of distribution and clearance parameters were also allometrically scaled, both a priori and based on standardization to a body weight of 70 Kg and set exponents (1 for the central and peripheral volumes of distribution and 0.75 for clearance). When analyzing continuous and categorical factors separately, the Pearson correlation test and one-way test ANOVA were utilized. To determine if the covariates could account for the variance in the model’s parameters, a Wald test was used. The level of significance was fixed at 5% in all studies. Reducing −2LL values, improving parameter precision as reflected by relative standard error, decreasing parameter values’ between-subject variability, and ensuring each covariate on a parameter is physiologically sound all play a role in deciding whether or not to include it in the final model.

2.2.3. Model Evaluation

Goodness-of-fit tests and visualizations were used to help determine the pool of possible models and pick one with the fewest errors or inconsistencies [33]. Relative standard errors (RSE%) were also used to evaluate the accuracy of the parameter estimates. Non-hierarchical models were evaluated using statistically significant numerical criteria, such as the log-likelihood, Akaike, and Bayesian information criteria.

The plots of observed values vs. predicted values for the population and individual weighted residuals versus concentrations or time were used for the graphical evaluation of goodness of fit. The predictive performance, stability, and robustness of the model were further evaluated using visual predictive check plots (VPCs). VPCs provide a graphical representation of the comparison between the observed data and the model’s predicted distribution. A total of 1000 Monte Carlo runs and 90% prediction intervals were used to create the VPCs.

2.3. Simulations

The resultant model was utilized to replicate the C-t profiles of amisulpride across three weight distribution values. There were three simulated subject groups of 1000 subjects each: (a) subjects weighing 50 Kg, (b) subjects weighing 70 Kg, and (c) subjects weighing 100 Kg.

Amisulpride blood concentrations were also simulated at steady state in the final model-based simulations using typical parameter estimates under regular oral administration of regularly used dosage regimens selected at (a) 200 mg, (b) 400 mg, and (c) 800 mg amisulpride. To serve as a tool for treatment regimen selection for diverse clinical populations, the simulated concentrations, represented by population projected values, were compared with the upper border of the indicated therapeutic range (320 ng/mL) and the laboratory alert level (640 ng/mL). Simulx^® was used for all simulations (Monolix^TM 2021R2, Simulation Plus Inc., Lancaster, CA, USA).

3. Results

The amisulpride C-t data of the 24 male and female subjects, who completed the two periods of the study, were included in the computational analysis. The mean age of the study population was 29 years (range 21–43 years), the mean body weight was 78.3 Kg (range 55–98.7 Kg), the mean height was 177 cm (range 165–187 cm), and the mean BMI was 26.5 kg/m² (range 18.9–29.9 Kg/m²). In total, 1056 C-t values were analyzed, while less than 5% of the samples were below the lower limit of quantification.

3.1. Developed Model

The kinetics of amisulpride were best explained by a two-compartment model with first-order oral absorption and elimination. The development path of models, along with their description and statistical criteria, is shown in Table 1. A wide variety of approaches were applied to model dual peaks. Based on the aforementioned models and their evaluation criteria, dual peaks of amisulpride were best described by two parallel first-order absorption processes. The final model was a two-compartment setup wherein the first-order absorption rate was followed by a second-order absorption rate, lag time, and first-order elimination (Table 1). The physiological characteristics of amisulpride absorption led to the need for a better model, and the term Tlag was developed to indicate the lag time of the second first-order process relative to the first.

For the examined models of residual error, the proportional error model (Equation (4)) led to the optimal performance of the residual variability consisting of a multiplicative coefficient b:

$${\mathrm{C}}_{\mathrm{ij}}={\mathrm{f}}_{\mathrm{ij}}+\mathrm{b}·{\mathrm{f}}_{\mathrm{ij}}·{\mathsf{\epsilon }}_{\mathrm{ij}}$$

(4)

where ${\mathrm{C}}_{\mathrm{ij}}$ is the j_th observed concentration of amisulpride for the i_th individual, ${\mathrm{f}}_{\mathrm{ij}}$ is the projected value from the model for the i_th subject, and ε_ij refers to the random error, considered to be normally distributed with mean 0 and variance 1.

The model parameter estimates along with their RSE (%) for each parameter of the final best model are shown in

Table 2. Final model parameter estimates.

Parameters (Units)	Value	Standard Error	Relative Standard Error (%)	p-Value
Fixed effects
ka1 (h−1)	0.76	0.16	21.1
ka2 (h−1)	0.91	0.17	18.6
z	0.30	0.08	29.0
Tlag2 (h)	1.95	0.16	8.38
CL/F (ml/h)	57.87	4.34	7.49
V1/F (ml)	202.12	22.62	39.0
Q/F (ml/h)	46.74	9.45	11.2
V2/F (ml)	467.11	120.07	20.2
Beta weight on CL	0.82	0.32	25.2	0.01
Random effects
ω_ka1	1.32	0.32	23.8
ω_ka2	0.43	0.14	31.8
ω_z	1.46	0.35	23.9
ω_Tlag2	0.32	0.06	19.4
ω_CL	0.22	0.04	20.3
ω_V1	0.076	0.007	10.1
ω_Q	0.65	0.14	21.3
ω_V2	0.5	0.16	32.5
Correlations
p(Q, CL)	0.8	0.15	18.8
p(ka1, z)	−0.68	0.19	28.5
Error model parameters
b	0.27	0.01	4.79
Estimated log-likelihood and information criteria
−2LL	3254.61
AIC	3294.61
BIC	3313.5
BICc	3340.97

Key: ka1: absorption rate constant of the first absorption process, ka2: second absorption rate constant, Tlag2: lag time of the second absorption rate ka2, z: ratio of dose fractions absorbed either by the first or the second absorption process, F: bioavailability fraction, V1/F: apparent volume of distribution of the central compartment, V2/F: apparent volume of distribution of the peripheral compartment, CL/F: apparent clearance, Q/F: apparent inter-compartment clearance, Beta weight on CL/F: allometric scaling factor for weight log transformed and centered around a standard 70 kg weight, b: proportional component of the error model, p: Pearson’s correlation coefficients of random effects, −2LL: 2 Loglikelihood, AIC: Akaike information criterion, BIC: Bayesian information criterion, BICc: Corrected Bayesian information criterion.

. The model parameters estimated were the first absorption rate constant (ka1 = 0.76 h⁻¹) and the second absorption rate constant (ka2 = 0.91 h⁻¹) with a lag time (Tlag2 = 1.95 h) in the central compartment. The ratio of dose fractions absorbed either by the first (z) or the second (1–z) absorption processes were equal to 0.30 and 0.70, respectively. The apparent volumes of distribution (V1/F = 202.12 mL and V2/F = 467.11 mL), apparent intercompartmental clearance (Q/F = 46.74 mL/h), and clearance from the central compartment (CL/F = 57.87 mL/h) were also calculated.

From the available covariates, bodyweight, which was log-transformed and centered around a standard 70 Kg was found to be an important covariate on CL (p = 0.01) and improved the final model. Thus, the model function for the apparent clearance is given by

CL = CL_pop/F (Weight/70)^0.82 e^ηCL/F

(5)

The Q/F and CL/F random effects were also found to be correlated (R = 0.8), as were ka1 and z (R = −0.68).

The relatively small RSE (%) results confirmed the accuracy and reliability of the parameter estimates (Table 2). The relevant VPC plot verified that the model’s prediction ability and robustness correctly described the data (Figure 1). The generated model’s prediction interval incorporates experimental concentration data over all percentiles, as depicted by the visual depiction of predictive performance. Figure 1 also depicts a typical individual’s dual peaks in a spaghetti plot. An example of a graphical model evaluation criterion is shown in Figure 2a, which superimposes the results of several models onto the data to see how well they describe the data. This is further confirmed by the fact that both the individual weighted residuals vs. time (Figure 2b) and concentration (Figure 2c) exhibit a balanced distribution around the zero line (Figure 2c).

3.2. Simulations

As quoted above, during the model’s development, body weight significantly affected the apparent clearance. To investigate the impact of body weight on amisulpride kinetics, simulations were performed using the final model. All parameter estimations were held constant while the bodyweight distribution’s extremes fluctuated; the selected bodyweight values were 50, 70, and 100 Kg. As can be seen in Figure 3, higher plasma concentrations are produced as body weight decreases. The simulated profiles obviously affected the decrease in amisulpride clearance in relation to the subject weight.

Furthermore, the final model was utilized to replicate amisulpride C-t profiles after oral administration of three regularly used dose regimens at steady-state (Figure 4). Daily dosages of 200 mg, 400 mg, and 800 mg were chosen and simulated at steady-state. The therapeutic reference range for amisulpride is 100–320 ng/mL, according to consensus standards for therapeutic drug monitoring [8]. The model-based simulation findings showed that the recommended dose of amisulpride was less than 200 mg in order to maintain the concentration in the therapeutic reference range and not exceed the top limit of the reference range (320 ng/mL). Similarly, the results of the model-based simulation revealed that the suggested dose of amisulpride was less than 400 mg based on the laboratory alert level (640 ng/mL) [11].

4. Discussion

Amisulpride kinetics shows high interindividual variability, and a significant proportion of patients have concentration levels that are outside the recommended range [13,14]. Furthermore, dual peaks appear in the majority of profiles, indicating most likely absorption complexity. The utilized amisulpride C-t data were taken from a crossover bioequivalence study in 24 participants; thus, using 48 C-t profiles of amisulpride to perform the analysis. Several combinations of structural and error models, absorption kinetics, and initial parameter estimates were investigated. Table 1 shows several illustrative models created during the model development process. The best performance was found in the case of a two-compartment disposition model with two parallel first-order processes, the second of which had a lag-time relative to the first. Elimination from the central compartment occurred in all cases using first-order kinetics.

Table 2 shows the population parameter estimations as well as their RSE% estimates. The clearance and volume of distribution parameter estimations are extremely close to those reported in earlier investigations [23,24,25,26]. In two prior investigations [23,24], two-compartment models were used to characterize amisulpride kinetics. Despite the fact that amisulpride kinetics has been described by a one-compartment model structure, none of these models characterized the twin peaks of amisulpride kinetics [25,26]. One of the complexes in the absorption phase following a single oral dose is the double peak phenomenon [34,35]. With the contrast between reference and test formulation, complex absorption is also difficult to model for the right interindividual and intraindividual variability. Many methods have been utilized in the literature to model dual and multiple peaks in modeling involving principally extra compartments, lag durations, and modeling using two or more first and zero-order absorption rate constants for distinct fractions of the molecule [28,29,30,31,35,36,37,38,39].

Amisulpride has a low oral bioavailability (48%) [40,41], which could be related to its poor solubility in the high pH of the colon, due to its weak basic nature (pKa = 9.37) [18], or to its high binding affinity to the P-glycoprotein efflux pump [19]. Inadequate time for absorption in the gastrointestinal tract, in particular, is a typical reason for inadequate bioavailability. The time at the absorption site may be insufficient if the drug does not dissolve easily or cannot pass the epithelial barrier (for example, if it is highly ionized and polar). In such instances, bioavailability is both very variable and low. Thus, the double peak phenomena in amisulpride kinetics could be caused by delayed stomach emptying and/or absorption variability. Because very little drug absorption occurs from the stomach relative to the small intestine in the case of variable gastric emptying, the drug is held in the stomach until it is transported to the small intestine and subsequently absorbed [42]. The heterogeneity in absorption within different parts of the stomach, on the other hand, is another common cause of the multiple peak phenomena [33]. When absorption occurs in distinct gut sections, it signifies that the jejunum absorbs nothing or very little compared to the duodenum and ileum. As a result, these medications supersaturate and/or precipitate as they pass from the stomach to the small intestine, and absorption may be delayed because they must pass through the small intestine to be digested and absorbed.

Covariate effects were explored for their impact on model parameters in order to explain the interindividual heterogeneity in amisulpride kinetics. Body weight was the only covariate that had a significant effect on clearance. This finding was supported by additional investigations [23,25]. None of the other covariates investigated had a significant effect on any of the amisulpride model parameters (i.e., p > 0.05) or improved the numerical or graphical criteria of the final model (Table 1). The population model developed was used to assess the impact of body weight on the kinetics of amisulpride (Figure 3). Higher plasma concentrations are created in simulated healthy persons when body weight drops.

For comparison, previously reported population models for amisulpride were fitted to our study’s concentration-time data [23,24,25,26]. The model estimates were those reported in the literature (

Table 3. Population models for amisulpride reported in the literature.

Clinical Study	Reeves et al., 2016 [23]	Reeves et al., 2017 [24]	Glatard et al., 2019 [25]	Huang et al., 2021 [26]
Patient population	Healthy elderly participants with Alzheimer’s disease	Healthy older people (n = 20) Alzheimer’s disease and very late onset schizophrenia-like psychosis (n = 31)	Patients with schizophrenia and schizotypal disorders	A retrospective study of data from psychiatric inpatients (Chinese patients with schizophrenia) (mean age = 32 years)
Sample size	45	51	242	121
Route of administration	oral 50 mg/day	oral 50 mg/day	oral	oral amisulpride with serum drug concentration monitoring
Software	Monolix	Monolix	NONMEM	ΝOΝΜΕΜ
Structural model	Two-compartment model with first-order elimination	Two-compartment with first-order absorption and elimination	One-compartment model with first-order absorption and elimination	One-compartment model with first-order absorption and elimination
Residual error model	proportional	proportional	proportional	proportional
Parameter estimates	ka = 0.87 h−1 Cl/F = 84 l/h V1/F = 668 l (men) V1/F = 399 (women) Q/F = 117 l/h V2/F = 808 l	ka = 0.83 h−1 Cl/F = 51.5 l/h V1/F = 440 l Q/F = 111 l/h V2/F = 741 l	ka = 0.9 h−1 Cl/F = 44 l/h V/F = 956 l	ka = 0.18 h−1 Cl/F = 61.1 l/h V1/F = 1720 l
Correlations	Between CL, Q, V1 and V2	NA	NA	NA
Covariates	V1/F: Gender (β_gender = −0.52) V1/F: weight V2/F: weight Cl/F: weight Q/F: weight	NA	CL/F: Age, Weight	CL/F: Age

Key: F: bioavailability fraction, V, volume of distribution, ka, absorption rate constant; V1/F: apparent volume of distribution of the central compartment, V2/F: apparent volume of distribution of the peripheral compartment, CL/F: apparent clearance, Q/F: apparent inter-compartment clearance; NA, not available.

) and were kept constant, whilst the covariates were subject-related. The fitting adequacy of various literature models was then investigated. Figure A1 shows that none of the published models can explain the double peak occurrence in amisulpride C-t data.

In a further step, we explored the recommended daily doses of amisulpride using our final model for simulations at steady-state amisulpride concentrations due to amisulpride plasma/serum levels showing large inter-individual variability, and a considerable percentage of patients having concentration levels outside the reference range (320 ng/mL) [13,42,43,44]. In a study conducted [43], 36% of patients’ amisulpride plasma levels exceeded the therapeutic reference level (320 ng/mL), and in another study, 54.4% had levels above the therapeutic reference level. According to Bowskill et al. (2012) [42], patients prescribed 401–800 mg/day had plasma concentrations ranging from 70 to 1960 mg/L. Several routine studies also reported higher plasma/serum concentration ranges. In a study with 506 patients, median concentration levels were found to be 529 ng/mL [13]. According to a retrospective study of 253 samples, the plasma concentration of amisulpride was 445.2 ± 231.5 ng/mL, which was far higher than the recommended range [44]. In a recent study, Huang et al. (2021) also examined a wide range of recommended daily doses (50–1200 mg) for Chinese psychotic patients, which indicated that more than 400 mg of amisulpride was over the recommended doses [26]. These high levels of amisulpride may be linked to specific adverse effects in certain patient groups, such as hyperprolactinemia in females or hypotension in older individuals [26]. Furthermore, age and gender were found to have a substantial effect on dose-corrected amisulpride plasma concentrations, which are higher in older patients and women, probably due to differences in the drug’s renal clearance [1]. Co-medication with lithium and clozapine is known to enhance dose-corrected amisulpride plasma concentrations [1]. In our investigation, simulations revealed that administering 200 mg of amisulpride based on the consensus criteria for therapeutic drug monitoring at the Neuropsychopharmacology level (320 ng/mL) and 400 mg based on the laboratory alert level (640 ng/mL) would be preferred (Figure 4). Consequently, there is a need to readjust the therapeutic dosage regimen levels of amisulpride and identify factors that may be associated with high concentration levels of amisulpride.

The “double peak” phenomenon is one of the issues that can occur during the absorption phase of orally administered drugs, and the underlying process may have significant therapeutic and drug interaction implications. Orally administered medications can cause problems during this phase of the absorption process. The double peak phenomenon that was seen in the pharmacokinetics of amisulpride was explained in this work by means of the development of a model that focuses on absorption kinetics. However, further research is required in this area because the kinetics of various medications, including alprazolam, ranitidine, avitriptan, piroxicam, phenazopyridine, dopamine, levodopa, and other dopamine-stimulating medicines, display multiple peaks. It is possible that the underlying process is unique in these instances; hence, modeling it would be an intriguing endeavor. In addition, it would be interesting to investigate the impact that double peak kinetics has on clinical outcomes by carrying out joint pharmacokinetic-pharmacodynamic simulations. One further possibility is to investigate whether there is a connection between the properties of the formulation, such as the excipients and the kind of formulation, and the presence of the double peak phenomenon, as well as the enhancement of this phenomenon. Finally, one unsolved issue in the field of bioequivalence is the investigation of the role that many peaks play in the correct selection of pharmacokinetic metrics and the evaluation of bioequivalence.

5. Conclusions

The purpose of this study was initially to develop a model for the description of double peaks in amisulpride after oral administration. A population model was found to adequately describe the dual peak phenomenon in amisulpride arising from absorption complexities and gastric emptying of a low soluble compound, using dual absorption rates with a lag time. A comparison with previously published models showed that none of the literature models was able to describe the double peak phenomenon of amisulpride C-t data. In addition, simulations have been performed to explore the impact of body weight, which was found in this study to significantly affect amisulpride kinetics on steady-state levels and examine the necessity of dose adjustment. These simulations showed that dosing regimens should be re-adjusted, while it was shown that low doses of amisulpride are more effective in healthy adults. As a result of these findings, there may be a need for personalized dosing regimens, as these findings may explain part of the variability in amisulpride exposure. Recommendations about the appropriate dosage regimen were also made.