Enhancing Explainable Machine Learning by Reconsidering Initially Unselected Items in Feature Selection for Classification
Abstract
1. Introduction
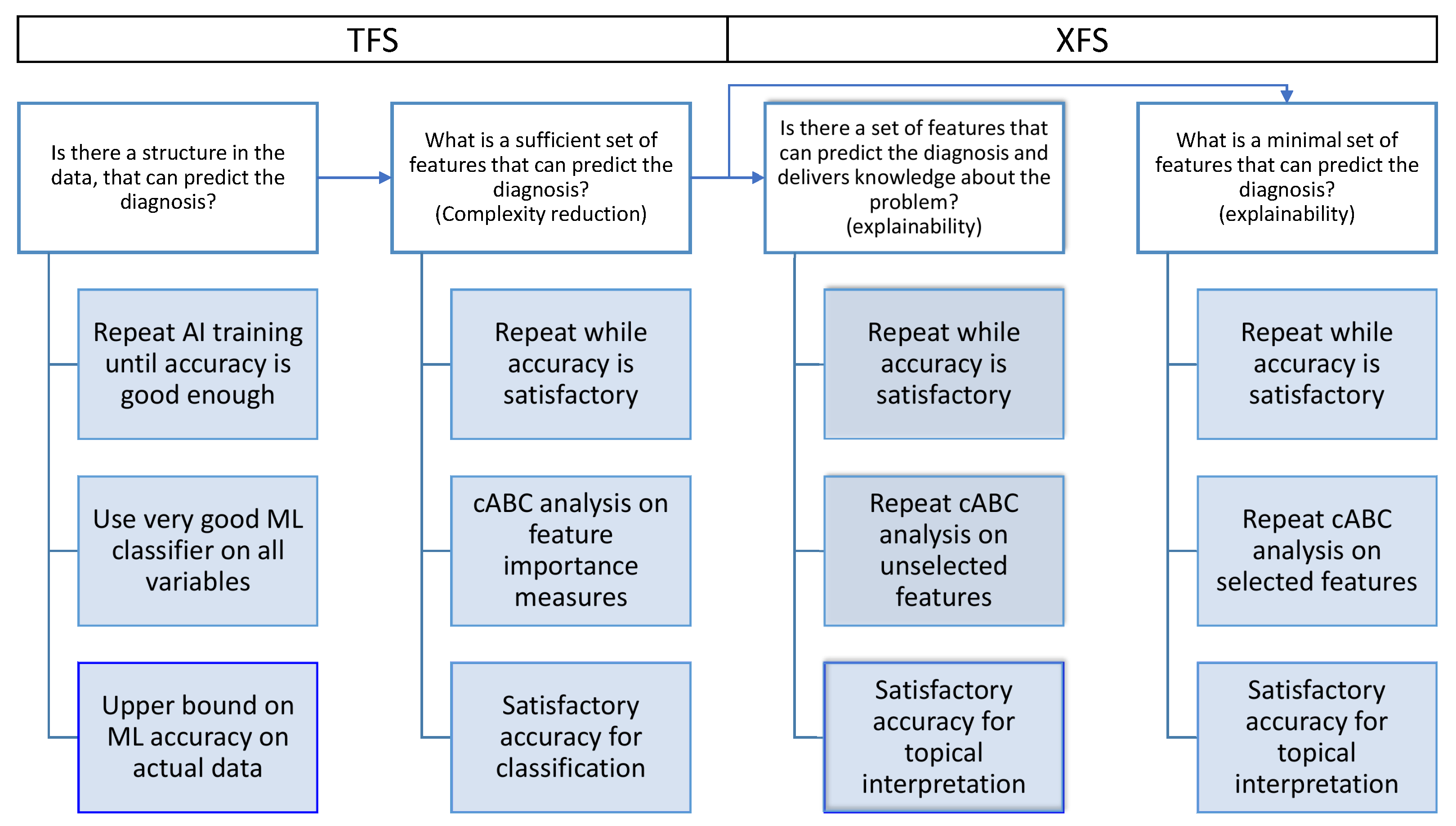
2. Methods
2.1. Algorithm
- Classification performance of algorithms trained with the selected features should be satisfactory, which is routinely checked. Ideally, it should not drop significantly from the performance obtained with all features. The classification performance must be at least better than chance, including the lower bound of the 95% confidence interval of classification performance measures, which should be higher than the level of guessing of the class assignment.
- Classification performance with the selected features should be better than classification performance when the training is conducted with the unselected features. This is not routinely checked. The difference between the respective classifications when training the algorithms with the selected features and when training the algorithm with the unselected features should be positive, e.g., with a lower bound of the 95% confidence interval > 0.
- If the difference in point 2 above is not satisfactorily greater than zero, but the classifier trained with the full set of features has satisfactory accuracy, then the unselected features should be reconsidered. If variables are omitted that are very strongly correlated with selected features, an assessment should be triggered of whether correlated variables might add relevant information that improves the (domain expert’s) interpretation of the feature set. In a new feature selection pass, the features already selected from the first pass are omitted. The final feature set is then the union of the two feature sets, provided that the second pass did not fail criterion 1.
2.2. Evaluations
2.2.1. Quantification of Feature Importance
2.2.2. Computation of the Set Size of the Selected Features
2.3. Experimental Setup
2.4. Data Sets
2.4.1. Iris Flower Data Example
2.4.2. Wine Quality Data Set
3. Results
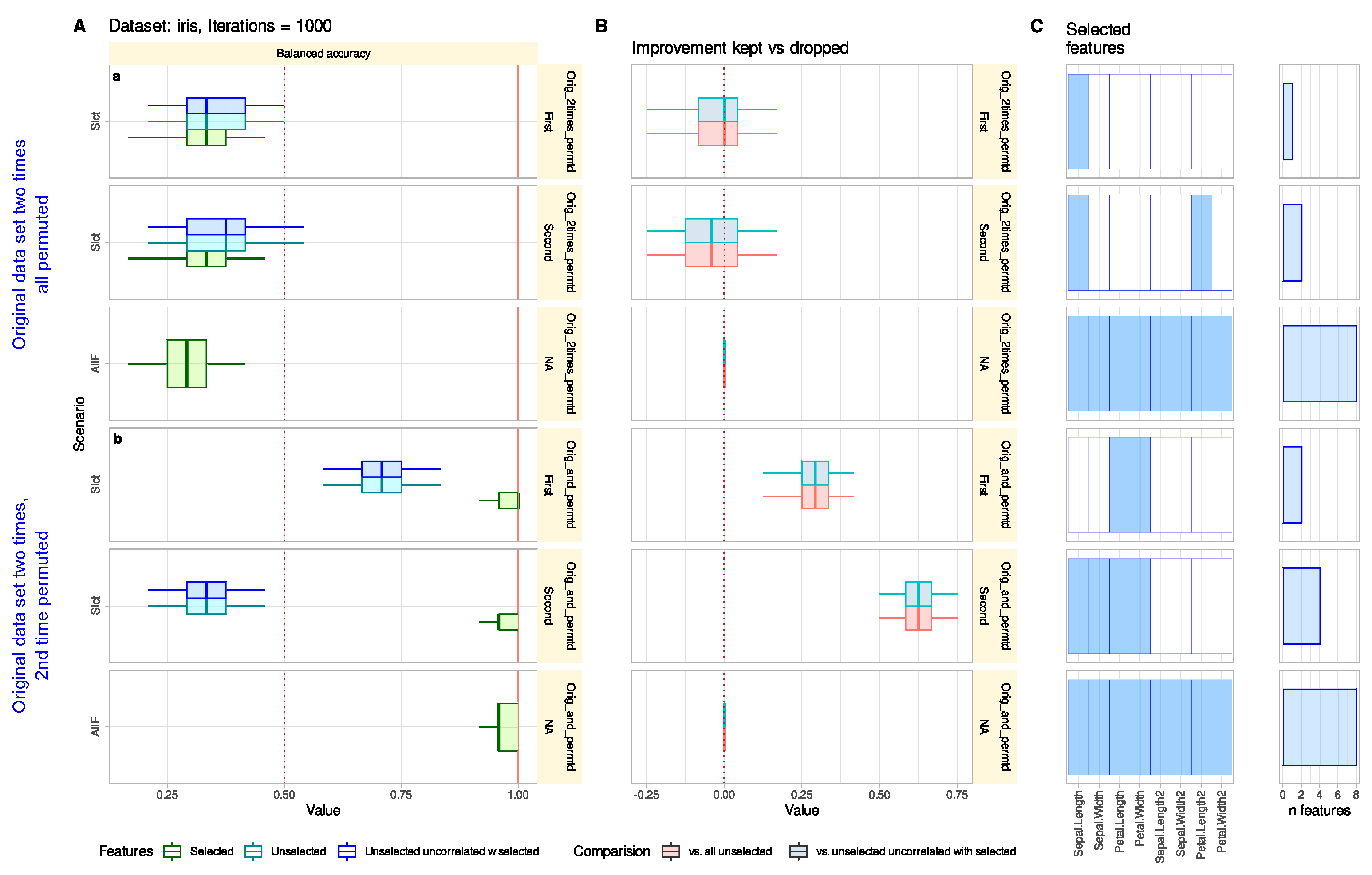
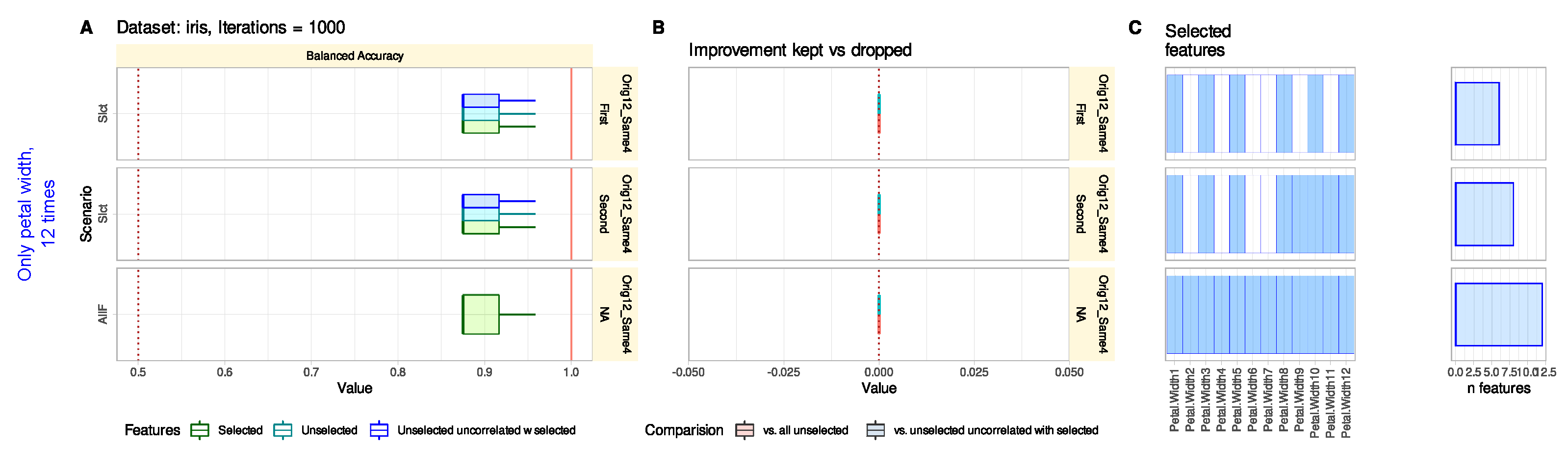
3.1. Iris Flower Data Set
3.1.1. Default Feature Selection Often Suffices and Removing Strongly Correlated Variables Is Not Necessary
3.1.2. Reconsidering Unselected Features Captures Information When Bad or Trivial Features Were Initially Selected
3.1.3. Reconsidering Unselected Features Does Not Tend to Add Uninformative Variables
3.1.4. Reconsidering Unselected Features Indicates Relevant Information That May Have Been Missed in The Knowledge Discovery Process
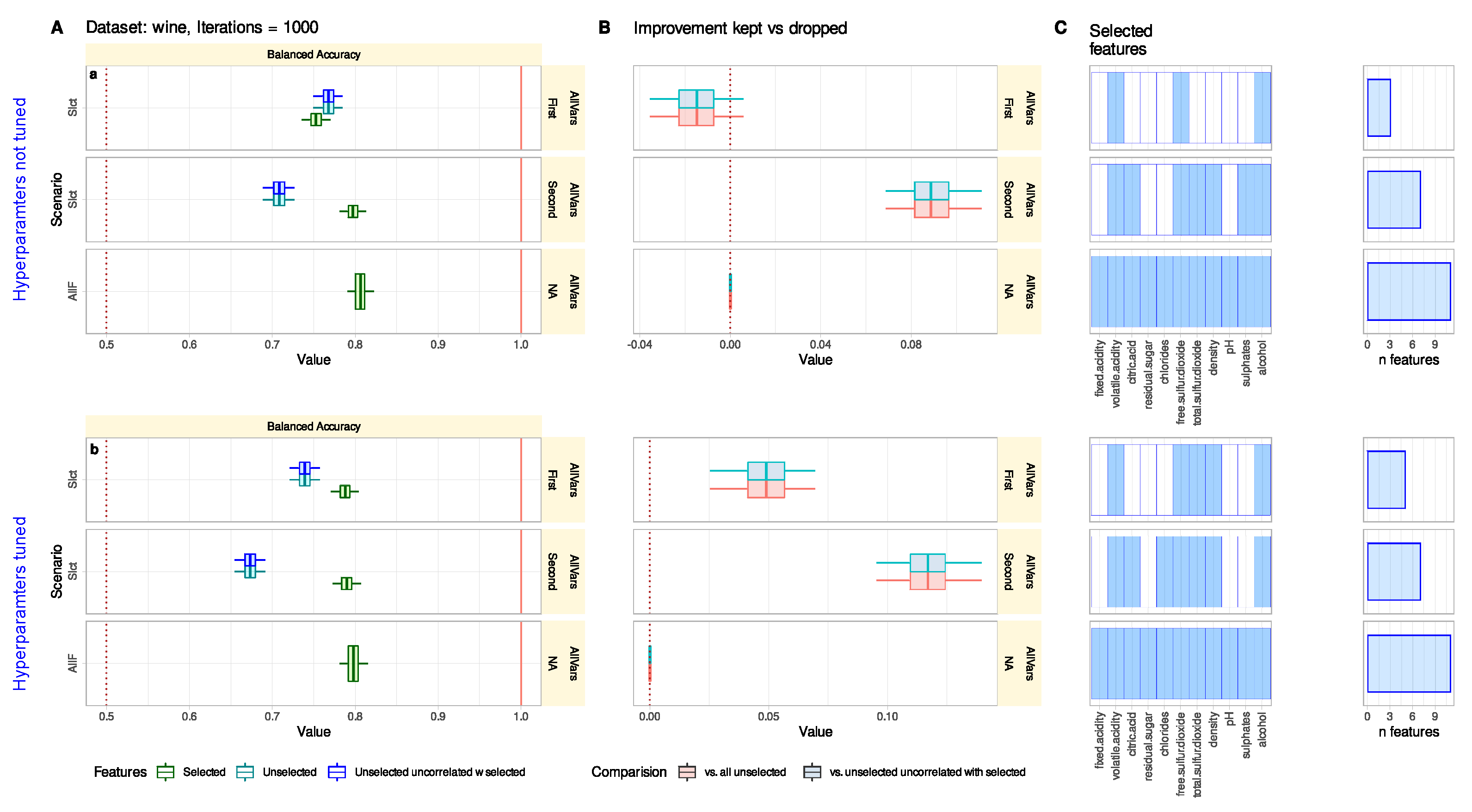
3.2. Wine Quality Data Set
Comparison of Classification Performance with Selected and Unselected Features Can Reveal Feature Selection Problems
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guyon, I. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Lotsch, J.; Kringel, D.; Ultsch, A. Explainable Artificial Intelligence (XAI) in Biomedicine: Making AI Decisions Trustworthy for Physicians and Patients. BioMedInformatics 2022, 2, 1. [Google Scholar] [CrossRef]
- Miller, G.A. The magical number seven plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef] [PubMed]
- Pudjihartono, N.; Fadason, T.; Kempa-Liehr, A.W.; O’Sullivan, J.M. A Review of Feature Selection Methods for Machine Learning-Based Disease Risk Prediction. Front. Bioinform. 2022, 2, 927312. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution. In Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Aboudi, N.E.; Benhlima, L. Review on wrapper feature selection approaches. In Proceedings of the 2016 International Conference on Engineering & MIS (ICEMIS), Agadir, Morocco, 22–24 September 2016; pp. 1–5. [Google Scholar]
- Chen, C.W.; Tsai, Y.H.; Chang, F.R.; Lin, W.C. Ensemble feature selection in medical datasets: Combining filter, wrapper, and embedded feature selection results. Expert Syst. 2020, 37, e12553. [Google Scholar] [CrossRef]
- Santosa, F.; Symes, W.W. Linear Inversion of Band-Limited Reflection Seismograms. Siam J. Sci. Stat. Comput. 1986, 7, 1307–1330. [Google Scholar] [CrossRef]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R N. 2002, 2, 18–22. [Google Scholar]
- Parr, T.; Turgutlu, K.; Csiszar, C.; Howard, J. Beware Default Random Forest Importances 2018. Available online: https://explained.ai/rf-importance (accessed on 3 September 2022).
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- Ultsch, A.; Lotsch, J. Computed ABC Analysis for Rational Selection of Most Informative Variables in Multivariate Data. PLoS ONE 2015, 10, e0129767. [Google Scholar] [CrossRef]
- Juran, J.M. The non-Pareto principle; Mea culpa. Qual. Prog. 1975, 8, 8–9. [Google Scholar]
- Lotsch, J.; Ultsch, A. Random Forests Followed by Computed ABC Analysis as a Feature Selection Method for Machine Learning in Biomedical Data; Advanced Studies in Classification and Data Science; Springer: Singapore, 2020; pp. 57–69. [Google Scholar]
- Ihaka, R.; Gentleman, R. R: A Language for Data Analysis and Graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 3 September 2022).
- Kuhn, M. Caret: Classification and Regression Training. 2018. Available online: https://cran.r-project.org/package=caret (accessed on 3 September 2022).
- Lötsch, J.; Malkusch, S.; Ultsch, A. Optimal distribution-preserving downsampling of large biomedical data sets (opdisDownsampling). PLoS ONE 2021, 16, e0255838. [Google Scholar] [CrossRef]
- Lötsch, J.; Mayer, B. A Biomedical Case Study Showing That Tuning Random Forests Can Fundamentally Change the Interpretation of Supervised Data Structure Exploration Aimed at Knowledge Discovery. BioMedInformatics 2022, 2, 544–552. [Google Scholar] [CrossRef]
- Good, P.I. Resampling Methods: A Practical Guide to Data Analysis; Birkhauser: Boston, MA, USA, 2006. [Google Scholar]
- Tille, Y.; Matei, A. Sampling: Survey Sampling. 2016. Available online: https://cran.r-project.org/package=sampling (accessed on 3 September 2022).
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The Balanced Accuracy and Its Posterior Distribution. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 3121–3124. [Google Scholar] [CrossRef]
- Anderson, E. The irises of the Gaspe peninsula. Bull. Am. Iris Soc. 1935, 59, 2–5. [Google Scholar]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Bannerman-Thompson, H.; Bhaskara Rao, M.; Kasala, S. Chapter 5-Bagging, Boosting, and Random Forests Using R. In Handbook of Statistics; Rao, C.R., Govindaraju, V., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 31, pp. 101–149. [Google Scholar] [CrossRef]
- Gupta, Y.K. Selection of important features and predicting wine quality using machine learning techniques. Procedia Comput. Sci. 2018, 125, 305–312. [Google Scholar] [CrossRef]
- Nebot, A.; Mugica, F.; Escobet, A. Modeling Wine Preferences from Physicochemical Properties using Fuzzy Techniques. In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications—SIMULTECH, Colmar, France, 21–23 July 2015. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Peterson, W.; Birdsall, T.; Fox, W. The theory of signal detectability. Trans. Ire Prof. Group Inf. Theory. 1954, 4, 171–212. [Google Scholar] [CrossRef]
- Khaire, U.M.; Dhanalakshmi, R. Stability of feature selection algorithm: A review. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1060–1073. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lötsch, J.; Ultsch, A. Enhancing Explainable Machine Learning by Reconsidering Initially Unselected Items in Feature Selection for Classification. BioMedInformatics 2022, 2, 701-714. https://doi.org/10.3390/biomedinformatics2040047
Lötsch J, Ultsch A. Enhancing Explainable Machine Learning by Reconsidering Initially Unselected Items in Feature Selection for Classification. BioMedInformatics. 2022; 2(4):701-714. https://doi.org/10.3390/biomedinformatics2040047
Chicago/Turabian StyleLötsch, Jörn, and Alfred Ultsch. 2022. "Enhancing Explainable Machine Learning by Reconsidering Initially Unselected Items in Feature Selection for Classification" BioMedInformatics 2, no. 4: 701-714. https://doi.org/10.3390/biomedinformatics2040047
APA StyleLötsch, J., & Ultsch, A. (2022). Enhancing Explainable Machine Learning by Reconsidering Initially Unselected Items in Feature Selection for Classification. BioMedInformatics, 2(4), 701-714. https://doi.org/10.3390/biomedinformatics2040047







