Multiscale Methods Framework with the 3D-RISM-KH Molecular Solvation Theory for Supramolecular Structures, Nanomaterials, and Biomolecules: Where Are We Going?
Abstract
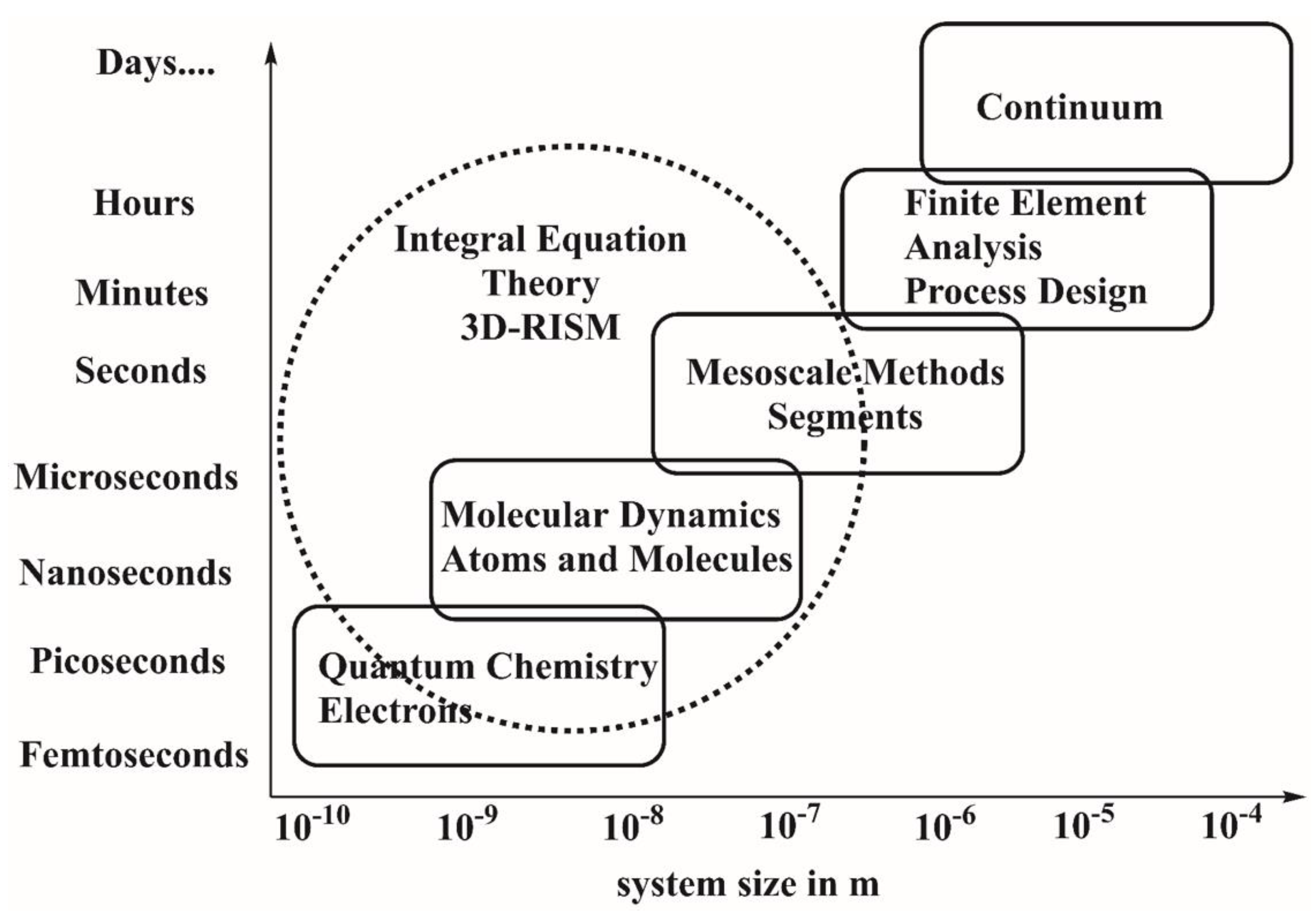
1. Introduction
2. Theoretical Background
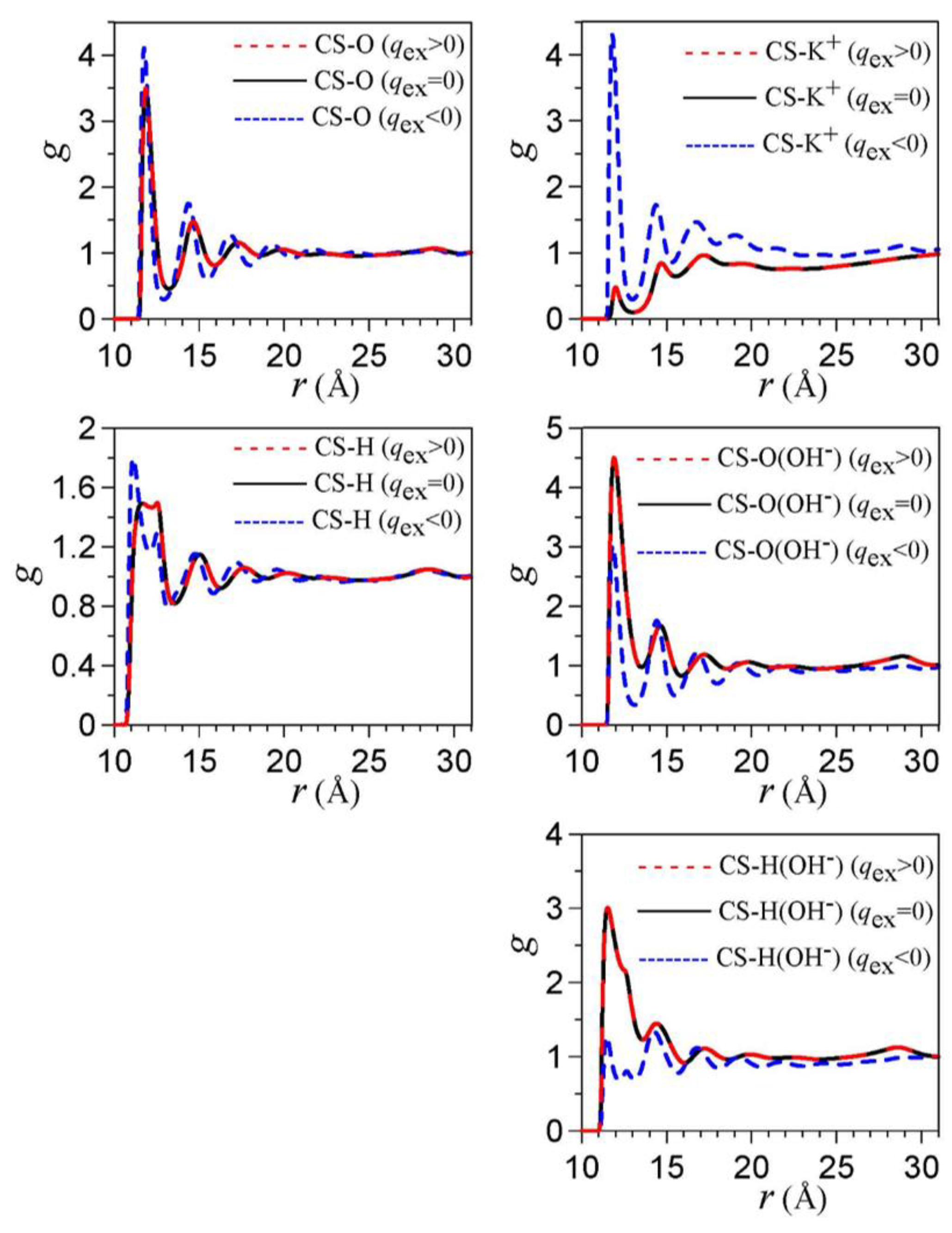
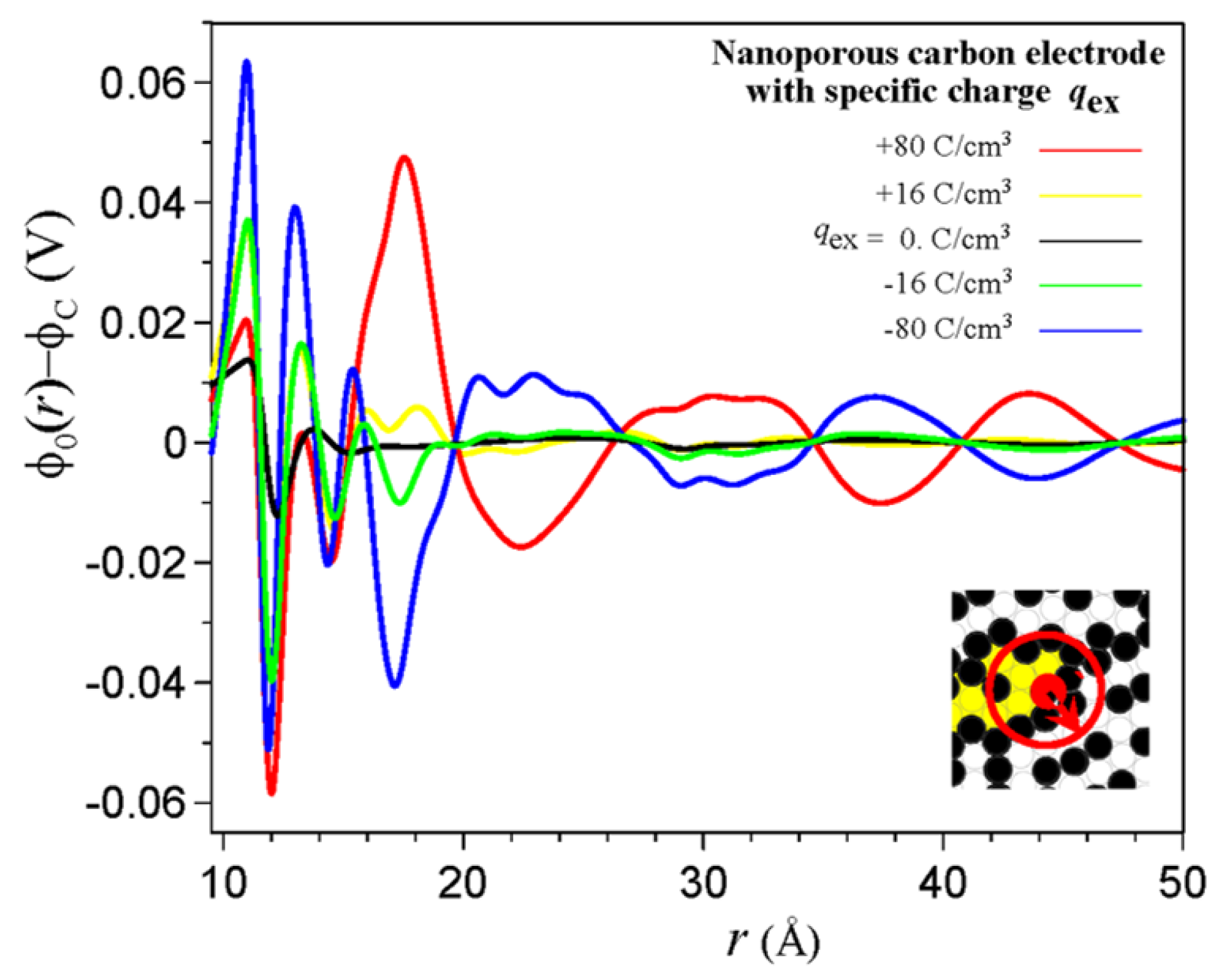
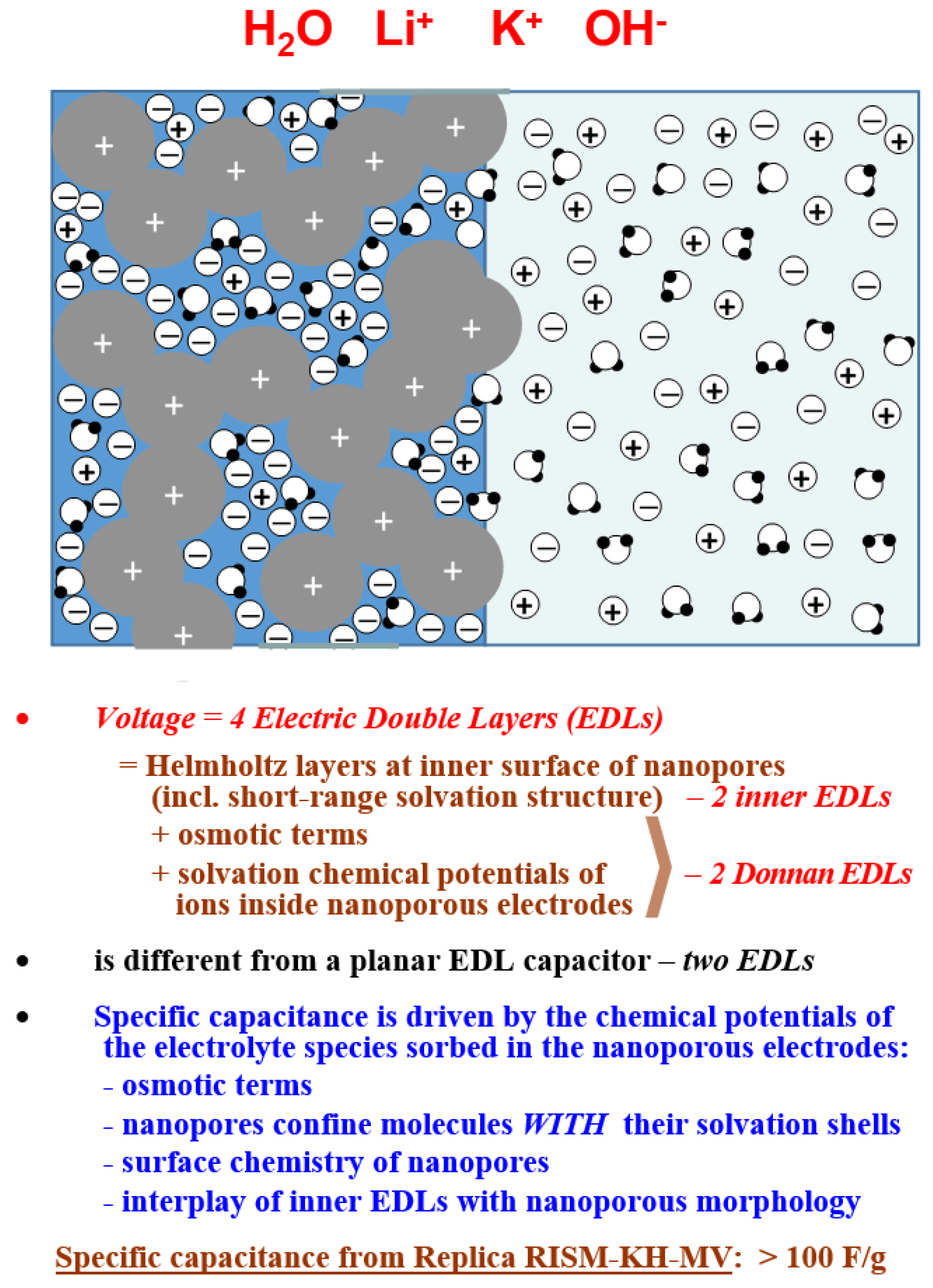
3. Electrical Double Layer in Nanoporous Materials
4. (Macro)Molecular Simulations with the 3D-RISM-KH Theory
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; van der Spoel, D. Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
- Gerez, G.; Di Remigio Eikås, R.; Rune Jensen, S.; Bjørgve, M.; Frediani, L. Cavity-Free Continuum Solvation: Implementation and Parametrization in a Multiwavelet Framework. J. Chem. Theory Comput. 2023, 19, 1986–1997. [Google Scholar] [CrossRef]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourik, T.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef] [PubMed]
- Vyboishchikov, S.F.; Voityuk, A.A. Solvation Free Energies for Aqueous and Nonaqueous Solutions Computed Using PM7 Atomic Charges. J. Chem. Inf. Model. 2021, 61, 4544–4553. [Google Scholar] [CrossRef] [PubMed]
- Klamt, A.; Diedenhofen, M. Calculation of Solvation Free Energies with DCOSMO-RS. J. Phys. Chem. A 2015, 119, 5439–5445. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, M.I.; Vanegas, J.M.; Pratt, L.R.; Muralidharan, A.; Rempe, S.B. Hydration Mimicry by Membrane Ion Channels. Annu. Rev. Phys. Chem. 2020, 71, 461–484. [Google Scholar] [CrossRef]
- Pratt, L.R.; Rempe, S.B. Quasi-chemical theory and implicit solvent models for simulations. AIP Conf. Proc. 1999, 492, 172–201. [Google Scholar] [CrossRef]
- Asthagiri, D.; Dixit, P.; Merchant, S.; Paulaitis, M.; Pratt, L.; Rempe, S.B.; Varma, S. Ion selectivity from local configurations of ligands in solutions and ion channels. Chem. Phys. Lett. 2010, 485, 1–7. [Google Scholar] [CrossRef]
- Rogers, D.M.; Rempe, S.B. Probing the thermodynamics of competitive ion binding using minimum energy structures. J. Phys. Chem. B 2011, 115, 9116–9129. [Google Scholar] [CrossRef]
- Rogers, D.M.; Jiao, D.; Pratt, L.R.; Rempe, S.B. Chapter Four—Structural models and molecular thermodynamics of hydration of ions and small molecules. Annu. Rep. Comput. Chem. 2012, 8, 71–127. [Google Scholar] [CrossRef]
- Hirata, F. (Ed.) Molecular Theory of Solvation. Understanding Chemical Reactivity; Kluwer: Dordrecht, The Netherlands, 2003; 358p. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory. Int. J. Mol. Sci. 2021, 22, 5061. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.-P.; McDonald, I.R. (Eds.) Chapter 11—Molecular Liquids. In Theory of Simple Liquids, 4th ed.; Academic Press: Oxford, UK, 2013; pp. 455–510. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. I. General formulation. J. Chem. Phys. 1986, 85, 5971–5976. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. II. Rational closures for integral equations. J. Chem. Phys. 1986, 85, 5977–5982. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. Numerical solution of the hypernetted chain equation for a solute of arbitrary geometry in three dimensions. J. Chem. Phys. 1995, 103, 360–364. [Google Scholar] [CrossRef]
- Beglov, D.; Roux, B. An Integral Equation To Describe the Solvation of Polar Molecules in Liquid Water. J. Phys. Chem. B 1997, 101, 7821–7826. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Three-dimensional density profiles of water in contact with a solute of arbitrary shape: A RISM approach. Chem. Phys. Lett. 1998, 290, 237–244. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Self-consistent description of a metal–water interface by the Kohn–Sham density functional theory and the three-dimensional reference interaction site model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Potentials of mean force of simple ions in ambient aqueous solution. I. Three-dimensional reference interaction site model approach. J. Chem. Phys. 2000, 112, 10391–10402. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Potentials of mean force of simple ions in ambient aqueous solution. II. Solvation structure from the three-dimensional reference interaction site model approach, and comparison with simulations. J. Chem. Phys. 2000, 112, 10403–10417. [Google Scholar] [CrossRef]
- Kovalenko, A. Three-dimensional RISM Theory for Molecular Liquids and Solid-Liquid Interfaces. In Molecular Theory of Solvation; Hirata, F., Ed.; Springer: Dordrecht, The Netherlands, 2003; pp. 169–275. [Google Scholar] [CrossRef]
- Chandler, D. Equilibrium structure and molecular motion in liquids. Acc. Chem. Res. 1974, 7, 246–251. [Google Scholar] [CrossRef]
- Lowden, L.J.; Chandler, D. Solution of a new integral equation for pair correlation functions in molecular liquids. J. Chem. Phys. 1973, 59, 6587–6595. [Google Scholar] [CrossRef]
- Chandler, D. Derivation of an integral equation for pair correlation functions in molecular fluids. J. Chem. Phys. 1973, 59, 2742–2746. [Google Scholar] [CrossRef]
- Johnson, J.; Case, D.A.; Yamazaki, T.; Gusarov, S.; Kovalenko, A.; Luchko, T. Small molecule hydration energy and entropy from 3D-RISM. J. Phys. Condens. Matter 2016, 28, 344002. [Google Scholar] [CrossRef] [PubMed]
- Imai, T.; Hiraoka, R.; Kovalenko, A.; Hirata, F. Water molecules in a protein cavity detected by a statistical-mechanical theory. J. Am. Chem. Soc. 2005, 127, 15334–15335. [Google Scholar] [CrossRef] [PubMed]
- Kondratenko, M.; Stoyanov, S.R.; Gusarov, S.; Kovalenko, A.; McCreery, R.L. Theoretical Modeling of Tunneling Barriers in Carbon-Based Molecular Electronic Junctions. J. Phys. Chem. C 2015, 119, 11286–11295. [Google Scholar] [CrossRef]
- Stoyanov, S.R.; Gusarov, S.; Kuznicki, S.M.; Kovalenko, A. Theoretical modeling of zeolite nanoparticle surface acidity for heavy oil upgrading. J. Phys. Chem. C 2008, 112, 6794–6810. [Google Scholar] [CrossRef]
- da Costa, L.M.; Stoyanov, S.R.; Gusarov, S.; Seidl, P.R.; de, M. Carneiro, J.W.; Kovalenko, A. Computational Study of the Effect of Dispersion Interactions on the Thermochemistry of Aggregation of Fused Polycyclic Aromatic Hydrocarbons as Model Asphaltene Compounds in Solution. J. Phys. Chem. A. 2014, 118, 896–908. [Google Scholar] [CrossRef]
- Genheden, S.; Luchko, T.; Gusarov, S.; Kovalenko, A.; Ryde, U. An MM/3D-RISM Approach for Ligand Binding Affinities. J. Phys. Chem. B 2010, 114, 8505–8516. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Towards A Molecular Theory for the van der Waals–Maxwell Description of Fluid Phase Transitions. J. Theor. Comput. Chem. 2002, 1, 381–406. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. A replica reference interaction site model theory for a polar molecular liquid sorbed in a disordered microporous material with polar chemical groups. J. Chem. Phys. 2001, 115, 8620–8633. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Description of a polar molecular liquid in a disordered microporous material with activating chemical groups by a replica RISM theory. Condens. Matter Phys. 2001, 4, 643–678. [Google Scholar]
- Tanimura, A.; Kovalenko, A.; Hirata, F. Molecular theory of an electrochemical double layer in a nanoporous carbon supercapacitor. Chem. Phys. Lett. 2003, 378, 638–646. [Google Scholar] [CrossRef]
- Tanimura, A.; Kovalenko, A.; Hirata, F. Structure of Electrolyte Solutions Sorbed in Carbon Nanospaces, Studied by the Replica RISM Theory. Langmuir 2007, 23, 1507–1517. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A. Molecular Description of Electrosorption in a Nanoporous Carbon Electrode. J. Comput. Theor. Nanosci. 2004, 1, 398–411. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. MTS-MD of Biomolecules Steered with 3D-RISM-KH Mean Solvation Forces Accelerated with Generalized Solvation Force Extrapolation. J. Chem. Theory Comput. 2015, 11, 1875–1895. [Google Scholar] [CrossRef]
- Imai, T.; Miyashita, N.; Sugita, Y.; Kovalenko, A.; Hirata, F.; Kidera, A. Functionality Mapping on Internal Surfaces of Multidrug Transporter AcrB Based on Molecular Theory of Solvation: Implications for Drug Efflux Pathway. J. Phys. Chem. B 2011, 115, 8288–8295. [Google Scholar] [CrossRef]
- Fafard, J.; Lyubimova, O.; Stoyanov, S.R.; Dedzo, G.K.; Gusarov, S.; Kovalenko, A.; Detellier, C. Adsorption of Indole on Kaolinite in Nonaqueous Media: Organoclay Preparation and Characterization, and 3D-RISM-KH Molecular Theory of Solvation Investigation. J. Phys. Chem. C 2013, 117, 18556–18566. [Google Scholar] [CrossRef]
- Malvaldi, M.; Bruzzone, S.; Chiappe, C.; Gusarov, S.; Kovalenko, A. Ab Initio Study of Ionic Liquids by KS-DFT/3D-RISM-KH Theory. J. Phys. Chem. B 2009, 113, 3536–3542. [Google Scholar] [CrossRef]
- Lyubimova, O.; Stoyanov, S.R.; Gusarov, S.; Kovalenko, A. Electric Interfacial Layer of Modified Cellulose Nanocrystals in Aqueous Electrolyte Solution: Predictions by the Molecular Theory of Solvation. Langmuir 2015, 31, 7106–7116. [Google Scholar] [CrossRef]
- Kovalenko, A.; Kobryn, A.E.; Gusarov, S.; Lyubimova, O.; Liu, X.; Blinov, N.; Yoshida, M. Molecular theory of solvation for supramolecules and soft matter structures: Application to ligand binding, ion channels, and oligomeric polyelectrolyte gelators. Soft Matter 2012, 8, 1508–1520. [Google Scholar] [CrossRef]
- Blinov, N.; Dorosh, L.; Wishart, D.; Kovalenko, A. Association Thermodynamics and Conformational Stability of β-Sheet Amyloid β(17-42) Oligomers: Effects of E22Q (Dutch) Mutation and Charge Neutralization. Biophys. J. 2010, 98, 282–296. [Google Scholar] [CrossRef] [PubMed]
- Casanova, D.; Gusarov, S.; Kovalenko, A.; Ziegler, T. Evaluation of the SCF Combination of KS-DFT and 3D-RISM-KH; Solvation Effect on Conformational Equilibria, Tautomerization Energies, and Activation Barriers. J. Chem. Theory Comput. 2007, 3, 458–476. [Google Scholar] [CrossRef] [PubMed]
- Percus, J.K.; Yevick, G.J. Analysis of Classical Statistical Mechanics by Means of Collective Coordinates. Phys. Rev. 1958, 110, 1–13. [Google Scholar] [CrossRef]
- Martynov, G.A.; Sarkisov, G.N. Exact equations and the theory of liquids. V. Mol. Phys. 1983, 49, 1495–1504. [Google Scholar] [CrossRef]
- Ballone, P.; Pastore, G.; Galli, G.; Gazzillo, D. Additive and non-additive hard sphere mixtures. Mol. Phys. 1986, 59, 275–290. [Google Scholar] [CrossRef]
- Kast, S.M.; Kloss, T. Closed-form expressions of the chemical potential for integral equation closures with certain bridge functions. J. Chem. Phys. 2008, 129, 236101. [Google Scholar] [CrossRef]
- Perkyns, J.S.; Lynch, G.C.; Howard, J.J.; Pettitt, B.M. Protein solvation from theory and simulation: Exact treatment of Coulomb interactions in three-dimensional theories. J. Chem. Phys. 2010, 132, 064106. [Google Scholar] [CrossRef]
- Stumpe, M.C.; Blinov, N.; Wishart, D.; Kovalenko, A.; Pande, V.S. Calculation of Local Water Densities in Biological Systems: A Comparison of Molecular Dynamics Simulations and the 3D-RISM-KH Molecular Theory of Solvation. J. Phys. Chem. B 2011, 115, 319–328. [Google Scholar] [CrossRef]
- Perkyns, J.S.; Pettitt, B.M. A site–site theory for finite concentration saline solutions. J. Chem. Phys. 1992, 97, 7656. [Google Scholar] [CrossRef]
- Kirkwood, J.G.; Buff, F.P. The Statistical Mechanical Theory of Solutions. I. J. Chem. Phys. 1951, 19, 774–777. [Google Scholar] [CrossRef]
- Harano, Y.; Imai, T.; Kovalenko, A.; Kinoshita, M.; Hirata, F. Theoretical study for partial molar volume of amino acids and polypeptides by the three-dimensional reference interaction site model. J. Chem. Phys. 2001, 114, 9506–9511. [Google Scholar] [CrossRef]
- Imai, T.; Harano, Y.; Kovalenko, A.; Hirata, F. Theoretical study for volume changes associated with the helix–coil transition of peptides. Biopolymers 2001, 59, 512–519. [Google Scholar] [CrossRef] [PubMed]
- Palmer, D.S.; Frolov, A.I.; Ratkova, E.L.; Fedorov, M.V. Towards a universal method for calculating hydration free energies: A 3D reference interaction site model with partial molar volume correction. J. Phys. Condens. Matter 2010, 22, 492101. [Google Scholar] [CrossRef] [PubMed]
- Luchko, T.; Blinov, N.; Limon, G.C.; Joyce, K.P.; Kovalenko, A. SAMPL5: 3D-RISM partition coefficient calculations with partial molar volume corrections and solute conformational sampling. J. Comput.-Aided Mol. Des. 2016, 30, 1115–1127. [Google Scholar] [CrossRef]
- Roy, D.; Blinov, N.; Kovalenko, A. Predicting Accurate Solvation Free Energy in n-Octanol Using 3D-RISM-KH Molecular Theory of Solvation: Making Right Choices. J. Phys. Chem. B 2017, 121, 9268–9273. [Google Scholar] [CrossRef]
- Kovalenko, A.; Ten-no, S.; Hirata, F. Solution of three-dimensional reference interaction site model and hypernetted chain equations for simple point charge water by modified method of direct inversion in iterative subspace. J. Comput. Chem. 1999, 20, 928–936. [Google Scholar] [CrossRef]
- Pulay, P. Convergence acceleration of iterative sequences. The case of scf iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Howard, J.J.; Perkyns, J.S.; Choudhury, N.; Pettitt, B.M. An Integral Equation Study of the Hydrophobic Interaction between Graphene Plates. J. Chem. Theory Comput. 2008, 4, 1928–1939. [Google Scholar] [CrossRef]
- Minezawa, N.; Kato, S. Efficient implementation of three-dimensional reference interaction site model self-consistent-field method: Application to solvatochromic shift calculations. J. Chem. Phys. 2007, 126, 054511. [Google Scholar] [CrossRef]
- Gusarov, S.; Pujari, B.S.; Kovalenko, A. Efficient treatment of solvation shells in 3D molecular theory of solvation. J. Comput. Chem. 2012, 33, 1478–1494. [Google Scholar] [CrossRef] [PubMed]
- Kobryn, A.E.; Gusarov, S.; Kovalenko, A. A closure relation to molecular theory of solvation for macromolecules. J. Phys. Condens. Matter 2016, 28, 404003. [Google Scholar] [CrossRef] [PubMed]
- Miyata, T.; Ebato, Y. Correction of Kovalenko-Hirata closure in Ornstein-Zernike integral equation theory for Lennard-Jones fluids. J. Mol. Liq. 2017, 245, 2–10. [Google Scholar] [CrossRef]
- Miyata, T.; Tange, K. Performance of Kobryn-Gusarov-Kovalenko closure from a thermodynamic viewpoint for one-component Lennard-Jones fluids. Chem. Phys. Lett. 2018, 700, 88–95. [Google Scholar] [CrossRef]
- Skinner, B.; Chen, T.; Loth, M.S.; Shklovskii, B.I. Theory of volumetric capacitance of an electric double layer supercapacitor. Phys. Rev. E 2011, 83, 56102–56111. [Google Scholar] [CrossRef]
- Feng, G.; Jiang, D.; Cummings, P.T. Curvature effect on the capacitance of electric double layers at ionic liquid/onion-like carbon interfaces. J. Chem. Theory Comput. 2012, 8, 1058–1063. [Google Scholar] [CrossRef]
- Given, J.A.; Stell, G. Comment on: Fluid distributions in two-phase random media: Arbitrary matrices. J. Chem. Phys. 1992, 97, 4573–4574. [Google Scholar] [CrossRef]
- Given, J.A. Liquid-state methods for random media: Random sequential adsorption. Phys. Rev. A 1992, 45, 816–824. [Google Scholar] [CrossRef]
- Given, J.A.; Stell, G.R. The replica Ornstein-Zernike equations and the structure of partly quenched media. Physica A 1994, 209, 495–510. [Google Scholar] [CrossRef]
- Lee, L.L. Chemical potentials based on the molecular distribution functions. An exact diagrammatical representation and the star function. J. Chem. Phys. 1992, 97, 8606–8616. [Google Scholar] [CrossRef]
- Kovalenko, A.; Gusarov, S. Multiscale methods framework: Self-consistent coupling of molecular theory of solvation with quantum chemistry, molecular simulations, and dissipative particle dynamics. Phys. Chem. Chem. Phys. 2018, 20, 2947–2969. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A. Multiscale Modeling of Solvation. In Springer Handbook of Electrochemical Energy; Breitkopf, C., Swider-Lyons, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 95–139. [Google Scholar] [CrossRef]
- Truchon, J.-F.; Pettitt, B.M.; Labute, P. A Cavity Corrected 3D-RISM Functional for Accurate Solvation Free Energies. J. Chem. Theory Comput. 2014, 10, 934–941. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Blinov, N.; Kovalenko, A. Octanol–Water Partition Coefficient from 3D-RISM-KH Molecular Theory of Solvation with Partial Molar Volume Correction. J. Phys. Chem. B 2015, 199, 5588–5597. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Yamaguchi, T.; Kovalenko, A.; Hirata, F. Structure of tert-Butyl Alcohol−Water Mixtures Studied by the RISM Theory. J. Phys. Chem. B 2002, 106, 5042–5049. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A.; Hirata, F. Compressibility of tert-Butyl Alcohol-Water Mixtures: The RISM Theory. J. Theor. Comput. Chem. 2003, 2, 193–203. [Google Scholar] [CrossRef]
- Johnson, R.S.; Yamazaki, T.; Kovalenko, A.; Fenniri, H. Molecular Basis for Water-Promoted Supramolecular Chirality Inversion in Helical Rosette Nanotubes. J. Am. Chem. Soc. 2007, 129, 5735–5743. [Google Scholar] [CrossRef]
- Yamazaki, T.; Fenniri, H.; Kovalenko, A. Structural Water Drives Self-assembly of Organic Rosette Nanotubes and Holds Host Atoms in the Channel. ChemPhysChem 2010, 11, 361–367. [Google Scholar] [CrossRef]
- Yoshida, N.; Imai, T.; Phongphanphanee, S.; Kovalenko, A.; Hirata, F. Molecular Recognition in Biomolecules Studied by Statistical-Mechanical Integral-Equation Theory of Liquids. J. Phys. Chem. B 2009, 113, 873–886. [Google Scholar] [CrossRef]
- Imai, T.; Oda, K.; Kovalenko, A.; Hirata, F.; Kidera, A. Ligand Mapping on Protein Surfaces by the 3D-RISM Theory: Toward Computational Fragment-Based Drug Design. J. Am. Chem. Soc. 2009, 131, 12430–12440. [Google Scholar] [CrossRef]
- Onishi, I.; Sunaba, S.; Yoshida, N.; Hirata, F.; Irisa, M. Role of Mg2+ Ions in DNA Hydrolysis by EcoRV, Studied by the 3D-Reference Interaction Site Model and Molecular Dynamics. J. Phys. Chem. B 2018, 122, 9061–9075. [Google Scholar] [CrossRef]
- Nikolić, D.; Blinov, N.; Wishart, D.; Kovalenko, A. 3D-RISM-Dock: A New Fragment-Based Drug Design Protocol. J. Chem. Theory Comput. 2012, 8, 3356–3372. [Google Scholar] [CrossRef]
- Blinov, N.; Dorosh, L.; Wishart, D.; Kovalenko, A. 3D-RISM-KH approach for biomolecular modelling at nanoscale: Thermodynamics of fibril formation and beyond. Molec. Simul. 2011, 37, 718–728. [Google Scholar] [CrossRef]
- Barth, E.; Schlick, T. Overcoming stability limitations in biomolecular dynamics. I. Combining force splitting via extrapolation with Langevin dynamics in LN. J. Chem. Phys. 1998, 109, 1617–1632. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Skeel, R.D.; Izaguirre, J.A. An impulse integrator for Langevin dynamics. Molec. Phys. 2002, 100, 3885–3891. [Google Scholar] [CrossRef]
- Ma, Q.; Izaguirre, J.A. Targeted mollified impulse: A multiscale stochastic integrator for long molecular dynamics simulations. Multiscale Model. Simul. 2003, 2, 1–21. [Google Scholar] [CrossRef]
- Henderson, T.M.; Izmaylov, A.F.; Scalmani, G.; Scuseria, G.E. Can short-range hybrids describe long-range-dependent properties? J. Chem. Phys. 2009, 131, 044108. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tuckerman, M.E.; Tobias, D.J.; Klein, M.L. Explicit reversible integrators for extended system dynamics. Molec. Phys. 1996, 87, 1117–1157. [Google Scholar] [CrossRef]
- Cheng, A.; Merz, K.M., Jr. Application of a multiple time step algorithm to biomolecular systems. J. Phys. Chem. B 1999, 103, 5396–5405. [Google Scholar] [CrossRef]
- Komeiji, J. Ewald summation and multiple time step methods for molecular dynamics simulation of biological molecules. J. Mol. Struct. Theochem. 2000, 530, 237–243. [Google Scholar] [CrossRef]
- Shinoda, W.; Mikami, M. Rigid-body dynamics in the isothermal-isobaric ensemble: A test on the accuracy and computational efficiency. J. Comput. Chem. 2003, 24, 920–930. [Google Scholar] [CrossRef]
- Minary, P.; Tuckerman, M.E.; Martyna, G.J. Long Time Molecular Dynamics for Enhanced Conformational Sampling in Biomolecular Systems. Phys. Rev. Lett. 2004, 93, 150201. [Google Scholar] [CrossRef] [PubMed]
- Luchko, T.; Gusarov, S.; Roe, D.R.; Simmerling, C.; Case, D.A.; Tuszynski, J.; Kovalenko, A. Three-Dimensional Molecular Theory of Solvation Coupled with Molecular Dynamics in Amber. J. Chem. Theory Comput. 2010, 6, 607–624. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, T.A.; Warshel, A. Frozen density functional approach for ab initio calculations of solvated molecules. J. Phys. Chem. 1993, 97, 8050–8053. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ros, P.; Ellis, D.E. Self-consistent molecular Hartree–Fock–Slater calculations I. The computational procedure. Chem. Phys. 1973, 2, 41–51. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.; van Gisbergen, S.; Fonseca Guerra, C.; Baerends, E.; Snijders, J.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Snijders, J.; te Velde, G.; Baerends, E. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- Verslus, L.; Ziegler, T. The determination of molecular structures by density functional theory. The evaluation of analytical energy gradients by numerical integration. J. Chem. Phys. 1988, 88, 322–328. [Google Scholar] [CrossRef]
- Gusarov, S.; Ziegler, T.A.; Kovalenko, A. Self-consistent combination of the three-dimensional RISM theory of molecular solvation with analytical gradients and the Amsterdam density functional package. J. Phys. Chem. A 2006, 110, 6083–6090. [Google Scholar] [CrossRef] [PubMed]
- Gusarov, S.; Fedorova, T.A.; Dmitriev, Y.Y.; Kovalenko, A. On Variational Estimates for Exchange-Correlation Interaction Obtained Within Super-CI Approach to MCSCF Approximation. Int. J. Quantum Chem. 2009, 109, 1672–1675. [Google Scholar] [CrossRef]
- ADF/AMS 2019.305, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2021; Available online: http://www.scm.com (accessed on 8 December 2021).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.; Kovalenko, A. Multiscale Methods Framework with the 3D-RISM-KH Molecular Solvation Theory for Supramolecular Structures, Nanomaterials, and Biomolecules: Where Are We Going? Thermo 2023, 3, 375-395. https://doi.org/10.3390/thermo3030023
Roy D, Kovalenko A. Multiscale Methods Framework with the 3D-RISM-KH Molecular Solvation Theory for Supramolecular Structures, Nanomaterials, and Biomolecules: Where Are We Going? Thermo. 2023; 3(3):375-395. https://doi.org/10.3390/thermo3030023
Chicago/Turabian StyleRoy, Dipankar, and Andriy Kovalenko. 2023. "Multiscale Methods Framework with the 3D-RISM-KH Molecular Solvation Theory for Supramolecular Structures, Nanomaterials, and Biomolecules: Where Are We Going?" Thermo 3, no. 3: 375-395. https://doi.org/10.3390/thermo3030023
APA StyleRoy, D., & Kovalenko, A. (2023). Multiscale Methods Framework with the 3D-RISM-KH Molecular Solvation Theory for Supramolecular Structures, Nanomaterials, and Biomolecules: Where Are We Going? Thermo, 3(3), 375-395. https://doi.org/10.3390/thermo3030023






