Abstract
Power electronic converter-based microgrids generally suffer from poor power delivery/handling capability during sudden load changes, especially during islanded operations. This is due to the lack of transient energy support to compensate for sudden load changes. The literature has suggested the use of adaptive droop control to provide compensation during transient conditions, thereby improving the power delivery capability. In this context, fuzzy logic-based adaptive droop control is a state-of-the-art technique that was developed based on empirical knowledge of the system. However, this way of designing the droop coefficient values without considering the mathematical knowledge of the system leads to instability during transient conditions. This problem further aggravates when dominant inductive load changes occur in the system. To address this limitation, this paper proposes an improved fuzzy logic-based adaptive droop control method. In the proposed methodology, the values of droop coefficients that are assigned for different membership functions are designed based on the stability analysis of the microgrid. In this analysis, the feasible range of active power–frequency droop values that could avoid instability during large inductive load changes is identified. Accordingly, the infeasible values are avoided in the design of the fuzzy controller. The performance of the proposed and the conventional fuzzy logic methods is verified through simulation in MATLAB/Simulink. From the results, it is identified that the proposed method has improved the power delivery capability of the microgrid by 14% compared to the conventional method.
1. Introduction
The use of power electronic converter-based microgrids is increasing at a rapid pace, and their power delivery issues have gained wide attention [1]. Droop control logic is popularly used in microgrids to avoid the need for separate communication links [2,3]. During small signal changes, droop control with its low dynamics helps to track the power requirements effectively [4,5]. However, under sudden load changes, especially during islanded operations, the droop control logic fails to handle the high-frequency dynamics and will lead to poor power handling [6]. To address these high-frequency dynamics during sudden large load changes, virtual inertia emulation through adaptive droop control is discussed in [7]. However, this method assumes that the parameters of the system are unaffected, which is not true in the case of sudden large load changes [8]. This presents a compelling need to study the role of sudden large load changes on droop coefficient values and, in turn, their effects on the power delivery capability of the microgrid.
An effective way of implementing adaptive droop control through fuzzy logic is discussed in [9,10,11]. The effect of load changes on the behavior of the droop values is not studied in [9], which is its main limitation. Fuzzy logic-based robust tuning of transient droop control is discussed in [10]. Commonly, the methods discussed in [9,10] are not suitable for single-machine systems operating in an islanding mode where the key objective is to maintain voltage and frequency in stable operating conditions. The method discussed in [11] can be adapted for a single-machine system operating in an islanded mode. Even though the methods discussed in [9,11] can be applied to single-machine systems, they did not consider the effect of sudden load changes on the behavior of the droop values. These sudden large load changes (especially reactive loads) with infeasible droop values could lead to instability and failure in power delivery. Additionally, the simulation time, which directly correlates with the computational burden, is longer in [11] due to four inputs and two outputs. Further, there are many indecisive situations in the design of this fuzzy controller. Recent advancements in microgrid control strategies have led to the development of various adaptive and robust methods. For instance, an adaptive sliding mode controller based on fuzzy logic was proposed to manage hybrid smart microgrid energy systems under uncertainty, effectively reducing chattering effects and enhancing stability [12]. Similarly, a novel control strategy combining integral sliding mode control with fuzzy adaptive PI control was introduced to ensure voltage stability in DC microgrids, demonstrating improved performance in the presence of system uncertainties [13]. Furthermore, a robust frequency control approach utilizing sliding mode control with linear matrix inequality techniques was developed for islanded microgrids, offering enhanced disturbance rejection capabilities [14]. These studies highlight the ongoing efforts to improve microgrid control systems through adaptive and robust methodologies, underscoring the relevance and potential impact of the proposed fuzzy logic-based adaptive droop control strategy in this evolving landscape. Given this, the following novel aspects are considered in the design of the proposed method in this paper. Firstly, the method can be applied to a single-machine system that can maintain frequency and voltage within stable limits. Secondly, stability analysis, which helps to identify a range of droop values that will enhance the power delivery capability, is included. Thirdly, the proposed fuzzy logic-based adaptive droop control strategy offers a practical and computationally efficient solution for real-time microgrid applications. Unlike data-driven or optimization-intensive methods such as ANFIS or genetic algorithms, the fuzzy logic controller relies on a limited rule base and does not require extensive training or iterative tuning. This inherent simplicity contributes to reduced implementation complexity and makes the controller suitable for real-time embedded deployment in resource-constrained environments.
The remaining sections of the paper are organized as follows. Section 2 describes the implementation of the proposed methodology. The results obtained from the proposed control method and the corresponding discussions are presented in Section 3. The conclusions of this proposed research are finally discussed in Section 4.
2. Proposed Methodology
The power controller in the proposed methodology is designed to operate with a combination of constant and variable values. The constant/fixed droop coefficient value (FD) is fixed at 0.5e−6. To this, an adaptive droop coefficient value (AD) is added, which acts to provide necessary compensation. In this work, FD is fixed at 5e−5 and AD is adjusted between ±5e−5.
Based on a mix of technical concepts, the extant literature, and industry norms, the FD and AD ranges were chosen. The FD was selected to strike a balance between system stability and power-sharing accuracy under typical load scenarios seen in low-voltage microgrids. According to IEEE Std. 1547 and IEEE Std. 2030.7, which offer recommendations for voltage and frequency regulation in inverter-based microgrids, these values are in accordance with those frequently utilized in droop-controlled inverter systems [15]. The fuzzy logic control system modulates the AD to adjust to real-time load fluctuations and system variables. The AD was intended to vary within a reasonable range of the FD. This strategy guarantees that the control mechanism is resilient, adaptable, and able to react to dynamic microgrid changes without sacrificing system performance. The chosen values are indicative of a practically applicable operating range; hence, the suggested method is generalizable for common microgrid applications, even though additional parameter sensitivity analysis may provide deeper insights into the range of applicability.
2.1. Identification of Feasible Range of Droop Coefficients
By considering the full range of AD, i.e., −5e−5 to 5e−5, it is observed from Eigenvalue analysis that with the conventional FDC method, with large inductive loads, the system is driven to instability as seen in Figure 1. In Figure 1, for values of loads greater than those corresponding to 1e−4, the poles of the system are going to the right half of the s-plane. From Figure 2, which represents the case of the proposed IFDC method, all the poles of the system remained in the left half of the s-plane for values of loads greater than those corresponding to 1e−4, thus ensuring stability.
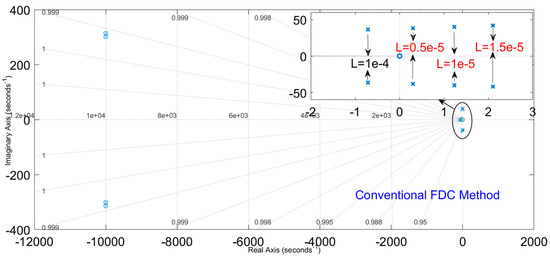
Figure 1.
Pole–zero plot of inductive loadings with an AD value of 2.5e−5.
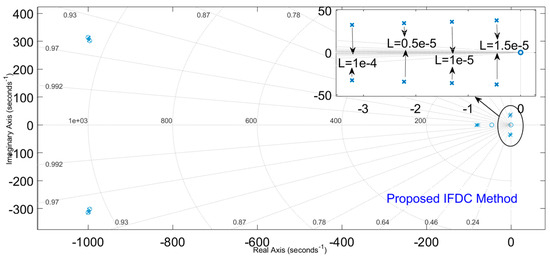
Figure 2.
Pole–zero plot of inductive loadings with an AD value of 2e−5.
In the proposed methodology, the AD range is considered to be from −5e−5 to 2e−5, which avoids the occurrence of instability. Through the analysis derived from Figure 1 and Figure 2, it is identified that the droop values from 2.5e−5 to 5e−5 are liable to cause instability in the case of large inductive load changes. Thus, in the design of the proposed controller, these values are discarded.
2.2. Proposed Improved Fuzzy Logic-Based Droop Control
In the proposed methodology, a fuzzy logic controller is developed to deliver the AD values. The details of the conventional fuzzy logic-based droop control (FDC) methodology can be found in [11]. In FDC, the fuzzy controllers take in four inputs and provide two outputs. This induces the conventional method to pose a large computational burden. To reduce this burden, in the proposed methodology, an improved fuzzy logic-based droop control (IFDC) is developed, which takes two inputs, viz., frequency (F) and the derivative of frequency (dF), and provides a single output (AD). The corresponding design of the IFDC is based on Figure 3. Figure 3a shows various membership functions of the IFDC of the output variable “AD”. The rule base of the proposed control methodology is shown in Figure 3b. In the proposed methodology, “AND” logic is used for combining the “if” conditions of the inputs F and dF. Based on the various combinations of inputs, various compensations in the form of AD are provided, whose descriptions and ranges are shown in Table 1.
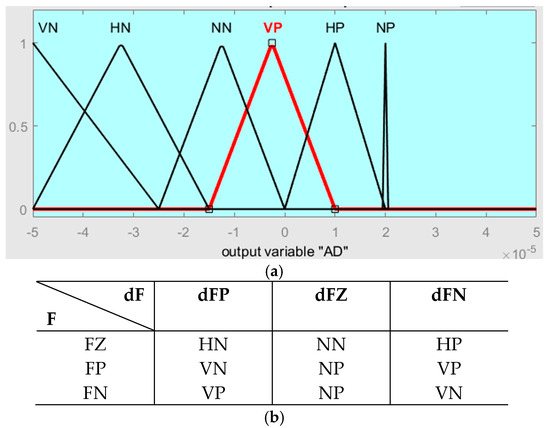
Figure 3.
Design of the proposed IFDC method: (a) membership functions of the output variable AD; (b) fuzzy rule base.

Table 1.
Design specifications of membership functions used in the proposed IFDC controller.
2.3. Small-Signal Stability Analysis
Eigenvalue analysis of the linearized system model is used to evaluate the small-signal stability of the suggested fuzzy logic-based adaptive droop control approach. By looking at the location of the system poles in the complex plane, this method enables evaluation of the local dynamic behavior of the system around a nominal operating point. Verifying if the system responds steadily to minor perturbations under inductive loading conditions is the aim of this analysis. After calculating the system state matrix’s eigenvalues, it was discovered that all of them fell within the left half of the s-plane, suggesting that the system is stable and has suitable damping properties.
Despite its relative simplicity, this approach is frequently utilized for preliminary validation in microgrid studies and offers important insights into the dynamic properties of the system. It would be difficult and outside the immediate purview of this work to derive a comprehensive nonlinear or Lyapunov-based proof of stability given the controller’s fuzzy logic component. However, the need for boundary condition analysis and more thorough theoretical treatment is recognized. To examine system behavior under a wider range of operating settings, including transient disturbances and fault scenarios, future studies should incorporate a thorough nonlinear stability assessment utilizing sophisticated methods like Lyapunov theory or phase portrait analysis.
3. Results and Discussion
The test setup consists of a single voltage source inverter-regulated distributed energy resource feeding two loads. The inverter receives the necessary gate pulse based on the decisions from the controller. The simulation is conducted for 160 s during which sudden inductive load switching is carried out at the 80th second and 90th second. Two different test cases, T1 and T2, are designed to verify the efficacy of the proposed method. In test case T1, a sudden reactive load of 7kVAr is connected and disconnected to the test setup at the 80th second and 90th second, respectively. In test case T2, similar conditions are ensured except that an 8kVAr load is used instead of a 7kVAr load in T1. Accordingly, the efficacy of the proposed research for the controller is ascertained through different variables, viz., frequency, active power, reactive power, and voltage. The results are compared with those of the conventional method. This comparison with respect to frequency and voltage is shown in Figure 4 and Figure 5, respectively. It is seen from Figure 4a and Figure 5a that the frequency and voltage magnitude results of both methods are satisfactory with no deviations during T1. During T2, as seen in Figure 4b and Figure 5b, the performance with the proposed IFDC method is satisfactory with no deviations. However, severe deviations in frequency and voltage magnitude are noticed with the conventional FDC method after the 80th second, leading to instability due to frequency and voltage magnitude.
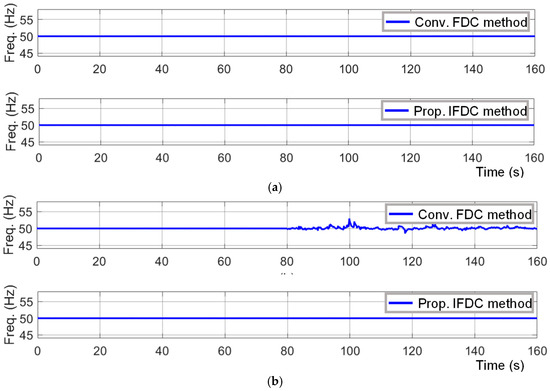
Figure 4.
Frequency results with the conventional FDC method and with the proposed IFDC method: (a) during test case T1; (b) during test case T2.
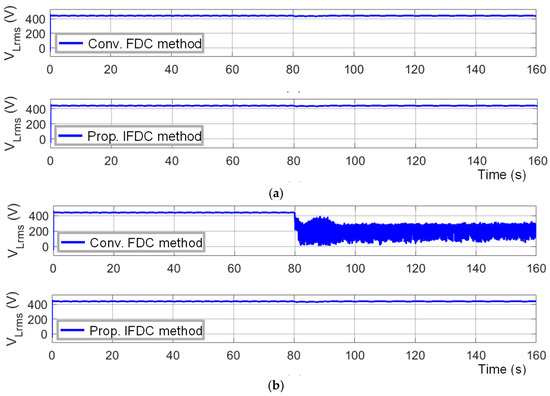
Figure 5.
Voltage results with the conventional FDC method and with the proposed IFDC method: (a) during test case T1; (b) during test case T2.
The results of the conventional and the proposed methods with respect to active and reactive power are shown in Figure 6 and Figure 7, respectively. It is seen from Figure 6a and Figure 7a that the active and reactive power deliveries with both methods are satisfactory during T1. During T2, as seen in Figure 6b and Figure 7b, the power delivery is satisfactory with the proposed method. However, during T2, when the conventional FDC method is deployed, the active and reactive power delivery fail after the load switch is turned on at the 80th second. This increase in power delivery with the proposed method from 7kVAr to 8kVAr amounts to a 14% improvement in power delivery capability. A summary of the comparison between the conventional and proposed methods with respect to different variables is presented in Table 2.
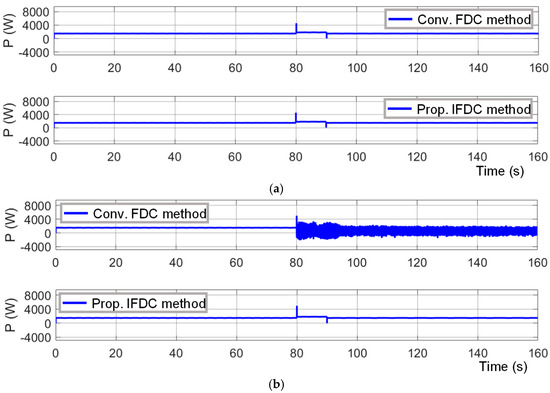
Figure 6.
Active power results with the conventional FDC method and with the proposed IFDC method: (a) during test case T1; (b) during test case T2.
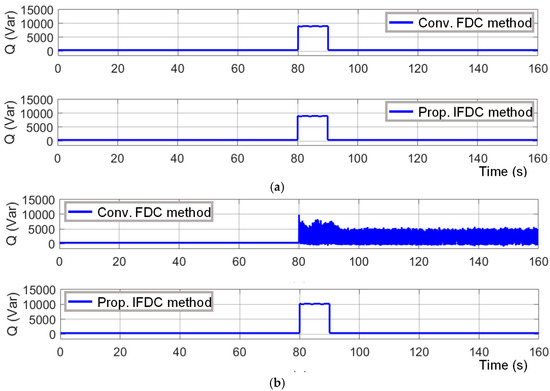
Figure 7.
Reactive power results with the conventional FDC method and with the proposed IFDC method: (a) during test case T1; (b) during test case T2.

Table 2.
Summary of the test results.
4. Conclusions
An improved fuzzy logic-based droop control (IFDC) approach, which introduces enhancements in two stages, is implemented in this work. To guarantee system stability and successful power delivery even in the face of abrupt and substantial fluctuations in inductive load, the first stage determines the viable range of droop coefficient values. When compared to traditional approaches, the second stage effectively reduces the simulation time (computational burden) by adding additional membership functions to the rule base. Although the study mostly concentrates on these enhancements without offering fresh experimental findings or extra comparisons, two test cases demonstrate the effectiveness of the suggested approach by demonstrating its capacity to sustain steady frequency, steady voltage, and a 14% boost in power handling capacity. Without needless detail, this method provides a targeted and concise illustration of the fundamental contributions of the IFDC method, highlighting its theoretical relevance and possible advantages for microgrid control.
Finally, it is understood from this work that the proposed IFDC method can enhance the power delivery capability of microgrids.
Author Contributions
Conceptualization, M.S. and Y.V.P.K.; methodology, M.S.; software, S.N.V.B.R.; validation, Y.V.P.K.; formal analysis, S.N.V.B.R.; investigation, M.S.; resources, Y.V.P.K.; data curation, M.S.; writing—original draft preparation, M.S.; writing—review and editing, Y.V.P.K.; visualization, S.N.V.B.R.; supervision, Y.V.P.K.; project administration, S.N.V.B.R.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Junior, R.S.R.; Machado, E.P.; Júnior, D.F. Development of a multivariable deadbeat controller in dq coordinates for the current loop of a grid-connected VSI. J. Control Autom. Electr. Syst. 2024, 35, 588–600. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Srikanth, M.; Kumar, Y.V.P. Improved Virtual Synchronous Generator-Based Control Scheme for Enhanced Transient Response in Microgrids. Eng. Proc. 2023, 56, 4. [Google Scholar] [CrossRef]
- Xiao, Z.-X.; Fang, H.-W. Impacts of P-f & Q-V Droop Control on MicroGrids Transient Stability. Phys. Procedia 2012, 24, 276–282. [Google Scholar]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Srikanth, M.; Kumar, Y.V.P.; Amir, M.; Mishra, S.; Iqbal, A. Improvement of Transient Performance in Microgrids: Comprehensive Review on Approaches and Methods for Converter Control and Route of Grid Stability. IEEE Open J. Ind. Electron. Soc. 2023, 4, 534–572. [Google Scholar] [CrossRef]
- Soni, N.; Doolla, S.; Chandorkar, M.C. Improvement of Transient Response in Microgrids Using Virtual Inertia. IEEE Trans. Power Deliv. 2013, 28, 1830–1838. [Google Scholar] [CrossRef]
- Srikanth, M.; Venkata Pavan Kumar, Y.A. State Machine-Based Droop Control Method Aided with Droop Coefficients Tuning through In-Feasible Range Detection for Improved Transient Performance of Microgrids. Symmetry 2023, 15, 1. [Google Scholar] [CrossRef]
- Yadav, M.; Jaiswal, P.; Singh, N. Fuzzy Logic-Based Droop Controller for Parallel Inverter in Autonomous Microgrid Using Vectored Controlled Feed-Forward for Unequal Impedance. J. Inst. Eng. India Ser. B 2021, 102, 691–705. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Robust Tuning of Transient Droop Gains Based on Kharitonov’s Stability Theorem in Droop-controlled Microgrids. IET Gener. Transm. Distrib. 2018, 12, 3495–3501. [Google Scholar] [CrossRef]
- Kumar, Y.V.P.; Bhimasingu, R. Fuzzy Logic Based Adaptive Virtual Inertia in Droop Control Operation of the Microgrid for Improved Transient Response. In Proceedings of the 2017 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Bangalore, India, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Tan, J.; Liu, W.; Zhao, X. Adaptive Sliding Mode Control Based on Fuzzy Logic for Hybrid Smart Microgrid Energy Systems under Uncertainty. Int. J. Energy Res. 2023, 47, 98–115. [Google Scholar]
- Zhang, Y.; Li, H.; Wang, S. Integral Sliding Mode Control Combined with Fuzzy Adaptive PI Control for Voltage Stability in DC Microgrids. Front. Energy Res. 2023, 11, 1278305. [Google Scholar]
- Liu, D.; Li, Q.; Zhang, L. Robust Frequency Control for Islanded Microgrids Using Sliding Mode Control with Linear Matrix Inequality (LMI) Techniques. Energy Syst. 2024, 15, 1539–1556. [Google Scholar]
- Std 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces (Revision of IEEE Std 1547-2003). IEEE: Piscataway, NJ, USA, 2018; pp. 1–138. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).